1. Introduction
Liquid crystals are multifunctional materials which form part of many biological material processes, such as sensor and actuator devices, natural super fibers, membranes, films, and drops [
1,
2,
3]. Other remarkable properties, such as film formation and surface pattern, can be found in biological plywoods, beetles’ cuticle [
1,
2,
3,
4], and cholesteric film formation flows of collagen solutions [
3,
4]. This paper presents the theory and simulation of a physiological actuator device whose functioning hinges on unique electro-mechanical properties of mesophases and is a prototypical example of responsive self-organizing materials [
1,
2,
5,
6,
7,
8,
9].
The functioning of outer hair cells (OHC) in the inner ear involves electric-field driven periodic curvature oscillations of liquid crystal (LC) elastic membranes that impart, by bending and oscillating [
9], momentum and flow to the contacting bulk viscoelastic fluids [
10]. This important phenomenon has been studied with several mechanical and mathematical modelling approaches using different constitutive equations [
11,
12,
13,
14,
15,
16,
17]. The electric field actuation of the liquid crystal membrane is known as flexoelectricity [
7,
8,
9] and it was studied and developed by Petrov and co-workers [
6,
7,
8]. The key role of OHC is sound amplification in the presence of bulk viscous dissipation and energy storage in the elastic flexoelectric membrane [
10,
11,
12,
13,
14]. Hence, the full description and understanding of OHC functioning has to include the frequency response of flexoelectric membranes embedded in viscous and viscoelastic media due to an oscillating electric
E field [
11,
15]. The input oscillating
E field, through the electromechanical flexoelectric effect, produces curvature oscillations in the elastic membrane that comprises the OHC surrounded by viscoelastic media [
9,
10,
15]. In turn, the oscillating elastic membrane displaces the contacting viscoelastic liquids through the mechanical visco-elastic and dissipation mechanisms [
10,
15]. The combined effect that allows the electro-mechanical energy conversion is based on the integration of the flexoelectric effect (
E field imposed on flexoelectric membrane) and the mechanical effect (membrane elasticity plus viscoelastic bulk fluid flow) [
10,
15].
A great deal of analytical approaches have been employed in order to simulate the changes in the average membrane curvature of a flexoelectric membrane as a function of the electrical field [
9,
10,
11,
12,
13]. Ricently Aguilar-Gutierrez et al. [
14], studied the curvature dissipation for liquid surfaces and mebranes from a generalized Boussiness-Scriven surface approach [
14]. Rabbits et al. [
15] developed a model based on a mixture-composite constitutive model. Their results show that the peak power efficiency is likely tunned to a specific frequency that depends on OHC length. Moreover, this tuning may contribute to the frequency selectivity of the cochlea [
15]. Other appraoches have employed electromecanical models with focus on hearing, composite membranes and isolated cochlear outer hair cells [
16,
17,
18]. From a mechanical-transduction point of view, some researchers have used voltage and tension-dependent mathematical models to describe lipid mobility in the outer hair cell plasma membrane, bending models with emphasis in cell electromotility, and genetics of the auditory hair cells [
19,
20,
21]. Some other electromechanical and rheological models have been proposed, which include electromagnetic mechanisms, the viscoelastic-relaxation dynamical response of the curvature through different rheological tests, including oscillatory and creep flow [
22,
23,
24]. From an electromechanical point of view, the reverse transduction, negative membrane capacitance, frequency response, and resonance curvature of these physical models [
25,
26,
27,
28], play an important role in the audition mechanisms of the cochlea and the energy output from the outer hair cells [
25,
26,
27,
28]. Other authors have focused in the description of the mammalian cochlear hair cells through power generation [
29], splay, energy, current noise spectrum, viscous fluid loss mechanisms, noise spectrum, stress of the membrane capacitance, and hair bundle motility [
30,
31,
32,
33].
In this context, we have developed several mathematical approaches to describe the flexoelectric membrane curvature through liquid crystal theory [
1,
2,
3,
6,
7,
8] and electrorheological models with emphasis in Outer Hair Cells (OHC) device modeling [
9,
10,
11,
12,
13,
14].
We would like to emphasize that “one of the main issues in this area is to find the monotonically and non-monotonic power dissipation in the system” induced by the changes in the curvature as a consequence of the imposed electrical field [
10,
12]; this power dissipation is characterized by a spectrum that depends on the electric field frequency and its specific features, such as resonant and antiresonance peaks, are the key issue of this this paper [
10,
12].
In order to include the physical nature of the fluids, several constitutive equations have been employed [
9,
10,
11,
12,
13,
14], from Euler (inviscid fluid) [
9] to Maxwell constitutive equations [
10], which have led to the governing ordinary differential equations that describe the changes in the curvature as a function of the electrical field [
9,
10,
11,
12]. Depending on the rheological equation of state, the shape of the power resonance can display several resonance curves in the regime of small inertia [
12] and zero inertia (Deborah number equal to zero) [
10,
12]. These resonance curves can be described in terms of linear ordinary differential equations, whose order (n) is defined by the total viscosity operator in the system [
10,
12]. For example, in the case of Euler and Newton fluids (n = 0), the power dissipation in the contacting bulk phases does not show resonance behavior [
9], but when the physical nature of the fluids is viscoelastic (Maxwell, n = 2), the system shows a resonance behavior as a function of the frequency [
10,
12].
The originality of this research consists of a critical and significant generalization of the above-mentioned works, including:
- (a)
The mathematical formulation developed here can be applied for any linear viscoelastic constitutive equation including fracctional linear operators;
- (b)
The viscosity operator choosen to characterize the rheology and the transfer momentum of the membrane into the viscoelastic liquid phases is the sum of a solvent and polymer contributions. When the solvent viscosities are zero, the system reduces to a previous model recently published [
9,
14]; and
- (c)
The effects of the solvent and polymer mechanisms induce a resonance and anti-resonance behavior (maximum and minimum), and the order of the electro-rheological model is three, whereas when the order of the dynamical equation is even, the system does not show a non-monotonic behavior. This new odd-even effect narrows down possible models from the outset.
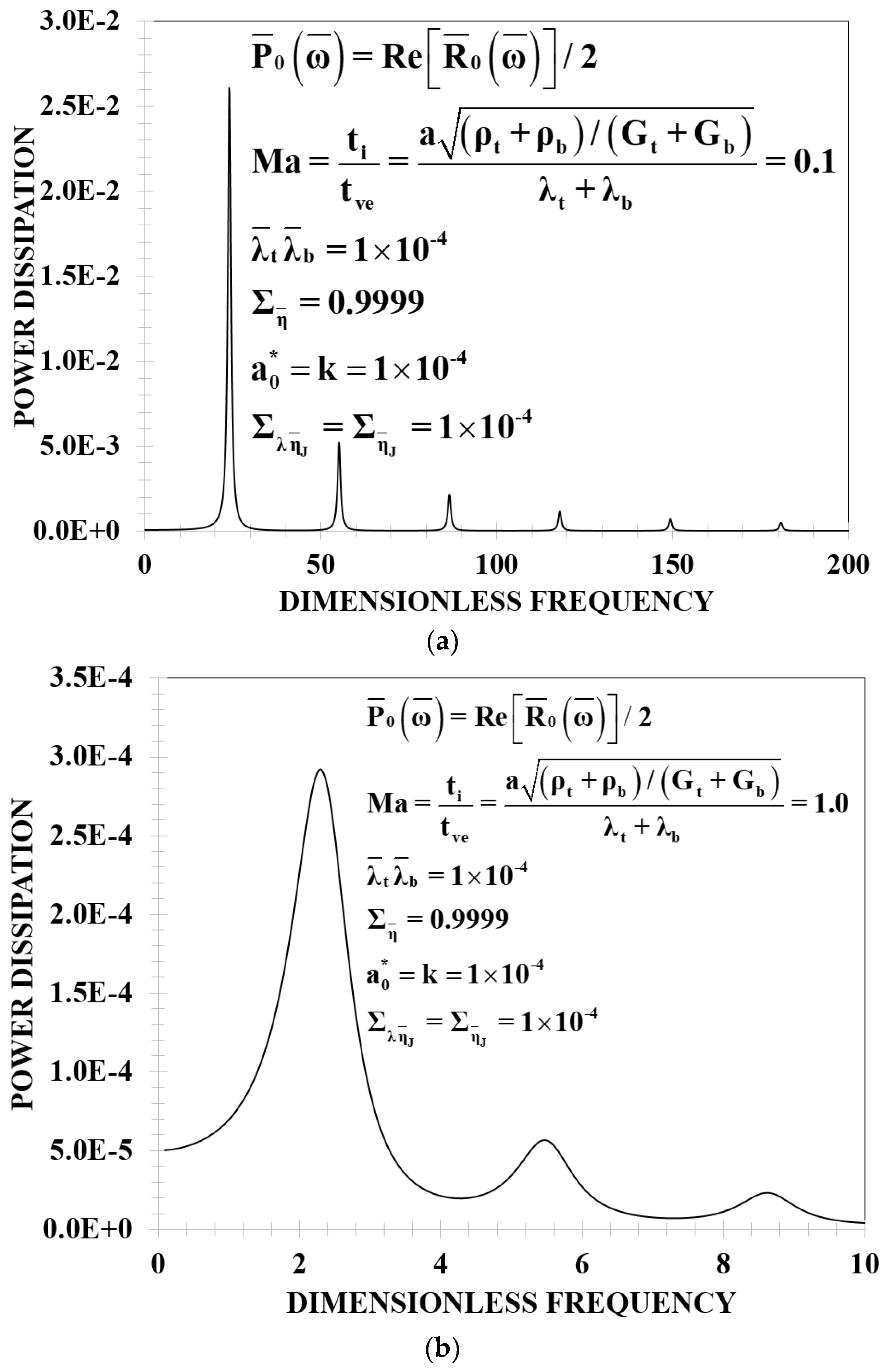
In general, the shape of the power resonance as well as the monotonical and non-monotonical behavior depend on the order of the ODE that describes the average membrane curvature as a function of the applied electrical field and the Deborah number [
14], which can be more properly interpreted as a reduced Mach number associated with the membrane speed propagation in the viscoelastic media. From extensive analysis based on an increasing order in classical viscoelastic models, it is found that: (i) for zero Mach numbers the power shows resonance behavior in the classical viscoelastic models (Maxwell, Jeffrey’s, and Burger’s models), meanwhile the non-monotonical behavior is displayed in the Jeffrey’s model (3ODE); (ii) when the inertia is included Ma ≠ 0, the system shows several resonance peaks, while at Ma >> 1 the system does not show any resonance peak at all. These generic findings narrow the range of relevant rheological conditions and rheological models, and allows us to establish connections between device output and material properties [
9,
10,
11,
12,
13,
14].
The three key issues to address in this energy conversion device are:
- (i)
The magnitude of the power P associated with the average curvature or volumetric rate flow delivered to the contacting of viscoelastic Jeffrey’s fluids from the imposed oscillating electric field E;
- (ii)
The minimum complexity of the Non-Newtonian model necessary to give the non-monotonically behavior in the power spectrum; and
- (iii)
The necessary material conditions to have a well-localized maximum and minimum resonant power peak (in the spectrum of power dissipation) as physiologically required [
25,
32].
As a partial summary, both the direct and converse membrane flexoelectric effects are sensor-actuator properties when membrane curvature and polarization are coupled as in nematic liquid crystals [
1,
2,
3,
6,
7,
8]. Membrane flexoelectricity due to its inherent sensor-actuator capabilities is an area of current interest in medicine, soft matter and biological materials [
33,
34,
35,
36,
37,
38].
The specific objectives of this paper are:
- (1)
Deriving a third-order dynamic linear model for a flexoelectric membrane attached to a capillary tube that contains Jeffrey’s viscoelastic fluids and is subjected to a fluctuating small amplitude electric field of arbitrary frequency.
- (2)
Computing the frequency response of the electrorheological device taking into account the viscoelastic nature of the contacting fluids;
- (3)
Using the modeling results to characterize the non-monotonic power spectrum associated to the role of membrane flexo-electricity and contacting fluid viscoelasticity of the device; and
- (4)
Identifying the material properties that lead to electromechanical conversion relevant to functioning of OHC.
To avoid repetition of lengthy derivations the reader is referred to [
10,
12]. In [
10] we describe the fluid viscoelasticity with a Maxwell fluid model, neglect momentum inertia (zero Deborah number: De = 0), and formulate the model in the time domain. In [
12] we extend the previous Maxwell model with the inertial mechanisms (Deborah number: De ≠ 0) and using the Fourier formalism two power resonance power peaks were found [
12] (see Appendices of ref. [
12]). These two early works do not show a minimum in the power spectrum [
10,
12], such as other mathematical approaches [
15]. In this research, we model the system in the frequency domain, including momentum inertia, and develop a generic approach that can be used in the future with any linear and fractional viscoelastic constitutive equation, as required by experimental results [
15]. The new approach is novel and significant because we extend the power spectrum with a well localized maximum and minimum, i.e., a non-monotonically behavior found in biological systems such as outer hair cell [
15] (see Figure 7 of ref. [
15]). This paper is organized as shown in
Figure 1.
Section 2 introduces the generic features of the dimensionless governing electro-rheological model of the electric field responsive membrane embedded in Jeffrey’s viscoelastic fluids. Dimensionless numbers and characteristic modes. The governing equation is based on the integration of: (i) the flexoelectric membrane shape equation applied to a circular membrane attached to the inner surface of a circular capillary; and (ii) the capillary flow of the contacting viscoelastic phases.
Section 3 presents the characteristic spectrum of the power output as a function of the Mach number and dimensionless numbers associated to the flexo-electric, viscoelastic and elastic mechanisms of the system.
Section 4 presents selected representative numerical results of the device (small and zero Mach numerical values).
Section 5 deals with the discussion of the numerical predictions, Biological applications, dominat mechanisms, and resonance conditions, respectively. The conclusions and future work are discussed in the last part of this research (
Section 6).
Appendix A and
Appendix B show scaling, dimensionless numbers, and some mathematical derivations of the power dissipation for the 3OD (third-order ordinary differential equation) model.
2. Mechanical Balance Equations
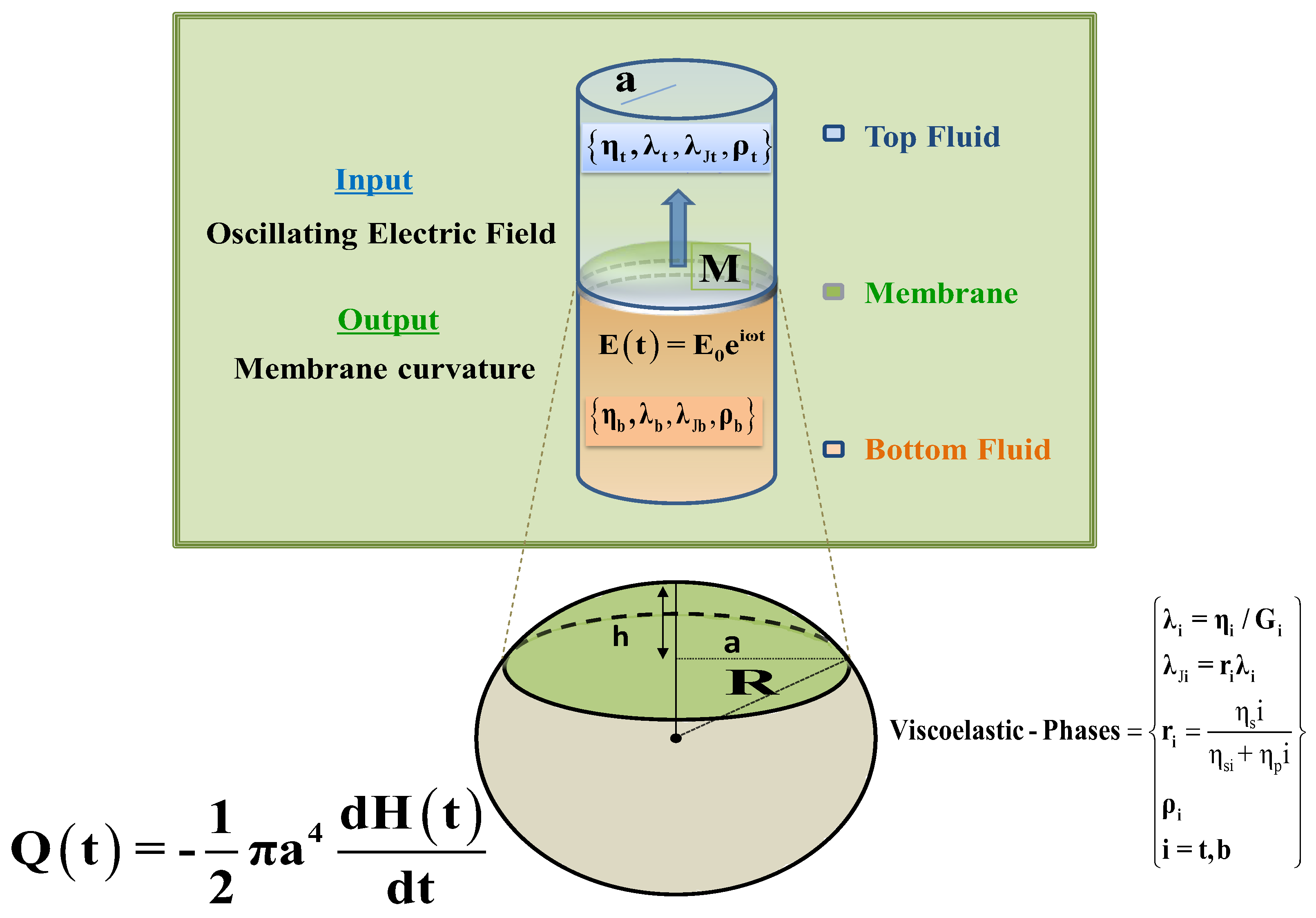
The physical setup and geometry of the flexoelectric membrane tethered to a capillary tube containing two viscoelastic fluids is defined in
Figure 2.
A capillary tube of radius “a” contains an edge-fixed flexoelectric membrane located at z = 0. Above and below the membrane there are two Jeffrey’s viscoelastic incompressible fluids with column heights z = L, solvent viscosities {η
sb, η
st}, polymer viscosities {η
pb, η
pt}, relaxation times {λ
b, λ
t}, and densities {ρ
b, ρ
t}. The total viscosity, relaxation and Jeffreys times can be expressed:
The pressures at the top of the upper layer and at the bottom of the lower layers are equal to a constant p (z = 0) = p (z = L) = p
0. By imposing a fluctuating electrical field
E(t) in the bottom, the membrane oscillates and displaces the upper and lower incompressible viscoelastic fluids; we emphasize that the Poiseuille flow is only generated by the flexoelectric effect of the membrane caused by the imposed
E(t) field, and body forces are neglected (null gravitational mechanisms) [
9,
10,
12].
The membranodynamic system contains the following primitive materials properties: (i) fluids viscoelastic properties
; (ii) membrane elasticity properties:
; (iii) geometry of the pipe and the membrane
; and (iv) flexoelectric force: {c
f, E
0}. The elastic moduli of the viscoelastic fluids are: G
i =η
i/λ
i; i = t, b. These parameters can be estimated from rheological and membrane experiments in steady and unsteady state [
9,
10] (and references therein).
2.1. Dimensionless Governing Equations
The coupled governing device equations are the dimensionless shape model, which is a force balance between the electrical field, pressure balance, and elastic storage membrane [
9,
10,
12]. The second equationis is the pressure balance with emerges of the momentum equation (Equation (2a)) and the total temporal viscosity operator, which is the sum of the top and bottom liquid viscoelastic phases [
12], which can be extended by any linear and non-linear viscoelastic equation [
9,
12]. In order to simplify the problem, dimensionless variables are used in the main equations to obtain dimensionless groups that facilitate the physical interpretation (see
Appendix A). The dimensionless shape equation is given by:
The pressure balance and the time viscosity operator are given by:
In Equation (2), the Mach
and flexoelectric
numbers are given by:
The parameters and scaling details of Equations (1)–(3) are given in
Appendix A. Equation (2a) is the z component of the momentum equation, which is a balance between the pressure gradient, and viscous and inertia mechanisms. The total viscosity operator given in Equation (2b) is completely general and can be used with any viscoelastic and fracctional viscoelastic model (See
Table 1). Notice that
is a time differential operator which is defined by
. In particular, in this research the Jeffreys viscosity model will be used, in order to obtain a third-order ODE that will describe the physics in this system. Combining Equations (1)–(3), the dynamical expression in terms of the Mach number is given by:
where the parameter
is the inverse of a characteristic length associated to the Mach number divided by the viscosity and multiplied by the time differential operator related to the inertia mechanisms. The solution of Equation (4) was already obtained in [
12] for a Maxwell fluid (see Appendix B of reference [
12]). Assuming non-slip conditions, i.e.,
and that the system must be bounded at
, the dimensionless non-homogeneous parametric Bessel differential equation is obtained. Once the velocity profile is obtained, the volumetric flow can be easily obtained using the Bessel function properties (see Appendix B of reference [
12]). The dimensionless volumetric flow
induced by the oscillations of the membrane in the viscoelastic phases, can be calculated from an integration in cylindrical coordinates:
In Equation (5) the following property of the Bessel functions was used: x
n+1J
n(x) = d[x J
1(x)]/dx = x J
0(x); and
can be interpreted as inertia-viscous non-linear differential operator
, and the parameter
was defined in Equation (4b). In the next step, the definition of the dimensionless volumetric flow is applied as the negative of the average membrane curvature time derivative [
9,
10,
12], i.e.,:
Combining Equations (5) and (6) gives:
Equation (7) is the general non-linear dynamical expression and can be expressed in terms of an Input (electrical field
E) and Output functions (average membrane curvature H or the volumetric flow rate Q). The corresponding transfer functions
and
are given by:
Equations (7) and (8) are non-linear differential equations that describe the relationship between the volumetric flow rate or the average membrane curvature and the electrical field E. In Equation (8b) it was assumed that the average membrane curvature is zero at time . On the other hand, Equation (8a) represents the dynamic evolution of the input (electrical field) and the output (average membrane curvature), and Equation (8b) is the transfer function of the (electrical field) and the output (volumetric flow rate), respectively. Notice both of them are regulated by the flexoelectric mechanisms through the dimensionless number asociated to the flexoelectric and viscoelastic mechanism through the time viscosity operator. Finally, both Equations (7) and (8) are the main model formulation results of this work.
2.2. Jeffrey’s Third-Order Ordinary Differential Equations
If the Bessel functions of the viscous-inertia defined in the operator
of Equation (8) are developed in a Mach (Ma << 1), number power series (see Appendix B of [
12]), the inertia-viscous operator
is the sum of the total viscosity, i.e.,
. In order to characterize the rheology and flow, the Jeffrey’s viscosity operator was used (
Table 1), which is the minimum model to obtain the non-monotonically behavior in the power spectrum, and is given by:
Once Equation (9) is substituted into Equations (8), and using the linear relation Equation (7), the following third-order differential equation in terms of an input variable {E(t)} and output variables {H(t), Q(t)} is obtained:
The output and input linear operators are given by the following differential operators:
The dimensionless coefficients of Equations (9)–(11) are given by:
The first term on the left hand side of Equation (11a) describes the retardation forces, the second and third terms are associated with inertia and viscous mechanisms, respectively; and the last one with the membrano-elastic mechanisms. The right-hand side describes the temporal evolution of the input driven force associated with flexo-electric mechanisms and the memory through the material parameters of the particular constitutive equation used in the system. A Newtonian model was obtained in [
9], a Maxwell second-order electro-rheological model was previously obtained in [
10,
12] using different mathematical approaches, and this Maxwell model was extended by taking into account the inertial mechanisms of the momentum fluids and finally non-linear extension (Newtonian) of these models was studied with a pertubation technique in terms of the Deborah number [
9,
10,
12].
2.2.1. Dimensionless Numbers
The governing Equations (11) and (12) contain seven dimensionless numbers:
which are associated with the following mechanisms: (i) Memory
: product of the viscoelastic dimensionless times
, and
, where
. This number
defines the elastic asymmetry of the fluids. When
(highly asymmetric case) one of the fluids is nearly inelastic, and when
(highly symmetric case) both fluids are equally elastic; (ii) Bulk Viscosity
: total viscosity in the system, where the elastic dimensionless moduli satisfy
. The numerical value of this number is controlled by the product between the two dimensionless Maxwell time numbers, i.e.,
. This dimensionless number is bounded by the maximum and minimum values of the Maxwell relaxation times, i.e.,
; (iii) The third group,
can be interpreted as a bulk viscosity weighted by the ratio between the solvent and total viscosity (solvent + polymer contributions). This dimensionless number is bounded by the following inequality:
; (iv) The fourth group is a bulk retardation viscosity weighted by the viscoelastic relaxation times, i.e.,
can be interpreted as a bulk viscosity weighted by the product between the solvent ratio
and the Maxwell relaxation times
. The maxima and minima values of this group are given by:
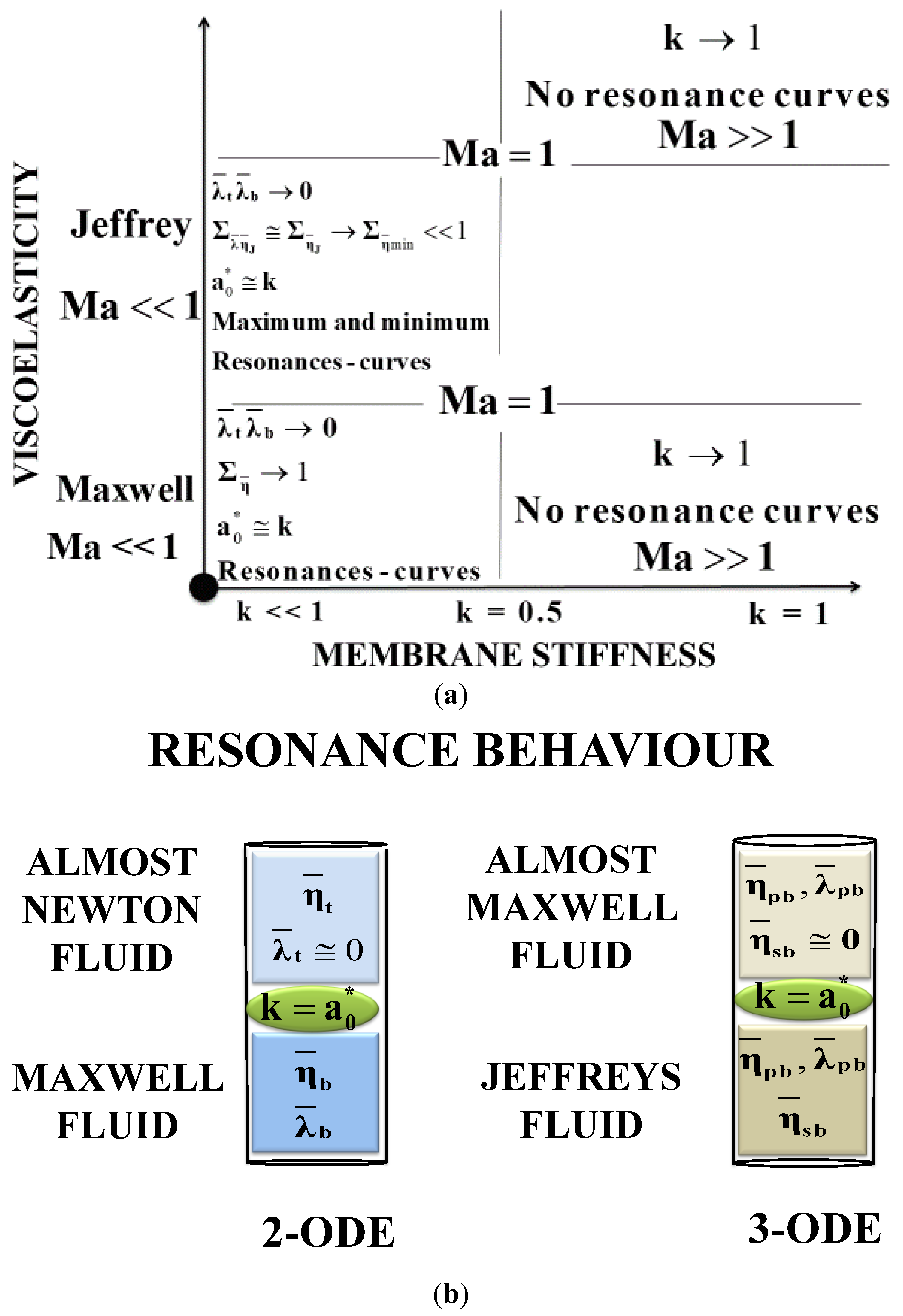
(v) Elastic ratio : dimensionless ratio between the membrane and the total system elasticity, . A floppy (soft) and stiff (rigid) membrane corresponds to k << 1 and k ≅ 1, respectively. The elastic ratio, is determined by the dimensionless elastic membrane modulus; (IV–V); (vi) The Mach number Ma is a ratio between the two velocities associated to viscoelasticity and bulk elastic forces and it is a measure of the inertia mechanism in the system; and finally (vii) the flexoelectric number is the dimensionless conversion of electric to bulk elastic energy or, equivalently, the static transfer function at zero frequency.
2.2.2. Response Mode Classification
It was demonstrated for a Maxwell fluid [
10,
12], that the important resonant characteristics are dominated by four dimensionless numbers
. In the extended Jeffrey’s model (Equations (11)–(13)) additional numbers are obtained by including inertial and solvent mechanisms
which can be interpreted as small perturbations to the previous Maxwell model [
10,
12]. According to the magnitudes of the main dimensionless numbers
, six case scenarios are possible i.e., the memory symmetry can be high (HS) or low (LS), the total viscosity high (HV), medium (MV), or low (LV), and the membrane can be floppy (FM) or stiff (SM), and these are summarized in
Table 2 [
10,
12]. The third and fourth columns are the contributions of the Jeffrey’s retardation mechanisms
, which are zero for the Maxwell model. For example, the first row {LS, LV, FM} corresponds to low symmetry, low viscosity, and floppy membrane [
10,
12]. This effective mode classification narrows the parametric envelope of biological significance. The specific numerical values in
Table 2 are selected to be characteristic of each mode; the last two columns are bulk retardation and weighted retardation viscosity, respectively, which will be defined in the next section.
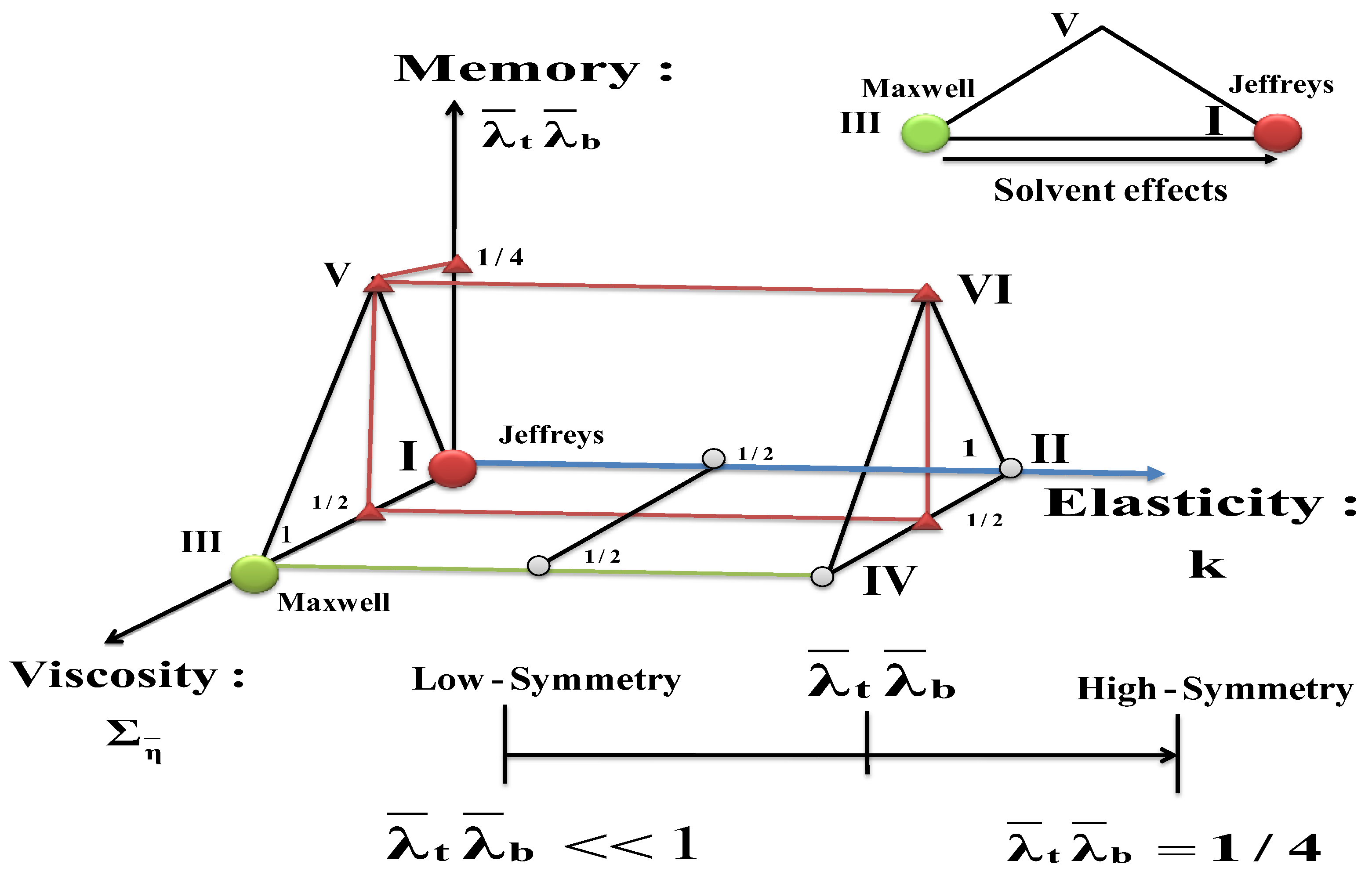
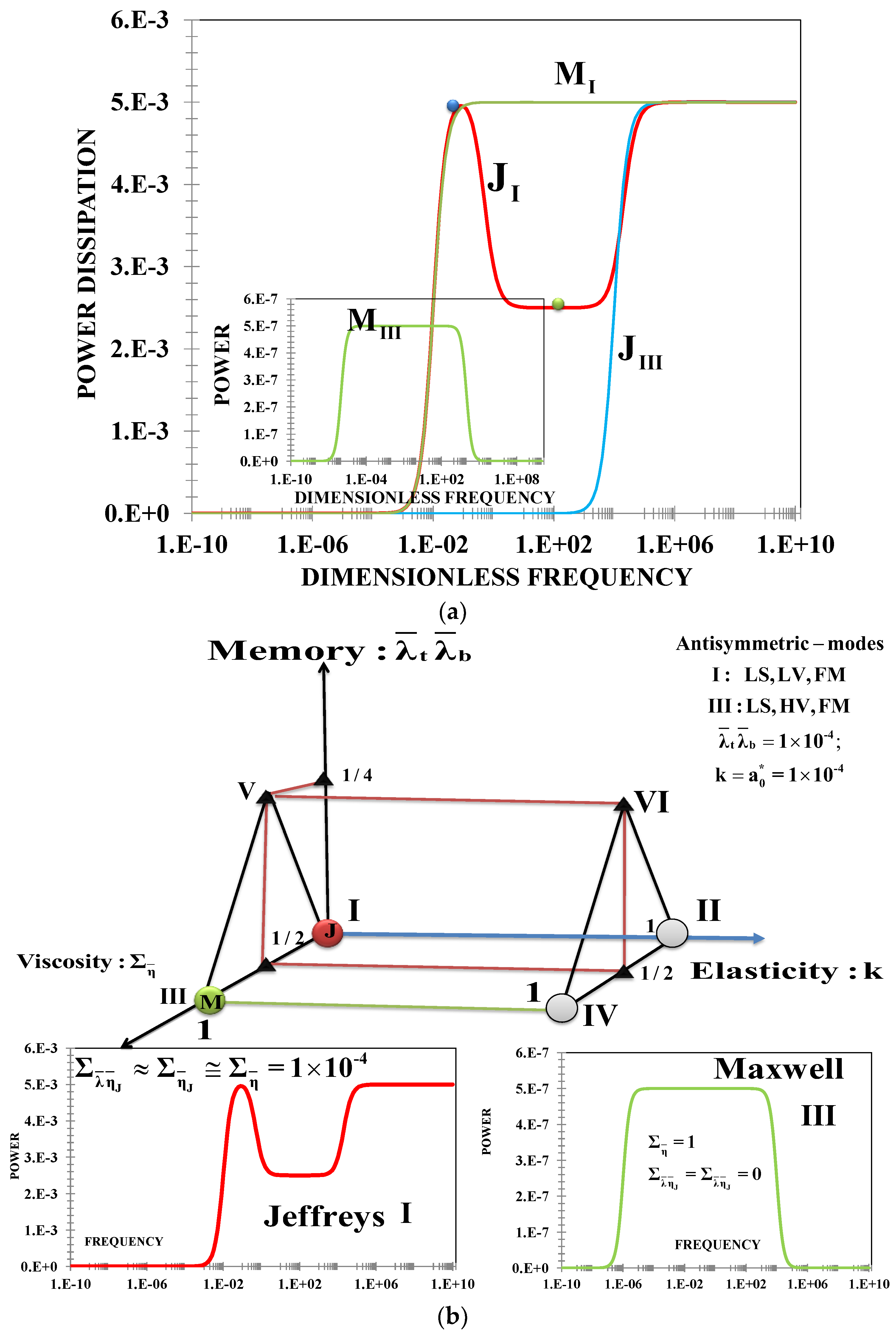
The six modes can be represented by the vertices of a prismatic 3D material space figure shown in
Figure 3, spanned by fluid memory, membrane elasticity, and total fluid viscosity
respectively.
These dimensionless numbers are completely determined by the numerical value of the memory number
and solvent and viscosities ratio through r
i = 0. For example, in the case of the asymmetric case, given a small value of the memory number, i.e.,
, the respective minimum and maximum values of the Maxwell relaxation times are
, the corresponding minimum and maximum values for the total bulk viscosity, bulk retardation viscosity, and weighted retardation viscosity are given by:
;
and the last one is
. For the symmetric case, the value of the memory number is
. Here, the Maxwell relaxation times are equal, i.e.,
, the bulk viscosity is fixed at
[
10,
12], and the values of the retardation bulk and average bulk viscosities can be chosen from the following ranges,
and
. The corresponding minimum and maximum values of the total bulk-viscosity (triangle) turn out to be a crucial material parameter in the energy conversion device. Finally, in this work we focus on the zone where the maximum and minimum of the Jeffrey’s model is found, and it is localized between modes I and III in the parametric 3D space, shown in
Figure 3. The other modes, do not display resonance and antiresonance behavior [
10,
12].
6. Conclusions
In this paper we explored the dynamics of the actuation flexoelectric mode [
1,
2,
6,
7,
8]. Using the flexoelectric shape equation in conjunction with a viscoelastic capillary flow model for the contacting phases, a new average curvature dynamic was obtained (Equations (12) and (13)). The third-order model for the electric field (input) and curvature or volumetric flow (output) is given by a balance of retardation, inertial, viscous, and elastic effects, originating from the flexoelectric membrane and the viscoelastic Jeffreys fluids (solvent and polymer mechanisms). Moreover, this new model (3ODE) can be interpreted as the sum of a second-order ordinary differential equation plus a small perturbation, which it is associated with retardation mechanisms. These third-order models are well known and they are associated to the jerk-force mechanism (timed derivative of acceleration) in ODEs, chaotic systems, and classic Newtonian mechanics [
34]. When the retardation mechanisms are zero, i.e.,
, the previous Maxwell model is recovered with inertial and inertialess mechanisms [
10,
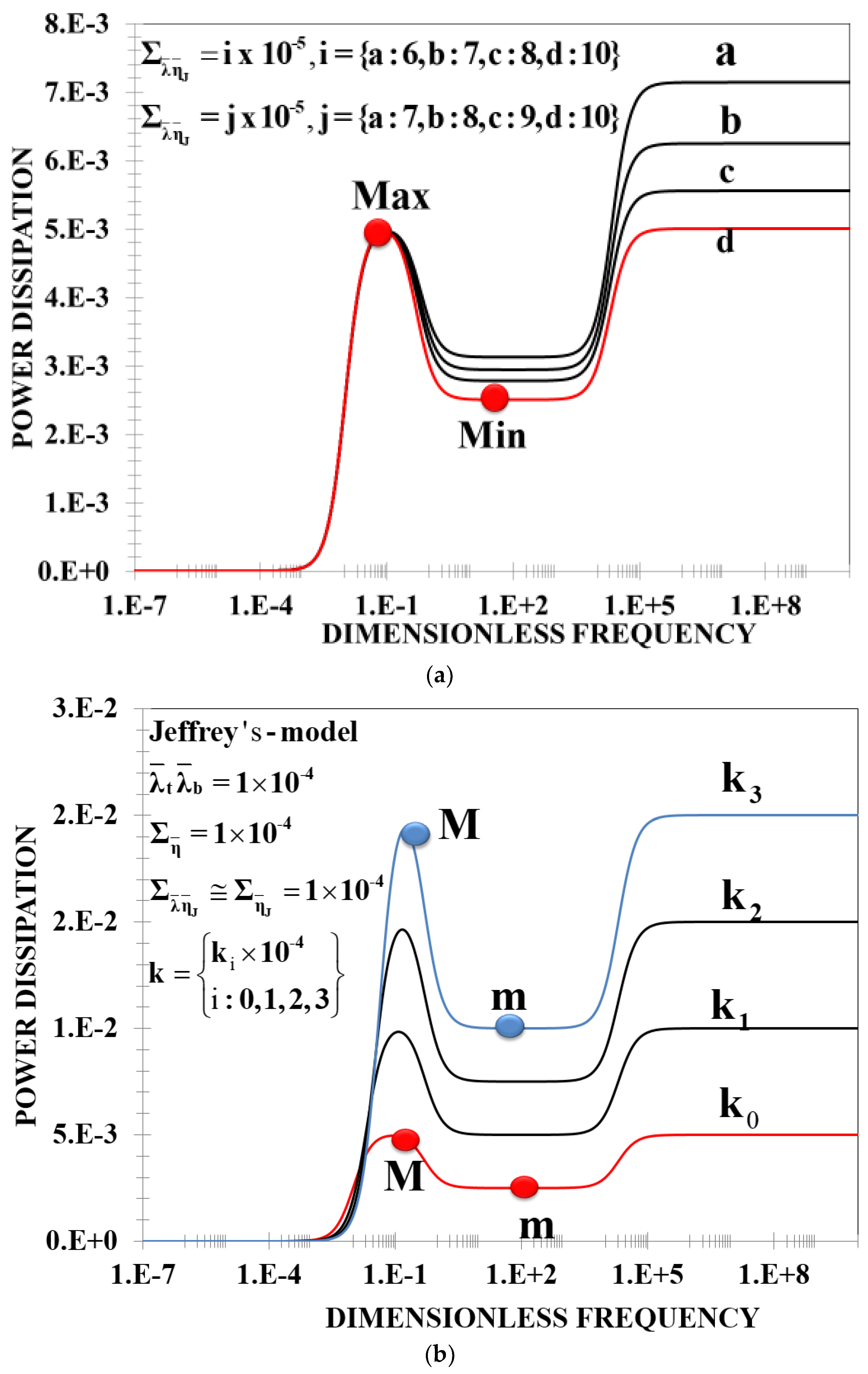
12]. Using dimensionless variables, and taking into account the inertia mechanisms in the system, the physics can be described with seven dimensionless numbers (Equations (11) and (21)). These dimensionless numbers are associated with the inertia, retardation, memory, viscous, elastic membrane, and flexoelectric mechanisms. A thorough parametric study was performed to identify the conditions that lead to the appearance of a maximum (resonance behavior) or a minimum (anti-resonance behavior) in the power spectrum (
Table 3). The maximum and minimum are found in mode I (
Figure 5), when the system presents a: (i) large asymmetry between the viscoelastic phases (one on phases is weakly elastic and the other one completely viscoelastic); (ii) minimum total bulk viscosity; (iii) small elasticity; and (iv) the flexoelectric mechanisms are of the order of the elasticity of the membrane [
10,
12]. The mathematical condition to reach the maximum and minimum are given when the maximum values of the retardation mechanisms are equal to the minimum value of the dissipation energy, i.e.,
. The above mathematical condition implies that the solvent and polymer viscosities play an important role in the resonance and anti-resonance behaviour (
Figure 6a,b). Physically, this means that in order to get a non-monotonically increasing behavior, a contrast in the liquid phases is necessary with one of them being weakly elastic and the other one being highly viscoelastic (Equations (22) and (23)). For example, if one of the viscoelastic phases is characterized by the Jeffrey’s or Maxwell model, the other one must be represented by the Maxwell or the Newtonian constitutive equation, respectively. It is important to note that the Maxwell and Jeffrey’s times are not independent and they satisfy a linear relation, whose slope is given by a ratio between the solvent viscosity and the polymer contribution to the bulk viscosity (
Section 2). The non-monotonically behaviour has been reported using a mechano-electrical model as a consequence of the outer hair cell length [
15] (see [
15], Figure 7b). In constrast, the lector-rheological model used here, showed that the solvent and the polymer mechanisms induced a similar non-monotonic behaviour in the power dissipation as a function of the applied electrical field. Here, the maximum and minimum is controlled by coupling effects between the solvent and the polymer contributions of the liquid viscoelastic phases (
Figure 6a). The numerical values of maximum and minimum is controlled by the elastic ratio k and the flexoelectric mechanisms trough the flexoelectric number
. Notice that in order to have the maximum and minimum in the system, the flexoelectric number
must be of the same order as k, i.e.,
(
Figure 6b). When the asymmetry of the viscoelastic phases increases, the power peak and the resonance width decrease and increase, respectively. These effects are shown in
Figure 6 and
Figure 7 and summarized in
Table 3. Furthermore, optimization of the power device can be obtained by minimizing the stored elastic membrane energy and maximizing the power dissipation. This was discussed in previous works [
9,
10,
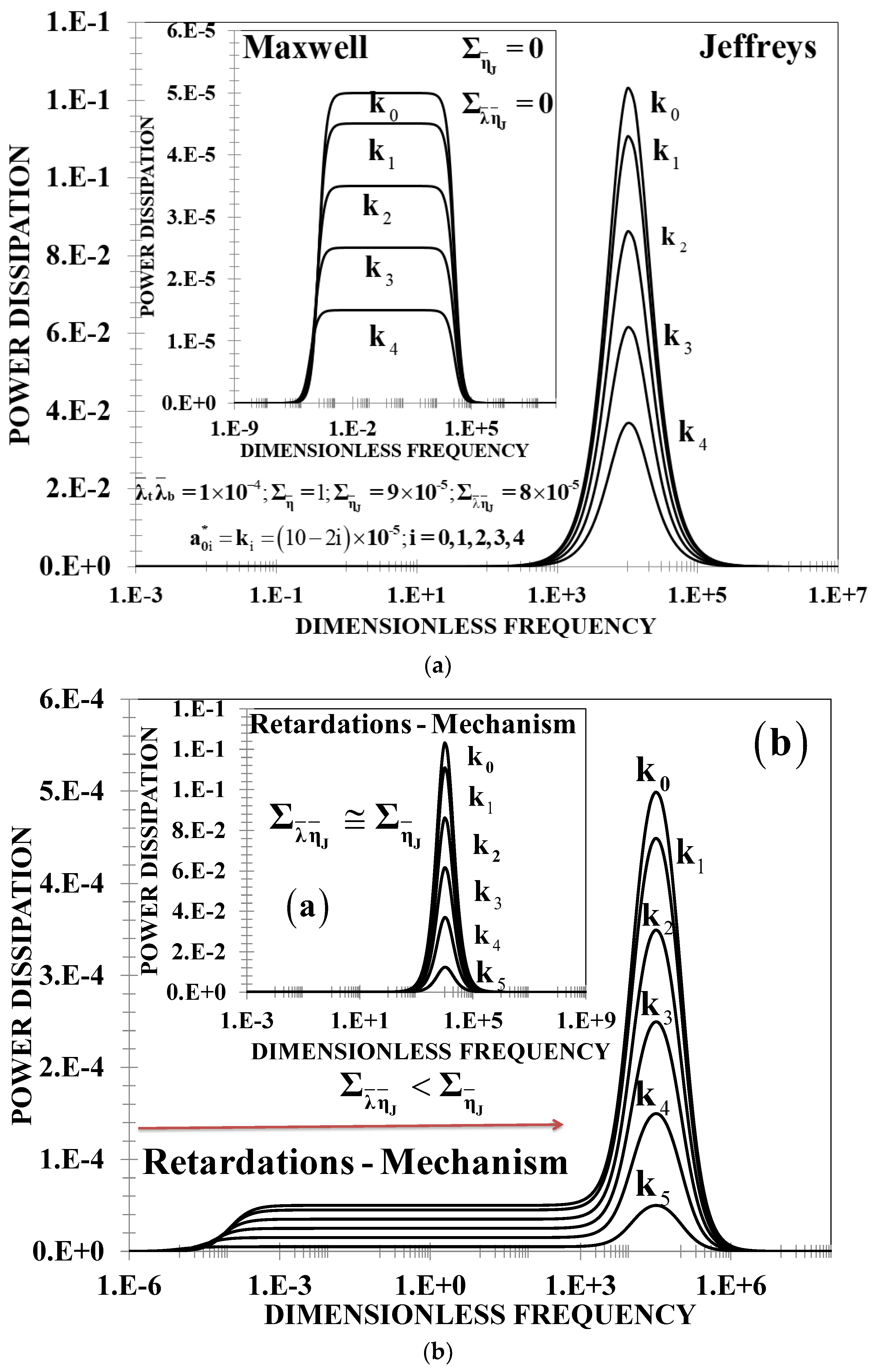
12]. In addition, when one of the solvent contributions is small in comparison with the other solvent phase, a close expression for the power dissipation is found (small Mach number, Ma << 1, Equations (16), (20) and (21)).
Physically, the dissipation dominates over the elastic storage membrane mechanisms in the resonance behavior [
9,
10,
12,
15]. The effect of the resonance behavior through the Mach number is to display more resonant peaks which can be associated to biological processes (see the Deborah number in [
10,
12]). The inclusion of new rheological parameters through higher models can be done by changing the Jeffrey’s viscosity operator given in
Table 1.
The merits of this research is to extend the previous theory [
1,
2,
6,
7,
8,
9,
10,
12], for any particular linear or fractional viscoelastic constitutive equation, through the generalized viscosity differential operator given in
Table 1.
In particular, the Jeffreys viscosity function was chosen to include the solvent and polymer mechanisms. When the inertia is included in the system through the Mach number several resonance peaks are found, which, from a biological point of view, could be relevant (
Figure 4). In the inertialess regime (Ma = 0), a third-order differential equation (3ODE) was found (Equations (10)–(12)). This electro-rheological model led to a non-monotonically decreasing behavior, which is directly related to the new viscosities associated with the retardation mechanisms, which are linked by the solvent and polymer contributions. Lastly, a qualitative evaluation of the present model predictions based on a non-monotonically power profile, indicates that the Helfrich-Flexoelectric-Jeffrey’s fluid model possesses the necessary physics to qualitatively capture the electro-mechanical power conversion phenomena. Future extensions include higher-order and fractional viscoelastic models, non-linear viscoelasticity, and mass transfer induced by shear forces [
35,
36]. Heat dissipation and non-linear effects due to high frequencies, compressible systems (density as a function of the pressure drop), and others diseases which can affect the hearing system (hypercholesterolemia, hyperglycemia, genetic problems, etc.) lie outside of the scope of the present research [
37,
38,
39,
40,
41]. A posible path to continue this research is to exted it to new models in the regime of nonlinear viscoelasticity (large deformations). The nonlinearity induced by large deformations can be explored with two approaches. The nonlinearity comes from the flexoelectric membrane or can be induced through the viscoelastic liquid phases. These new approaches must be explored through analytical and numerical algoritms and can be a starting point of new reaserch. The present theory, model, and computations contribute to the evolving fundamental understanding of biological shape actuation through electromechanical couplings [
1,
2,
3,
4,
9,
10,
11,
12,
35,
36,
37] involving liquid crystallinity.