Onset of Convection in the Presence of a Precipitation Reaction in a Porous Medium: A Comparison of Linear Stability and Numerical Approaches
Abstract
:1. Introduction
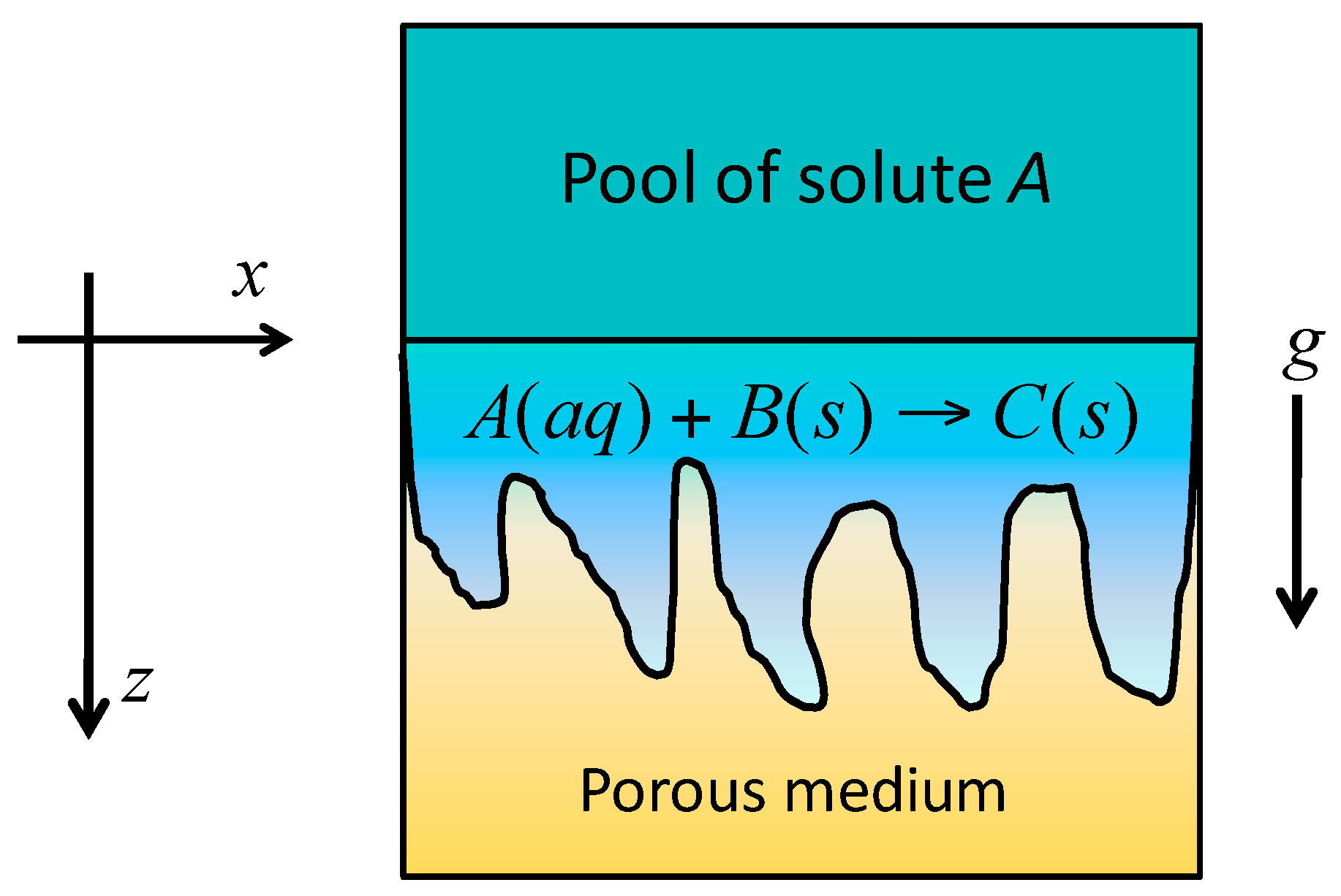
2. Model
2.1. Governing Equations and Scaling
2.2. Linear Stability Analysis
3. Results
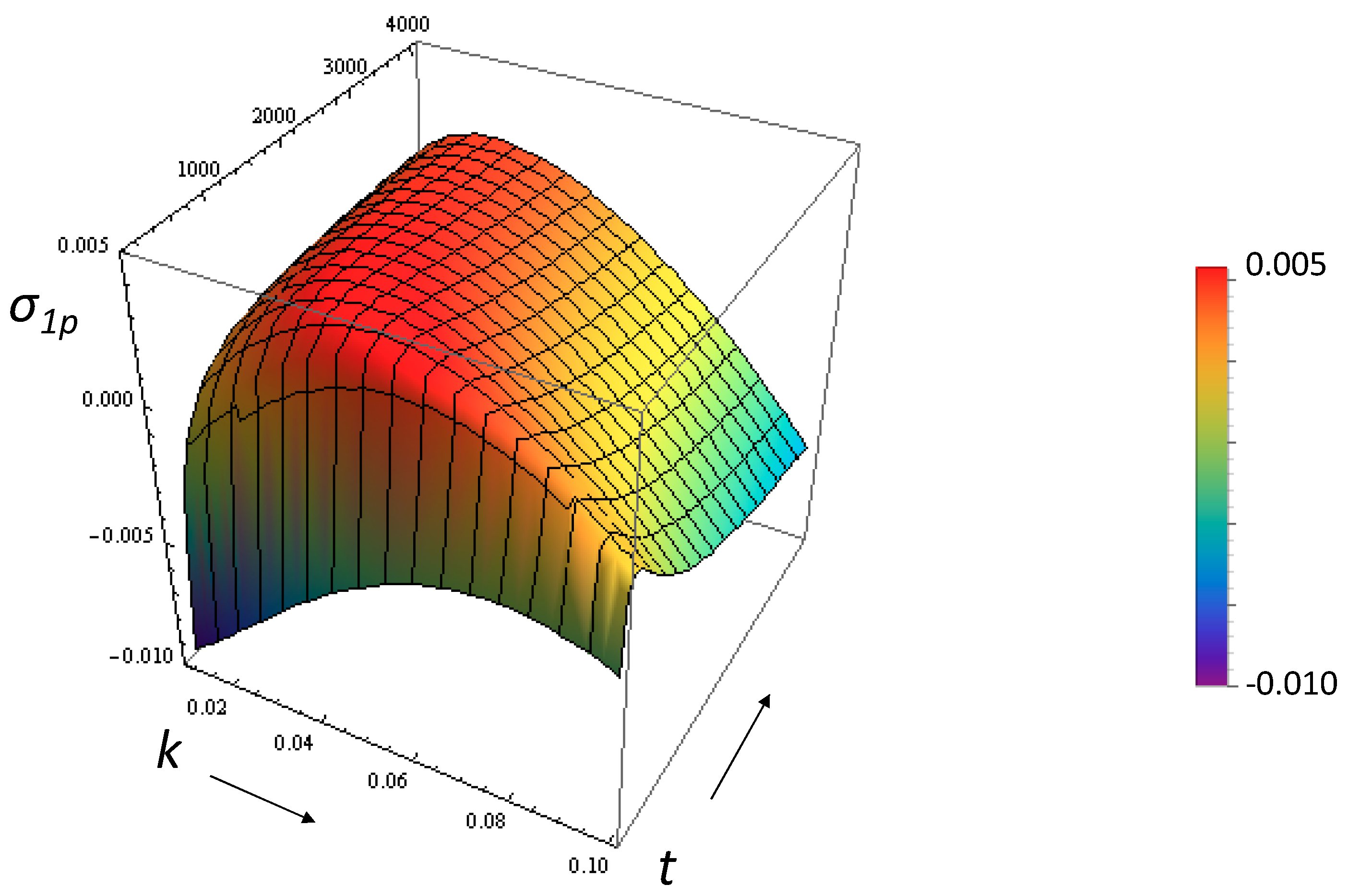
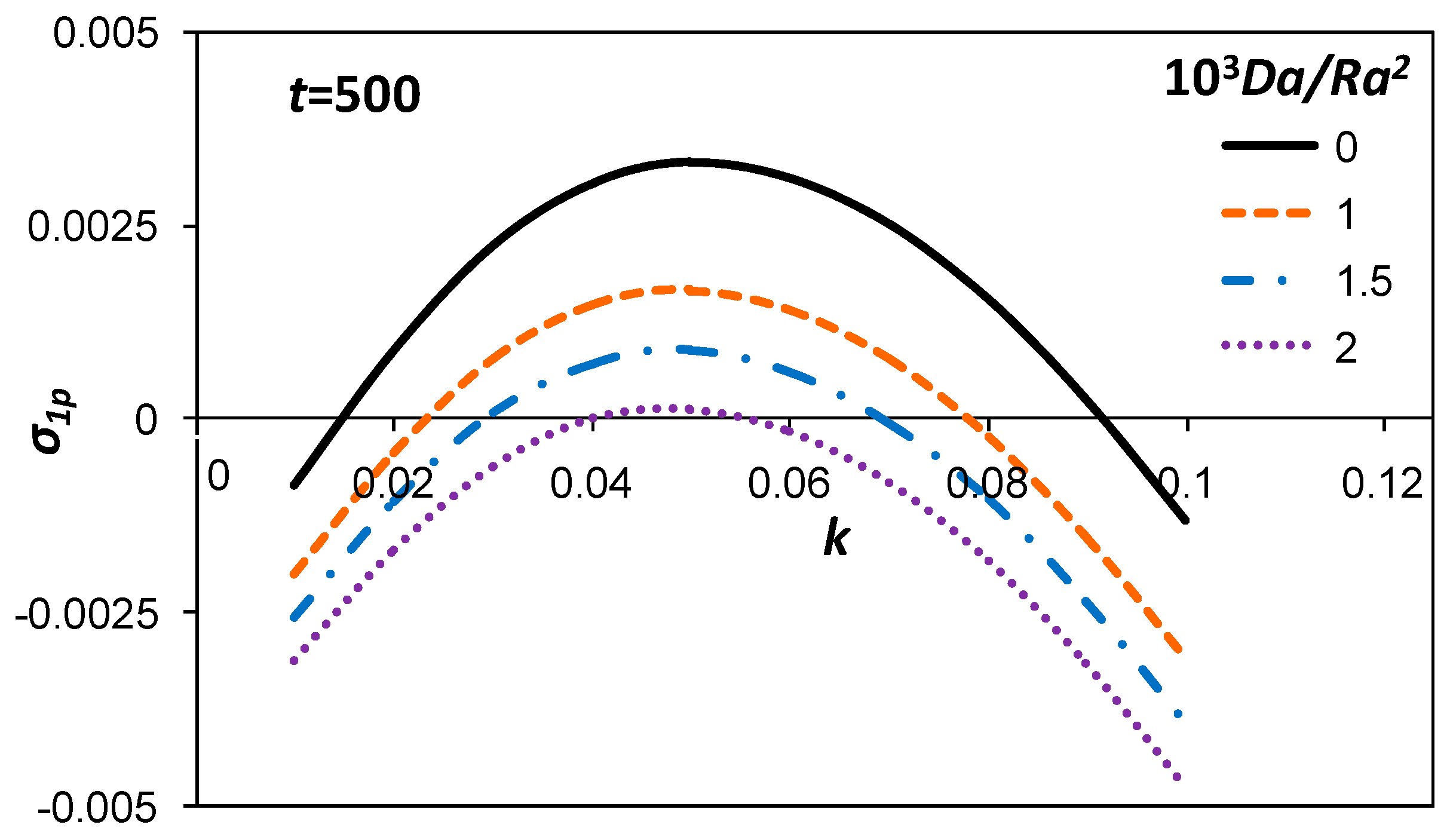
3.1. Growth Rate of the Perturbation
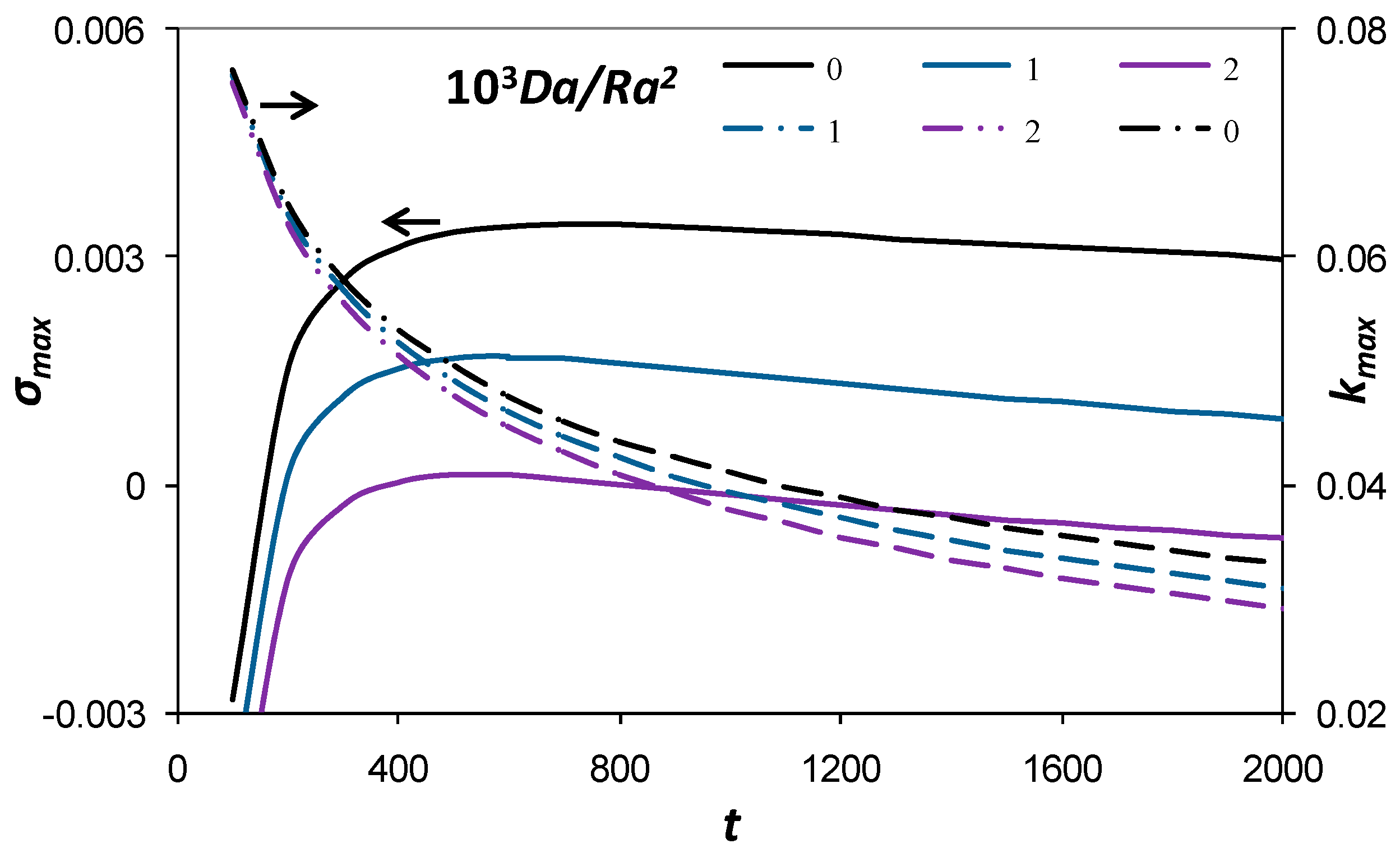
3.2. Maximum Growth Rate and Corresponding Wave Number
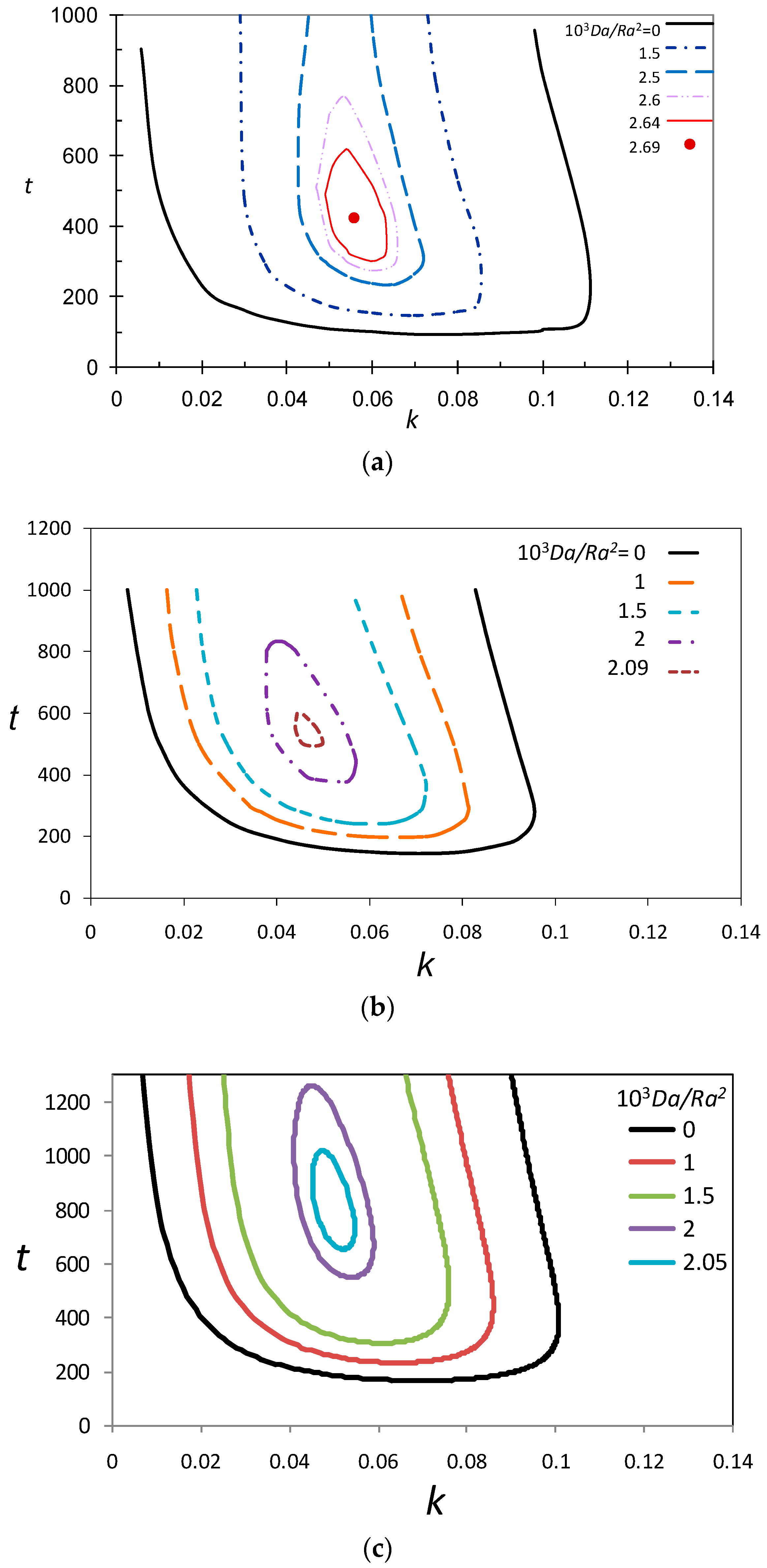
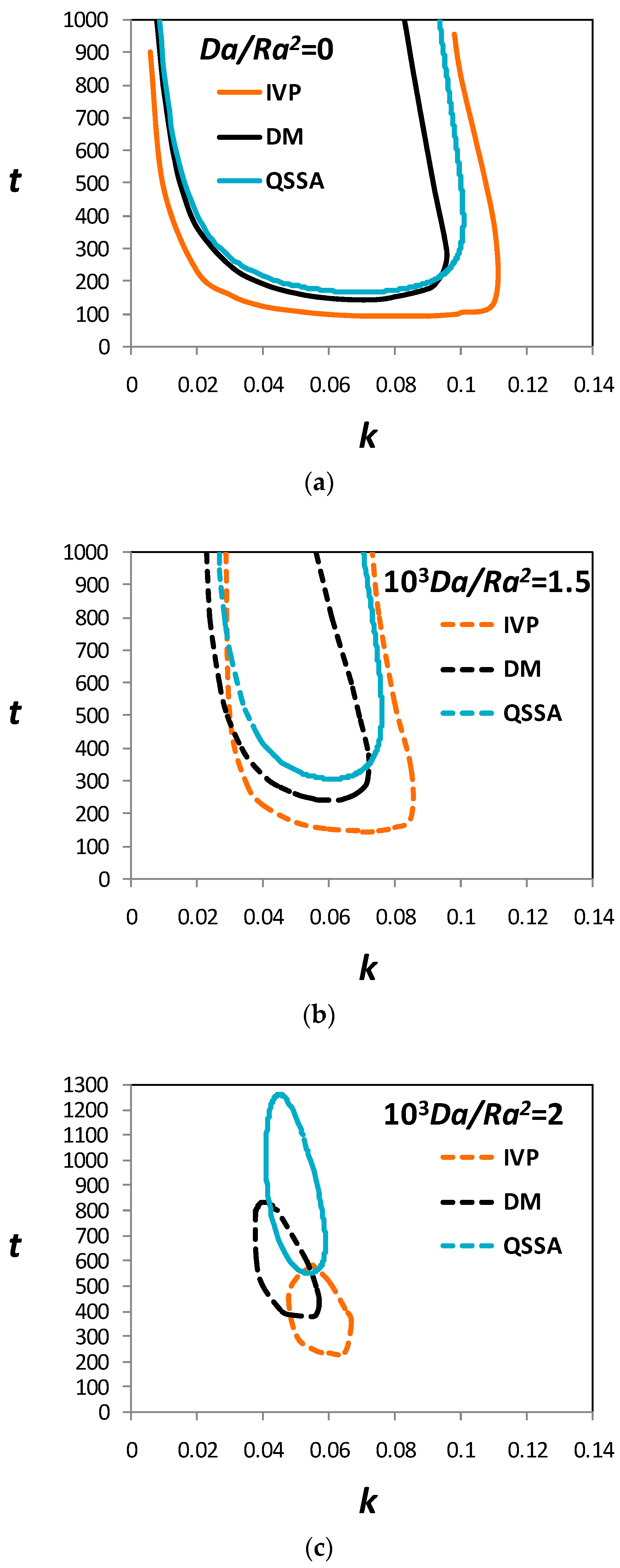
3.3. Marginal Stability Curves
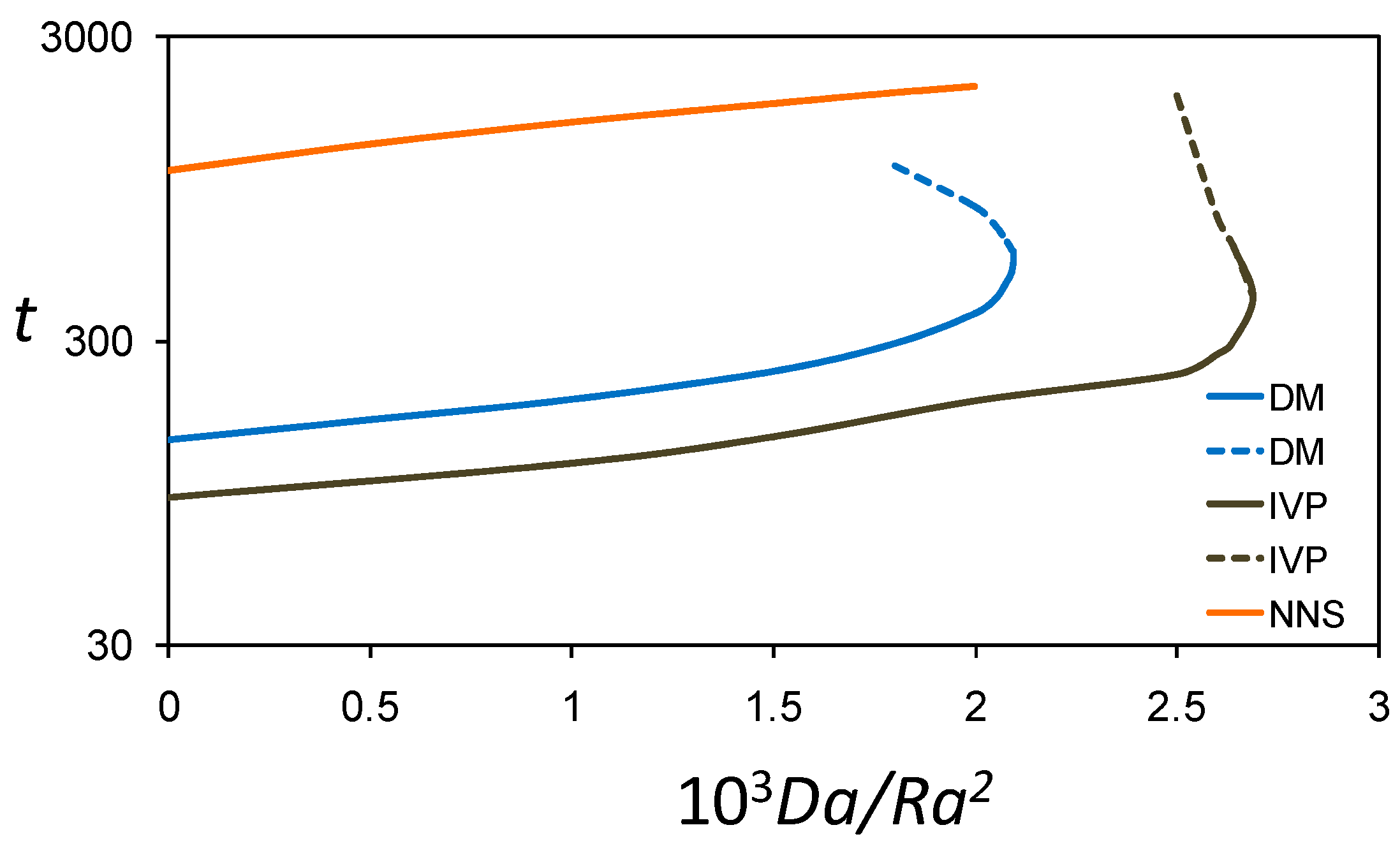
3.4. Time for Onset of Convection
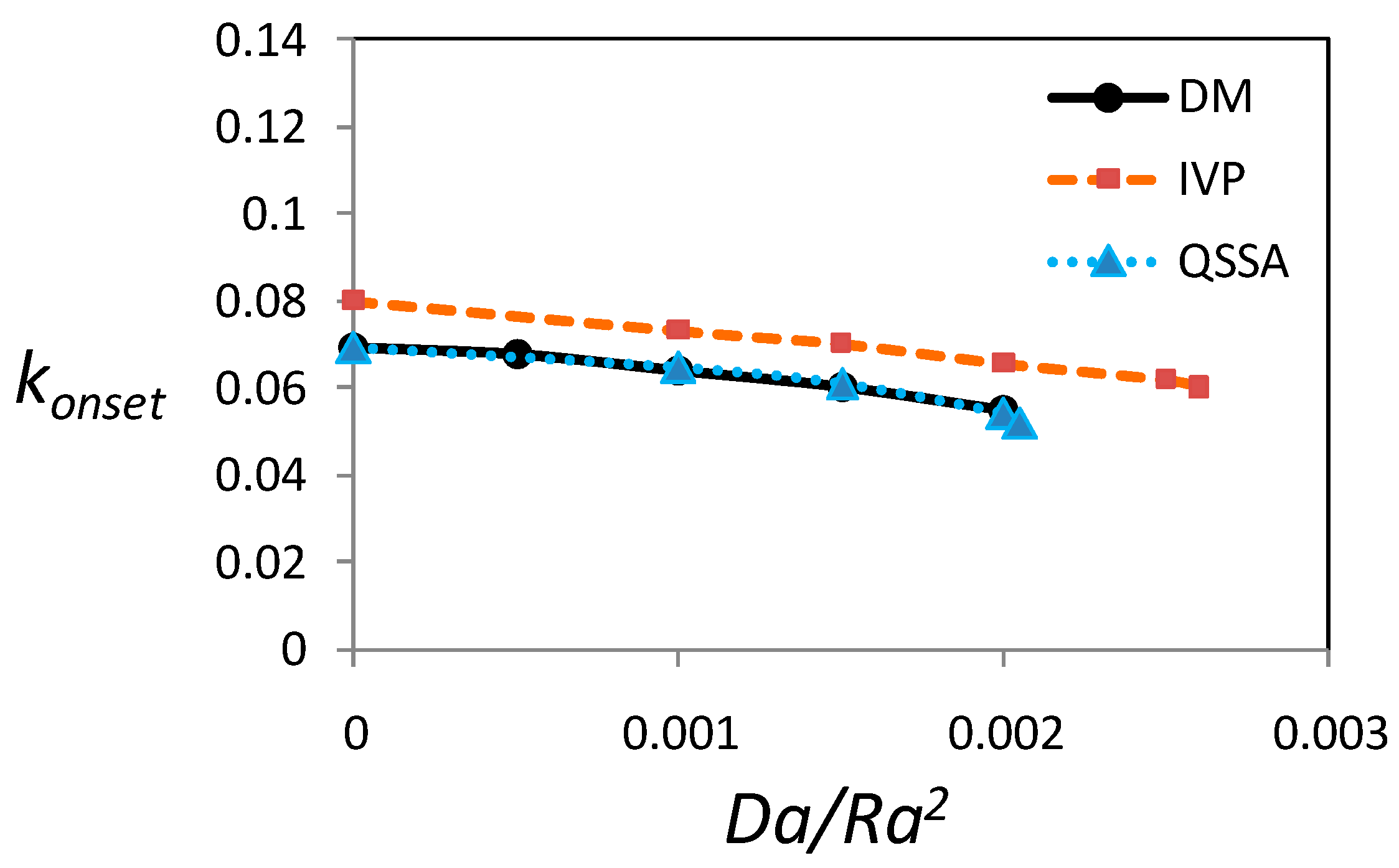
3.5. Critical Wave Number at the Onset of Instability
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D.W. Scaling behavior of convective mixing, with application to geological storage of CO2. AIChE J. 2007, 53, 1121–1131. [Google Scholar] [CrossRef]
- Ennis-King, J.; Paterson, L. Coupling of geochemical reactions and convective mixing in the long-term geological storage of carbon dioxide. Int. J. Greenh. Gas Control 2007, 1, 86–93. [Google Scholar] [CrossRef]
- Andres, J.T.H.; Cardoso, S.S. Onset of convection in a porous medium in the presence of chemical reaction. Phys. Rev. E 2011, 83, 046312. [Google Scholar] [CrossRef] [PubMed]
- Ghesmat, K.; Hassanzadeh, H.; Abedi, J. The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media: CO2 storage in saline aquifers. J. Fluid Mech. 2011, 673, 480–512. [Google Scholar] [CrossRef]
- Andres, J.T.H.; Cardoso, S.S. Convection and reaction in a diffusive boundary layer in a porous medium: Nonlinear dynamics. Chaos 2012, 22, 037113. [Google Scholar] [CrossRef] [PubMed]
- Ghoshal, P. Studies on Dissolution-Driven Convection with Precipitating and Non-Precipitating Chemical Reactions in Porous Media. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Cardoso, S.S.S.; Andres, J.T.H. Geochemistry of silicate-rich rocks can curtail spreading of carbon dioxide in subsurface aquifers. Nat. Commun. 2014, 5, 5743. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.C.; Kim, Y.H. The effect of chemical reaction on the onset of gravitational instabilities in a fluid saturated within a vertical Hele-Shaw cell: Theoretical and numerical studies. Chem. Eng. Sci. 2015, 134, 632–647. [Google Scholar]
- Linden, P.F. Perspectives in Fluid Dynamics, Chapter 6: Convection in the Environment; Batchelor, G.K., Moffatt, H.K., Worster, M.G., Eds.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Riaz, A.; Hesse, M.; Tchelepi, H.A.; Orr, F.M. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 2006, 548, 87–111. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Selim, A.; Ennis-King, J.P. The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media; Springer: Dordrecht, The Netherlands, 2008; pp. 85–110. [Google Scholar]
- Commonwealth Scientific and Industrial Research Organisation (CSIRO). Fastflo Tutorial Guide; CSIRO: Canberra, Australia, 2000. [Google Scholar]
- Kim, M.C.; Choi, C.K. Effects of first-order chemical reaction on gravitational instability in a porous medium. Phys. Rev. E 2014, 90, 053016. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.C.; Choi, C.K. Some theoretical aspects on the onset of buoyancy-driven convection in a fluid-saturated porous medium heated impulsively from below. Korean J. Chem. Eng. 2015, 32, 2400–2405. [Google Scholar] [CrossRef]
- Ward, T.J.; Cliffe, K.A.; Jensen, O.E.; Power, H. Dissolution-driven porous medium convection in the presence of chemical reaction. J. Fluid Mech. 2014, 747, 316–349. [Google Scholar] [CrossRef]
- Slim, A.C. Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech. 2014, 741, 461–491. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H.; Green, C.P.; Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control 2015, 40, 238–266. [Google Scholar] [CrossRef]
- Tilton, N.; Daniel, D.; Riaz, A. The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids 2013, 25, 092107. [Google Scholar] [CrossRef]
- Marini, L. Geological Sequestration of Carbon Dioxide: Thermodynamics, Kinetics, and Reaction Path Modeling; Elsevier: Amsterdam, The Netherlands, 2007; Volume 11. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghoshal, P.; Kim, M.C.; Cardoso, S.S.S. Onset of Convection in the Presence of a Precipitation Reaction in a Porous Medium: A Comparison of Linear Stability and Numerical Approaches. Fluids 2018, 3, 1. https://doi.org/10.3390/fluids3010001
Ghoshal P, Kim MC, Cardoso SSS. Onset of Convection in the Presence of a Precipitation Reaction in a Porous Medium: A Comparison of Linear Stability and Numerical Approaches. Fluids. 2018; 3(1):1. https://doi.org/10.3390/fluids3010001
Chicago/Turabian StyleGhoshal, Parama, Min Chan Kim, and Silvana S. S. Cardoso. 2018. "Onset of Convection in the Presence of a Precipitation Reaction in a Porous Medium: A Comparison of Linear Stability and Numerical Approaches" Fluids 3, no. 1: 1. https://doi.org/10.3390/fluids3010001



