Nonlinear Convection in a Partitioned Porous Layer
Abstract
:1. Introduction
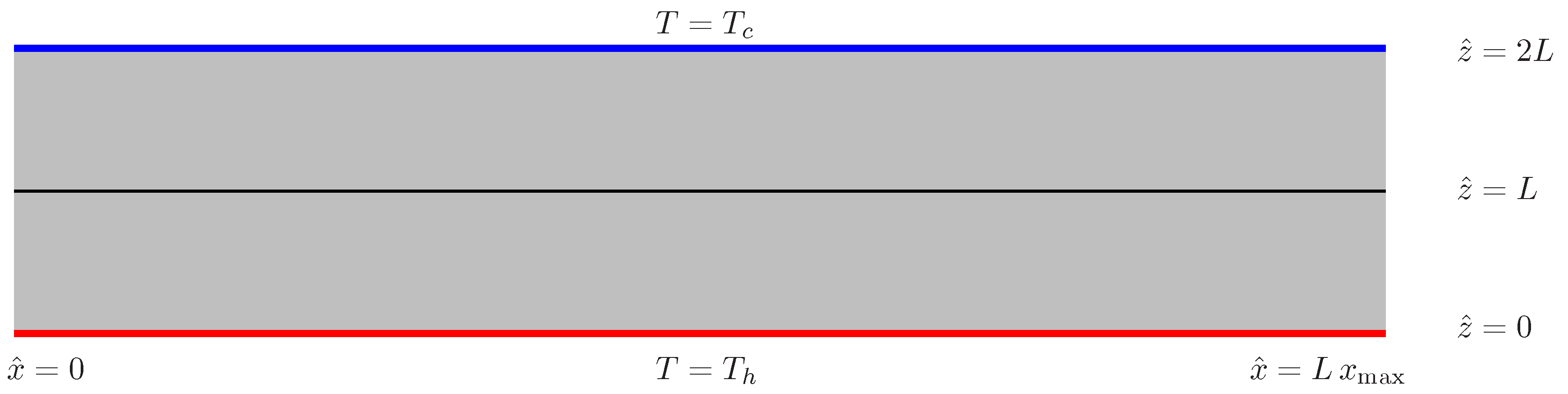
2. Governing Equations
3. Numerical Method
4. Results and Discussion
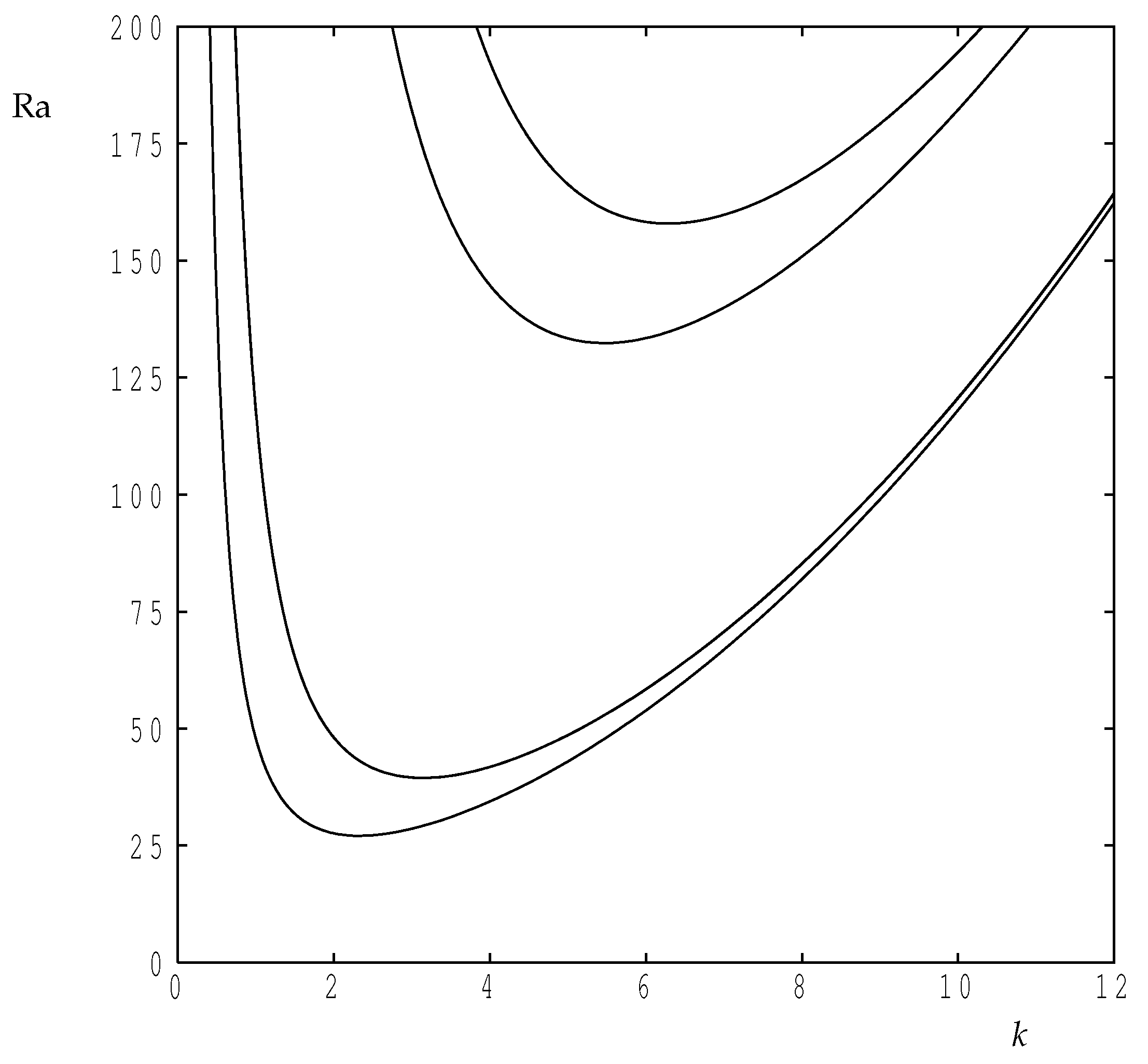
4.1. Linearised Theory
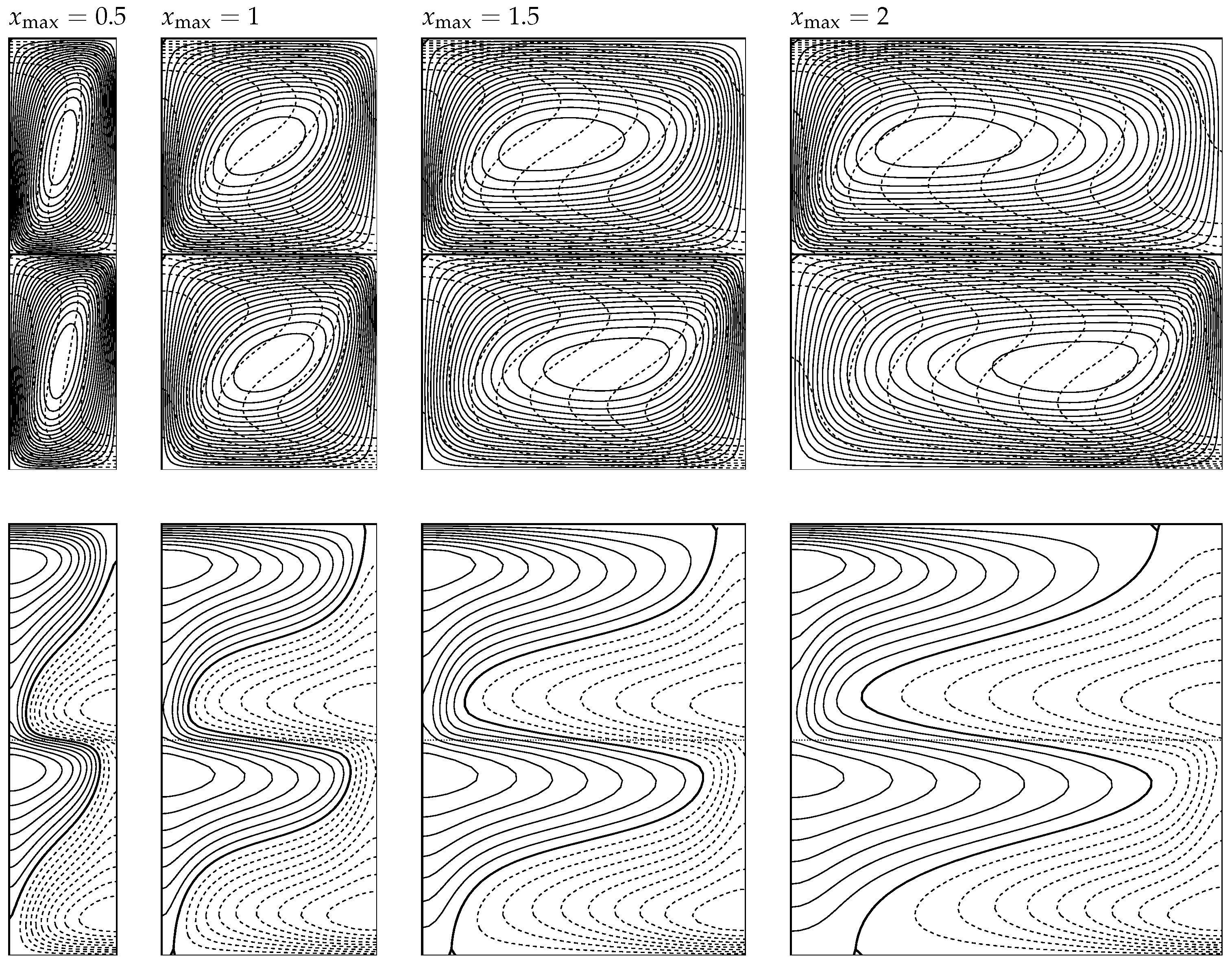
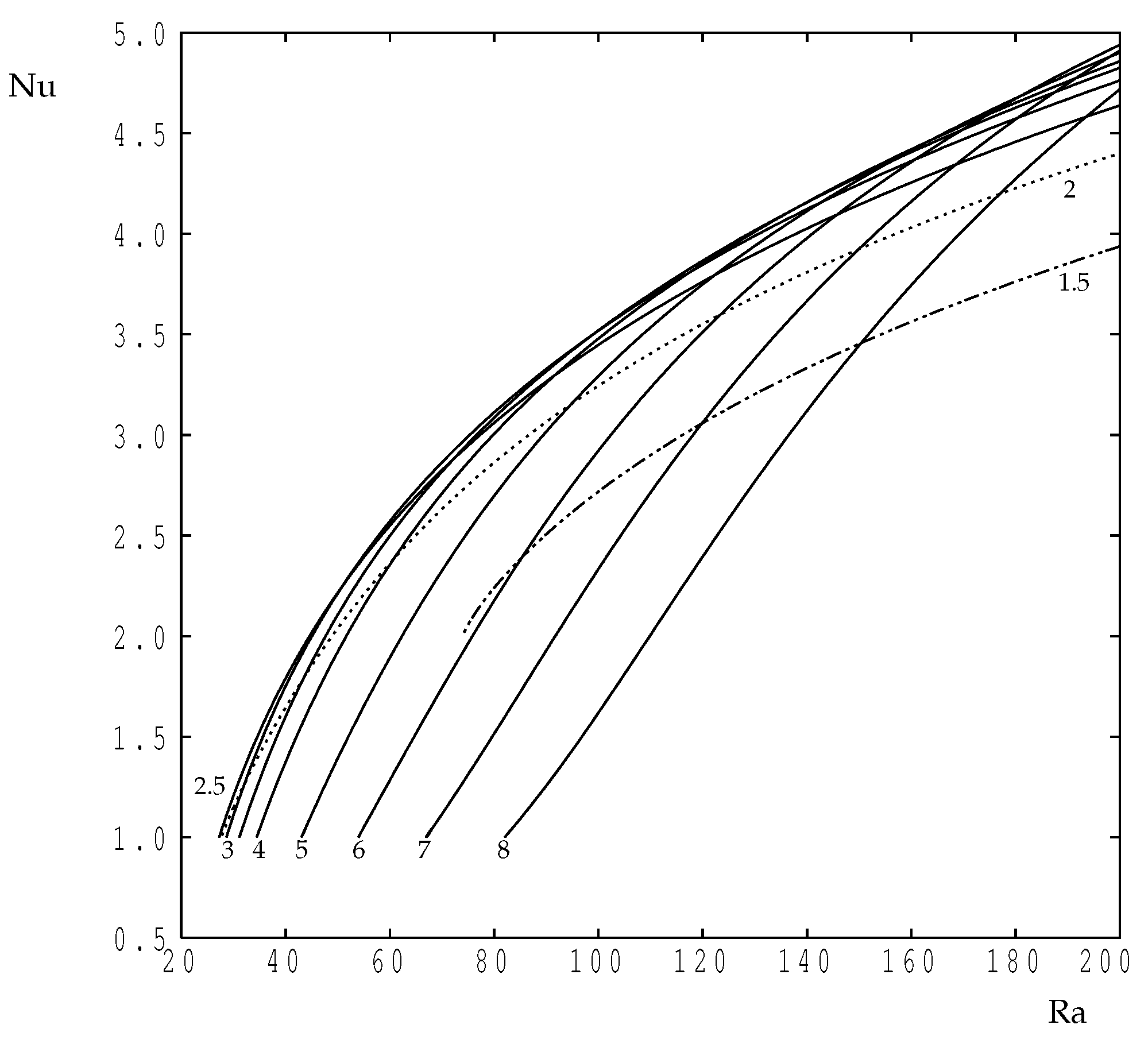
4.2. Nonlinear Flows
5. Conclusions
Conflicts of Interest
Abbreviations
| C | heat capacity |
| g | gravity |
| k | wavenumber () |
thermal conductivity of the porous medium | |
| K | permeability |
| L | height of one sublayer |
Nusselt number | |
| NX | number of intervals in the x-direction |
| NZ | number of intervals in the z-direction |
| p | pressure |
| Ra | Darcy–Rayleigh number |
| t | time |
| T | dimensional temperature |
upper (cold) boundary temperature | |
lower (hot) boundary temperature | |
| u | horizontal velocity |
| w | vertical velocity |
| x | horizontal coordinate |
width of the computational domain | |
| z | vertical coordinate |
| CGIs | CpG islands |
| β | expansion coefficient |
temperature drop across a sublayer | |
| θ | temperature |
| λ | value defined in Equation (21) |
| μ | dynamic viscosity |
| ρ | density |
| σ | value defined in Equation (21) |
| ψ | streamfunction |
| c | critical value |
| f | fluid |
| pm | porous medium |
| ^ | dimensional quantity |
| + | immediately above the interface |
| − | immediately below the interface |
Appendix A. Accuracy Considerations

| NX × NZ | Nu |
|---|---|
| 12 × 16 | 4.4238 |
| 24 × 32 | 4.5451 |
| 48 × 64 | 4.5720 |
| NX × NZ | Error | |
|---|---|---|
| 12 × 16 | 27.762 | 2.45% |
| 24 × 32 | 27.265 | 0.62% |
| 48 × 64 | 27.129 | 0.15% |
References
- Georghitza, St.I. The marginal stability in porous inhomogeneous media. Proc. Camb. Phil. Soc. 1961, 57, 871–877. [Google Scholar] [CrossRef]
- Masuoka, T.; Katsuhara, T.; Nakazono, Y.; Isozaki, S. Onset of convection and flow patterns in a porous layer of two different media. Heat Transf. Jpn. Res. 1979, 7, 39–52. [Google Scholar] [CrossRef]
- Rana, R.; Horne, R.N.; Cheng, P. Natural convection in a multi-layered geothermal reservoir. J. Heat Transf. 1979, 101, 411–416. [Google Scholar] [CrossRef]
- McKibbin, R.; O’Sullivan, M.J. Onset of convection in a layered porous medium heated from below. J. Fluid Mech. 1980, 96, 375–393. [Google Scholar] [CrossRef]
- McKibbin, R.; O’Sullivan, M.J. Heat transfer in a layered porous medium heated from below. J. Fluid Mech. 1981, 111, 141–173. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Riley, D.S. The three-dimensional stability of finite-amplitude convection in a layered porous medium heated from below. J. Fluid Mech. 1990, 211, 437–461. [Google Scholar] [CrossRef]
- Mojtabi, A.; Rees, D.A.S. The onset of the convection in Horton-Rogers-Lapwood experiments: The effect of conducting bounding plates. Int. J. Heat Mass Transf. 2011, 54, 293–301. [Google Scholar] [CrossRef] [Green Version]
- Falsaperla, P.; Mulone, G.; Straughan, B. Rotating porous convection with prescribed heat flux. Int. J. Eng. Sic. 2010, 48, 685–692. [Google Scholar] [CrossRef]
- Riahi, D.N. Nonlinear convection in a porous layer with finite conducting boundaries. J. Fluid Mech. 1983, 129, 153–171. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Mojtabi, A. The effect of conducting boundaries on weakly nonlinear Darcy–Bénard convection. Transp. Porous Media 2011, 88, 45–63. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Mojtabi, A. The effect of conducting boundaries on Lapwood-Prats convection. Int. J. Heat Mass Transf. 2013, 65, 765–778. [Google Scholar] [CrossRef] [Green Version]
- Saleh, H.; Saeid, N.H.; Hashim, I.; Mustafa, Z. Effect of conduction in bottom wall on Darcy–Bénard convection in a porous enclosure. Transp. Porous Media 2011, 88, 357–368. [Google Scholar] [CrossRef]
- Jang, J.Y.; Tsai, W.L. Thermal instability of two horizontal porous layers with a conductive partition. Int. J. Heat Mass Transf. 1988, 31, 993–1003. [Google Scholar]
- Postelnicu, A. Thermal stability of two fluid porous layers separated by a thermal barrier. In Proceedings of the 3rd Baltic Heat Transfer Conference, Gdansk, Poland, 22–24 September 1999; pp. 443–450.
- Patil, P.M.; Rees, D.A.S. The onset of convection in a porous layer with multiple horizontal solid partitions. Int. J. Heat Mass Transf. 2014, 68, 234–246. [Google Scholar] [CrossRef] [Green Version]
- Straughan, B. Nonlinear stability of convection in a porous layer with solid partitions. J. Math. Fluid Mech. 2014, 16, 727–736. [Google Scholar] [CrossRef]
- Genç, G.; Rees, D.A.S. The onset of convection in horizontally partitioned porous layers. Phys. Fluids 2011, 23, 064107. [Google Scholar] [CrossRef] [Green Version]
- Rees, D.A.S.; Genç, G. Onset of convection in porous layers with multiple horizontal partitions. Int. J. Heat Mass Transf. 2011, 54, 3081–3089. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P.; Genç, G. Weakly nonlinear convection in a porous layer with multiple horizontal partitions. Transp. Porous Media 2014, 103, 437–448. [Google Scholar] [CrossRef] [Green Version]
- De la Torres Juarez, M.; Busse, F.H. Stability of two-dimensional convection in a fluid-saturated porous medium. J. Fluid Mech. 1995, 292, 305–323. [Google Scholar] [CrossRef]


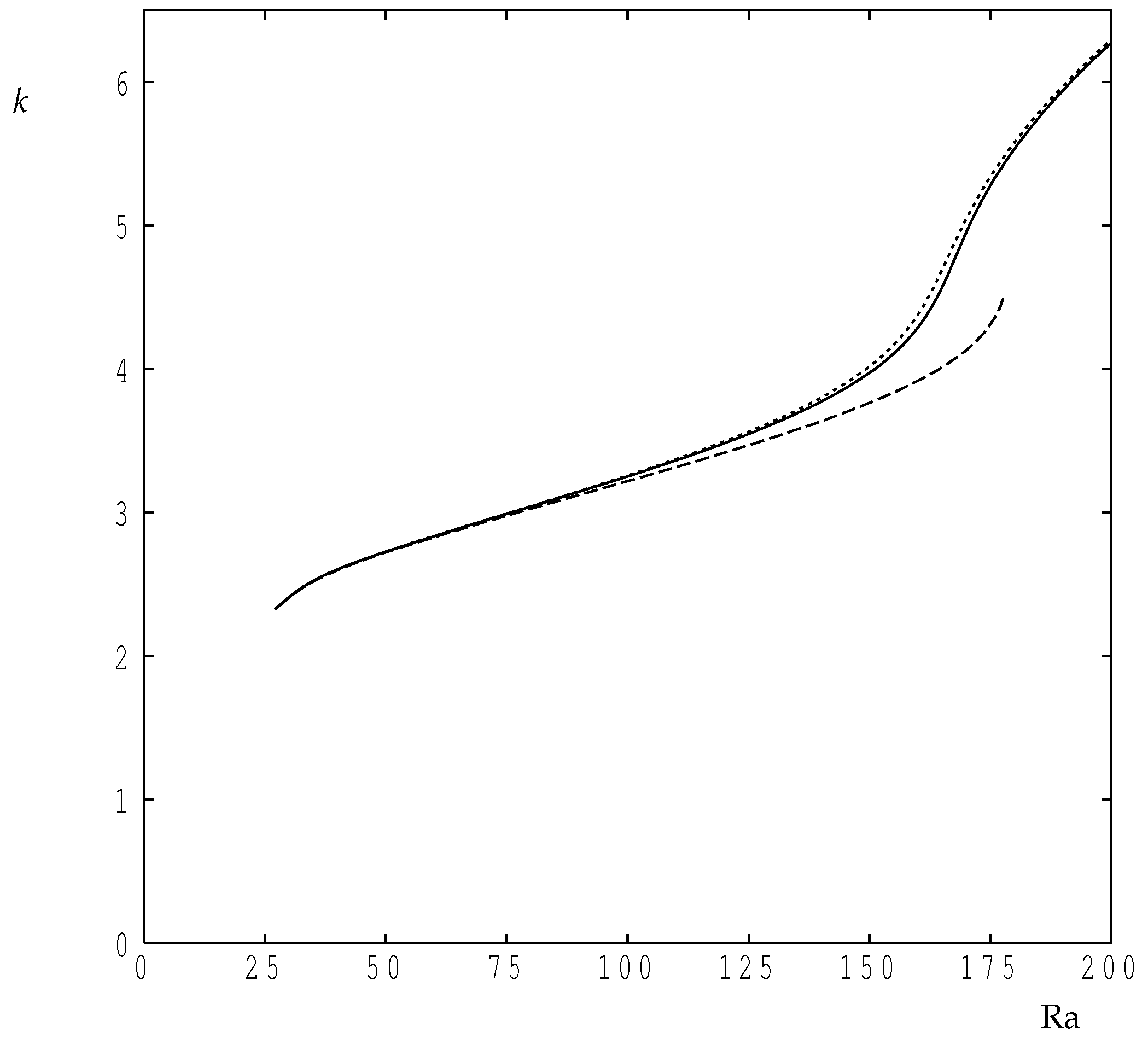
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, D.A.S. Nonlinear Convection in a Partitioned Porous Layer. Fluids 2016, 1, 24. https://doi.org/10.3390/fluids1030024
Rees DAS. Nonlinear Convection in a Partitioned Porous Layer. Fluids. 2016; 1(3):24. https://doi.org/10.3390/fluids1030024
Chicago/Turabian StyleRees, D. Andrew S. 2016. "Nonlinear Convection in a Partitioned Porous Layer" Fluids 1, no. 3: 24. https://doi.org/10.3390/fluids1030024






