Design and Control of Cooperativity in Spin-Crossover in Metal–Organic Complexes: A Theoretical Overview
Abstract
:1. Introduction
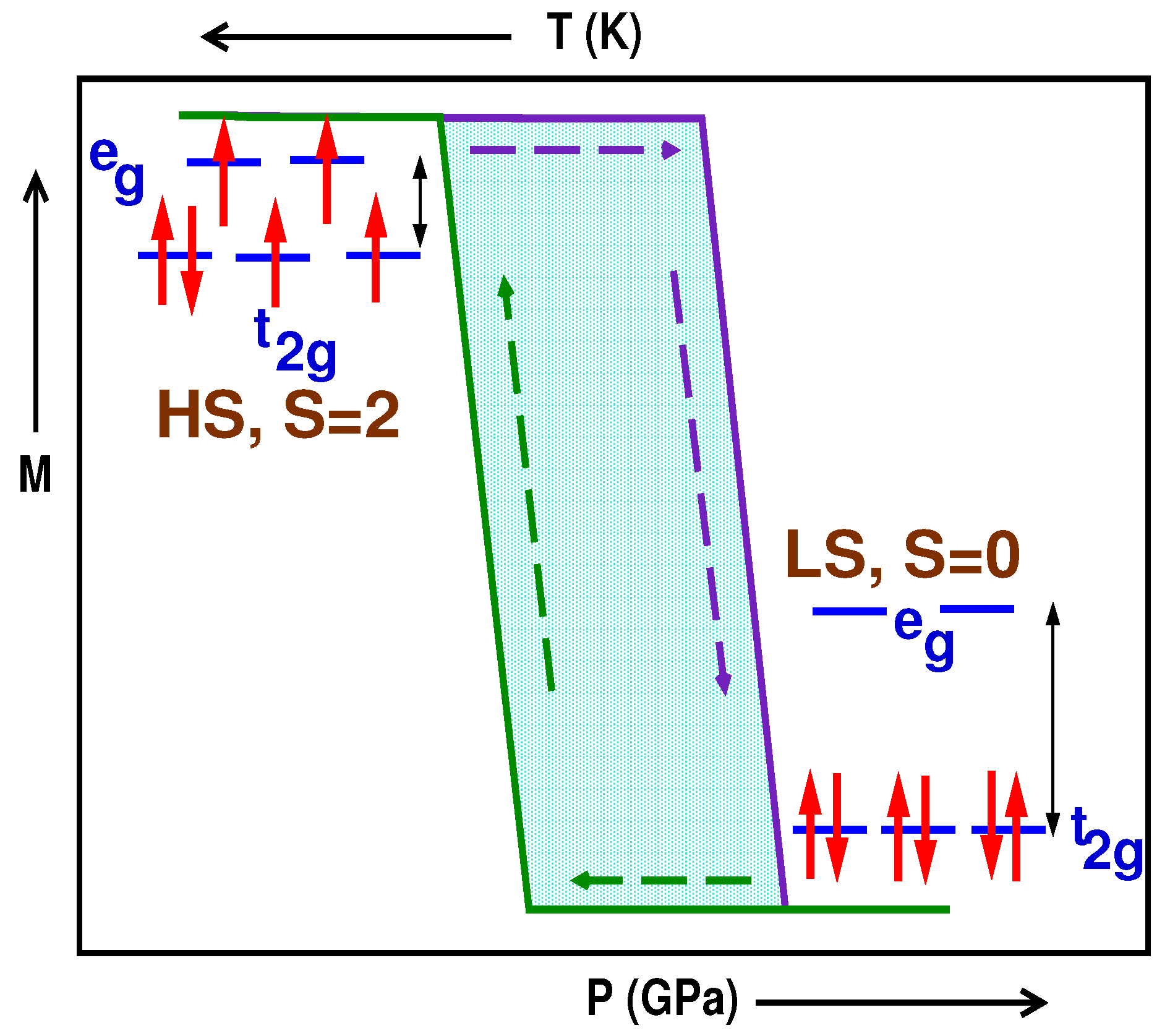
2. Experimental Evidences of Cooperativity
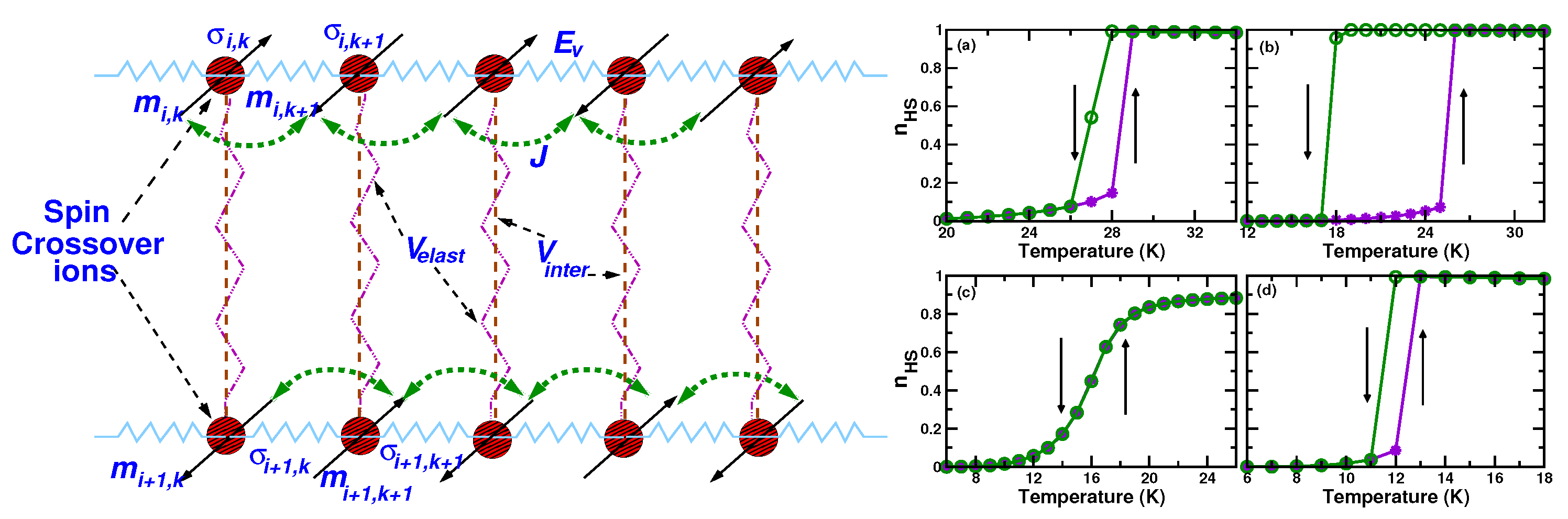
3. Theoretical Models on Cooperativity
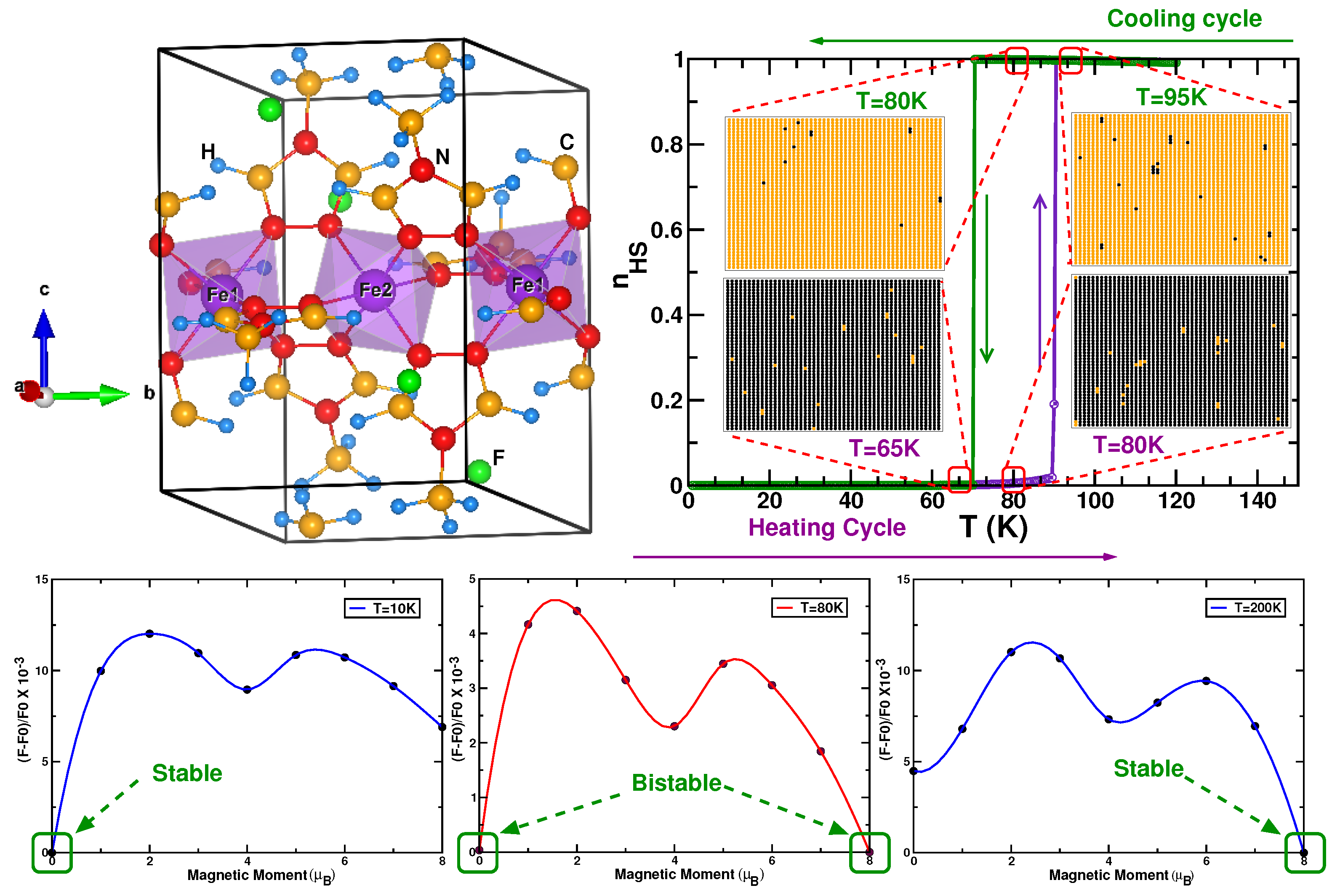
4. Ab Initio Studies on Materials Showing Cooperativity
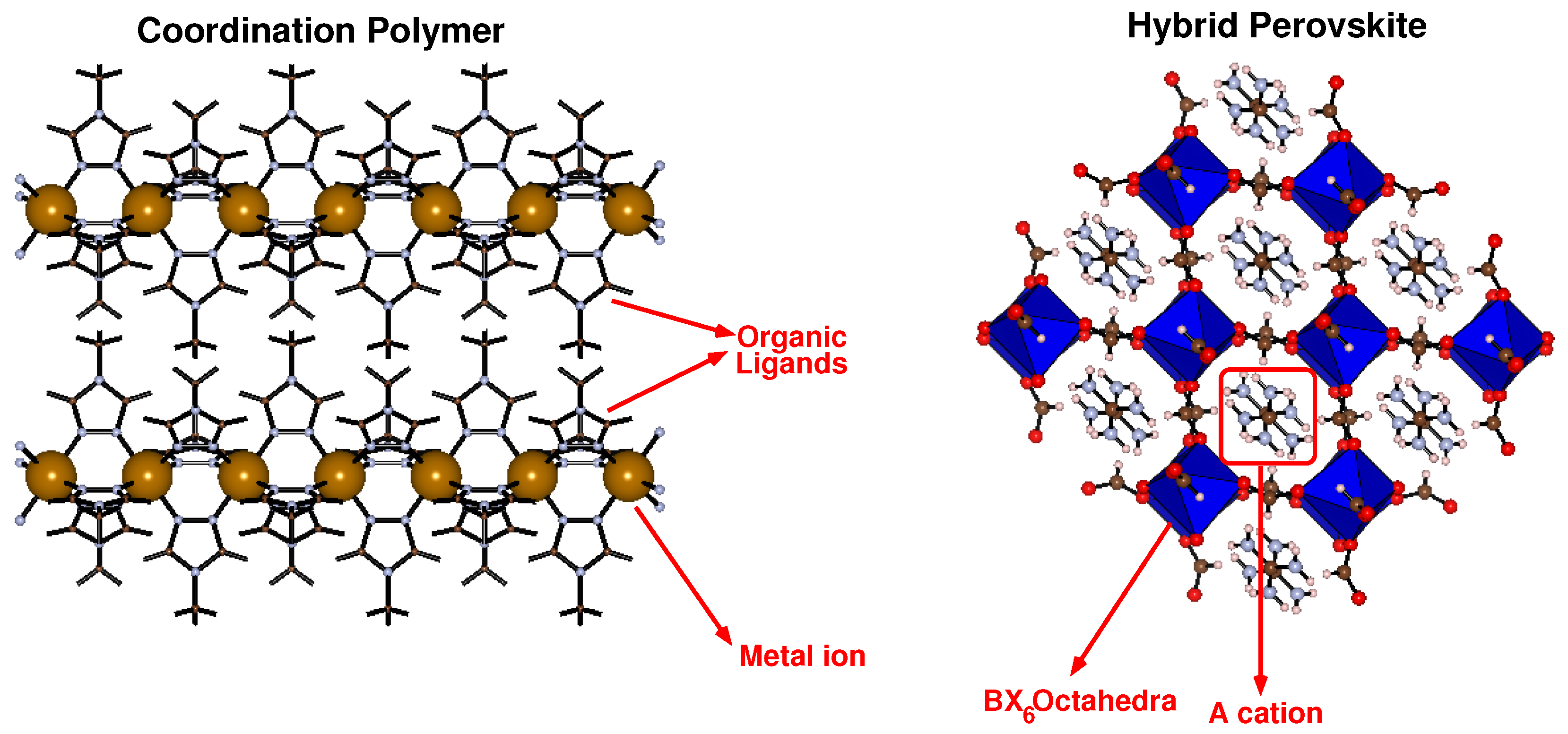
4.1. Linear or 1-d Coordination Polymers
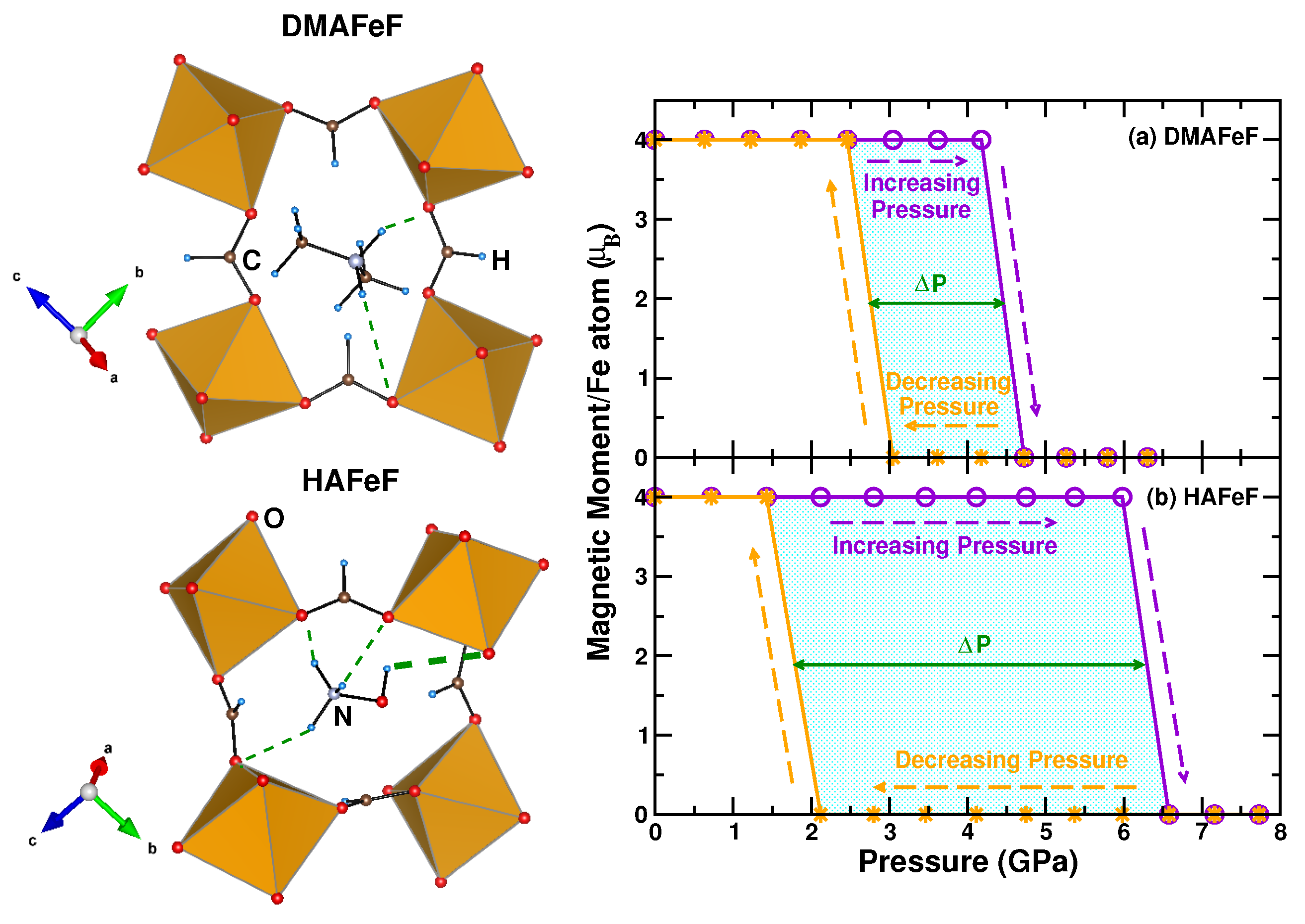
4.2. Hybrid Perovskites
5. Summary and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SCO | Spin crossover |
| MOF | Metal organic framework |
| LS | Low Spin |
| HS | High Spin |
| EXAFS | Extended X-ray absorption Fine Structure |
| FT-IR | Fourier Transform Infrared Spectroscopy |
| UV-vis | Ultraviolet and visible |
| EPR | Electron Paramagnetic Resonance |
| SR | Muon Spin Relaxation |
| PAS | Positron Annihilation Spectroscopy |
| NRS | Nuclear Resonant Scattering of synchroton radiation |
| LIESST | Light induced spin state trapping |
| SQUID | Superconducting quantum interference device |
| trz | triazole |
| btr | bis-triazole |
| bipy | 4,4’-bipyridine |
| bpea | 1,2-bis(4-pyridyl)ethane |
| bppa | 1,3-bis(4-pyridyl)propane |
| hyetrz | 4-(2’-hydroxyethyl)-1,2,4-triazole |
| MC | Monte Carlo |
| DFT | Density functional theory |
| CASSCF | Complete active space self consistent field |
| CASPT2 | Complete active space with second order perturbation theory |
| CC | Couple cluster theory |
| CCSD(T) | Coupled Cluster single-double and perturbative triple |
| VASP | Vienna Ab-initio Simulation Package |
| PBE | Perdew, Burke and Ernzerhof |
| AIMD | Ab-initio Molecular dynamics |
| DMAFeF | Dimethyl ammonium Iron Formate |
| HAFeF | Hydroxyl ammonium Iron Formate |
References
- Létard, J.-F.; Guionneau, P.; Goux-Capes, L. Spin Crossover in Transition Metal Compounds I-III; Gütlich, P., Goodwinpp, H., Eds.; Springer: Berlin, Germany, 2004; pp. 221–249. [Google Scholar]
- Linares, J.; Codjovi, E.; Garcia, Y. Pressure and Temperature Spin Crossover Sensors with Optical Detection. Sensors 2012, 12, 4479–4492. [Google Scholar] [CrossRef] [PubMed]
- Cobo, S.; Molnár, G.; Real, J.A.; Bousseksou, A. Multilayer Sequential Assembly of Thin Films that Display Room-Temperature Spin Crossover with Hysteresis. Angew. Chem. Int. Ed. 2006, 45, 5786–5789. [Google Scholar] [CrossRef] [PubMed]
- Saha-Dasgupta, T.; Oppeneer, P.M. Computational design of magnetic metal–organic complexes and coordination polymers with spin-switchable functionalities. MRS Bull. 2014, 39, 614–620. [Google Scholar] [CrossRef]
- Brooker, S.; Kitchen, J.A. Nano-magnetic materials: Spin crossover compounds vs. single molecule magnets vs. single chain magnets. Dalton Trans. 2009, 7331–7340. [Google Scholar] [CrossRef] [PubMed]
- Ohkoshi, S.I.; Imoto, K.; Tsunobuchi, Y.; Takano, S.; Tokoro, H. Light-induced spin-crossover magnet. Nat. Chem. 2011, 3, 564–569. [Google Scholar] [CrossRef] [PubMed]
- Halder, G.J.; Kepert, C.J.; Moubaraki, B.; Murray, K.S.; Cashion, J.D. Guest-Dependent Spin Crossover in a Nanoporous Molecular Framework Material. Science 2002, 298, 1762–1765. [Google Scholar] [CrossRef] [PubMed]
- Olguín, J.; Brooker, S. Spin crossover active iron(II) complexes of selected pyrazole-pyridine/pyrazine ligands. Coord. Chem. Rev. 2011, 255, 203–240. [Google Scholar] [CrossRef]
- Batten, S.R.; Champness, N.R.; Chen, X.M.; Garcia-Martinez, J.; Kitagawa, S.; Öhrström, L.; O’Keeffe, M.; Suh, M.P.; Reedijk, J. Terminology of metal–organic frameworks and coordination polymers (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1715–1724. [Google Scholar] [CrossRef] [Green Version]
- Ozarowski, A.; Shunzhong, Y.; McGarvey, B.R.; Mislankar, A.; Drake, J.E. EPR and NMR study of the spin-crossover transition in bis(4,4’-bi-1,2,4-triazole)bis(thiocyanato)iron hydrate and bis(4,4’-bi-1,2,4-triazole)bis(selenocyanato)iron hydrate. X-ray structure determination of Fe(4,4’-bi-1,2,4-triazole)2(SeCN)2·H2O. Inorg. Chem. 1991, 30, 3167–3174. [Google Scholar] [CrossRef]
- Yann Garcia, N.N.A.; Naik, A.D. Crystal Engineering of Fe-II Spin Crossover Coordination Polymers Derived from Triazole or Tetrazole Ligands. Chimia 2013, 67, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.; Wheatley, P. Gas Storage in Nanoporous Materials. Angew. Chem. Int. Ed. 2008, 47, 4966–4981. [Google Scholar] [CrossRef] [PubMed]
- Kreno, L.E.; Leong, K.; Farha, O.K.; Allendorf, M.; Van Duyne, R.P.; Hupp, J.T. Metal–Organic Framework Materials as Chemical Sensors. Chem. Rev. 2012, 112, 1105–1125. [Google Scholar] [CrossRef] [PubMed]
- Horcajada, P.; Chalati, T.; Serre, C.; Gillet, B.; Sebrie, C.; Baati, T.; Eubank, J.F.; Heurtaux, D.; Clayette, P.; Kreuz, C.; et al. Porous metal–organic-framework nanoscale carriers as a potential platform for drug delivery and imaging. Nat. Mater. 2010, 9, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Czaja, A.U.; Trukhan, N.; Muller, U. Industrial applications of metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1284–1293. [Google Scholar] [CrossRef] [PubMed]
- Cheetham, A.K.; Rao, C.N.R. There’s Room in the Middle. Science 2007, 318, 58–59. [Google Scholar] [CrossRef] [PubMed]
- Garcia, Y.; Niel, V.; Muñoz, M.C.; Real, J.A. Spin Crossover in 1D, 2D and 3D Polymeric Fe(II) Networks. In Spin Crossover in Transition Metal Compounds I; Gütlich, P., Goodwin, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 229–257. [Google Scholar]
- Krober, J.; Codjovi, E.; Kahn, O.; Groliere, F.; Jay, C. A spin transition system with a thermal hysteresis at room temperature. J. Am. Chem. Soc. 1993, 115, 9810–9811. [Google Scholar] [CrossRef]
- Setifi, F.; Milin, E.; Charles, C.; Thétiot, F.; Triki, S.; Gómez-García, C.J. Spin Crossover Iron(II) Coordination Polymer Chains: Syntheses, Structures, and Magnetic Characterizations of [Fe(aqin)2(μ2-M(CN)4)] (M = Ni(II), Pt(II), aqin = Quinolin-8-amine). Inorg. Chem. 2014, 53, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Schonfeld, S.; Lochenie, C.; Thoma, P.; Weber, B. 1D iron(II) spin crossover coordination polymers with 3,3[prime or minute]-azopyridine-kinetic trapping effects and spin transition above room temperature. CrystEngComm 2015, 17, 5389–5395. [Google Scholar] [CrossRef]
- Bauer, W.; Lochenie, C.; Weber, B. Synthesis and characterization of 1D iron(II) spin crossover coordination polymers with hysteresis. Dalton Trans. 2014, 43, 1990–1999. [Google Scholar] [CrossRef] [PubMed]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing Optoelectronic Properties of Metal Halide Perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef] [PubMed]
- Mitzi, D.B.; Feild, C.A.; Harrison, W.T.A.; Guloy, A.M. Conducting tin halides with a layered organic-based perovskite structure. Nature 1994, 369, 467–469. [Google Scholar] [CrossRef]
- Náfrádi, B.; Szirmai, P.; Spina, M.; Lee, H.; Yazyev, O.V.; Arakcheeva, A.; Chernyshov, D.; Gibert, M.; Forró, L.; Horváth, E. Optically switched magnetism in photovoltaic perovskite CH3NH3(Mn:Pb)I3. Nat. Commun. 2016, 7, 13406. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chen, Q.; Li, G.; Luo, S.; Song, T.B.; Duan, H.S.; Hong, Z.; You, J.; Liu, Y.; Yang, Y. Interface engineering of highly efficient perovskite solar cells. Science 2014, 345, 542–546. [Google Scholar] [CrossRef] [PubMed]
- Heo, J.H.; Song, D.H.; Han, H.J.; Kim, S.Y.; Kim, J.H.; Kim, D.; Shin, H.W.; Ahn, T.K.; Wolf, C.; Lee, T.W.; et al. Planar CH3NH3PbI3 Perovskite Solar Cells with Constant 17.2% Average Power Conversion Efficiency Irrespective of the Scan Rate. Adv. Mater. 2015, 27, 3424–3430. [Google Scholar] [CrossRef] [PubMed]
- Burschka, J.; Pellet, N.; Moon, S.J.; Humphry-Baker, R.; Gao, P.; Nazeeruddin, M.K.; Gratzel, M. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 2013, 499, 316–319. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Hu, K.; Gao, S.; Kobayashi, H. Formate-Based Magnetic Metal–Organic Frameworks Templated by Protonated Amines. Adv. Mater. 2010, 22, 1526–1533. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Dalal, N.S.; Toby, B.H.; Kroto, H.W.; Cheetham, A.K. Order-Disorder Antiferroelectric Phase Transition in a Hybrid Inorganic–Organic Framework with the Perovskite Architecture. J. Am. Chem. Soc. 2008, 130, 10450–10451. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Ramachandran, V.; Clark, R.J.; Zhou, H.D.; Toby, B.H.; Dalal, N.S.; Kroto, H.W.; Cheetham, A.K. Multiferroic Behavior Associated with an Order-Disorder Hydrogen Bonding Transition in Metal–Organic Frameworks (MOFs) with the Perovskite ABX3 Architecture. J. Am. Chem. Soc. 2009, 131, 13625–13627. [Google Scholar] [CrossRef] [PubMed]
- Weng, D.F.; Wang, Z.M.; Gao, S. Framework-structured weak ferromagnets. Chem. Soc. Rev. 2011, 40, 3157–3181. [Google Scholar] [CrossRef] [PubMed]
- Stroppa, A.; Jain, P.; Barone, P.; Marsman, M.; Perez-Mato, J.M.; Cheetham, A.K.; Kroto, H.W.; Picozzi, S. Electric Control of Magnetization and Interplay between Orbital Ordering and Ferroelectricity in a Multiferroic Metal–Organic Framework. Angew. Chem. Int. Ed. 2011, 50, 5847–5850. [Google Scholar] [CrossRef] [PubMed]
- Di Sante, D.; Stroppa, A.; Jain, P.; Picozzi, S. Tuning the Ferroelectric Polarization in a Multiferroic Metal–Organic Framework. J. Am. Chem. Soc. 2013, 135, 18126–18130. [Google Scholar] [CrossRef] [PubMed]
- Stroppa, A.; Barone, P.; Jain, P.; Perez-Mato, J.M.; Picozzi, S. Hybrid Improper Ferroelectricity in a Multiferroic and Magnetoelectric Metal–Organic Framework. Adv. Mater. 2013, 25, 2284–2290. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Stroppa, A.; Nabok, D.; Marino, A.; Rubano, A.; Paparo, D.; Matsubara, M.; Nakotte, H.; Fiebig, M.; Picozzi, S.; et al. Switchable electric polarization and ferroelectric domains in a metal–organic-framework. Npj Quant. Mater. 2016, 1, 16012. [Google Scholar] [CrossRef]
- Tian, Y.; Stroppa, A.; Chai, Y.; Yan, L.; Wang, S.; Barone, P.; Picozzi, S.; Sun, Y. Cross coupling between electric and magnetic orders in a multiferroic metal–organic framework. Sci. Rep. 2014, 4, 6062. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Stroppa, A.; Chai, Y.S.; Barone, P.; Perez-Mato, M.; Picozzi, S.; Sun, Y. High-temperature ferroelectricity and strong magnetoelectric effects in a hybrid organic–inorganic perovskite framework. Phys. Status Solidi Rapid Res. Lett. 2015, 9, 62–67. [Google Scholar] [CrossRef]
- Zhao, W.P.; Shi, C.; Stroppa, A.; Di Sante, D.; Cimpoesu, F.; Zhang, W. Lone-Pair-Electron-Driven Ionic Displacements in a Ferroelectric Metal–Organic Hybrid. Inorg. Chem. 2016, 55, 10337–10342. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Aguirre, L.C.; Pato-Doldán, B.; Stroppa, A.; Yáñez-Vilar, S.; Bayarjargal, L.; Winkler, B.; Castro-García, S.; Mira, J.; Sánchez-Andújar, M.; Señarís-Rodríguez, M.A. Room-Temperature Polar Order in [NH4][Cd(HCOO)3]—A Hybrid Inorganic–Organic Compound with a Unique Perovskite Architecture. Inorg. Chem. 2015, 54, 2109–2116. [Google Scholar] [CrossRef] [PubMed]
- Kamminga, M.E.; Stroppa, A.; Picozzi, S.; Chislov, M.; Zvereva, I.A.; Baas, J.; Meetsma, A.; Blake, G.R.; Palstra, T.T.M. Polar Nature of (CH3NH3)3Bi2I9 Perovskite-Like Hybrids. Inorg. Chem. 2017, 56, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Ptak, M.; Maczka, M.; Gagor, A.; Sieradzki, A.; Stroppa, A.; Di Sante, D.; Perez-Mato, J.M.; Macalik, L. Experimental and theoretical studies of structural phase transition in a novel polar perovskite-like [C2H5NH3][Na0.5Fe0.5(HCOO)3] formate. Dalton Trans. 2016, 45, 2574–2583. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Di Sante, D.; Stroppa, A. Strain Tuning of Ferroelectric Polarization in Hybrid Organic Inorganic Perovskite Compounds. J. Phys. Chem. Lett. 2015, 6, 4553–4559. [Google Scholar] [CrossRef] [PubMed]
- Mazzuca, L.; Cañadillas-Delgado, L.; Rodríguez-Velamazán, J.A.; Fabelo, O.; Scarrozza, M.; Stroppa, A.; Picozzi, S.; Zhao, J.P.; Bu, X.H.; Rodríguez-Carvajal, J. Magnetic Structures of Heterometallic M(II)–M(III) Formate Compounds. Inorg. Chem. 2017, 56, 197–207. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, H.; Chakraborty, S.; Saha-Dasgupta, T. Cationic Effect on Pressure Driven Spin-State Transition and Cooperativity in Hybrid Perovskites. Chem. Mater. 2016, 28, 8379–8384. [Google Scholar] [CrossRef]
- Cambi, L.; Szegö, L. Über die magnetische Susceptibilität der komplexen Verbindungen. Berichte der Deutschen Chemischen Gesellschaft (A B Ser.) 1931, 64, 2591–2598. [Google Scholar] [CrossRef]
- Stoufer, R.C.; Busch, D.H.; Hadley, W.B. Unusual Magnetic Properties of Some Six-Coördinate Cobalt(II) Complexes 1—Electronic Isomers. J. Am. Chem. Soc. 1961, 83, 3732–3734. [Google Scholar] [CrossRef]
- Madeja, K.; König, E. Zur frage der bindungsverhältnise in komplexverbindungen des eisen(II) mit 1,10-phenanthrolin. J. Inorg. Nucl. Chem. 1963, 25, 377–385. [Google Scholar] [CrossRef]
- Kojima, N.; Murakami, Y.; Komatsu, T.; Yokoyama, T. EXAFS study on the spin-crossover system, [Fe(4-NH2trz)3](R-SO3)2. Synth. Met. 1999, 103, 2154. [Google Scholar] [CrossRef]
- Okabayashi, J.; Ueno, S.; Wakisaka, Y.; Kitazawa, T. Temperature-dependent EXAFS study for spin crossover complex: Fe(pyridine)2Ni(CN)4. Inorg. Chim. Acta 2015, 426, 142–145. [Google Scholar] [CrossRef]
- Koenig, E.; Madeja, K. 5T2-1A1 Equilibriums in some iron(II)-bis(1,10-phenanthroline) complexes. Inorg. Chem. 1967, 6, 48–55. [Google Scholar] [CrossRef]
- Gütlich, Philipp, G.H.A. Spin Crossover in Transition Metal Compounds I; Springer: Berlin, Germany, 2004. [Google Scholar]
- Molnár, G.; Kitazawa, T.; Dubrovinsky, L.; McGarvey, J.J.; Bousseksou, A. Pressure tuning Raman spectroscopy of the spin crossover coordination polymer Fe(C5H5N)2[Ni(CN)4]. J. Phys. Condens. Matter 2004, 16, S1129. [Google Scholar] [CrossRef]
- Tuchagues, J.P.; Bousseksou, A.; Molnár, G.; McGarvey, J.J.; Varret, F. The Role of Molecular Vibrations in the Spin Crossover Phenomenon. In Spin Crossover in Transition Metal Compounds III; Springer: Berlin/Heidelberg, Germany, 2004; pp. 84–103. [Google Scholar]
- Hauser, A. Light-Induced Spin Crossover and the High-Spin→Low-Spin Relaxation. In Spin Crossover in Transition Metal Compounds II; Springer: Berlin/Heidelberg, Germany, 2004; pp. 155–198. [Google Scholar]
- Krivokapic, I.; Zerara, M.; Daku, M.L.; Vargas, A.; Enachescu, C.; Ambrus, C.; Tregenna-Piggott, P.; Amstutz, N.; Krausz, E.; Hauser, A. Spin-crossover in cobalt(II) imine complexes. Coord. Chem. Rev. 2007, 251, 364–378. [Google Scholar] [CrossRef]
- Gütlich, P.; Gaspar, A.B.; Garcia, Y. Spin state switching in iron coordination compounds. Beilstein J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed]
- Decurtins, S.; Gütlich, P.; Köhler, C.; Spiering, H.; Hauser, A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron(II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. [Google Scholar] [CrossRef]
- Hauser, A. Reversibility of light-induced excited spin state trapping in the Fe(ptz)6(BF4)2, and the Zn1−xFex(ptz)6(BF4)2 spin-crossover systems. Chem. Phys. Lett. 1986, 124, 543–548. [Google Scholar] [CrossRef]
- Létard, J.F.; Capes, L.; Chastanet, G.; Moliner, N.; Létard, S.; Real, J.A.; Kahn, O. Critical temperature of the LIESST effect in iron(II) spin crossover compounds. Chem. Phys. Lett. 1999, 313, 115–120. [Google Scholar] [CrossRef]
- Enachescu, C.; Machado, H.; Menendez, N.; Codjovi, E.; Linares, J.; Varret, F.; Stancu, A. Static and light induced hysteresis in spin-crossover compounds: Experimental data and application of Preisach-type models. Phys. B Condens. Matter 2001, 306, 155–160. [Google Scholar] [CrossRef]
- Baldé, C.; Bauer, W.; Kaps, E.; Neville, S.; Desplanches, C.; Chastanet, G.; Weber, B.; Létard, J.F. Light-Induced Excited Spin-State Properties in 1D Iron(II) Chain Compounds. Eur. J. Inorg. Chem. 2013, 2013, 2744–2750. [Google Scholar] [CrossRef]
- Weber, B.; Tandon, R.; Himsl, D. Synthesis, Magnetic Properties and X-ray Structure Analysis of a 1-D Chain Iron(II) Spin Crossover Complex with wide Hysteresis. Zeitschrift für Anorganische und Allgemeine Chemie 2007, 633, 1159–1162. [Google Scholar] [CrossRef]
- Bauer, W.; Scherer, W.; Altmannshofer, S.; Weber, B. Two-Step versus One-Step Spin Transitions in Iron(II) 1D Chain Compounds. Eur. J. Inorg. Chem. 2011, 2011, 2803–2818. [Google Scholar] [CrossRef]
- Weber, B.; Kaps, E.S.; Desplanches, C.; Létard, J.F. Quenching the Hysteresis in Single Crystals of a 1D Chain Iron(II) Spin Crossover Complex. Eur. J. Inorg. Chem. 2008, 2008, 2963–2966. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Miyashita, S.; Nishino, M. Elastic interaction among transition metals in one-dimensional spin-crossover solids. Phys. Rev. B 2007, 75, 094112. [Google Scholar] [CrossRef]
- Willenbacher, N.; Spiering, H. The elastic interaction of high-spin and low-spin complex molecules in spin-crossover compounds. J. Phys. C Solid State Phys. 1988, 21, 1423–1439. [Google Scholar] [CrossRef]
- Spiering, H.; Willenbacher, N. Elastic interaction of high-spin and low-spin complex molecules in spin-crossover compounds. II. J. Phys. Condens. Matter 1989, 1, 10089–10105. [Google Scholar] [CrossRef]
- Spiering, H.; Boukheddaden, K.; Linares, J.; Varret, F. Total free energy of a spin-crossover molecular system. Phys. Rev. B 2004, 70, 184106. [Google Scholar] [CrossRef]
- Banerjee, H.; Kumar, M.; Saha-Dasgupta, T. Cooperativity in spin-crossover transition in metalorganic complexes: Interplay of magnetic and elastic interactions. Phys. Rev. B 2014, 90, 174433. [Google Scholar] [CrossRef]
- Timm, C. Collective effects in spin-crossover chains with exchange interaction. Phys. Rev. B 2006, 73, 014423. [Google Scholar] [CrossRef]
- D’Avino, G.; Painelli, A.; Boukheddaden, K. Vibronic model for spin crossover complexes. Phys. Rev. B 2011, 84, 104119. [Google Scholar] [CrossRef]
- Miralles, J.; Castell, O.; Caballol, R.; Malrieu, J.P. Specific CI calculation of energy differences: Transition energies and bond energies. Chem. Phys. 1993, 172, 33–43. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Siegbahn, P.E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Fouqueau, A.; Mer, S.; Casida, M.E.; Daku, L.M.L.; Hauser, A.; Mineva, T.; Neese, F. Comparison of density functionals for energy and structural differences between the high-[5T2g:(t2g)4(eg)2] and low-[1A1g:(t2g)6(eg)0] spin states of the hexaquoferrous cation [Fe(H2O)6]2+. J. Chem. Phys. 2004, 120, 9473–9486. [Google Scholar] [CrossRef] [PubMed]
- Ordejón, B.; de Graaf, C.; Sousa, C. Light-Induced Excited-State Spin Trapping in Tetrazole-Based Spin Crossover Systems. J. Am. Chem. Soc. 2008, 130, 13961–13968. [Google Scholar] [CrossRef] [PubMed]
- Pierloot, K.; Vancoillie, S. Relative energy of the high-(T2g5) and low-(A1g1) spin states of [Fe(H2O)6]2+, [Fe(NH3)6]2+, and [Fe(bpy)3]2+: CASPT2 versus density functional theory. J. Chem. Phys. 2006, 125, 124303. [Google Scholar] [CrossRef] [PubMed]
- Watts, J.D.; Gauss, J.; Bartlett, R.J. Coupled cluster methods with noniterative triple excitations for restricted open shell Hartree Fock and other general single determinant reference functions. Energies and analytical gradients. J. Chem. Phys. 1993, 98, 8718–8733. [Google Scholar] [CrossRef]
- Maldonado, P.; Kanungo, S.; Saha-Dasgupta, T.; Oppeneer, P.M. Two-step spin-switchable tetranuclear Fe(II) molecular solid: Ab initio theory and predictions. Phys. Rev. B 2013, 88, 020408. [Google Scholar] [CrossRef]
- Sarkar, S.; Tarafder, K.; Oppeneer, P.M.; Saha-Dasgupta, T. Spin-crossover in cyanide-based bimetallic coordination polymers-insight from first-principles calculations. J. Mater. Chem. 2011, 21, 13832–13840. [Google Scholar] [CrossRef]
- Jeschke, H.O.; Salguero, L.A.; Rahaman, B.; Buchsbaum, C.; Pashchenko, V.; Schmidt, M.U.; Saha-Dasgupta, T.; Valentí, R. Microscopic modeling of a spin crossover transition. New J. Phys. 2007, 9, 448. [Google Scholar] [CrossRef]
- Tarafder, K.; Kanungo, S.; Oppeneer, P.M.; Saha-Dasgupta, T. Pressure and Temperature Control of Spin-Switchable Metal–Organic Coordination Polymers from Ab Initio Calculations. Phys. Rev. Lett. 2012, 109, 077203. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Alvarez, S. Distortion Pathways of Transition Metal Coordination Polyhedra Induced by Chelating Topology. Chem. Rev. 2015, 115, 13447–13483. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Buhks, E.; Navon, G.; Bixon, M.; Jortner, J. Spin conversion processes in solutions. J. Am. Chem. Soc. 1980, 102, 2918–2923. [Google Scholar] [CrossRef]
- Hauser, A.; Guetlich, P.; Spiering, H. High-spin .fwdarw. low-spin relaxation kinetics and cooperative effects in the hexakis(1-propyltetrazole)iron bis(tetrafluoroborate) and [Zn1−xFex(ptz)6](BF4)2(ptz = 1-propyltetrazole) spin-crossover systems. Inorg. Chem. 1986, 25, 4245–4248. [Google Scholar] [CrossRef]
- Létard, J.F.; Guionneau, P.; Rabardel, L.; Howard, J.A.K.; Goeta, A.E.; Chasseau, D.; Kahn, O. Structural, Magnetic, and Photomagnetic Studies of a Mononuclear Iron(II) Derivative Exhibiting an Exceptionally Abrupt Spin Transition. Light-Induced Thermal Hysteresis Phenomenon. Inorg. Chem. 1998, 37, 4432–4441. [Google Scholar] [CrossRef] [PubMed]
- Morgan, G.G.; Murnaghan, K.D.; Müller-Bunz, H.; McKee, V.; Harding, C.J. A Manganese(III) Complex that Exhibits Spin Crossover Triggered by Geometric Tuning. Angew. Chem. 2006, 118, 7350–7353. [Google Scholar] [CrossRef]
- Martinho, P.N.; Gildea, B.; Harris, M.M.; Lemma, T.; Naik, A.D.; Müller-Bunz, H.; Keyes, T.E.; Garcia, Y.; Morgan, G.G. Cooperative Spin Transition in a Mononuclear Manganese(III) Complex. Angew. Chem. 2012, 124, 12765–12769. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, H.; Chakraborty, S.; Saha-Dasgupta, T. Design and Control of Cooperativity in Spin-Crossover in Metal–Organic Complexes: A Theoretical Overview. Inorganics 2017, 5, 47. https://doi.org/10.3390/inorganics5030047
Banerjee H, Chakraborty S, Saha-Dasgupta T. Design and Control of Cooperativity in Spin-Crossover in Metal–Organic Complexes: A Theoretical Overview. Inorganics. 2017; 5(3):47. https://doi.org/10.3390/inorganics5030047
Chicago/Turabian StyleBanerjee, Hrishit, Sudip Chakraborty, and Tanusri Saha-Dasgupta. 2017. "Design and Control of Cooperativity in Spin-Crossover in Metal–Organic Complexes: A Theoretical Overview" Inorganics 5, no. 3: 47. https://doi.org/10.3390/inorganics5030047




