Self-Homodyne Detection in Optical Communication Systems
Abstract
:1. Introduction
2. Overview of Self-Homodyne Detection
2.1. Concept and Early Work
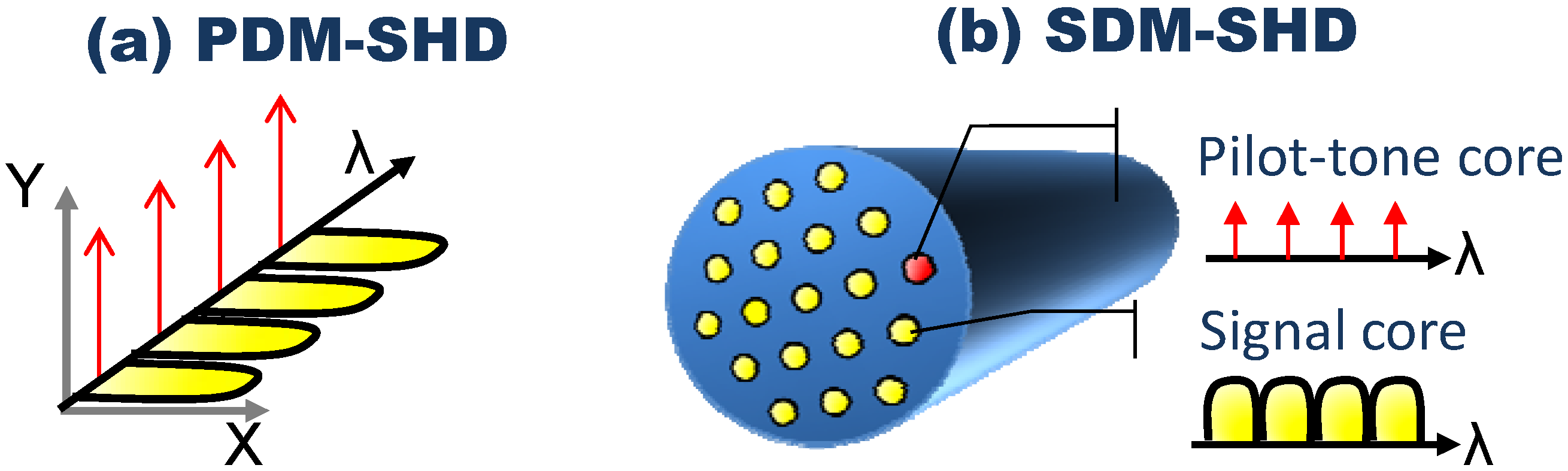
2.2. Penalty Compared to Intradyne Detection
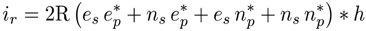
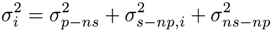
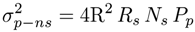
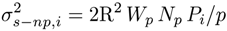
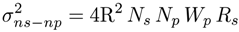
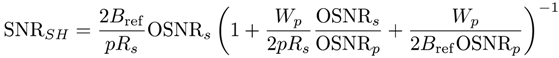
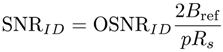
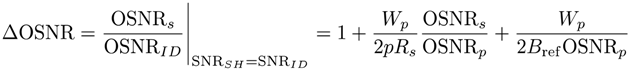
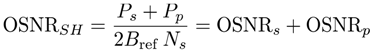
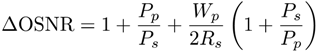
2.3. DSP Savings and Phase Noise Cancellation
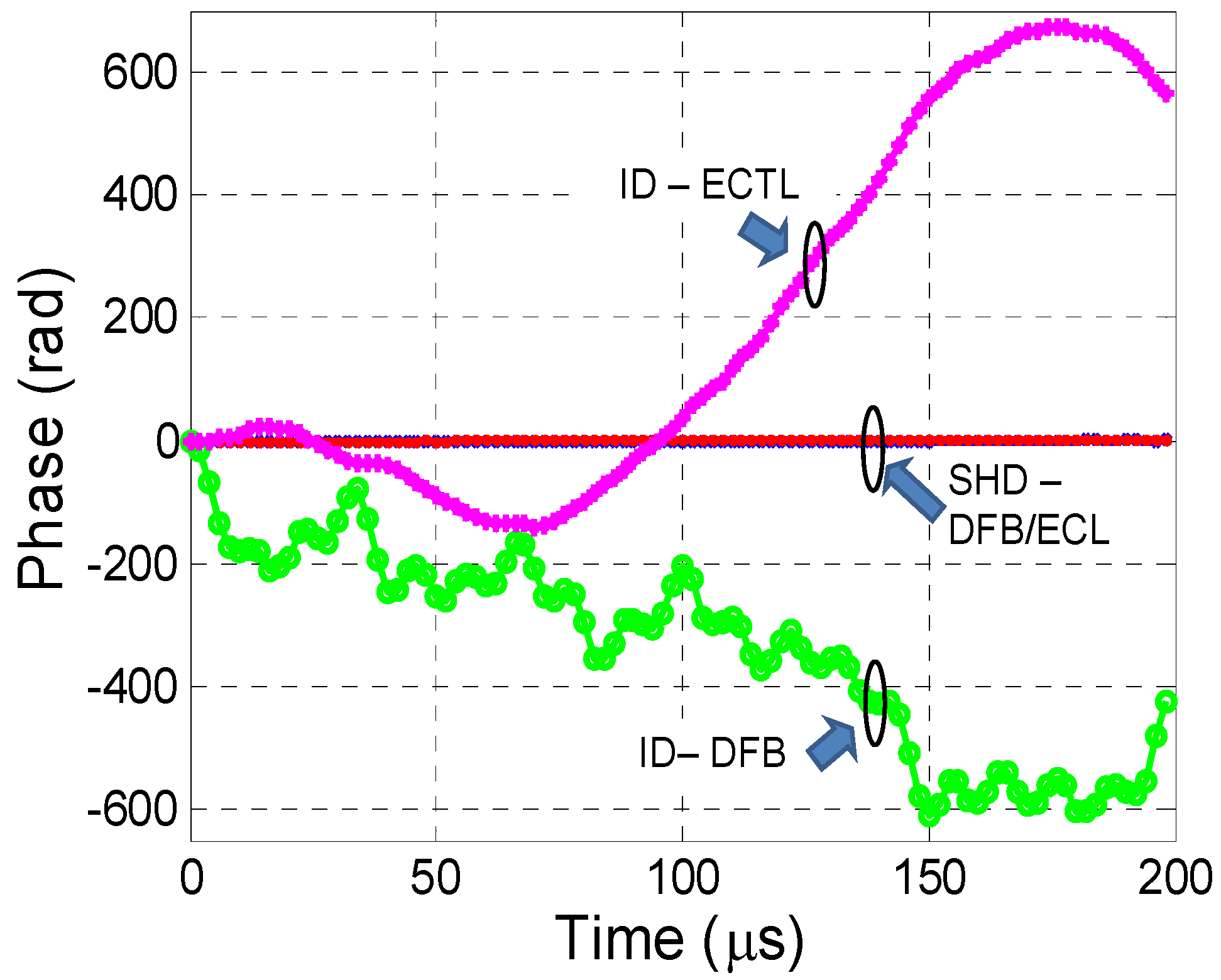

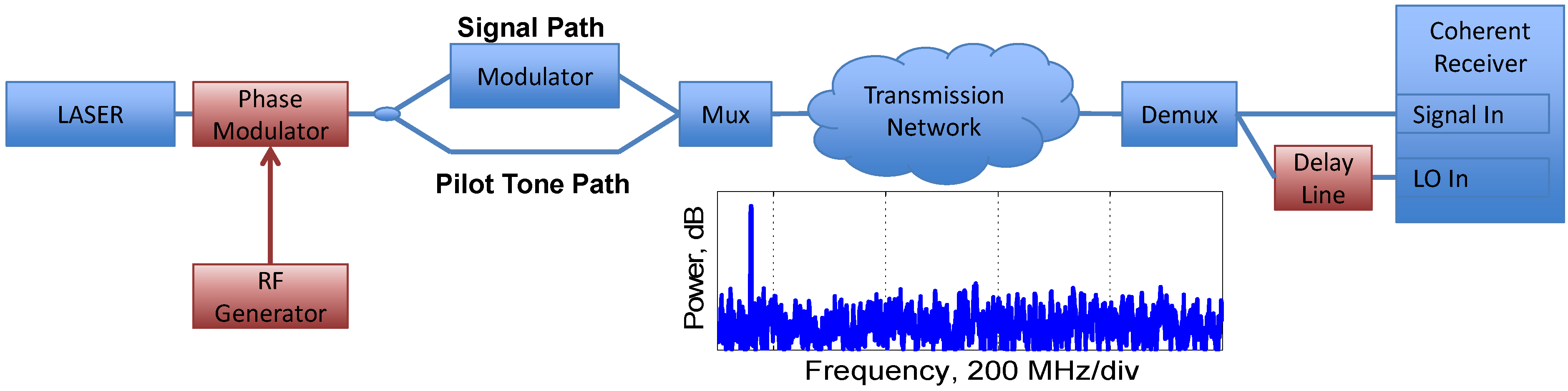
2.4. Requirement for Receiver Polarization Control of Pilot-Tone
2.5. Other Pilot-Tone Transmission Schemes
3. PDM-SHD: Implementations and Developments
3.1. PDM-SHD Transmission and Advanced Modulation Formats
3.2. Developments of PDM-SHD
3.2.1. Spectral Interleaving of Signal/PT
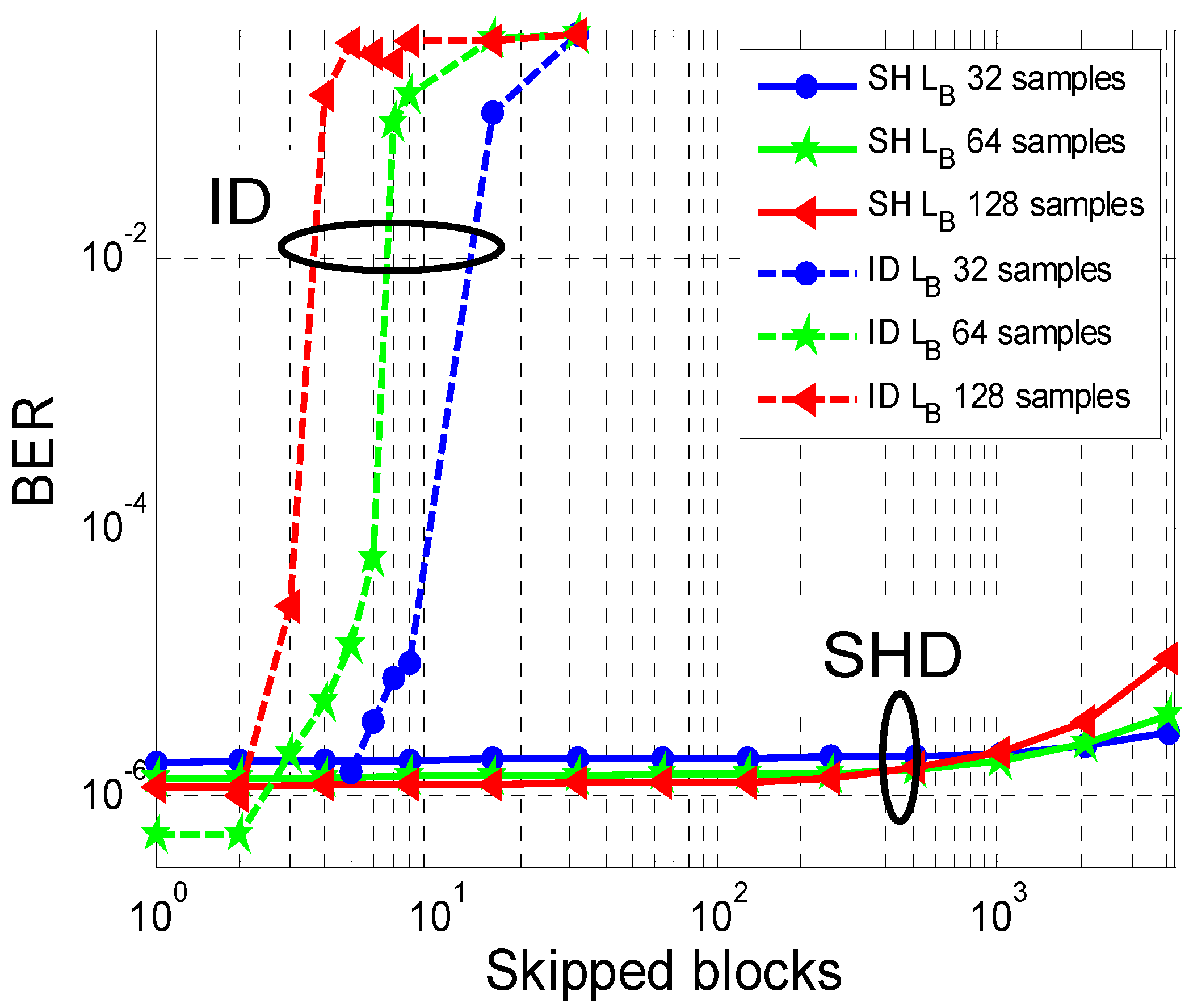
3.2.2. Digital Self-Homodyne Detection
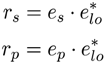
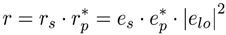
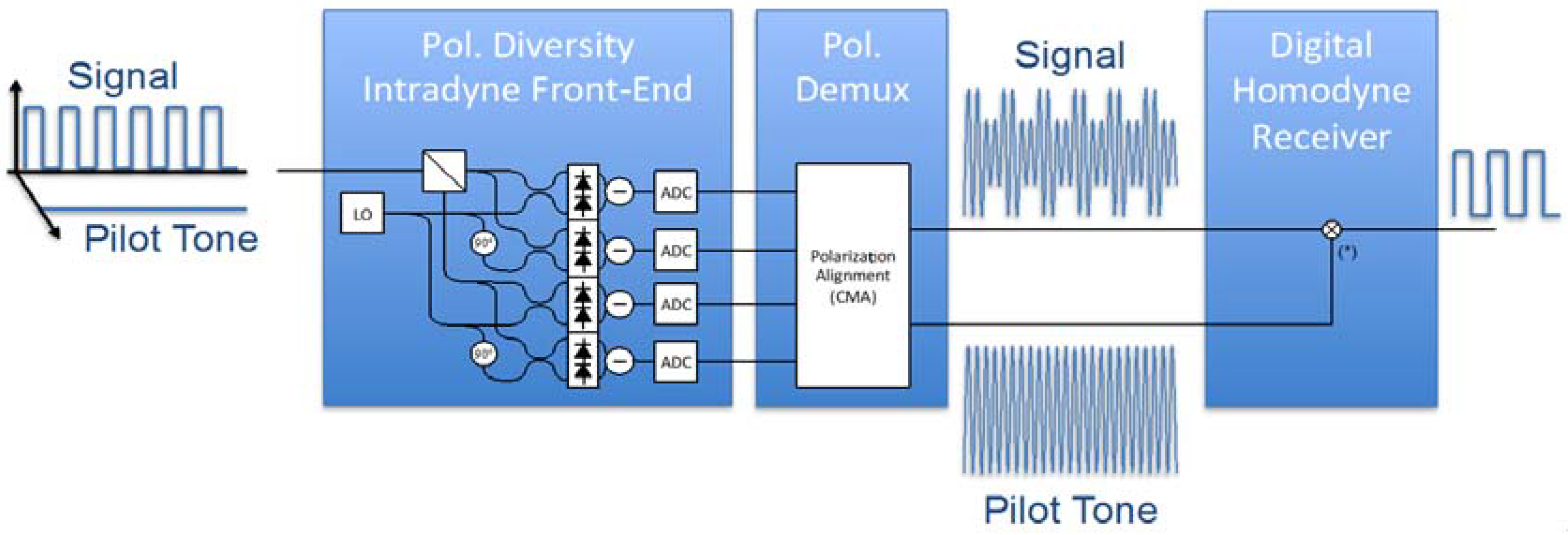
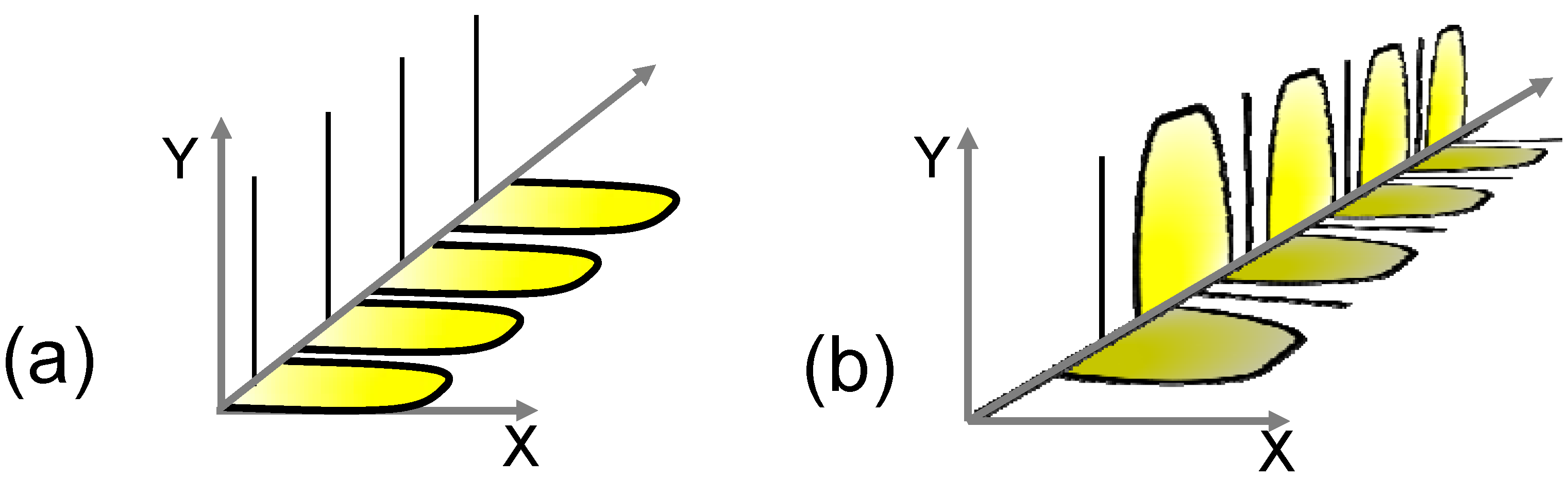
4. SDM- SHD: Implementations and Developments
4.1. Transmission
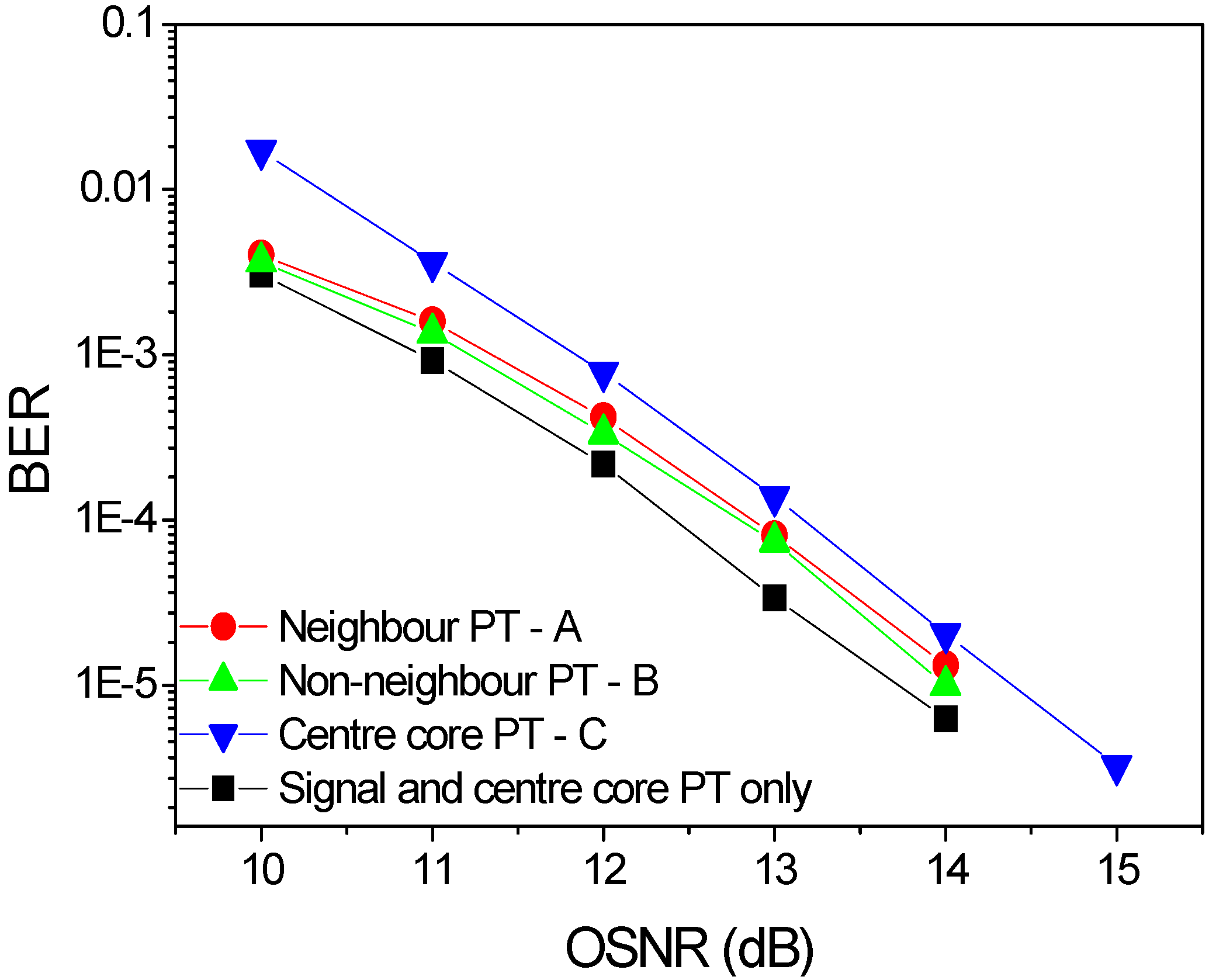

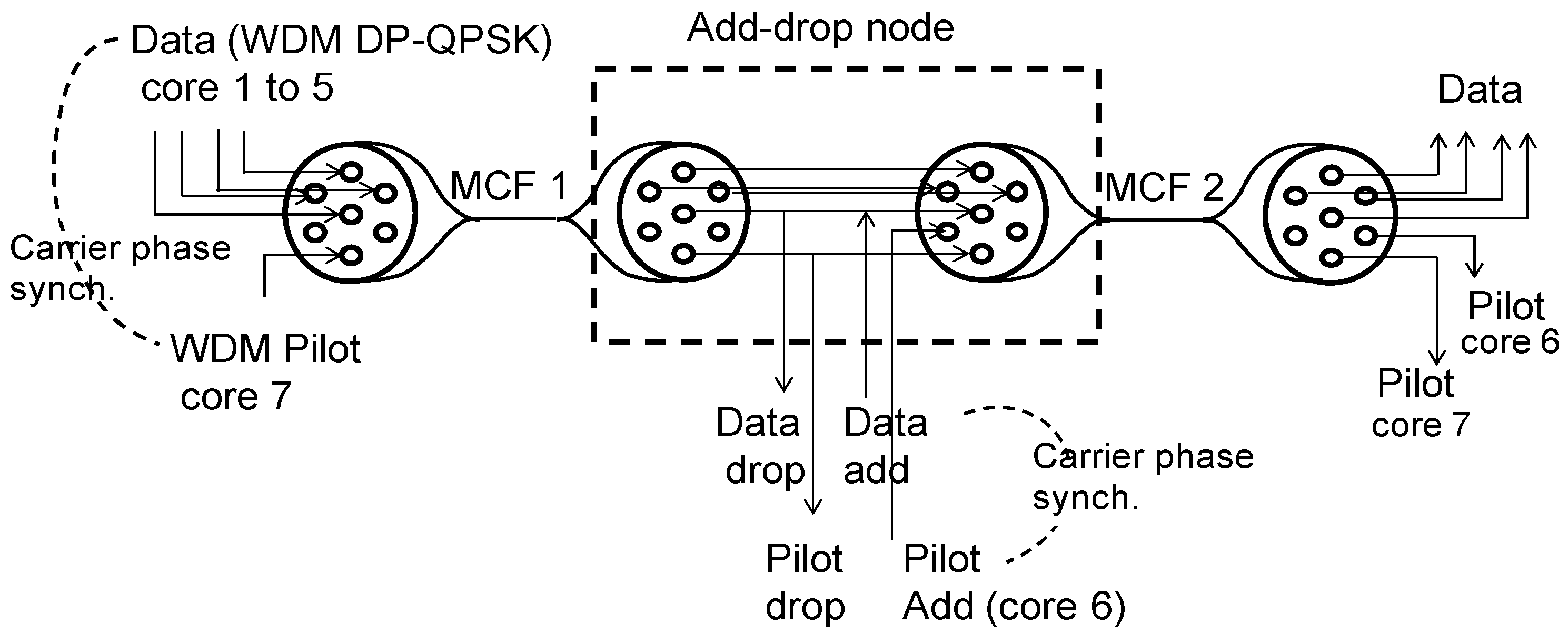
4.2. Moves towards Networking
4.3. Path Length Alignment Scheme
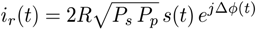
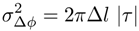
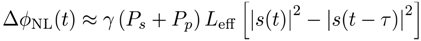
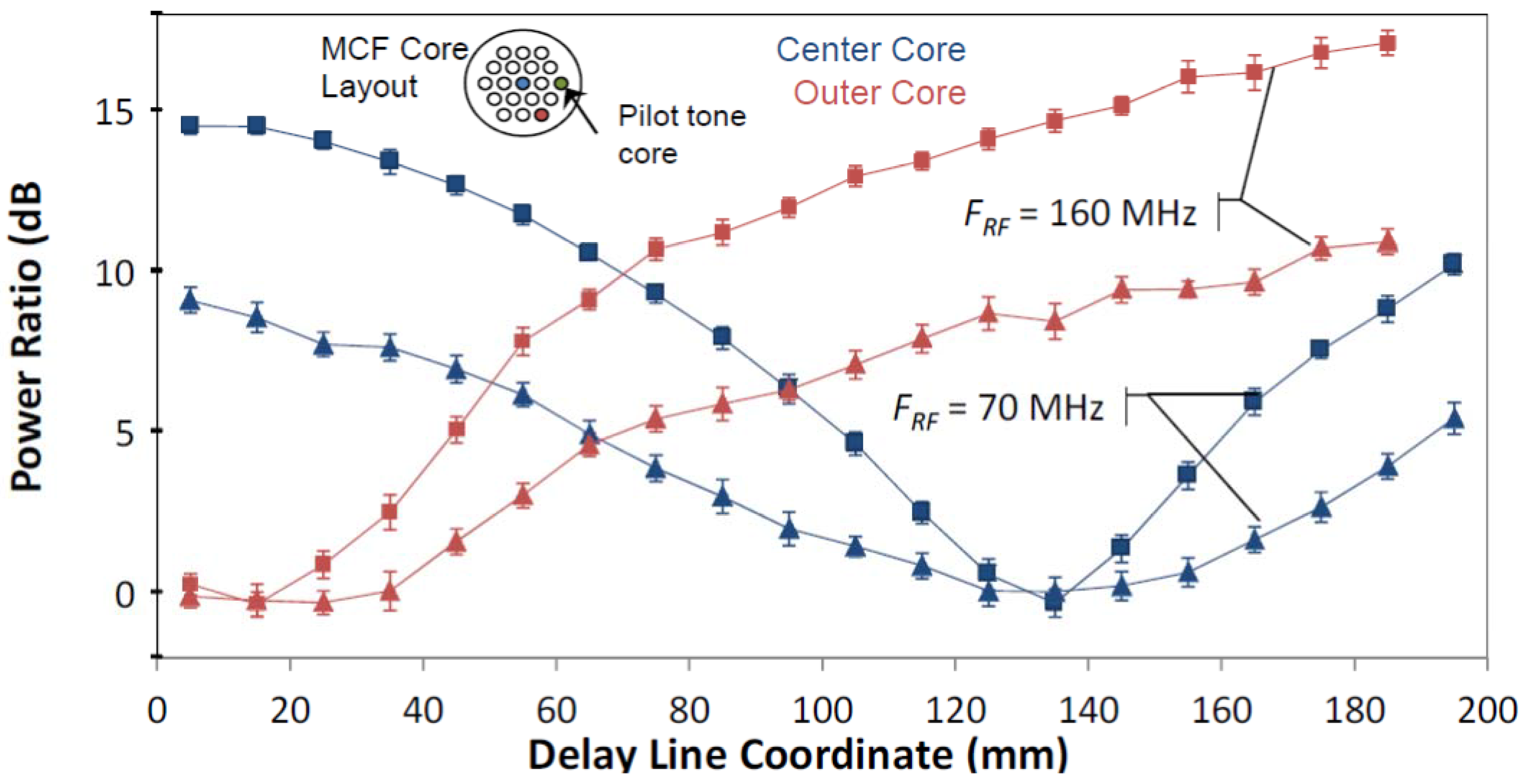
5. Summary and Future Challenges
Acknowledgments
Authors Contributions
Conflicts of Interest
References
- Miyazaki, T.; Kubota, F. PSK self-homodyne detection using a pilot carrier for multibit/symbol transmission with inverse-RZ signal. IEEE Photonics Technol. Lett. 2005, 17, 1334–1336. [Google Scholar] [CrossRef]
- Miyazaki, T. Linewidth-Tolerant QPSK Homodyne Transmission Using a Polarization-Multiplexed Pilot Carrier. IEEE Photonics Technol. Lett. 2006, 18, 388–390. [Google Scholar] [CrossRef]
- Johannisson, P.; Sjödin, M.; Karlsson, M.; Tipsuwannakul, E.; Andrekson, P. Cancellation of nonlinear phase distortion in self-homodyne coherent systems. IEEE Photonics Technol. Lett. 2010, 22, 802–824. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Delgado-Mendinueta, J.M.; Sakaguchi, J.; Luis, R.S.; Klaus, W.; Awaji, Y; Wada, N.; Kanno, A.; Kawanishi, T. 105 Tb/s Transmission System Using Low-cost, MHz Linewidth DFB Lasers Enabled by Self-Homodyne Coherent Detection and a 19-Core Fiber. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013.
- Nakamura, M.; Kamio, Y.; Lu, G.-W.; Miyazaki, T. Ultimately phase-noise tolerant QPSK homodyne using a spectrum-sliced ASE light source. IEICE Electron. Express 2007, 4, 406–410. [Google Scholar] [CrossRef]
- Nakamura, M.; Kamio, Y.; Lu, G.-W.; Miyazaki, T. Ultimate Linewidth-Tolerant 20-Gbps QPSK-Homodyne Transmission Using a Spectrum-Sliced ASE Light Source. In Proceedings of the Optical Fiber Communication and the National Fiber Optic Engineers Conference, OFC/NFOEC 2007, Anaheim, CA, USA, 25–29 March 2007.
- Nakamura, M.; Kamio, Y.; Miyazaki, T. QPSK-Homodyne Transmission using a Multi-Wavelength Fabry-Perot Laser Diode. In Proceedings of the Lasers and Electro-Optics Conference, Baltimore, MD, USA, 6–11 May 2007.
- Nakamura, M.; Kamio, Y. Linewidth-tolerant, ISI-suppressed 15-Gbit/s 64-QAM transmission over 120-km SSMF. In Proceedings of the 34th European Conference on Optical Communication, ECOC 2008, Brussels, Belgium, 21–25 September 2008.
- Nakamura, M.; Kamio, Y. 30-Gbps (5-Gsymbol/s) 64-QAM Self-Homodyne Transmission over 60-km SSMF Using Phase-Noise Cancelling Technique and ISI-Suppression Based on Electronic Digital Processing. In Proceedings of the Optical Fiber Communication 2009, San Diego, CA, USA, 22–26 March 2009.
- Kamio, Y.; Nakamura, M.; Miyazaki, T. 80-Gb/s 256-QAM signals using phase noise and DGD-tolerant pilot-carrier-aided homodyne detection. In Proceedings of the 33rd European Conference and Ehxibition of Optical Communication (ECOC), Berlin, Germany, 16–20 September 2007.
- Luis, R.S.; Puttnam, B.J.; Mendinueta, J.-M.D.; Sakaguchi, J.; Shinada, S.; Kamio, Y.; Wada, N.; Nakamura, M. Self-homodyne coherent OFDM packet transmission without carrier frequency or common phase error estimation. In Proceedings of the IEEE 4th International Conference on Photonics, Malaka, Malaysia, 28–30 October 2013; pp. 123–125.
- Delgado Mendinueta, J.M.; Puttnam, B.J.; Sakaguchi, J.; Luis, R.S.; Klaus, W.; Awaji, Y.; Kanno, A.; Kawanishi, T. Investigation of Receiver DSP Carrier Phase Estimation Rate for Self-Homodyne Space-Division Multiplexing Communication Systems. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013.
- Delgado Mendinueta, J.M.; Puttnam, B.J.; Sakaguchi, J.; Luis, R.S.; Klaus, W.; Awaji, Y.; Kanno, A.; Kawanishi, T. Energy Efficient Carrier Phase Recovery for Self-Homodyne Polarization-Multiplexed QPSK. In Proceedings of the 18th OptoElectronics and Communications Conference, Kyoto, Japan, 30 June–4 July 2013.
- Sjödin, M.; Agrell, E.; Lu, G.-W.; Johannisson, P.; Karlsson, M.; Andrekson, P. Interleaved polarization division multiplexing in self-homodyne coherent WDM systems. In Proceedings of the 36th European Conference and Exhibition on Optical Communication (ECOC), Torino, Italy, 19–23 September 2010.
- Sjödin, M.; Agrell, E.; Johannisson, P.; Lu, G.-W.; Andrekson, P.A.; Karlsson, M. Filter optimization for self-homodyne coherent WDM systems using interleaved polarization division. IEEE J. Light. Technol. 2011, 29, 1219–1226. [Google Scholar] [CrossRef]
- Zhu, B.; Taunay, T.F.; Fishteyn, M.; Liu, X.; Chandrasekhar, S.; Yan, M.F.; Fini, J.M.; Monberg, E.M.; Dimarcello, F.V. 112-Tb/SDM DWDM transmission with 14-b/s/Hz aggregate spectral efficiency over a 76.8-km seven-core fiber. Opt. Express 2011, 19, 16665–16671. [Google Scholar] [CrossRef]
- Klaus, W.; Sakaguchi, J.; Puttnam, B.J.; Awaji, Y.; Wada, N.; Kobayashi, T.; Watanabe, M. Free-space coupling optics for multi-core fibers. In Proceedings of the IEEE Photonics Society Summer Topical Meeting Series, Seattle, WA, USA, 9–11 July 2012.
- Sakaguchi, J.; Puttnam, B.J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Imamura, K.; Inaba, H.; Mukasa, K.; et al. 19-core fiber transmission of 19 × 100 × 172-Gb/s SDM-WDM-PDM-QPSK signals at 305 Tb/s. In Proceedings of the National Fiber Optic Engineers Conference on Optical Fiber Communication Conference and Exposition (OFC/NFOEC), Los Angeles, CA, USA, 4–8 March 2012.
- Feuer, M.D.; Nelson, L.E.; Zhou, X.; Woodward, S.L.; Isaac, R.; Zhu, B.; Taunay, T.F.; Fishteyn, M.; Fini, J.M.; Yan, M.F. Joint Digital Signal Processing Receivers for Spatial Superchannels. IEEE Photonics Technol. Lett. 2012, 24, 1957–1960. [Google Scholar] [CrossRef]
- Camatel, S.; Ferrero, V. Homodyne coherent detection of ASK and PSK signals performed by a subcarrier optical phase-locked loop. IEEE Photonics Technol. Lett. 2006, 18, 142–144. [Google Scholar] [CrossRef]
- Sjödin, M.; Johannisson, P.; Karlsson, M.; Tong, Z.; Andrekson, P.A. OSNR requirements for self-homodyne coherent systems. IEEE Photonics Technol. Lett. 2010, 22, 91–93. [Google Scholar] [CrossRef]
- Luis, R.; Puttnam, B.; Mendinueta, J.; Klaus, W.; Sakaguchi, J.; Awaji, Y.; Kawanishi, T.; Kanno, A.; Wada, N. OSNR Penalty of Self-Homodyne Coherent Detection in Spatial-Division-Multiplexing Systems. IEEE Photonics Technol. Lett. 2014, 26, 477–479. [Google Scholar] [CrossRef]
- Essiambre, R.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. IEEE J. Light. Technol. 2010, 28, 662–701. [Google Scholar]
- Rebola, J.; Cartaxo, A. Q-factor estimation and impact of 248 spontaneous-spontaneous beat noise on the performance of optically 249 preamplified systems with arbitrary optical filtering. IEEE J. Light. Technol. 2003, 21, 87–95. [Google Scholar] [CrossRef]
- Luis, R.S.; Puttnam, B.J.; Mendinueta, J.-M.D.; Sakaguchi, J.; Shinada, S.; Nakamura, M.; Kamio, Y.; Wada, N. Self-homodyne detection of polarization-multiplexed pilot tone signals using a polarization diversity coherent receiver. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013.
- Le Taillandier de Gabory, E.; Arikawa, M.; Hashimoto, Y.; Ito, T.; Fukuchi, K. A shared carrier reception and processing scheme for compensating frequency offset and phase noise of space-division multiplexed signals over multicore fibers. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013.
- Kuschnerov, M.; Bex, T.; Kainzmaier, P. Energy Efficient Digital Signal Processing. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), San Francisco, CA, USA, 9–13 March 2013.
- Savory, S.J. Digital Coherent Optical Receivers: Algorithms and Subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Sakaguchi, J.; Delgado-Mendinueta, J.M.; Klaus, W.; Awaji, Y; Wada, N.; Kanno, A.; Kawanishi, T. Investigating self-homodyne coherent detection in a 19 channel space-division-multiplexed transmission link. Opt. Express 2013, 21, 1561–1566. [Google Scholar] [CrossRef]
- Luis, R.S.; Puttnam, B.J.; Mendinueta, J.M.D.; Sakaguchi, J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T. In-service method of path length alignment in SDM systems with self-homodyne detection. In Proceedings of the 18th OptoElectronics and Communications Conference, Kyoto, Japan, 30 June–4 July 2013.
- Meyr, H.; Moeneclaey, M.; Fechtel, S.A. Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing; John Wiley & Sons, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Noé, R.; Heidrich, H.; Hoffmann, D. Endless polarization control systems for coherent optics. IEEE J. Light. Technol. 1988, 6, 1199–1207. [Google Scholar] [CrossRef]
- Hidayat, A.; Koch, B.; Mirvoda, V.; Zhang, H.; Bhandare, S.; Ibrahim, S.K.; Sandel, D.; Noe, R. Fast Optical Endless Polarization Tracking with LiNbO3 Component. In Proceedings of the Optical Fiber communication/National Fiber Optic Engineers Conference, San Diego, CA, USA, 24–28 February 2008.
- Koch, B.; Noé, R.; Mirvoda, V.; Sandel, D. 20 krad/s Endless Optical Polarisation and Phase Control. Electron. Lett. 2013, 49, 483–485. [Google Scholar] [CrossRef]
- Pfau, T.; Peveling, R.; Hoffinann, S.; Bhandare, S.; Ibrahim, S.; Sandel, D.; Adamczyk, O.; Porrmann, M.; Noe, R.; Achiam, Y.; et al. PDL-Tolerant Real-time Polarization-Multiplexed QPSK Transmission with Digital Coherent Polarization Diversity Receiver. In Proceedings of the Digest of the IEEE/LEOS Summer Topical Meetings, Portland, OR, USA, 23–25 July 2007.
- Koch, B.; Noé, R.; Mirvoda, V.; Griesser, H.; Bayer, S.; Wernz, H. Record 59-krad/s Polarization Tracking in 112-Gb/s640-km PDM-RZ-DQPSK Transmission. IEEE Photonics Technol. Lett. 2010, 22, 1407–1409. [Google Scholar] [CrossRef]
- Koch, B.; Noé, R.; Mirvoda, V.; Sandel, D.; Jan, O.; Puntsri, K. 20-Gb/s PDM-RZ-DPSK Transmission with 40 krad/s Endless Optical Polarization Tracking. IEEE Photonics Technol. Lett. 2013, 25, 798–801. [Google Scholar]
- Kamio, Y.; Miyazaki, T. Pilot-Symbol-Aided Self-Homodyne Detection for High-Efficiency Optical-Fiber Transmission System. In Proceedings of the Pacific Rim Conference on Lasers and Electro-Optics, CLEO/Pacific Rim 2005, Tokyo, Japan, 30 July–2 August 2005.
- Lu, G.-W.; Nakamura, M.; Kamio, Y.; Miyazaki, T. 40-Gb/s QPSK with Inserted Pilot Symbols Using Self-Homodyne Detection. In Proceedings of the Optical Fiber Communication and the National Fiber Optic Engineers Conference, OFC/NFOEC 2007, Anaheim, CA, USA, 25–29 March 2007.
- Lu, G.-W.; Nakamura, M.; Kamio, Y.; Miyazaki, T. 40-Gb/s QPSK and 20-Gb/s PSK with inserted pilot symbols using self-homodyne detection. Opt. Express 2007, 15, 7660–7666. [Google Scholar] [CrossRef]
- Kikuchi, K. Phase-diversity homodyne detection of multilevel optical modulation with digital carrier phase estimation. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 563–570. [Google Scholar] [CrossRef]
- Nakazawa, M.; Yoshida, M.; Kasai, K.; Hongou, J. 20 msymbol/s, 64 and 128 QAM coherent optical transmission over 525 km using heterodyne detection with frequency-stabilised laser. Electron. Lett. 2006, 42, 710–712. [Google Scholar] [CrossRef]
- Nakazawa, M.; Hirooka, T.; Yoshida, M.; Kasai, K. Ultrafast Coherent Optical Transmission. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 363–376. [Google Scholar] [CrossRef]
- Okamoto, S.; Toyoda, K.; Omiya, T.; Kasai, K.; Yoshida, M.; Nakazawa, M. 512 QAM (54 Gbit/s) coherent optical transmission over 150 km with an optical bandwidth of 4.1 GHz. In Proceedings of the 36th European Conference and Exhibition on Optical Communication, Torino, Italy, 19–23 September 2010.
- Omiya, T.; Yoshida, M.; Nakazawa, M. 1 Tbit/s 256 QAM-OFDM transmission over 560 km with 14.3 bit/s/Hz spectral efficiency. In Proceedings of the 18th OptoElectronics and Communications Conference held jointly with 2013 International Conference on Photonics in Switching (OECC/PS), Kyoto, Japan, 30 June–4 July 2013.
- Nakamura, M.; Kamio, Y.; Miyazaki, T. PMD- and Dispersion-Tolerance of QPSK Homodyne Detection using a Polarization-Multiplexed Pilot Carrier. In Proceedings of the European Conference on Optical Communications, ECOC 2006, Cannes, France, 24–28 September 2006.
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Real-time 40-Gbit/s 16-QAM self-homodyne using a polarization-multiplexed pilot-carrier. In Proceedings of the Digest of the IEEE/LEOS Summer Topical Meetings, Acapulco, Mexico, 21–23 July 2008.
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Linewidth-tolerant real-time 40-Gbit/s 16-QAM self-homodyne detection using a pilot carrier and ISI suppression based on electronic digital processing. Opt. Lett. 2010, 35, 13–15. [Google Scholar] [CrossRef]
- Kamio, Y.; Nakamura, M.; Miyazaki, T. Pilot-Carrier Based Linewidth-Tolerant 8PSK Self-homodyne using Only One Modulator. In Proceedings of the 33rd European Conference and Ehxibition of Optical Communication (ECOC), Berlin, Germany, 16–20 September 2007.
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Linewidth-tolerant 30 Gbit/s 8-PSK self-homodyne using single modulator and phase-noise cancelling technique. Electron. Lett. 2009, 45, 368–369. [Google Scholar] [CrossRef]
- Qu, Z.; Fu, S.; Zhang, M; Tang, M; Shum, P.; Liu, D. Analytical Investigation on Self-Homodyne Coherent System Based on Few-Mode Fiber. IEEE Photonics Technol. Lett. 2014, 26, 74–77. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Sakaguchi, J.; Delgado-Mendinueta, J.M.; Klaus, W.; Awaji, Y; Wada, N.; Kanno, A.; Kawanishi, T. Investigating self-homodyne coherent detection in a 19-core spatial-division-multiplexed transmission link. In Proceedings of the 38th European Conference and Exhibition on Optical Communications (ECOC), Amsterdam, The Netherlands, 16–20 September 2012.
- ITU. Recommendation G.975 forward Error Correction for Submarine Systems. In Proceedings of the World Telecommunications Standardization Assembly, Montreal, QC, Canada, 27 September–6 October 2000.
- Puttnam, B.J.; Delgado-Mendinueta, J.M.; Sakaguchi, J.; Luis, R.S.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T. 210Tb/s Self-Homodyne PDM-WDM-SDM Transmission with DFB lasers in a 19-Core Fiber. In Proceedings of the IEEE Photonics Society Summer Topical Meeting Series, Waikoloa, HI, USA, 8–10 July 2013.
- Maher, R.; Thomsen, B. Dynamic linewidth measurement technique using digital intradyne coherent receivers. Opt. Express 2011, 19, B313–B322. [Google Scholar] [CrossRef]
- Le Taillandier de Gabory, E.; Arikawa, M.; Ito, T.; Fukuchi, K. DWDM transmission of 128 Gb/s PM-16QAM signal over 1815km of 7-core MCF using shared carrier reception for improving the received signal quality. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013.
- Amaya, N.; Irfan, M.; Zervas, G.; Nejabati, R.; Simeonidou, D.; Sakaguchi, J.; Klaus, W.; Puttnam, B.J.; Miyazawa, T.; Awaji, Y.; et al. First Fully-Elastic Multi-Granular Network with Space/Frequency/Time Switching Using Multi-Core Fibres and Programmable Optical Nodes. In Proceedings of the European Conference and Exhibition on Optical Communication, London, UK, 16–20 September 2012.
- Amaya, N.; Irfan, M.; Zervas, G.; Nejabati, R.; Simeonidou, D.; Sakaguchi, J.; Klaus, W.; Puttnam, B.J.; Miyazawa, T.; Awaji, Y.; et al. Fully-elastic multi-granular network with space/frequency/time switching using multi-core fibres and programmable optical nodes. Opt. Express 2013, 21, 8658–8872. [Google Scholar]
- Feuer, M.D.; Nelson, L.E.; Abedin, K.; Zhou, X.; Taunay, T.F.; Fini, J.F.; Zhu, B.; Isaac, R.; Harel, R.; Cohen, G.; et al. ROADM System for Space Division Multiplexing with Spatial Superchannels. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013.
- Sakaguchi, J; Klaus, W.; Puttnam, B.J.; Miyazawa, T.; Awaji, Y; Delgado-Mendinueta, J.M.; Luis, R.S.; Wada, N. SDM-WDM hybrid reconfigurable add-drop nodes for self-homodyne photonic networks. In Proceedings of the IEEE Photonics Society Summer Topical Meeting Series, Waikoloa, HI, USA, 8–10 July 2013.
- Amaya, N.; Yan, S.; Channegowda, M.; Rofoee, B.R.; Shu, Y.; Rashidi, M.; Ou, Y.; Zervas, G.; Nejabati, R.; Simeonidou, D.; et al. First Demonstration of Software Defined Networking (SDN) over Space Division Multiplexing (SDM) Optical Networks. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013.
- Amaya, N.; Yan, S.; Channegowda, M.; Rofoee, B.R.; Shu, Y.; Rashidi, M.; Ou, Y.; Zervas, G.; Nejabati, R.; Simeonidou, D.; et al. Software defined networking (SDN) over space division multiplexing (SDM) optical networks: Features, benefits and experimental demonstration. Opt. Express 2014, 22, 3638–3647. [Google Scholar] [CrossRef]
- Zan, Z.; Lowery, A.J. Experimental demonstration of a flexible and stable semiconductor laser linewidth emulator. Opt. Express 2014, 18, 13880–13885. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Puttnam, B.J.; Luís, R.S.; Delgado Mendinueta, J.M.; Sakaguchi, J.; Klaus, W.; Kamio, Y.; Nakamura, M.; Wada, N.; Awaji, Y.; Kanno, A.; et al. Self-Homodyne Detection in Optical Communication Systems. Photonics 2014, 1, 110-130. https://doi.org/10.3390/photonics1020110
Puttnam BJ, Luís RS, Delgado Mendinueta JM, Sakaguchi J, Klaus W, Kamio Y, Nakamura M, Wada N, Awaji Y, Kanno A, et al. Self-Homodyne Detection in Optical Communication Systems. Photonics. 2014; 1(2):110-130. https://doi.org/10.3390/photonics1020110
Chicago/Turabian StylePuttnam, Benjamin J., Ruben S. Luís, José Manuel Delgado Mendinueta, Jun Sakaguchi, Werner Klaus, Yukiyoshi Kamio, Moriya Nakamura, Naoya Wada, Yoshinari Awaji, Atsushi Kanno, and et al. 2014. "Self-Homodyne Detection in Optical Communication Systems" Photonics 1, no. 2: 110-130. https://doi.org/10.3390/photonics1020110



