Explicit Solutions for the (2 + 1)-Dimensional Jaulent–Miodek Equation Using the Integrating Factors Method in an Unbounded Domain

Abstract

In this work, we prove that the integrating factors can be used as a reduction method. Analytical solutions of the Jaulent–Miodek (JM) equation are obtained using integrating factors as an extension of a recent work where, through hidden symmetries, the JM was reduced to ordinary differential equations (ODEs). Some of these ODEs had no quadrature. We here derive several new solutions for these non-solvable ODEs.

1. Introduction

Nonlinear partial differential equations (NLPDEs) play an important role in various branches of scientific such as fluid mechanics, optical fibers, medical (breast cancer), oceans engineering, and other applications [1,2,3]. Analytical solutions for these equations are obtained using the homotopy perturbation method, Darboux transformation, variational iteration, Painlevé expansions, the homogeneous balance method, the Jacobi elliptic function, the exp-function method, and extended tanh-function [4,5,6,7,8,9,10,11,12,13]. The (2 + 1)-dimensional Jaulent–Miodek (JM) evolution equation is a highly nonlinear partial differential, previously solved analytically using several methods such as Hirota’s bilinear method [14], leading to a multiple-soliton solution of this equation.

Generalized solitary solution and generalized compacton-like solutions were also obtained using the exp-function method in [12] for the JM equation by introducing a new a complex variable that transforms the PDE to an ODE and then assumes the solution in the form of exponential terms with constants that are determined later. Applying the direct symmetry method in [15] leads to symmetry reductions and some new exact solutions of the JM equation. In [4], the Homotopy perturbation method was applied to solve the JM equation. In the JM equation [16], optimal hidden symmetries were detected, and the JM equation reduces to an ODE through these hidden symmetries. Some of the obtained ODEs were found to be non-integrable. This is where our work begins. We solve these equations using the Lie integrating factors.

The paper is constituted of five sections. In Section 2, an introduction to the Jaulent–Miodek equation is shown. In Section 3, the reduction of the JM equation to an ordinary differential equation (ODE) occurs in three steps. For each Lie vector, the following steps apply:

• The JM partial differential equation variables (x, y, t) are reduced to a PDE in two variables (r, s) whose Lie symmetries are evaluated.
• These symmetries are used for a further reduction of independent variables from (r, s) to one variable ($\eta$).
• The resulting ODE non-solvable equations, through their corresponding Integrating Factors are reduced to new solvable ones.

Section 4 contains an analysis of our results, and Section 5 contains conclusions.

2. Mathematical Model

The four JM models [1] have the following forms:

$$w_t=-{\left(w_{xx}-2w^3\right)}_x+\frac{3}{2}(w_x{\partial }_x{}^{-1}{w}_y+w{w}_y)$$

(1a)

$$w_t=\frac{1}{2}{\left(w_{xx}-2w^3\right)}_x+\frac{3}{2}(-\frac{1}{4}{\partial }_x{}^{-1}{w}_{yy}+w{w}_y)$$

(1b)

$$w_t=-\frac{1}{4}{\left(w_{xx}-2w^3\right)}_x-\frac{3}{4}(\frac{1}{4}{\partial }_x{}^{-1}{w}_{yy}+w_x{\partial }_x{}^{-1}{w}_y)$$

(1c)

$$w_t=2{\left(w_{xx}-2w^3\right)}_x-\frac{3}{4}({\partial }_x{}^{-1}{w}_{yy}-2w_x{\partial }_x{}^{-1}{w}_y-6w{w}_y)$$

(1d)

where w(x, y, t) is an analytic function with respect to the variables x, y, and t; the subscripts denote the partial derivatives and $\left({\partial }_x{}^{-1}f\right)\left(x\right)={{\displaystyle \int }}_{-\infty }^{x}f\left(t\right)dt$ and ${\partial }_x{}^{-1}{\partial }_x={\partial }_x{\partial }_x{}^{-1}=1$.

We choose to work on Equation (1c) where we use the transformation $w=u_x$ to overcome the integral term. This leads to a fourth order differential equation:

$$u_{xt}+\frac{1}{4}{u}_{xxxx}-\frac{3}{2}{\left(u_x\right)}^2{u}_{xx}+\frac{3}{16}{u}_{yy}+\frac{3}{4}{u}_{xx}{u}_y=0.$$

(2)

An investigation of its Lie vectors using Maple results in eight Lie vectors:

$$\begin{gathered} X_1=\frac{\partial }{\partial t},X_2=\frac{\partial }{\partial y},X_3=\frac{\partial }{\partial x}, X_4=\frac{\partial }{\partial u}, X_5=t\frac{\partial }{\partial u}, X_6=t\frac{\partial }{\partial x}+\frac{4}{3}y\frac{\partial }{\partial u}, X_7=\frac{x}{3}\frac{\partial }{\partial x}+\frac{2}{3}y\frac{\partial }{\partial y}+t\frac{\partial }{\partial t}, \\ {X}_8=-\frac{8}{3}y\frac{\partial }{\partial x}+t\frac{\partial }{\partial y}+\frac{2}{3}x\frac{\partial }{\partial u}. \end{gathered}$$

(3)

3. Reduction of the Independent Variables in Jaulent–Miodek Equation (2)

In this paragraph, we will study, among the eight Lie vectors obtained in [16], only those vectors leading to ODEs with no quadrature.

3.1. Reduction of the JM Partial Differential, Equation (2), Using $X_8$

The optimal vector $X_8=-\frac{8}{3}y\frac{\partial }{\partial x}+t\frac{\partial }{\partial y}+\frac{2}{3}x\frac{\partial }{\partial u}$ reduces Equation (2) (where variable u is a dependent variable, and (x, y, t) are the independent variables) to a PDE of the form

$$\frac{3}{4}r{F}_{rs}+\frac{9}{8}{F}_s+\frac{9}{8}s{F}_{ss}+\frac{81}{1024}{r}^4{F}_{ssss}-\frac{243}{512}{F}_{ss}{r}^4{\left(F_s\right)}^2=0$$

(4)

where F is the new independent variable and $r=t \mathrm{and} s=\mathrm{¾}tx+y^2$. This equation has six Lie vectors:

$$\begin{gathered} V_1=r^{3/2}\frac{\partial }{\partial s}+\frac{\partial }{\partial f},V_2=r^{3/2}\frac{\partial }{\partial s}+r\frac{\partial }{\partial f},V_3=r\frac{\partial }{\partial r}+\frac{4}{3}S\frac{\partial }{\partial s}+\frac{\partial }{\partial f},V_4=r\frac{\partial }{\partial r}+\frac{4}{3}S\frac{\partial }{\partial s}+r\frac{\partial }{\partial f}, \\ {V}_5=r^{3/2}\frac{\partial }{\partial r}+\frac{3}{2}S\sqrt{r}\frac{\partial }{\partial s}+\frac{\partial }{\partial f},V_6=r^{3/2}\frac{\partial }{\partial r}+\frac{3}{2}S\sqrt{r}\frac{\partial }{\partial s}+r\frac{\partial }{\partial f}. \end{gathered}$$

(5)

Only $V_5$ is found to be a hidden symmetry [1] (Hidden symmetries are different from the original equation Lie vectors.). This vector is used to transform JM to a nonlinear fourth degree ordinary differential equation of the form

$${\theta }_{\eta \eta \eta \eta }-6{\theta }_{\eta \eta }{\theta }_{\eta }{}^2=0$$

(6)

where $\eta =\frac{3}{4}\frac{tx+y^2}{t^{\frac{3}{2}}}.$ In the original work [16], Equation (6) was solved using its hidden vectors through successive Lie reductions. We here will use the integrating factors and compare the results.

3.1.1. Integrating Factor Technique to Obtain an Explicit Solution

We first deduce Equation (6) Integrating Factors using Maple:

$${\mu }_1={\theta }_{\eta },{\mu }_2=1.$$

(7)

These Integrating Factors reduces Equation (6) to

$${\theta }_{\eta \eta }{}^2-{\theta }_{\eta }{}^4+c=0.$$

(8)

This equation possesses symmetry vectors

$$Y_1=\frac{\partial }{\partial \eta },Y_2=\frac{\partial }{\partial \theta }.$$

(9)

These two vectors are used to reduce Equation (8) to a differential order.

$Y_1$ Reductions of Equation (8)

Vector $Y_1$ reduces Equation (8) to a first order, ordinary differential equation of the form

$$\frac{d\phi \left(\lambda \right)}{d\lambda }=\phi {\left(\lambda \right)}^2.$$

(10)

This equation has a closed-form solution:

$$\phi \left(\lambda \right)=\frac{1}{-\lambda +c}.$$

(11)

Back-substituting for the variable $\lambda =\eta , \phi \left(\lambda \right)=\frac{d\theta }{d\eta }$ and integrating Equation (11), we obtain

$$\theta \left(\eta \right)=-\ln \left(-\eta +c\right)+c_1$$

(12)

where $\eta =\frac{\frac{3}{4}tx+y^2}{t^{\frac{3}{2}}}$, and c and $c_1$ are integration constants. Then, back-substituting, we obtain

$$\theta \left(\eta \right)=F\left(r,s\right)+\frac{2}{\sqrt{t}}$$

(13)

where $F\left(r,s\right)=u\left(x,y,t\right)-\frac{2}{3}\frac{yx}{t}-\frac{16}{27}\frac{y^3}{t^2}$. Hence,

$$u\left(x,y,t\right)=\frac{2}{3}\frac{yx}{t}+\frac{16}{27}\frac{y^3}{t^2}-\frac{2}{\sqrt{t}}+\ln \left(-\frac{\frac{3}{4}tx+y^2}{t^{\frac{3}{2}}}+c\right)+c_1.$$

(14)

Back to the original variable $w=u_x$, we obtain;

$$w\left(x,y,t\right)=\frac{2y}{3t}-\frac{3t}{4\left(\frac{3}{4}tx+y^2-c\sqrt{t^3}\right)}.$$

(15)

This result is different from the one obtained in [1]:

$$w\left(x,y,t\right)=\frac{2y}{3t}+\frac{3t}{4\left(y^2+\frac{3}{4}xt\right)}.$$

Our results are plotted in Figure 1a–d for different times: 03, 0.5, 0.8, and 1.2 s.

The previously results show that, with time marching, a parabolic middle peak upward advancing front wave remains, while the rest of the peaks reverse.

$Y_2$ Reductions of Equation (8)

We continue the reduction of Equation (8) to a first-order ODE of the form using vector $Y_2$:

$$\frac{d\phi \left(\lambda \right)}{d\lambda }=\phi \left(\lambda \right).$$

(16)

This equation has a closed-form solution:

$$\phi \left(\lambda \right)=e^{\lambda }.$$

(17)

Back-substituting by $\phi \left(\lambda \right)=\frac{d\theta \left(\eta \right)}{d\eta }$, $\lambda =\theta \left(\eta \right)$, we obtain

$$\theta \left(\eta \right)=\ln \left(-\frac{1}{\eta +c}\right)+c_1,\eta =\frac{s}{r^{\frac{3}{2}}}$$

(18)

where $\theta \left(\eta \right)=F\left(r,s\right)+\frac{2}{\sqrt{r}}$, $c_1$ and c are integration constants. By back-substituting variables (r, s) by $s=\frac{3}{4}tx+y^2, r=t$, we obtain

$$F\left(r,s\right)=-\frac{2}{\sqrt{r}}+\ln \left(-\frac{1}{\frac{s}{r^{\frac{3}{2}}}+c}\right)+c_1$$

(19)

where $F\left(r,s\right)=u\left(x,y,t\right)-\frac{2}{3}\frac{yx}{t}-\frac{16}{27}\frac{y^3}{t^2}$. Hence,

$$u\left(x,y,t\right)=\frac{2}{3}\frac{yx}{t}+\frac{16}{27}\frac{y^3}{t^2}-\frac{2}{\sqrt{t}}+\ln \left(\frac{-1}{\frac{\frac{3}{4}tx+y^2}{t^{\frac{3}{2}}}}+c\right)+c_1.$$

(20)

Then, back to the original variable $w=u_x$, we obtain

$$w\left(x,y,t\right)=\frac{2y}{3t}-\frac{3}{\left(3x+4\frac{y^2}{t}+4c\sqrt{t^3}\right)}.$$

(21)

This result is plotted in Figure 2a–d as shown with different times and c values;

The result obtained in Equation (21) is different from the one obtained in [16] using hidden symmetries:

$$ww\left(x,y,t\right)=\frac{2y}{3t}+\frac{3t}{4\left(y^2+\frac{3}{4}xt\right)}.$$

3.2. $\left(X_2+X_5\right)$ Similarity Reduction of Equation (2)

$\left(X_2+X_5\right)$ Lie vector reduces Equation (2) to

$$F_{rs}+\frac{3}{4}s{F}_{rr}+\frac{1}{4}{F}_{rrrr}-\frac{3}{2}{F}_{rr}{\left(F_r\right)}^2=0.$$

(22)

This equation possesses five Lie vectors:

$$\begin{gathered} V_1=\frac{\partial }{\partial r}+\frac{\partial }{\partial F}, V_2=\frac{\partial }{\partial r}+s\frac{\partial }{\partial F}, V_3=\frac{3s}{4}\frac{\partial }{\partial r}+\frac{\partial }{\partial s}+\frac{\partial }{\partial F}, V_4=\frac{3s}{4}\frac{\partial }{\partial r}+\frac{\partial }{\partial s}+s\frac{\partial }{\partial F} , \\ {V}_5=\left(\frac{r}{3}+\frac{5s^2}{8}\right)\frac{\partial }{\partial r}+s\frac{\partial }{\partial s}+\frac{\partial }{\partial F}. \end{gathered}$$

(23)

Testing these vectors shows that the first two vectors are inherited from the original vectors as $X_3+X_4\to V_1,\hspace{0.17em}{X}_3+X_5\to V_2$, while V₃, V₄, and V₅ are hidden vectors.

3.2.1. ${\mathit{V}}_4$ Reduction of Equation (22)

We choose here to work only with the V₄ Lie hidden vector, as it leads, in [1], to an ODE with no analytic solution:

$${\theta }^{\prime \prime \prime \prime }-6{\left({\theta }^{\prime }\right)}^2{\theta }^{″}+6{\theta }^{\prime }{\theta }^{″}-\frac{3}{2}{\theta }^{″}=0$$

(24)

where $\eta =-\frac{8}{3}x+t^2,\mathrm{and}\theta \left(\eta \right)=u\left(x,y,t\right)-ty-\frac{4}{3}x.$

As this equation has no analytic solution, we thus investigate the integrating factor method.

Integrating Factor Technique to Obtain Explicit Solutions

Equation (24) has two Integrating Factors:

$${\mu }_1={\theta }_{\eta },{\mu }_2=1.$$

(25)

They are used to reduce Equation (24) to a differential order:

$$2{\theta }_{\eta \eta }{}^2-2{\theta }_{\eta }{}^4+4{\theta }_{\eta }{}^3-3{\theta }_{\eta }{}^2=0.$$

(26)

This equation has two closed solutions:

$$\begin{gathered} \theta \left(\eta \right)={\tanh }^{-1}(\sqrt{6}/2\tanh (\frac{\sqrt{6}}{2}\eta +\frac{\sqrt{6}}{2}c)) \\ \pm \frac{1}{6}\frac{(\sqrt{2}\cosh (\frac{\sqrt{6}}{2}\eta +\frac{\sqrt{6}}{2}c)\sqrt{3}{\tanh }^{-1}(\frac{1}{3}\cosh \left(\frac{\sqrt{6}}{2}\eta +\frac{\sqrt{6}}{2}c\right)\sqrt{3})\sqrt{6}}{\sqrt{\cosh {\left(\frac{\sqrt{6}}{2}\eta +\frac{\sqrt{6}}{2}c\right)}^2}}+c_1 \end{gathered}$$

(27)

where c and c₁ are constants of integration. By back substitution for 𝜂 and θ(𝜂), we obtain

$$\begin{array}{c}u\left(x,y,t\right)= ty+\frac{4}{3}x+{\tanh }^{-1}\left(\frac{\sqrt{6}}{2}\tanh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c\right)\right)\pm \frac{1}{4}\\ \ast \frac{(\sqrt{2}\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c\right)\sqrt{3}{\tanh }^{-1}\left(\frac{1}{3}\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c\right)\sqrt{3}\right)\sqrt{6}}{\sqrt{\cosh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c\right)}^2}}+c_1.\end{array}$$

(28)

Differentiate $u(x,y,t)$ w, r, t (x) once, we obtain

$$\begin{gathered} \begin{array}{cc}w\left(x,y,t\right)& =\frac{4}{3}+\frac{-4+4\tanh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c \right)}^2}{1-\frac{3}{2}\tanh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c \right)}^2}\hfill \\ & \mp \frac{4}{3}\frac{\sqrt{6}\sinh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2} c\right){\tanh }^{-1}\left(\frac{1}{3}\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)\sqrt{3}\right)}{\sqrt{\cosh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)}^2}}\mp \hfill \\ & \frac{4}{3}\frac{\sqrt{2}\sinh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)}{1-\frac{1}{3}\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)\sqrt{\cosh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}x+t^2\right)+\frac{\sqrt{6}}{2}c\right)}^2}}\hfill \end{array} \\ \pm \frac{4}{3}\frac{\sqrt{6}\sinh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}\mathrm{x}+{\mathrm{t}}^2\right)+\frac{\sqrt{6}}{2}\mathrm{c}\right){\tanh }^{-1}\left(\frac{1}{3}\cosh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}\mathrm{x}+{\mathrm{t}}^2\right)+\frac{\sqrt{6}}{2}\mathrm{c}\right)\sqrt{3}\right)\sinh \left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}\mathrm{x}+{\mathrm{t}}^2\right)+\frac{\sqrt{6}}{2}\mathrm{c}\right)}{{(\cosh {\left(\frac{\sqrt{6}}{2}\left(-\frac{8}{3}\mathrm{x}+{\mathrm{t}}^2\right)+\frac{\sqrt{6}}{2}\mathrm{c}\right)}^2)}^{3/2}}. \end{gathered}$$

(29)

This result contains two solutions: one is positive and the other is negative, and the two are plotted as shown in Figure 3 for constant c = 0 and 1. Positive solutions are plotted in Figure 3a,b, while negative ones are plotted in Figure 3c,d.

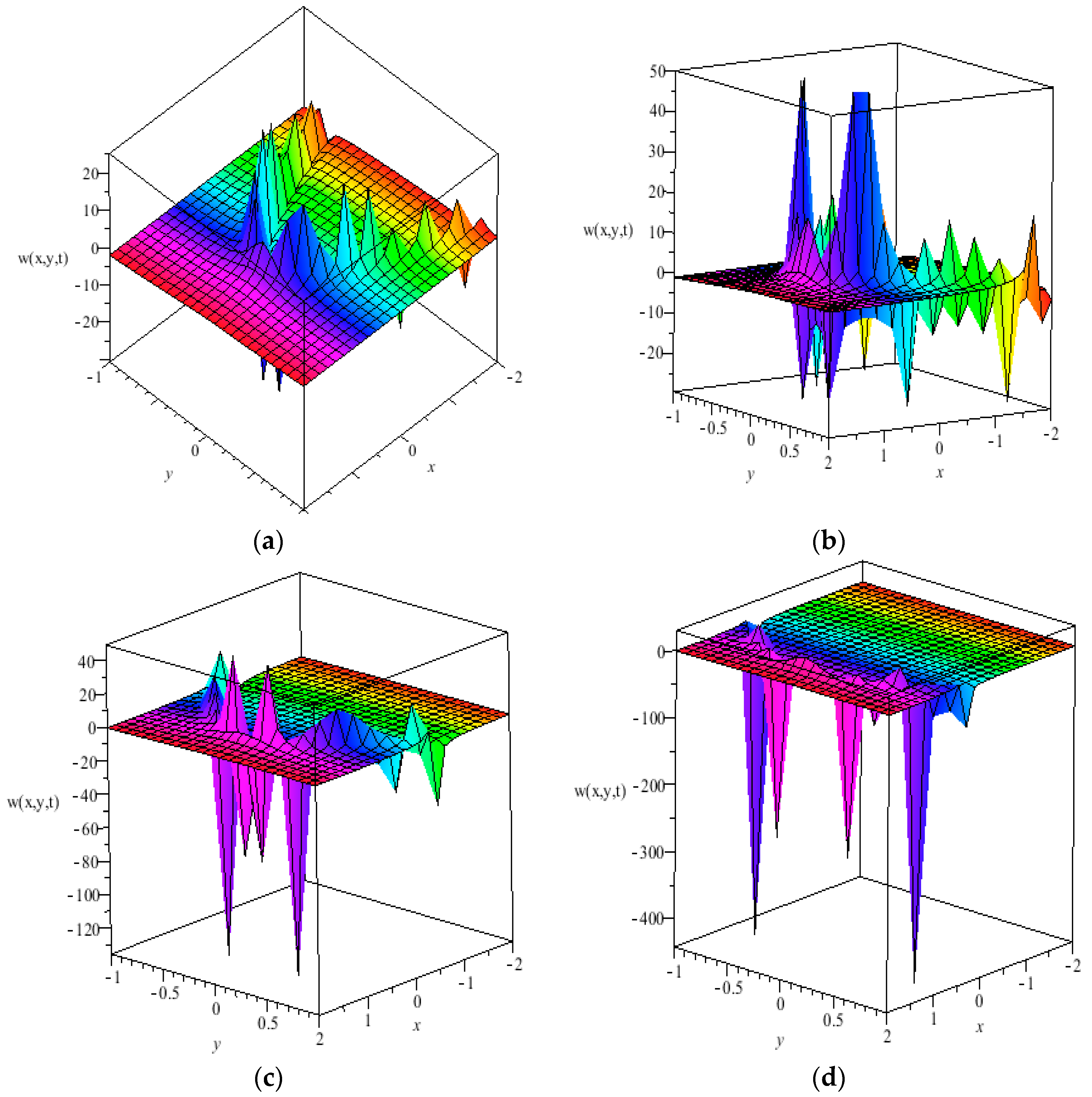
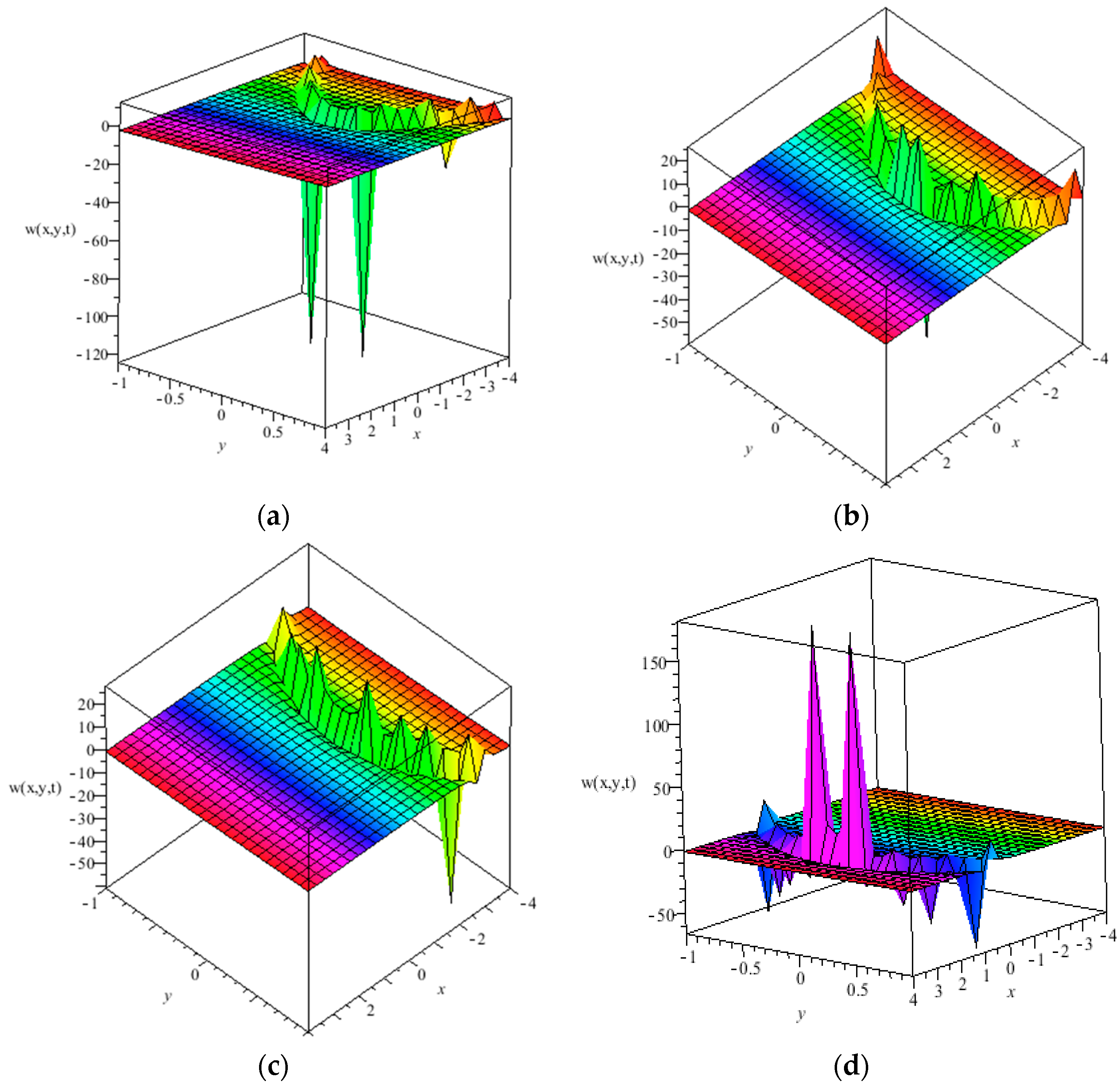
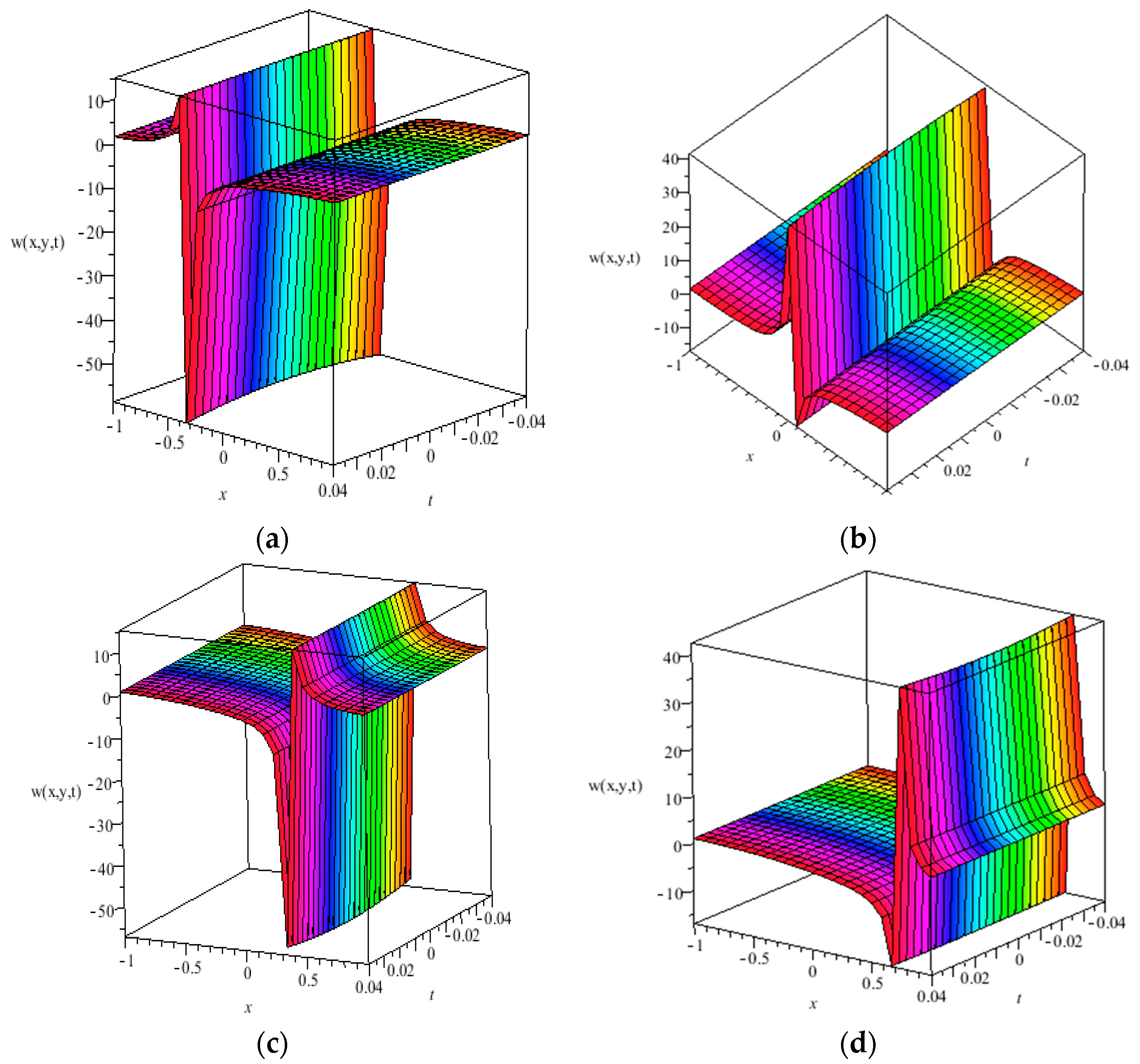
4. Analysis of Results

We then compare our results for vector V₄; Equation (29) using the integrating Lie factor, with solutions obtained in [16] using two levels of hidden symmetries:

$$w(x,y,t)=\frac{4}{3}+\frac{4{(\mathrm{sech}(\frac{\sqrt{6}}{4}(t^2-\frac{8}{3}x)))}^2}{1-{(\frac{1}{\sqrt{2}}+\frac{\sqrt{6}}{2}\tanh (\frac{\sqrt{6}}{4}(t^2-\frac{8}{3}x)))}^2}$$

(30)

$$w(x,y,t)=\frac{\pm 4\hspace{0.17em}\left(\pm 6\mp 2{\left(\cosh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\right)}^2+\sqrt{2}\sinh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\hspace{0.17em}{\left(\cosh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\right)}^2-3\sqrt{2}\sinh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\right)}{\left(-3+5{\left(\cosh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\right)}^2+\sqrt{3}\sinh \left(\sqrt{\frac{2}{3}}\left(3t^2-8x\right)\right)\right)\hspace{0.17em}\left(3-5{\left(\cosh \left(\frac{1}{\sqrt{6}}\left(3t^2-8x\right)\right)\right)}^2+\sqrt{3}\sinh \left(\sqrt{\frac{2}{3}}\left(3t^2-8x\right)\right)\right)}.$$

(31)

We find that these results obtained in [1], Equations (30) and (31), are different from our solution described in Equation (29).

5. Conclusions

In the present work, new solutions are found for the JM Equation (2);

• For vector X₈ we replaced two successive Lie reduction processes used in [16] with a unique integrating process that led to new solutions.
• For vectors X₂ + X₅, we solved ODEs with no quadrature and obtained a new solution (Equation (29)) using an integrating factor, different from the solutions in [16] that resulted from a two consecutive Lie reductions.
• Thus, we can say that the advantages of using integrating factors are as follows:
  • New and different solutions are obtained if we use a Lie symmetry reduction from A to z.
  • The reduction stages are reduced via Lie symmetry reduction.
  • In practice, the integrating factor method perhaps obtains the solution more easily than does the Lie reduction.
  • The problems of the Lie symmetry reduction method (back substitution problems) are thus overcome.