General Solution of the Extended Plate Model Including Diffusion, Slow Transfer Kinetics and Extra-Column Effects for Isocratic Chromatographic Elution
Abstract
:1. Introduction
2. Theory
2.1. General Description of the Chromatographic Elution Based on the Extended Plate Model
- (i)
- The solute crosses a fixed length L inside the column.
- (ii)
- The column is divided into N equal microscopic theoretical plates.
- (iii)
- The interaction between solute and stationary phase in each theoretical plate is determined by a linear isotherm:where and are the solute concentration in the mobile phase and stationary phase, respectively, at equilibrium inside the i theoretical plate, and and the corresponding number of moles.
2.2. Extra-Column Effects
2.3. Peak Profile
2.4. Evaluation of Peak Profile Moments
2.4.1. General Method
- (i)
- The equations describing the elution process (in this work, the sum of Equation Systems (31) and (29)) are first outlined.
- (ii)
- The system of differential equations is transformed to a system of algebraic equations in the Laplace space, which is a function of the variable r.
- (iii)
- The peak function is then obtained in the Laplace space (r-domain): F(r).
- (iv)
- To obtain the moments about the origin, the following property of the Laplace transformation is considered [10]:
- (v)
- For the moment of order n, the system of equations in the Laplace space describing the elution is derived n fold with regard to r. Then, it is solved to obtain the corresponding derivative after making r = 0 (see Equation (36)).
- (vi)
- The peak parameters are obtained from the moments about the origin.
2.4.2. Transformation of the System of Differential Equations into the Laplace Space
2.4.3. Solution for the Mean and Variance of the Peak Profile
3. Experimental Section
3.1. Reagents and Columns
3.2. Apparatus and Measurement of Peak Parameters
4. Results and Discussion
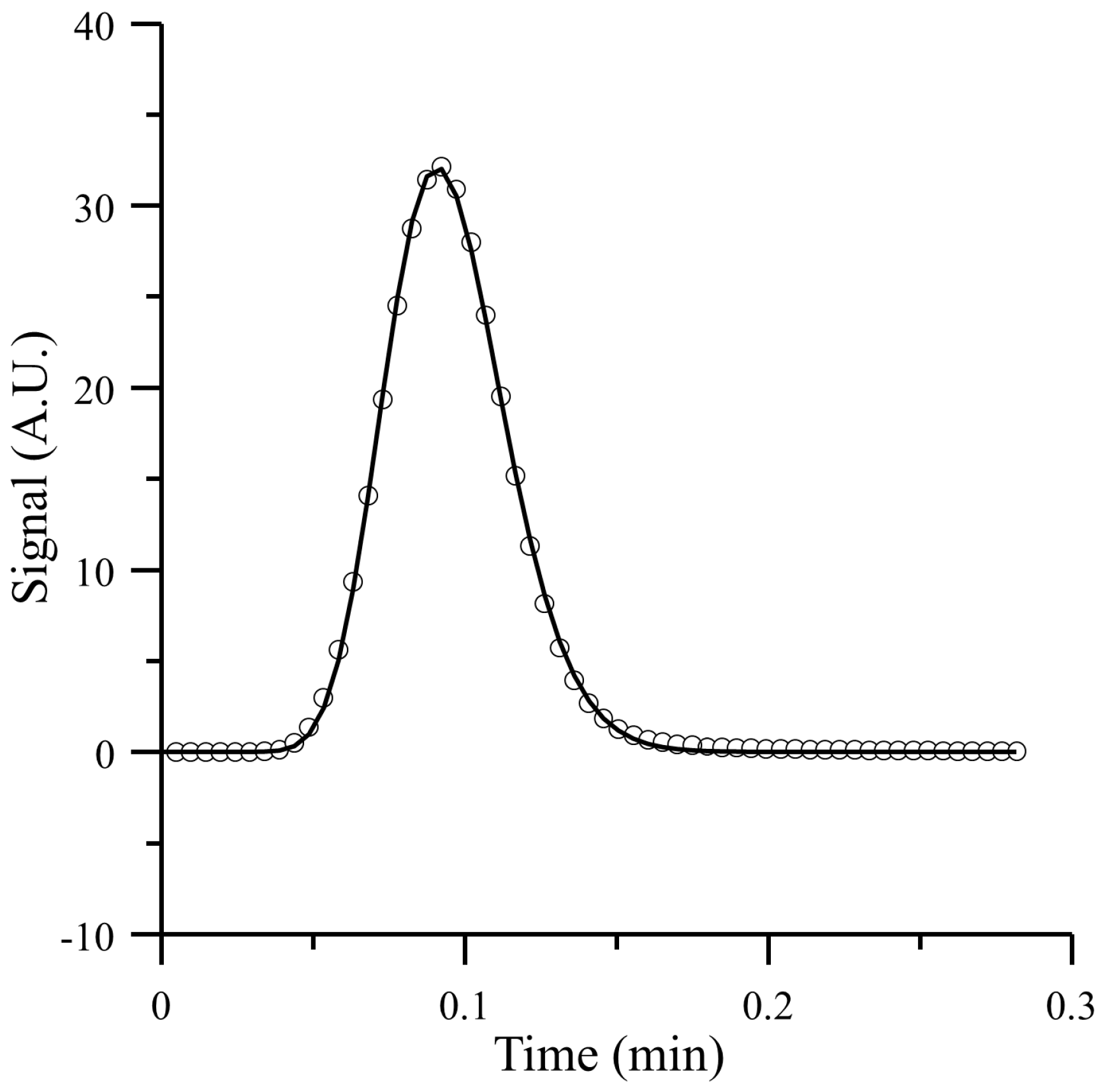
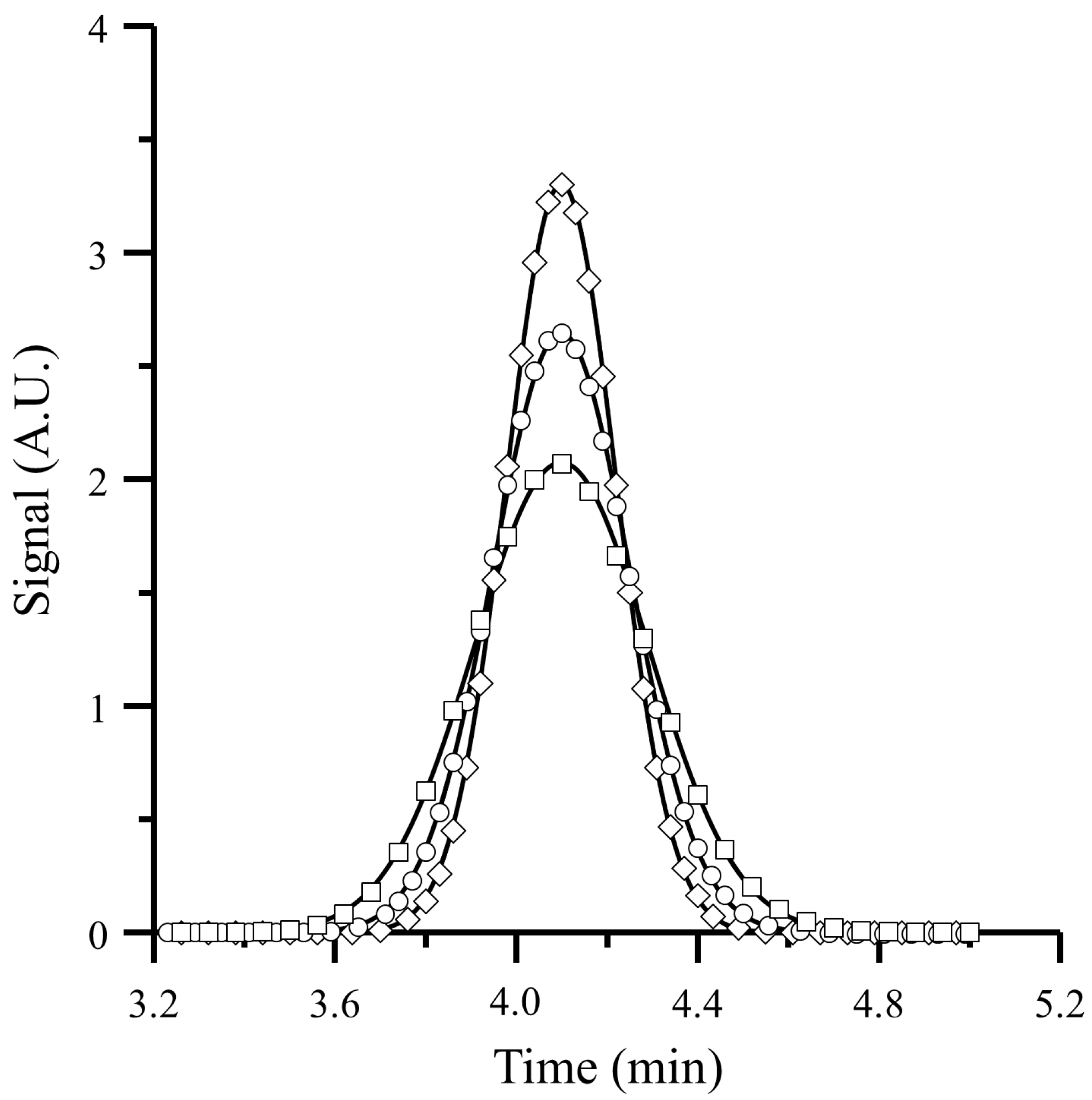
4.1. Comparison of the Proposed Model with a Simulation Approach
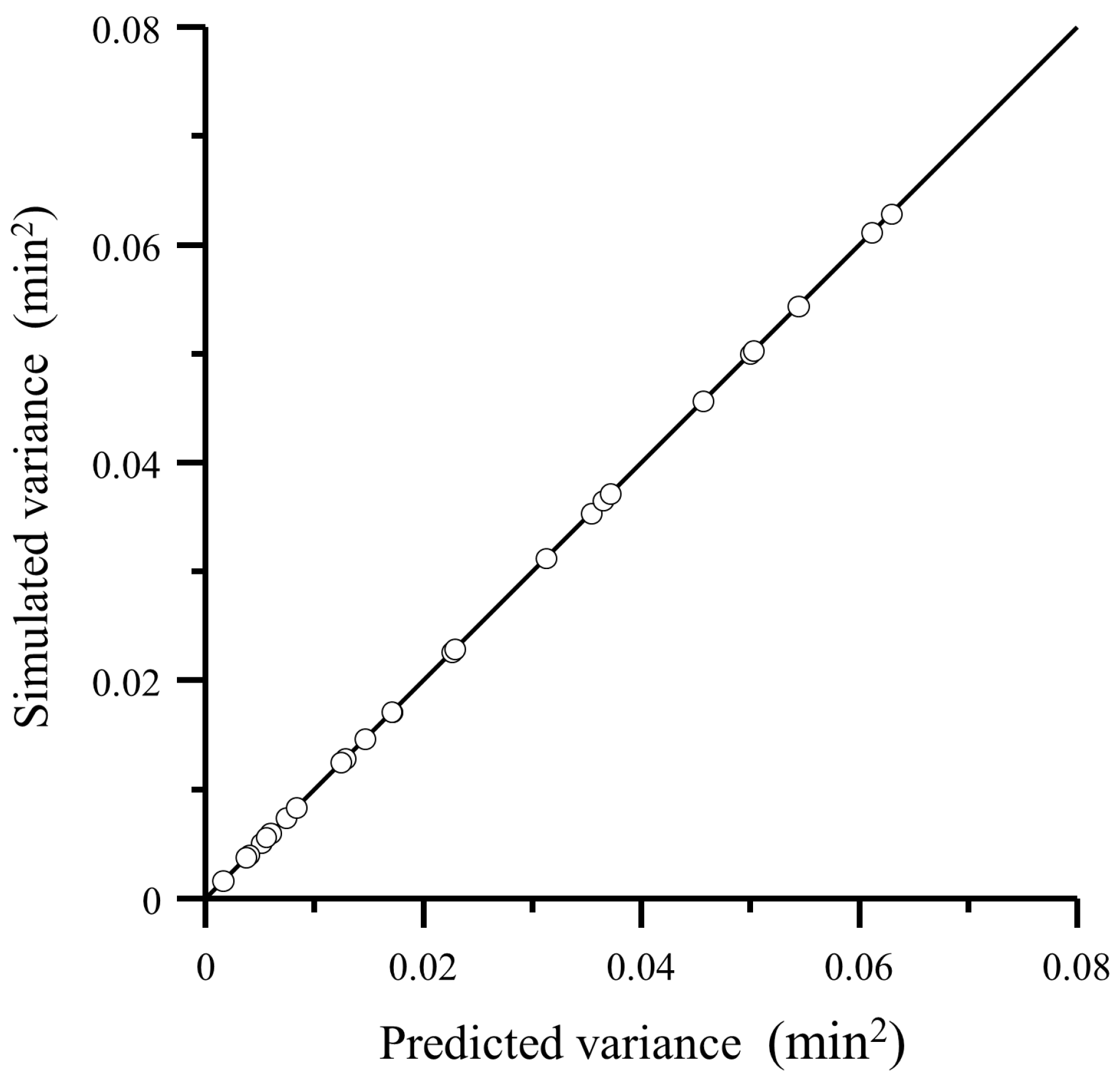
4.2. Comparison of Predicted Variance with Experimental Data
4.3. Variance Components
- (i)
- Equilibrium between the mobile phase and stationary phase according to a Craig process:
- (ii)
- Convection or flow through the column:
- (iii)
- Slow mass transfer between the phases:
- (iv)
- Mobile phase diffusion:
- (v)
- Stationary phase diffusion:
- (vi)
- Extra-column dispersion given by Equation (49) that includes convection, diffusion and dispersion due to the Taylor-Aris regime.
4.4. Equation Describing the Theoretical Plate Height
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Glossary
| A, B, C | van Deemter equation constants |
| AV, BV, CV | constants in the variance-flow rate equation, where the variance is expressed in volume units |
| a0 | initial moles of solute in the mobile phase associated to the first theoretical plate |
| ai | moles of solute in the mobile phase associated to the i theoretical plate |
| moles of solute in the mobile phase at equilibrium in the i theoretical plate | |
| solute concentration in the mobile phase at equilibrium in the i theoretical plate | |
| bi | moles of solute in the stationary phase associated to the i theoretical plate |
| moles of solute in the stationary phase at equilibrium with the mobile phase in the i theoretical plate | |
| solute concentration in the stationary phase at equilibrium associated to the i theoretical plate | |
| c | solute concentration in the mobile phase as a function of t and x |
| Dm, Ds | solute longitudinal diffusion coefficient in the mobile phase and stationary phase |
| dm, ds | diffusion transfer kinetic constants in the mobile phase and stationary phase |
| dext | diffusion transfer kinetic constant in the mobile phase in the extra-column tubing |
| F | flow rate |
| F(r) | peak function in the r-domain |
| f(t) | peak function in the time-domain |
| Φ | volume phase ratio |
| H | column plate height (H = L/N) |
| Hext | extra-column plate height (Hext = Lext/M) |
| i | plate index |
| J | molar flow per unit area and time due to the longitudinal diffusion |
| K | distribution coefficient or partition constant |
| k | solute retention factor (k = KΦ) |
| kf | rate of mass transfer between phases |
| L | column length |
| m | kinetic constant for the solute slow mass transfer from the mobile phase to the stationary phase |
| M | number of theoretical plates in the extra-column tubing |
| N | efficiency or number of column theoretical plates |
| ni | total moles of solute in the i theoretical plate |
| change in the total moles of solute per time unit | |
| q | solute concentration in the stationary phase as a function of t and x |
| q* | solute concentration in the stationary phase at equilibrium with the solute in the mobile phase at concentration c |
| r | Laplace variable |
| s | kinetic constant for the solute slow mass transfer from the stationary phase to the mobile phase |
| t | time coordinate |
| t0 | column dead time |
| tcol | solute retention time associated to the column |
| text | solute retention time associated to the extra-column tubing |
| tR | solute retention time or peak mean time (time at the peak maximum for symmetrical peaks) |
| u | linear flow velocity |
| Vm | mobile phase volume associated to a theoretical plate |
| Vs | stationary phase volume associated to a theoretical plate |
| x | axial coordinate |
| γm, γs | obstruction to the diffusion transfer factors in the mobile phase and stationary phase |
| μk | kth moment about the origin |
| σ2 | peak variance |
| column variance | |
| variance associated to the longitudinal diffusion | |
| variance associated to the eddy dispersion | |
| variance associated to the extra-column dispersion | |
| variance associated to the slow mass transfer | |
| τ | mass transfer kinetic parameter related to the flow in the column |
| τext | mass transfer kinetic parameter related to the flow in the extra-column tubing |
| ν | mass-transfer rate constant between both phases (ν = m + s) |
Appendix
A.1. Extra-Column Contribution
A.2. Column Contribution
A.2.1. Zero-Order Derivative
A.2.2. First-Order Derivative
A.2.3. Second-Order Derivative
References
- Martin, A.J.P.; Synge, R.L.M. A new form of chromatogram employing two liquid phases. Biochem. J. 1941, 35, 1358–1368. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.J.P.; Synge, R.L.M. Separation of the higher monoamino acids by counter-current liquid-liquid extraction: The amino-acid composition of wool. Biochem. J. 1941, 35, 91–121. [Google Scholar] [CrossRef] [PubMed]
- Howard, G.A.; Martin, A.J.P. The separation of the C12-C18 fatty acids by reversed-phase partition chromatography. Biochem. J. 1950, 46, 532–538. [Google Scholar] [CrossRef]
- Ettre, L.S. Obituary A.J.P. Martin (1910–2002). J. Chromatogr. A 2002, 972, 131–136. [Google Scholar]
- Craig, L.C. Identification of small amounts of organic compounds by distribution studies: Separation by counter-current distribution. J. Biol. Chem. 1944, 155, 519–534. [Google Scholar] [CrossRef]
- Williamson, B.; Craig, L.C. Identification of small amounts of organic compounds by distribution studies. V. Calculation of theoretical curves. J. Biol. Chem. 1947, 168, 687–697. [Google Scholar] [PubMed]
- Felinger, A. Data Analysis and Signal Processing in Chromatography; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Said, A.S. Theoretical plate concept in chromatography. AIChE J. 1956, 2, 477–481. [Google Scholar] [CrossRef]
- Said, A.S. Theoretical plate concept in chromatography: Part II. AIChE J. 1959, 5, 69–72. [Google Scholar] [CrossRef]
- Baeza-Baeza, J.J.; García-Álvarez-Coque, M.C. A theoretical plate model accounting for slow kinetics in chromatographic elution. J. Chromatogr. A 2011, 1218, 5166–5174. [Google Scholar] [CrossRef] [PubMed]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 4th ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Giddings, J.C. The nature of eddy diffusion. Anal. Chem. 1966, 38, 490–491. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. Relationship between trans-column eddy diffusion and retention in liquid chromatography: Theory and experimental evidence. J. Chromatogr. A 2010, 1217, 6350–6365. [Google Scholar] [CrossRef] [PubMed]
- Grinias, J.P.; Bunner, B.; Gilar, M.; Jorgenson, J.W. Measurement and modeling of extra-column effects due to injection and connections in capillary liquid chromatography. Chromatography 2015, 2, 669–690. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. On the extra-column band-broadening contributions of modern, very high pressure liquid chromatographs using 2.1 mm I.D. columns packed with sub-2 μm particles. J. Chromatogr. A 2010, 1217, 7677–7689. [Google Scholar] [CrossRef] [PubMed]
- Miyabe, K.; Guiochon, G. Fundamental interpretation of the peak profiles in linear reversed-phase liquid chromatography. Adv. Chromatogr. 2000, 40, 1–113. [Google Scholar] [PubMed]
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography; Academic Press, Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Hao, W.; Di, B.; Chen, Q.; Wang, J.; Yang, Y.; Sun, X. Study of the peak variance in isocratic and gradient liquid chromatography using the transport model. J. Cromatogr. A 2013, 1295, 67–81. [Google Scholar] [CrossRef] [PubMed]
- Felinger, A.; Guiochon, G. Comparison of the kinetic models of linear chromatography. Chromatographia 2004, 60, S175–S180. [Google Scholar] [CrossRef]
- Czok, M.; Guiochon, G. The physical sense of simulation models of liquid chromatography: Propagation through a grid or solution of the mass balance equation. Anal. Chem. 1990, 62, 189–200. [Google Scholar] [CrossRef]
- Gao, H.; Lin, B. A simplified numerical method for the general rate model. Comput. Chem. Eng. 2010, 34, 277–285. [Google Scholar] [CrossRef]
- Câmara, L.D.T. Stepwise model evaluation in simulated moving-bed separation of ketamine. Chem. Eng. Technol. 2014, 37, 301–309. [Google Scholar] [CrossRef]
- Van Deemter, J.J.; Zuiderweg, F.J.; Klinkenberg, A. Longitudinal diffusion and resistance to mass transfer as causes of non-ideality in chromatography. Chem. Eng. Sci. 1996, 5, 271–289. [Google Scholar] [CrossRef]
- Hawkes, S.J. Modernization of the Van Deemter equation for chromatographic zone dispersion. J. Chem. Educ. 1983, 60, 393–398. [Google Scholar] [CrossRef]
- Golshan-Shirazi, S.; Guiochon, G. Review of the various models of linear chromatography and their solutions. In Theoretical Advancement in Chromatography and Related Separation Techniques; Dondi, F., Guiochon, G., Eds.; NATO ASI Series; Kluver Academic Publishers: Berlin, Germany, 1992; Volume 383, pp. 61–92. [Google Scholar]
- Giddings, J.C.; Eyring, H. A molecular dynamic theory of chromatography. Anal. Chem. 1955, 59, 416–421. [Google Scholar] [CrossRef]
- Felinger, A. Molecular dynamic theories in chromatography. J. Chromatogr. A 2008, 1184, 20–41. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y. The statistical theory of linear capillary chromatography with uniform stationary phase. J. Chromatogr. A 2007, 1144, 221–244. [Google Scholar] [CrossRef] [PubMed]
- Tijssen, R. The mechanism and importance of zone spreading. In Handbook in HPLC; Kaltz, E., Eksteen, R., Schoenmakers, P., Miller, N., Eds.; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Gritti, F.; Guiochon, G. Mass transfer kinetics, band broadening and column efficiency. J. Chromatogr. A 2012, 1221, 2–40. [Google Scholar] [CrossRef] [PubMed]
- Miyabe, K. Moment analysis of chromatographic behavior in reversed-phase liquid chromatography. J. Sep. Sci. 2009, 32, 757–770. [Google Scholar] [CrossRef] [PubMed]
- Knox, J.H.; Scott, H.P. B and C terms in the Van Deemter equation for liquid chromatography. J. Chromatogr. 1983, 282, 297–313. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. General HETP equation for the study of mass-transfer mechanisms in RPLC. Anal. Chem. 2006, 78, 5329–5347. [Google Scholar] [CrossRef] [PubMed]
- Usher, K.M.; Simmons, C.R.; Dorsey, J.G. Modeling chromatographic dispersion: A comparison of popular equations. J. Chromatogr. A 2008, 1200, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Knox, J.H. Band dispersion in chromatography: A new view of A-term dispersion. J. Chromatogr. A 1999, 831, 3–15. [Google Scholar] [CrossRef]
- Knox, J.H. Band dispersion in chromatography: A universal expression for the contribution from the mobile zone. J. Chromatogr. A 2002, 960, 7–18. [Google Scholar] [CrossRef]
- Desmet, G.; Broeckhoven, K.; de Smet, J.; Deridder, S.; Baron, G.V.; Gzil, P. Errors involved in the existing B-term expressions for the longitudinal diffusion in fully porous chromatographic media: Part I: Computational data in ordered pillar arrays and effective medium theory. J. Chromatogr. A 2008, 1188, 171–188. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Ghosal, S. Characterizing dispersion in microfluidic channel. Lap Chip 2009, 9, 2537–2550. [Google Scholar] [CrossRef] [PubMed]

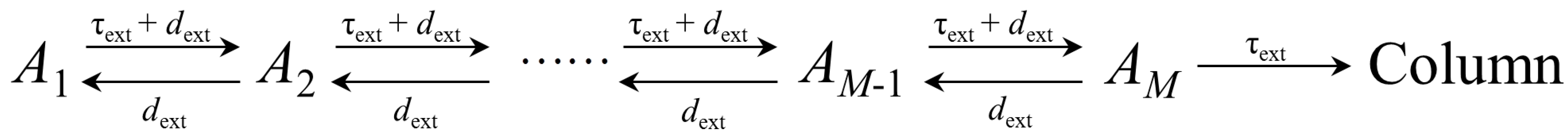
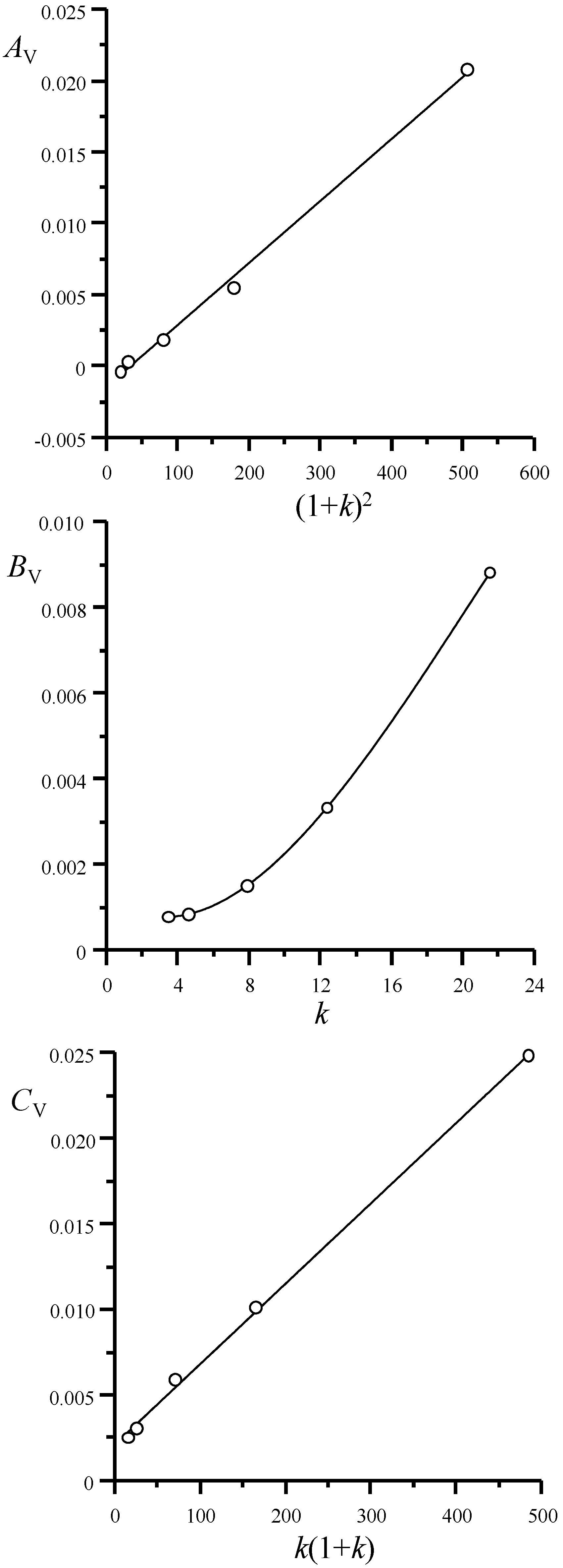
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baeza-Baeza, J.J.; García-Álvarez-Coque, M.C. General Solution of the Extended Plate Model Including Diffusion, Slow Transfer Kinetics and Extra-Column Effects for Isocratic Chromatographic Elution. Separations 2016, 3, 11. https://doi.org/10.3390/separations3020011
Baeza-Baeza JJ, García-Álvarez-Coque MC. General Solution of the Extended Plate Model Including Diffusion, Slow Transfer Kinetics and Extra-Column Effects for Isocratic Chromatographic Elution. Separations. 2016; 3(2):11. https://doi.org/10.3390/separations3020011
Chicago/Turabian StyleBaeza-Baeza, Juan José, and María Celia García-Álvarez-Coque. 2016. "General Solution of the Extended Plate Model Including Diffusion, Slow Transfer Kinetics and Extra-Column Effects for Isocratic Chromatographic Elution" Separations 3, no. 2: 11. https://doi.org/10.3390/separations3020011




