Methods and Tools for Robust Optimal Control of Batch Chromatographic Separation Processes
Abstract
:1. Introduction
1.1. Solvent Composition Trajectory Elution Strategies
1.2. PDE-Constrained Dynamic Optimization
1.3. Nonlinear Robust Optimization of Uncertain Dynamic Systems
1.4. Aim and Scope
- i)
- To formulate a nominal open-loop optimal control problem and its robust counterpart, including penalty on the difference on the zero-order hold control discretization, to find optimal control trajectories that remain feasible for all perturbations from the uncertainty set.
- ii)
- To develop a numerically efficient framework for simulation of a Lyapunov differential equation, enabling the computation of the robustified inequality constraint margin in the counterpart problem.
- iii)
- To assess the robustness of general elution trajectories, for both batch elution and cyclic-steady-state operation, and to benchmark with that of the conventional liner trajectories.
1.5. Outline of the Paper
2. Process Description
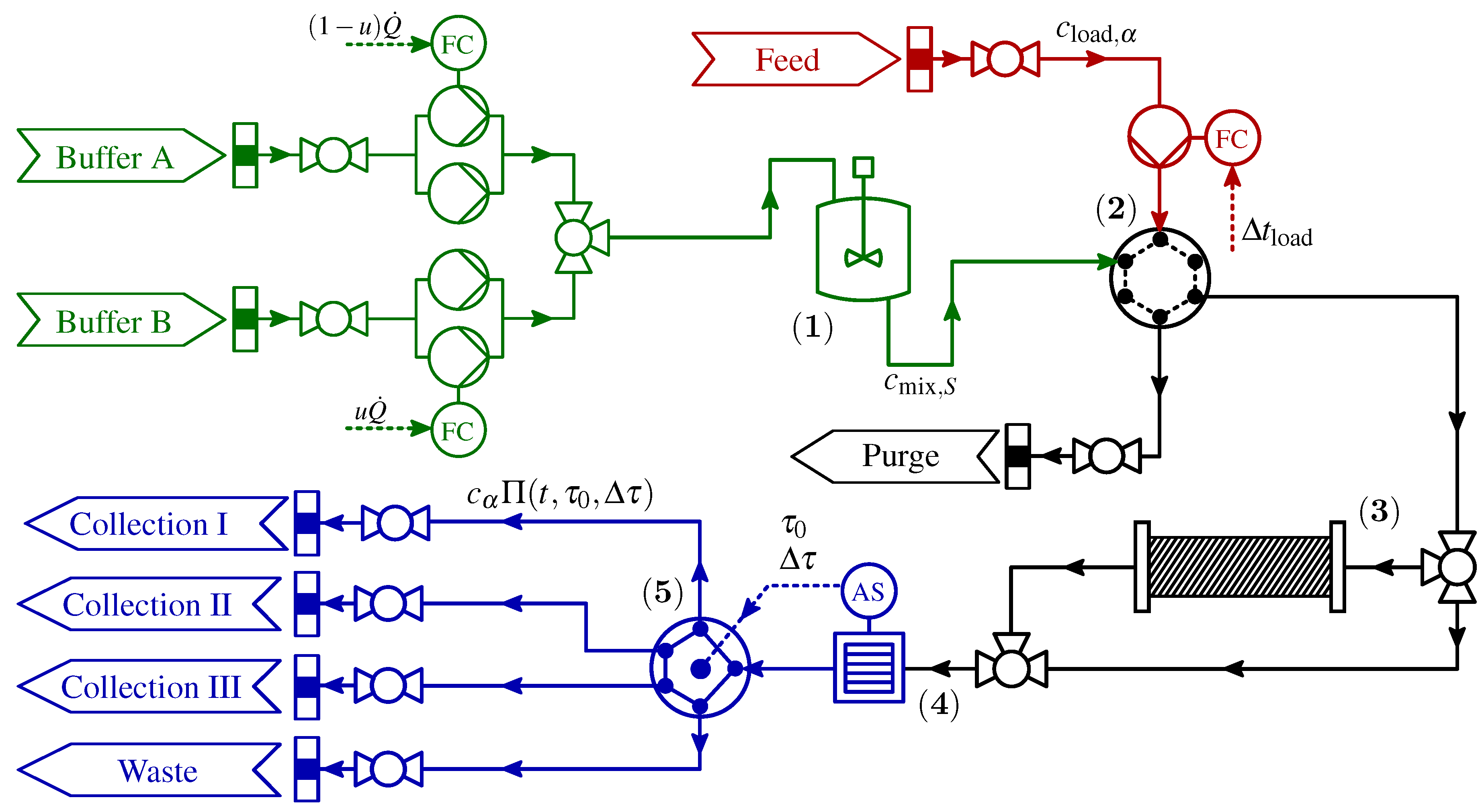
| Parameter | Description | Value | Unit |
|---|---|---|---|
| volumetric flow rate | |||
| sample load duration | s | ||
| buffer mixing unit volume | |||
| column length | m | ||
| column diameter | m | ||
| particle diameter | m | ||
| interstitial porosity of the column | − | ||
| apparent particle porosity | − | ||
| total porosity of the column | − | ||
| a | apparent dispersion coefficient | ||
| interstitial velocity | |||
| kinetic rate constant | |||
| self-association equilibrium constant | − | ||
| ν | stoichiometric constant | − | |
| adsorption capacity |
2.1. Control Signal Uncertainties
3. Mathematical Modeling
| Component | α | |||
|---|---|---|---|---|
| Insulin aspart | A | |||
| desB30 insulin | B | |||
| Insulin methyl ester | C |
3.1. Spatial Discretization
4. Problem Formulation
- i)
- Optimal control strategy I is exclusively concerned with the batch elution operation mode, where the limit cycle criteria are relaxed and the upper fractionating interval endpoint bounds the temporal horizon, i.e., .
- ii)
- Optimal control strategy II is concerned with the comprehensive CSS operation mode, where the temporal horizon includes the column regeneration and re-equilibration modes.
4.1. Cyclic-Steady-State Criteria Formulation
4.2. Open-loop Optimal Control Problem Formulation
4.3. Robust Counterpart Problem Formulation
5. Methods and Tools
5.1. The JModelica.org Toolchain
5.1.1. Optimization
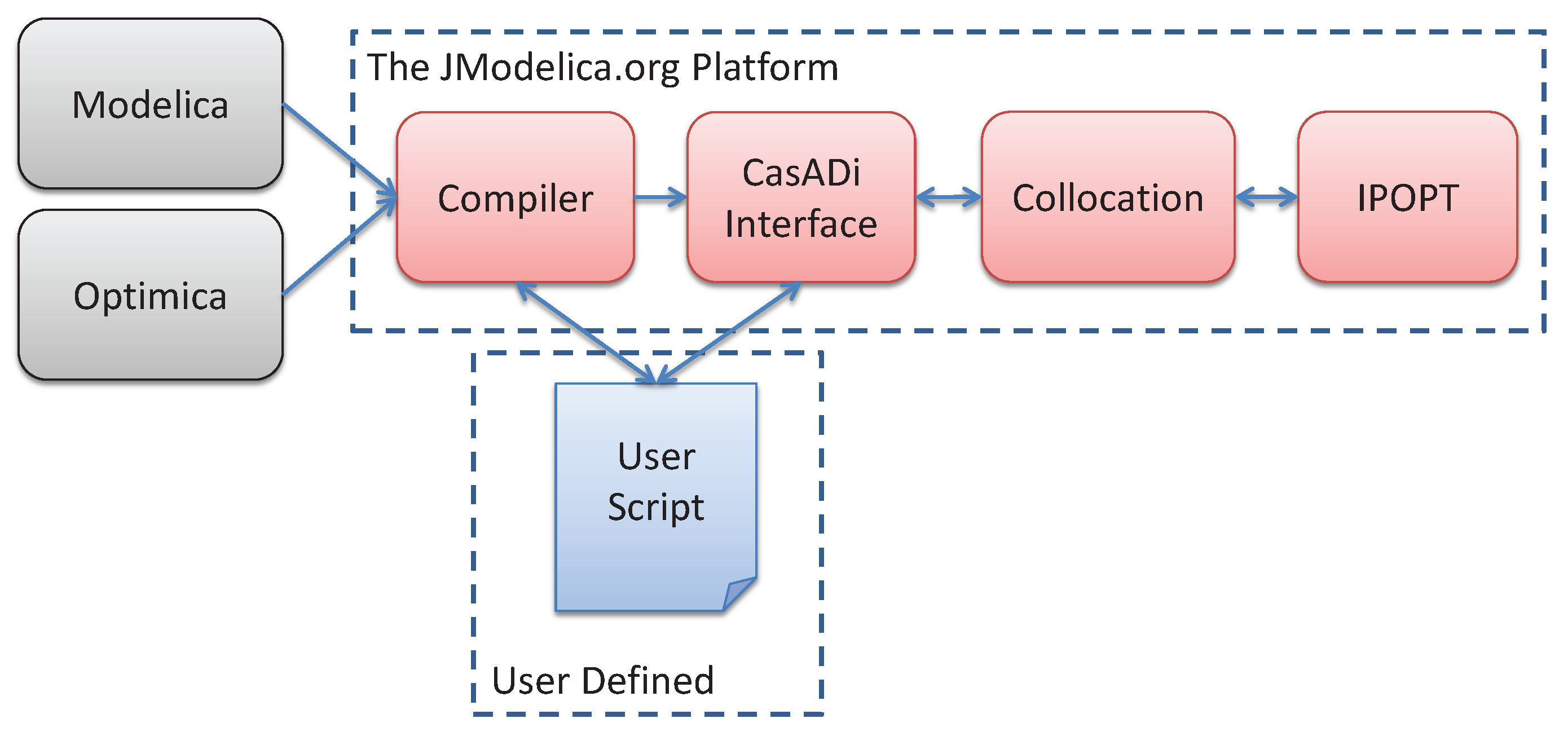
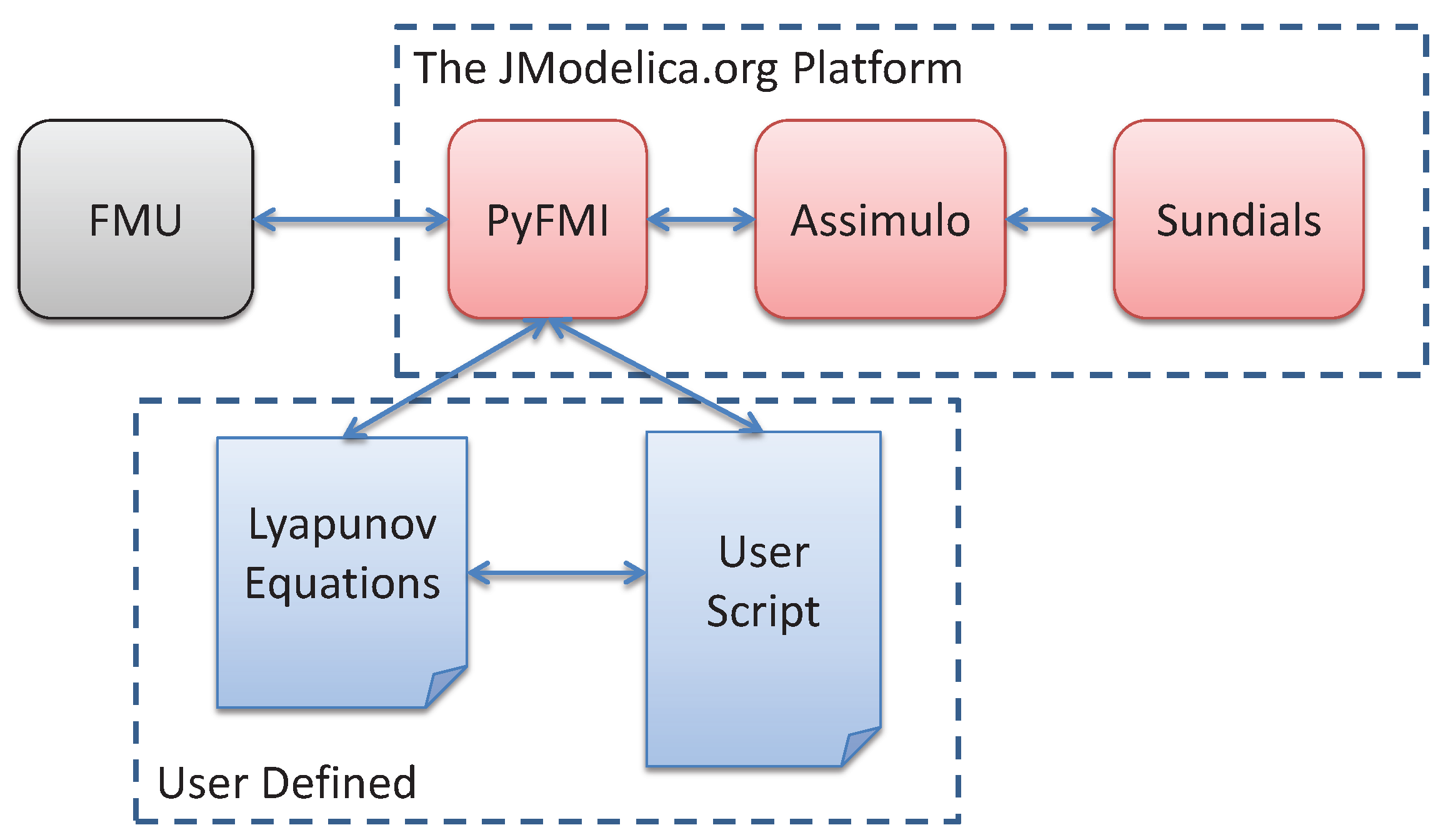
5.1.2. Simulation
5.2. Transcription of the Dynamic Optimization Problem
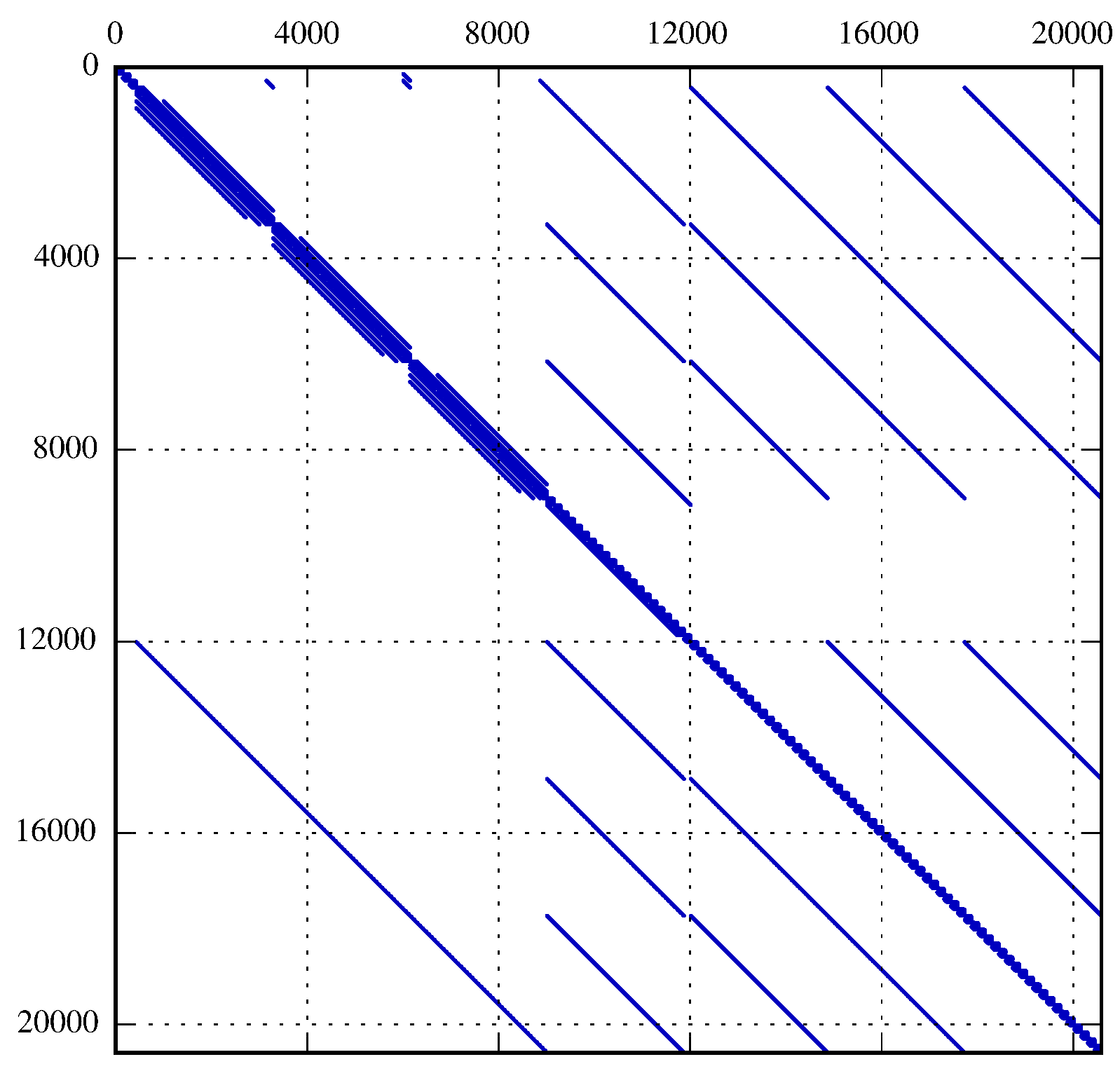
5.3. Simulation Setup and Coupling of the Lyapunov Equation

6. Results and Discussion
| Solutions to the Open-loop Optimal | Solutions to the Robust Counterpart | |||||
|---|---|---|---|---|---|---|
| Control Problem (Equation (11)) | Problem (Equation (19)) | |||||
| a | ||||||
| Solutions to the Open-loop Optimal | Solutions to the Robust Counterpart | |||||
|---|---|---|---|---|---|---|
| Control Problem (Equation (11)) | Problem (Equation (19)) | |||||
6.1. Optimal Control Strategy I—Nominal and Robustified Elution Trajectories in the Batch Elution Operation Mode
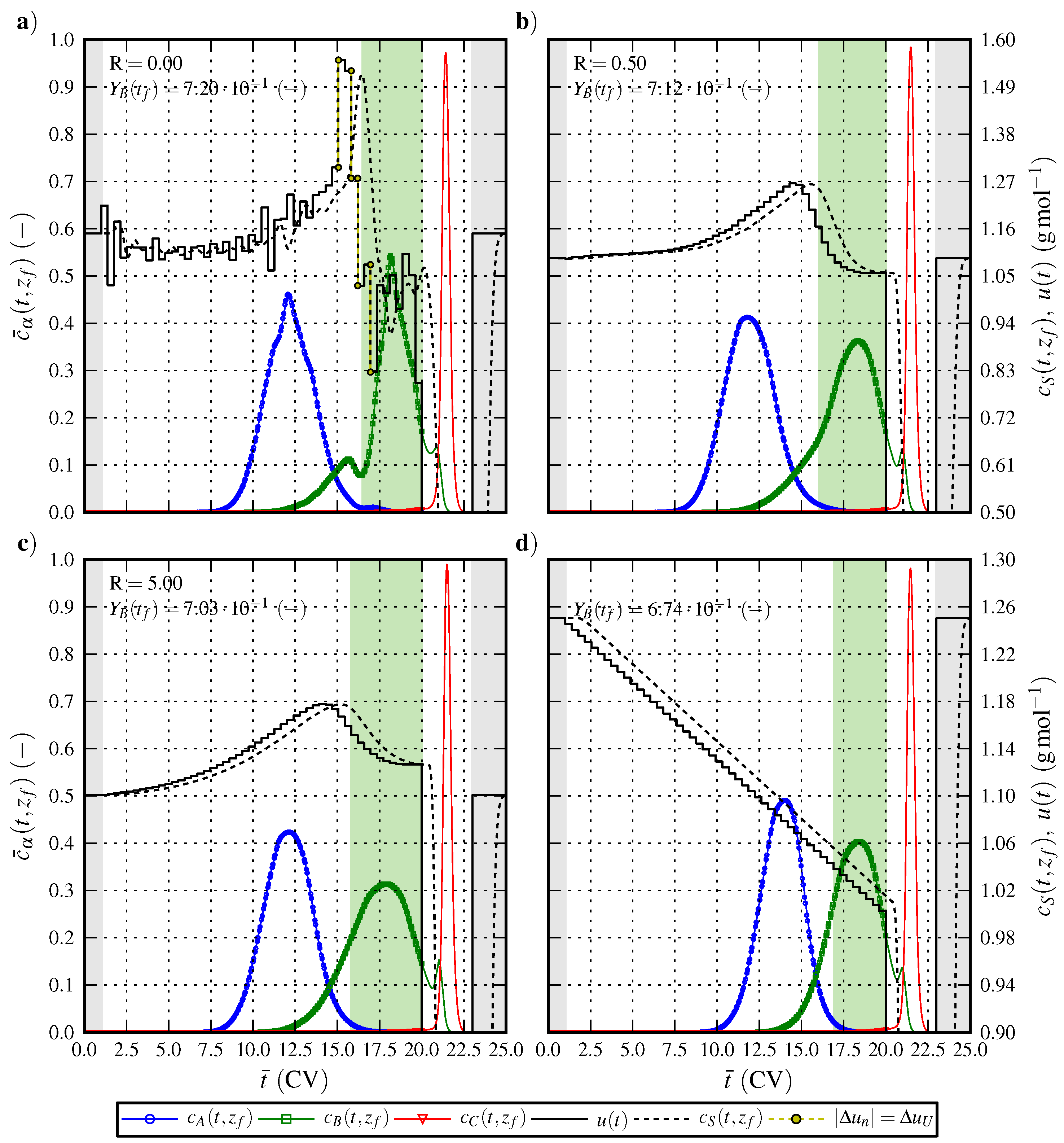
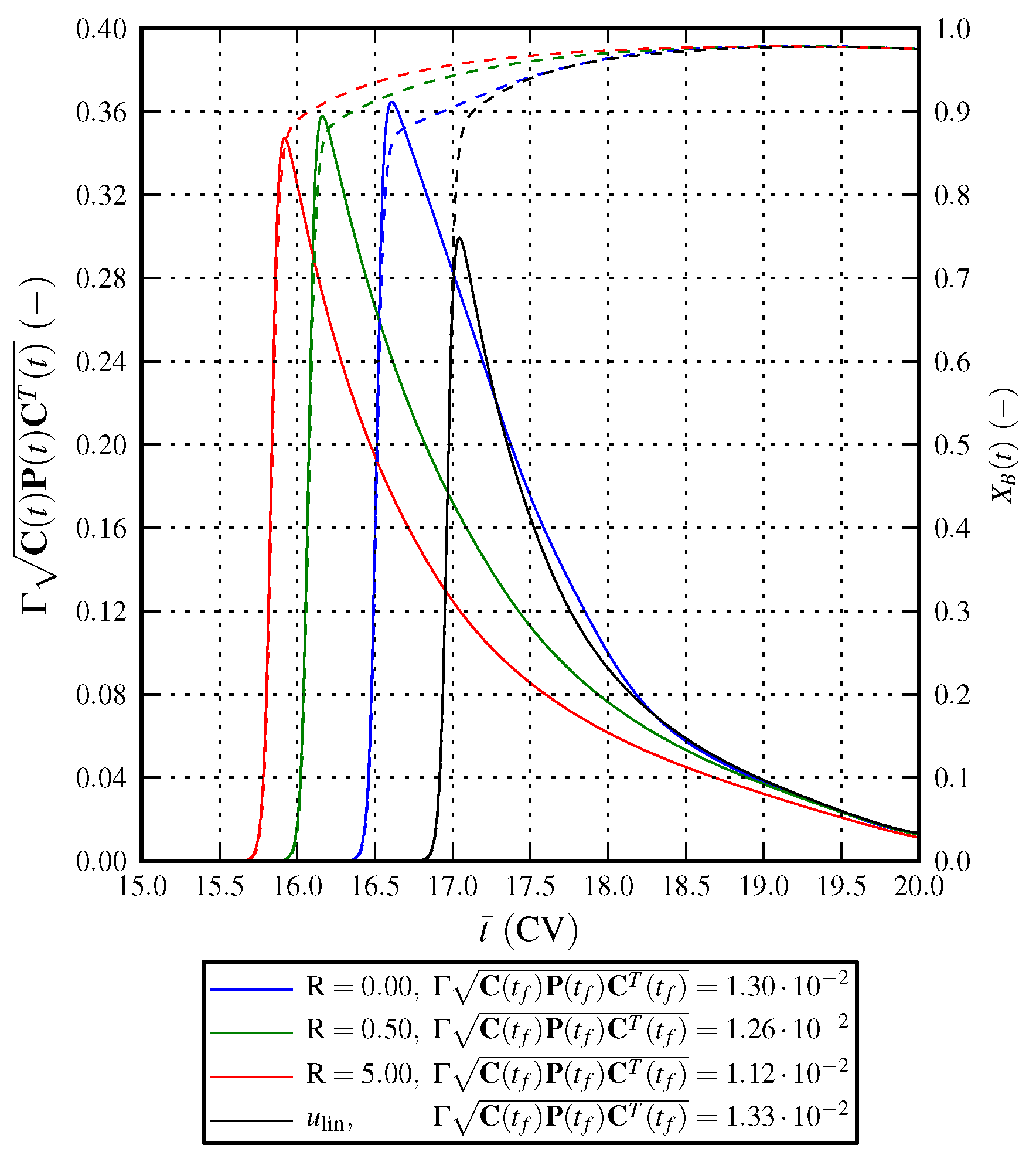

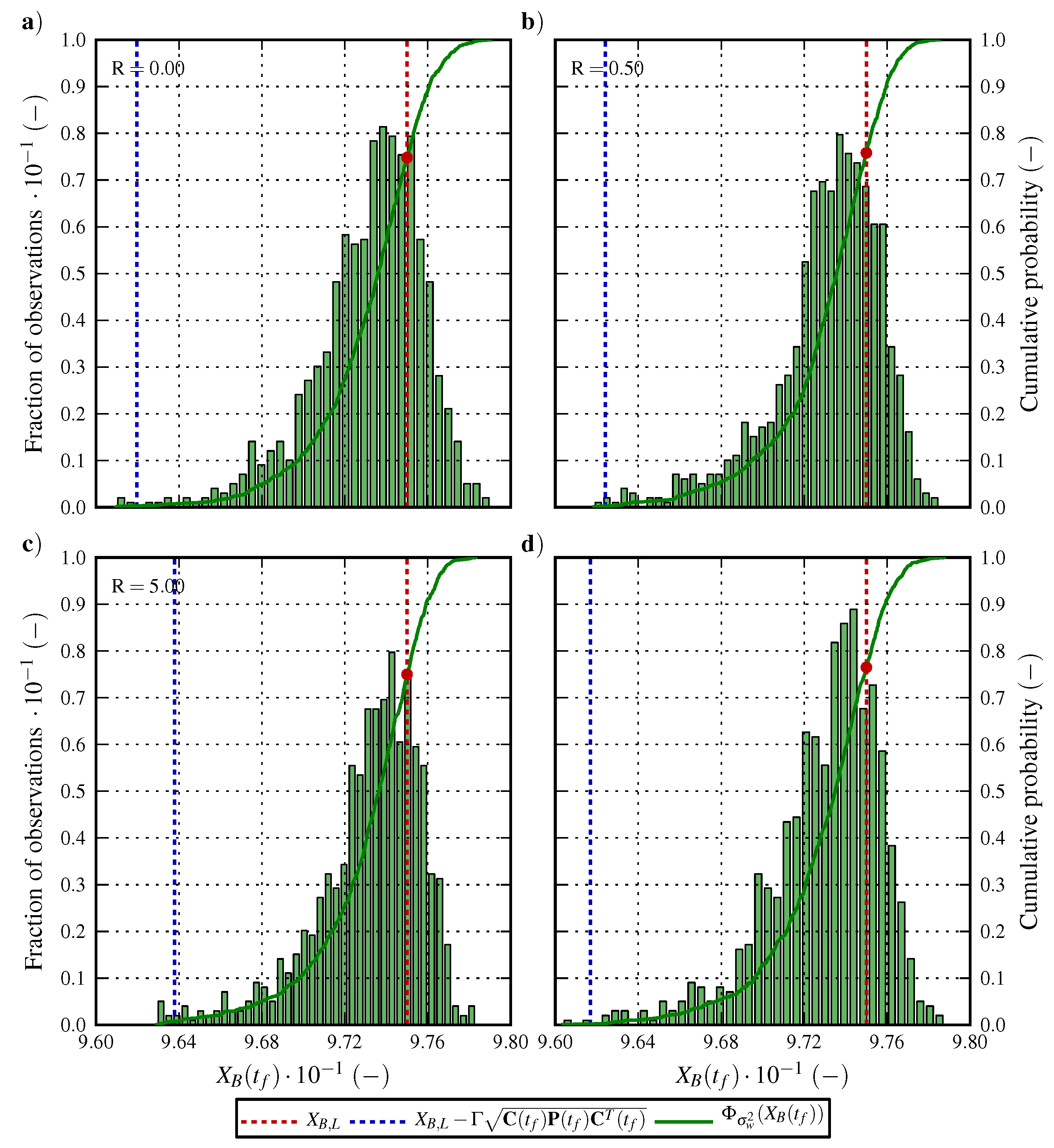
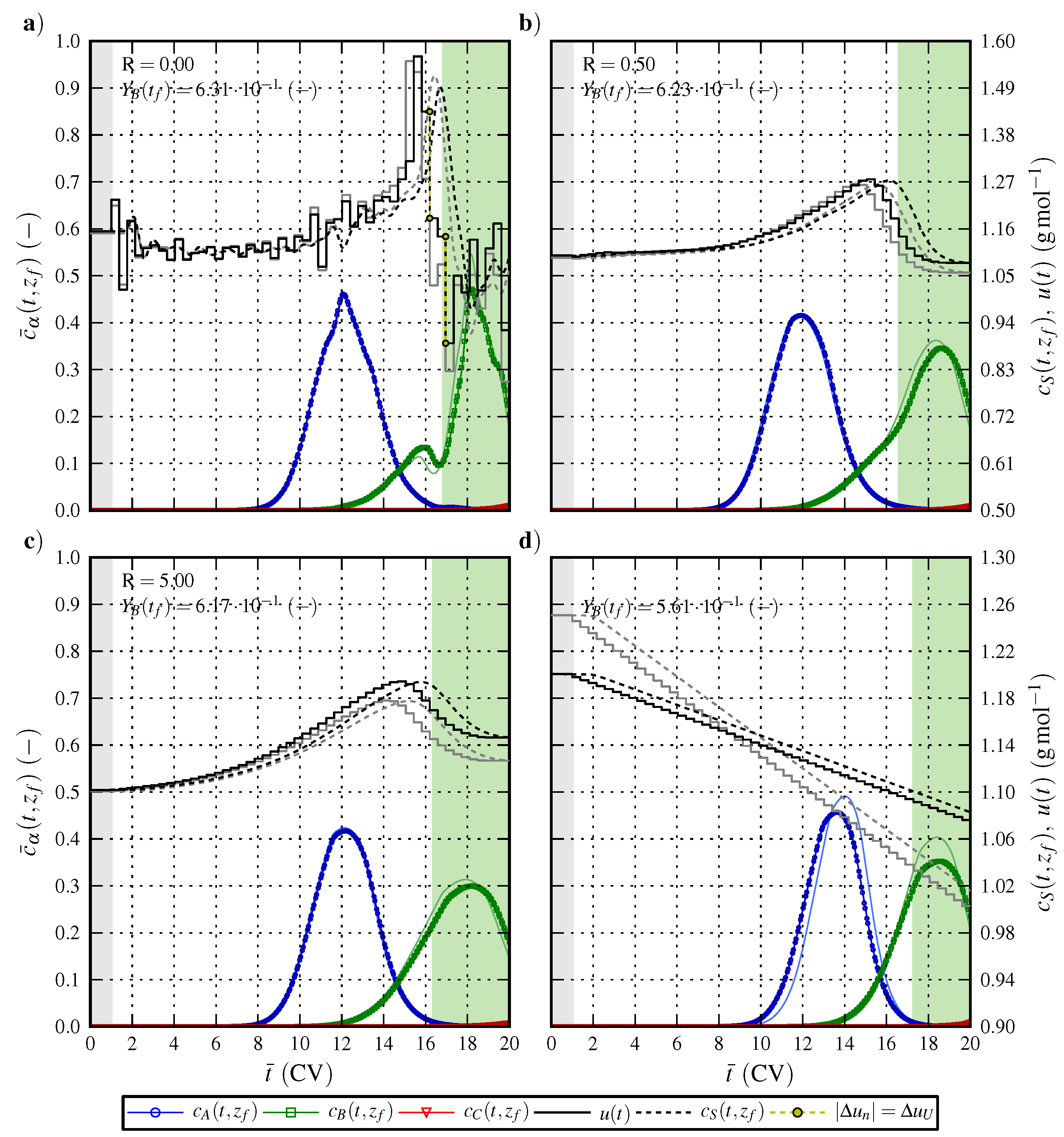
6.2. Optimal Control Strategy II—Nominal and Robustified Elution Trajectories in the Cyclic-Steady-State Operation Mode
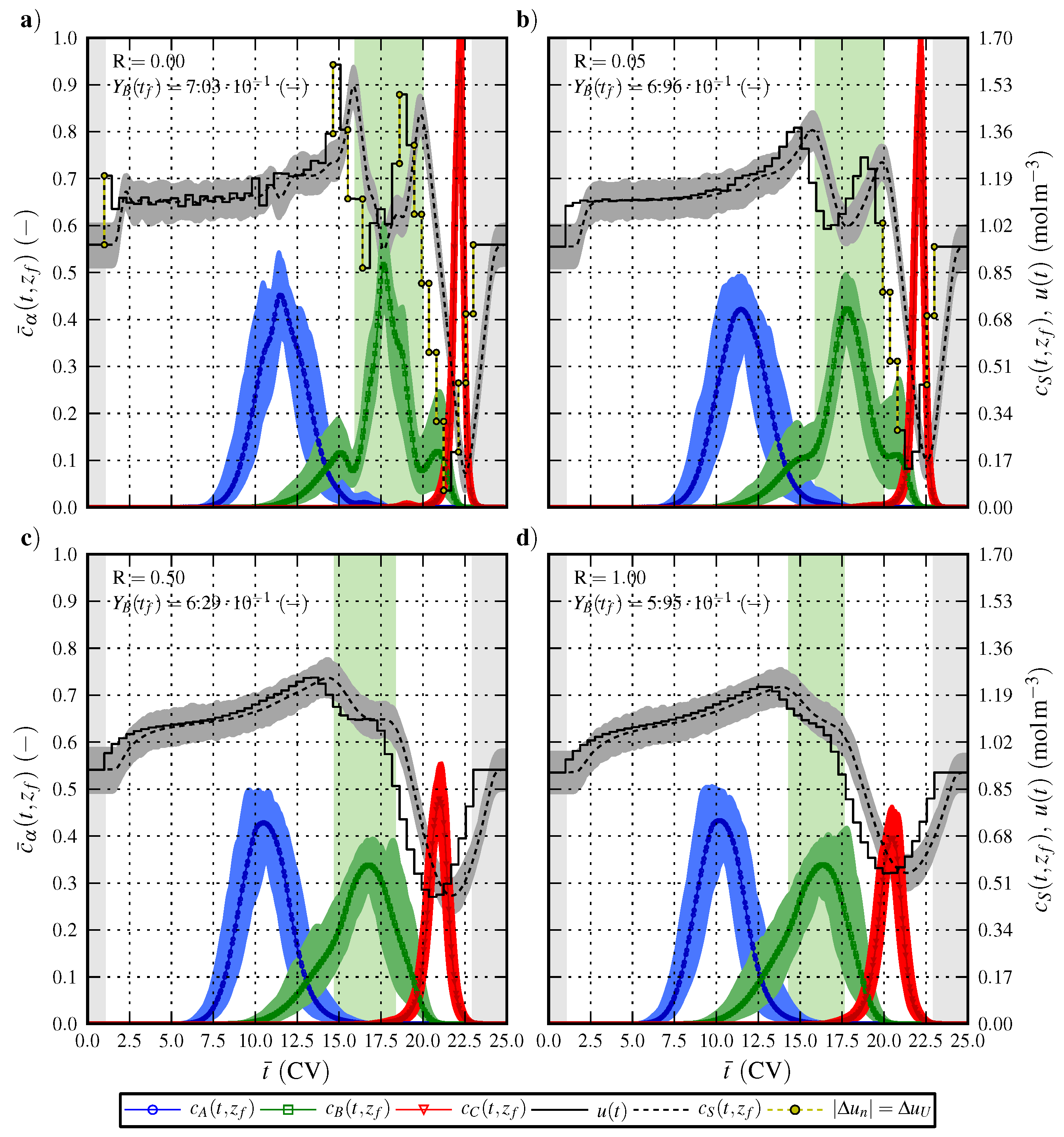

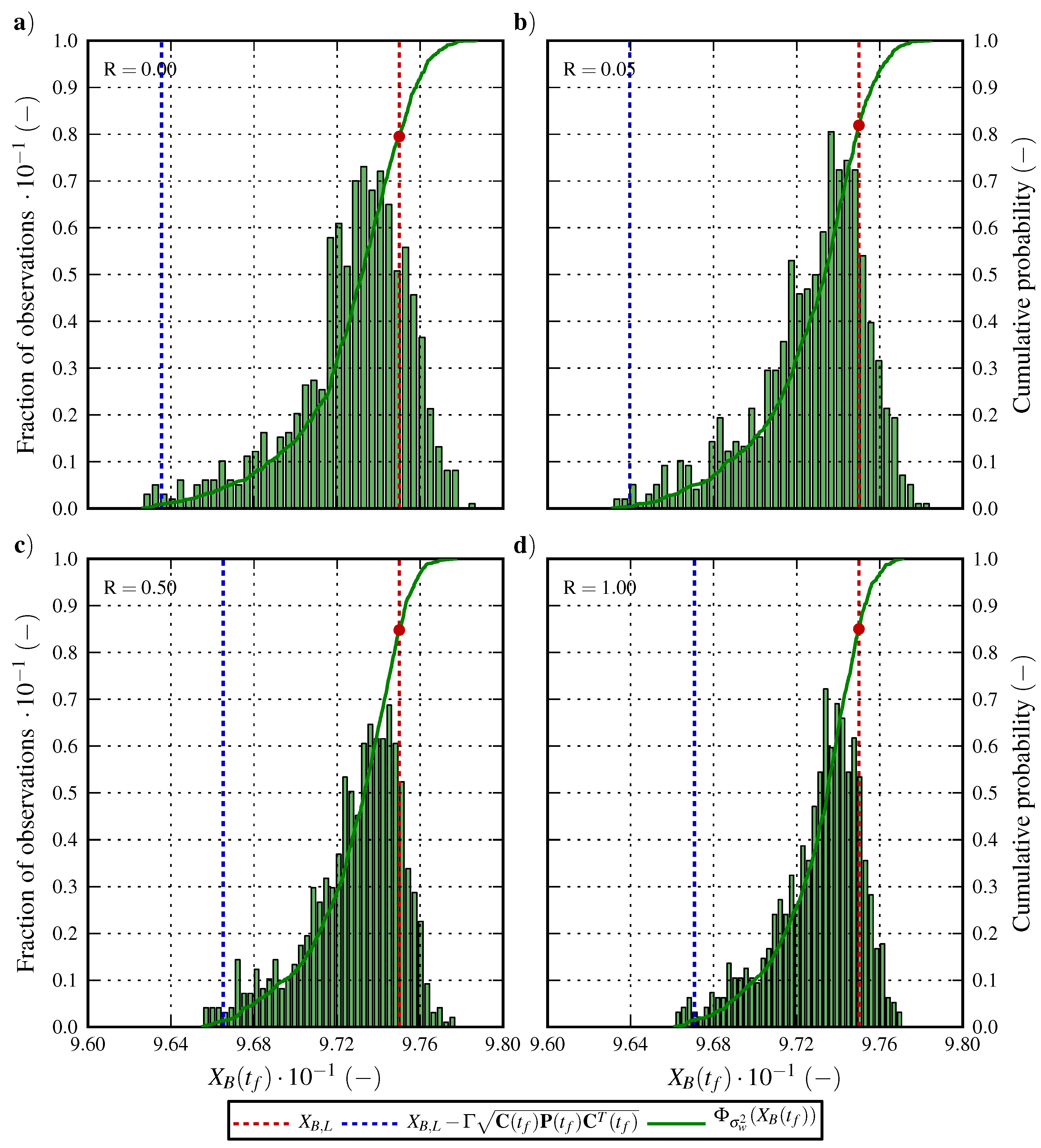

7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ündey, C.; Ertunç, S.; Mistretta, T.; Looze, B. Applied advanced process analytics in biopharmaceutical manufacturing: Challenges and prospects in real-time monitoring and control. J. Process Control 2010, 20, 1009–1018. [Google Scholar] [CrossRef]
- Jungbauer, A. Chromatographic media for bioseparation. J. Chromatogr. A 2005, 1065, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Wisniewski, E.; Boschetti, E.; Jungbauer, A. Biotechnology and biopharmaceutical manufacturing, processing, and preservation. In Drug Manufacturing Technology Series, 1st ed.; Avis, K.E., Wu, V.L., Eds.; Interpharm Press, Inc.: Buffalo Grove, IL, USA, 1996; Volume 2. [Google Scholar]
- Department of Health and Human Services U.S. Food and Drug Administration. Pharmaceutical cGMPs for the 21st Century: A Risk-based Approach; U.S. Food and Drug Administration: Silver Spring, MD, USA, 2004.
- Chirino, A.; Mire-Sluis, A. Characteristics biological products and assessing comparability following manufacturing changes. Nat. Biotechnol. 2004, 22, 1383–1391. [Google Scholar] [CrossRef] [PubMed]
- Rathore, A.S.; Yu, M.; Yeboah, S.; Sharma, A. Case study and application of process analytical technology (PAT) towards bioprocessing: Use of on-line high-performance liquid chromatography (HPLC) for making real-time pooling decisions for process chromatography. Biotechnol. Bioeng. 2008, 100, 306–316. [Google Scholar] [CrossRef] [PubMed]
- Close, E.J.; Salm, J.R.; Bracewell, D.G.; Sorensen, E. A model based approach for identifying robust operating conditions for industrial chromatography with process variability. Chem. Eng. Sci. 2014, 116, 284–295. [Google Scholar] [CrossRef]
- Jiang, C.; Flansburg, L.; Ghose, S.; Jorjorian, P.; Shukla, A.A. Defining process design space for a hydrophobic interaction chromatography (HIC) purification step: Application of quality by design (QbD) principles. Biotechnol. Bioeng. 2010, 107, 985–997. [Google Scholar] [CrossRef] [PubMed]
- Harms, J.; Wang, X.; Kim, T.; Yang, X.; Rathore, A.S. Defining process design space for biotech products: Case study of pichia pastoris fermentation. Biotechnol. Prog. 2008, 24, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Rathore, A.; Winkle, H. Quality by design for biopharmaceuticals. Nat. Biotechnol. 2009, 27, 26–34. [Google Scholar] [CrossRef] [PubMed]
- Mota, J.P.B.; Araújo, J.M.M.; Rodrigues, R.C.R. Optimal design of simulated moving-bed processes under flow rate uncertainty. AIChE J. 2007, 53, 2630–2642. [Google Scholar] [CrossRef]
- Degerman, M.; Westerberg, K.; Nilsson, B. A model-based approach to determine the design space of preparative chromatography. Chem. Eng. Technol. 2009, 32, 1195–1202. [Google Scholar] [CrossRef]
- Westerberg, K.; Broberg Hansen, E.; Degerman, M.; Budde Hansen, T.; Nilsson, B. Model-based process challenge of an industrial ion-exchange chromatography step. Chem. Eng. Technol. 2012, 35, 183–190. [Google Scholar] [CrossRef]
- Borg, N.; Westerberg, K.; Andersson, N.; von Lieres, E.; Nilsson, B. Effects of uncertainties in experimental conditions on the estimation of adsorption model parameters in preparative chromatography. Comput. Chem. Eng. 2013, 55, 148–157. [Google Scholar] [CrossRef]
- Snyder, L.R.; Dolan, J.W. High-Performance Gradient Elution: The Practical Application of the Linear-Solvent-Strength Model; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Sreedhar, B.; Wagler, A.; Kaspereit, M.; Seidel-Morgenstern, A. Optimal cut-times finding strategies for collecting a target component from overloaded elution chromatograms. Comput. Chem. Eng. 2013, 49, 158–169. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. The distortion of gradient profiles in reversed-phase liquid chromatography. J. Chromatogr. A 2014, 1340, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Tarafder, A.; Aumann, L.; Müller-Späth, T.; Morbidelli, M. Improvement of an overloaded, multi-component, solvent gradient bioseparation through multiobjective optimization. J. Chromatogr. A 2007, 1167, 42–53. [Google Scholar] [CrossRef] [PubMed]
- Damtew, A.; Sreedhar, B.; Seidel-Morgenstern, A. Evaluation of the potential of nonlinear gradients for separating a ternary mixture. J. Chromatogr. A 2009, 1216, 5355–5364. [Google Scholar] [CrossRef] [PubMed]
- Nikitas, P.; Pappa-Louisi, A.; Papachristos, K. Optimisation technique for stepwise gradient elution in reversed-phase liquid chromatography. J. Chromatogr. A 2004, 1033, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Holmqvist, A.; Magnusson, F. Open-loop optimal control of batch chromatographic separation processes using direct collocation. J. Process Control 2015. submitted for publication. [Google Scholar]
- Holmqvist, A.; Magnusson, F.; Nilsson, B. Dynamic multi-objective optimization of batch chromatographic separation processes. Computer Aided Chemical Engineering 2015, Volume 37, 815–820. [Google Scholar]
- ICH Harmonised Tripartite Guideline. Pharmaceutical Development Q8(R2), Annex to Pharmaceutical Development, Step 4, August 2009. Available online: http://www.ich.org/products/guidelines/quality/article/quality-guidelines.html (accessed on 10 July 2015).
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Daubechies, I., Weinan, E., Lenstra, J.K., Süli, E., Eds.; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Schmidt-Traub, H.; Schulte, M.; Seidel-Morgenstern, A. Preparative Chromatography, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Lienqueo, M.E.; Mahn, A.; Salgado, J.C.; Asenjo, J.A. Current insights on protein behaviour in hydrophobic interaction chromatography. J. Chromatogr. B 2007, 849, 53–68. [Google Scholar] [CrossRef] [PubMed]
- Mahn, A.; Lienqueo, M.E.; Asenjo, J.A. Optimal operation conditions for protein separation in hydrophobic interaction chromatography. J. Chromatogr. B 2007, 849, 236–242. [Google Scholar] [CrossRef] [PubMed]
- Biegler, L.T.; Ghattas, O.; Heinkenschloss, M.; van Bloemen Waanders, B. Large-scale PDE-constrained optimization. In Lecture Notes in Computational Science and Engineering; Barth, T.J., Griebel, M., Keyes, D.E., Nieminen, R.M., Roose, D., Schlick, T., Eds.; Springer: Berlin, Germany, 2003; Volume 30. [Google Scholar]
- Wendl, S.; Pesch, H.; Rund, A. On a state-constrained PDE optimal control. In Recent Advances in Optimization and its Applications in Engineering; Diehl, M., Glineur, F., Jarlebring, E., Michiels, W., Eds.; Springer: Berlin, Germany, 2010; pp. 429–438. [Google Scholar]
- Herzog, R.; Kunisch, K. Algorithms for PDE-constrained optimization. GAMM-Mitteilungen 2010, 33, 163–176. [Google Scholar] [CrossRef]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Betts, J. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; SIAM’s Advances in Design and Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Davis, M.E. Numerical Methods and Modeling for Chemical Engineers, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Schiesser, W.E. The Numerical Method of Lines: Integration of Partial Differential Equations, 1st ed.; Academic Press: San Diago, CA, USA, 1991. [Google Scholar]
- Gao, W.; Engell, S. Iterative set-point optimization of batch chromatography. Comput. Chem. Eng. 2005, 29, 1401–1409. [Google Scholar] [CrossRef]
- Dünnebier, G.; Engell, S.; Epping, A.; Hanisch, F.; Jupke, A.; Klatt, K.U.; Schmidt-Traub, H. Model-based control of batch chromatography. AIChE J. 2001, 47, 2493–2502. [Google Scholar] [CrossRef]
- Kawajiri, Y.; Biegler, L.T. Optimization strategies for simulated moving bed and PowerFeed processes. AIChE J. 2006, 52, 1343–1350. [Google Scholar] [CrossRef]
- Nagrath, D.; Messac, A.; Bequette, B.W.; Cramer, S.M. A hybrid model framework for the optimization of preparative chromatographic processes. Biotechnol. Prog. 2004, 20, 162–178. [Google Scholar] [CrossRef] [PubMed]
- Sreedhar, B.; Damtew, A.; Seidel-Morgenstern, A. Theoretical study of preparative chromatography using closed-loop recycling with an initial gradient. J. Chromatogr. A 2009, 1216, 4976–4988. [Google Scholar] [CrossRef] [PubMed]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Shu, C.W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Quarteroni, A., Ed.; Springer: Berlin, Germany, 1998; Volume 1697, pp. 325–432. [Google Scholar]
- John, V.; Novo, J. On (essentially) non-oscillatory discretizations of evolutionary convection–diffusion equations. J. Comput. Phys. 2012, 231, 1570–1586. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Programm. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Griewank, A. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Püttmann, A.; Schnittert, S.; Naumann, U.; von Lieres, E. Fast and accurate parameter sensitivities for the general rate model of column liquid chromatography. Comput. Chem. Eng. 2013, 56, 46–57. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 2004, 28, 971–983. [Google Scholar] [CrossRef]
- Mitra, K. Multiobjective optimization of an industrial grinding operation under uncertainty. Chem. Eng. Sci. 2009, 64, 5043–5056. [Google Scholar] [CrossRef]
- Pinto, J.C. On the costs of parameter uncertainties. Effects of parameter uncertainties during optimization and design of experiments. Chem. Eng. Sci. 1998, 53, 2029–2040. [Google Scholar]
- Logist, F.; Houska, B.; Diehl, M.; van Impe, J.F. Robust multi-objective optimal control of uncertain (bio)chemical processes. Chem. Eng. Sci. 2011, 66, 4670–4682. [Google Scholar] [CrossRef]
- Houska, B.; Diehl, M. Nonlinear robust optimization of uncertainty affine dynamic systems under the L-infinity norm. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design (CACSD), Yokohama, Japan, 8–10 September 2010; pp. 1091–1096.
- Houska, B.; Logist, F.; Impe, J.V.; Diehl, M. Robust optimization of nonlinear dynamic systems with application to a jacketed tubular reactor. J. Process Control 2012, 22, 1152–1160. [Google Scholar] [CrossRef]
- Klatt, K.U.; Hanisch, F.; Dünnebier, G.; Engell, S. Model-based optimization and control of chromatographic processes. Comput. Chem. Eng. 2000, 24, 1119–1126. [Google Scholar] [CrossRef]
- Shan, Y.; Seidel-Morgenstern, A. Optimization of gradient elution conditions in multicomponent preparative liquid chromatography. J. Chromatogr. A 2005, 1093, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Hansen, S.K.; Skibsted, E.; Staby, A.; Hubbuch, J. A label-free methodology for selective protein quantification by means of absorption measurements. Biotechnol. Bioeng. 2011, 108, 2661–2669. [Google Scholar] [CrossRef] [PubMed]
- Sherwood, T.K.; Pigford, R.L.; Wilke, C.R. Mass Transfer; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Mollerup, J.M. A review of the thermodynamics of protein association to ligands, protein adsorption, and adsorption isotherms. Chem. Eng. Technol. 2008, 31, 864–874. [Google Scholar] [CrossRef]
- Forssén, P.; Arnell, R.; Fornstedt, T. An improved algorithm for solving inverse problems in liquid chromatography. Comput. Chem. Eng. 2006, 30, 1381–1391. [Google Scholar] [CrossRef]
- Cornel, J.; Tarafder, A.; Katsuo, S.; Mazzotti, M. The direct inverse method: A novel approach to estimate adsorption isotherm parameters. J. Chromatogr. A 2010, 1217, 1934–1941. [Google Scholar] [CrossRef] [PubMed]
- Hahn, T.; Sommer, A.; Osberghaus, A.; Heuveline, V.; Hubbuch, J. Adjoint-based estimation and optimization for column liquid chromatography models. Comput. Chem. Eng. 2014, 64, 41–54. [Google Scholar] [CrossRef]
- Johansson, K.; Frederiksen, S.S.; Degerman, M.; Breil, M.P.; Mollerup, J.M.; Nilsson, B. Combined effects of potassium chloride and ethanol as mobile phase modulators on hydrophobic interaction and reversed-phase chromatography of three insulin variants. J. Chromatogr. A 2015, 1381, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Sweby, P.K. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Shu, C. High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. Soc. Ind. Appl. Math. 2009, 51, 82–126. [Google Scholar] [CrossRef]
- Schellinger, A.P.; Stoll, D.R.; Carr, P.W. High speed gradient elution reversed-phase liquid chromatography. J. Chromatogr. A 2005, 1064, 143–156. [Google Scholar] [CrossRef] [PubMed]
- Schellinger, A.P.; Carr, P.W. Isocratic and gradient elution chromatography: A comparison in terms of speed, retention reproducibility and quantitation. J. Chromatogr. A 2006, 1109, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Navarro, A.; Caruel, H.; Rigal, L.; Phemius, P. Continuous chromatographic separation process: Simulated moving bed allowing simultaneous withdrawal of three fractions. J. Chromatogr. A 1997, 770, 39–50. [Google Scholar] [CrossRef]
- Aumann, L.; Stroehlein, G.; Morbidelli, M. Parametric study of a 6-column countercurrent solvent gradient purification (MCSGP) unit. Biotechnol. Bioeng. 2007, 98, 1029–1042. [Google Scholar] [CrossRef] [PubMed]
- Osberghaus, A.; Hepbildikler, S.; Nath, S.; Haindl, M.; von Lieres, E.; Hubbuch, J. Optimizing a chromatographic three component separation: A comparison of mechanistic and empiric modeling approaches. J. Chromatogr. A 2012, 1237, 86–95. [Google Scholar] [CrossRef] [PubMed]
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Biegler, L.T.; Cervantes, A.M.; Wächter, A. Advances in simultaneous strategies for dynamic process optimization. Chem. Eng. Sci. 2002, 57, 575–593. [Google Scholar] [CrossRef]
- Houska, B.; Diehl, M. Robust nonlinear optimal control of dynamic systems with affine uncertainties. In Proceedings of the 48th IEEE Conference on Decision and Control, 2009 held jointly with the 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 2274–2279.
- Åkesson, J.; Årzén, K.E.; Gäfvert, M.; Bergdahl, T.; Tummescheit, H. Modeling and optimization with Optimica and JModelica.org—Languages and tools for solving large-scale dynamic optimization problems. Comput. Chem. Eng. 2010, 34, 1737–1749. [Google Scholar]
- Elmqvist, H.; Mattsson, S.E. Modelica—The next generation modeling language an international design effort. In Proceedings of the 1st World Congress of System Simulation, Singapore, 1–4 September 1997; pp. 1–3.
- Åkesson, J. Optimica—An extension of modelica supporting dynamic optimization. In Proceedings of the 6th International Modelica Conference, Bielefeld, Germany, 3–4 March 2008.
- Blochwitz, T.; Otter, M.; Åkesson, J.; Arnold, M.; Clauss, C.; Elmqvist, H.; Friedrich, M.; Junghanns, A.; Mauss, J.; Neumerkel, D.; et al. Functional mockup interface 2.0: The standard for tool independent exchange of simulation models. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3 September 2012.
- Andersson, J. A General-purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, Arenberg Doctoral School, KU Leuven, Leuven, Belgium, 2013. [Google Scholar]
- Lennernäs, B. A CasADi Based Toolchain for JModelica.org. Master’s Thesis, Lund University, Lund, Sweden, 2013. [Google Scholar]
- Andersson, C.; Führer, C.; Åkesson, J. Assimulo: A unified framework for ODE solvers. Math. Comput. Simul. 2015, 116, 26–43. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Magnusson, F.; Åkesson, J. Collocation methods for optimization in a modelica environment. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012.
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-algebraic Problems, 2nd ed.; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Dassault Systèmes. Dymola—Multi-Engineering Modeling and Simulation—Version 2015 FD01. Available online: http://www.dymola.com/ (accessed on 30 April 2015).
- Curtis, A.; Powell, M.J.; Reid, J.K. On the estimation of sparse Jacobian matrices. J. Appl. Math. 1974, 13, 117–120. [Google Scholar] [CrossRef]
- HSL. A Collection of Fortran Codes for Large Scale Scientific Computation. Available online: http://www.hsl.rl.ac.uk (accessed on 10 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holmqvist, A.; Andersson, C.; Magnusson, F.; Åkesson, J. Methods and Tools for Robust Optimal Control of Batch Chromatographic Separation Processes. Processes 2015, 3, 568-606. https://doi.org/10.3390/pr3030568
Holmqvist A, Andersson C, Magnusson F, Åkesson J. Methods and Tools for Robust Optimal Control of Batch Chromatographic Separation Processes. Processes. 2015; 3(3):568-606. https://doi.org/10.3390/pr3030568
Chicago/Turabian StyleHolmqvist, Anders, Christian Andersson, Fredrik Magnusson, and Johan Åkesson. 2015. "Methods and Tools for Robust Optimal Control of Batch Chromatographic Separation Processes" Processes 3, no. 3: 568-606. https://doi.org/10.3390/pr3030568





