Network Analysis Identifies Crosstalk Interactions Governing TGF-β Signaling Dynamics during Endoderm Differentiation of Human Embryonic Stem Cells
Abstract
:1. Introduction
2. Methods
2.1. Cell Culture and Treatment
2.1.1. Human ESC Maintenance
2.1.2. Experimental Induction of Endoderm from hESCs
2.1.3. Measuring Experimental Dynamics of Signaling Molecules
2.2. Identification of Network Interactions from Experimental Time Series Signaling Data
2.2.1. Details of DBN Algorithm
2.2.2. Constructing the DBNs
3. Results and Discussion
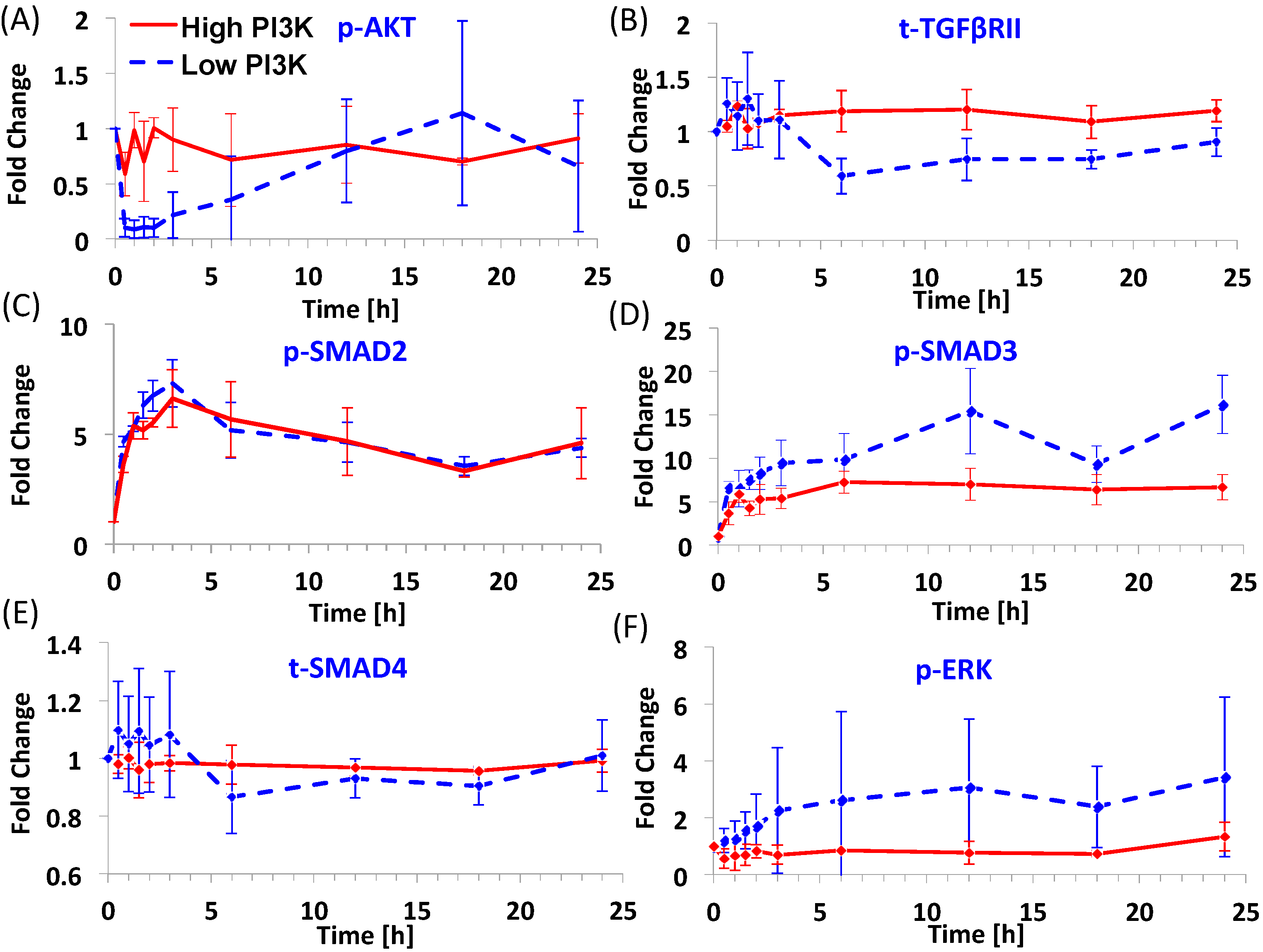
3.1. Dynamics of Signaling Molecules during Endoderm Induction
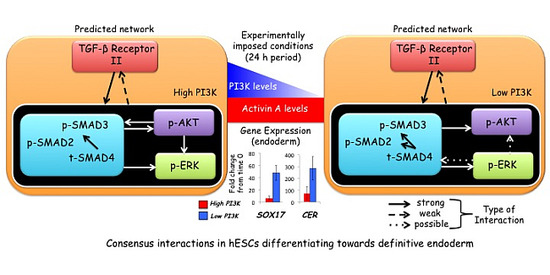
3.2. Predictions of Network Interactions by DBN Analysis on Entire Time Series
3.2.1. DBN Analysis and Consensus Graph
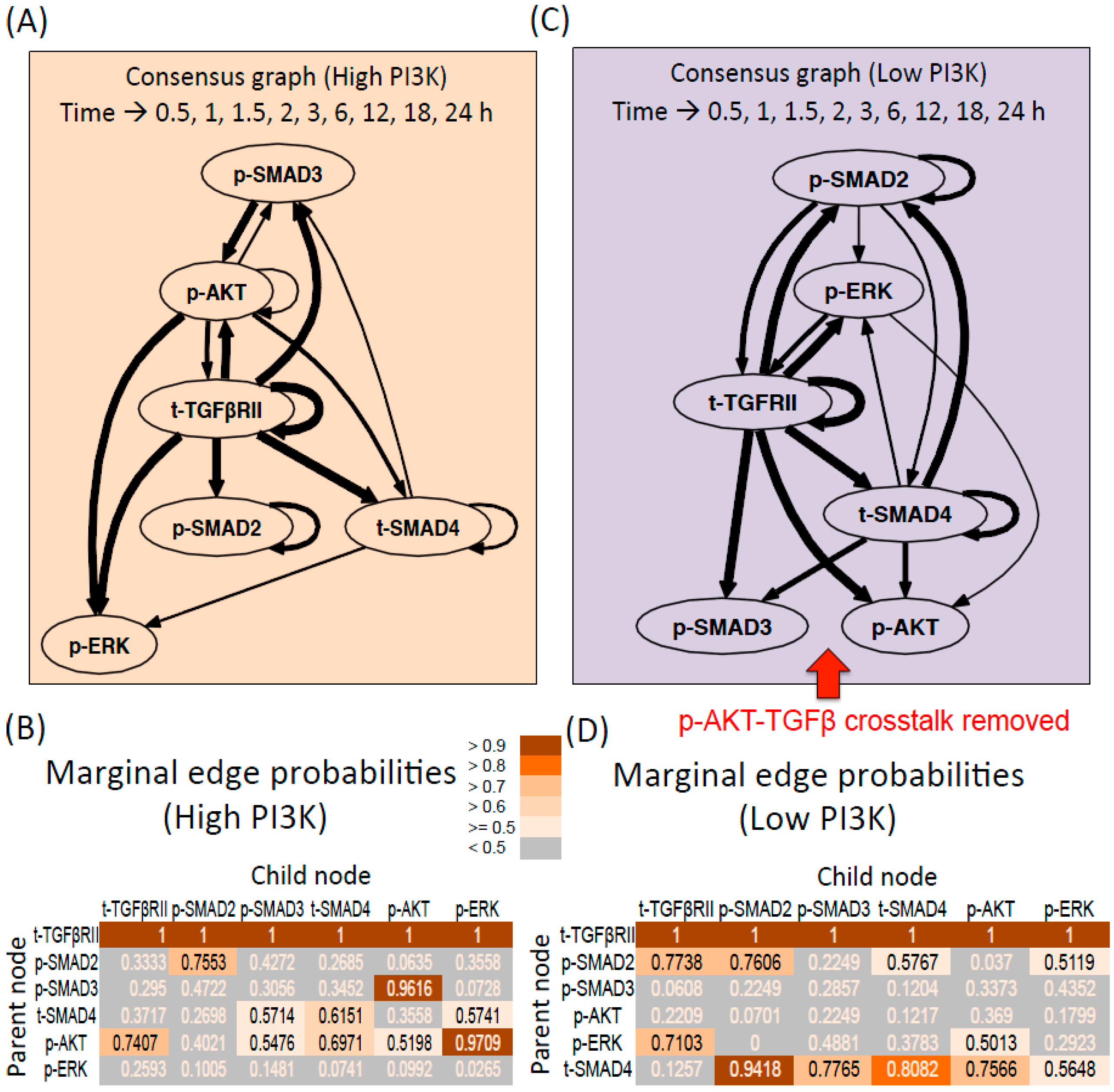
3.2.2. High PI3K Condition
3.2.3. Low PI3K Condition
3.2.4. Comparison between Digraphs of High and low PI3K Conditions
Influence of Total Receptor Levels
Interactions between Intracellular Molecules
3.2.5. Change-points Inferred by cpBGe Model
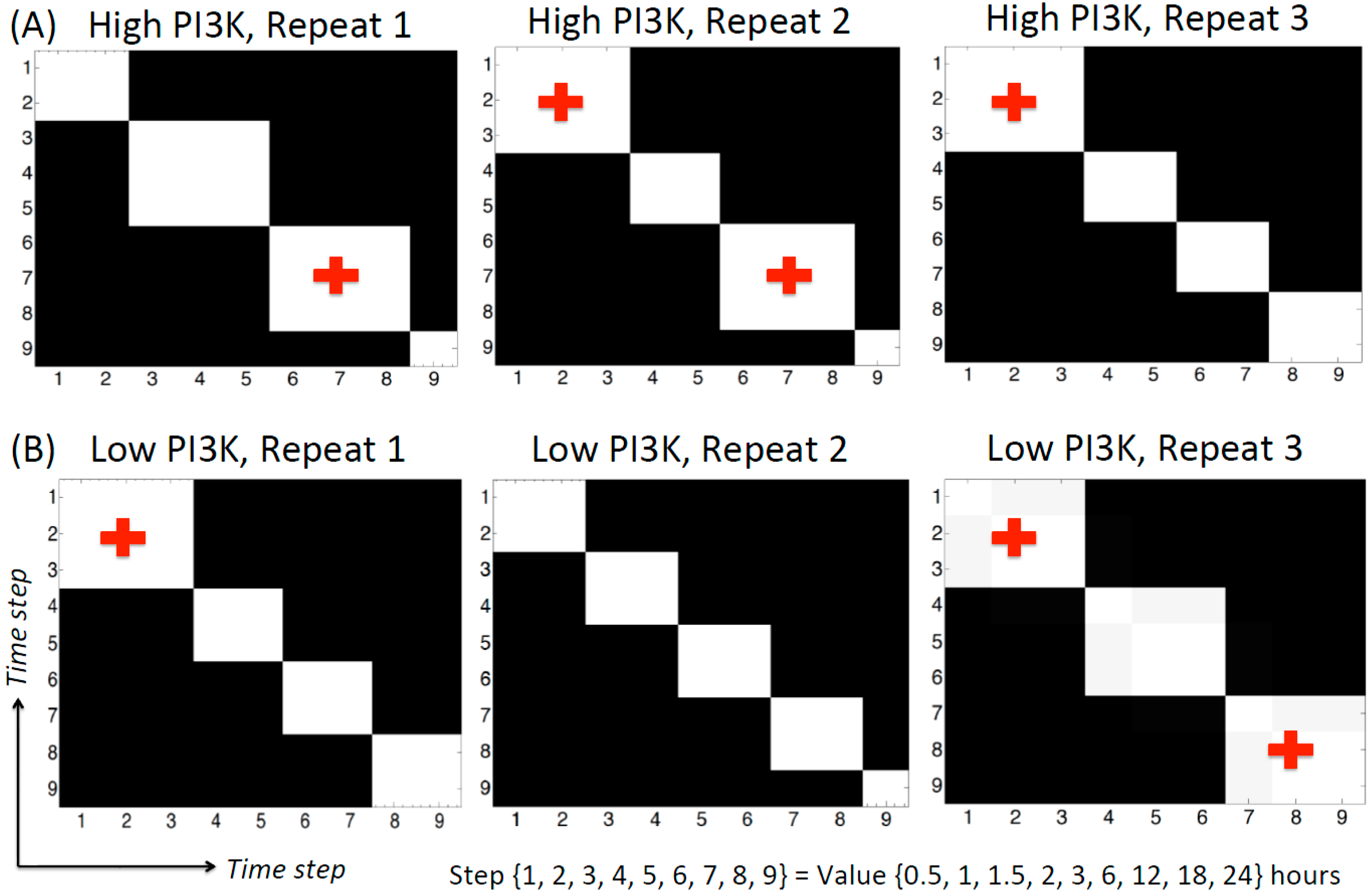
3.3. Changes in Regulatory Structure across Time Zones
3.3.1. High PI3K Condition
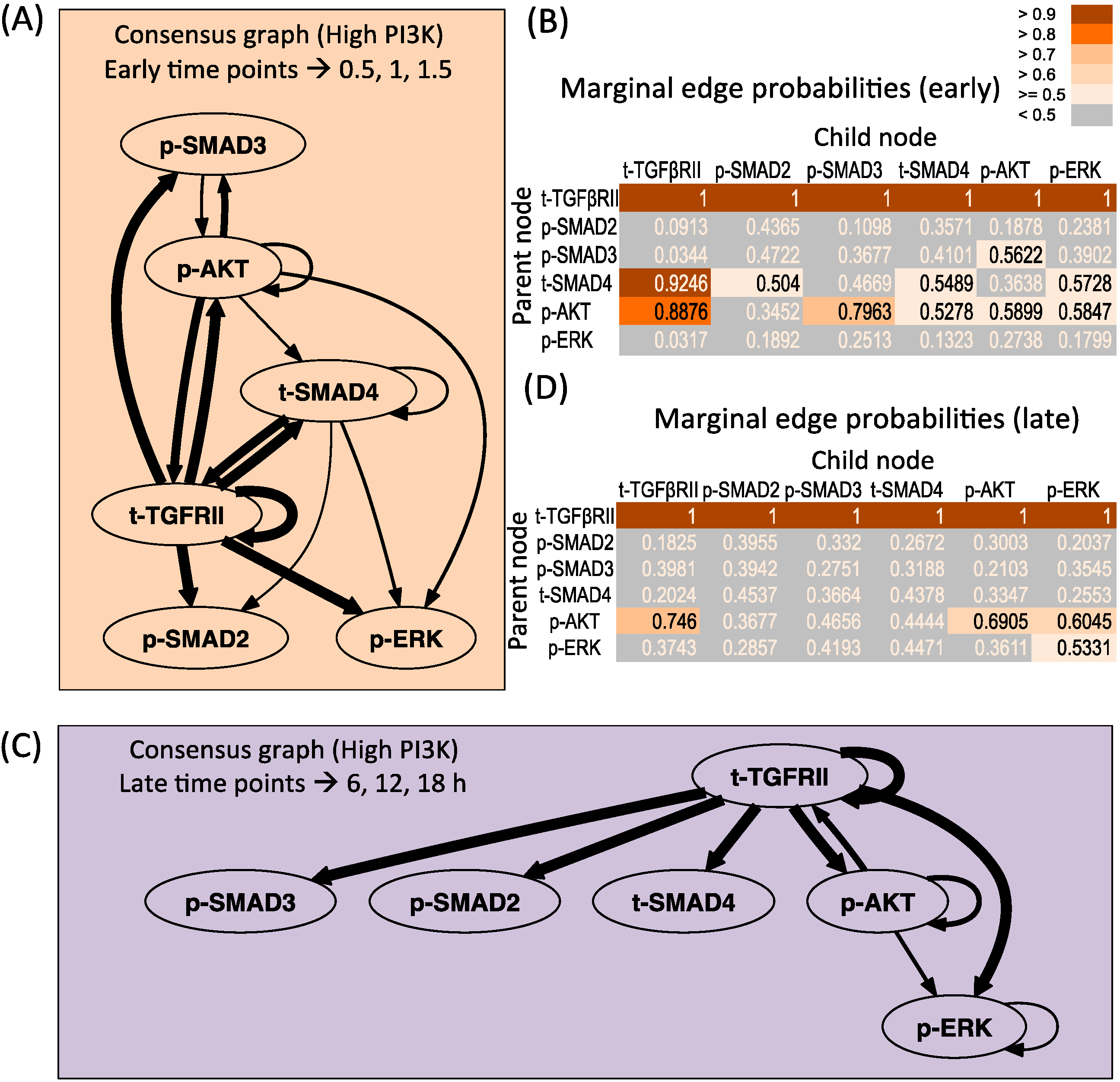
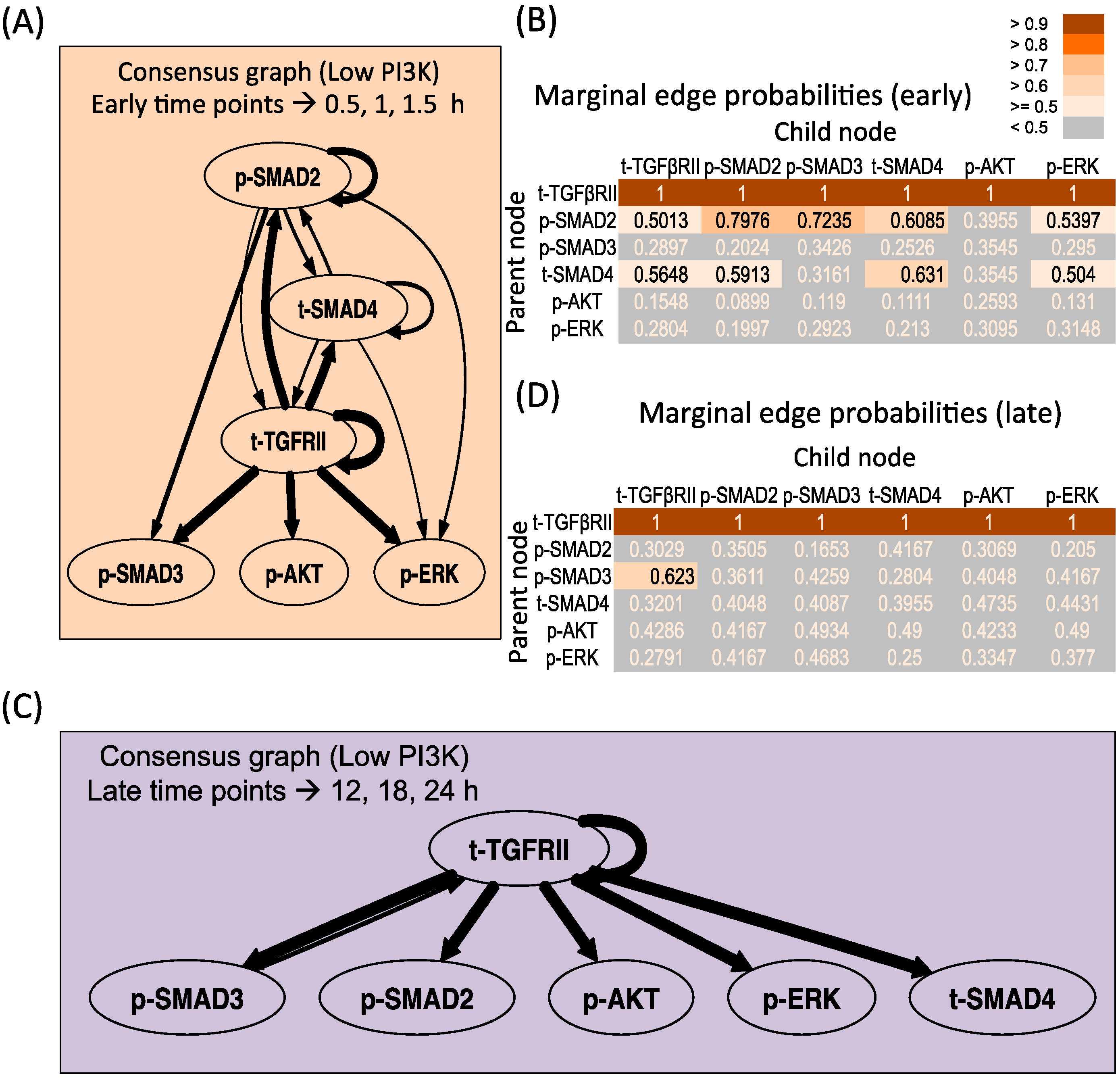
3.3.2. Low PI3K Condition
3.4. Correlation between Molecule Pairs in the Early and Late Time Zones
3.4.1. Influence of Total Receptor Levels
3.4.2. Intracellular Regulation by p-AKT
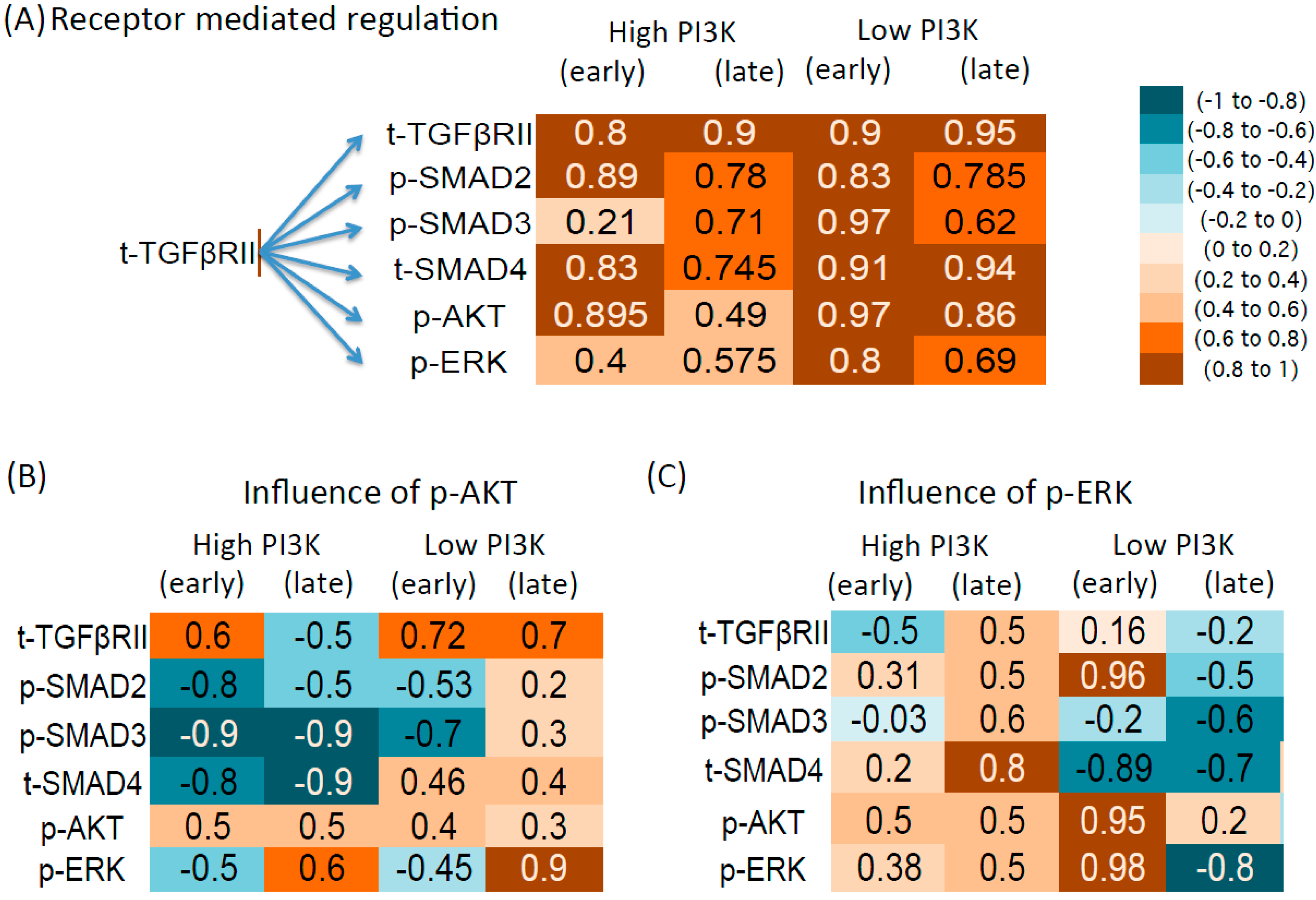
3.4.3. Intracellular Regulation by p-ERK
3.5. Network Regulation during Endoderm Differentiation
4. Conclusions
Acknowledgments
Author Contributions
Nomenclature
| DBN | Dynamic Bayesian Network |
| DE | Definitive Endoderm |
| hESCs | Human Embryonic Stem Cells |
| p-SMAD2 | phosphorylated SMAD2 |
| p-SMAD3 | phosphorylated SMAD3 |
| p-AKT | phosphorylated AKT |
| p-ERK | phosphorylated ERK |
| TGFβ | Transforming growth factor-beta |
| t-TGFβRII | total TGFβ receptor 2 |
| t-SMAD4 | total SMAD4 |
Conflicts of Interest
References
- Semb, H. Definitive endoderm: A key step in coaxing human embryonic stem cells into transplantable beta-cells. Biochem. Soc. Trans. 2008, 36, 272–275. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, M.; Mathew, S.; Task, K.; Barner, S.; Banerjee, I. Potential for pancreatic maturation of differentiating human embryonic stem cells is sensitive to the specific pathway of definitive endoderm commitment. PLoS One 2014, 9, e94307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.; Browning, V.L.; Odorico, J.S. Activin, bmp and fgf pathways cooperate to promote endoderm and pancreatic lineage cell differentiation from human embryonic stem cells. Mech. Dev. 2011, 128, 412–427. [Google Scholar] [CrossRef] [PubMed]
- McLean, A.B.; D’Amour, K.A.; Jones, K.L.; Krishnamoorthy, M.; Kulik, M.J.; Reynolds, D.M.; Sheppard, A.M.; Liu, H.; Xu, Y.; Baetge, E.E. Activin a efficiently specifies definitive endoderm from human embryonic stem cells only when phosphatidylinositol 3-kinase signaling is suppressed. Stem Cells 2007, 25, 29–38. [Google Scholar] [CrossRef] [PubMed]
- D’Amour, K.A.; Agulnick, A.D.; Eliazer, S.; Kelly, O.G.; Kroon, E.; Baetge, E.E. Efficient differentiation of human embryonic stem cells to definitive endoderm. Nat. Biotechnol. 2005, 23, 1534–1541. [Google Scholar] [CrossRef] [PubMed]
- Nostro, M.C.; Sarangi, F.; Ogawa, S.; Holtzinger, A.; Corneo, B.; Li, X.; Micallef, S.J.; Park, I.-H.; Basford, C.; Wheeler, M.B. Stage-specific signaling through tgfβ family members and wnt regulates patterning and pancreatic specification of human pluripotent stem cells. Development 2011, 138, 861–871. [Google Scholar] [CrossRef] [PubMed]
- Basma, H.; Soto-Gutierrez, A.; Yannam, G.R.; Liu, L.; Ito, R.; Yamamoto, T.; Ellis, E.; Carson, S.D.; Sato, S.; Chen, Y.; et al. Differentiation and transplantation of human embryonic stem cell-derived hepatocytes. Gastroenterology 2009, 136, 990–999. [Google Scholar] [CrossRef] [PubMed]
- Sulzbacher, S.; Schroeder, I.S.; Truong, T.T.; Wobus, A.M. Activin a-induced differentiation of embryonic stem cells into endoderm and pancreatic progenitors—The influence of differentiation factors and culture conditions. Stem Cell Reviews Rep. 2009, 5, 159–173. [Google Scholar] [CrossRef]
- Mathew, S.; Jaramillo, M.; Zhang, X.; Zhang, L.A.; Soto-Gutierrez, A.; Banerjee, I. Analysis of alternative signaling pathways of endoderm induction of human embryonic stem cells identifies context specific differences. BMC Syst. Biol. 2012, 6, 154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richardson, T.; Kumta, P.N.; Banerjee, I. Alginate encapsulation of human embryonic stem cells to enhance directed differentiation to pancreatic islet-like cells. Tissue Eng. Part A 2014, 20, 3198–3211. [Google Scholar] [CrossRef] [PubMed]
- Attisano, L.; Wrana, J.L.; Montalvo, E.; Massague, J. Activation of signalling by the activin receptor complex. Mol. Cell. Biol. 1996, 16, 1066–1073. [Google Scholar] [PubMed]
- Massague, J.; Seoane, J.; Wotton, D. Smad transcription factors. Genes Dev. 2005, 19, 2783–2810. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.Y.; Hill, C.S. Tgf-beta superfamily signaling in embryonic development and homeostasis. Dev. Cell 2009, 16, 329–343. [Google Scholar] [CrossRef] [PubMed]
- Dalton, S. Signaling networks in human pluripotent stem cells. Curr. Opin. Cell Biol. 2013, 25, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Avery, S.; Zafarana, G.; Gokhale, P.J.; Andrews, P.W. The role of smad4 in human embryonic stem cell self-renewal and stem cell fate. Stem Cells 2010, 28, 863–873. [Google Scholar] [PubMed]
- Sakaki-Yumoto, M.; Liu, J.M.; Ramalho-Santos, M.; Yoshida, N.; Derynck, R. Smad2 is essential for maintenance of the human and mouse primed pluripotent stem cell state. J. Biol. Chem. 2013, 288, 18546–18560. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.M.; Reynolds, D.; Cliff, T.; Ohtsuka, S.; Mattheyses, A.L.; Sun, Y.; Menendez, L.; Kulik, M.; Dalton, S. Signaling network crosstalk in human pluripotent cells: A smad2/3-regulated switch that controls the balance between self-renewal and differentiation. Cell Stem Cell 2012, 10, 312–326. [Google Scholar] [CrossRef] [PubMed]
- Pauklin, S.; Vallier, L. The cell-cycle state of stem cells determines cell fate propensity. Cell 2013, 155, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Needham, C.J.; Bradford, J.R.; Bulpitt, A.J.; Westhead, D.R. A primer on learning in bayesian networks for computational biology. PLoS Comput. Biol. 2007, 3, e129. [Google Scholar] [CrossRef] [PubMed]
- Woolf, P.J.; Prudhomme, W.; Daheron, L.; Daley, G.Q.; Lauffenburger, D.A. Bayesian analysis of signaling networks governing embryonic stem cell fate decisions. Bioinformatics 2005, 21, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Zielinski, R.; Przytycki, P.F.; Zheng, J.; Zhang, D.; Przytycka, T.M.; Capala, J. The crosstalk between egf, igf, and insulin cell signaling pathways—Computational and experimental analysis. BMC Syst. Biol. 2009, 3, 88. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Heinrich, R.; Neel, B.G.; Rapoport, T.A. Mathematical models of protein kinase signal transduction. Mol. Cell 2002, 9, 957–970. [Google Scholar] [CrossRef] [PubMed]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Grzegorczyk, M.; Husmeier, D. Improvements in the reconstruction of time-varying gene regulatory networks: Dynamic programming and regularization by information sharing among genes. Bioinformatics 2011, 27, 693–699. [Google Scholar] [CrossRef] [PubMed]
- Grzegorczyk, M.; Husmeier, D. Non-homogeneous dynamic bayesian networks for continuous data. Mach. Learn. 2011, 83, 355–419. [Google Scholar] [CrossRef]
- Azhar, N.; Ziraldo, C.; Barclay, D.; Rudnick, D.A.; Squires, R.H.; Vodovotz, Y.; Pediatric Acute Liver Failure Study Group. Analysis of serum inflammatory mediators identifies unique dynamic networks associated with death and spontaneous survival in pediatric acute liver failure. PLoS One 2013, 8, e78202. [Google Scholar] [CrossRef] [PubMed]
- Emr, B.; Sadowsky, D.; Azhar, N.; Gatto, L.A.; An, G.; Nieman, G.F.; Vodovotz, Y. Removal of inflammatory ascites is associated with dynamic modification of local and systemic inflammation along with prevention of acute lung injury: In vivo and in silico studies. Shock 2014, 41, 317–323. [Google Scholar] [CrossRef] [PubMed]
- Aerts, J.M.; Haddad, W.M.; An, G.; Vodovotz, Y. From data patterns to mechanistic models in acute critical illness. J. Crit. Care 2014, 29, 604–610. [Google Scholar] [CrossRef] [PubMed]
- Dojer, N.; Gambin, A.; Mizera, A.; Wilczynski, B.; Tiuryn, J. Applying dynamic bayesian networks to perturbed gene expression data. BMC Bioinf. 2006, 7, 249. [Google Scholar] [CrossRef]
- Chang, R.; Shoemaker, R.; Wang, W. Systematic search for recipes to generate induced pluripotent stem cells. PLoS Comput. Biol. 2011, 7, e1002300. [Google Scholar] [CrossRef] [PubMed]
- Grzegorczyk, M.; Husmeier, D. A non-homogeneous dynamic bayesian network with sequentially coupled interaction parameters for applications in systems and synthetic biology. Stat. Appl. Genet. Mol. Biol. 2012, 11. [Google Scholar] [CrossRef]
- Yu, J.; Smith, V.A.; Wang, P.P.; Hartemink, A.J.; Jarvis, E.D. Advances to bayesian network inference for generating causal networks from observational biological data. Bioinformatics 2004, 20, 3594–3603. [Google Scholar] [CrossRef] [PubMed]
- Schmierer, B.; Hill, C.S. Tgfbeta-smad signal transduction: Molecular specificity and functional flexibility. Nat. Rev. Mol. Cell Biol. 2007, 8, 970–982. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Wang, X.-F. Signaling cross-talk between tgf-β/bmp and other pathways. Cell Res. 2008, 19, 71–88. [Google Scholar] [CrossRef]
- Zhang, Y.E. Non-smad pathways in tgf-β signaling. Cell Res. 2008, 19, 128–139. [Google Scholar] [CrossRef]
- Conery, A.R.; Cao, Y.; Thompson, E.A.; Townsend, C.M., Jr.; Ko, T.C.; Luo, K. Akt interacts directly with smad3 to regulate the sensitivity to tgf-beta induced apoptosis. Nat. Cell Biol. 2004, 6, 366–372. [Google Scholar] [CrossRef] [PubMed]
- Danielpour, D.; Song, K. Cross-talk between igf-i and tgf-β signaling pathways. Cytokine Growth Factor Rev. 2006, 17, 59–74. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Wang, H.; Krebs, T.L.; Danielpour, D. Novel roles of akt and mtor in suppressing tgf-beta/alk5-mediated smad3 activation. EMBO J. 2006, 25, 58–69. [Google Scholar] [CrossRef] [PubMed]
- Remy, I.; Montmarquette, A.; Michnick, S.W. Pkb/akt modulates tgf-β signalling through a direct interaction with smad3. Nat. Cell Biol. 2004, 6, 358–365. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhou, F.; ten Dijke, P. Signaling interplay between transforming growth factor-β receptor and pi3k/akt pathways in cancer. Trends Biochem. Sci. 2013, 38, 612–620. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Kang, J.; Ko, T.C.; Evers, B.M.; Chung, D.H. Inhibition of transforming growth factor-beta/smad signaling by phosphatidylinositol 3-kinase pathway. Cancer Lett. 2006, 242, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Ye, F.; Ding, H.; Chen, K.; Jiang, H.; Shen, X. Protein tyrosine phosphatase 1b regulates tgf beta 1-induced smad2 activation through pi3 kinase-dependent pathway. Cytokine 2006, 35, 88–94. [Google Scholar] [CrossRef] [PubMed]
- Aksamitiene, E.; Kiyatkin, A.; Kholodenko, B.N. Cross-talk between mitogenic ras/mapk and survival pi3k/akt pathways: A fine balance. Biochem. Soc. Trans. 2012, 40, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, A.F.; Banga, J.R. Reverse engineering and identification in systems biology: Strategies, perspectives and challenges. J. R. Soc. Interface 2014, 11, 20130505. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, I.; Maiti, S.; Parashurama, N.; Yarmush, M. An integer programming formulation to identify the sparse network architecture governing differentiation of embryonic stem cells. Bioinformatics 2010, 26, 1332–1339. [Google Scholar] [CrossRef] [PubMed]
- Chemmangattuvalappil, N.; Task, K.; Banerjee, I. An integer optimization algorithm for robust identification of non-linear gene regulatory networks. BMC Syst. Biol. 2012, 6, 119. [Google Scholar] [CrossRef] [PubMed]
- Guillen-Gosálbez, G.; Miró, A.; Alves, R.; Sorribas, A.; Jiménez, L. Identification of regulatory structure and kinetic parameters of biochemical networks via mixed-integer dynamic optimization. BMC Syst. Biol. 2013, 7, 113. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Fernandez, M.; Rehberg, M.; Kremling, A.; Banga, J.R. Simultaneous model discrimination and parameter estimation in dynamic models of cellular systems. BMC Syst. Biol. 2013, 7, 76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Penfold, C.A.; Wild, D.L. How to infer gene networks from expression profiles, revisited. Interface Focus 2011, 1, 857–870. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.P.; Tzou, W.S. Computational methods for discovering gene networks from expression data. Brief Bioinform. 2009, 10, 408–423. [Google Scholar] [PubMed]
- Bansal, M.; Belcastro, V.; Ambesi-Impiombato, A.; Di Bernardo, D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007, 3. [Google Scholar] [CrossRef]
- Tegner, J.; Yeung, M.K.; Hasty, J.; Collins, J.J. Reverse engineering gene networks: Integrating genetic perturbations with dynamical modeling. Proc. Natl. Acad. Sci. USA 2003, 100, 5944–5949. [Google Scholar] [CrossRef] [PubMed]
- Molinelli, E.J.; Korkut, A.; Wang, W.; Miller, M.L.; Gauthier, N.P.; Jing, X.; Kaushik, P.; He, Q.; Mills, G.; Solit, D.B.; et al. Perturbation biology: Inferring signaling networks in cellular systems. PLoS Comput. Biol. 2013, 9, e1003290. [Google Scholar] [CrossRef] [PubMed]
- Galvin-Burgess, K.E.; Travis, E.D.; Pierson, K.E.; Vivian, J.L. Tgf-β-superfamily signaling regulates embryonic stem cell heterogeneity: Self-renewal as a dynamic and regulated equilibrium. Stem Cells 2013, 31, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Dai, W.; Hahn, J. Mathematical modeling and analysis of crosstalk between mapk pathway and smad-dependent tgf-β signal transduction. Processes 2014, 2, 570–595. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathew, S.; Sundararaj, S.; Banerjee, I. Network Analysis Identifies Crosstalk Interactions Governing TGF-β Signaling Dynamics during Endoderm Differentiation of Human Embryonic Stem Cells. Processes 2015, 3, 286-308. https://doi.org/10.3390/pr3020286
Mathew S, Sundararaj S, Banerjee I. Network Analysis Identifies Crosstalk Interactions Governing TGF-β Signaling Dynamics during Endoderm Differentiation of Human Embryonic Stem Cells. Processes. 2015; 3(2):286-308. https://doi.org/10.3390/pr3020286
Chicago/Turabian StyleMathew, Shibin, Sankaramanivel Sundararaj, and Ipsita Banerjee. 2015. "Network Analysis Identifies Crosstalk Interactions Governing TGF-β Signaling Dynamics during Endoderm Differentiation of Human Embryonic Stem Cells" Processes 3, no. 2: 286-308. https://doi.org/10.3390/pr3020286