Dynamic Modeling of Cell-Free Biochemical Networks Using Effective Kinetic Models
Abstract
:1. Introduction
2. Results
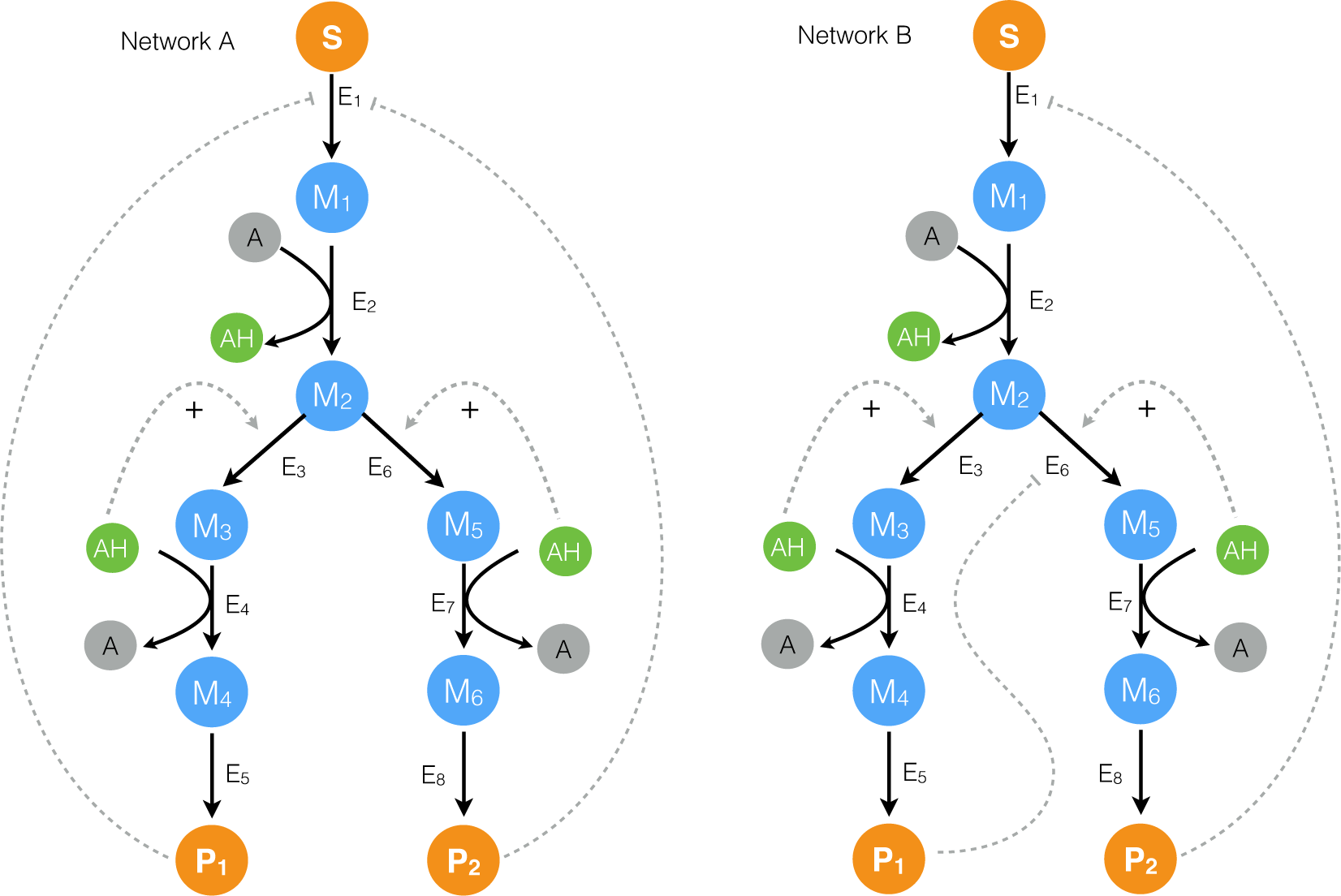
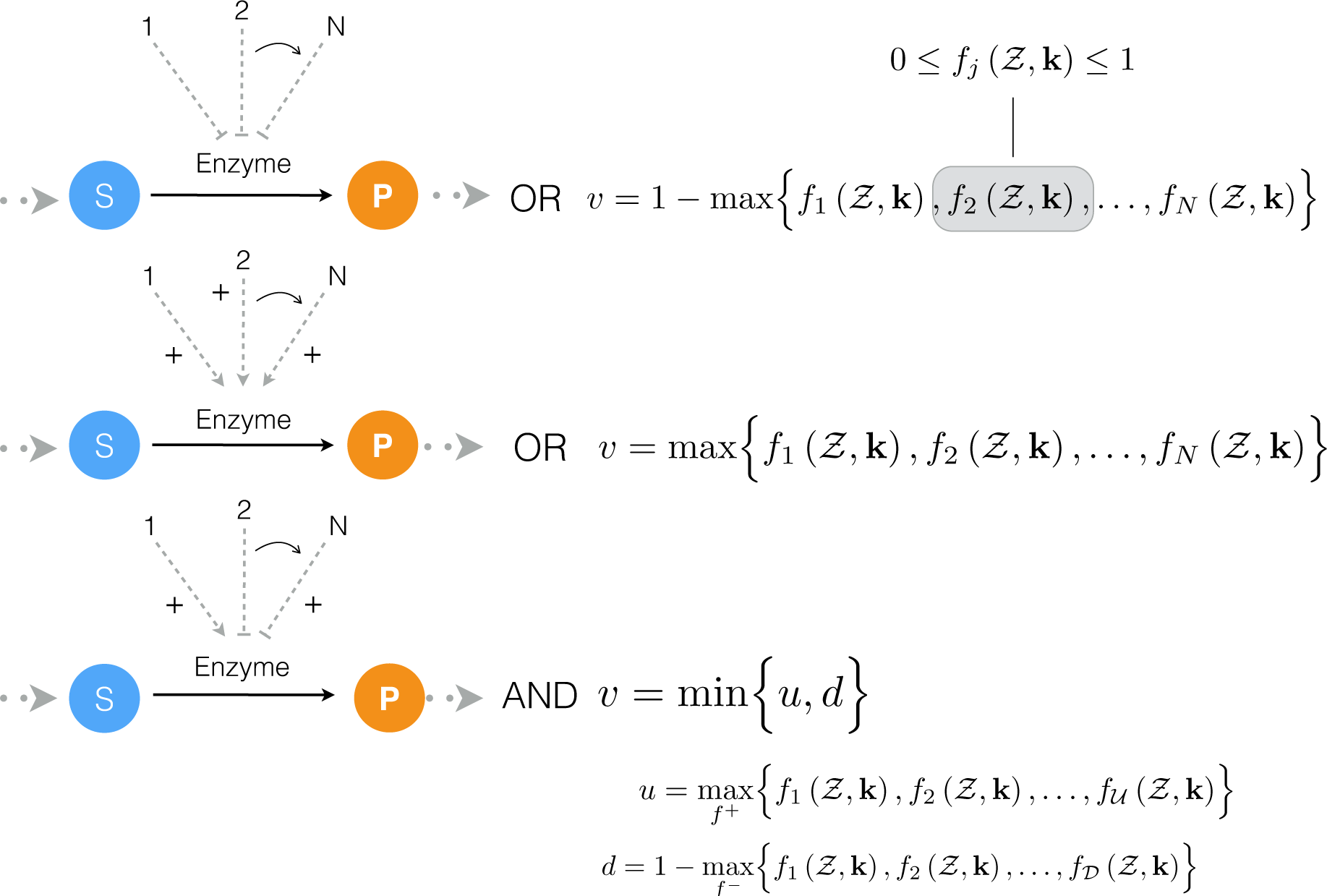
2.1. Formulation and Properties of Effective Cell-Free Metabolic Models
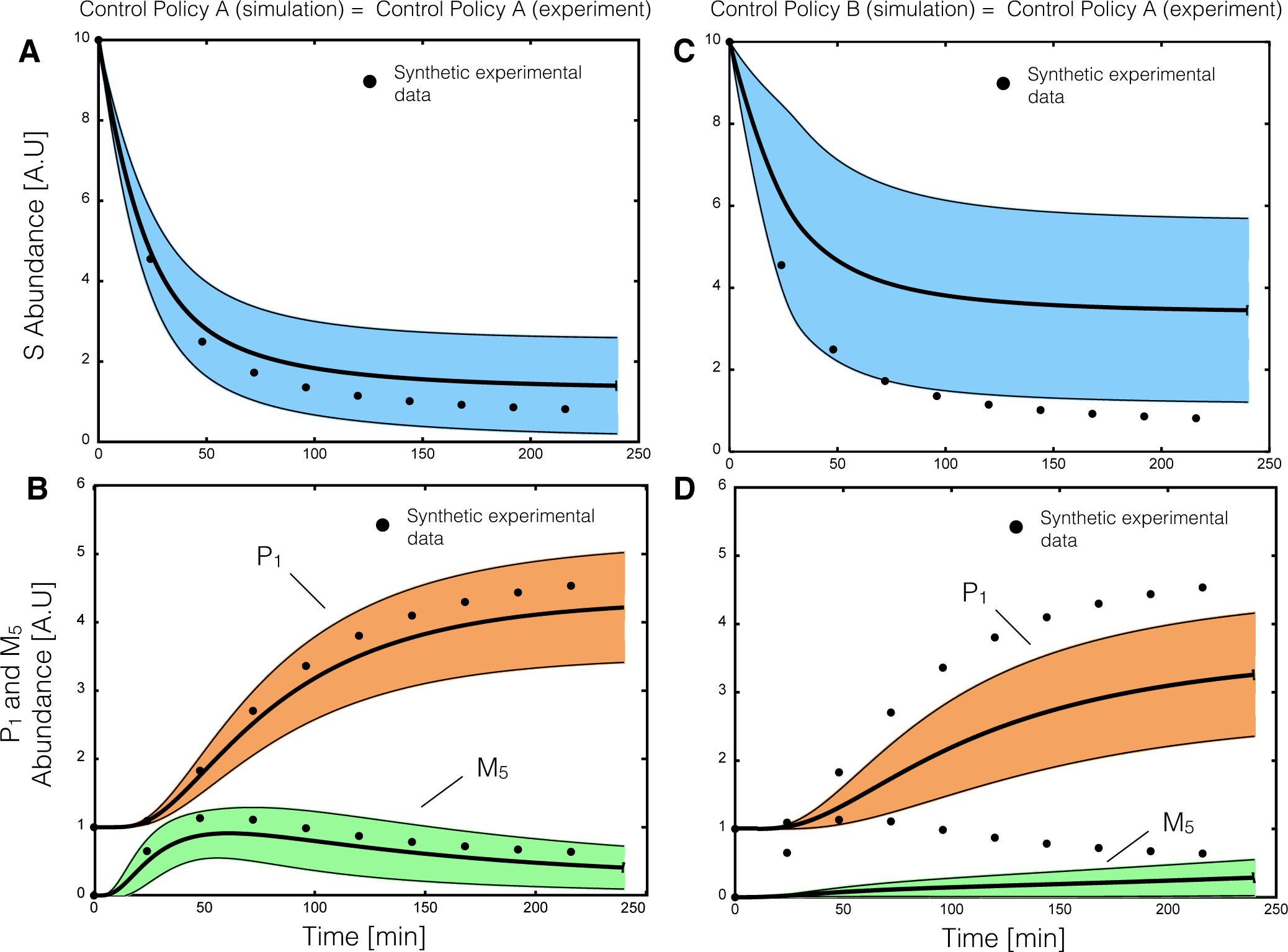
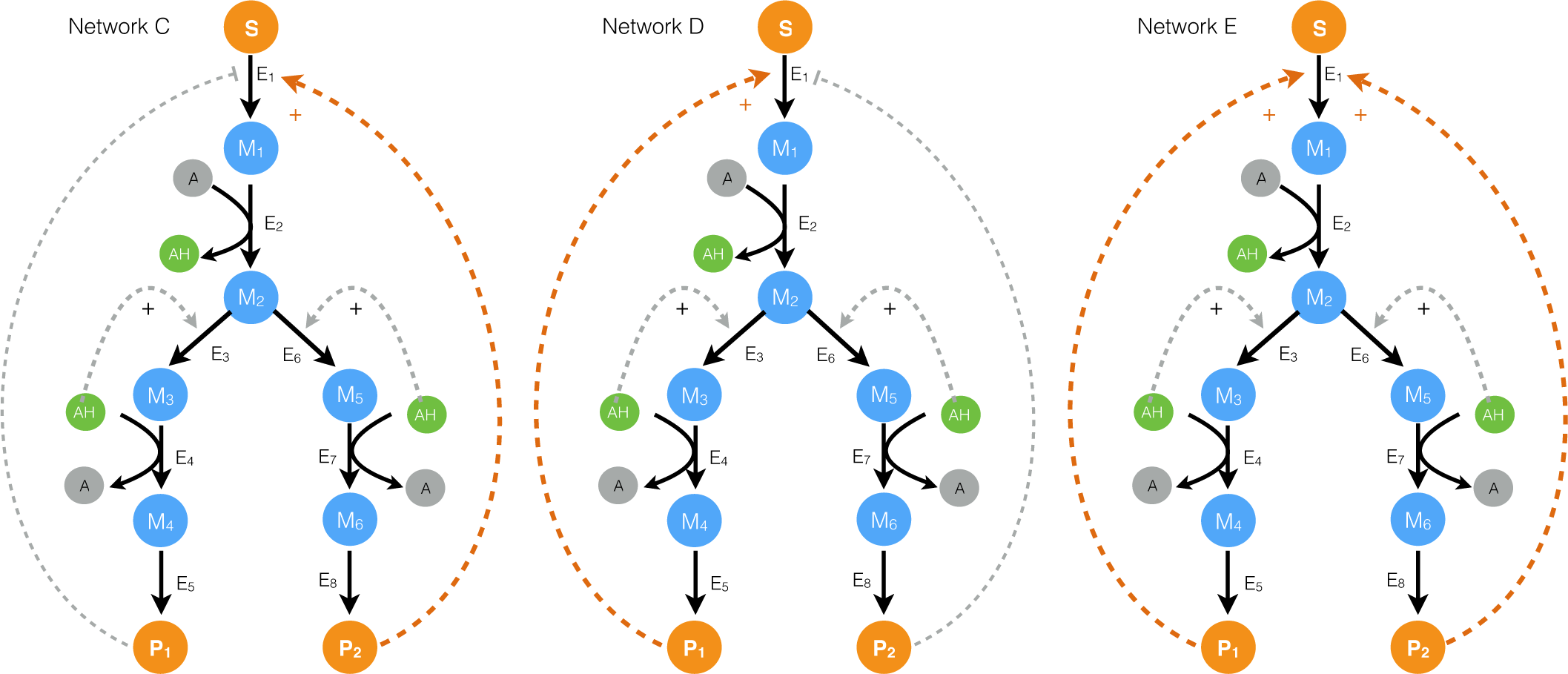
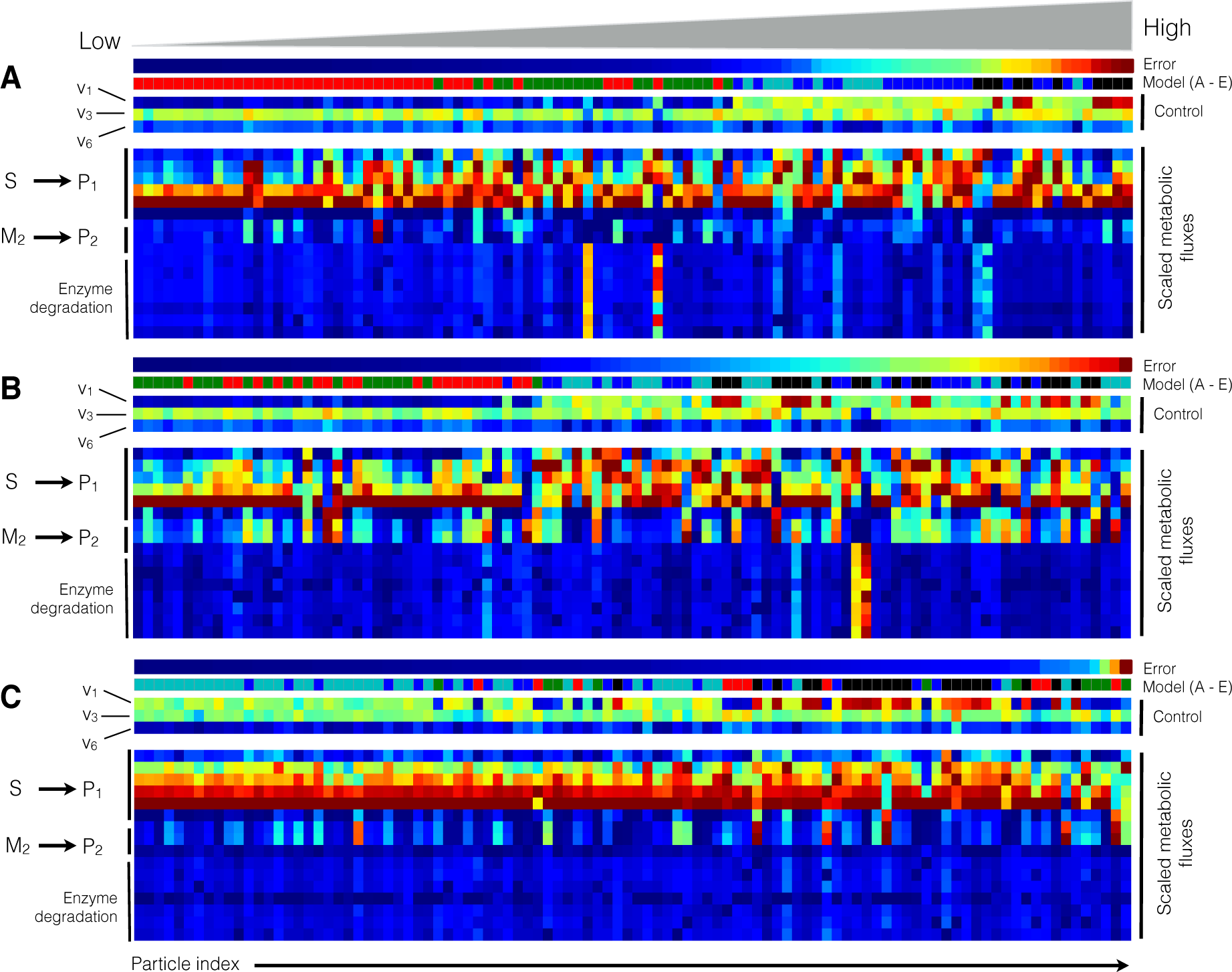
2.2. Estimating Parameters and Effective Allosteric Regulatory Structures
3. Discussion
4. Materials and Methods
4.1. Formulation and Solution of the Model Equations
Estimation of model parameters and structures from synthetic experimental data
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fredrickson, A.G. Formulation of structured growth models. Biotechnol. Bioeng. 1976, 18, 1481–1486. [Google Scholar]
- Domach, M.M.; Leung, S.K.; Cahn, R.E.; Cocks, G.G.; Shuler, M.L. Computer model for glucose-limited growth of a single cell of Escherichia coli B/r-A. Biotechnol. Bioeng. 1984, 26, 203–216. [Google Scholar]
- Steinmeyer, D.; Shuler, M. Structured model for Saccharomyces cerevisiae. Chem. Eng. Sci. 1989, 44, 2017–2030. [Google Scholar]
- Wu, P.; Ray, N.G.; Shuler, M.L. A single-cell model for CHO cells. Ann. N. Y. Acad. Sci. 1992, 665, 152–187. [Google Scholar]
- Castellanos, M.; Wilson, D.B.; Shuler, M.L. A modular minimal cell model: Purine and pyrimidine transport and metabolism. Proc. Natl. Acad. Sci. USA 2004, 101, 6681–6686. [Google Scholar]
- Atlas, J.C.; Nikolaev, E.V.; Browning, S.T.; Shuler, M.L. Incorporating genome-wide DNA sequence information into a dynamic whole-cell model of Escherichia coli: Application to DNA replication. IET Syst. Biol. 2008, 2, 369–382. [Google Scholar]
- Dhurjati, P.; Ramkrishna, D.; Flickinger, M.C.; Tsao, G.T. A cybernetic view of microbial growth: Modeling of cells as optimal strategists. Biotechnol. Bioeng. 1985, 27, 1–9. [Google Scholar]
- Kompala, D.S.; Ramkrishna, D.; Jansen, N.B.; Tsao, G.T. Investigation of bacterial growth on mixed substrates: Experimental evaluation of cybernetic models. Biotechnol. Bioeng. 1986, 28, 1044–1055. [Google Scholar]
- Kim, J.I.; Song, H.S.; Sunkara, S.R.; Lali, A.; Ramkrishna, D. Exacting predictions by cybernetic model confirmed experimentally: Steady state multiplicity in the chemostat. Biotechnol. Prog. 2012, 28, 1160–1166. [Google Scholar]
- Varner, J.; Ramkrishna, D. Metabolic engineering from a cybernetic perspective: Aspartate family of amino acids. Metab. Eng. 1999, 1, 88–116. [Google Scholar]
- Song, H.S.; Morgan, J.A.; Ramkrishna, D. Systematic development of hybrid cybernetic models: Application to recombinant yeast co-consuming glucose and xylose. Biotechnol. Bioeng. 2009, 103, 984–1002. [Google Scholar]
- Song, H.S.; Ramkrishna, D. Cybernetic models based on lumped elementary modes accurately predict strain-specific metabolic function. Biotechnol. Bioeng. 2011, 108, 127–140. [Google Scholar]
- Lewis, N.E.; Nagarajan, H.; Palsson, B.O. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 2012, 10, 291–305. [Google Scholar]
- Edwards, J.S.; Palsson, B.O. The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. USA 2000, 97, 5528–5533. [Google Scholar]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.Ø. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3(3), 121. [Google Scholar]
- Oh, Y.K.; Palsson, B.O.; Park, S.M.; Schilling, C.H.; Mahadevan, R. Genome-scale reconstruction of metabolic network in Bacillus subtilis based on high-throughput phenotyping and gene essentiality data. J. Biol. Chem. 2007, 282, 28791–28799. [Google Scholar]
- Feist, A.M.; Herrgård, M.J.; Thiele, I.; Reed, J.L.; Palsson, B.Ø. Reconstruction of biochemical networks in microorganisms. Nat. Rev. Microbiol. 2009, 7, 129–143. [Google Scholar]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.O. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar]
- Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3(3), 119. [Google Scholar]
- Hyduke, D.R.; Lewis, N.E.; Palsson, B.Ø. Analysis of omics data with genome-scale models of metabolism. Mol. Biosyst. 2013, 9, 167–174. [Google Scholar]
- McCloskey, D.; Palsson, B.Ø.; Feist, A.M. Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 2013, 9, 661. [Google Scholar]
- Zomorrodi, A.R.; Suthers, P.F.; Ranganathan, S.; Maranas, C.D. Mathematical optimization applications in metabolic networks. Metab. Eng. 2012, 14, 672–686. [Google Scholar]
- Jewett, M.C.; Calhoun, K.A.; Voloshin, A.; Wuu, J.J.; Swartz, J.R. An integrated cell-free metabolic platform for protein production and synthetic biology. Mol. Syst. Biol. 2008, 4, 220. [Google Scholar]
- Matthaei, J.H.; Nirenberg, M.W. Characteristics and stabilization of DNAase-sensitive protein synthesis in E. coli extracts. Proc. Natl. Acad. Sci. USA 1961, 47, 1580–1588. [Google Scholar]
- Nirenberg, M.W.; Matthaei, J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. USA 1961, 47, 1588–1602. [Google Scholar]
- Lu, Y.; Welsh, J.P.; Swartz, J.R. Production and stabilization of the trimeric influenza hemagglutinin stem domain for potentially broadly protective influenza vaccines. Proc. Natl. Acad. Sci. USA 2014, 111, 125–130. [Google Scholar]
- Hodgman, C.E.; Jewett, M.C. Cell-free synthetic biology: Thinking outside the cell. Metab. Eng. 2012, 14, 261–269. [Google Scholar]
- Morris, M.K.; Saez-Rodriguez, J.; Clarke, D.C.; Sorger, P.K.; Lauffenburger, D.A. Training signaling pathway maps to biochemical data with constrained fuzzy logic: Quantitative analysis of liver cell responses to inflammatory stimuli. PLoS Comput. Biol. 2011, 7, e1001099. [Google Scholar]
- Brown, K.S.; Sethna, J.P. Statistical mechanical approaches to models with many poorly known parameters. Phys. Rev. E 2003, 68, 021904. [Google Scholar]
- Covert, M.W.; Schilling, C.H.; Palsson, B. Regulation of gene expression in flux balance models of metabolism. J. Theor. Biol. 2001, 213, 73–88. [Google Scholar]
- Covert, M.W.; Knight, E.M.; Reed, J.L.; Herrgard, M.J.; Palsson, B.O. Integrating high-throughput and computational data elucidates bacterial networks. Nature 2004, 429, 92–96. [Google Scholar]
- Varner, J.D. Large-scale prediction of phenotype: Concept. Biotechnol. Bioeng. 2000, 69, 664–678. [Google Scholar]
- Song, H.S.; Ramkrishna, D. Prediction of dynamic behavior of mutant strains from limited wild-type data. Metab. Eng. 2012, 14, 69–80. [Google Scholar]
- Gadkar, K.G.; Doyle, F.J., 3rd; Crowley, T.J.; Varner, J.D. Cybernetic model predictive control of a continuous bioreactor with cell recycle. Biotechnol. Prog. 2003, 19, 1487–1497. [Google Scholar]
- Heijnen, J.J. Approximative kinetic formats used in metabolic network modeling. Biotechnol. Bioeng. 2005, 91, 534–545. [Google Scholar]
- Savageau, M.A. Biochemical systems theory: Operational differences among variant representations and their significance. J. Theor. Biol. 1991, 151, 509–530. [Google Scholar]
- Visser, D.; Heijnen, J.J. Dynamic simulation and metabolic re-design of a branched pathway using linlog kinetics. Metab. Eng. 2003, 5, 164–176. [Google Scholar]
- Hadlich, F.; Noack, S.; Wiechert, W. Translating biochemical network models between different kinetic formats. Metab. Eng. 2009, 11, 87–100. [Google Scholar]
- Tran, L.M.; Rizk, M.L.; Liao, J.C. Ensemble modeling of metabolic networks. Biophys. J 2008, 95, 5606–5617. [Google Scholar]
- Luan, D.; Zai, M.; Varner, J.D. Computationally derived points of fragility of a human cascade are consistent with current therapeutic strategies. PLoS Comput. Biol. 2007, 3(3), e142. [Google Scholar]
- Song, S.O.; Varner, J. Modeling and analysis of the molecular basis of pain in sensory neurons. PLoS One 2009, 4, e6758. [Google Scholar]
- Tasseff, R.; Nayak, S.; Salim, S.; Kaushik, P.; Rizvi, N.; Varner, J.D. Analysis of the molecular networks in androgen dependent and independent prostate cancer revealed fragile and robust subsystems. PLoS One 2010, 5, e8864. [Google Scholar]
- Tasseff, R.; Nayak, S.; Song, S.O.; Yen, A.; Varner, J.D. Modeling and analysis of retinoic acid induced differentiation of uncommitted precursor cells. Integr. Biol. 2011, 3(3), 578–591. [Google Scholar]
- Nayak, S.; Siddiqui, J.K.; Varner, J.D. Modelling and analysis of an ensemble of eukaryotic translation initiation models. IET Syst. Biol. 2011, 5, 2. [Google Scholar]
- Lequieu, J.; Chakrabarti, A.; Nayak, S.; Varner, J.D. Computational modeling and analysis of insulin induced eukaryotic translation initiation. PLoS Comput. Biol 2011, 7, e1002263. [Google Scholar]
- Machta, B.B.; Chachra, R.; Transtrum, M.K.; Sethna, J.P. Parameter space compression underlies emergent theories and predictive models. Science 2013, 342, 604–607. [Google Scholar]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry; W.H. Freeman: New York, NY, USA, 2002. [Google Scholar]
- Peskov, K.; Goryanin, I.; Demin, O. Kinetic model of phosphofructokinase-1 from Escherichia coli. J. Bioinform. Comput. Biol. 2008, 6, 843–867. [Google Scholar]
- Keseler, I.M.; Mackie, A.; Peralta-Gil, M.; Santos-Zavaleta, A.; Gama-Castro, S.; Bonavides-Martínez, C.; Fulcher, C.; Huerta, A.M.; Kothari, A.; Krummenacker, M.; et al. EcoCyc: Fusing model organism databases with systems biology. Nucleic Acids Res 2013, 41, D605–D612. [Google Scholar]
- Huang, Z.; Mou, L.; Shen, Q.; Lu, S.; Li, C.; Liu, X.; Wang, G.; Li, S.; Geng, L.; Liu, Y.; et al. ASD v2.0: Updated content and novel features focusing on allosteric regulation. Nucleic Acids. Res. 2014, 42, D510–D516. [Google Scholar]
- Link, H.; Kochanowski, K.; Sauer, U. Systematic identification of allosteric protein-metabolite interactions that control enzyme activity in vivo. Nat. Biotechnol. 2013, 31, 357–361. [Google Scholar]
- Kremling, A.; Fischer, S.; Gadkar, K.; Doyle, F.J.; Sauter, T.; Bullinger, E.; Allgöwer, F.; Gilles, E.D. A benchmark for methods in reverse engineering and model discrimination: Problem formulation and solutions. Genome Res 2004, 14, 1773–1785. [Google Scholar]
- Gadkar, K.G.; Gunawan, R.; Doyle, F.J., III. Iterative approach to model identification of biological networks. BMC Bioinform 2005, 6, 155. [Google Scholar]
- Eaton, J.W.; Bateman, D.; Hauberg, S. GNU Octave Version 3.0.1 Manual: A High-Level Interactive Language for Numerical Computations; CreateSpace Independent Publishing Platform: North Charleston, SC, USA, 2009. [Google Scholar]
- Song, S.O.; Chakrabarti, A.; Varner, J.D. Ensembles of signal transduction models using Pareto Optimal Ensemble Techniques (POETs). Biotechnol. J 2010, 5, 768–780. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization, Proceedings of the International Conference on Neural Networks, Perth, Western Australia, Australia, 27 November 1995; pp. 1942–1948.



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/)
Share and Cite
Wayman, J.A.; Sagar, A.; Varner, J.D. Dynamic Modeling of Cell-Free Biochemical Networks Using Effective Kinetic Models. Processes 2015, 3, 138-160. https://doi.org/10.3390/pr3010138
Wayman JA, Sagar A, Varner JD. Dynamic Modeling of Cell-Free Biochemical Networks Using Effective Kinetic Models. Processes. 2015; 3(1):138-160. https://doi.org/10.3390/pr3010138
Chicago/Turabian StyleWayman, Joseph A., Adithya Sagar, and Jeffrey D. Varner. 2015. "Dynamic Modeling of Cell-Free Biochemical Networks Using Effective Kinetic Models" Processes 3, no. 1: 138-160. https://doi.org/10.3390/pr3010138




