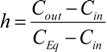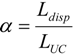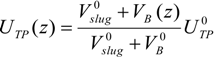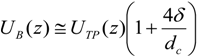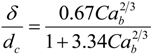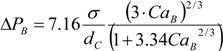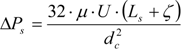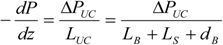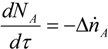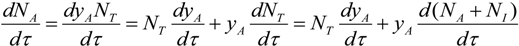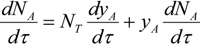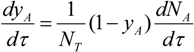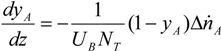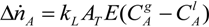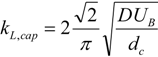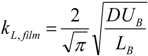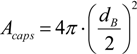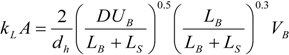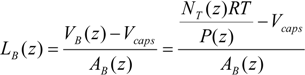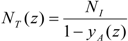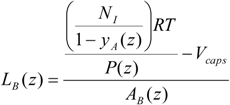1. Introduction
An effective exploitation of the advantages of microscale operation for industrial production processes requires a reliable and robust numbering-up procedure. For multiphase systems, one must not only ensure uniform flow rates of each phase but also similar flow structures [
1] and residence time distributions [
2,
3] in the individual microchannels, if the optimal performance is to be achieved [
4]. Furthermore, in reactive systems, multiplicities can arise, leading to drastic differences in the behavior between otherwise identical microchannels [
5]. The problem is compounded by the greater significance of fabrication tolerances at the microscale, since even slight discrepancies can give rise to considerable changes in volumetric flow rates, which scale with the fourth power of the channel diameter [
6,
7].
Passive distribution strategies thus necessitate high-precision machining, usually entail large upstream pressure drops and are unable to adapt to changing operating conditions, such as fouling [
8]. An active approach, in which the flow in each microchannel is monitored and regulated using simple non-invasive probes and actuators overcome these shortcomings [
9].
Even so, the multiplicities in reactive flows still represent a particularly severe challenge, since they can not only diminish performance but may also lead to hazardous runaway situations or reactor failure. In polymerizations, for instance, the reaction and hydrodynamics are strongly coupled through the viscosity of the reaction medium. Should, for whatever reason, the flow in one channel be less than that in the others, the resulting increase in the residence time will yield higher conversion and thus viscosities, increasing the resistance to flow and lowering the flow rate still further. If no remedial action is taken, this self-reinforcing mechanism amplifies any flow divergence and can ultimately cause the channel concerned to plug.
Of course, such multiplicities are by no means confined to microscale systems. In multiphase flow in microchannels, on the other hand, certain reactive hydrodynamic multiplicities can arise which are unlikely or even impossible in macroscale equipment, due to the intensified interaction in the biphasic flow. In an alternating gas-liquid slug flow with absorption, for example, the gas uptake reduces the size of the gas slugs, thus, changing the pressure drop characteristics of the flow, raising the channel residence time and thus enhancing the absorption still further. Conversely, reactions that generate gas or decrease viscosity exert a stabilizing influence on the uniformity of the flow distribution over parallel microchannels.
The objective of the work presented here was to elucidate the relevance of such microscale-specific phenomena in the parallelization of multiphase flows in microchannels and to establish if it might be feasible to utilize self-regulating behavior in order to ameliorate irregularities in flow distribution.
3. Gas-Liquid Model Equations
As shown in previous work, bubble length and bubble velocity play an important role for hydrodynamics and the mass transfer in the slug-flow regime. Even though some studies have focused on the possibility of the expansion of the bubble due to the inherent pressure drop [
12,
13], and in more recent studies [
14,
15] due to mass transfer from the liquid into the gas phase, none of them has considered the fact that, for very reactive systems, the effect of the consumption may well exceed that of the expansion of the bubble or the case where the mass transfer occurs from the gas to the liquid phase. The model presented in this work couples hydrodynamics with mass transfer and thus accounts for the change in the size of the bubble as a result of chemical absorption.
When the length of the bubble alters, several parameters are affected, starting with the superficial velocity. Since the volume of the unit cell comprising a single bubble and the associated slug is changing along the channel length, the two-phase superficial velocity will be a function of the position as given in Equation (4). This entails that all parameters that are velocity-dependent are also location-dependent, i.e., capillary and Reynolds numbers, film thickness and mass transfer coefficients.
In slug flow, it is known that bubbles travel faster than the nominal superficial velocity due to the presence of a thin liquid wall film surrounding the bubble. The true velocity can be approximated by a simple mass balance in round capillaries, as expressed in Equation (5) (a deviation of no more than 5% was reported by [
3]). In this equation, δ represents the film thickness and can be obtained by the expression found by Aussillous and Quéré [
16], describing the extent of significant films in micro-channels (Equation (6)).
As can be seen, the film thickness is a function of the capillary number, Ca = μU/πσ which in turn is a function of the velocity and therefore also of the location as stated earlier.
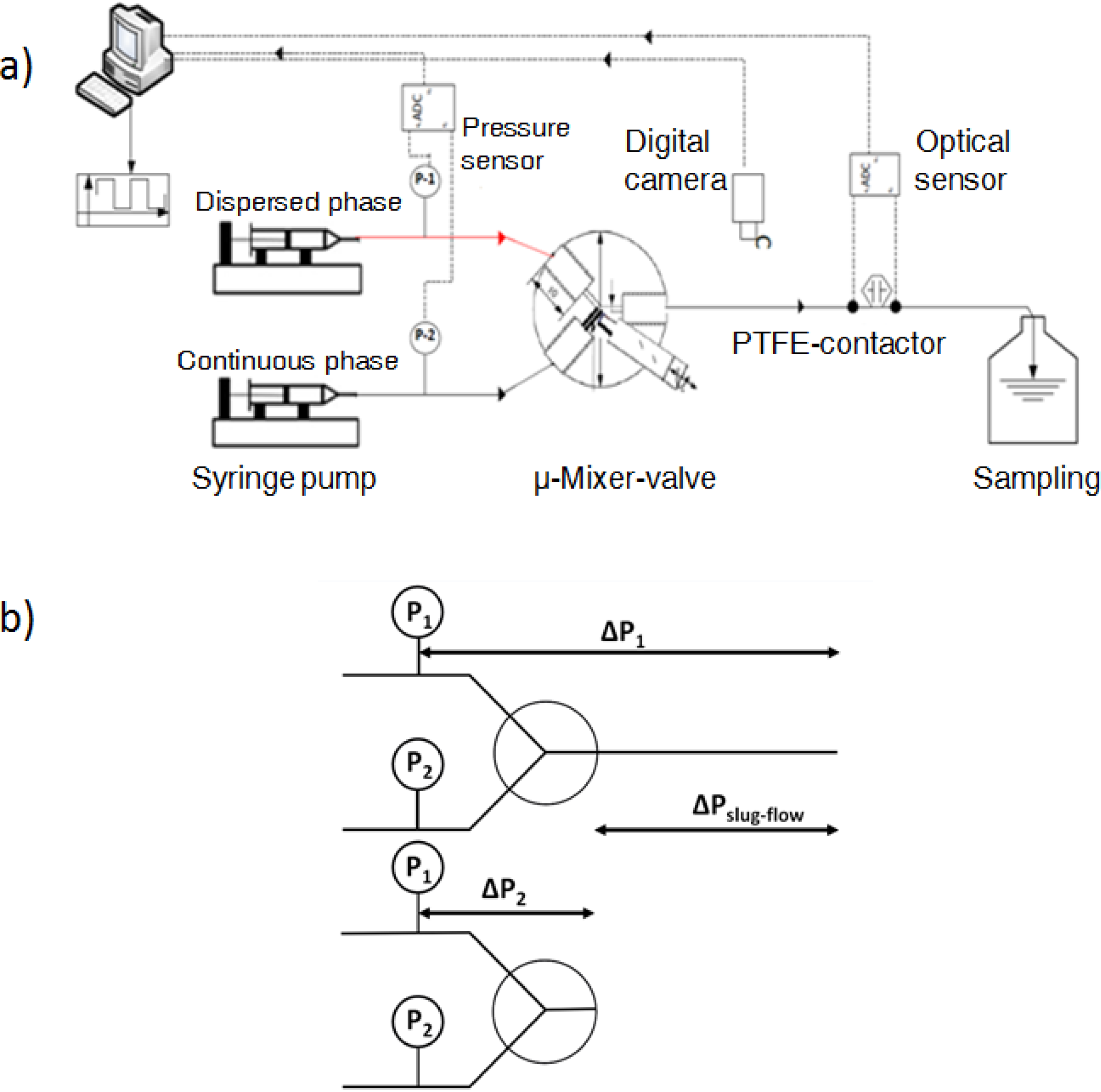
To describe the hydrodynamics, the pressure drop must be defined. In this work, the pressure drop is taken according to the unit cell based model presented by Warnier
et al. [
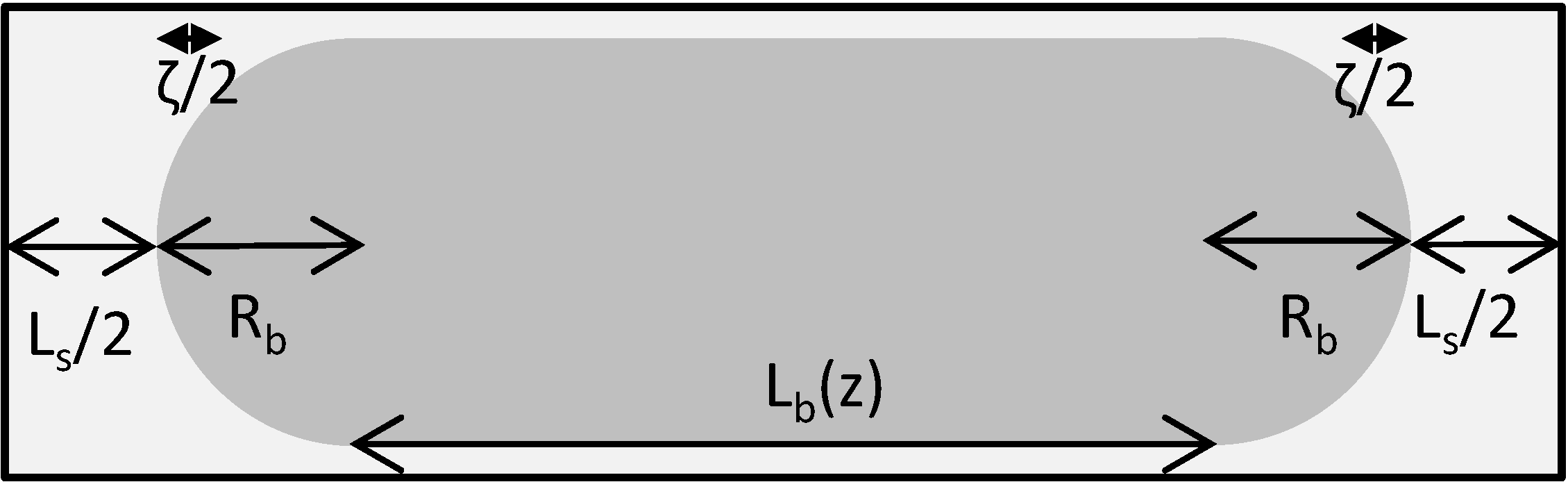
13]. In this model the pressure drop across a unit cell (presented in
Figure 3) is defined by the individual contributions of the liquid slug and the pressure drop generated by the presence of the bubble.
Figure 3.
Unit cell representation. Lb represents the length of the bubble, Ls represents the slug length Rb is the bubble diameter and ζ accounts for the liquid in the cap region.
Figure 3.
Unit cell representation. Lb represents the length of the bubble, Ls represents the slug length Rb is the bubble diameter and ζ accounts for the liquid in the cap region.
The individual bubble pressure is described by the corrected Bretherton’s approximation, and the liquid slug pressure drop is described by the fully developed Hagen-Poiseuille with a correction for the amount of liquid in the domed bubble cap region (ζ).
The differential pressure drop can then be obtained as:
However, the length of the bubble is not constant along the channel length. In the case of gas absorption into the liquid phase, for instance, it is necessary to couple the mass transfer with the pressure drop in order to determine how the bubble contracts along the channel length.
The change in the number of moles for the absorbed component with respect to the residence time can be given by:
since the number of moles of the inert is not changing with time Equation (12) becomes:
yielding:
The residence time for the bubble is given by the bubble velocity yielding:
The chemical system used for this study was the widely studied chemical absorption of CO
2 in NaOH [
17]. First a pseudo 1st order reaction was assumed, but since the reaction was found to be fast enough, the chemical absorption was then simply accounted for by the inclusion of the enhancement factor. Finally, the change in the molar flow due to chemical absorption can be given by:
As for determining the mass transfer coefficient, several studies conducted on mass transfer in gas-liquid slug flow [
18,
19,
20,
21] were considered. In this work most of the available models were examined, with particular emphasis on the models of Vandu
et al. [
18] and Yue
et al. [
19], as they allow the introduction of changes in the parameters along the length of the channel. Vandu’s model treats the cap and wall film contributions separately according to:
Yue’s model, on the other hand, considers the overall mass transfer across the entire interface:
Finally, the link between the mass transfer and the pressure drop is given by the bubble length, since a relationship between bubble length and the total number of moles can be expressed as:
the total number of moles is linked to the molar fraction by the relationship:
yielding the influence of all parameters on the bubble length:
It is important to notice that the expansion due to the pressure drop presented in previous works is included in this model as well, since the volume of the bubble is calculated by using the pressure at each location.
5. Conclusions
In this paper, a model has been developed to describe the behavior of a multiphase slug flow in circular microchannels. The model couples the hydrodynamics, reaction and mass transfer phenomena, and for gas-liquid systems, it accounts for both the contraction of the gas phase due to reactive absorption and the inherent change in volume linked to the pressure drop.
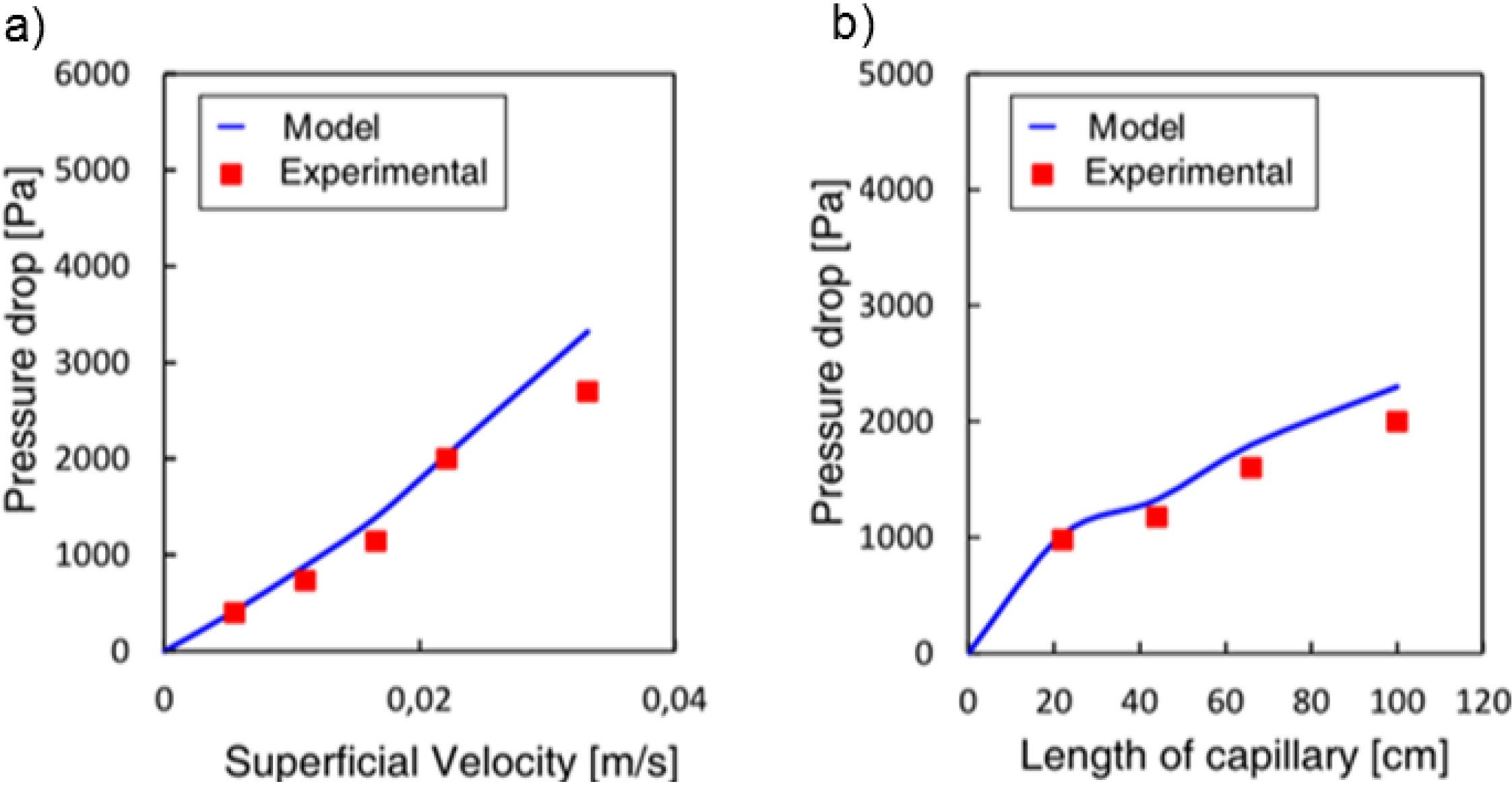
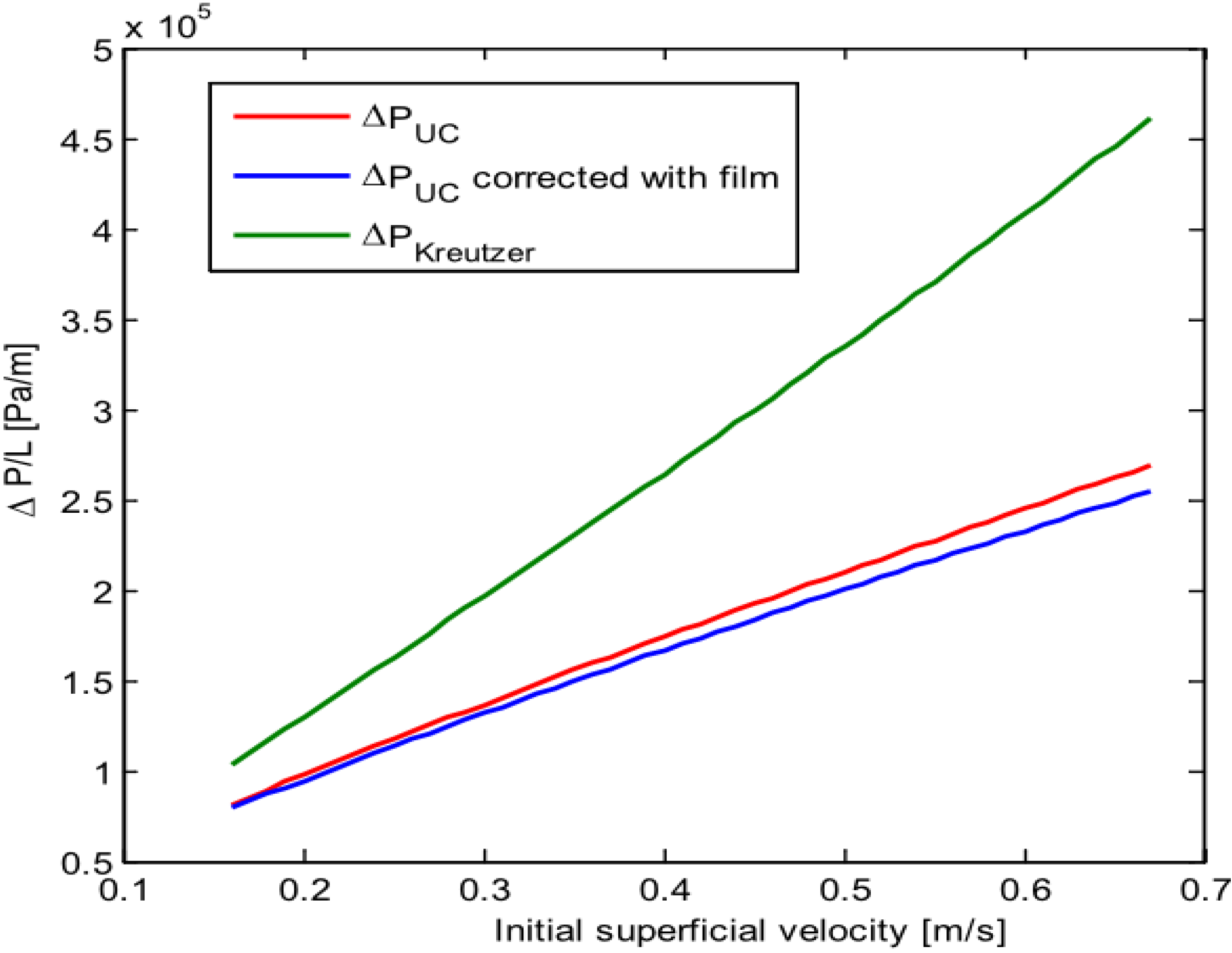
The model was first validated by comparing the results obtained with results from other researchers yielding results of the same order of magnitude. For the pressure drop it gave results consistent with those obtained by Warnier
et al. [
13], and to a lesser extent, Kreutzer
et al. [
22]. For the mass transfer characteristics, the model predicted mass transfer coefficient values in close agreement with those from the most recent publications, like the experimental results of Sobieszuk
et al. [
20] and Yue
et al. [
19]. Furthermore, the model was tested to get an idea of how large the effect of the film surrounding the bubble is on the hydrodynamics, showing only a slight deviation from the case without film. Finally, the effect of the slug geometry was studied, as it was found that this could play an important role for instabilities, and the work of Jovanovic
et al. [
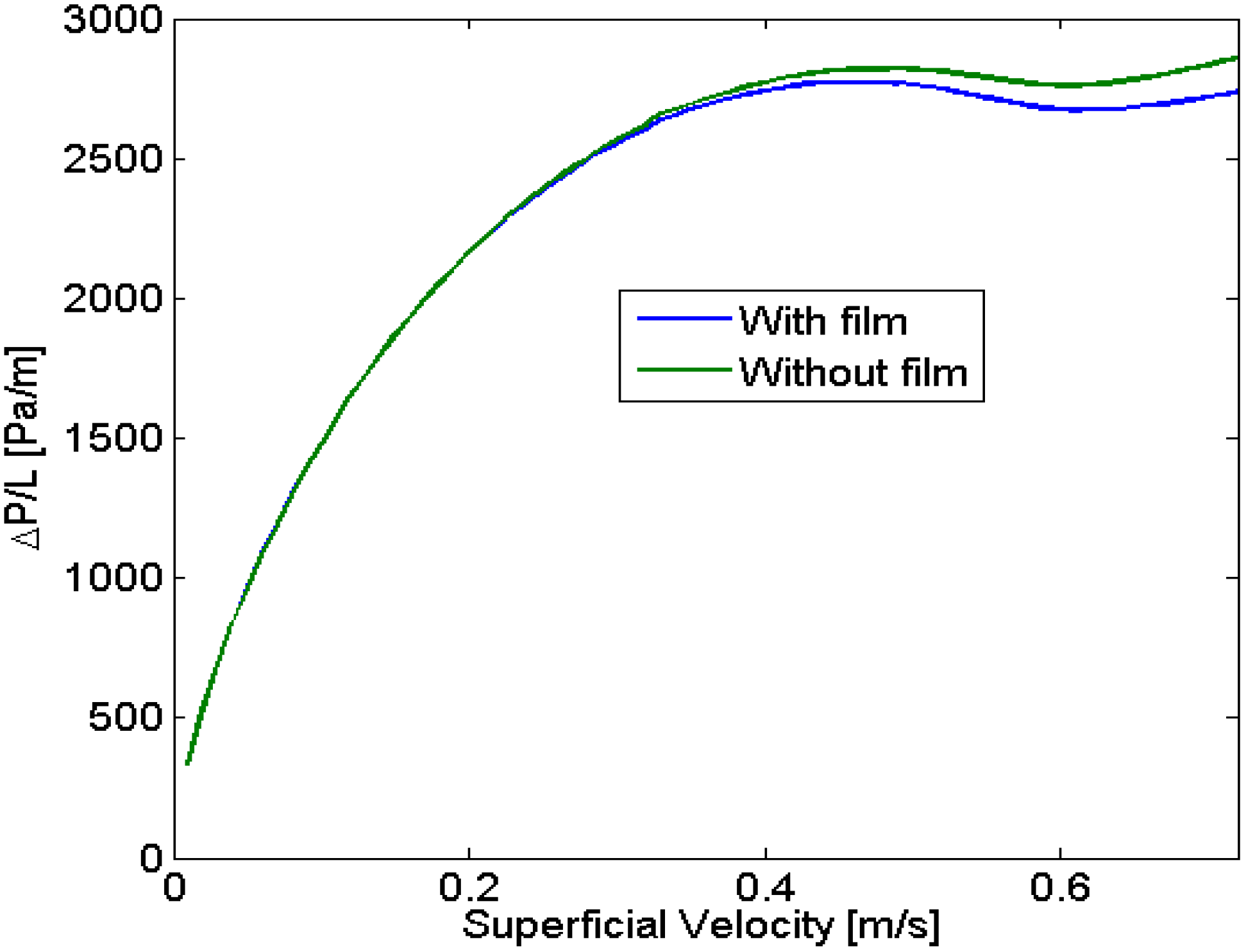
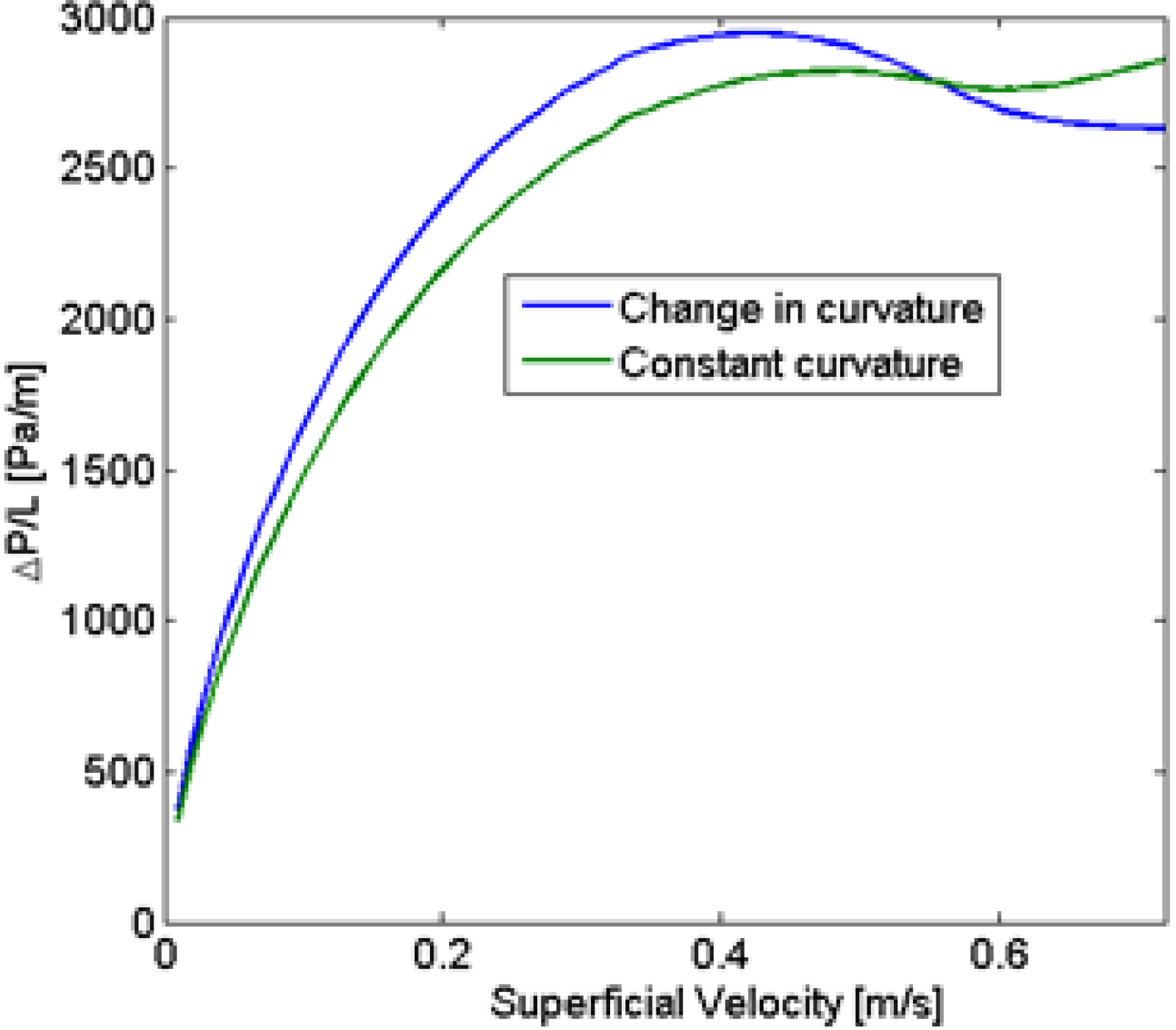
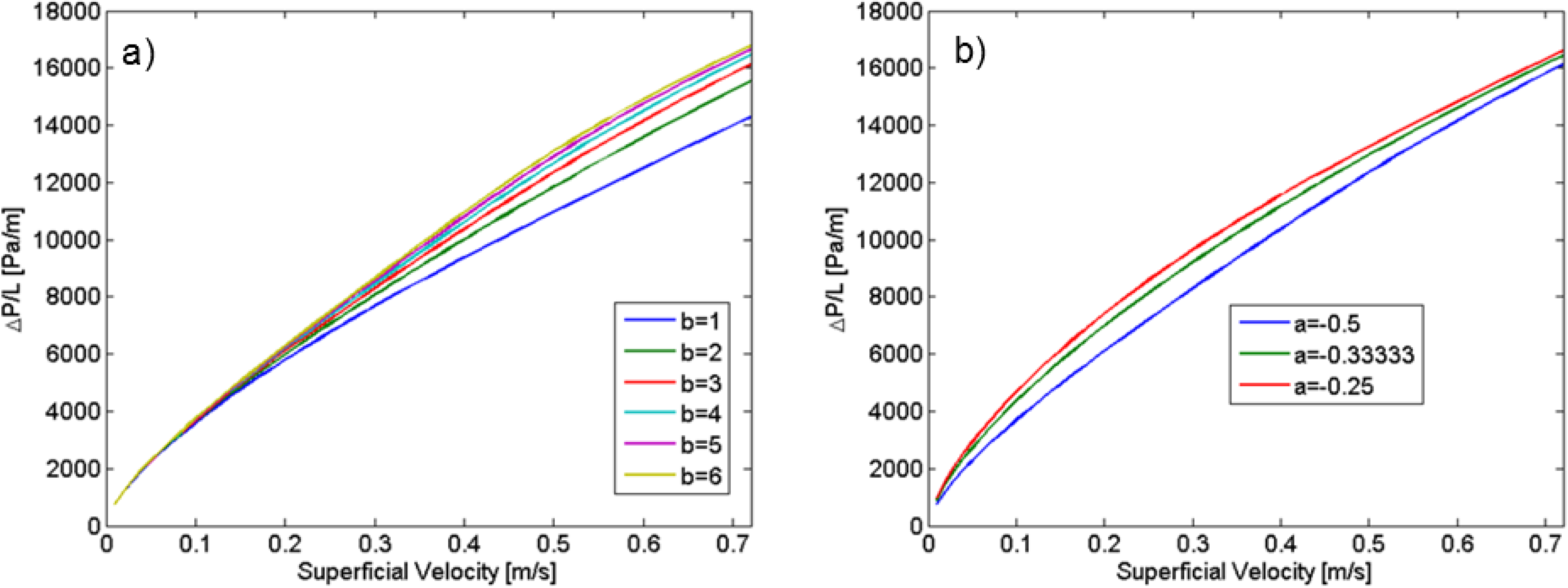
23] has shown that it was not constant but a function of the velocity.
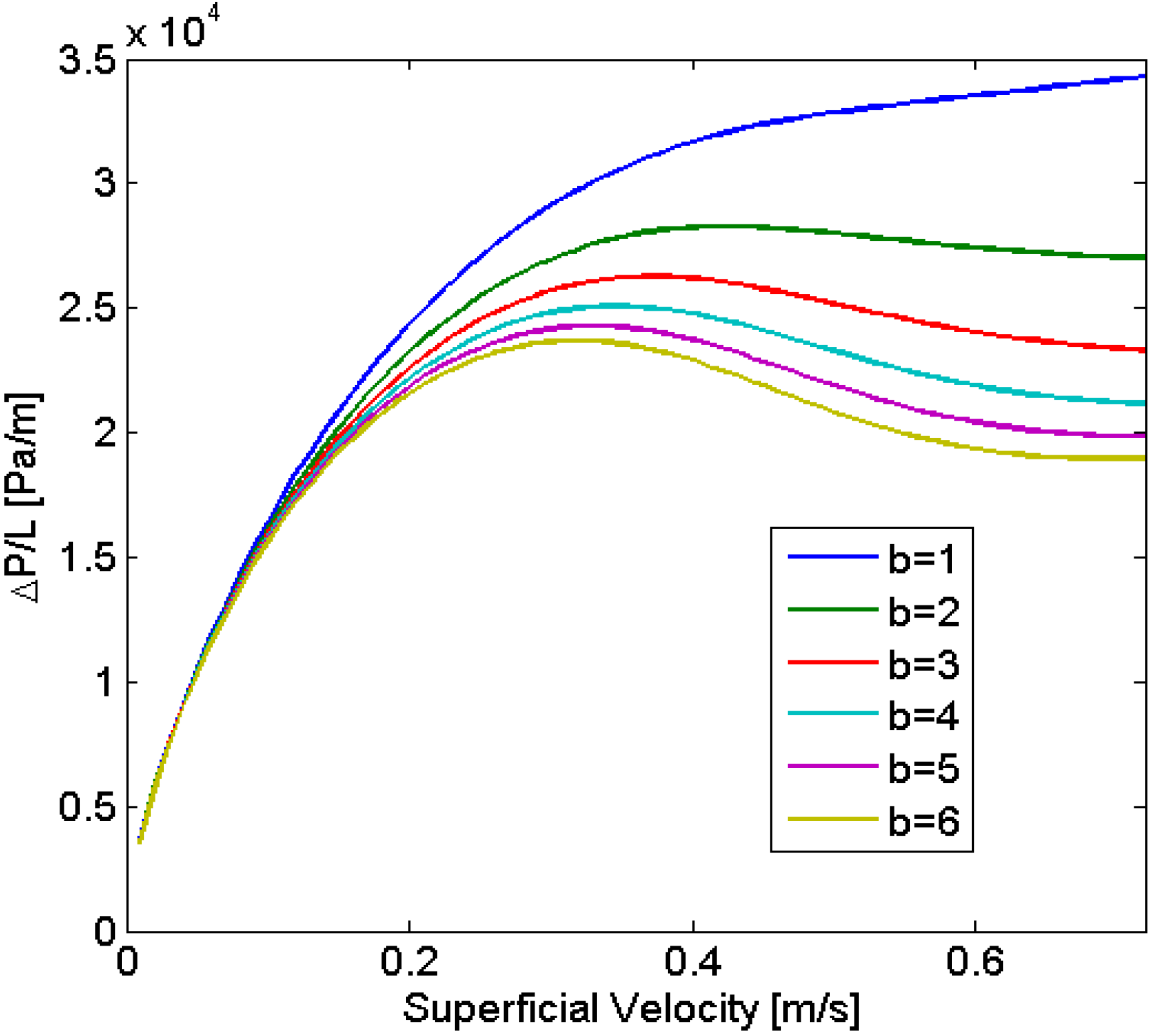
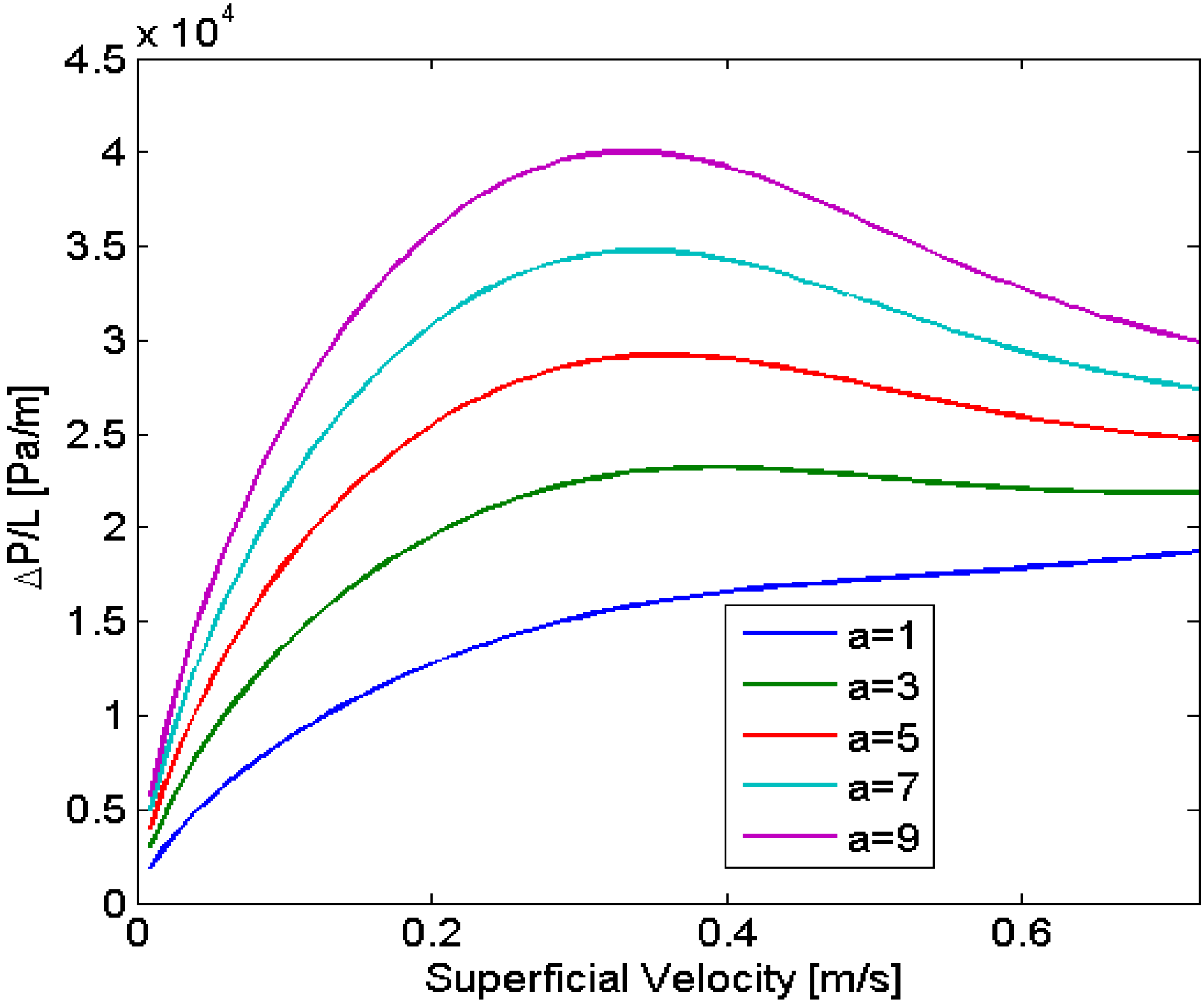
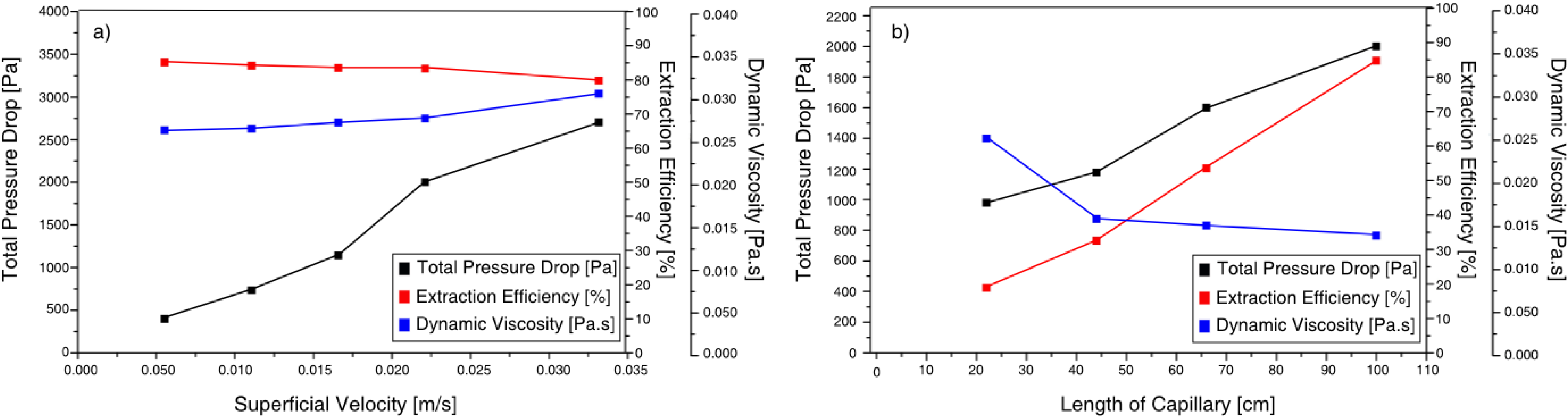
The model was used to analyze the stability of the flow for a gas-liquid system establishing that multiplicities can arise in particular cases, such as long bubbles, or for systems with changes in viscosity. These results led to the study of systems with decreasing viscosity, since this can enable one to achieve a better distribution in parallelized microchannels. Experimental results obtained for an aqueous-ionic liquid-system found a good agreement between the experimental and predicted values (11% and 13% error, depending on the parameter varied).
The results demonstrate that the coupling between flow structure, the extent of reaction/extraction and pressure drop can result in multiple operating states, thus, making an active measurement and control strategy to ensure uniform behavior and optimal performance essential.