A Generalized Measure for the Optimal Portfolio Selection Problem and its Explicit Solution
Abstract
:1. Introduction
2. Main Results
2.1. Optimal Portfolios for Special Cases
2.1.1. Optimal Portfolio Selection With MV Measure
2.1.2. Optimal Portfolio Selection With MSD
2.1.3. Optimal Portfolio Selection With Sharpe Ratio
2.1.4. Optimal Portfolio With Generalized Sharpe Ratio
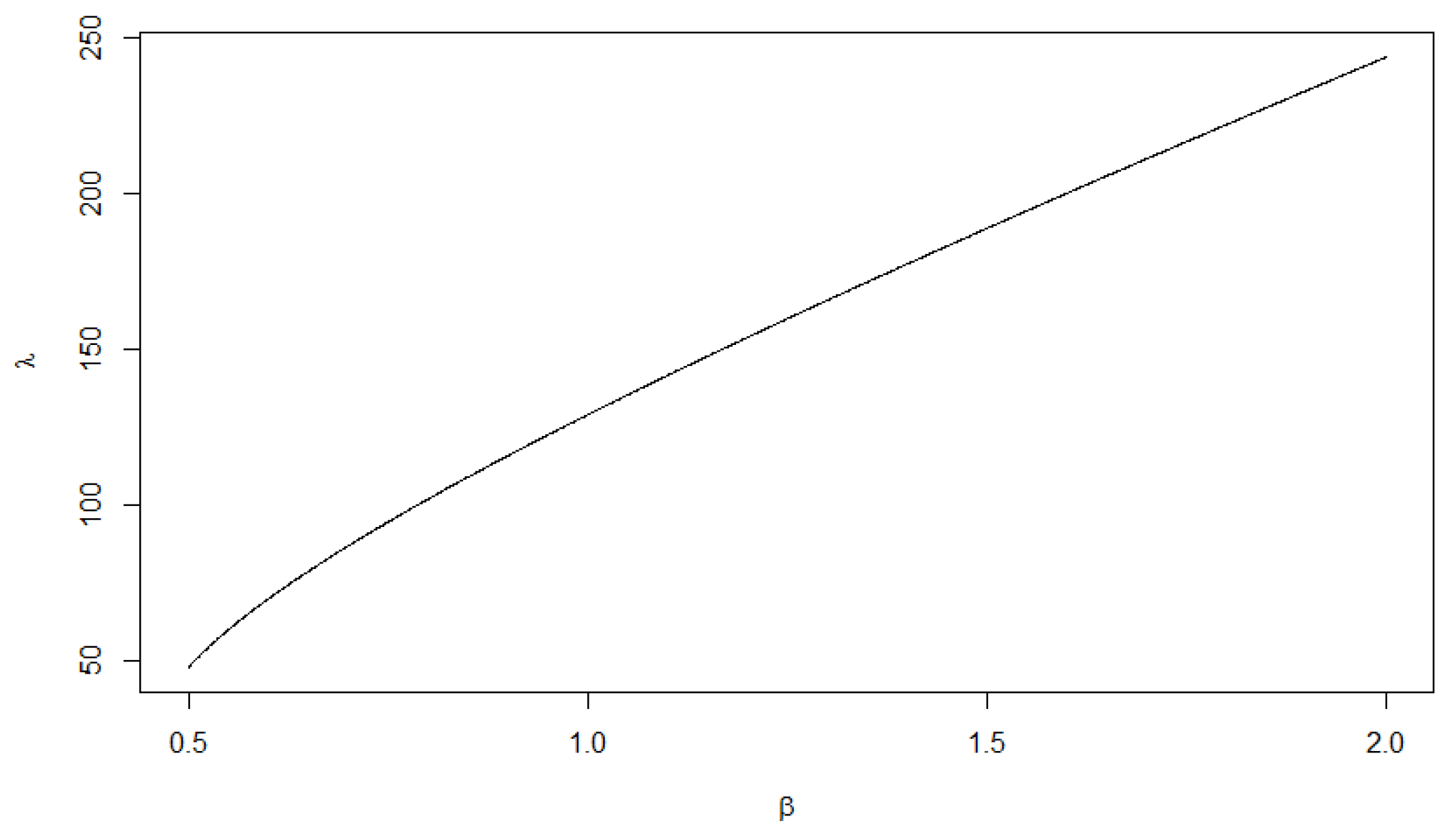
3. Numerical Illustrations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proofs
References
- Bera, Samaresh, Praveen Gupta, and Sudip Misra. 2015. D2S: Dynamic demand scheduling in smart grid using optimal portfolio selection strategy. IEEE Transactions on Smart Grid 6: 1434–42. [Google Scholar] [CrossRef]
- Best, Michael J., and Robert R. Grauer. 1990. The efficient set mathematics when mean-variance problems are subject to general linear constraints. Journal of Economics and Business 42: 105–20. [Google Scholar] [CrossRef]
- Castellano, Rosella, and Roy Cerqueti. 2014. Mean–Variance portfolio selection in presence of infrequently traded stocks. European Journal of Operational Research 234: 442–49. [Google Scholar] [CrossRef]
- Elton, Edwin J., and Martin J. Gruber. 1987. Modern Portfolio Theory and Investment Analysis. New York: Wiley. [Google Scholar]
- Fletcher, Jonathan. 2015. Exploring the benefits of using stock characteristics in optimal portfolio strategies. The European Journal of Finance 23: 1–19. [Google Scholar] [CrossRef] [Green Version]
- Fulga, Cristinca. 2016. Portfolio optimization under loss aversion. European Journal of Operational Research 251: 310–22. [Google Scholar] [CrossRef]
- Graham, John R., Campbell R. Harvey, and Manju Puri. 2015. Capital allocation and delegation of decision-making authority within firms. Journal of Financial Economics 115: 449–70. [Google Scholar] [CrossRef]
- Landsman, Zinoviy, and Emiliano A. Valdez. 2003. Tail conditional expectations for elliptical distributions. North American Actuarial Journal 7: 55–71. [Google Scholar] [CrossRef]
- Landsman, Zinoviy. 2008a. Minimization of the root of a quadratic functional under an affine equality constraint. Journal of Computational and Applied Mathematics 216: 319–27. [Google Scholar] [CrossRef]
- Landsman, Zinoviy. 2008b. Minimization of the root of a quadratic functional under a system of affine equality constraints with application to portfolio management. Journal of Computational and Applied Mathematics 220: 739–48. [Google Scholar] [CrossRef]
- Landsman, Zinoviy, and Udi Makov. 2016. Minimization of a function of a quadratic functional with application to optimal portfolio selection. Journal of Optimization Theory and Application 170: 308–22. [Google Scholar] [CrossRef]
- Li, Bin, and Steven C. H. Hoi. 2014. Online portfolio selection: A survey. ACM Computing Surveys (CSUR) 46: 35. [Google Scholar] [CrossRef]
- Luenberger, David G. 1984. Linear and Nonlinear Programming. Boston: Addison-Wesley. [Google Scholar]
- Markowitz, Harry. 2014. Mean–variance approximations to expected utility. European Journal of Operational Research 234: 346–55. [Google Scholar] [CrossRef]
- Panjer, Harry H., and Phelim. P. Boyle, eds. 1998. Financial economics: With Applications to Investments, Insurance, and Pensions. Schaumburg: Society of Actuaries. [Google Scholar]
- Qin, Zhongfeng. 2015. Mean-variance model for portfolio optimization problem in the simultaneous presence of random and uncertain returns. European Journal of Operational Research 245: 480–88. [Google Scholar] [CrossRef]
- Ray, Pritee, and Mamata Jenamani. 2016. Mean-variance analysis of sourcing decision under disruption risk. European Journal of Operational Research 250: 679–89. [Google Scholar] [CrossRef]
- Schaible, Siegfried, and Toshidide Ibaraki. 1983. Fractional programming. European Journal of Operational Research 12: 325–38. [Google Scholar] [CrossRef]
- Sharpe, William F. 1966. Mutual fund performance. The Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Sharpe, William F. 1998. The Sharpe Ratio. Streetwise-The Best of the Journal of Portfolio Management. Princeton: Princeton University Press, pp. 169–85. [Google Scholar]
- Shen, Yang, Xin Zhang, and Tak Kuen Siu. 2014. Mean–variance portfolio selection under a constant elasticity of variance model. Operations Research Letters 42: 337–42. [Google Scholar] [CrossRef]
- Steinbach, Marc C. 2001. Markowitz Revisted: Mean-Variance models in financial portfolio analysis. SIAM Review 43: 31–85. [Google Scholar] [CrossRef]
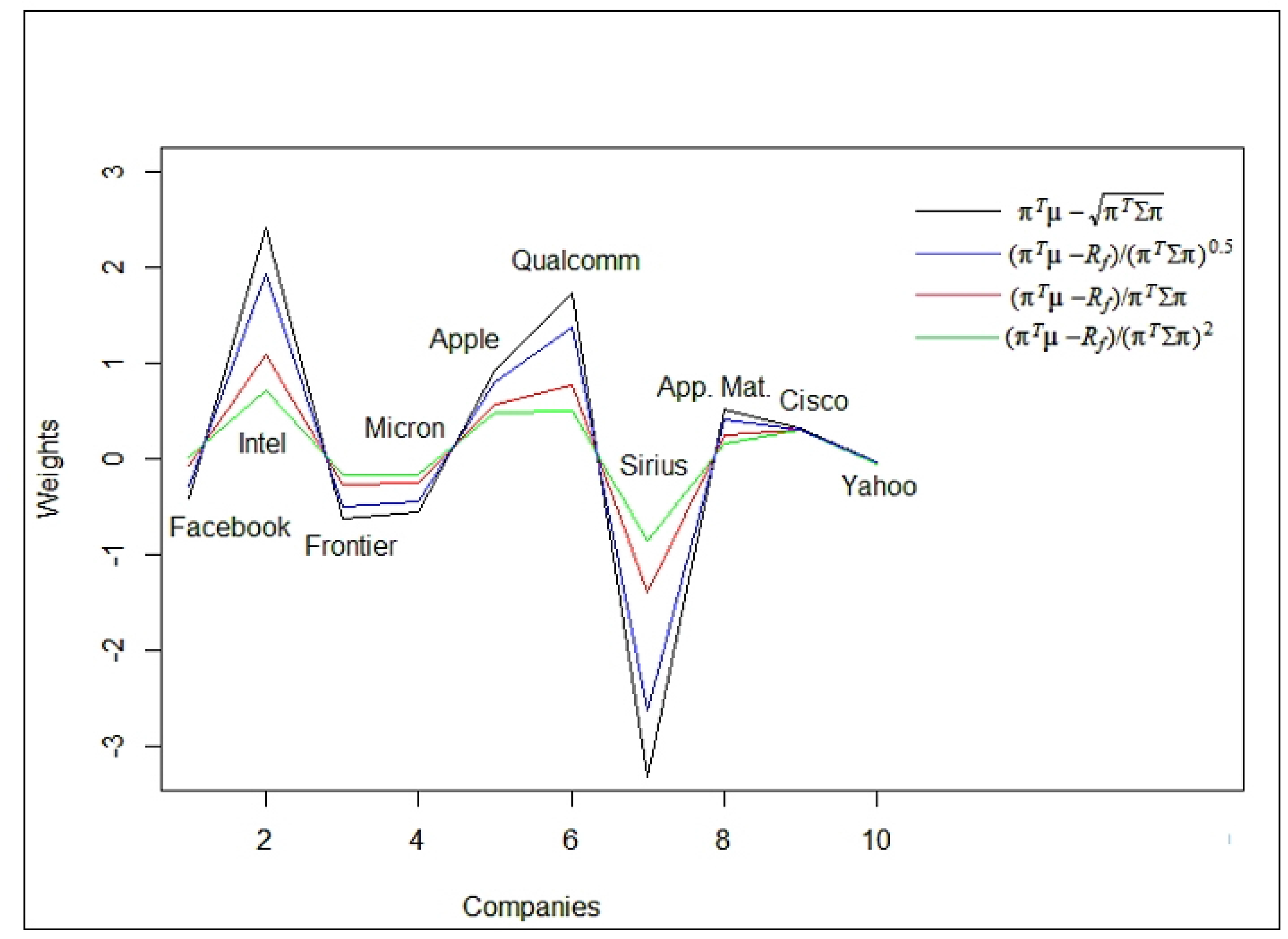
| Stock | Intel | Frontier | Micron | Apple | |
|---|---|---|---|---|---|
| Mean | 0.000868097 | −0.000608624 | −0.006684089 | −0.006902419 | −6.1631 × 10 |
| Stock | Qualcomm | Sirius | App. Mat. | Cisco | Yahoo |
| Mean | 0.001046047 | 0.000763278 | 0.002049615 | −2.57636 × 10 | 0.001925747 |
| Intel | Frontier | Micron | Apple | ||
| 0.000175 | 0.000038 | 0.000054 | 0.000063 | −0.000014 | |
| Intel | 0.000038 | 0.000174 | 0.000075 | 0.000213 | −0.000014 |
| Frontier | 0.000054 | 0.000075 | 0.000685 | 0.000031 | −0.000001 |
| Micron | 0.000063 | 0.000213 | 0.000031 | 0.001031 | 0.000048 |
| Apple | −0.000014 | −0.000014 | −0.000001 | 0.000048 | 0.000124 |
| Qualcomm | Sirius | App. Mat. | Cisco | Yahoo | |
| 0.000029 | −0.000015 | −0.000019 | 0.000006 | 0.000010 | |
| Intel | 0.000030 | 0.000086 | 0.000024 | 0.000028 | 0.000047 |
| Frontier | 0.000084 | −0.000014 | 0.000071 | 0.000050 | 0.000095 |
| Micron | 0.000027 | 0.000023 | 0.000050 | −0.000002 | 0.000047 |
| Apple | −0.000002 | 0.000012 | 0.000015 | −0.000010 | 0.000046 |
| Qualcomm | Sirius | App. Mat. | Cisco | Yahoo | |
| Qualcomm | 0.000108 | 0.000054 | 0.000038 | 0.000054 | 0.000075 |
| Sirius XM | 0.000054 | 0.000097 | 0.000049 | 0.000044 | 0.000060 |
| App. Mat. | 0.000038 | 0.000049 | 0.000235 | 0.000046 | 0.000086 |
| Cisco | 0.000054 | 0.000044 | 0.000046 | 0.000084 | 0.000037 |
| Yahoo | 0.000075 | 0.000060 | 0.000086 | 0.000037 | 0.000316 |
| Utility Function | ||||||
| 61.78 | −0.282 | 1.938 | −0.496 | −0.432 | 0.809 | |
| 47.6 | −0.402 | 2.418 | −0.627 | −0.542 | 0.937 | |
| 128.8 | −0.071 | 1.094 | −0.264 | −0.238 | 0.584 | |
| 243.7 | 0.019 | 0.727 | −0.163 | −0.154 | 0.486 | |
| Utility Function | ||||||
| 1.382 | −2.613 | 0.419 | 0.314 | −0.0391 | ||
| 1.731 | −3.313 | 0.516 | 0.319 | −0.0377 | ||
| 0.766 | −1.382 | 0.247 | 0.305 | −0.041 | ||
| 0.499 | −0.847 | 0.173 | 0.301 | −0.042 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landsman, Z.; Makov, U.; Shushi, T. A Generalized Measure for the Optimal Portfolio Selection Problem and its Explicit Solution. Risks 2018, 6, 19. https://doi.org/10.3390/risks6010019
Landsman Z, Makov U, Shushi T. A Generalized Measure for the Optimal Portfolio Selection Problem and its Explicit Solution. Risks. 2018; 6(1):19. https://doi.org/10.3390/risks6010019
Chicago/Turabian StyleLandsman, Zinoviy, Udi Makov, and Tomer Shushi. 2018. "A Generalized Measure for the Optimal Portfolio Selection Problem and its Explicit Solution" Risks 6, no. 1: 19. https://doi.org/10.3390/risks6010019




