Deflation Risk and Implications for Life Insurers
Abstract
:1. Introduction
2. Framework
2.1. Inflation and Real Interest Rate Dynamics
2.2. Risk-Neutral Dynamics
2.3. Derivative Valuation
3. Estimation Method
4. Application to the US Inflation
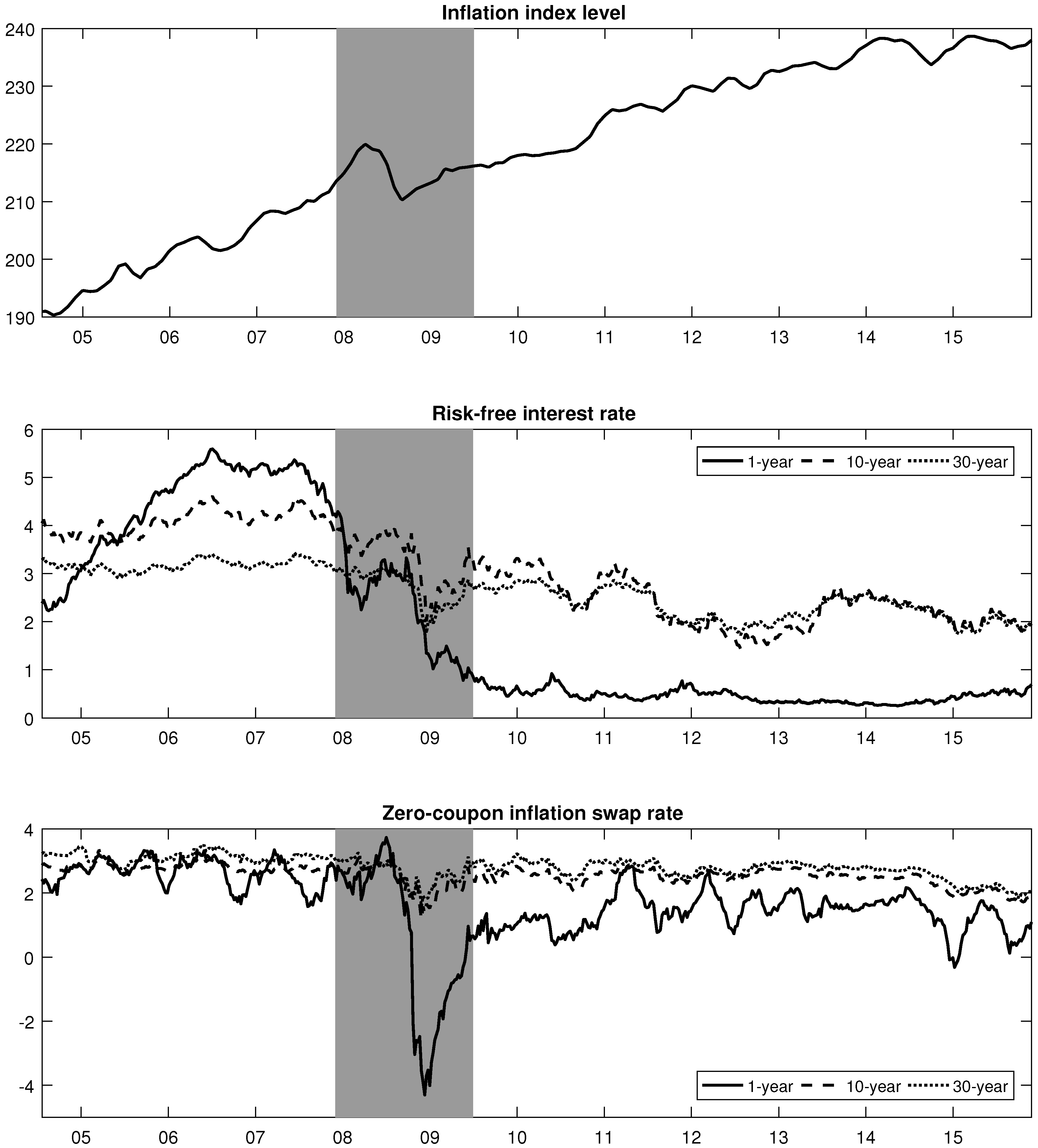
4.1. Data
4.2. Estimation Results
4.3. Estimation of Nested Models
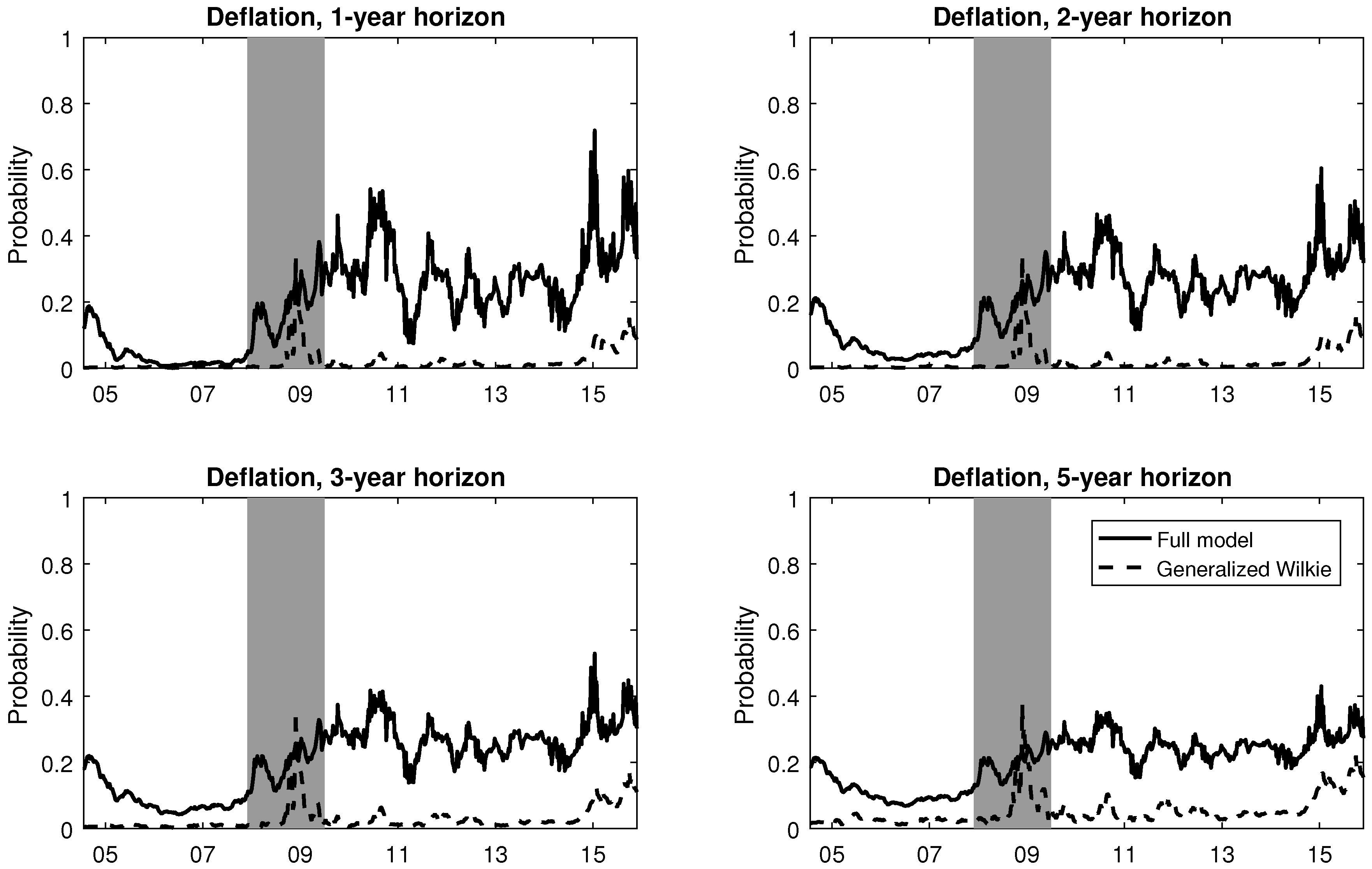
4.4. Deflation Risk through Time
5. Impacts of Deflation on Life Insurance
5.1. Impacts on the Discount Rate
5.2. Impacts of Embedded Optionalities
6. Concluding Remarks
Acknowledgments
Conflicts of Interest
Appendix A. Model Under the Risk-Neutral Measure
Appendix B. Derivative Valuation
Appendix B.1. Zero-Coupon Bonds
Appendix B.2. Inflation Swaps
Appendix B.3. Cap and Floor Options
Appendix C. Distribution of the Inflation Index Level
References
- A. Bohnert, N. Gatzert, and A. Kolb. “Assessing inflation risk in non-life insurance.” Insur. Math. Econ. 66 (2016): 86–96. [Google Scholar] [CrossRef]
- M. Mittelstaedt. “Deflation ’Worst Possible World’ for Life Insurers.” 2010. Available online: http://www. theglobeandmail.com/globe-investor/investment-ideas/deflation-worst-possible-world-for-life-insurers/ article1320807/ (accessed on 14 July 2016).
- E. Dimitriou, and B. Ahmedov. “Insurance and Inflation Risk: Under the Radar? ” 2014. Available online: http://www.pimco.co.uk/insights/viewpoints/viewpoints/insurance-and-inflation-risk-under-the-radar (accessed on 14 July 2016).
- A. Koursaris, and V. Knava. “Insurance: Market-consistency and ESGs.” 2010. Available online: http://www.theactuary.com/archive/old-articles/part-3/insurance-3A-market-consistency-and-esgs/ (accessed on 14 July 2016).
- I. Fisher. The Theory of Interest. New York, NY, USA: The Macmillan Co., 1930. [Google Scholar]
- S. Heston, and S. Nandi. “A closed-form GARCH option valuation model.” Rev. Financ. Stud. 13 (2000): 585–625. [Google Scholar] [CrossRef]
- M. Fleckenstein, F.A. Longstaff, and H. Lustig. “Deflation Risk.” Working Paper. Unpulished work. 2014. [Google Scholar]
- K.C. Ahlgrim, and S.P. D’Arcy. “The Effect of Deflation or High Inflation on the Insurance Industry.” Working Paper. Unpulished work. 2012. [Google Scholar]
- A. Wilkie. “Stochastic investment models: Theory and applications.” Insur. Math. Econ. 6 (1987): 65–83. [Google Scholar] [CrossRef]
- S.N. Singor, L.A. Grzelak, D.D. Van Bragt, and C.W. Oosterlee. “Pricing inflation products with stochastic volatility and stochastic interest rates.” Insur. Math. Econ. 52 (2013): 286–299. [Google Scholar] [CrossRef]
- S.L. Heston. “A closed-form solution for options with stochastic volatility with applications to bond and currency options.” Rev. Financ. Stud. 6 (1993): 327–343. [Google Scholar] [CrossRef]
- A. Ang, G. Bekaert, and M. Wei. “Do macro variables, asset markets, or surveys forecast inflation better? ” J. Monet. Econ. 54 (2007): 1163–1212. [Google Scholar] [CrossRef]
- A.W. Phillips. “The relation between unemployment and the rate of change of money wage rates in the United Kingdom, 1861–1957.” Economica 25 (1958): 283–299. [Google Scholar] [CrossRef]
- M. Pond, and C. Mirani. “Market Strategy Americas.” Technical Report. Barclays Capital, 2011. [Google Scholar]
- Y. Kitsul, and J.H. Wright. “The economics of options-implied inflation probability density functions.” J. Financ. Econ. 110 (2013): 696–711. [Google Scholar] [CrossRef]
- O. Vasicek. “An equilibrium characterization of the term structure.” J. Financ. Econ. 5 (1977): 177–188. [Google Scholar] [CrossRef]
- F. Black, and M. Scholes. “The pricing of options and corporate liabilities.” J. Political Econ. 81 (1973): 637–654. [Google Scholar] [CrossRef]
- L. Kilian, and S. Manganelli. “Quantifying the risk of deflation.” J. Money Credit Bank. 39 (2007): 561–590. [Google Scholar] [CrossRef]
- R. Bansal, and A. Yaron. “Risks for the long run: A potential resolution of asset pricing puzzles.” J. Financ. 59 (2004): 1481–1509. [Google Scholar] [CrossRef]
- D. Creal. “A survey of sequential Monte Carlo methods for economics and finance.” Econom. Rev. 31 (2012): 245–296. [Google Scholar] [CrossRef]
- P. Christoffersen, K. Jacobs, and C. Ornthanalai. “Dynamic jump intensities and risk premiums: Evidence from S&P500 returns and options.” J. Financ. Econ. 106 (2012): 447–472. [Google Scholar]
- C. Ornthanalai. “Levy jump risk: Evidence from options and returns.” J. Financ. Econ. 112 (2014): 69–90. [Google Scholar] [CrossRef]
- C. Bardgett, E. Gourier, and M. Leippold. “Inferring Volatility Dynamics and Risk Premia from the S&P 500 and VIX Markets.” Working Paper. Unpulished work. 2015. [Google Scholar]
- S. Julier, and J. Uhlmann. “A New Extension of the Kalman Filter to Nonlinear Systems.” In Proceedings of the AeroSence: 11th International Symposium Aerospace/Defense Sensing, Simulation and Controls, Orlando, FL, USA, 20–25 April 1997; pp. 182–193.
- E.A. Wan, and R. Van Der Merwe. “The unscented Kalman filter for nonlinear estimation.” In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158.
- P. Christoffersen, C. Dorion, K. Jacobs, and L. Karoui. “Nonlinear Kalman filtering in affine term structure models.” Manag. Sci. 60 (2014): 2248–2268. [Google Scholar] [CrossRef]
- P. Carr, and L. Wu. “Stock options and credit default swaps: A joint framework for valuation and estimation.” J. Financ. Econom. 8 (2010): 409–449. [Google Scholar] [CrossRef]
- M. Boudreault, G. Gauthier, and T. Thomassin. “Recovery rate risk and credit spreads in a hybrid credit risk model.” J. Credit Risk 9 (2013): 3–39. [Google Scholar] [CrossRef]
- J. Kerkhof. “Inflation derivatives explained.” In Fixed Income Quantitative Research. New York, NY, USA: Lehman Brothers, 2005, pp. 1–80. [Google Scholar]
- M.J. Fleming, and J. Sporn. “Trading activity and price transparency in the inflation swap market.” Econ. Policy Rev. 19 (2013): 49–62. [Google Scholar] [CrossRef]
- B. Dumas, J. Fleming, and R.E. Whaley. “Implied volatility functions: Empirical tests.” J. Financ. 53 (1998): 2059–2106. [Google Scholar] [CrossRef]
- The National Bureau of Economic Research (NBER). “US Business Cycle Expansions and Contraction.” 2016. Available online: http://www.nber.org/cycles.html/ (accessed on 15 July 2016).
- B. Rémillard. Statistical Methods for Financial Engineering. London, UK: Chapman & Hall, 2013. [Google Scholar]
- J.H. Christensen, J.A. Lopez, and G.D. Rudebusch. “Do central bank liquidity facilities affect interbank lending rates? ” J. Bus. Econ. Stat. 32 (2014): 136–151. [Google Scholar] [CrossRef]
- T. Hoshi, and A.K. Kashyap. “Japan’s financial crisis and economic stagnation.” J. Econ. Perspect. 18 (2004): 3–26. [Google Scholar] [CrossRef]
- M. Dorfman, A. Kling, and J. Russ. “The Impact of Deflation on Insurance Companies Offering Participating Life Insurance.” Working Paper. Unpulished work. 2006. [Google Scholar]
- P. Pflaumer. “Methods for estimating selected life table parameters using the Gompertz Distribution.” In Proceedings of the Joint Statistical Meetings, Social Statistics Section, Miami Beach, FL, USA, 30 July 2011–4 August 2011; pp. 733–747.
- J.R. Brown, O.S. Mitchell, and J.M. Poterba. “Mortality Risk, Inflation Risk, and Annuity Products.” Working Paper. Unpulished work. 2000. [Google Scholar]
- F. Esscher. “On the probability function in the collective theory of risk.” Skandinavisk Aktuarietidskrift 15 (1932): 175–195. [Google Scholar]
- J. Gil-Pelaez. “Note on the inversion theorem.” Biometrika 38 (1951): 481–482. [Google Scholar] [CrossRef]
- M. Kendall, and A. Stuart. The Advanced Theory of Statistics. New York, NY, USA: Macmillan Publishing Co., 1977, Volume 1. [Google Scholar]
- 1.In this study, inflation risk refers to both the risks of deflation (inflation rates being too low) and high inflation (too high).
- 2.For instance, US Social Security benefits do not decrease if the cost-of-living adjustment is negative, as prescribed by the Social Security Act. It is the same in Canada: the Canada Pension Plan payments do not decrease in case of deflation. Note that other private and public pension plans may provide similar protections.
- 3.Generally, the nominal interest rate is modelled directly, without special emphasis on the dynamics of underlying economic quantities. Modelling the real interest rate and the expected inflation rate separately allows for more flexibility, and has the advantage of capturing the risk associated specifically to these two factors.
- 4.Phillips curve models of inflation link the expected inflation to some measure of the output gap.
- 5.Time series of realized inflation rates is obtained by a simple transformation of inflation index levels.
- 7.Over a short period of time, it is known from a first-order Taylor expansion that .
- 8.In an earlier version of their paper, Fleckenstein et al. [7] do have stochastic volatility. However, the variance could be negative in the model, which is inconsistent with the definition of this quantity.
- 9.In an unreported study, we find that the addition of the long-run trend only has a marginal impact on the model fit, as this latent variable is quite steady in time.
- 10.If the inflation swap rate is 1.25% and the maturity is 5 years, then a cash flow of will be exchanged at maturity.
- 11.Year-on-year inflation options are caps and floors that make payments on an annual basis. The payment is the difference between some strike rate and the annual inflation. In contrast, zero-coupon inflation options make only one payment as it is the case with zero-coupon inflation swaps. This payment is based on the cumulative inflation from inception up to the maturity date.
- 12.The European inflation cap case is done without any loss of generality since one could simply use put-call parity to price European inflation floor or put options.
- 13.Since is latent, there is no way to recover as in a typical GARCH framework.
- 14.For a review of recent developments in filtering methods for economics and finance applications, see Creal [20].
- 15.The standard deviation of the error is proportional to the size of the observed implied volatility. This is consistent with the assumption that relative error on implied volatility should be approximately Gaussian.
- 16.The parameters of the UKF technique have been assumed to be , , and , as proposed in Wan and Van Der Merwe [25].
- 18.Quasi-likelihood means here that the first two moments of the posterior distribution have a second order precision, and a posterior Gaussian distribution has to be assumed.
- 19.Series ID: CPIAUCNS.
- 20.Series ID: USD1MTD156N to USD6MTD156N and DSWP1 to DSWP30.
- 21.Series ID: USSWIT1 to USSWIT30.
- 22.We focus on Wednesday data because it is the least likely day to be a holiday, and it is least likely to be affected by weekend effects. For more details on the advantages of using Wednesday data, see Dumas et al. [31].
- 23.Series IDs starting with USIZF and USIZC are chosen.
- 24.For caps, we verify that their prices are greater than or equal to . For floors, .
- 25.In this study, we use the recessions as defined by the National Bureau of Economic Research [32].
- 26.Note that at the beginning of the sample, only index levels, nominal bond prices, and swap prices are available. Then, starting in October 2009, option implied volatilities were available and were used in the estimation as measurements.
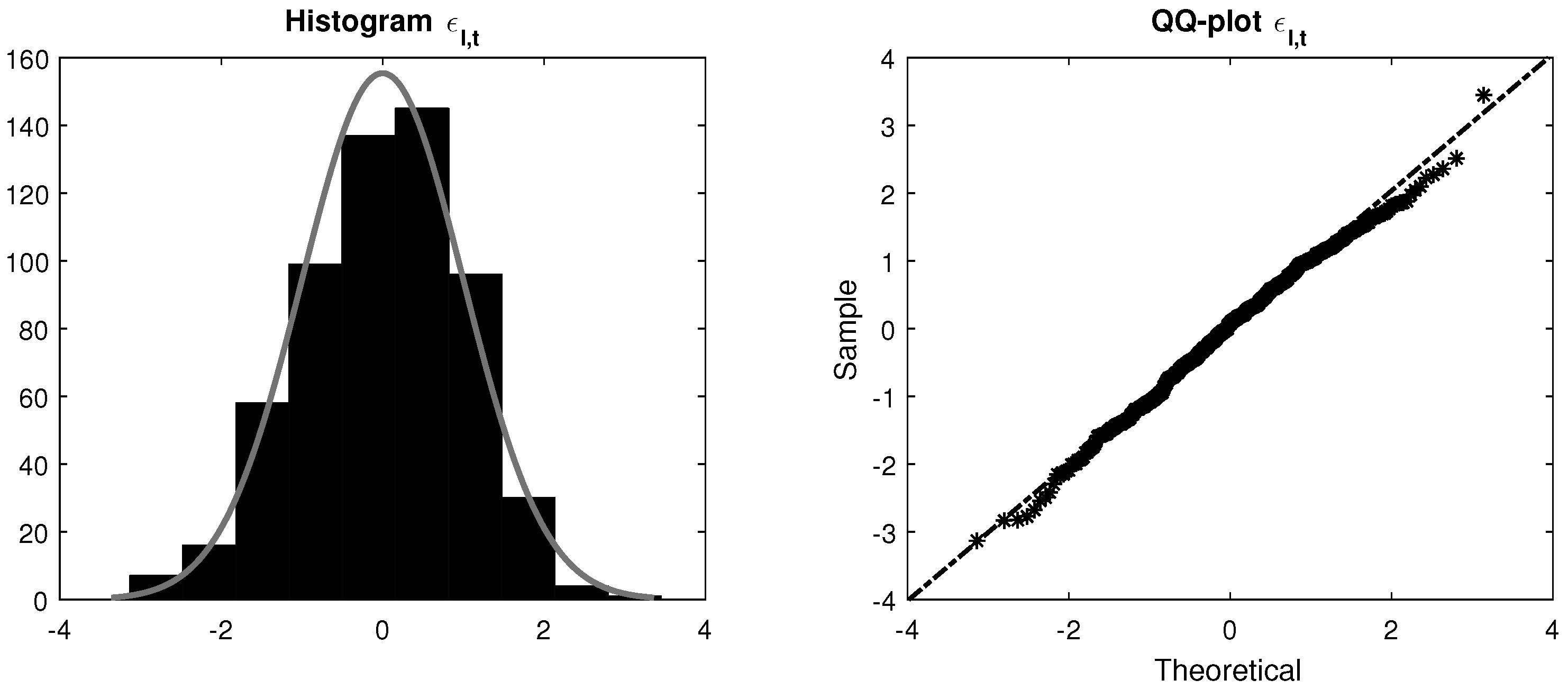
- 27.The p-values associated to the chi-square and the Jarque–Bera goodness of fit tests are 0.116 and 0.114, respectively.
- 28.From a statistical perspective, this is the equivalent of setting for each t, and assuming that . Therefore, by assuming an expected inflation rate of zero, the real interest is therefore equal to the nominal interest rate.
- 29.As inflation caps and floors depend on the real interest rate, we cannot use the option dataset in the model estimation. See Equation (6) for more details.
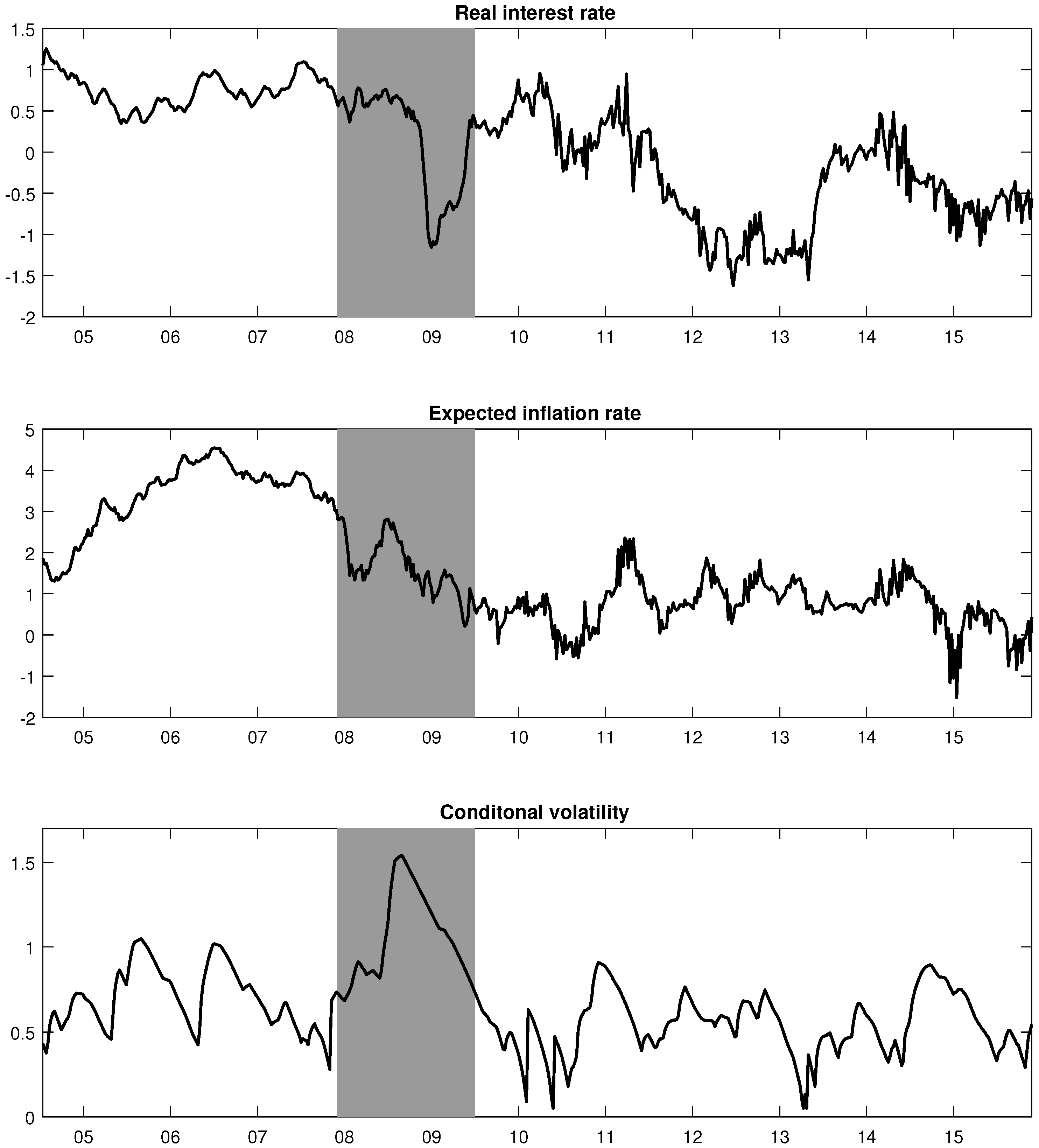
- 30.For the full model, the filtered expected inflation rate decreased during the post-recession era, as seen in Figure 2, and this could to some extent explain the high 1-year deflation probabilities during that period.
- 31.Typically, the ratio of risk-neutral to physical probabilities are generally higher than one for tail risk. For a discussion on this, see Fleckenstein et al. [7].
- 32.Note that our results are robust to other types of life insurance products, such as deferred annuities.
- 33.The Gompertz survivor function is approximated by , where and . These parameters are estimated by Pflaumer [37] while using the 2006 National Vital Statistics Reports life table for females in the US.
- 34.It is the average 5-year real rate over the 2004–2014 period, as given by the US Department of the Treasury.
- 35.Time of death and other relevant rates are sampled through a Monte Carlo simulation engine. The number of paths is set to .
- 36.Indeed, the expected value of the portfolio value should be approximately the same across the various models. Therefore, comparing the pricing performance is futile, as only the average behaviour of the discount rate is important in calculating the expected future payments.
- 37.Commonly, decreases in the inflation index level make future payments smaller. However, the added protection does not reduce the paid amount in the case of deflation.
- 38.The NIR model cannot separate the respective effects of the real interest rate and the expected inflation.
- 39.In a robustness test, life insurance policies have been used instead of annuities. The results were qualitatively the same, meaning that risk measures obtained with the full model were higher than the ones of the GW model.
- 40.As explained in previous sections, options contain critical information about the tails of the inflation index distribution. Additionally, flexible modelling assumptions are of paramount importance to capture the evolution of market-consistent risk measures.




| Dynamics | Parameter | Interpretation |
|---|---|---|
| Real interest rate | θ | Unconditional level of real interest rate under |
| Unconditional level of real interest rate under | ||
| κ | Speed of mean reversion | |
| σ | Volatility of the real interest rate innovations | |
| Initial real interest rate | ||
| ρ | Correlation coefficient between real interest rate and | |
| expected inflation innovations | ||
| Expected inflation | ν | Unconditional level of expected inflation under |
| Unconditional level of expected inflation under | ||
| β | Speed of mean reversion | |
| γ | Volatility of the expected inflation innovations | |
| Initial expected inflation rate | ||
| Conditional variance | w | Unconditional level of variance |
| a | ARCH parameter | |
| b | GARCH parameter (i.e., persistence) | |
| c | Asymmetry parameter | |
| Initial variance level | ||
| Error standard deviations | Standard deviation of bonds | |
| Standard deviation of swaps | ||
| Homoskedastic standard deviation of implied volatilities | ||
| Adjustment parameter for option maturity | ||
| Adjustment parameter for option strike |
| Panel A: Risk-Free Interest Rates | ||||||||
| Maturity | Mean | SD | Min | Median | Max | |||
| 1/12 | 1.655 | 1.965 | 0.148 | 0.202 | 0.263 | 3.114 | 5.805 | 593 |
| 1/6 | 1.731 | 1.955 | 0.189 | 0.242 | 0.348 | 3.172 | 5.723 | 593 |
| 1/4 | 1.793 | 1.943 | 0.223 | 0.279 | 0.468 | 3.231 | 5.679 | 593 |
| 1/6 | 1.948 | 1.874 | 0.320 | 0.443 | 0.734 | 3.388 | 5.540 | 593 |
| 1 | 1.886 | 1.873 | 0.250 | 0.419 | 0.618 | 3.573 | 5.591 | 593 |
| 2 | 2.048 | 1.709 | 0.339 | 0.624 | 1.117 | 3.669 | 5.425 | 593 |
| 3 | 2.255 | 1.563 | 0.427 | 0.937 | 1.639 | 3.807 | 5.279 | 593 |
| 4 | 2.450 | 1.426 | 0.554 | 1.265 | 1.998 | 3.824 | 5.167 | 593 |
| 5 | 2.615 | 1.300 | 0.717 | 1.546 | 2.284 | 3.862 | 5.062 | 593 |
| 7 | 2.843 | 1.097 | 1.088 | 1.907 | 2.665 | 3.862 | 4.868 | 593 |
| 10 | 2.989 | 0.899 | 1.432 | 2.165 | 2.927 | 3.832 | 4.606 | 593 |
| 30 | 2.620 | 0.481 | 1.719 | 2.166 | 2.660 | 3.090 | 3.436 | 593 |
| Panel B: Inflation Swap Rates | ||||||||
| Maturity | Mean | SD | Min | Median | Max | |||
| 1 | 1.652 | 1.217 | −4.301 | 1.170 | 1.740 | 2.520 | 3.732 | 593 |
| 2 | 1.856 | 0.962 | −3.605 | 1.449 | 1.878 | 2.536 | 3.460 | 593 |
| 3 | 2.018 | 0.757 | −2.047 | 1.672 | 2.033 | 2.583 | 3.335 | 593 |
| 4 | 2.145 | 0.620 | −1.112 | 1.811 | 2.157 | 2.605 | 3.280 | 593 |
| 5 | 2.249 | 0.535 | −0.478 | 1.946 | 2.295 | 2.640 | 3.271 | 593 |
| 6 | 2.329 | 0.467 | 0.218 | 2.092 | 2.396 | 2.651 | 3.249 | 593 |
| 7 | 2.397 | 0.417 | 0.504 | 2.207 | 2.474 | 2.687 | 3.160 | 593 |
| 8 | 2.454 | 0.381 | 0.768 | 2.306 | 2.537 | 2.713 | 3.195 | 593 |
| 9 | 2.503 | 0.347 | 0.988 | 2.364 | 2.575 | 2.733 | 3.096 | 593 |
| 10 | 2.549 | 0.321 | 1.173 | 2.429 | 2.621 | 2.760 | 3.110 | 593 |
| 12 | 2.606 | 0.308 | 1.346 | 2.488 | 2.673 | 2.811 | 3.130 | 593 |
| 15 | 2.674 | 0.310 | 1.336 | 2.540 | 2.742 | 2.883 | 3.300 | 593 |
| 20 | 2.733 | 0.321 | 1.267 | 2.595 | 2.808 | 2.950 | 3.360 | 593 |
| 25 | 2.773 | 0.333 | 1.414 | 2.637 | 2.845 | 2.991 | 3.390 | 593 |
| 30 | 2.815 | 0.342 | 1.573 | 2.677 | 2.877 | 3.035 | 3.500 | 593 |
| Maturity | Mean | N | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.775 | 1.586 | 1.361 | 1.299 | 1.382 | 1.695 | 2.028 | 1.589 | 2868 |
| 2 | 2.616 | 2.289 | 1.896 | 1.804 | 1.949 | 2.326 | 2.617 | 2.214 | 2916 |
| 3 | 3.166 | 2.766 | 2.236 | 2.102 | 2.251 | 2.723 | 3.192 | 2.633 | 2862 |
| 5 | 4.043 | 3.505 | 2.757 | 2.584 | 2.745 | 3.325 | 3.882 | 3.263 | 2465 |
| 7 | 4.811 | 4.192 | 3.263 | 2.920 | 3.072 | 3.863 | 4.515 | 3.805 | 2212 |
| 10 | 5.727 | 5.059 | 4.249 | 3.225 | 3.451 | 4.459 | 5.250 | 4.489 | 2085 |
| 15 | 6.682 | 5.852 | 4.954 | 3.667 | 3.422 | 4.913 | 5.863 | 5.050 | 1856 |
| 20 | 7.453 | 6.416 | 5.312 | 3.787 | 3.170 | 5.145 | 6.349 | 5.376 | 1807 |
| 30 | 8.656 | 7.290 | 5.860 | 3.990 | 3.005 | 5.525 | 7.108 | 5.919 | 1626 |
| Real Interest Rate | Expected Inflation | Conditional Variance | Error Standard Deviations | ||||
|---|---|---|---|---|---|---|---|
| θ | 3.54 | ν | 3.48 | w | 9.13 | 8.36 | |
| (4.34) | (1.98) | (1.26) | (2.32) | ||||
| 3.24 | 7.05 | a | 6.43 | 1.89 | |||
| (8.70) | (9.45) | (1.91) | (5.00) | ||||
| κ | 9.99 | β | 9.92 | b | 9.87 | 4.78 | |
| (1.44) | (7.56) | (3.22) | (2.99) | ||||
| σ | 3.64 | γ | 7.55 | c | 1.12 | 1.25 | |
| (9.04) | (5.20) | (2.72) | (3.68) | ||||
| 2.03 | 3.58 | 3.61 | 1.35 | ||||
| (2.24) | (7.53) | (1.69) | (3.14) | ||||
| ρ | 7.08 | ||||||
| (1.14) | |||||||
| Panel A: Nominal Interest Rate Model | |||||||
| Nominal Interest Rate | Expected Inflation | Conditional Variance | Error Standard Deviations | ||||
| θ | 7.85 | ν | - | w | - | 1.48 | |
| (1.81) | - | - | (2.53) | ||||
| 1.02 | - | a | - | - | |||
| (6.22) | - | - | - | ||||
| κ | 9.98 | β | - | b | - | - | |
| (2.27) | - | - | - | ||||
| σ | 6.42 | γ | - | c | - | - | |
| (6.06) | - | - | - | ||||
| 7.60 | - | - | - | ||||
| (1.60) | - | - | - | ||||
| ρ | - | ||||||
| - | |||||||
| Panel B: Generalized Wilkie’s [9] (GW) Model | |||||||
| Real Interest Rate | Expected Inflation | Conditional Variance | Error Standard Deviations | ||||
| θ | - | ν | 1.26 | w | 9.32 | - | |
| - | (2.33) | (1.41) | - | ||||
| - | 1.40 | a | - | 1.56 | |||
| - | (7.57) | - | (2.44) | ||||
| κ | - | β | 1.00 | b | - | - | |
| - | (6.33) | - | - | ||||
| σ | - | γ | 2.34 | c | - | - | |
| - | (3.90) | - | - | ||||
| - | 5.04 | - | - | ||||
| - | (2.60) | - | - | ||||
| ρ | - | ||||||
| - | |||||||
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bégin, J.-F. Deflation Risk and Implications for Life Insurers. Risks 2016, 4, 46. https://doi.org/10.3390/risks4040046
Bégin J-F. Deflation Risk and Implications for Life Insurers. Risks. 2016; 4(4):46. https://doi.org/10.3390/risks4040046
Chicago/Turabian StyleBégin, Jean-François. 2016. "Deflation Risk and Implications for Life Insurers" Risks 4, no. 4: 46. https://doi.org/10.3390/risks4040046





