Qualitative Properties of Difference Equation of Order Six

Abstract

In this paper we study the qualitative properties and the periodic nature of the solutions of the difference equation

$$x_{n+1}=\alpha x_{n-2}+{\displaystyle \frac{\beta x_{n-2}^2}{\gamma x_{n-2}+\delta x_{n-5}}},n=0,1,...,$$

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary positive real numbers and $\alpha ,\beta ,\gamma ,\delta$are positive constants. In addition, we derive the form of the solutions of some special cases of this equation.

1. Introduction

This paper deals with behavior of the solutions of the difference equation

$$x_{n+1}=\alpha x_{n-2}+{\displaystyle \frac{\beta x_{n-2}^2}{\gamma x_{n-2}+\delta x_{n-5}}},n=0,1,...,$$

(1.1)

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary positive real numbers and $\alpha ,\beta ,\gamma ,\delta$are constants. In addition, we obtain the form of solution of some special cases.

Recently, there has been great interest in studying difference equation systems. One of the reasons for this is a necessity for some techniques which can be used in investigating equations arising in mathematical models describing real life situations in population biology, economics, probability theory, genetics, psychology, and so forth.

Difference equations appear naturally as discrete analogues and as numerical solutions of differential and delay differential equations having applications in biology, ecology, economy, physics, and so on. Although difference equations are very simple in form, it is extremely difficult to understand thoroughly the behaviors of their solution (see [1,2,3,4,5,6,7,8,9] and the references cited therein). Recently, a great effort has been made in studying the qualitative analysis of rational difference equations and rational difference system (see [10,11,12,13,14,15,16,17,18,19,20,21,22,23]).

Elabbasy et al. [8] studied the boundedness, global stability, periodicity character and gave the solution of some special cases of the difference equation.

$$x_{n+1}=\frac{\alpha x_{n-l}+\beta x_{n-k}}{A{x}_{n-l}+B{x}_{n-k}}$$

Elabbasy and Elsayed [9] investigated the local and global stability, boundedness, and gave the solution of some special cases of the difference equation

$$x_{n+1}={\displaystyle \frac{a{x}_{n-l}{x}_{n-k}}{b{x}_{n-p}+c{x}_{n-q}}}.$$

In [13], Elsayed investigated the solution of the following non-linear difference equation

$$x_{n+1}=a{x}_n+\frac{b{x}_n^2}{c{x}_n+d{x}_{n-1}^2}.$$

Keratas et al. [24] obtained the solution of the following difference equation

$$x_{n+1}=\frac{x_{n-5}}{1+x_{n-2}{x}_{n-5}}.$$

Saleh et al. [25] investigated the dynamics of the solution of difference equation

$$y_{n+1}=A+\frac{y_n}{y_{n-k}}.$$

Yalçınkaya [26] has studied the following difference equation

$$x_{n+1}=\alpha +{\displaystyle \frac{x_{n-m}}{x_n^k}}.$$

For other related work on rational difference equations, see [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49].

Below, we outline some basic definitions and some theorems that we will need to establish our results.

Let I be some interval of real numbers and let

$$F:I^{k+1}\to I,$$

be a continuously differentiable function. Then for every set of initial conditions $x_{-k},x_{-k+1},...$, $x_0\in I,$ the difference equation

$$x_{n+1}=F(x_n,x_{n-1},...,x_{n-k}),n=0,1,...,$$

(1.2)

has a unique solution ${\left\{x_n\right\}}_{n=-k}^{\infty }$.

A point $\overline{x}\in I$ is called an equilibrium point of Equation (1.2) if

$$\overline{x}=f(\overline{x},\overline{x},...,\overline{x}).$$

That is, $x_n=\overline{x}$ for $n\ge 0,$is a solution of Equation (1.2), or equivalently, $\overline{x}$ is a fixed point of f.

DEFINITION 1.1. 

(Equilibrium Point)

A point $\overline{x}\in I$ is called an equilibrium point of Equation (1.2) if

$$\overline{x}=f(\overline{x},\overline{x},...,\overline{x}).$$

That is, $x_n=\overline{x}$ for $n\ge 0,$is a solution of Equation (1.2), or equivalently, $\overline{x}$ is a fixed point of f.

DEFINITION 1.2. 

(Periodicity)

A Sequence ${\left\{x_n\right\}}_{n=-k}^{\infty }$is said to be periodic with period p if $x_{n+p}=x_n$for all $n\ge -k.$

DEFINITION 1.3. 

(Fibonacci Sequence)

The sequence

$$\begin{array}{ccc}\hfill {\left\{F_m\right\}}_{m=1}^{\infty }& =& \{1,2,3,5,8,13,....\}i.e.,F_m=F_{m-1}+F_{m-2}\ge 0,\hfill \\ \hfill F_{-2}& =& 0,F_{-1}=1,\hfill \end{array}$$

is called Fibonacci Sequence.

DEFINITION 1.4. 

(Stability)

(i)

The equilibrium point $\overline{x}$ of Equation (1.2) is locally stable if for every $ϵ>0,$there exists $\delta >0$such that for all $x_{-k},x_{-k+1},...,x_{-1}$,$x_0\in I$with

$$\left|x_{-k}-\overline{x}\right|+\left|x_{-k+1}-\overline{x}\right|+...+\left|x_0-\overline{x}\right|<\delta ,$$

we have

$$\left|x_n-\overline{x}\right|<ϵ\text{for}\text{all}n\ge -k.$$

(ii)

The equilibrium point $\overline{x}$of Equation (1.2) is locally asymptotically stable if $\overline{x}$is locally stable solution of Equation (1.2) and there exists $\gamma >0,$ such that for all $x_{-k},x_{-k+1},...,x_{-1}$, $x_0\in I$with

$$\left|x_{-k}-\overline{x}\right|+\left|x_{-k+1}-\overline{x}\right|+...+\left|x_0-\overline{x}\right|<\gamma ,$$

we have

$$\underset{n\to \infty }{lim}{x}_n=\overline{x}.$$

(iii)

The equilibrium point $\overline{x}$of Equation (1.2) is global attractor if for all $x_{-k},x_{-k+1},...,x_{-1}$, $x_0\in I,$we have

$$\underset{n\to \infty }{lim}{x}_n=\overline{x}.$$

(iv)

The equilibrium point $\overline{x}$of Equation (1.2) is globally asymptotically stable if $\overline{x}$is locally stable, and $\overline{x}$is also a global attractor of Equation (1.2).

(v)

The equilibrium point $\overline{x}$of Equation (1.2) is unstable if $\overline{x}$is not locally stable.

(vi)

The linearized equation of Equation (1.2) about the equilibrium $\overline{x}$is the linear difference equation

$$y_{n+1}={\displaystyle \sum _{i=0}^k}{\displaystyle \frac{\partial F(\overline{x},\overline{x},...,\overline{x})}{\partial x_{n-i}}}{y}_{n-i}.$$

(1.3)

Theorem A. 

[38] Assume that $p,q\in R$and$k\in \{0,1,2,...\}$. Then

$$\left|p\right|+\left|q\right|<1,$$

is a sufficient condition for the asymptotic stability of the difference equation

$$x_{n+1}+p{x}_n+q{x}_{n-k}=0,n=0,1,....$$

The following theorem will be useful for establishing the results in this paper.

Theorem B. 

[39] Let $[\alpha ,\beta ]$ be an interval of real numbers assume that $g:{[\alpha ,\beta ]}^2\to [\alpha ,\beta ],$ is a continuous function and consider the following equation

$$x_{n+1}=g(x_n,x_{n-1}),n=0,1,...,$$

(1.4)

satisfying the following conditions :

(a)

$g(x,y)$ is non-decreasing in $x\in$$[\alpha ,\beta ]$ for each fixed $y\in [\alpha ,\beta ]$ and $g(x,y)$ is non-increasing in $y\in$$[\alpha ,\beta ]$ for each fixed $x\in [\alpha ,\beta ].$

(b)

For any $(m,M)\in [\alpha ,\beta ]\times [\alpha ,\beta ]$ that is a solution of the system

$$M=g(M,m)andm=g(m,M),$$

we have that

$$m=M.$$

Then Equation (1.4) has a unique equilibrium $\overline{x}\in [\alpha ,\beta ]$ and every solution of Equation (1.4) converges to $\overline{x}.$

2. Local Stability of the Equilibrium Point of Equation (1.1)

In this section we study the local stability properties of the equilibrium point of Equation (1.1). The equilibrium points of Equation (1.1) are given by the relation

$$\overline{x}=\alpha \overline{x}+{\displaystyle \frac{\beta {\overline{x}}^2}{\gamma \overline{x}+\delta \overline{x}}},$$

or

$${\overline{x}}^2(1-\alpha )(\gamma +\delta )=\beta {\overline{x}}^2.$$

If $(1-\alpha )(\gamma +\delta )\ne \beta ,$ then the unique equilibrium point is $\overline{x}=0.$

Let $f:{(0,\infty )}^2⟶(0,\infty )$ be a continuously differentiable function defined by

$$f(u,v)=\alpha u+{\displaystyle \frac{\beta u^2}{\gamma u+\delta v}}.$$

(2.1)

Therefore

$${\left(\frac{\partial f}{\partial u}\right)}_{\overline{x}}=\alpha +\frac{\beta \gamma +2\beta \delta }{{(\gamma +\delta )}^2},{\left(\frac{\partial f}{\partial v}\right)}_{\overline{x}}=\frac{-\beta \delta }{{(\gamma +\delta )}^2}.$$

Then the linearized equation of Equation (1.1) about $\overline{x}$ is

$$y_{n+1}-\left(\alpha +\frac{\beta \gamma +2\beta \delta }{{(\gamma +\delta )}^2}\right)y_n+\left(\frac{\beta \delta }{{(\gamma +\delta )}^2}\right)y_{n-1}=0.$$

(2.2)

Theorem 1. 

Assume that$\beta (\gamma +3\delta )<{(\gamma +\delta )}^2(1-\alpha ),\alpha <1.$Then the equilibrium point $\overline{x}=0$of Equation (1.1) is locally asymptotically stable.

Proof: 

From Theorem A, it follows that Equation (2.2) is asymptotically stable if

$$\left|\alpha +\frac{\beta \gamma +2\beta \delta }{{(\gamma +\delta )}^2}\right|+\left|\frac{\beta \delta }{{(\gamma +\delta )}^2}\right|<1,$$

or

$$\alpha +\frac{\beta \gamma +3\beta \delta }{{(\gamma +\delta )}^2},$$

and so

$$\beta (\gamma +3\delta )<{(\gamma +\delta )}^2(1-\alpha ),$$

which completes the proof.

3. Global Attractivity of the Equilibrium Point of Equation (1.1)

In this section we investigate the global attractivity character of solutions of Equation (1.1).

Theorem 2. 

The equilibrium point $\overline{x}$ of Equation (1.1) is a global attractor if $\gamma (1-\alpha )\ne \beta .$

Proof: 

Let $\alpha ,\beta$ are real numbers and assume that $g:{[\alpha ,\beta ]}^2\to [\alpha ,\beta ],$be a function defined by Equation (2.1).

Suppose that $(m,M)$is a solution of the system

$$M=g(M,m)andm=g(m,M).$$

Then from Equation (1.1), we see that

$$M=\alpha M+{\displaystyle \frac{\beta M^2}{\gamma M+\delta m}},m=\alpha m+{\displaystyle \frac{\beta m^2}{\gamma m+\delta M}}.$$

Therefore

$$M(1-\alpha )={\displaystyle \frac{\beta M^2}{\gamma M+\delta m}},m(1-\alpha )={\displaystyle \frac{\beta m^2}{\gamma m+\delta M}},$$

or,

$$\gamma (1-\alpha )(M^2-m^2)=b(M^2-m^2),c(1-\alpha )\ne \beta ,$$

thus

$$M=m.$$

From Theorem B, it follows that $\overline{x}$ is a global attractor of Equation (1.1) and then the proof is complete.

4. Boundedness of Solutions of Equation (1.1)

In this section we study the boundedness of solution of Equation (1.1)

Theorem 3. 

Every solution of Equation(1.1) is bounded if $\left(\alpha +{\displaystyle \frac{\beta }{\gamma }}\right)<1.$

Proof: 

Let ${\left\{x_n\right\}}_{n=-5}^{\infty }$be a solution of Equation (1.1). It follows from Equation (1.1) that

$$x_{n+1}=\alpha x_{n-2}+{\displaystyle \frac{\beta x_{n-2}^2}{\gamma x_{n-2}+\delta x_{n-5}}}\le \alpha x_{n-2}+\frac{\beta x_{n-2}^2}{\gamma x_{n-2}}=\left(\alpha +\frac{\beta }{\gamma }\right)x_{n-2}.$$

Then

$$x_{n+1}\le x_{n-2},\text{for}\text{all}n\ge 0.$$

Then the sub-sequences ${\left\{x_{3n-1}\right\}}_{n=-5}^{\infty },$ ${\left\{x_{3n-2}\right\}}_{n=-5}^{\infty }$ and ${\left\{x_{3n}\right\}}_{n=-5}^{\infty }$ are decreasing and so are bounded from above by $M=max\{x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0\}.$

In order to confirm the result in this section we consider some numerical examples for $x_{-5}=10,x_{-4}=5,x_{-3}=8,x_{-2}=2,x_{-1}=9,x_0=7,\alpha =0.5,\beta =6,\gamma =9,\delta =10.$ (See Figure 1) and $x_{-5}=10,x_{-4}=5,x_{-3}=8,x_{-2}=2,x_{-1}=9,x_0=7,\alpha =0.6,\beta =6,\gamma =7,\delta =12.$ (See Figure 2).

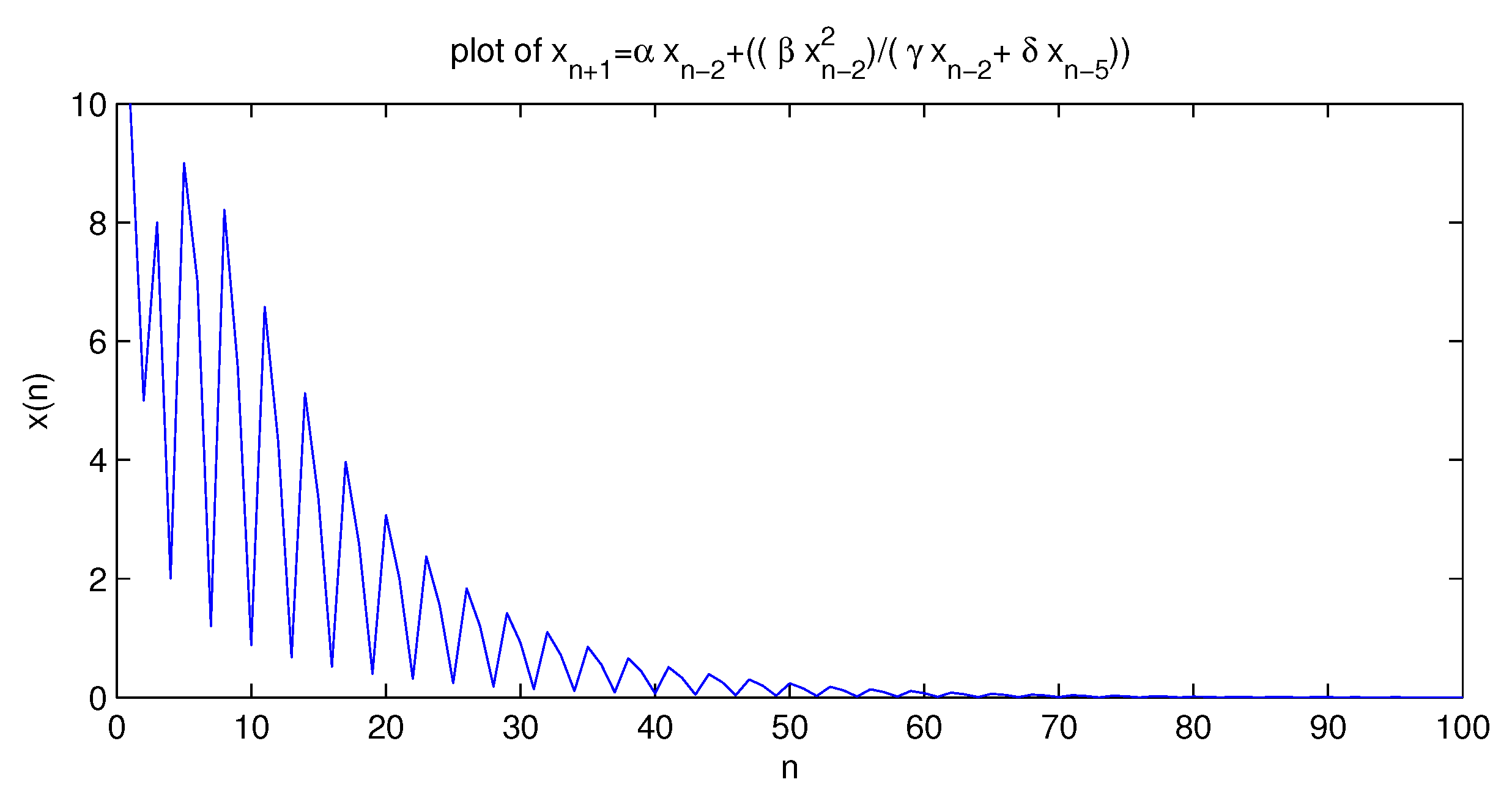
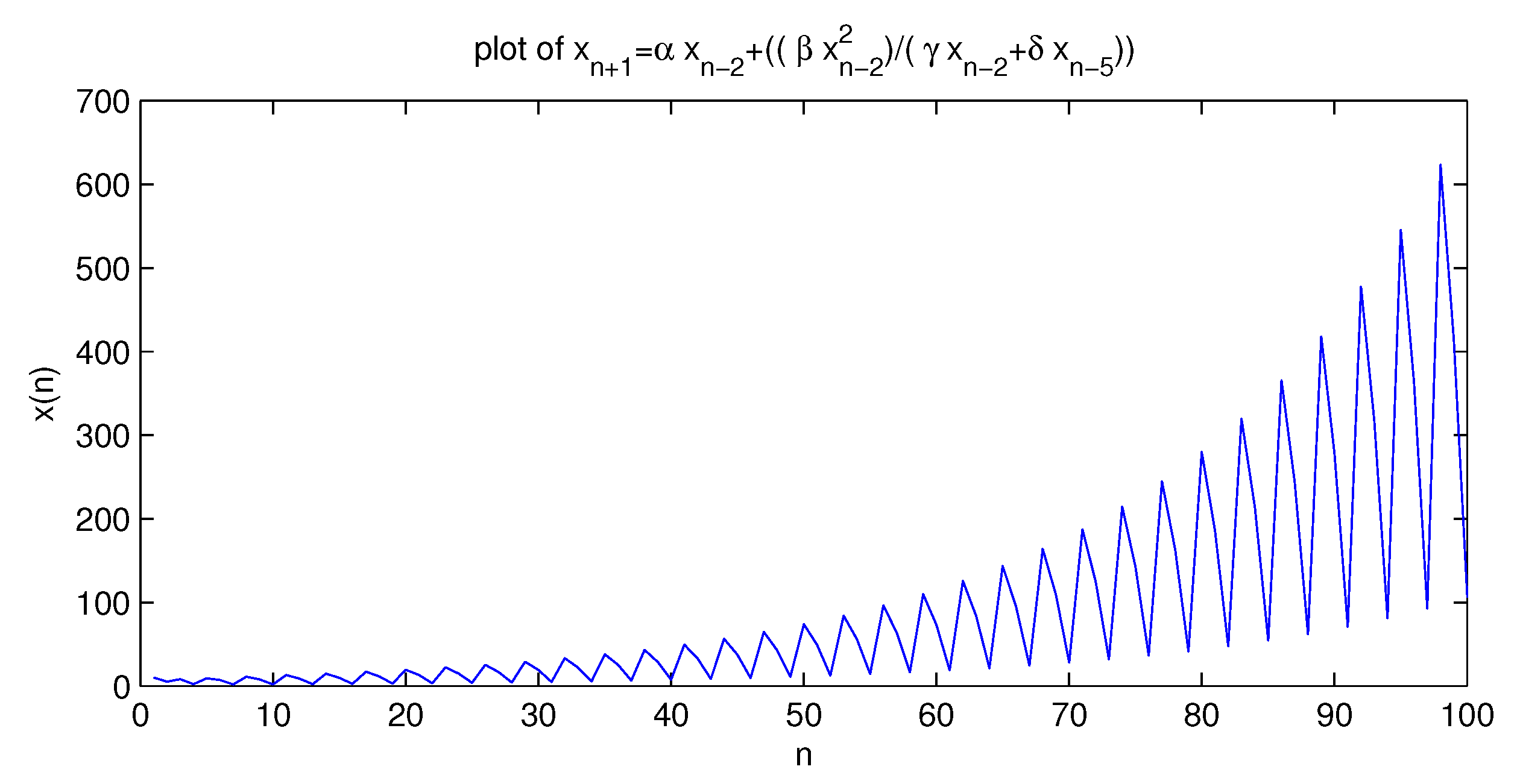
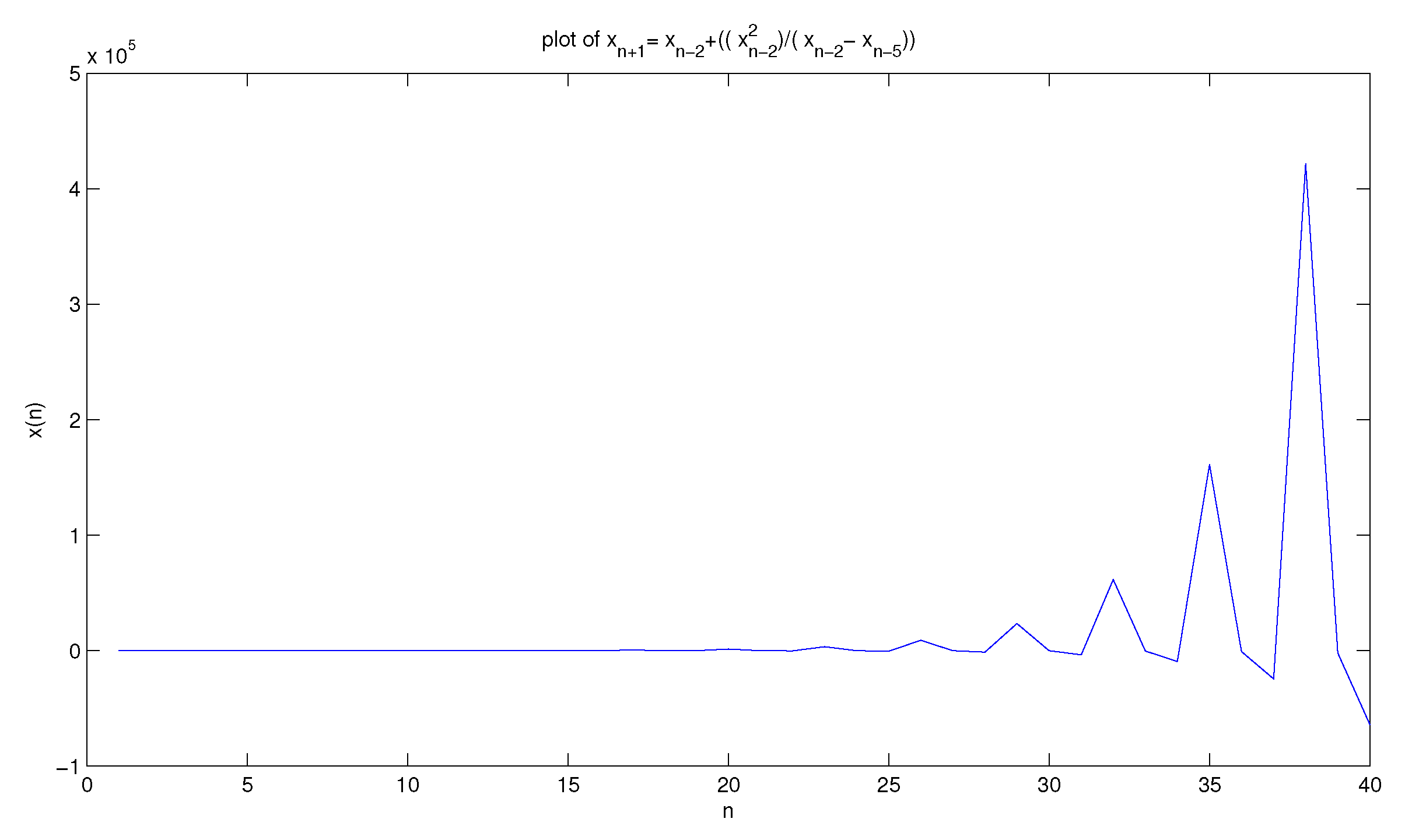
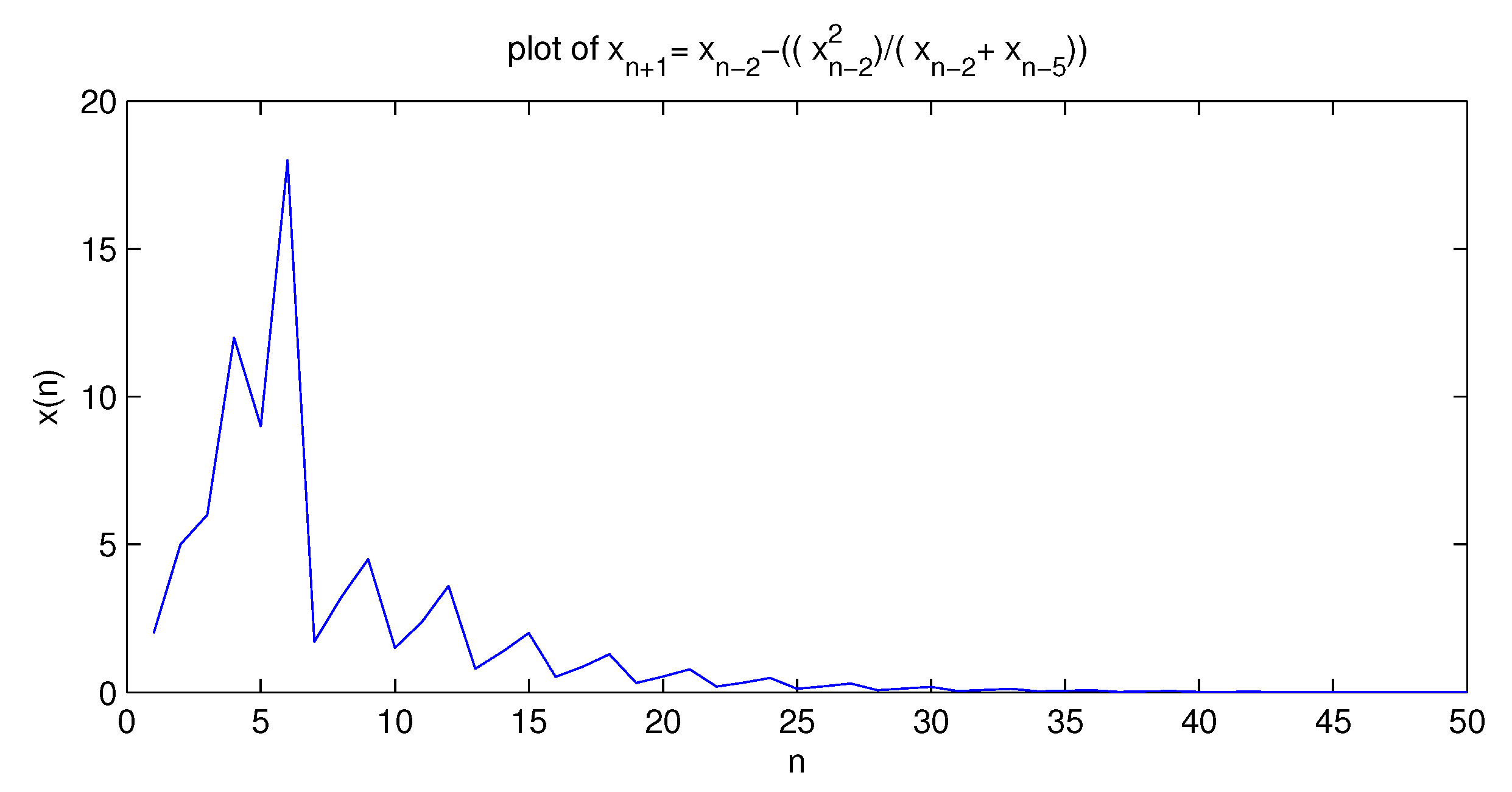
5. Special Cases of Equation (1.1)

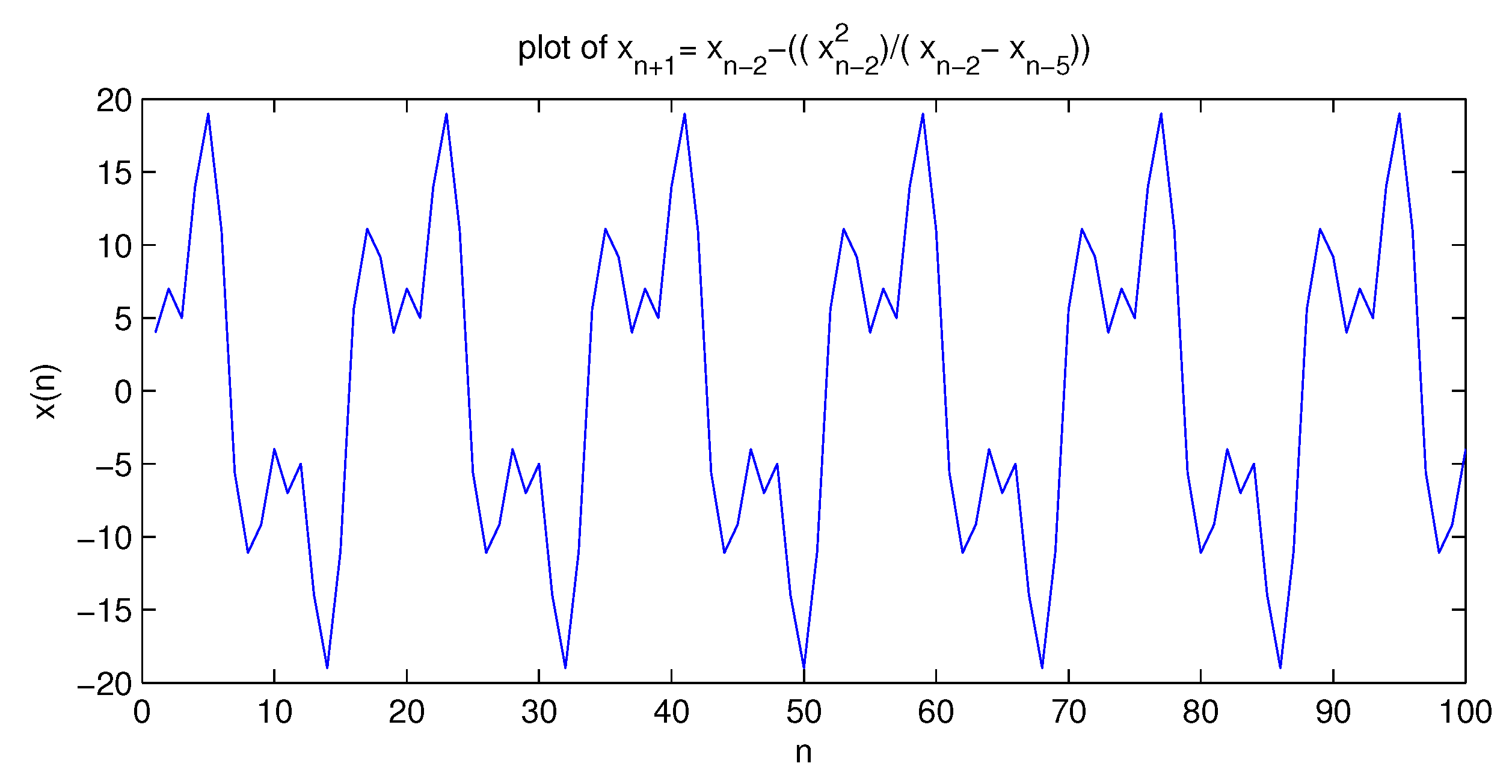
5.1. First Equation

In this section we study the following special case of Equation (1.1)

$$x_{n+1}=x_{n-2}+\frac{x_{n-2}^2}{x_{n-2}+x_{n-5}}$$

(5.1)

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary real numbers.

Theorem 4. 

Let${\left\{x_n\right\}}_{n=-5}^{\infty }$be a solution of Equation (5.1) then for $n=0,1,2,...$

$$\begin{array}{ccc}\hfill x_{3n-1}& =& k{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right),x_{3n-2}=h{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right),\hfill \\ \hfill x_{3n}& =& r{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}}\right),\hfill \end{array}$$

where $x_{-5}=t,$ $x_{-4}=q,$ $x_{-3}=p,$ $x_{-2}=r,$ $x_{-1}=k,$ $x_0=h,$ ${\left\{f_m\right\}}_{m=1}^{\infty }=\{1,1,2,3,5,8,13,...\}.$

Proof: 

We prove that the forms given are solutions of Equation (5.1) by using mathematical induction. First, we let $n=0,$ then the result holds. Second, we assume that the expressions are satisfied for $n-1,n-2$. Our objective is to show that the expressions are satisfied for n. That is;

$$\begin{array}{ccc}\hfill x_{3n-8}& =& r{\displaystyle \prod _{i=1}^{n-2}}\left({\displaystyle \frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}}\right),x_{3n-7}=k{\displaystyle \prod _{i=1}^{n-2}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right),\hfill \\ \hfill x_{3n-6}& =& h{\displaystyle \prod _{i=1}^{n-2}}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right),x_{3n-5}=r{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}}\right),\hfill \\ \hfill x_{3n-4}& =& k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right),x_{3n-3}=h{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right).\hfill \end{array}$$

Now, it follows from Equation (5.1) that,

$$\begin{array}{ccc}\hfill x_{3n-1}& =& x_{3n-4}+\frac{x_{3n-4}^2}{x_{3n-4}+x_{3n-7}}\hfill \\ & =& k{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}\right)+\frac{k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)}{k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)+k{\displaystyle \prod _{i=1}^{n-2}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)}\hfill \\ & =& k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)+\frac{{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)\left({\displaystyle \frac{f_{2n-1}k+f_{2n-2}q}{f_{2n-2}k+f_{2n-3}q}}\right)}{\left({\displaystyle \frac{f_{2n-1}k+f_{2n-2}q}{f_{2n-2}k+f_{2n-3}q}}\right)+1}\hfill \\ & =& k{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}}\right)\left(1+{\displaystyle \frac{f_{2n-1}k+f_{2n-2}q}{f_{2n-1}k+f_{2n-2}q+f_{2n-2}k+f_{2n-3}q}}\right)\hfill \\ & =& k{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}\right)\left(1+{\displaystyle \frac{f_{2n-1}k+f_{2n-2}q}{f_{2n}k+f_{2n-1}q}}\right)\hfill \\ & =& k{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}\right)\left({\displaystyle \frac{f_{2n+1}k+f_{2n}q}{f_{2n}k+f_{2n-1}q}}\right).\hfill \end{array}$$

Therefore

$$x_{3n-1}=k{\displaystyle \prod _{i=1}^n}\left(\frac{f_{2i+1}k+f_{2i}q}{f_{2i}k+f_{2i-1}q}\right).$$

Also, we see from Equation (5.1) that,

$$\begin{array}{ccc}\hfill x_{3n-2}& =& x_{3n-5}+{\displaystyle \frac{x_{3n-5}^2}{x_{3n-5}+x_{3n-8}}}\hfill \\ & =& r{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}\right)+\frac{r{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}}\right)\left({\displaystyle \frac{f_{2n-1}r+f_{2n-2}t}{f_{2n-2}r+f_{2n-3}t}}\right)}{\left({\displaystyle \frac{f_{2n-1}r+f_{2n-2}t}{f_{2n-2}r+f_{2n-3}t}}\right)+1}\hfill \\ & =& r{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}\right)\left(1+\frac{f_{2n-1}r+f_{2n-2}t}{f_{2n-1}r+f_{2n-2}t+f_{2n-2}r+f_{2n-3}t}\right)\hfill \\ & =& r{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}r+f_{2i}t}{f_{2i}r+f_{2i-1}t}\right)\left(\frac{f_{2n+1}r+f_{2n}t}{f_{2n}r+f_{2n-1}t}\right).\hfill \end{array}$$

Then

$$x_{3n-2}=h{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right).$$

Also, wee see from Equation (5.1) that,

$$\begin{array}{ccc}\hfill x_{3n}& =& x_{3n-3}+{\displaystyle \frac{x_{3n-3}^2}{x_{3n-3}+x_{3n-6}}}\hfill \\ & =& h{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}h+f_{2i}p}{f_{2i}r+f_{2i-1}t}\right)+\frac{h{\displaystyle \prod _{i=1}^{n-1}}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right)\left({\displaystyle \frac{f_{2n-1}h+f_{2n-2}p}{f_{2n-2}h+f_{2n-3}p}}\right)}{\left({\displaystyle \frac{f_{2n-1}h+f_{2n-2}p}{f_{2n-2}h+f_{2n-3}p}}\right)+1}\hfill \\ & =& h{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}\right)\left(1+\frac{f_{2n-1}h+f_{2n-2}p}{f_{2n-1}h+f_{2n-2}p+f_{2n-2}h+f_{2n-3}p}\right)\hfill \\ & =& h{\displaystyle \prod _{i=1}^{n-1}}\left(\frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}\right)\left(\frac{f_{2n+1}h+f_{2n}p}{f_{2n}h+f_{2n-1}p}\right)\hfill \end{array}$$

Thus

$$x_{3n}=h{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{2i+1}h+f_{2i}p}{f_{2i}h+f_{2i-1}p}}\right).$$

Hence, the proof is complete.

We will confirm our result by considering some numerical examples assume $x_{-5}=3,x_{-4}=5,x_{-3}=9,x_{-2}=2,x_{-1}=9,x_0=4.$ (See Figure 3).

5.2. Second Equation

In this section we solve a more specific form of Equation (1.1)

$$x_{n+1}=x_{n-2}+\frac{x_{n-2}^2}{x_{n-2}-x_{n-5}},$$

(5.2)

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary real numbers.

Theorem 5. 

Let${\left\{x_n\right\}}_{n=-5}^{\infty }$be a solution of Equation (5.3). Then for $n=0,1,2,...$

$$\begin{array}{ccc}\hfill x_{3n-1}& =& k{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{i+2}k-f_{i}q}{f_{i}k-f_{i-2}q}}\right),x_{3n-2}=h{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{i+2}h-f_{i}p}{f_{i}h-f_{i-2}p}}\right),\hfill \\ \hfill x_{3n}& =& r{\displaystyle \prod _{i=1}^n}\left({\displaystyle \frac{f_{i+2}r-f_{i}t}{f_{i}r-f_{i-2}t}}\right)\hfill \end{array}$$

where $x_{-5}=t,x_{-4}=q,x_{-3}=p,x_{-2}=r,x_{-1}=k,x_0=h,$ ${\left\{f_m\right\}}_{m=-1}^{\infty }=\{1,0,1,1,2,3,5,8,13,...\}.$

Proof: 

The proof is the same as for Theorem 4 and is therefore omitted.

To confirm our result assume $x_{-5}=3,x_{-4}=5,x_{-3}=9,x_{-2}=2,x_{-1}=9,x_0=4.$ (See Figure 4).

5.3. Third Equation

In this section we deal with the following special case of Equation (1.1)

$$x_{n+1}=x_{n-2}-\frac{x_{n-2}^2}{x_{n-2}+x_{n-5}},$$

(5.3)

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary real numbers.

Theorem 6. 

Let ${\left\{x_n\right\}}_{n=-5}^{\infty }$ be a solution of Equation(5.5) then for $n=0,1,2,....$

$$x_{3n-1}={\displaystyle \frac{kq}{f_{n}k+f_{n+1}q}},x_{3n-2}={\displaystyle \frac{rt}{f_{n}r+f_{n+1}t}},x_{3n}={\displaystyle \frac{hp}{f_{n}h+f_{n+1}p}},$$

where$x_{-5}=t,x_{-4}=q,x_{-3}=p,x_{-2}=r,x_{-1}=k,x_0=h,{\left\{f_m\right\}}_{m=-1}^{\infty }=\{1,0,1,1,2,3,5,8,13,...\}.$

Proof: 

For $n=0$, the result holds. Now suppose that $n>0$ and that our assumption holds for $n-2,n-3.$ That is,

$$\begin{array}{ccc}\hfill x_{3n-8}& =& {\displaystyle \frac{rt}{f_{n-2}r+f_{n-1}t}},x_{3n-7}={\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}},\hfill \\ \hfill x_{3n-6}& =& {\displaystyle \frac{hp}{f_{n-2}h+f_{n-1}p}},x_{3n-5}={\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}},\hfill \\ \hfill x_{3n-4}& =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}},x_{3n-3}={\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}.\hfill \end{array}$$

Now, it follows from Equation (5.3) that,

$$\begin{array}{ccc}\hfill x_{3n-1}& =& x_{3n-4}-\frac{x_{3n-4}^2}{x_{3n-4}+x_{3n-7}}\hfill \\ & =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}}-\left(\frac{{\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}}{\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}}}{{\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}}+{\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}}}\right)\hfill \\ & =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}}-\left(\frac{{\displaystyle \frac{kq}{f_{n-2}k+f_{n-1}q}}\left(f_{n-2}k+f_{n-1}q\right)}{f_{n-2}k+f_{n-1}q+f_{n-1}k+f_{n}q}\right)\hfill \\ & =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}}\left(1-\frac{f_{n-2}k+f_{n-1}q}{f_{n-2}k+f_{n-1}q+f_{n-1}k+f_{n}q}\right)\hfill \\ & =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}}\left(\frac{f_{n-2}k+f_{n-1}q+f_{n-1}k+f_{n}q+f_{n-2}k+f_{n-1}q}{f_{n-2}k+f_{n-1}q+f_{n-1}k+f_{n}q}\right)\hfill \\ & =& {\displaystyle \frac{kq}{f_{n-1}k+f_{n}q}}\left(\frac{f_{n-1}k+f_{n}q}{f_{n}k+f_{n+1}q}\right)={\displaystyle \frac{kq}{f_{n}k+f_{n+1}q}}.\hfill \end{array}$$

Also, from Equation (5.3), we see that,

$$\begin{array}{ccc}\hfill x_{3n}& =& x_{3n-3}-\frac{x_{3n-3}^2}{x_{3n-3}+x_{3n-6}}\hfill \\ & =& {\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}-\left(\frac{{\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}{\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}}{{\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}+{\displaystyle \frac{hp}{f_{n-2}h+f_{n-1}p}}}\right)\hfill \\ & =& {\displaystyle \frac{hp}{f_{n-1}k+f_{n}q}}-\left(\frac{{\displaystyle \frac{hp}{f_{n-2}h+f_{n-1}p}}\left(f_{n-2}h+f_{n-1}p\right)}{f_{n-2}h+f_{n-1}p+f_{n-1}h+f_{n}p}\right)\hfill \\ & =& {\displaystyle \frac{hp}{f_{n-1}h+f_{n}p}}\left(1-\frac{f_{n-2}h+f_{n-1}p}{f_{n-2}h+f_{n-1}p+f_{n-1}h+f_{n}p}\right)\hfill \\ & =& {\displaystyle \frac{hp}{f_{n-1}h+f_{n}p}}\left(\frac{f_{n-1}h+f_{n}p}{f_{n}h+f_{n+1}p}\right)={\displaystyle \frac{hp}{f_{n}h+f_{n+1}p}}.\hfill \end{array}$$

Also, from Equation (5.3), we get,

$$\begin{array}{ccc}\hfill x_{3n-2}& =& x_{3n-5}-\frac{x_{3n-5}^2}{x_{3n-5}+x_{3n-8}}\hfill \\ & =& {\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}-\left(\frac{{\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}{\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}}{{\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}+{\displaystyle \frac{rt}{f_{n-2}r+f_{n-1}t}}}\right)\hfill \\ & =& {\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}-\left(\frac{{\displaystyle \frac{rt}{f_{n-2}r+f_{n-1}t}}\left(f_{n-2}r+f_{n-1}t\right)}{f_{n-2}r+f_{n-1}t+f_{n-1}r+f_{n}t}\right)\hfill \\ & =& {\displaystyle \frac{rt}{f_{n-1}r+f_{n}t}}\left(\frac{f_{n-1}r+f_{n}t}{f_{n}r+f_{n+1}t}\right)={\displaystyle \frac{rt}{f_{n}r+f_{n+1}t}}.\hfill \end{array}$$

Hence, the proof is complete.

We consider a numerical example of this special case, assume $x_{-5}=2,x_{-4}=5,x_{-3}=6,x_{-2}=12,x_{-1}=9,x_0=18.$ (See Figure 5).

5.4. Fourth Equation

In this section we deal with the form of solution of the following equation

$$x_{n+1}=x_{n-2}-\frac{x_{n-2}^2}{x_{n-2}-x_{n-5}},$$

(5.4)

where the initial conditions $x_{-5},x_{-4},x_{-3},x_{-2},x_{-1},x_0$ are arbitrary real numbers.

Theorem 7. 

Let ${\left\{x_n\right\}}_{n=-5}^{\infty }$ be a solution of Equation (5.4) Then every solution of Equation (5.4) is periodic with period 18. Moreover, ${\left\{x_n\right\}}_{n=-5}^{\infty }$ takes the form

$$\left\{\begin{array}{c}t,q,p,r,k,h,{\displaystyle \frac{-rt}{r-t}},{\displaystyle \frac{-kq}{k-q}},{\displaystyle \frac{-hp}{h-p}},-t,-q,-p,\\ -r,-k,-h,{\displaystyle \frac{rt}{r-t}},{\displaystyle \frac{kq}{k-q}},{\displaystyle \frac{hp}{h-p}},t,q,p,r,k,h,...\end{array}\right\},$$

or,

$$\begin{array}{ccc}\hfill x_{18n-5}& =& t,x_{18n-4}=q,x_{18n-3}=p,x_{18n-2}=r,x_{18n-1}=k,\hfill \\ \hfill x_{18n}& =& h,x_{18n+1}=\frac{-rt}{r-t},x_{18n+2}=\frac{-kq}{k-q},x_{18n+3}=\frac{-hp}{h-p},\hfill \\ \hfill x_{18n+4}& =& -t,x_{18n+5}=-q,x_{18n+6}=-p,x_{18n+7}=-r,x_{18n+8}=-k,\hfill \\ \hfill x_{18n+9}& =& -h,x_{18n+10}=\frac{rt}{r-t},x_{18n+11}=\frac{kq}{k-q},x_{18n+12}=\frac{hp}{h-p},\hfill \end{array}$$

where $x_{-5}=t,x_{-4}=q,x_{-3}=p,x_{-2}=r,x_{-1}=k,x_0=h,x_{-5}\ne x_{-2},x_{-4}\ne x_0,x_{-3}\ne x_{-1}.$

Proof: 

The proof is the same as the proof of Theorem 6 and thus will be omitted.

Figure 6 shows the solution when $x_{-5}=4,x_{-4}=7,x_{-3}=5,x_{-2}=14,x_{-1}=19,x_0=11.$

6. Conclusions

In this paper we investigated the global attractivity, boundedness and the solutions of some special cases of Equation (1.1). In Section 2 we proved when $\beta (\gamma +3\delta )<{(\gamma +\delta )}^2(1-\alpha )$, Equation (1.1) has local stability. In Section 3 we showed that the unique equilibrium of Equation (1.1) is globally asymptotically stable if $\gamma (1-\alpha )\ne \beta .$ In Section 4 we investigated that the solution of Equation (1.1) is bounded if $\left(\alpha +{\displaystyle \frac{\beta }{\gamma }}\right)<1$. In Section 5 we obtained the form of the solution of four special cases of Equation (1.1) and gave numerical examples of each of the case with different initial values.