Tight State-Independent Uncertainty Relations for Qubits
Abstract
:1. Introduction
1.1. Entropic Uncertainty Relations
1.2. State-Independent Uncertainty Relations for Standard Deviations
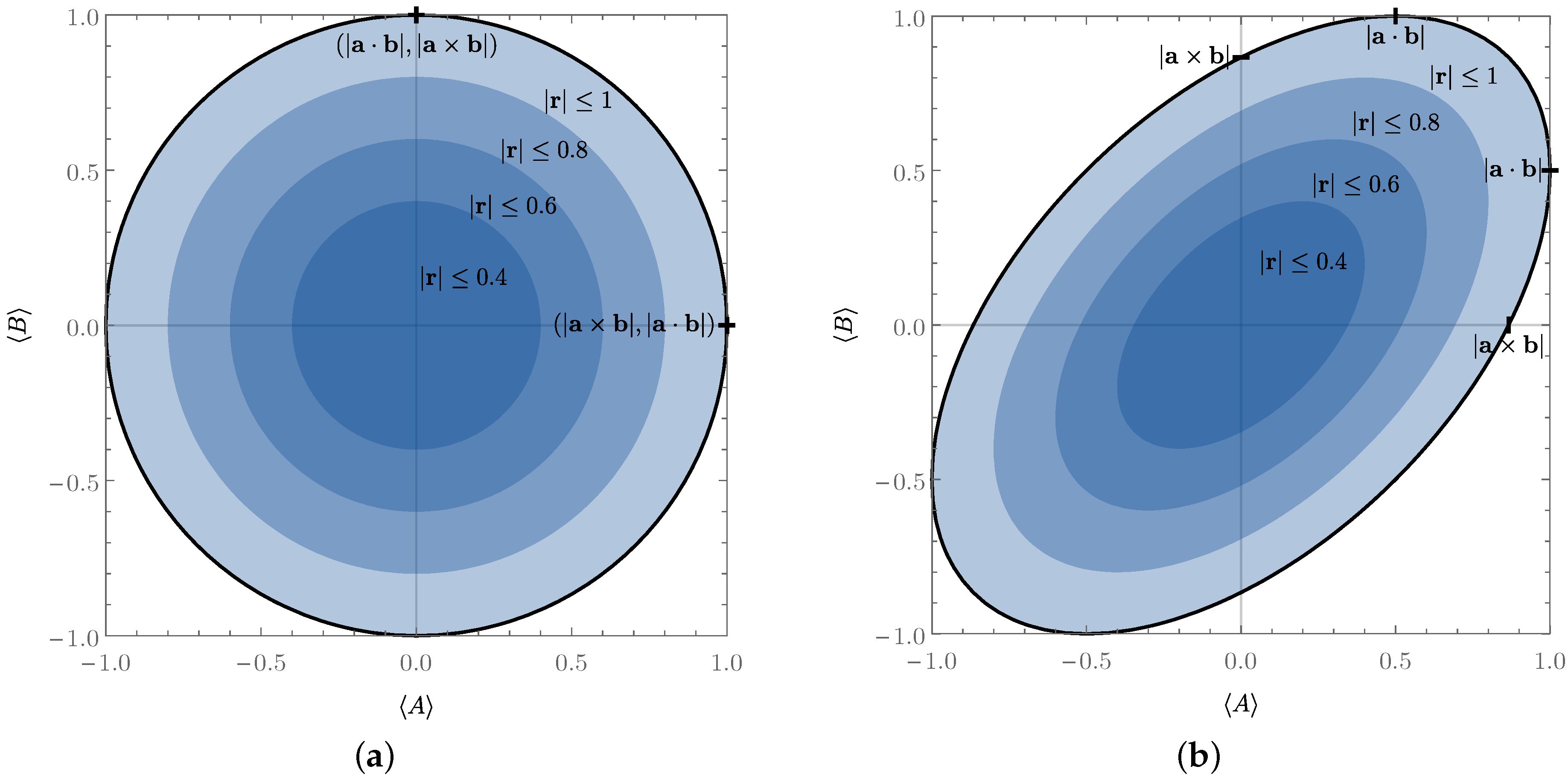
2. A Unified Approach to Qubit Uncertainty Relations
2.1. For Two Observables
2.2. Generalisation to More Observables
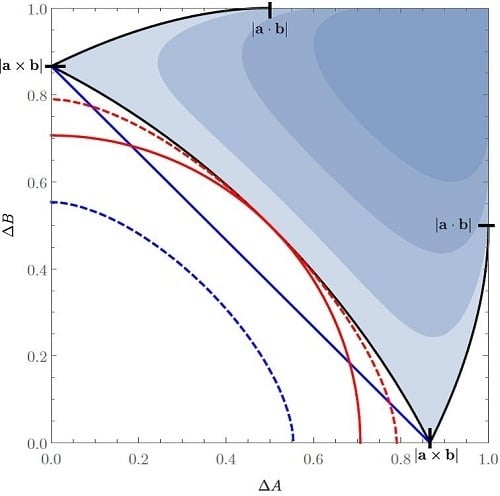
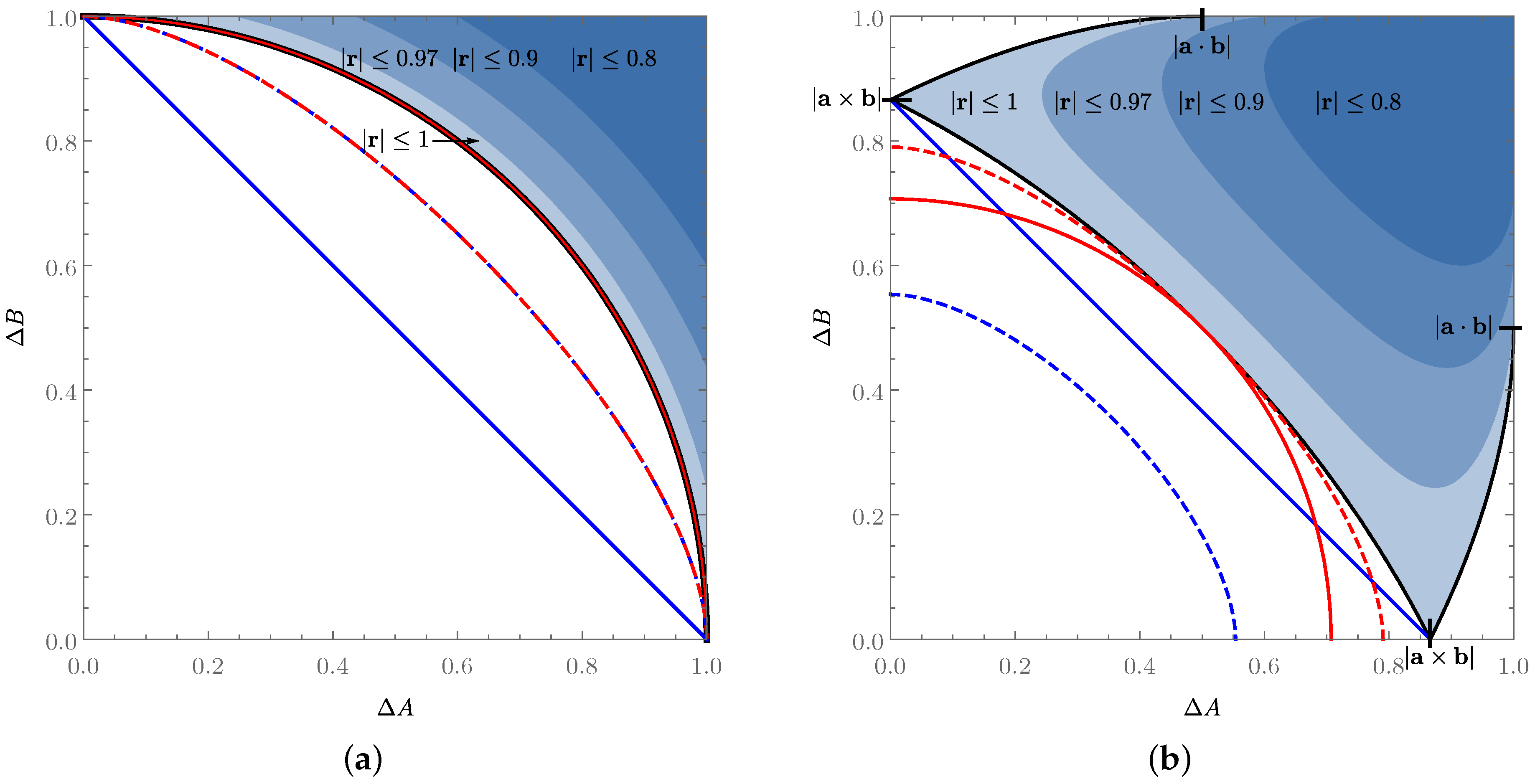
3. Uncertainty Relations in Terms of Standard Deviations
3.1. Uncertainty Relation for Two Pauli Observables
3.2. Uncertainty Relations for n Pauli Observables
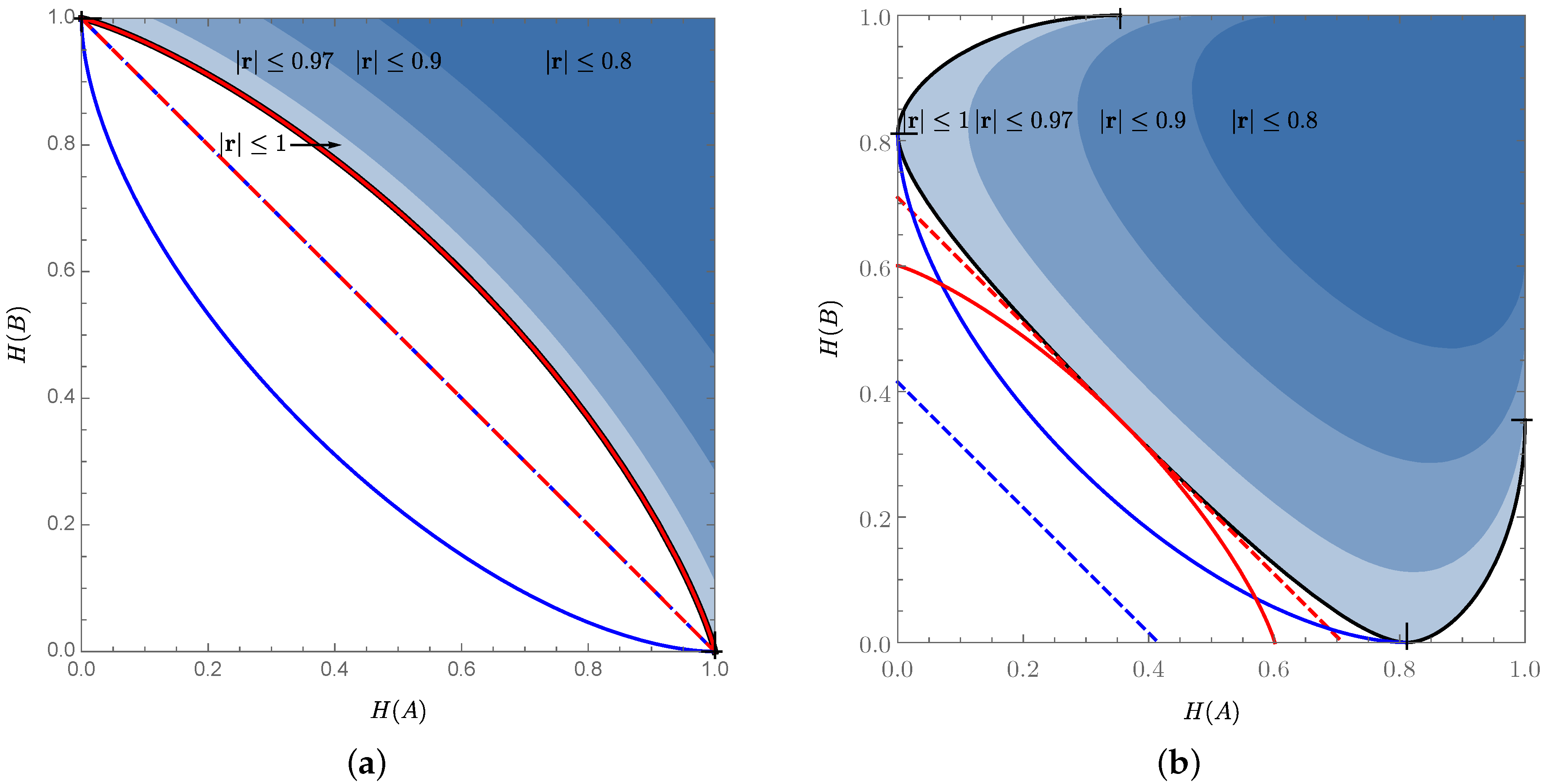
4. Entropic Uncertainty Relations
5. Higher Dimensional Systems
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Robertson, H.P. The uncertainty principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement. Phys. Rev. A 2003, 67, 042105. [Google Scholar] [CrossRef]
- Hall, M.J.W. Prior information: How to circumvent the standard joint-measurement uncertainty relation. Phys. Rev. A 2004, 69, 052113. [Google Scholar] [CrossRef]
- Branciard, C. Error-tradeoff and error-disturbance relations for incompatible quantum measurements. Proc. Natl. Acad. Sci. USA 2013, 110, 6742–6747. [Google Scholar] [CrossRef] [PubMed]
- Busch, P.; Lahti, P.; Werner, R.F. Proof of Heisenberg’s error-disturbance relation. Phys. Rev. Lett. 2013, 111, 160405. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, M. Disproving Heisenberg’s error-disturbance relation. 2013; arXiv:1308.3540. [Google Scholar]
- Dressel, J.; Nori, F. Certainty in Heisenberg’s uncertainty principle: Revisiting definitions for estimation errors and disturbance. Phys. Rev. A 2014, 89, 022106. [Google Scholar] [CrossRef]
- Busch, P.; Lahti, P.; Werner, R.F. Colloquium: Quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys. 2014, 86, 1261. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl. 1930, 14, 296–303. [Google Scholar]
- Kaniewski, J.; Tomamichel, M.; Wehner, S. Entropic uncertainty from effective anticommutators. Phys. Rev. A 2014, 90, 012332. [Google Scholar] [CrossRef]
- Maccone, L.; Pati, A.K. Stronger uncertainty relations for all incompatible observables. Phys. Rev. Lett. 2014, 113, 260401. [Google Scholar] [CrossRef] [PubMed]
- Hirschman, I.I., Jr. A note on entropy. Am. J. Math. 1957, 79, 152–156. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in quantum mechanics. Phys. Rev. Lett. 1983, 50, 631–633. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef] [PubMed]
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic uncertainty relations and their applications. 2015; arXiv:1511.04857. [Google Scholar]
- Garrett, A.J.M.; Gull, S.F. Numerical study of the information uncertainty principle. Phys. Lett. A 1990, 151, 453–458. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, J. Optimal entropic uncertainty relation in two-dimensional Hilbert space. Phys. Lett. A 1998, 244, 189–195. [Google Scholar] [CrossRef]
- Ghirardi, G.; Marinatto, L.; Romano, R. An optimal entropic uncertainty relation in a two-dimensional Hilbert space. Phys. Lett. A 2003, 317, 32–36. [Google Scholar] [CrossRef]
- De Vicente, J.I.; Sánchez-Ruiz, J. Improved bounds on entropic uncertainty relations. Phys. Rev. A 2008, 77, 042110. [Google Scholar] [CrossRef]
- Abdelkhalek, K.; Schwonnek, R.; Maassen, H.; Furrer, F.; Duhme, J.; Raynal, P.; Englert, B.G.; Werner, R.F. Optimality of entropic uncertainty relations. 2015; arXiv:1509.00398. [Google Scholar]
- Huang, Y. Variance-based uncertainty relations. Phys. Rev. A 2012, 86, 024101. [Google Scholar] [CrossRef]
- Li, J.L.; Qiao, C.F. Reformulating the quantum uncertainty relation. Sci. Rep. 2015, 5, 12708. [Google Scholar] [CrossRef] [PubMed]
- Busch, P.; Lahti, P.; Werner, R.F. Heisenberg uncertainty for qubit measurements. Phys. Rev. A 2014, 89, 012129. [Google Scholar] [CrossRef]
- Dammeier, L.; Schwonnek, R.; Werner, R.F. Uncertainty relations for angular momentum. New J. Phys. 2015, 17, 093046. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Busch, P. Qubit uncertainty tutorial; 12th International Workshop on Quantum Physics and Logic, Oxford, UK, 17 July 2015. Available online: https://www.cs.ox.ac.uk/qpl2015/slides/busch-tutorial.pdf (accessed on 22 February 2016).
- Branciard, C. Deriving tight error-trade-off relations for approximate joint measurements of incompatible quantum observables. Phys. Rev. A 2014, 89, 022124. [Google Scholar] [CrossRef]
- Hofmann, H.F.; Takeuchi, S. Violation of local uncertainty relations as a signature of entanglement. Phys. Rev. A 2003, 68, 032103. [Google Scholar] [CrossRef]
- Bertlmann, R.A.; Krammer, P. Bloch vector for qudits. J. Phys. A Math. Theor. 2008, 41, 235303. [Google Scholar] [CrossRef]
- Kimura, G. The Bloch vector for N-level systems. Phys. Lett. A 2003, 314, 339–349. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbott, A.A.; Alzieu, P.-L.; Hall, M.J.W.; Branciard, C. Tight State-Independent Uncertainty Relations for Qubits. Mathematics 2016, 4, 8. https://doi.org/10.3390/math4010008
Abbott AA, Alzieu P-L, Hall MJW, Branciard C. Tight State-Independent Uncertainty Relations for Qubits. Mathematics. 2016; 4(1):8. https://doi.org/10.3390/math4010008
Chicago/Turabian StyleAbbott, Alastair A., Pierre-Louis Alzieu, Michael J. W. Hall, and Cyril Branciard. 2016. "Tight State-Independent Uncertainty Relations for Qubits" Mathematics 4, no. 1: 8. https://doi.org/10.3390/math4010008