1. Introduction
The necessity to study supersonic gas jets arises, first, due to the wide use of such flows in various technological apparatuses and, second, due to the high level of force, thermal, and pulsating loads generated when such supersonic flows impinge onto obstacles. The discharge of supersonic jets is normally accompanied with a high level of acoustic noises emitted into ambient space. In the case of jets impinging onto obstacles, the onset of self-oscillation regimes, featuring the emission of high-intensity sound, is possible. The much more complex internal structure of supersonic jets in comparison with that of subsonic jets is due to the involvement of curvilinear compression shocks, closed internal zones with subsonic flows, mixing layers, and flow regions with high gradients of flow quantities. All of these factors necessitate fundamental and applied studies of the shock-wave structure, mixing characteristics, and acoustic emission properties of supersonic gas jets. Results of the study of jet flows, including supersonic jets, have been described in sufficient detail in previous publications [
1,
2,
3,
4,
5,
6,
7].
At present, the search is being conducted for effective methods of controlling the mass transfer process by affecting the initial section of the mixing layer [
8]. A significant effect of streamwise vortex structures on the processes of mass transfer in the mixing layer is reported [
9]. The formation of streamwise vortices is realized with the use of vortex generators of various types. The results of the use of protrusions located at the nozzle exit and the formation of a disturbance in the jet flow, the so-called “tabs”, for the intensification of mixing in the jet shear layer were presented in References [
10,
11]. Microtabs of small dimensions applied on the nozzle inner surface were used to form streamwise vortices in the supersonic jet mixing layer. The minimum thickness of the used microtab was 0.06 mm [
12]. In the experiments, the azimuthal non-uniformity at the distribution of the measured pressure was observed as a result of formation of streamwise vortex structures. Using chevrons and tabs in nozzles of turbofan engines allows the jet noise to be substantially reduced [
13]. Optimal configurations of nozzles with chevrons and tabs were found, which made it possible to reduce the noise level by 2.7 dB with a minor loss in thrust (approximately 0.06%).
Another type of vortex generator is the injection of a microjet into the main stream, which was described in detail in Reference [
14]. The degree of influence of the microjet on the main jet was studied by varying the total pressure in the microjet. It was shown that the mixing efficiency depends on the shape of the microjet. It was also shown that when the 16 transverse microjets of the nitrogen are injected, the overall level of broadband noise from the twin jet is reduced and the high-frequency discrete noise is decreased [
15]. A decrease in the level of acoustic disturbances for a supersonic jet with an obstacle when several microjets are injected into the main stream was noted in Reference [
16].
The results of computational studies on the methods of reducing the noise level in supersonic jets in the presence of various vortex generators—including chevrons, tabs and microjets—were presented in Reference [
17]. An experimental and numerical study of underexpanded free sonic jet flows issuing from rectangular, elliptical, and slot nozzles was undertaken in Reference [
18]. In the works of References [
19,
20], the authors validated an in-house RANS numerical tool, employing a k-epsilon turbulence model with a specific compressibility correction, by comparing the numerical results with the experimental ones reported by Woodmansee et al. [
21] concerning an air underexpanded jet. The numerical model was able to capture the key features of underexpanded jets (Mach disk, triple point, slip line, barrel shocks, etc.) and showed very good agreement with the centerline and radial profiles of temperature and pressure [
20]. Moreover, a study of a hydrogen underexpanded jet was also performed [
22].
High-resolution planar particle image velocimetry was used to measure turbulent quantities in the region downstream of the Mach disk in an axisymmetric underexpanded jet issued from a convergent nozzle [
23]. An experimental study was carried out to provide detailed data on nozzle inlet and exit conditions and near-field development for convergent round nozzles operated at N
pr (N
pr is the nozzle pressure ratio) corresponding to high subsonic and supersonic (underexpanded) jet plumes [
24]. The existence of the Taylor-Goertler vortices around the inner zone of the gas jets was demonstrated in free gas jets submerged in water by means of an optical probe [
25]. In Reference [
26], the ability of the Particle Image Velocimetry (PIV) technique to provide correct measurements of the velocity field in steady supersonic underexpanded hot free jets was reported. The influence of nozzle exit conditions on the near-field development of underexpanded jets and study acoustics was investigated in References [
24,
27].
The studies to be overviewed here, aimed at revealing the physical mechanisms behind the production of strong flow pulsations by supersonic jets impinging onto obstacles, were motivated by the tendency toward the minimization of the adverse action of flows on engineering structures. The latter implies the reduction of the vibration level of structural elements and the provision for the safe departure of space-rocket systems from the launch pad. Despite the fact that the lift-off process lasts for a length time of only a few seconds, the emergence of flow pulsations accompanied with intense acoustic disturbances at the location of the propulsion system may inflict damages both to the rocket itself and to the launch building.
Currently, activities aimed at the development of new-generation, future technology-manned transportation vehicles using a reentry system that includes a multijet system necessary for deceleration near the landing surface are under way,
Figure 1 [
28]. The application of such a multijet system necessitates the study of the detailed shock-wave structure of the flow in free high-pressure supersonic jets and in jets impinging onto the surface under landing conditions.
Difficulties in the study of physical mechanisms within the indicated activities consist in the existence of a multitude of fundamental points to be taken into consideration. Among such points are problems in the hydrodynamic instability of supersonic shear flows (boundary layer and mixing layer), the development of small perturbations and their interaction with compression shocks, the mechanisms of acoustic emission by high-speed flows, the emergence of self-oscillations, and the shock-wave structure of supersonic non-isobaric jets.
2. Spatial Structure in the Jet Shear Layer of a Supersonic Underexpanded Jet
In the present review, we describe some results of the studies of the three-dimensional (3D) structure of the mixing layer and the shock-wave structure of supersonic jet flows which were performed at Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch of the Russian Academy of Science (ITAM SB RAS) during past two decades. A review of earlier publications is given in monographs [
4,
5]. An important contribution to the studies of the detailed gas-dynamic structure of supersonic non-isobaric jets was the experimental discovery of the 3D pattern of the flow in the mixing layer of a supersonic underexpanded jet [
29,
30].
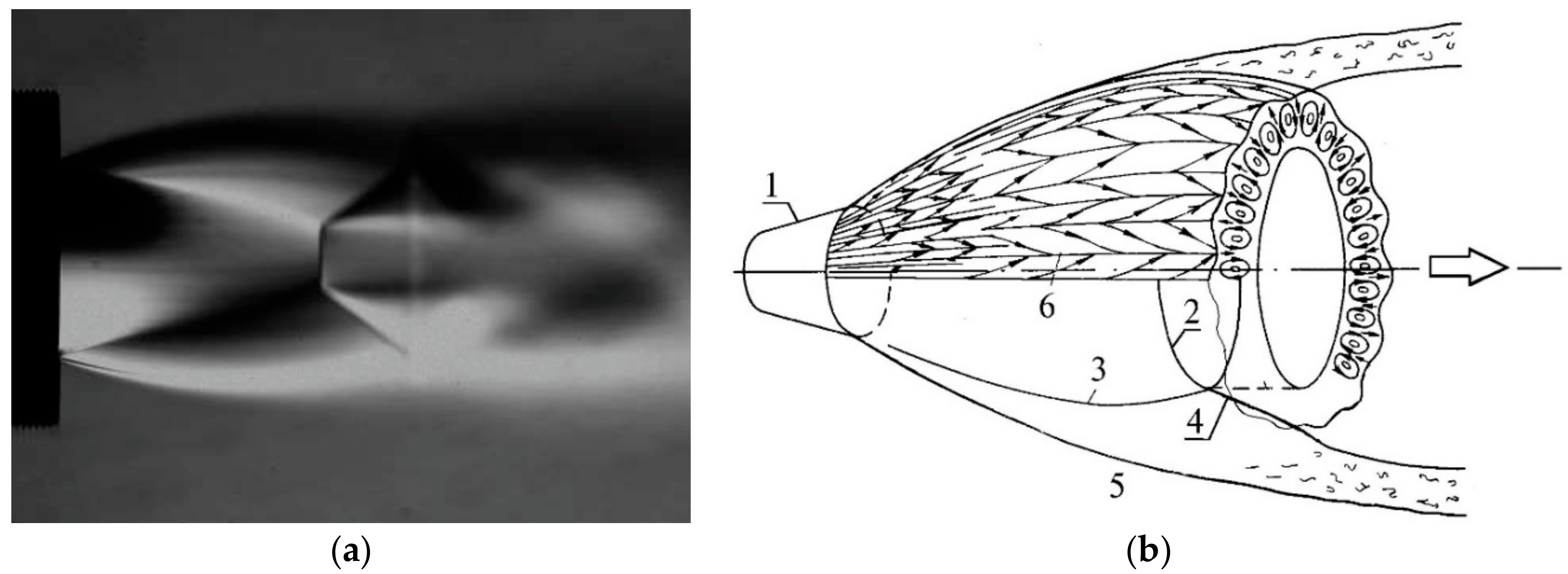
Figure 2 shows a schlieren photo of a supersonic underexpanded jet (N
pr = 5.0, where N
pr = P
0/P
c—nozzle pressure ratio; P
0—total pressure; P
c—pressure in the ambient space) exhausted from a convergent nozzle with a small surface roughness, and the diagram of the flow in the presence of streamwise vortical structures [
30] formed in the mixing layer of the jet. Here, the schlieren photo refers to a flow regime in which the initial disturbances due to the roughness of the inner nozzle surface were very small and, hence, the longitudinal streaks due to the presence of azimuthal disturbances were seen indistinctly.
Detection the 3D flow structure in the shear layer of supersonic jets is a problem of great scientific significance because it involves both the physical nature and the formation mechanism of vortices. Experimentally, a substantial influence of the level of the initial stationary disturbances in the mixing layer, formed in the immediate vicinity of the nozzle exit during jet discharge, was revealed. An experimental confirmation of the existence of streamwise vortical structures in the mixing layer of supersonic underexpanded jets was obtained in References [
31,
32].
The study of the physical mechanisms of the origination of streamwise vortices in jet mixing layers is impossible without a detailed description of the shock-wave structure of supersonic non-isobaric jets. In previous publications [
33,
34,
35,
36], the results of an experimental study of the gas-dynamic structure of supersonic jets and the characteristics of stationary streamwise vortical structures formed in the jet mixing layer were reported. A determining role of the level of the initial disturbances formed on the inner surface of the nozzle in the vicinity of the nozzle outlet was demonstrated in Reference [
33].
A determining role of the curvature of flow streamlines in the mixing layer of supersonic jets was demonstrated in References [
35,
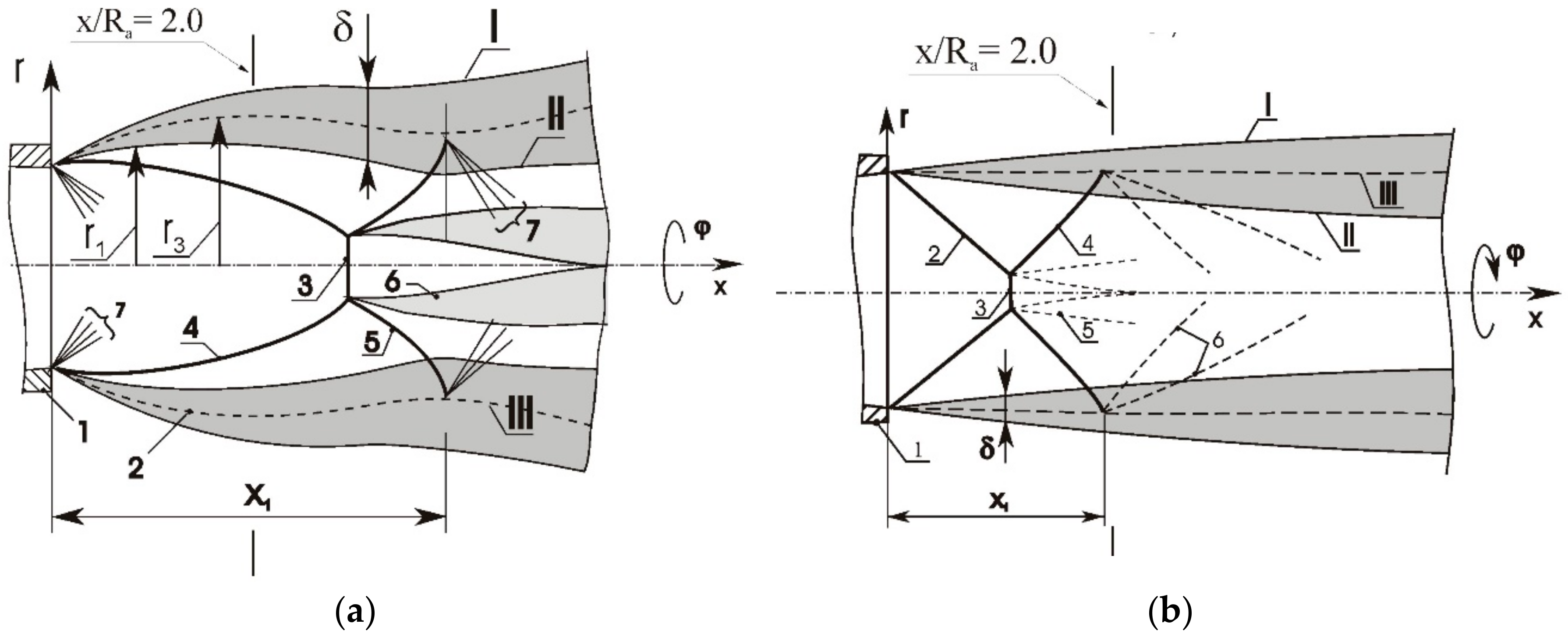
36] by means of comparison of the root-mean-square value of azimuthal non-uniformities for two jets, an underexpanded jet and an overexpanded jet. Here, the jet Mach numbers for both plumes jets are identical and equal to M
j = 1.71; the nozzle outlet diameters are also identical and equal to 30 mm; yet, the design Mach numbers at the nozzle exit are different, equal to M
a = 1.0 and 2.0 (see
Figure 3). This is why, at identical values of stagnation pressure in the settling chamber (nozzle pressure ratio N
pr = 5.0), for the Mach 1 nozzle a non-calculated ratio of a supersonic underexpanded jet (n
p = 2.64), and in the Mach 2 nozzle (n
p = 0.64) an overexpansion regime, was implemented. Here n
p = P
a/P
c is the non-calculated pressure ratio, P
a is the pressure at the nozzle exit, and P
c is the pressure in the ambient space.
Although the Mach numbers for both jets were identical (M
j = 1.71), mixing layer parameters were close to each other, and the levels of initial azimuthal disturbances in the mixing layers of the initial lengths of the jets were nearly identical, the streamline curvatures were essentially different. That is why the registered increase of the intensity of artificial stationary disturbances for underexpanded jets in comparison with overexpanded jets points to a considerable effect of the streamline curvature on the development of streamwise vortical disturbances in the mixing layer. The latter result confirms the previous conclusion about the determining role of the Taylor-Goertler instability in the development of stationary azimuthal disturbances in the mixing layer of supersonic jets (
Figure 4).
In the numerical study of Reference [
36], an important role of the Goertler flow instability on the development of streamwise vortices in the mixing layer of supersonic jets was shown. In Reference [
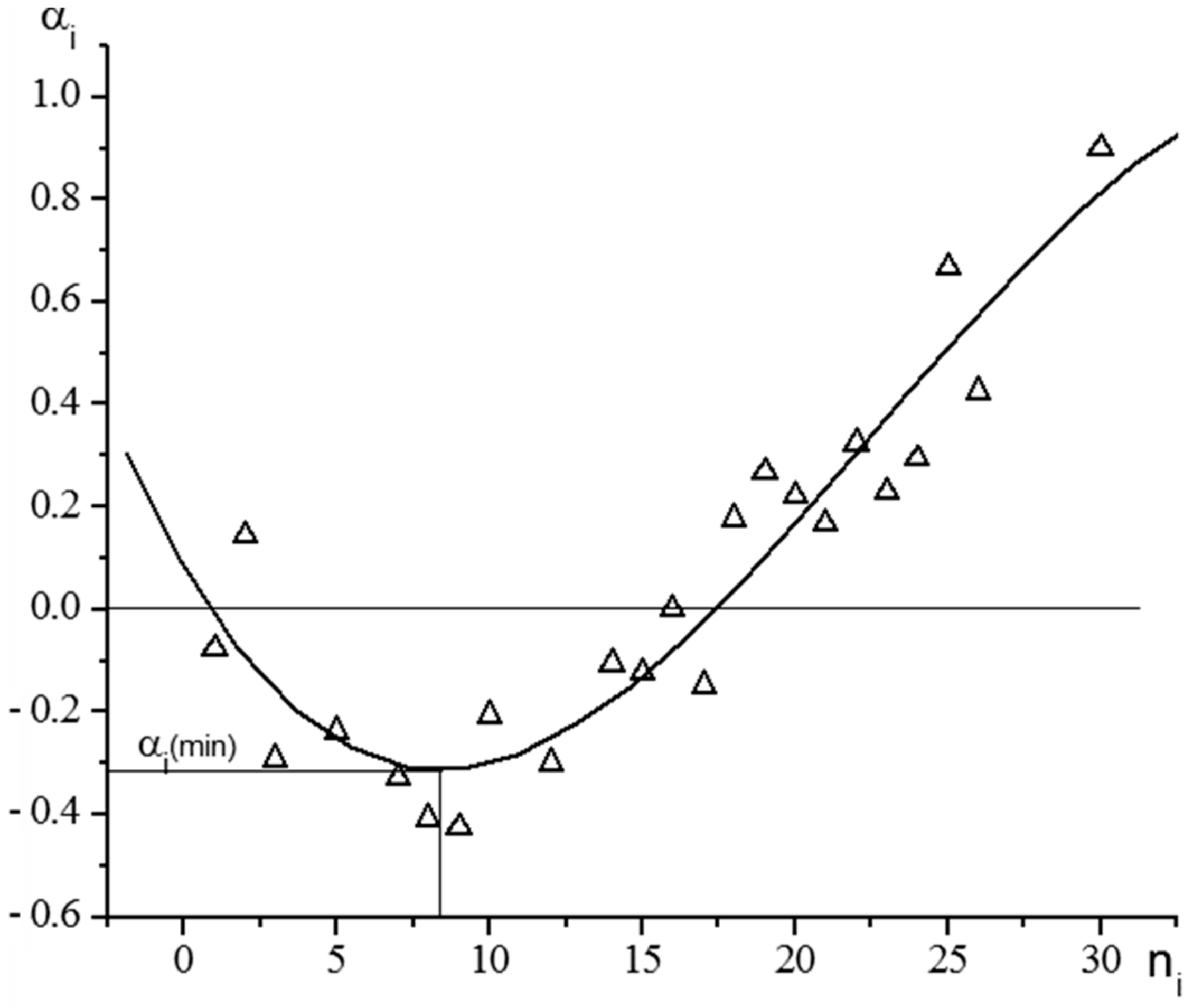
37], spectral characteristics of 3D stationary disturbances in the mixing layer of a supersonic underexpanded jet were analyzed. The conditions for the growth of such disturbances were identified, and the dependence of spectral characteristics on the regime of jet discharge from the nozzle was refined. The evolution of streamwise vortical structures in the mixing layer of the initial length of underexpanded jets results, first, in the formation of large Goertler disturbances (whose azimuthal size is comparable with the mixing-layer thickness) and, second, in the decay of small-scale disturbances. A maximum growth of the amplitude is observed for the disturbances with wavenumber n = 8, and this result is in satisfactory agreement with the numerical results of Reference [
36] (
Figure 5).
In analyzing the experimental data, an assumption was adopted that the mean flow in the mixing layer was superimposed with small-amplitude harmonic-type disturbances [
36]. Then, the formula by which a mode of the disturbed flow can be calculated is:
where An(r, x) is the amplitude of the spectral component of Goertler disturbances and n
i is the azimuthal wavenumber related to the characteristic size of the disturbances by the formula λn = 2πr/n
i. The wavelength λn refers to the transverse size of a pair of streamwise vortices. The variable α is a complex quantity that can be represented as:
where α′
r is the streamwise wavenumber, and iα′ is the increment of disturbance growth in the longitudinal direction. The formula by which the increment of the n
i-th mode can be determined is:
where Δx = x
2 − x
1 is the distance between two cross-sections of the jet, and An (x
1) and An (x
2) are the amplitudes of components with the corresponding wavenumbers in these cross-sections. The normalization of the streamwise coordinate by the nozzle outlet radius can be used to render Formula (4) to a dimensionless form:
Negative value of growth increment α
i(min) in
Figure 5 points toward maximal increasing with wavenumber n
i = 8. Moreover, we can see that for n
i > 16, azimuthal disturbances (small streamwise vortices) decrease with distance from the nozzle exit. For example, the modification of artificial azimuthal disturbances with n
i = 6 is shown below (nozzle with six chevrons).
The gas-dynamic structure of the initial length of an overexpanded submerged jet exhausting from a shaped flat nozzle with geometric Mach number 4 was presented in Reference [
38]. It was shown that stationary streamwise vortical structures develop in the jet mixing layer analogously to the flow in axisymmetric underexpanded jets. The presence of intense vortices formed in corner configurations of the flat nozzle was revealed as well. Visualized pictures of flow structure performed using the laser-knife technique were presented. The visualization was performed using the scattering of laser radiation on condensate microparticles which formed as a result of nitrogen supercooling.
The intensification of mixing processes in high-speed flows is a fundamental problem in aero-gas-dynamics, which is also related to the search for methods to control sound-generation processes. At ITAM SB RAS, studies aimed at the investigation of mechanisms of mixing intensification in supersonic shear layers due to the generation of streamwise vortical structures with vortex generators are under way. Various vortex generators, such as corrugations, chevrons, tabs, lobulated mixers (corrugations), and microjets interacting with the mixing layer of the primary jet, are known. A local action forms an additional perturbation in the flow, to be transformed into a streamwise vortex. The formation of such streamwise vortices structures leads to a substantial intensification of the transfer of mass in the jet mixing layer [
8,
39].
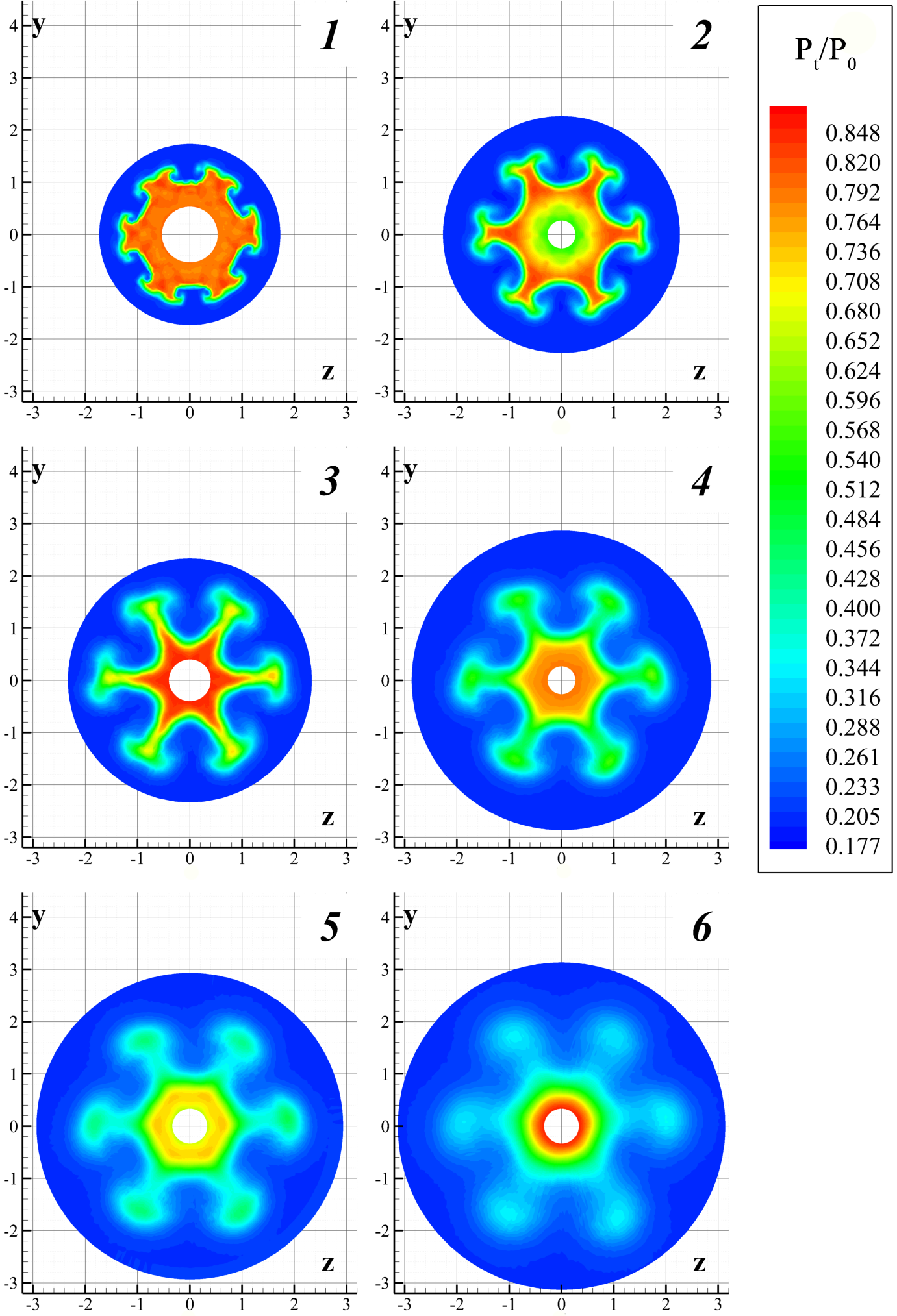
In a jet exhausting out of a nozzle with six chevrons, a more complex flow pattern is registered: the jet boundaries become more smeared, and the presence of the chevrons leads to the emergence of a series of compression shocks interacting with one another and intersecting at the axis. The Mach disk in the first cell of the jet is not registered (
Figure 6).
The experimentally obtained contour lines of total pressures measured in various cross-sections of a jet emanating from a nozzle provided with chevrons are shown in
Figure 7; here, results of numerical calculations comply with the experimental data of Reference [
40]. As a result of the interaction of chevrons with the jet flow, the transformation of the steady-state jet structure and the formation of mushroom-like large-scale vortical structures were registered. Each chevron gave birth to a pair of counter-rotating streamwise vortices shaped like mushrooms. The transformation of the formed vortical disturbances, the increase of the amplitude of azimuthal non-uniformities to x/R
a = 3, and the dissipation of disturbances observed on moving farther from the nozzle exit all can be traced. It should be noted here that, at the given geometry of vortex generators, in the jet mixing layer there forms the main mode of azimuthal disturbances with n
p = 6 being close to the most unstable mode of azimuthal disturbances (see
Figure 5). The mushroom-like large-scale vortex structures were also registered in subsonic jets without chevrons [
9].
The influence of vortex generators on the characteristics of the acoustic emission of supersonic jets was analyzed in Reference [
41]. It was found that the injection of air microjets into a subsonic or supersonic jet resulted in a change of the noise frequency spectrum, namely, in noise reduction in the low-frequency portion of the spectrum and in noise amplification in the high-frequency region. The injection of water into jets also resulted in the suppression of the discrete tone of noise for all examined regimes. It was found that the effectiveness of the impact of liquid injection on the reduction of acoustic emission increased with increasing the water concentration in the jet. It should also be noted that the revealing the substantial effect due to vortex generators on the acoustic-emission pattern of supersonic jets is of vital importance.
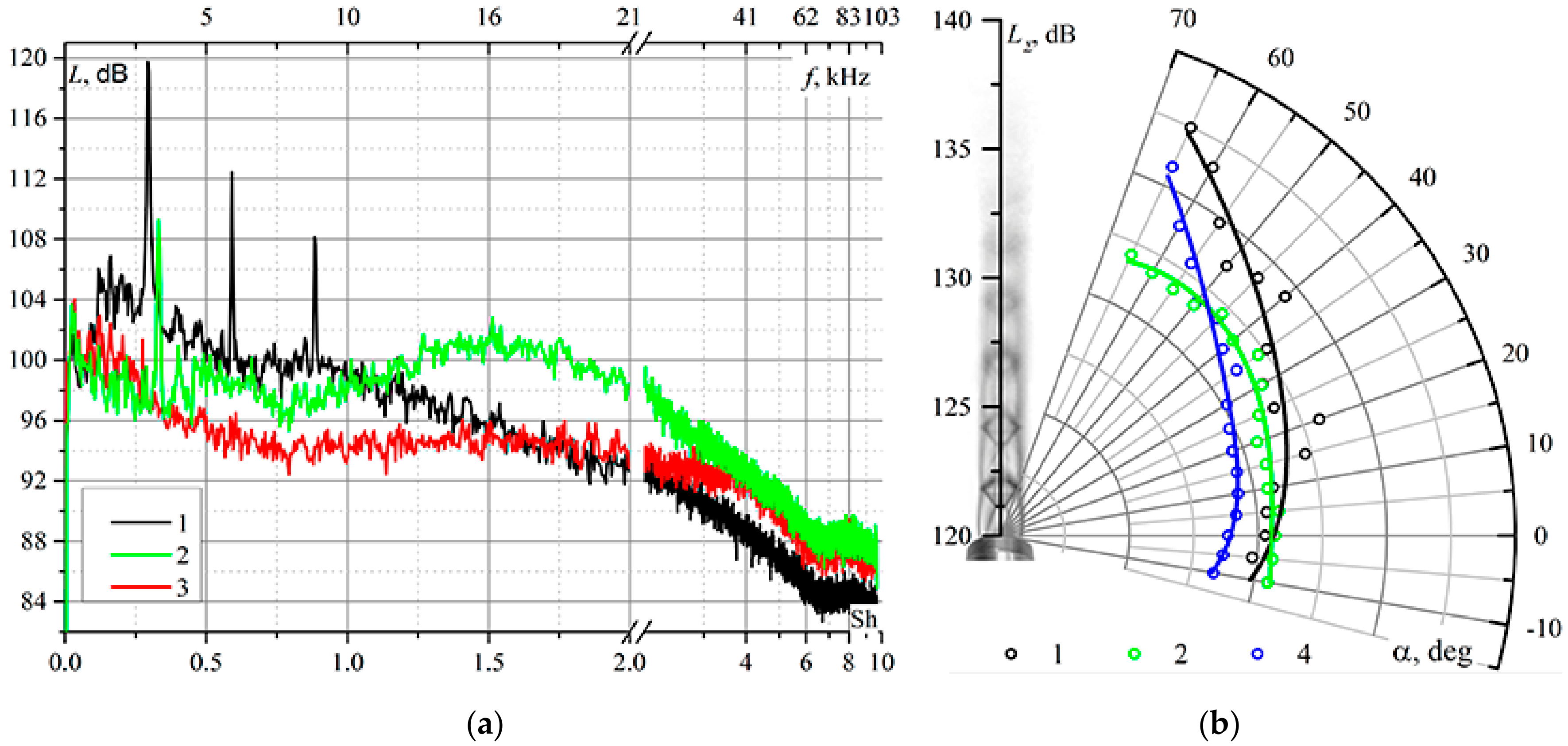
The microjet facility was a cylindrical head with a hollow internal channel, to which six conical micronozzles were connected. The micronozzles were arranged in a hexagon, with the azimuthal angular spacing between them being 60°. Each of the microjets was exhausted by a convergent nozzle, or micronozzle, with an outlet diameter of d
j = 0.7 mm. From inside, the micronozzles were contoured like cones (convergent micronozzles). It was found that, as the injected microjets grew in intensity, there occurred a proportional reduction of the level of low-frequency noise and a corresponding increase in the level of high-frequency noise (
Figure 8a). A minimum intensity of microjets at which a full suppression of discrete tone occurred in the spectrum of acoustic-pressure pulsations was identified. The use of chevrons substantially altered the frequency spectrum of the acoustic noise, promoting its reduction in the region of low frequencies and a considerable amplification of the shock-wave-induced noise component.
A jet noise reduction phenomenon observed during the use of vortex generators at a low Strouhal number was observed. Here, the boundary value of the frequency range in which the jet noise reduction occurred under the action of vortex generators underwent changes. The reduction of noise in the low-frequency portion of the spectrum under the action of chevrons amounted to 5–8 dB, whereas at the injection of microjets this reduction had a value of 3–5 dB. The injection of microjets promoted the reduction of the overall level of the jet-induced noise by 2–3 dB uniformly throughout the entire range of observation angles α (
Figure 8b). The presence of chevrons provided a profound noise reduction only for angles α > 45°; this reduction reached 5 dB. At smaller values of α the overall total noise level changed insignificantly.
A brief review of publications devoted to the study of the mechanisms of interaction of supersonic underexpanded jets with flat finite-size obstacles for determining the influence of involved geometric and gas-dynamic parameters (nozzle exit Mach number, nozzle pressure ratio, obstacle sizes, nozzle-to-obstacle separation) was given in References [
5,
28].
An experimental study of specific features of the shock-wave structure of a single supersonic non-isobaric jet exhausted in external supersonic flow was performed with the aim of determining the base pressure and studying the gas-dynamic structure of the flow [
42]. Schlieren photos in the vicinity of the stern cut points to a substantial difference of the gas-dynamic structure of a supersonic jet in the external supersonic flow from a jet exhausted into ambient space (
Figure 9).
Performing studies of high-speed jet flows using numerical calculation methods necessitates the comparison of calculated and experimental data, or the verification of the calculated data. Obtaining detailed reliable experimental data with completely documented test conditions (test case) is a difficult engineering problem that can only be solved as a result of joint efforts of specialists working in various fields. Related examples illustrating the solution of some particular problems are given in References [
43,
44,
45,
46,
47].
The use of obliquely cut nozzles in the reentry systems of future technology-manned reentry new-generation space vehicles calls for studies of the gas-dynamic flow structure of such jets [
28].
The availability of test cases is important not only to verify the adequacy of numerical results, but also to test new measured data obtained by other methods and in other experimental facilities. Research along this line is under way both at our institute and in other organizations. In a recent publication [
43], detailed data on the flow field in a supersonic underexpanded jet were reported, and Reference [
44] gave an example of using experimental data for the refinement of the calculation procedure and, in particular, for updating the model of turbulent mixing in supersonic jets.
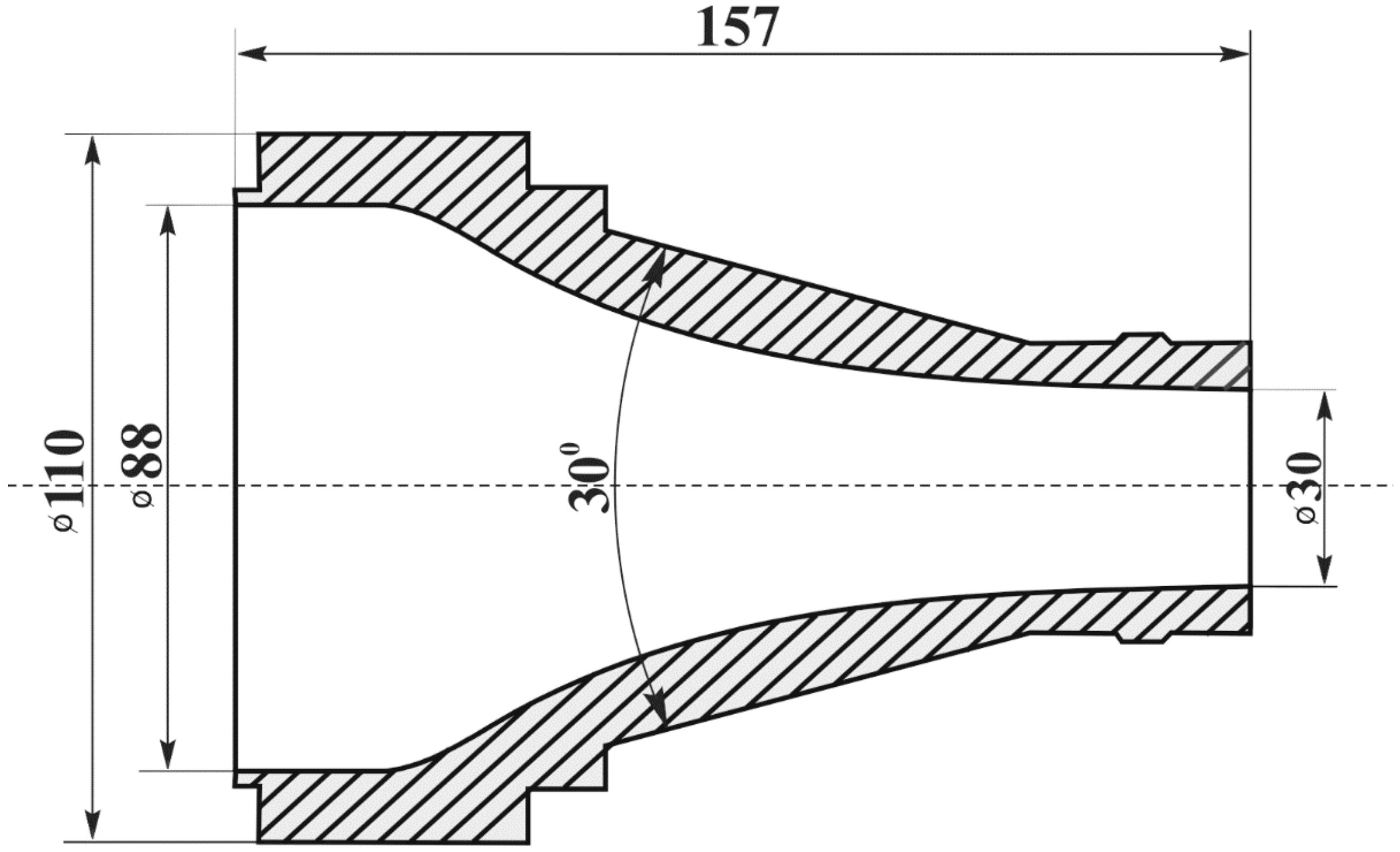
Below, we discuss the results of an experimental study of the gas-dynamic structure of a supersonic underexpanded jet described in Reference [
45]; the gained data can be used to test the results of numerical studies. The underexpanded supersonic jet was discharged from a convergent nozzle. The inner shaping of the nozzle ensured a smoothly converging passage from an 88-mm to a 30-mm nozzle outlet diameter (
Figure 10). The inner surface of the nozzle was shaped with a Vitoshinskii [
46] profile (Formula (5)) and had a minimum instrumental roughness of 0.25 μm.
where r(x) is the radius, R
in is the radius of the nozzle inlet, L is the length of the nozzle, and x is the longitudinal coordinate.
The gas-dynamic parameters at the nozzle exit were as follows: Mach number Ma = 1.0; Reynolds number based on the parameters at the nozzle exit Red = Ua∙Da/ν = 2.29∙106; np = Pa/Pc = 2.64 (here, Pa is the pressure at the nozzle exit; Pc is the pressure in ambient space equal to the pressure in the Eiffel chamber; T0 is the stagnation temperature in the settling chamber; Tc = 282 K is the temperature in the Eiffel chamber; Tw = 276 K is the nozzle wall temperature; Npr = P0/Pc = 5.0 is the nozzle pressure ratio; and δa/Da~0.03 is the relative thickness of boundary layer at the nozzle exit).
The shock-wave structure of the flow is seen in schlieren visualization pictures; it refers to the gas-dynamic jet discharge regime described above. At 5 ms of exposure, the photos show the averaged flow pattern (
Figure 11a), whereas at 2 μs of exposure, the instantaneous flow pattern is shown (
Figure 11b). Visualization of the flow in the diametral plane with a short exposure of 5 ns performed using the laser-knife technique is shown in
Figure 11c.
At long exposures, the steady-state shock-wave structure of the supersonic flow is clearly seen; it involves compression shocks, shock waves, mixing layers, and jet boundaries (
Figure 11a). Alternating dark and light bands are seen; those bands are indicative of azimuthal nonuniformities of the optical density of flow over the initial lengths of the jets (
Figure 11b). In the instantaneous photos (
Figure 11b), various vortical structures—such as, for example, streamwise vortices—formed in the shear flow are observed.
A cell structure of the jet flow involving the initial length of the jet, the first barrel, the Mach disk, the barrel shock, and the reflected shock is clearly seen. The flow in front of the Mach disk (a dark region in
Figure 11c) features a high flow velocity and a low gas density. As particles traverse the normal shock, a jump-like decrease of flow velocity occurs [
47]. This process leads to an enhanced concentration of light-scattering particles and an increased brightness of this flow region. Inside the jet behind the Mach disk, in the region behind the triple point origin in result of interaction of the compression shocks, the formation of periodic dark spots in the regions located symmetrically about the jet axis is observed. The transverse size of the dark spots increases in the downstream direction. The position of these structures corresponds to the inner mixing layer (shear layer) origin behind the triple point where the barrel shock, the reflected shock, and the normal compression shock (or Mach disk) interact with each other. It should be noted that in one interesting work [
48], this shear layer was identified as only a slip line. At some distance from the Mach disk, the inner mixing layers merge together to form an axial turbulent flow.
The distributions of Pitot pressure measured in the jet cross-section x/R
a = 2.0 at various times (years) are shown in
Figure 12a. Apart from the data obtained at the jet facility of the T-326 wind tunnel, ITAM SB RAS, with the use of a shaped convergent nozzle (
Figure 10), the graph contains data obtained at the vertical jet facility (VJF) of ITAM SB RAS during the discharge of a jet out of a convergent nozzle with N
pr = 5.0 and an outlet diameter of D
a = 20 mm [
33].
The root-mean-square deviation of pressure from its mean value obtained by averaging results over various measurement series is characterized by Curve 2 in
Figure 12b.
Some deviation of pressure is registered in jet regions with large radial gradients of flow quantities, at the barrel shock (r/R
a ≈ 0.6) and in the mixing layer (r/R
a ≈ 1.3). In those regions, the root-mean-square deviation of Pitot pressure from its mean value amounts to 5–6%, this being due to both the inaccuracies in the positioning of the pressure hole of the microprobe and the inaccuracies in maintaining the gas-dynamic regime of the flow (N
pr). An additional source for the difference of the measured values from the mean pressure in the mixing layer can be the stationary streamwise vortical structures mentioned above [
30,
31,
32,
33,
34,
35,
36,
37]. In the weakly gradient segments of the jet, in the compressed layer and at the outer boundary, the measurement error was 0.5–0.9%.
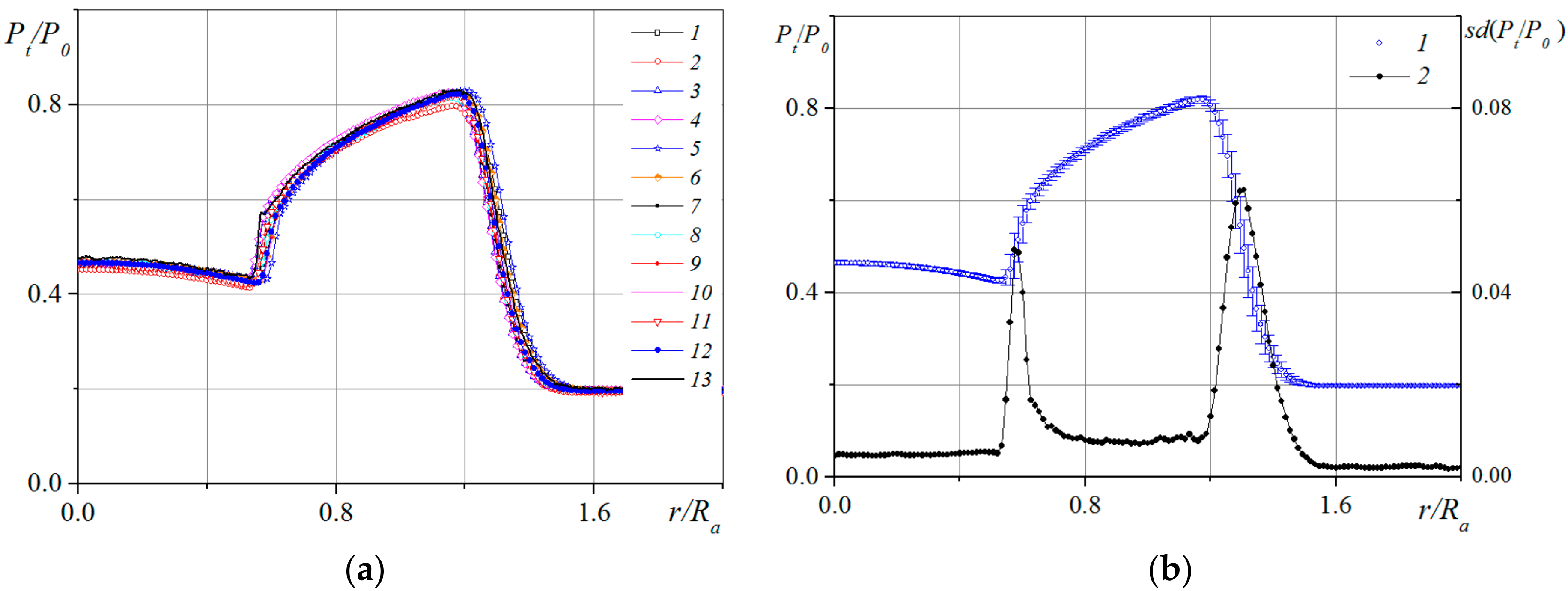
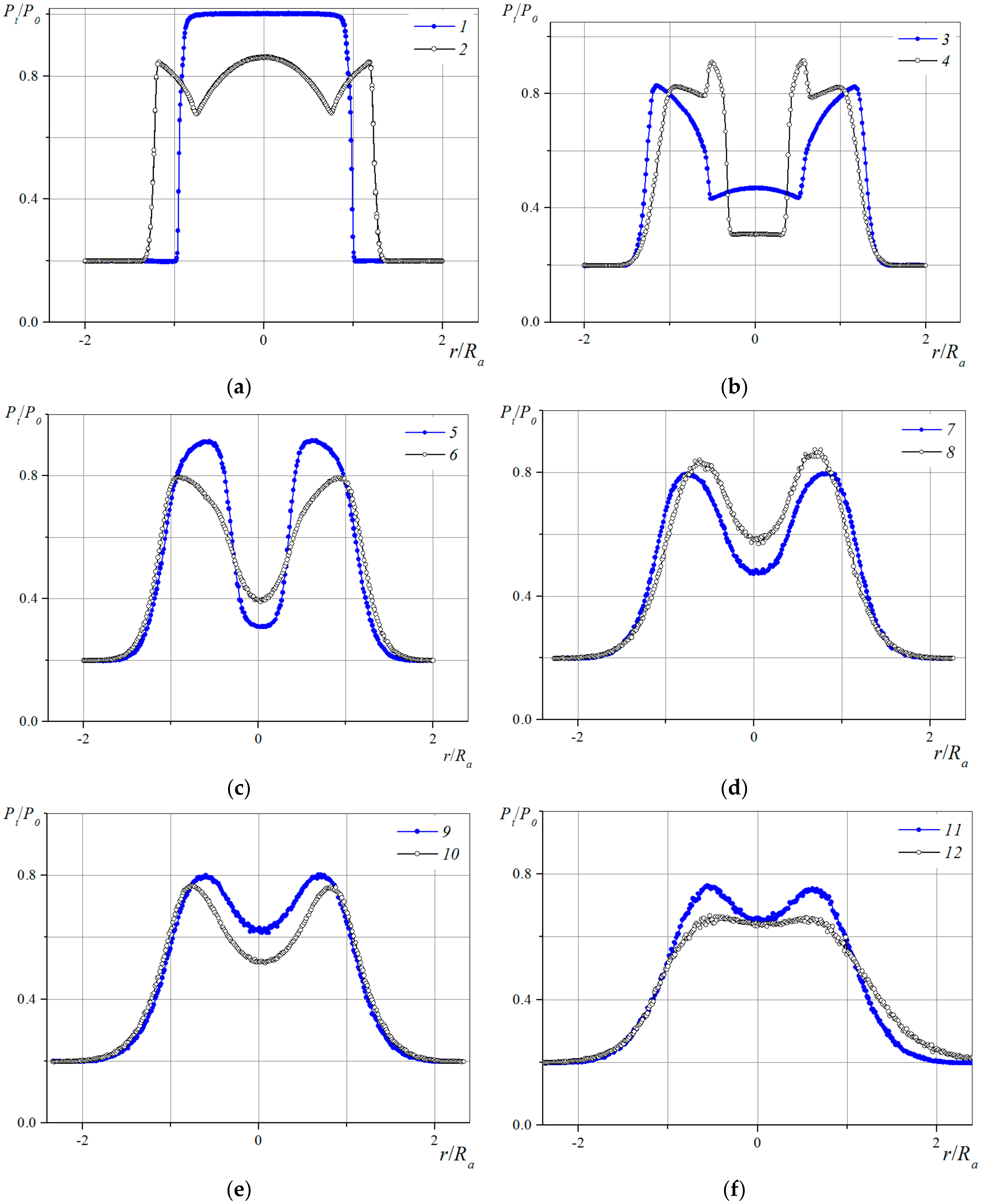
Radial distributions of the relative Pitot pressure measured at a jet facility of the T-326 wind tunnel ITAM SB RAS in various cross-sections of a supersonic underexpanded jet exhausting into ambient space are shown in
Figure 13 [
45]. The experimental data were obtained at the initial (x/R
a ≤ 3.0) and transient (x/R
a ≥ 3.0) lengths of the jet at x/R
a = 0.03–12.0.
At the exit from the nozzle (Curve 1,
Figure 13a), there forms a profile with a uniform distribution of the measured Pitot pressure, equal to the stagnation pressure at the inlet to the nozzle (P
t/P
0 = 1.0). In the downstream region (Curve 2) at the axis there forms a parabolic profile, and a barrel shock originates. The radial position of the barrel shock corresponds to the minimum P
t/P
0 = 0.68 observed at r/R
a = ±0.79.
In the cross-section x/R
a = 2.0 (curve 3 in
Figure 13b), the barrel shock is registered at r/R
a = ±0.5–0.6. At r/R
a > ±0.6, further increase of pressure in the compressed layer of the jet occurs; this pressure attains its highest value at the inner boundary of the mixing layer (P
t/P
0 = 0.82, r/R
a = ±1.16). The least thickness of the mixing layer is observed in the vicinity of the nozzle exit (Curve 1,
Figure 13a) and the largest thickness, at the maximum distance from the exit (Curve 12 in
Figure 13f). An increase in mixing-layer thickness with distance from nozzle outlet is registered.
In the flow region behind the Mach disc, the radial pressure profile exhibits rather an intricate behavior (Curve 4 in
Figure 13b). At the jet axis, a substantial decrease of pressure due to the pressure losses behind the Mach disk is observed. Behind the triple point, there forms an inner mixing layer. The rise of pressure in the region r/R
a = ±0.5 refers to the flow region in which the compression of the flow proceeds first in the barrel shock, and then in the reflected shock. The latter results in smaller losses of total pressure; according to the measurements, a maximum P
t/P
0 = 0.91, r/R
a = ±0.5 is observed in Curve 4 (
Figure 13b). On increasing the radius at which the Pitot tube was installed, the measured pressure decreases to 0.8, with this circumstance being due to the increase of total pressure losses (the stream does not traverse the reflected shock because the Mach number in this region has a larger magnitude). Farther on, we observe a weak increase of measured pressure in the compressed layer to a maximum of P
t/P
0 = 0.82 at r/R
a = ±1 at the inner boundary and a decrease of pressure in the mixing layer to 0.2, the region of which corresponds to the outer jet boundary.
As the flow moves downstream, the pressure profiles become smoother (
Figure 13c–f), and the pressure maxima and minima slope more gently. In the central portion of the jet, the measured total pressure values show oscillations.
In some cross-sections of the jet, a slight asymmetry of total pressure profiles measured, e.g., at x/R
a = 7.0 (Curve 8,
Figure 13d), 10.0, and 12.0 (Curves 11 and 12,
Figure 13f) is observed. Probably, this asymmetry is related to some effect due to the traversing-gear pylon necessary for the displacement of the Pitot microtube.
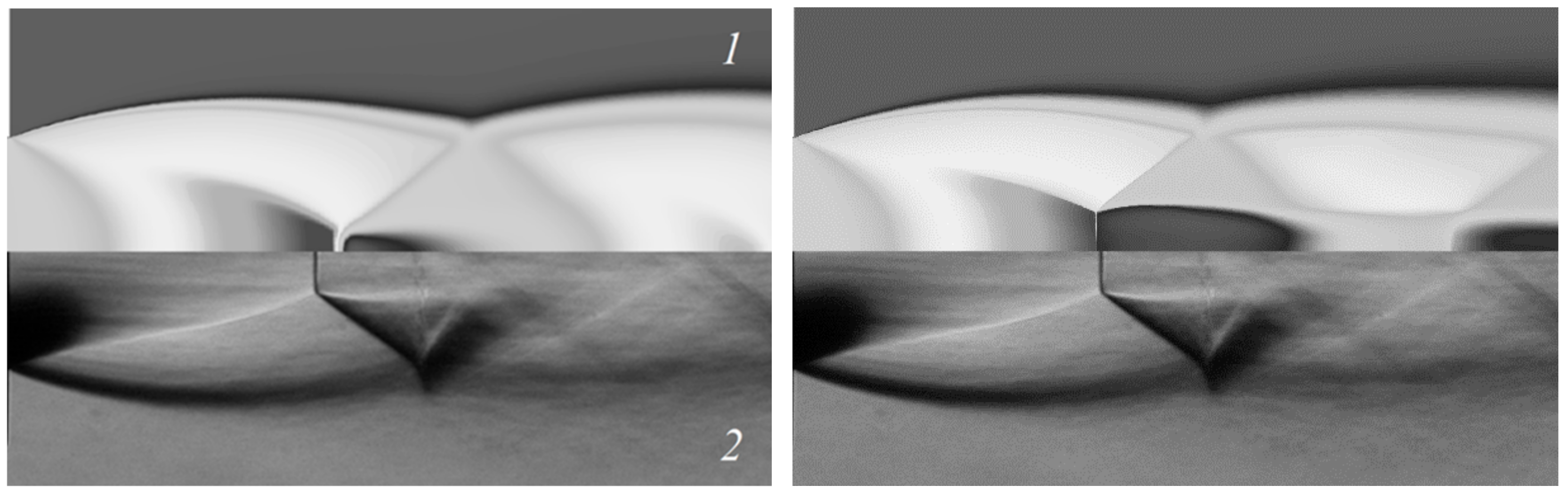
The use of experimental data to test numerical data was attempted in Reference [
43]. The flow in a supersonic underexpanded jet (M
a = 1, N
pr = 5) was modeled with Reynolds-averaged Navier-Stokes equations using the Spalarat-Allmaras SST models of turbulence [
49]. The calculated data qualitatively resemble the experimental data; however, some difference between the two datasets is also observed (
Figure 14). The Mach disk was located 4 mm (~x/R
a = 0.27) farther from the nozzle exit, its diameter being two times smaller than that in the experiment. A possible reason for the observed difference in the positions of Mach disks can be the overproduction of turbulent viscosity, which can be due to the form of the Coakley q-ω turbulence model (
Figure 14, left) [
50] used in the calculations. The use of the SST model of turbulence (
Figure 14, right) yields a better agreement between the calculated and experimental data.
The necessity of gaining experimental data concerning the structure of supersonic jets for testing results of numerical studies was noted in Reference [
42]. Also, we would like to mention here the publication of Reference [
51], in which experimental data concerning the structure of a supersonic overexpanded jet emanating into ambient space were reported. In that work, visualization results and detailed data for the longitudinal axial profile of the jet and for its radial pressure profiles measured with the help of a Pitot microtube at various distances from the nozzle exit to the examined section were reported. In the experiments, a simple Laval nozzle with a conical diverging section was used. The nozzle was designed for a nozzle exit Mach number of 3.005.