Flight Load Assessment for Light Aircraft Landing Trajectories in Windy Atmosphere and Near Wind Farms
Abstract
:1. Introduction
1.1. Wind Turbines Impact on Aviation
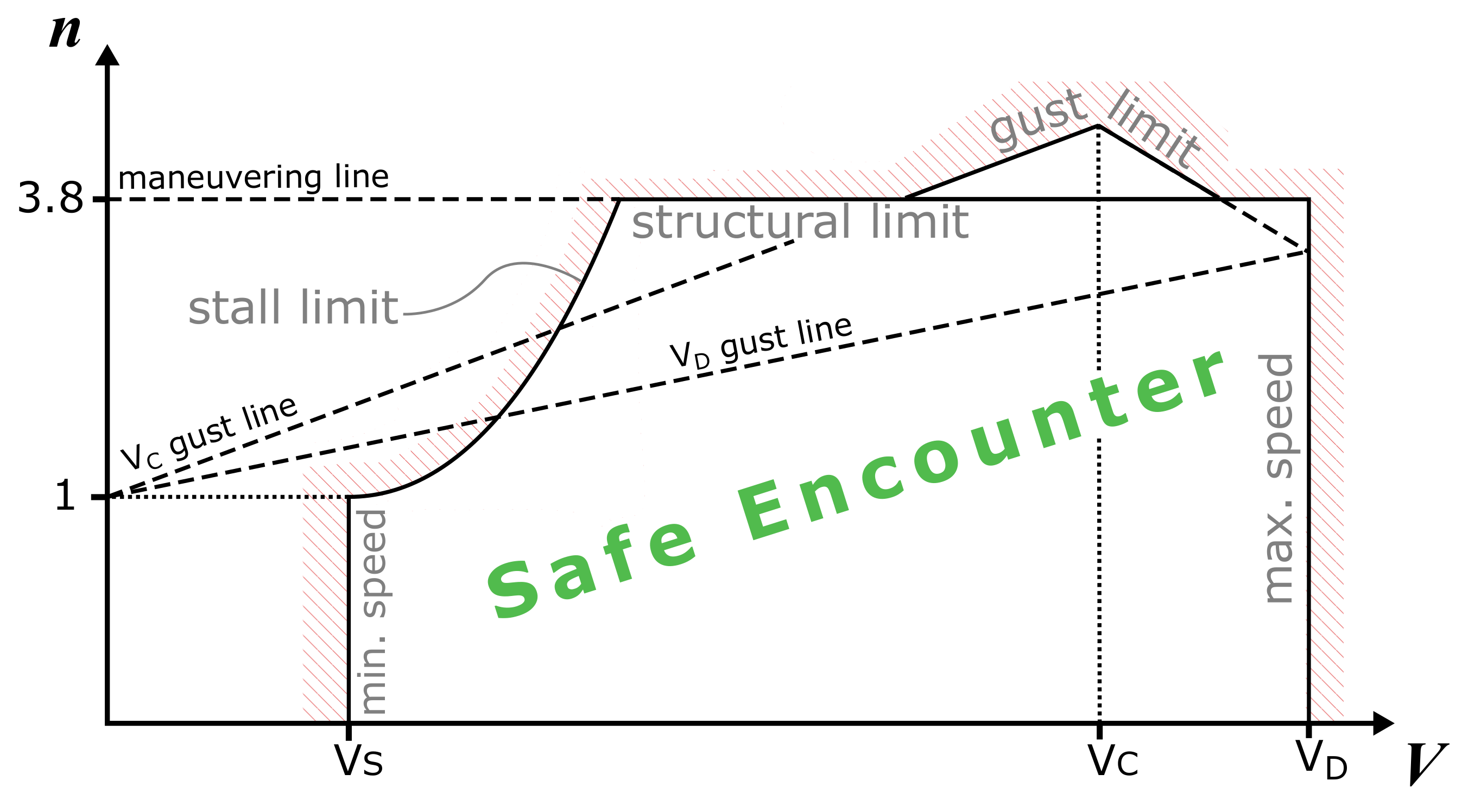
1.2. Aircraft Load Factor and V-n Diagram
1.3. Modelling
1.4. The Importance of Aeronautical Studies
1.5. Present Work and Structure of the Article
2. Methodology
2.1. Automatic Navigation in JSBSim
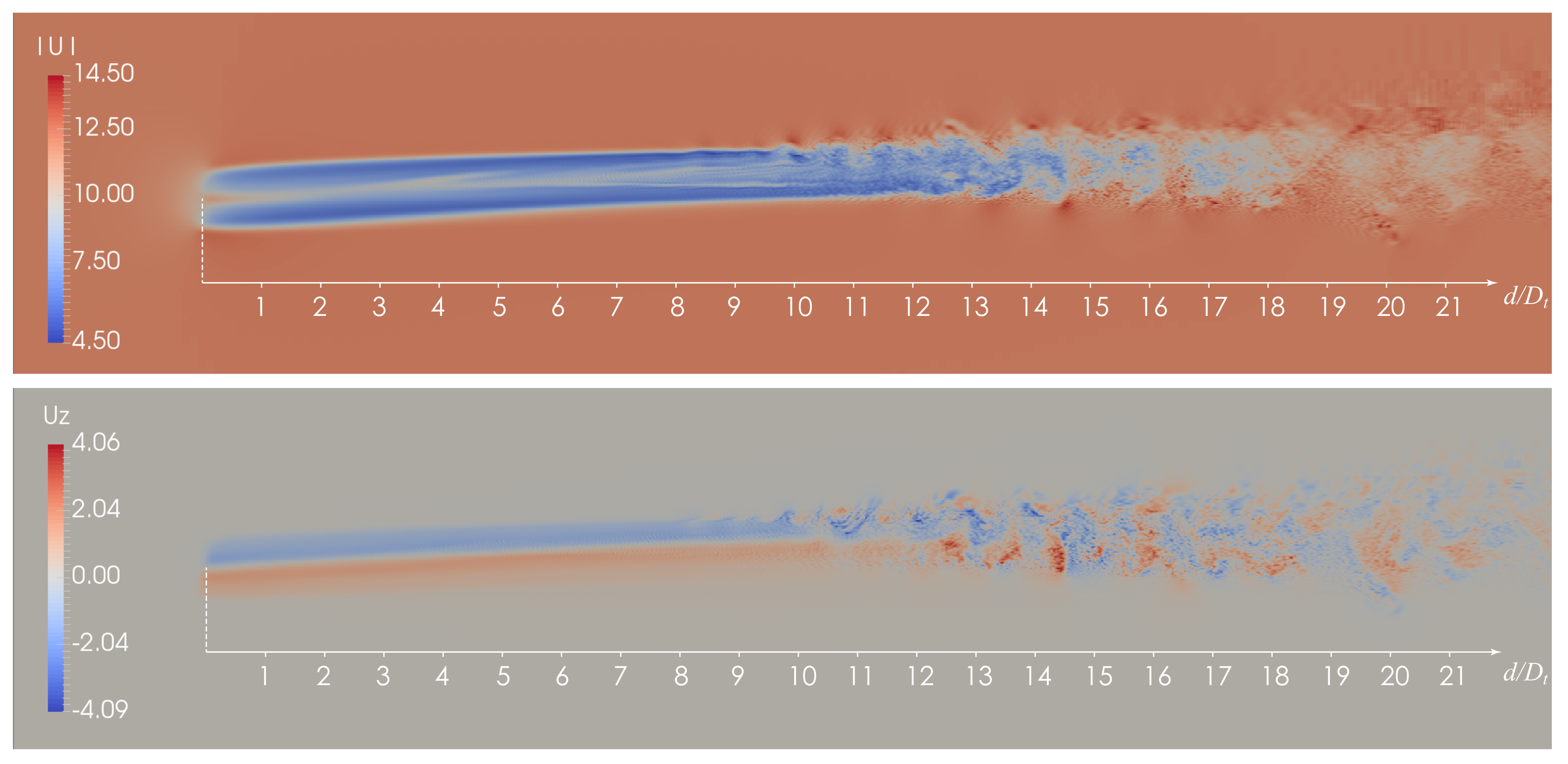
2.2. CFD Models
2.3. Coupling, Geo-Referentiation and Wind Interpolation
- JSBSim transmits the instantaneous aircraft position in a spherical, Earth-fixed reference frame;
- WiReS converts latitude and longitude coordinates to the UTM Cartesian coordinate system; altitude is untouched;
- WiReS uses this new form of the aircraft center of gravity position to directly access the mesh and interpolate the wind velocity vector field;
- WiReS transforms the wind velocity vector to the more common (for aeronautic applications) north-east-down reference frame and passes it back to the original instance of JSBSim;
- JSBSim acquires the wind velocity vector and uses it to update the aircraft velocity vector relative to the wind.
- Finally, all aerodynamic parameters are altered, thus taking into account the effects of the wind in that exact location on Earth, and the aircraft position is propagated to the next time frame.
3. Results
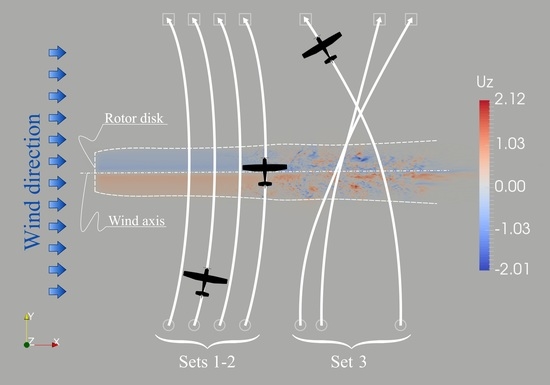
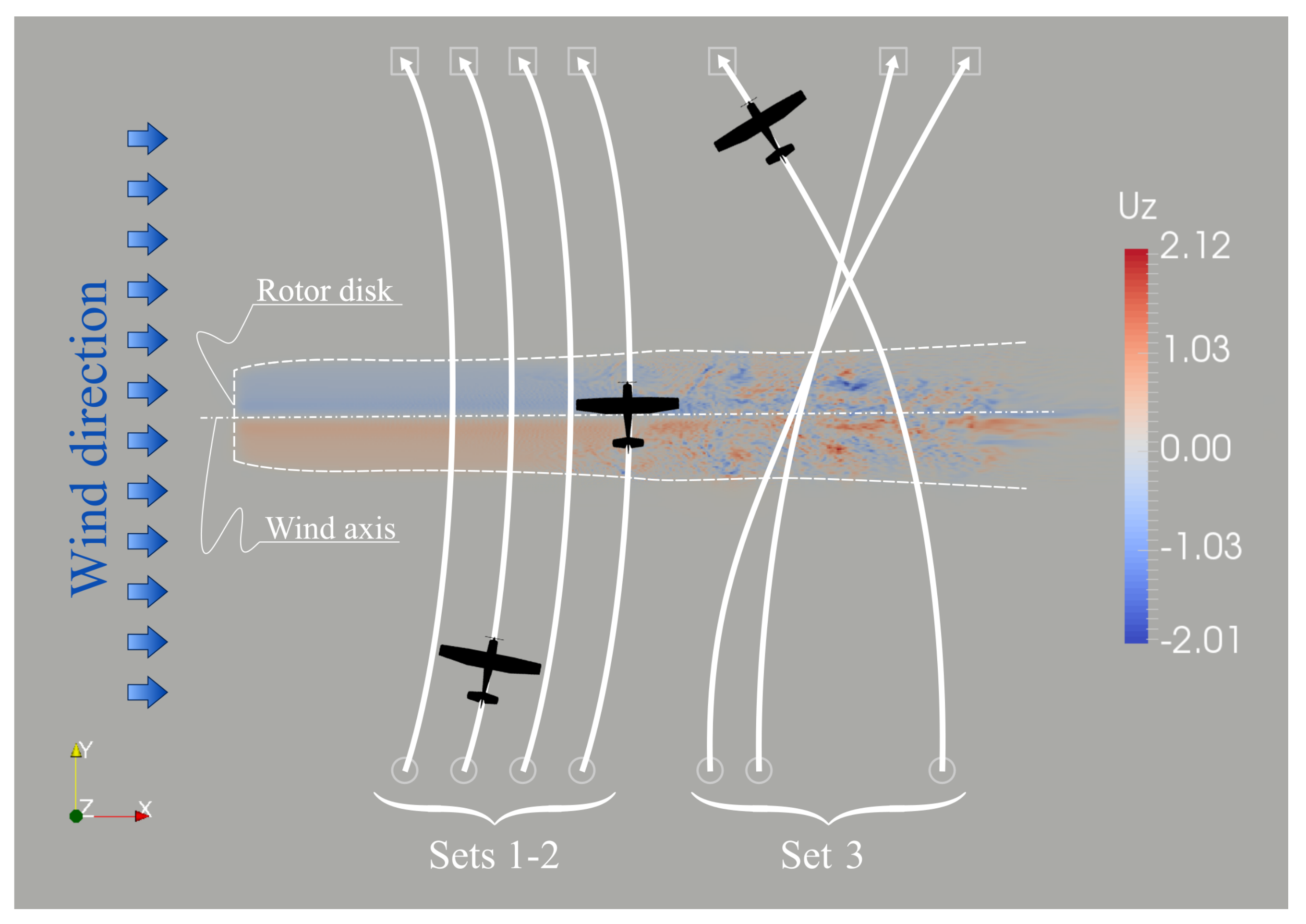
3.1. Scenarios Description
- Set 1
- comprises 20 deterministic simulations associated with an initial aircraft speed of 50 kn (≈ 93 ·) and flight path angle equal to . Initial ground position is assigned manually with respect to the turbine disk so as to achieve crossing distances d at integer multiples of the rotor diameter, i.e., crossings at . Initial altitude is also assigned manually in order to achieve crossings exactly through the middle of the wake. Final position is symmetrical to the initial one with respect to the wind axis, and is marked by a way-point. With this set-up, the aircraft realizes an ideal wake encounter by crossing the wake at the exact wind axis and with a heading at crossing of 0 (i.e., north).
- Set 2
- resembles Set 1 in every aspect but the aircraft initial speed, which is now set to 100 kn. These first two sets are referred to as the deterministic ones, and were set-up for performing a controllable trend study on the effects of distance to the rotor and aircraft speed.
- Set 3
- is the Montecarlo set, consisting of 100 random simulations. With reference to Figure 6: (i) initial horizontal position is uniformly distributed within the region interested by the turbine wake, while vertical position is fixed at a prescribed distance from the wind axis; (ii) initial speed is also uniformly distributed between 50 and 100 kn; (iii) initial altitude is assigned as a Gaussian variable of and , where is the turbine hub height above ground; (iv) initial heading is always set to north; (v) initial flight path angle is set to ; (vi) final position way-point coordinates are assigned similarly to the initial ones; (vii) final altitude that commands the gliding autopilot at every instant is assigned to be 65 over the final way-point in all cases. In this way, the aircraft undergoes a more or less steep turn during the wake encounter, crosses the wake at different heights, incidence angle and at variable rates of descent. This attempt was meant to reproduce the natural variability lying under potential realistic wake encounter scenarios.
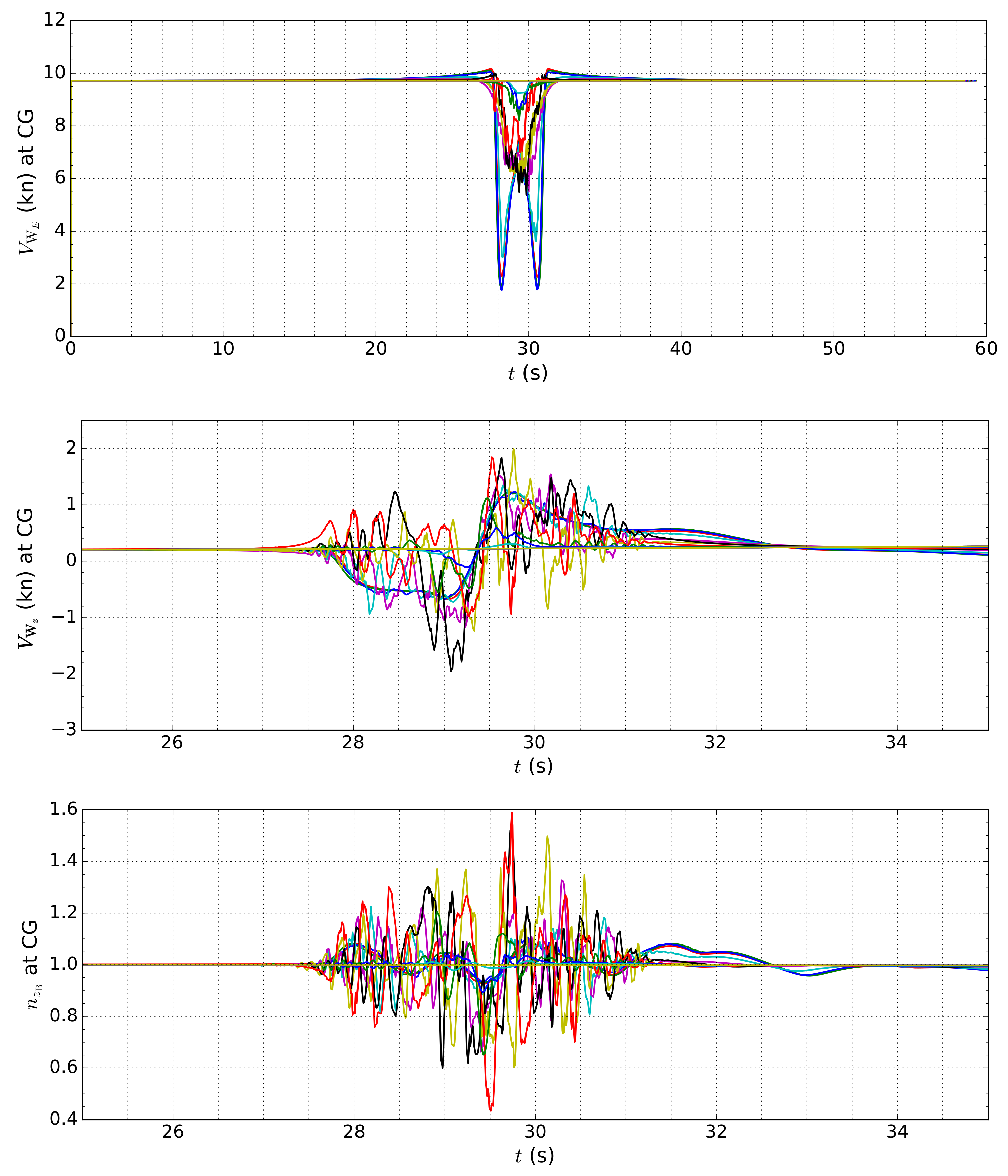
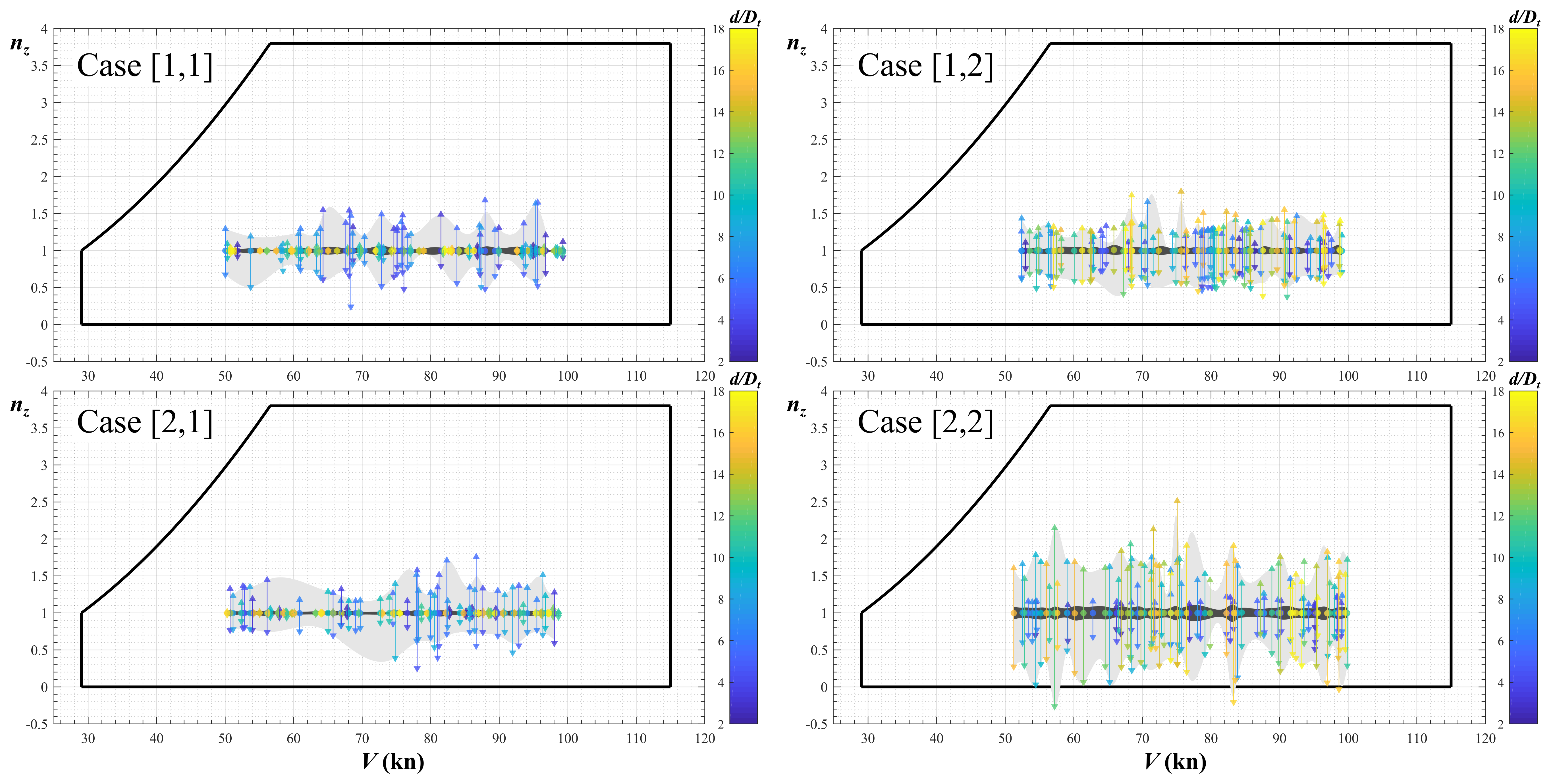
3.2. Analysis of Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Angle of attack | |
| Aileron, elevator, rudder deflection | |
| Normalized throttle | |
| Mean value and standard deviation of a Gaussian distributed variable | |
| Aircraft mass factor for the computation of the limit gust load factor | |
| Air density | |
| Bank, elevation, heading angles | |
| Azimuth angle of the main wind velocity vector | |
| Azimuth angle between main wind velocity and turbine axis | |
| Shaft power | |
| a | Inertial acceleration |
| Wing span | |
| Mean aerodynamic chord length | |
| d | Downwind distance from wind turbine rotor plane |
| g | Gravitational acceleration |
| Turbine hub height | |
| Altitude above Sea Level | |
| Horizontal tail arm, | |
| Vertical tail arm, | |
| n | Normal load factor |
| Roll, pitch, yaw angular velocities | |
| t | Time |
| Position of the aerodynamic center of the horizontal tail along the x-axis in the body reference frame | |
| Position of the aerodynamic center of the vertical tail along the x-axis in the body reference frame | |
| Body reference frame | |
| Position of the center of gravity along the x-axis in the body reference frame | |
| Wind reference frame | |
| Reference gust speed | |
| Gust speed | |
| Lift coefficient | |
| Lift coefficient slope | |
| Lift coefficient derivative w.r.t. time derivative of the angle of attack | |
| Pitching moment coefficient derivative w.r.t. pitch angular velocity | |
| Turbine diameter | |
| Empirical factor for the computation of the limit gust normal load factor | |
| Central moments of inertia | |
| Turbine rotor radius | |
| S | Aircraft reference area |
| Horizontal tail area | |
| Vertical tail area | |
| Wing area | |
| V | Aircraft velocity vector |
| V | Aircraft velocity magnitude |
| Aircraft design cruise speed, design dive speed and design stall speed | |
| Aircraft vertical speed | |
| Wind velocity magnitude | |
| Wind velocity component along the axis | |
| Wind velocity component along the East direction | |
| W | Aircraft weight |
| Aircraft empty weight | |
| Aircraft maximum take-off weight | |
| B | Subscript for body reference frame |
| L | Subscript for aerodynamic lift |
| W | Subscript for wind reference frame and wind parameters |
References
- Global Wind Energy Council. Global Wind Report: Annual Market Update 2015; Global Wind Energy Council: Brussels, Belgium, 2016. [Google Scholar]
- Federal Agency for Wind Energy. Windenergieprojekte unter Berücksichtigung von Luftverkehr und Radaranlagen; Wind Energy Projects under Limitations of Aviation and Radar Facilities; Bundesverband WindEnergie e.V., Federal Agency for Wind Energy: Berlin, Germany, 2017. (In German)
- Airspace & Safety Initiative Windfarm Working Group. Managing the Impact of Wind Turbines on Aviation; Airspace & Safety Initiative Windfarm Working Group: Hampshire, UK, 2013. [Google Scholar]
- U.S. Department of Transportation—Federal Aviation Administration. Recommended Standard Traffic Patterns and Practices for Aeronautical Operations at Airports without Operating Control Towers; U.S. Department of Transportation: Washington, DC, USA, 1993.
- Keränen, R.; Pettazzi, A.; Alku Catalina, L.; Salsón, S. Weather Radar and Abundant Wind Farmin—Impacts on Data Quality and Mitigation by Doppler Dual-Polarization. In Proceedings of the ERAD2014 8th European Conference on Radar in Meteorology and Hydrology, Garmisch-Partenkirchen, Germany, 1–5 September 2014. [Google Scholar]
- Gilman, P.; Husser, L.; Miller, B.; Peterson, L. Federal Interagency Wind Turbine Radar Interference Mitigation Strategy; Report for U.S. Department of Energy; U.S. Department of Energy: Washington, DC, USA, 2016.
- Hall, W.; Rico-Ramirez, M.A.; Krämer, S. Offshore wind turbine clutter characteristics and identification in operational C–band weather radar measurements. Q. J. R. Metereol. Soc. 2017, 143, 720–730. [Google Scholar] [CrossRef]
- European Aviation Safety Agency (EASA). Annual Aviation Safety Review; EASA: Cologne, Germany, 2017. [Google Scholar]
- Bureau of Aircraft Accidents Archives (B3A). Available online: http://www.baaa-acro.com (accessed on 5 April 2018).
- Glabeke, G. The Influence of Wind Turbine Induced Turbulence on Ultralight Aircraft, a CFD Analysis. Ph.D. Thesis, VIVES University of Applied Sciences, Oostende, Belgium, 2011. [Google Scholar]
- Van der Wall, B.; Fischenberg, D.; Lehmann, P.; van der Wall, L. Impact of Wind Energy Rotor Wakes on Fixed-Wing Aircraft and Helicopters. In Proceedings of the 42nd European Rotorcraft Forum, Lille, France, 5–8 September 2016. [Google Scholar]
- Mulinazzi, T.E.; Zheng, Z. Wind Farm Turbulence Impacts on General Aviation Airports in Kansas; Kansas Department of Transportation: Topeka, KS, USA, 2014.
- Wang, Y.; White, M.; Barakos, G. Wind Turbine Wake Encounter Study; Civil Aviation Authority: London, UK, 2015.
- European Aviation Safety Agency. EASA Certification Specifications for Very Light Aeroplanes; EASA: Cologne, Germany, 2003. [Google Scholar]
- Sanderse, B.; van der Pijl, S.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind Energy 2011, 14, 799–819. [Google Scholar] [CrossRef]
- Carrión, M.; Woodgate, M.; Steijl, R.; Barakos, G.N.; Gomez-Iradi, S.; Munduate, X. Understanding wind-turbine wake breakdown using computational fluid dynamics. AIAA J. 2015, 53, 588–602. [Google Scholar] [CrossRef]
- Troldborg, N.; Zahle, F.; Sørensen, N.; Réthoré, P. Comparison of wind turbine wake properties in non-uniform inflow predicted by different rotor models. J. Phys. Conf. Ser. 2014, 555, 012100. [Google Scholar] [CrossRef]
- Kalvig, S.; Manger, E.; Hjertager, B. Comparing different CFD wind turbine modelling approaches with wind tunnel measurements. J. Phys. Conf. Ser. 2014, 555. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Leonardi, S. Large Eddy Simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy Wiley Online Libr. 2015, 8, 1047–1060. [Google Scholar] [CrossRef]
- Martinez, L.; Leonardi, S.; Churchfield, M.; Moriarty, P. A Comparison of Actuator Disk and Actuator Line wind turbine models and best practices for their use. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Hardin, J. The velocity field induced by a helical vortex filament. Phys. Fluids 1982, 25. [Google Scholar] [CrossRef]
- Kocurek, D. Lifting Surface Performance Analysis for Horizontal Axis Wind Turbines; Solar Energy Research Institute: Golden, CO, USA, 1987. [Google Scholar]
- Schmidt, J.; Daniele, E.; Stoevesandt, B. Böenbelastung von UL-Flugzeugen durch den Turbulenten Nachlauf von Windenergieanlagen; Internal Report; Fraunhofer-Institute for Wind Energy Systems (IWES): Oldenburg, Germany, 2015. (In German) [Google Scholar]
- Schmidt, J.; Daniele, E.; Stoevesandt, B. Ergänzende Ergebnisauswertung zur Gefährdung von ULF durch WEA für den Standort Linnich-Boslar; Internal Report; Fraunhofer-Institute for Wind Energy Systems (IWES): Oldenburg, Germany, 2015. (In German) [Google Scholar]
- Schmidt, J.; Daniele, E.; Stoevesandt, B. Preliminary Assessment of the Impact of the Fairview Wind Project on Small Aircrafts at the Stayner Aerodrome; Internal Report; Fraunhofer-Institute for Wind Energy Systems (IWES): Oldenburg, Germany, 2016. [Google Scholar]
- Padfield, G.; Manimala, B.; Turner, G. A Severity Analysis for Rotorcraft Encounters with Vortex Wakes. J. Am. Helicopter Soc. 2004, 49, 445–456. [Google Scholar] [CrossRef]
- De Marco, A.; D’Auria, J. Collision Risk Studies with 6DOF Flight Simulations when Aerodrome Obstacle Standards Cannot Be Met. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences (ICAS 2014), St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- JSBSim: An Open Source, Platform-Independent, Flight Dynamics & Control Software Library in C++. Available online: http://jsbsim.sourceforge.net/ (accessed on 10 April 2018).
- OpenFOAM, Free CFD Software, The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 10 April 2018).
- Project Jupyter. Available online: http://jupyter.org/ (accessed on 10 April 2018).
- GitHub of the Aircraft Design Group of the University of Naples Federico II. Available online: https://github.com/Aircraft-Design-UniNa/WiReS (accessed on 10 April 2018).
- Ziegler, J.G.; Nichols, N.B.; Rochester, N.Y. Optimum Settings for Automatic Controllers. Trans. ASME 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Vollmer, L.; van Dooren, M.; Trabucchi, D.; Schneemann, J.; Steinfeld, G.; Witha, B.; Trujillo, J.; Kühn, M. First comparison of LES of an offshore wind turbine wake with dual-Doppler lidar measurements in a German offshore wind farm. J. Phys. Conf. Ser. 2015, 625. [Google Scholar] [CrossRef]
- Mikkelsen, R. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Jha, P.K.; Churchfield, M.J.; Moriarty, P.J.; Schmitz, S. Guidelines for Volume Force Distributions within Actuator Line Modeling of Wind Turbines on Large-Eddy Simulation-Type Grids. J. Sol. Energy Eng. 2014, 136, 031003. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, J.; Mikkelsen, R. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2009. [Google Scholar]
- Rahimi, H.; Garcia, A.M.; Stoevesandt, B.; Peinke, J.; Schepers, G. An engineering model for wind turbines under yawed conditions derived from high fidelity models. Wind Energy 2018. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Snyder, J. Map Projections—A Working Manual; United States Governmental Printing Office: Washington, DC, USA, 1983.
- Cessna C172 Skyhawk Specifications. Available online: http://cessna.txtav.com/en/piston/cessna-skyhawk (accessed on 10 April 2018).
- Comco Ikarus C42 Specifications. Available online: http://www.comco-ikarus.de/Pages/produkte-comco/c42a.php (accessed on 10 April 2018).
- Foto by Frank Schwichtenberg (CC BY-SA 3.0). Available online: https://commons.wikimedia.org/wiki/File%3ACessna_172R_Skyhawk_(D-EEJJ)_04.jpg (accessed on 10 April 2018).
- Foto by Ian Kirk from Broadstone, Dorset, UK (CC BY 2.0). Available online: https://commons.wikimedia.org/wiki/File%3AIkarus_C42_Compton_Abbas_30th_June_2013_(9218593234).jpg (accessed on 10 April 2018).
- HPC Cluster EDDY. Available online: www.uni-oldenburg.de/fk5/wr/hochleistungsrechnen/hpc-facilities/eddy/ (accessed on 10 April 2018).
 aileron ,
aileron ,  elevator ,
elevator ,  rudder and
rudder and  throttle , on the right vertical axis. These are the superposition of the initial trim command and autopilots actions; (b) time histories of the angular speed components in body axes:
throttle , on the right vertical axis. These are the superposition of the initial trim command and autopilots actions; (b) time histories of the angular speed components in body axes:  roll rate p,
roll rate p,  pitch rate q and
pitch rate q and  yaw rate r; (c) time histories of the Euler angles:
yaw rate r; (c) time histories of the Euler angles:  bank angle ,
bank angle ,  elevation-angle and
elevation-angle and  heading angle on the right vertical axis; and (d) 3D representation of the trajectory, with ground track and side-view projections. Altitude is not to scale.
heading angle on the right vertical axis; and (d) 3D representation of the trajectory, with ground track and side-view projections. Altitude is not to scale.
 aileron ,
aileron ,  elevator ,
elevator ,  rudder and
rudder and  throttle , on the right vertical axis. These are the superposition of the initial trim command and autopilots actions; (b) time histories of the angular speed components in body axes:
throttle , on the right vertical axis. These are the superposition of the initial trim command and autopilots actions; (b) time histories of the angular speed components in body axes:  roll rate p,
roll rate p,  pitch rate q and
pitch rate q and  yaw rate r; (c) time histories of the Euler angles:
yaw rate r; (c) time histories of the Euler angles:  bank angle ,
bank angle ,  elevation-angle and
elevation-angle and  heading angle on the right vertical axis; and (d) 3D representation of the trajectory, with ground track and side-view projections. Altitude is not to scale.
heading angle on the right vertical axis; and (d) 3D representation of the trajectory, with ground track and side-view projections. Altitude is not to scale.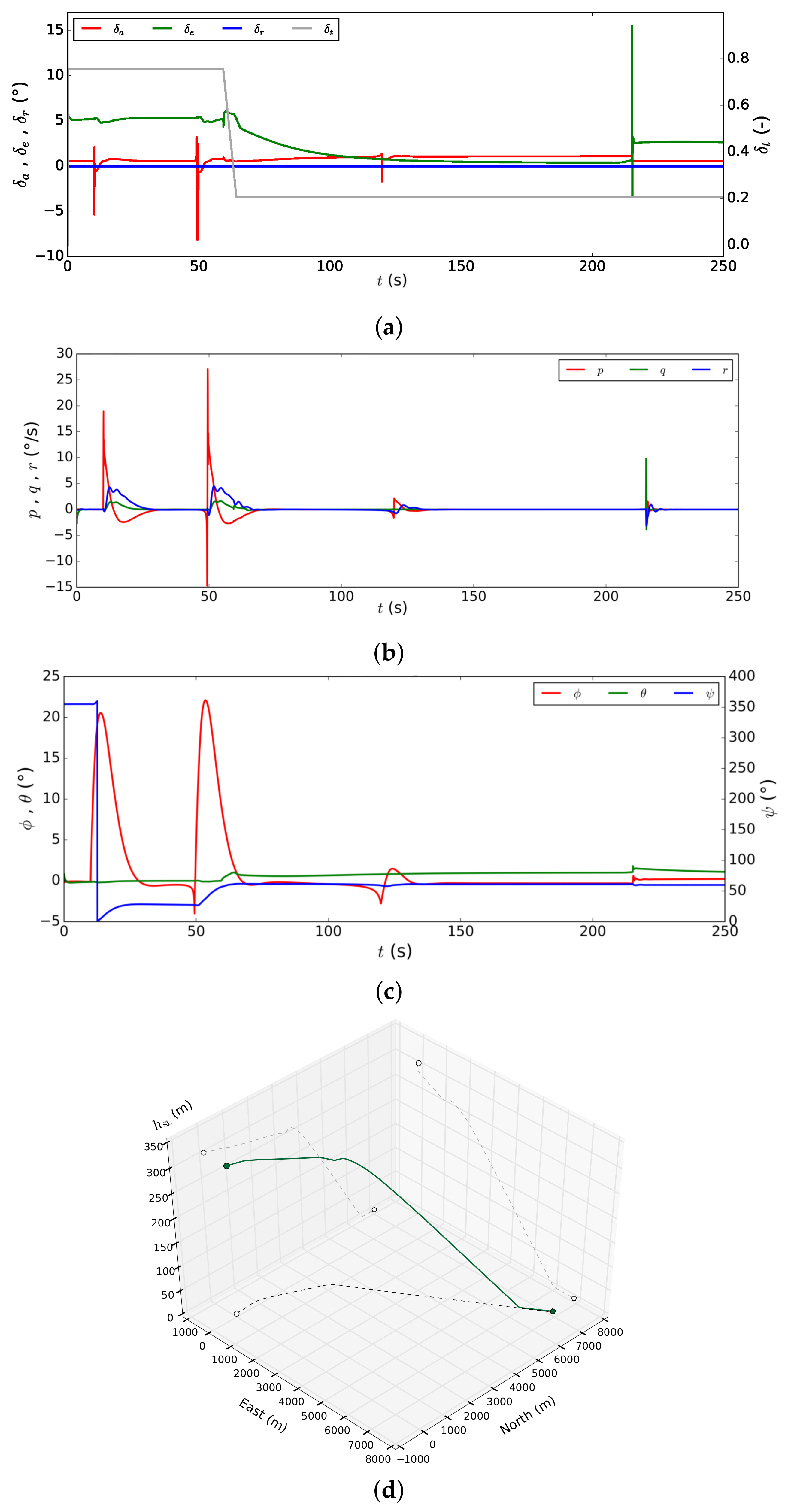
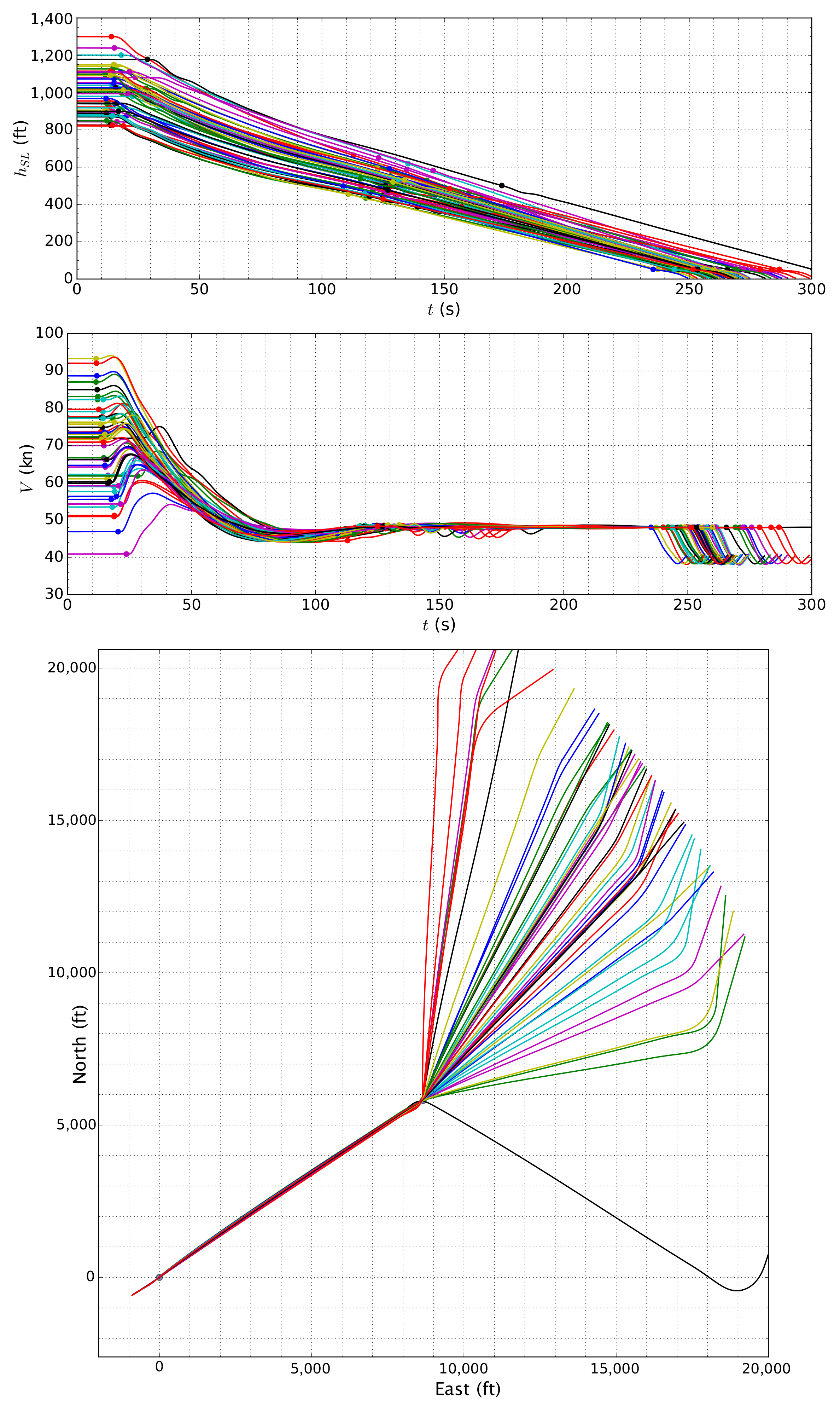

 50 kn in-axis;
50 kn in-axis;  100 kn in-axis;
100 kn in-axis;  50 kn off-axis;
50 kn off-axis;  100 kn off-axis;
100 kn off-axis;  Sets 3 in-axis;
Sets 3 in-axis;  Sets 3 off-axis.
Sets 3 off-axis.
 50 kn in-axis;
50 kn in-axis;  100 kn in-axis;
100 kn in-axis;  50 kn off-axis;
50 kn off-axis;  100 kn off-axis;
100 kn off-axis;  Sets 3 in-axis;
Sets 3 in-axis;  Sets 3 off-axis.
Sets 3 off-axis.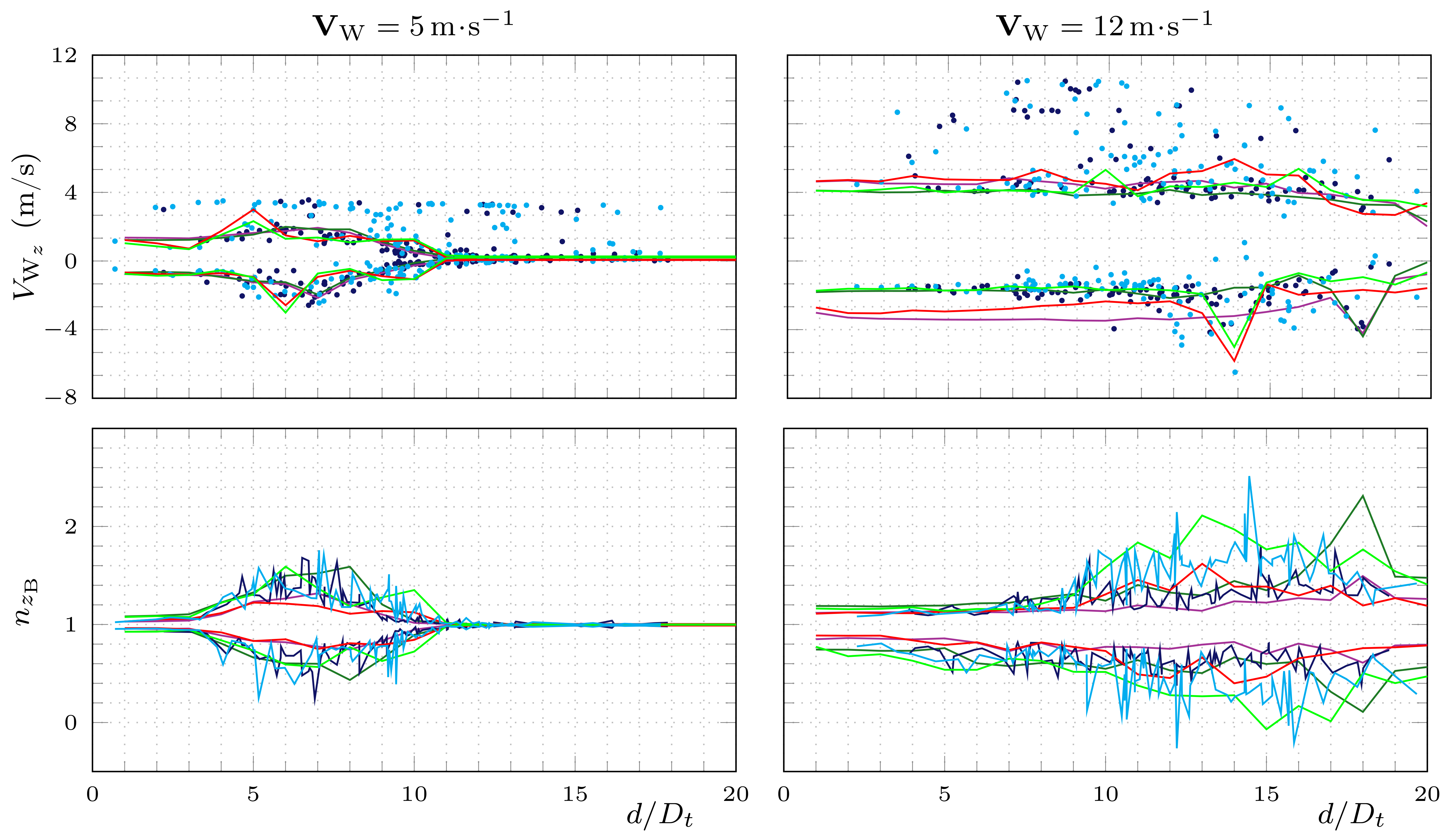
| Cessna 172 | Ikarus C42 | Custom | Units | |||||
|---|---|---|---|---|---|---|---|---|
| Seats | 4 | 2 | 2 | – | ||||
| 174 | (16.2) | 135 | (12.5) | 142 | (13.2) | () | ||
| 36.1 | (11) | 31.0 | (9.45) | 29.5 | (9.00) | () | ||
| 4.9 | (1.5) | – | 4.0 | (1.2) | () | |||
| 21.9 | (2.03) | – | 17.9 | (1.66) | () | |||
| 15.7 | (4.78) | – | 12.9 | (3.93) | () | |||
| 16.5 | (1.53) | – | 13.5 | (1.25) | () | |||
| 15.7 | (4.78) | – | 12.9 | (3.93) | () | |||
| 1640 | (744) | 583 | (264) | 596 | (270) | () | ||
| 2550 | (1157) | 1041 | (472) | – | () | |||
| 948 | (1285) | – | 261 | (353) | () | |||
| 1346 | (1825) | – | 371 | (503) | () | |||
| 1967 | (2667) | – | 542 | (735) | () | |||
| 180 | (134) | 100 | (75) | 100 | (75) | () | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varriale, C.; De Marco, A.; Daniele, E.; Schmidt, J.; Stoevesandt, B. Flight Load Assessment for Light Aircraft Landing Trajectories in Windy Atmosphere and Near Wind Farms. Aerospace 2018, 5, 42. https://doi.org/10.3390/aerospace5020042
Varriale C, De Marco A, Daniele E, Schmidt J, Stoevesandt B. Flight Load Assessment for Light Aircraft Landing Trajectories in Windy Atmosphere and Near Wind Farms. Aerospace. 2018; 5(2):42. https://doi.org/10.3390/aerospace5020042
Chicago/Turabian StyleVarriale, Carmine, Agostino De Marco, Elia Daniele, Jonas Schmidt, and Bernhard Stoevesandt. 2018. "Flight Load Assessment for Light Aircraft Landing Trajectories in Windy Atmosphere and Near Wind Farms" Aerospace 5, no. 2: 42. https://doi.org/10.3390/aerospace5020042