Damage Detection in a Composite T-Joint Using Guided Lamb Waves
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
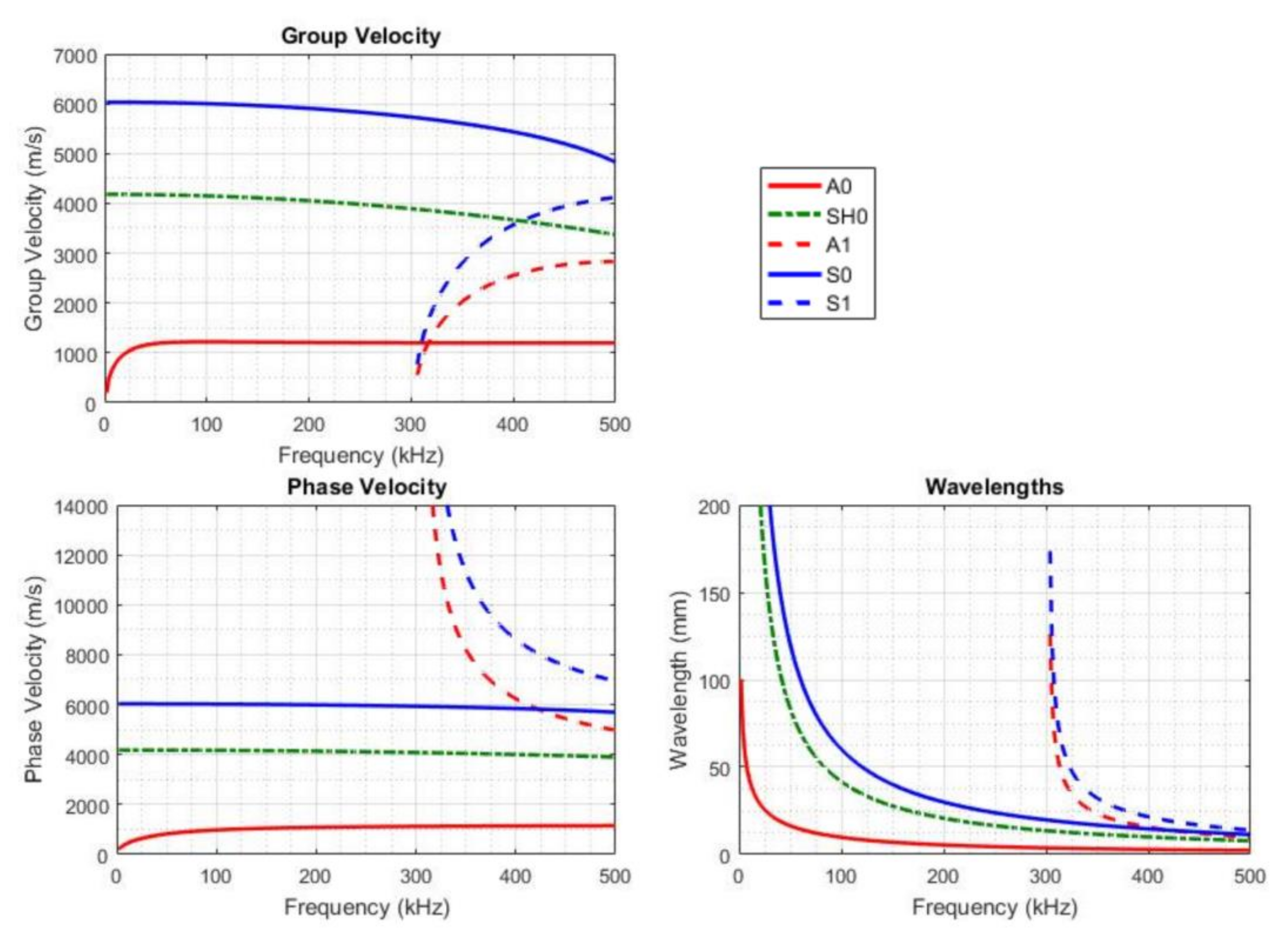
2.2. Theoretical Dispersion Curves
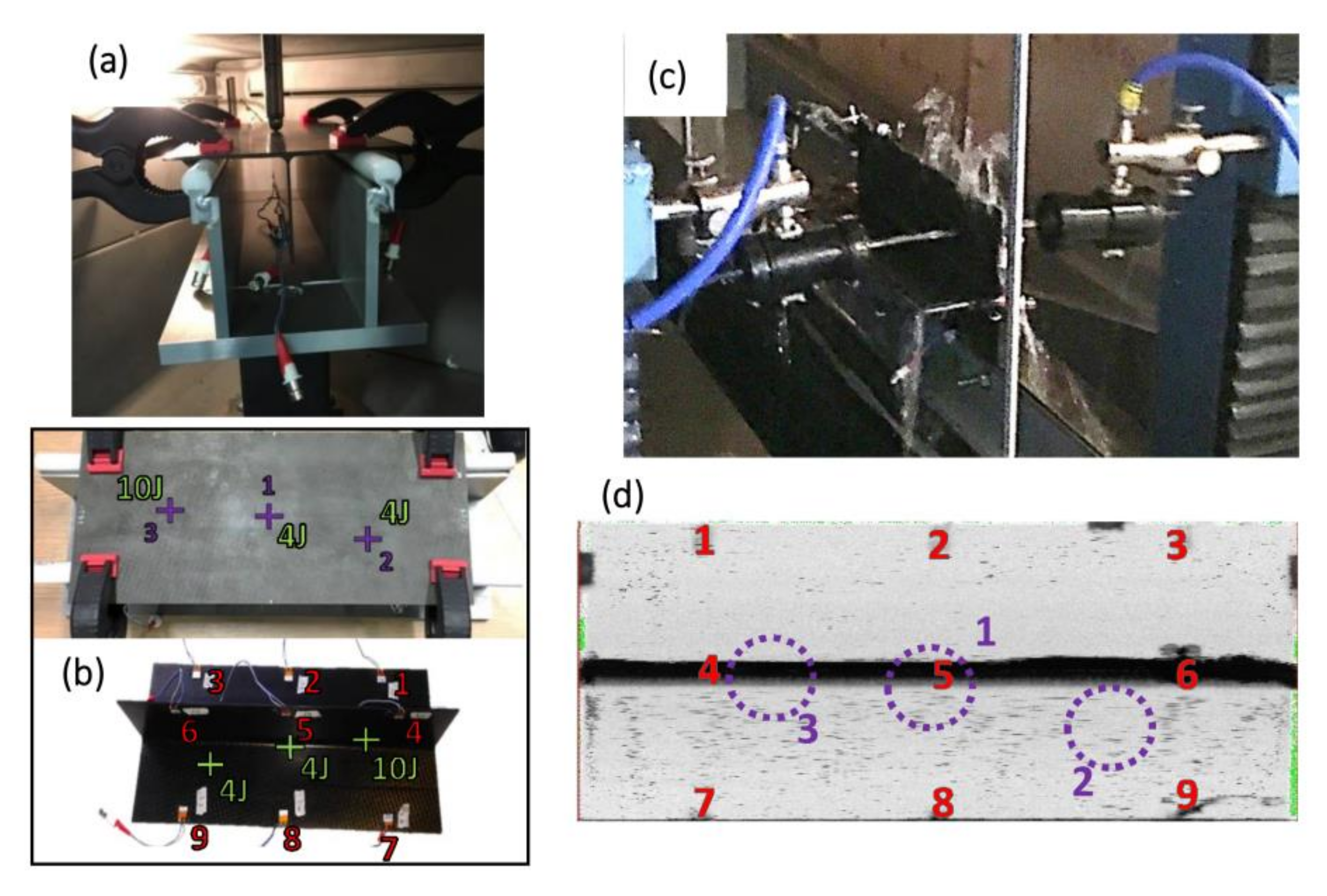
2.3. Guided Wave Experiments
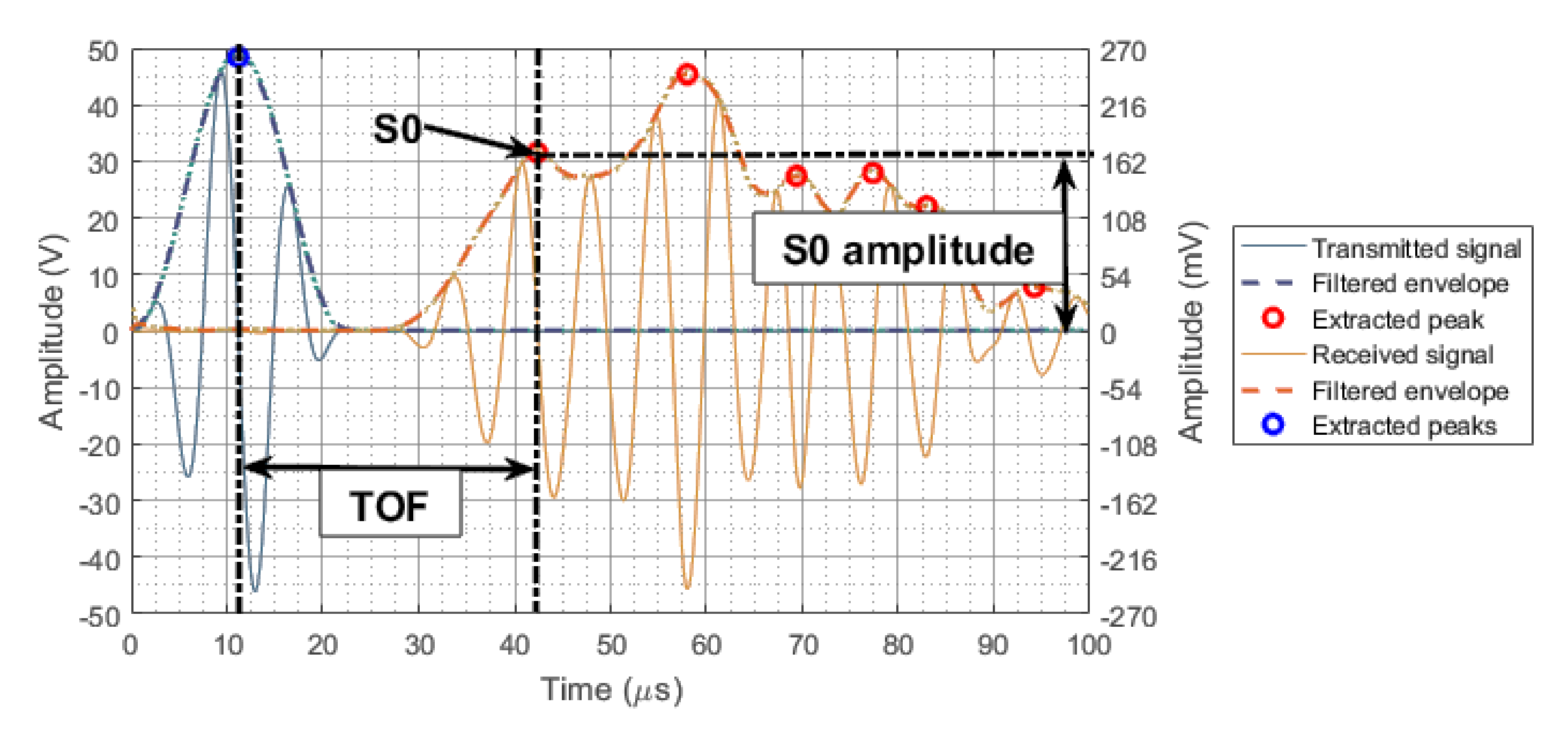
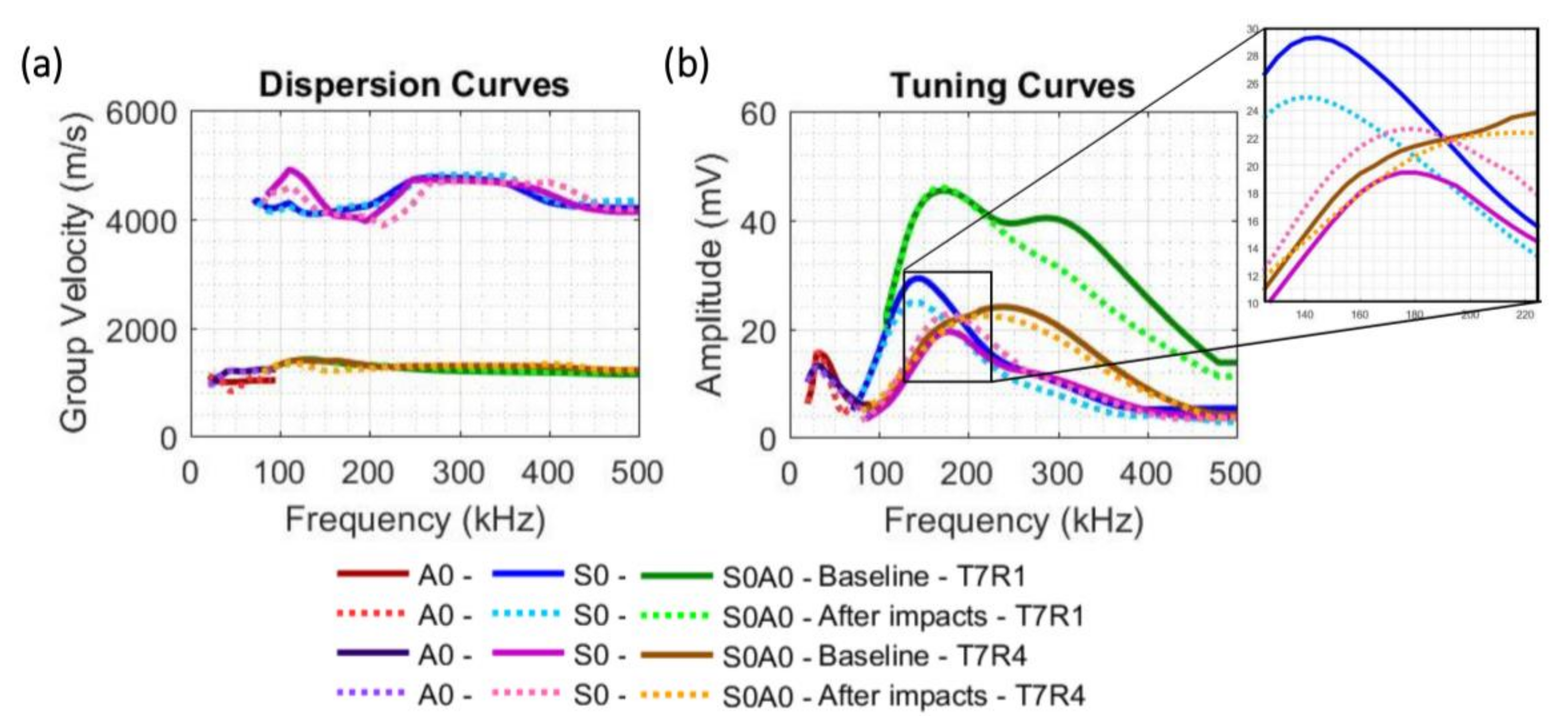
2.4. Dispersion and Tuning Curves Determination Method
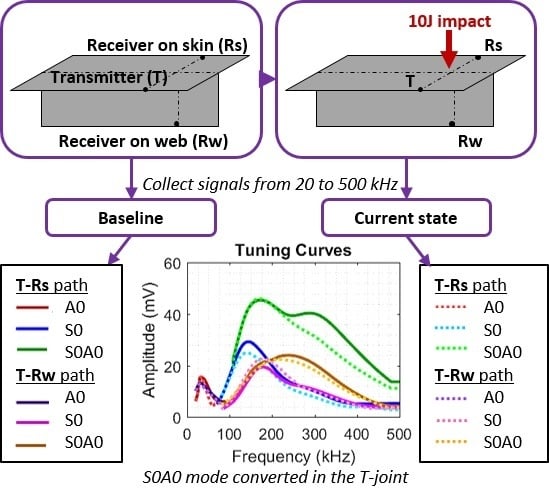
2.5. Impact Damage Initiation
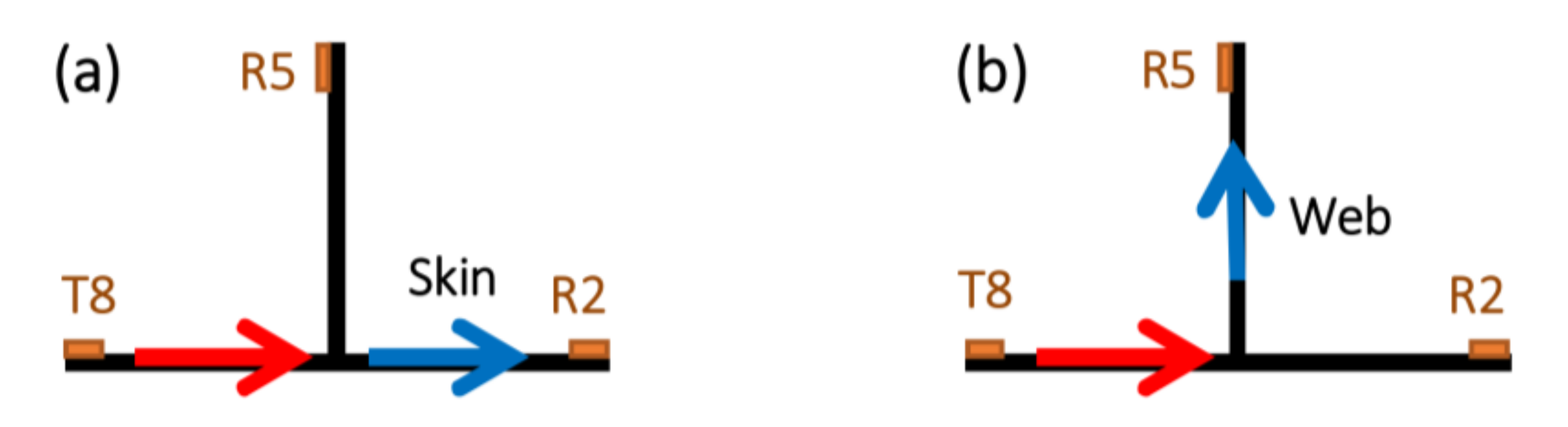
- A first impact of 4J has been introduced under the web in the middle of the T-joint, at location ‘1’ shown in Figure 5b, and guided waves signals have been collected afterwards. Some results of signal comparison between the pristine structure and after this 4J impact are presented in the following section.
- Then, two more impacts at different locations have been executed: an impact of 4J slightly offset from the web of the T-joint approximately between transducers ‘3’ and ‘9’ at location ‘2’ presented in Figure 5b and an impact of 10J under the web of the T-joint approximately between transducers ‘1’ and ‘7’ at location ‘3’ as shown in Figure 5b. Guided waves signals have been collected afterwards and some results of signal comparison between the pristine structure and after these three impacts are discussed in Section 3.
3. Results and Discussion
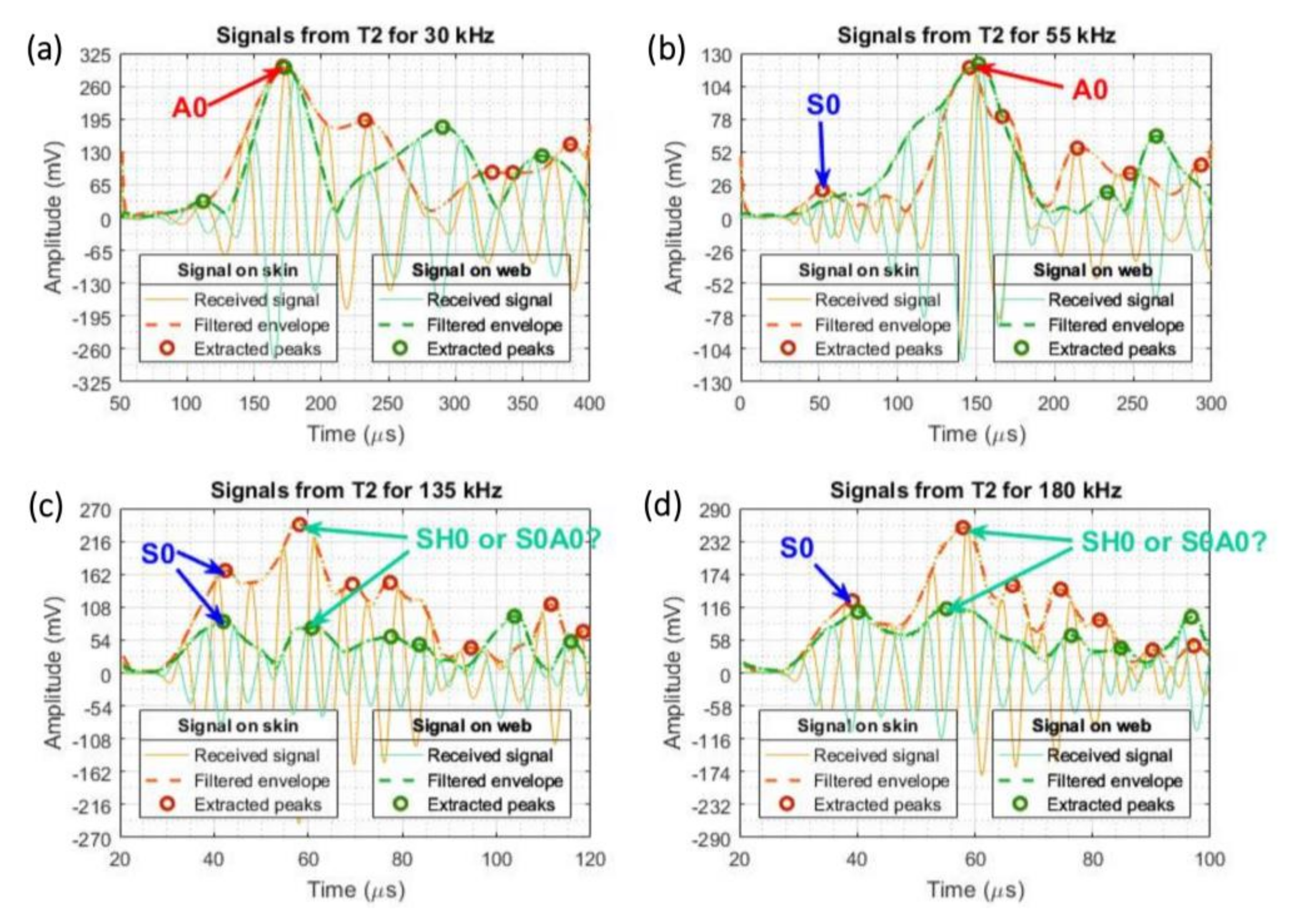
3.1. Identification of Lamb Waves Fundamental Modes
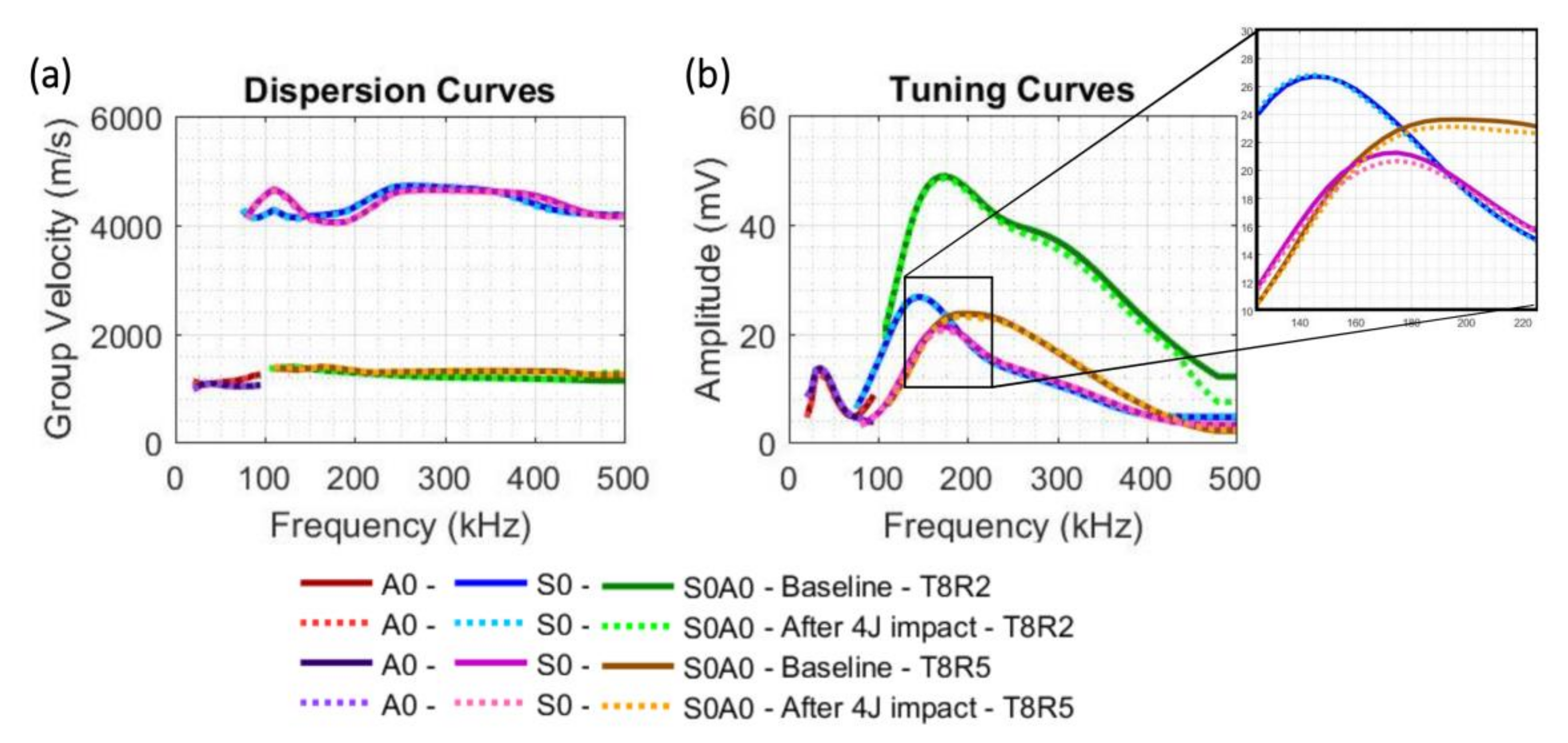
3.2. Dispersion and Tuning Curves
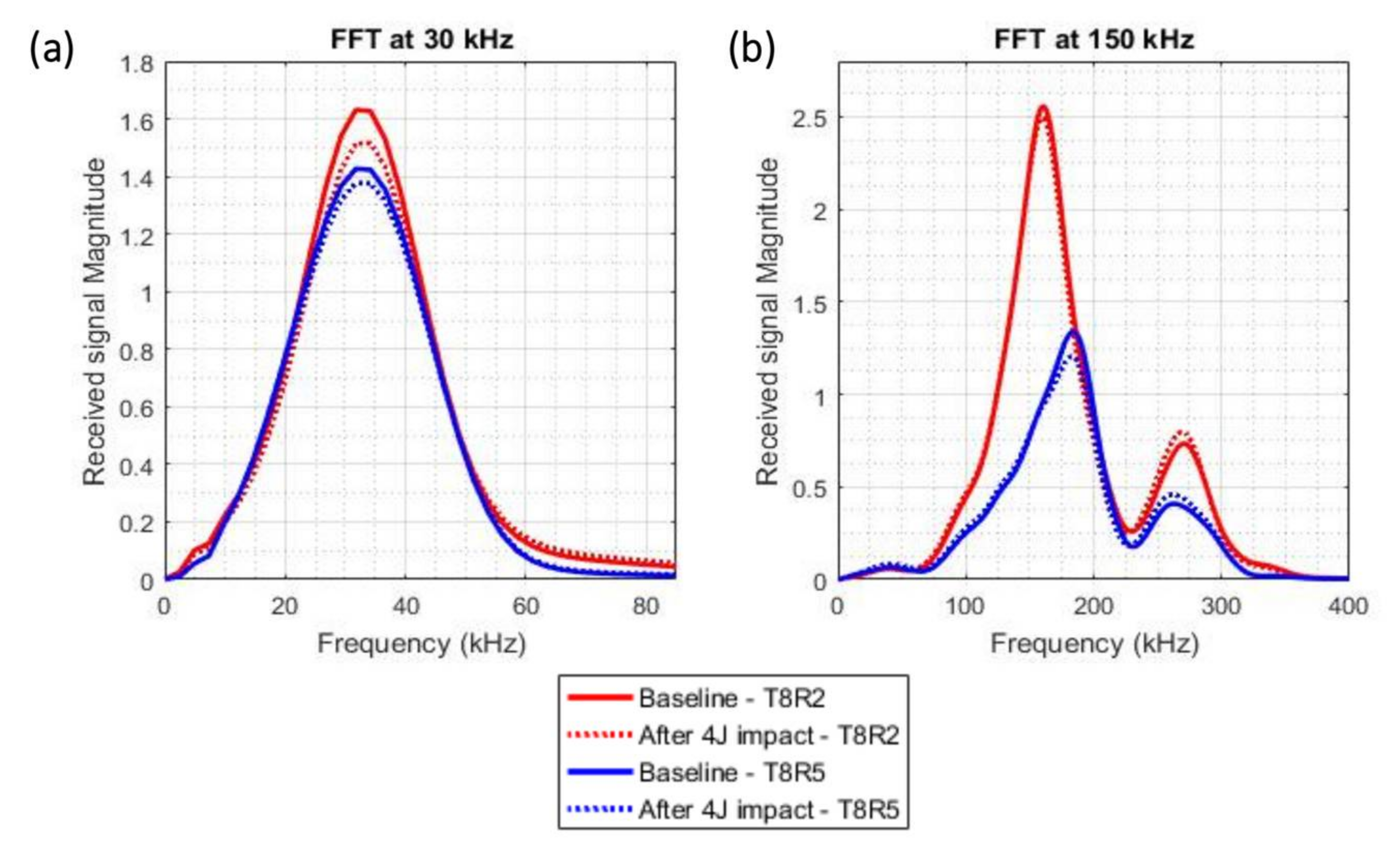
3.3. Signal Comparison between the Baseline and Signal Acquired after a 4J Impact
3.4. Signal Comparison between the Baseline and Signal Acquired after a 10J Impact
3.5. Discussion
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Giurgiutiu, V. Structural Health Monitoring of Aerospace Composites; Academic Press: Waltham, MA, USA, 2016; ISBN 9780124096059. [Google Scholar]
- Richardson, M.O.W.; Wisheart, M.J. Review of low-velocity impact properties of composite materials. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1123–1131. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L. Identification of Damage Using Lamb Waves: From Fundamentals to Applications; Springer Science & Business Media: Berlin, Germany, 2009; Volume 48, ISBN 9781848827837. [Google Scholar]
- Balageas, D.; Fritzen, C.; Güemes, A. Structual Health Monitoring; Wiley-ISTE: London, UK, 2006; ISBN 9781905209019. [Google Scholar]
- Gresil, M.; Giurgiutiu, V. Guided wave propagation in composite laminates using piezoelectric wafer active sensors. R. Soc. Aeronaut. J. 2013, 117, 971–995. [Google Scholar] [CrossRef]
- Diamanti, K.; Soutis, C. Structural health monitoring techniques for aircraft composite structures. Prog. Aerosp. Sci. 2010, 46, 342–352. [Google Scholar] [CrossRef]
- Rose, J.L.; Morrow, P. An Introduction to Ultrasonic Guided Waves. In Proceedings of the 4th Middle East NDT Conference and Exhibition, Manama, Kingdom of Bahrain, 2–5 December 2007. [Google Scholar]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Interaction of Lamb mode (Ao) with structural discontinuity and generation of “turning modes” in a T-joint. Ultrasonics 2011, 51, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Sizing of interface delamination in a composite T-joint using time-of-flight of Lamb Waves. J. Intell. Mater. Syst. Struct. 2011, 22, 757–768. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Barnard, D.; Dayal, V. Finite element simulation of core inspection in helicopter rotor blades using guided waves. Ultrasonics 2015, 62, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Soorgee, M.H. A mode conversion based feature for crack depth evaluation in homogenous plates based on 3D simulated Lamb waves. In Proceedings of the 3rd Iranian International NDT Conference, Tehran, Iran, 21–22 February 2016. [Google Scholar]
- Benmeddour, F.; Grondel, S.; Assaad, J.; Moulin, E. Study of the fundamental Lamb modes interaction with asymmetrical discontinuities. NDT E Int. 2008, 41, 330–340. [Google Scholar] [CrossRef]
- Quaegebeur, N.; Micheau, P.; Masson, P.; Maslouhi, A. Structural health monitoring strategy for detection of interlaminar delamination in composite plates. Smart Mater. Struct. 2010, 19, 085005. [Google Scholar] [CrossRef]
- Testoni, N.; de Marchi, L.; Marzani, A. Detection and characterization of delaminations in composite plates via air-coupled probes and warped-domain filtering. Compos. Struct. 2016, 153, 773–781. [Google Scholar] [CrossRef]
- Monaco, E.; Boffa, N.D.; Memmolo, V.; Ricci, F.; Testoni, N.; De Marchi, L.; Marzani, A.; Hettler, J.; Tabatabaeipour, M.; Delrue, S.; et al. Methodologies for Guided Wave-Based SHM System Implementation on Composite Wing Panels: Results and Perspectives from SARISTU Scenario 5. In Smart Intelligent Aircraft Structures (SARISTU); Springer: Cham, Switzerland, 2016; pp. 495–527. [Google Scholar]
- Janarthan, B.; Mitra, M.; Mujumdar, P.M. Damage detection in stiffened composite panels using Lamb wave. In Proceedings of the 6th European Workshop on Structural Health Monitoring (EWSHM 2012), Dresden, Germany, 3–6 July 2012; Volume 2, pp. 1033–1041. [Google Scholar]
- Gresil, M.; Giurgiutiu, V. Prediction of attenuated guided waves propagation in carbon fibre composites using Rayleigh damping model. J. Intell. Mater. Syst. Struct. 2015, 26, 2151–2169. [Google Scholar] [CrossRef]
- Lee, B.C.; Staszewski, W.J. Sensor location studies for damage detection with Lamb waves. Smart Mater. Struct. 2007, 16, 399–408. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]
- Kesavan, A.; Deivasigamani, M.; John, S.; Herszberg, I. Damage detection in T-joint composite structures. Compos. Struct. 2006, 75, 313–320. [Google Scholar] [CrossRef]
- Kesavan, A.; John, S.; Herszberg, I. Strain-based Structural Health Monitoring of Complex Composite Structures. Struct. Health Monit. 2008, 7, 203–213. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, D.; Wang, Y.; Rahim, G. In-service structural health monitoring of a full-scale composite horizontal tail. J. Wuhan Univ. Technol. Sci. Ed. 2015, 30, 1215–1224. [Google Scholar] [CrossRef]
- Ma, X.; Bian, K.; Lu, J.; Xiong, K. Experimental Research on Detection for Interface Debond of CFRP T-joints under Tensile Load. Compos. Struct. 2016, 158, 359–368. [Google Scholar] [CrossRef]
- Kapoor, H.; Soni, S.R. Experimental structural health monitoring of Z-fibre reinforced co-cured composite pi-joints using Lamb wave propagation. In Proceedings of the SPIE—Nondestructive Characterization for Composite Materials, Aerospace Engineering, Civil Infrastructure, and Homeland Security, San Diego, CA, USA, 8–12 March 2009; Volume 7294, pp. 1–9. [Google Scholar] [CrossRef]
- Kapoor, H.; Blackshire, J.L.; Soni, S.R. Damage detection in z-Fibre reinforced, co-cured composite Pi-Joint using pitch–catch ultrasonic analysis and scanning laser vibrometry. Struct. Longev. 2010, 3, 221–238. [Google Scholar]
- Swenson, E.D.; Soni, S.R.; Kapoor, H. Lamb wave propagation in Z-pin reinforced co-cured composite pi-joints. Proc. SPIE 2010, 7649, 76490D. [Google Scholar] [CrossRef]
- Geetha, G.K.; Mahapatra, D.R.; Gopalakrishnan, S.; Hanagud, S. Laser Doppler imaging of delamination in a composite T-joint with remotely located ultrasonic actuators. Compos. Struct. 2016, 147, 197–210. [Google Scholar] [CrossRef]
- Okabe, Y.; Fujibayashi, K.; Shimazaki, M.; Soejima, H.; Ogisu, T. Delamination detection in composite laminates using dispersion change based on mode conversion of Lamb waves. Smart Mater. Struct. 2010, 19, 115013. [Google Scholar] [CrossRef]
- LAMSS (Laboratory for Active Materials and Smart Structures) and University of South Carolina. SAFE_DISPERSION_GUI. 2014. Available online: http://www.me.sc.edu/research/lamss/html/software.html (accessed on 1 June 2017).
- Wang, X.; Lu, Y.; Tang, J. Damage detection using piezoelectric transducers and the Lamb wave approach: I. System analysis. Smart Mater. Struct. 2008, 17, 1–15. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. 2002, 11, 269–278. [Google Scholar] [CrossRef]
- Sherafat, M.H.; Guitel, R.; Quaegebeur, N.; Hubert, P.; Lessard, L.; Masson, P. Structural health monitoring of a composite skin-stringer assembly using within-the-bond strategy of guided wave propagation. Mater. Des. 2016, 90, 787–794. [Google Scholar] [CrossRef]
- Si, L.; Wang, Q. Rapid multi-damage identification for health monitoring of laminated composites using piezoelectric wafer sensor arrays. Sensors (Switzerland) 2016, 16, 638. [Google Scholar] [CrossRef] [PubMed]
- Kijanka, P.; Radecki, R.; Packo, P.; Staszewski, W.J.; Uhl, T. GPU-based local interaction simulation approach for simplified temperature effect modelling in Lamb wave propagation used for damage detection. Smart Mater. Struct. 2013, 22, 035014. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Philibert, M.; Soutis, C.; Gresil, M.; Yao, K. Damage Detection in a Composite T-Joint Using Guided Lamb Waves. Aerospace 2018, 5, 40. https://doi.org/10.3390/aerospace5020040
Philibert M, Soutis C, Gresil M, Yao K. Damage Detection in a Composite T-Joint Using Guided Lamb Waves. Aerospace. 2018; 5(2):40. https://doi.org/10.3390/aerospace5020040
Chicago/Turabian StylePhilibert, Marilyne, Constantinos Soutis, Matthieu Gresil, and Kui Yao. 2018. "Damage Detection in a Composite T-Joint Using Guided Lamb Waves" Aerospace 5, no. 2: 40. https://doi.org/10.3390/aerospace5020040