1. Introduction
Consider the well-known ARFIMA
model given by:
where
is a sequence of uncorrelated (not necessarily independent) random variables, such that
and
(stationary AR(
p)) and
(invertible MA(
q)) polynomials respectively.
This standard case of constant variance innovations has been considered in many traditional time series analysis with applications. However, in recent years, there has been a great number of developments based on time-dependent instantaneous innovation variance (or volatility) such that
In particular, the following cases have been considered:
- (i)
is a deterministic function of t or
- (ii)
follows the family of (G)ARCH process (see, [
1,
2]),
- (iii)
is another stochastic process.
These cases (i) to (iii) can be analysed with emphasis on different practical issues. However, in applications, we need additional assumptions on
, such as:
- (a)
to ensure Var() is finite, in (i)
- (b)
stationarity or stability of both and in (ii) and (iii)
Assumption (a) is imposed as it is natural to set bounds for the deterministic function
. In fact, Assumption (b) is required when
is a stochastic process. For case (i), the effect of non-stochastic and time-dependent instantaneous variance when
was studied by Niemi [
3] under the standard AR and MA regularity conditions on the zeros of
and
, respectively. In his work, Peiris [
4] argues that the results of Niemi [
3] can be extended to the ARFIMA family when
In (ii), it is known that
is strictly stationary if
is strictly stationary, and in particular,
is
-th order stationary if
is
-th order stationary. For the Integrated GARCH (IGARCH) model, Nelson [
5] and Bougerol and Picard [
6] have argued that IGARCH is strictly stationary under additional regularity conditions. For case (iii) with stochastic volatility, it is obvious that if
is
m-th order stationary, then
is
-th order stationary. Therefore, it can be argued that when
is a stationary stochastic process, the conditional likelihood estimation carried out by taking
cannot be significant since
is bounded. This would be useful in the estimation of parameters, especially in both cases (ii) and (iii). See the survey papers of McAleer [
7] and Shephard [
8] for the various extensions of (ii) and (iii).
An alternative way of modelling time-dependent volatilities has been extensively studied using ARMA models with time-dependent coefficients driven by constant variance innovations. See, for example, [
4,
9,
10,
11,
12,
13] and the references therein for details. However, this approach is not very attractive in applications, as it involves too many parameters to estimate.
Turning to applications in economic and financial time series, there are many popular directions of modelling and analysis of long-memory. Among others, the analysis of long-memory in inflation has been considered by Backus and Zin [
14], Hassler and Wolters [
15], Baillie, Chung and Tieslau [
16], and Caporale and Gil-Alana [
17]. In their paper, Delgado and Robinson [
18] considered a number of methods for the analysis of long-memory time series using ARFIMA. An alternative and a general approach is to use the ARFIMA family with conditional and stochastic volatility as considered by Baillie et al. [
19], Bollerslev and Mikkelsen [
20], Ling and Li [
21], Breidt et al. [
22], Deo and Hurvich [
23], and Bos et al. [
24]. In their recent paper, Bos et al. [
24] accommodate the stochastic volatility in ARFIMA modelling. Empirical evidence confirms that such models are very satisfactory in practice. Therefore, the aim of this paper is to extend the ARFIMA models with time-varying volatility to a general flexible class of time series models based on Gegenbauer polynomials together with the ARMA structure. The Gegenbauer ARMA (GARMA) model is a generalization of the ARFIMA model. Clearly, the former encompasses the latter as a special case. We will also extend the class of
k-factor Gegenbauer process following Woodward et al. [
25], Ferrara and Gueganand [
26], and Caporale and Gil-Alana [
17], by accommodating time-dependent volatility.
The organization of the paper is as follows.
Section 2 reviews the family of GARMA with constant variance (volatility).
Section 3 shows the existence and uniqueness of second-order solutions for the GARMA model with time-dependent volatility and develops new classes of GARMA-GARCH and GARMA-SV.
Section 4 presents the asymptotic results for the maximum likelihood estimator for the GARMA-GARCH model and reports a Monte Carlo likelihood method for estimating the GARMA-SV model.
Section 5 presents an illustrative example via simulation data, while
Section 6 demonstrate an empirical example using inflation data in France, Japan and the United States.
Section 7 gives concluding remarks.
2. Basic Results on GARMA with Constant Volatility
In this section, we review the family of GARMA processes with constant volatility. Based on the work of Gray et al. [
27] and Chung [
28], consider the family of time series generated by:
where the polynomials
and
are as defined before,
are real parameters and
is white noise with zero mean and variance
This process in (2) is known as Gegenbauer ARMA of order (
) or GARMA (
) and has the following properties:
The power spectrum is given by:
where
and
The process in (2) is stationary with long-memory when
and
or
and
The long-memory features are characterized by:
- –
hyperbolic decay of the autocorrelation function (ACF ) superimposed with a sinusoidal,
- –
unbounded spectrum at the Gegenbauer frequency,
In their recent papers, a modified class of generalized fractional processes has been studied by Shitan and Peiris [
29,
30].
Now, consider the following special case or the GARMA
process and its properties for later reference. That is, when
we have:
Suppose that the following regularity conditions are satisfied:
A Stationary Solution to GARMA Model
Under the regularity conditions in R1, there exists the Wold representation to (4) given by:
where
with
and the Gegenbauer coefficients
have the explicit representation:
such that
(
is the Gamma function; see [
31] for details). These coefficients
are recursively related by:
with initial values
and
An Invertible Solution to GARMA Model
Under the MA regularity conditions, there exists an invertible solution to (4) given by:
where
are obtained from (6) replacing
d by
with corresponding initial values.
The next section develops the class of GARMA() driven by time-dependent or stochastic innovations for later reference.
3. GARMA with Time-Dependent Innovations
Suppose that
in (4) is time-dependent. Consider the class of regular (in both AR and MA) GARMA(
) driven by time-dependent innovations satisfying:
where
is the time-dependent volatility.
Below, we establish the existence and uniqueness of second-order solutions to (4) with innovations in (8) under certain additional regularity conditions.
3.1. Unique Stable Solutions
We use the following general approach:
Let be a probability space, and let be the space of all real-valued random variables on with finite r-th order moments. Suppose that is sequence of random variables in and is the closed linear subspace of spanned by the elements Let be the closed linear subspace spanned by all of the elements by
In the case of
let
ξ and
ζ be any two random elements in
such that the inner product and the norm satisfy
respectively. It is easy to verify that
is a Hilbert space.
Intuitively, if the volatility process is stationary, it guarantees the existence of the second moment of , which enables us to establish the following two lemmas.
Lemma 1. Under the AR regularity conditions R1, if the innovation process is stationary, then the solution in (5) belongs to , i.e.,
Proof. Since the innovation process is stationary, is bounded. Hence the solution ☐
Lemma 2. Under the MA regularity conditions R2, if the innovation process is stationary, then an invertible solution to (7) belongs to or
The proof is similar to that of Lemma 1.
Lemma 3. Under the both AR and MA regularity conditions and stationarity of the innovation process, one has
The proof to this follows from Lemmas 1 and 2.
Next, we consider two special cases useful in applications.
3.2. Two Special Cases
Consider two popular cases where the innovations follow GARCH or SV processes.
3.2.1. GARMA(; u)-GARCH()
Suppose that
in (8) follows a GARCH(
) process, such that
where
r and
s are positive integers (both not simultaneously zero),
,
and
. It is well-known that an equivalent representation of the GARCH(
) process is:
where
and are serially uncorrelated with mean zero. Now, we state the following lemma:
Lemma 4. Let be generated by GARMA and follows (9).- (a)
If the AR regularity conditions and are satisfied, then is second-order stationary and
- (b)
If the MA regularity conditions are satisfied, then is invertible and
Proofs follow from Lemmas 1 and 2.
The next section develops the class of GARMA() driven by SV innovations or GARMA-SV.
3.2.2. GARMA()-SV
Suppose that
satisfies the following recursion
where
and
,
is a constant,
, and the disturbances
and
are mutually independent for all
t. Further assume that the roots of
and
lie outside the unit circle. Note that
measures the conditional volatility of the log-volatility.
Let
Then, it is known that there exists a sequence
, such that
with
Now, we have the following lemma:
Lemma 5. Under the AR regularity condition on the log-volatility process in (10) has uniquely determined solution, such thatwhere is the mean of the log-volatility process. It is clear from (11) that the log-volatility process
converges in the mean square to
κ and:
In their paper, Chesney and Scott [
32] have considered the case where
follows an AR(1) process, such that
where
is a positive constant, and
Lemma 6. The process in (12) is equivalent towhere , and . Note that Proof. Since we have Substituting for in (12) and noting that the lemma follows. ☐
Remark. Clearly, in (12) is not a martingale difference series, and hence, it is not useful in applications. However, this can be written as an ARMA(1,1) in the form:where and are given by This result can be extended to any general ARMA structure for the log-volatility process.
Lemma 7. Suppose that the SV process follows an ARMA() model as in (10). Then, the corresponding process satisfies and ARMA in the form:where and for with Proof. The proof follows from extending the approach in Lemma 6. ☐
Section 4 discusses the estimation of parameters.
4. Estimation of Parameters
This section discusses the estimation for the GARMA (p,d,q; u) model with time-dependent volatility. We divide the section into to two parts, namely, (i) the GARMA-GARCH and (ii) the GARMA-SV.
4.1. GARMA-GARCH Model
Suppose that
is generated by the GARMA (
p,
d,
q;
u)-GARCH(
r,
s) model (2), (8) and (9). Define
,
,
and
Let
, and let
be the true value of
in the interior of the compact set
Λ. The approximate log-likelihood function (excluding the constant) is given by
where
and
Assuming the initial values of are zero, an approximate maximum likelihood estimator of in Λ is obtained by maximizing the above function, which is asymptotically equivalent to the maximum likelihood (ML) estimator. For the case of a non-normal distribution, we can still use the same approach with the corresponding quasi-maximum likelihood (QML) estimator.
For the ARFIMA (
)-GARCH (
) model, Breidt et al. [
22] suggested the above approach. However, Ling and Li [
21] established the consistency and asymptotic normality of the corresponding ML estimator and showed that the information matrix is block-diagonal. Combining the results of Ling and Li [
21] and Chung [
28,
33], we can obtain the asymptotic results for the corresponding estimator of the GARMA-GARCH model.
Proposition 1. Let and be approximate ML estimators of u and based on a sample from a GARMA-GARCH model under the conditions in Lemma 4. Then, is asymptotically independent of and:where and and are two independent Brownian motions with mean zero and covarianceFurthermore,where is a random variable defined as As discussed in Chung [
28,
33], the convergence rates of
are faster than those of the remaining parameters. The off-diagonal blocks in the information matrix (with respect to the parameter
u and the remaining parameters) approach zero. Hence, the distribution of
is asymptotically independent of the remaining parameters.
Below, we report the asymptotic result of the remaining parameters.
Proposition 2. Based on the sample from the GARMA-GARCH model and under the conditions in Lemma 4, we havewhere and For the case of
u to be one, we can use the asymptotic result of Ling and Li [
21].
Following Gray et al. [
27] and Chung [
28], in practice, we use the grid search procedure for different value of
u over the range
to minimize the likelihood function. For selecting the order of the GARMA-GARCH model, we can use an information criterion, such as AIC and BIC. Furthermore, we can use the conventional
t test for the parameters except for
u. For testing the null hypothesis regarding
u, we can use the approach of Chung [
33] to obtain percentiles via simulations.
4.2. Estimation of GARMA-SV Model
Suppose that
are generated from the GARMA (
p,
d,
q;
u)-SV model (2), (8) with the SV structure
where
and
are independent.
From (18), we have and Further, Since is a latent process, the evaluation of the likelihood function requires integrating it with respect to .
As mentioned earlier, the evaluation of the likelihood function involves high-dimensional integration, which is difficult to calculate. Nevertheless, among others, Danielsson and Richard [
34], Shephard and Pitt [
35], Durbin and Koopman [
36,
37] and Liesenfeld and Richard [
38] suggested evaluating high-dimensional integrals using simulation methods and then maximizing the corresponding likelihood function. In this case, we use the Monte Carlo likelihood (MCL) estimator of Durbin and Koopman [
37]. In their recent paper, Bos et al. [
24] extended the MCL estimator for the estimation of parameters of ARFIMA-SV parameters. This approach creates a set of realized values for
by ‘importance sampling’. Conditional on
h and using the prediction error decomposition, it is clear that the density is given by:
where
is the one-step ahead prediction error,
is its variance and
h is from importance sampling.
From (19), we evaluate the simulated likelihood function based on the true density and the importance density using the results of Durbin and Koopman [
37]. We also extend the work of Bos et al. [
24], by replacing the autocovariance functions of the ARFIMA by those of the GARMA and use the results of McElroy and Holan [
39] to obtain the ML estimator. As a practical issue, we use the grid search procedure for different values of
u over the range
for minimizing the likelihood function.
Noting that
,
, we can consider that the information matrix of
has a block diagonal structure similar to the GARMA-GARCH case, where
. If the MCL approximates the true likelihood accurately, we can use the conventional
t test for the parameters except for
u. For testing the null hypothesis regarding
u, we can use the approach of Chung [
33] to obtain percentiles via simulations, based on Proposition 1. For this purpose, we need to replace
K in Proposition 1 with
, by noting
unlike the GARMA-GARCH process.
In the next section, we will investigate the finite sample properties of the MCL estimator. In selecting the order of the GARMA-SV model, we can use the MCL to calculate the information criterion, such as AIC and BIC.
It is worth mentioning a semi-parametric estimation procedure for the long-memory parameter under heteroskedasticity. See, for example, [
40]. For the GARMA-SV model, we extend this in two directions: one is to to replace the conditional heteroskedasticity by SV, and the other is to extend the ARFIMA to the GARMA. For the latter case regarding the GARMA process, Hidalgo and Soulier [
41] developed a log-periodogram regression estimator extending the work of Robinson and Henry [
40].
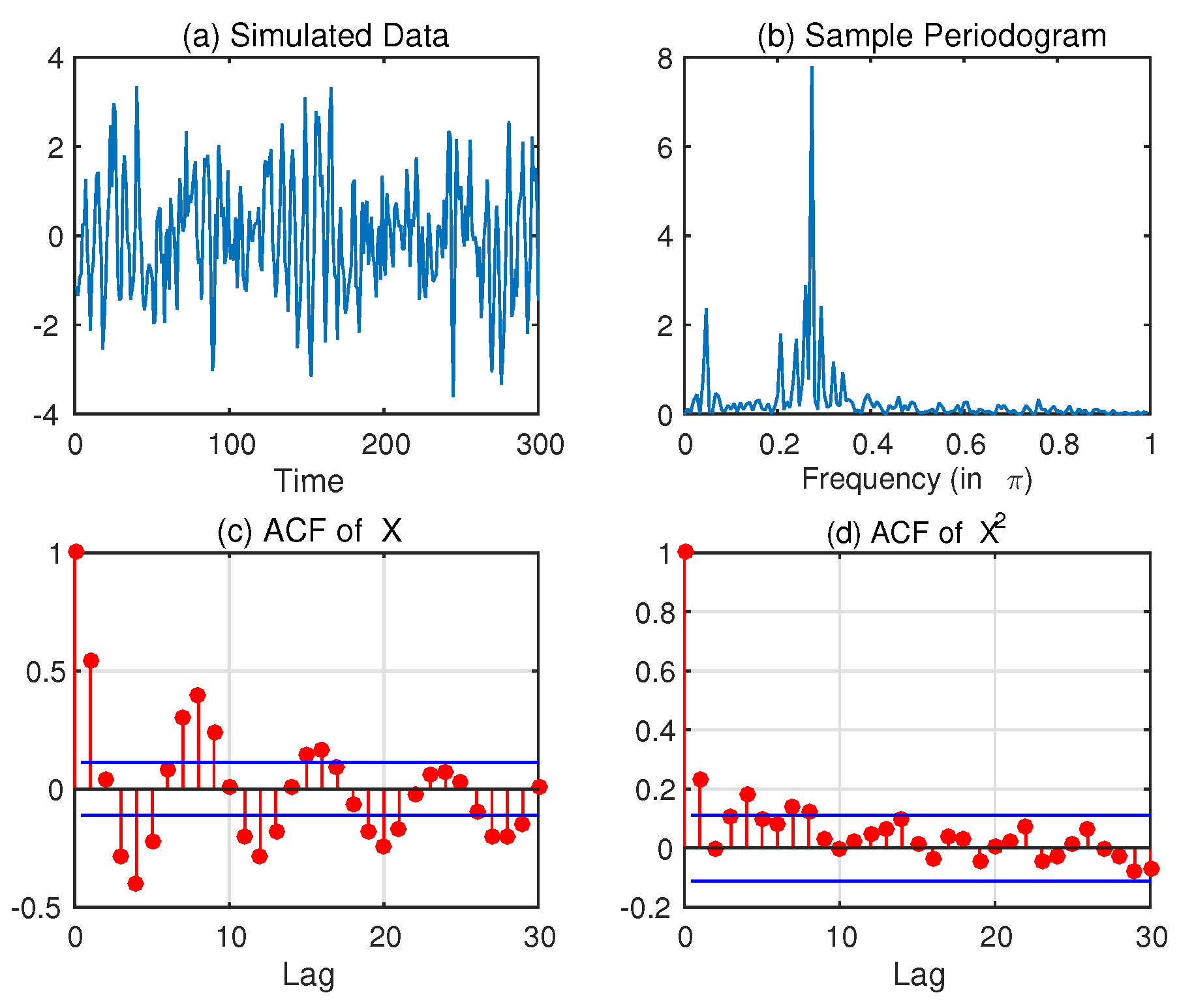
Now, look at a simulation study in order to illustrate certain properties of this GARMA-SV class.
6. Applications of GARMA-SV Models
We use the monthly consumer price index (CPI)
in three countries: France, Japan and the United States (U.S.) to illustrate the modelling described in this paper. The sample period starts from 1960M11 to 2015M11 in all three countries. The data source is the IMF’s International Financial Statistics published on the IMF web page. The CPIs are normalized at 100 for the year 2010. >From the price index series, we calculate the monthly inflation rates,
giving
observations. By removing the seasonal effects, regress the inflation rates on a series of monthly dummies
as
Define
, where
is the average of inflation rates and
is the residuals through the method of OLS.
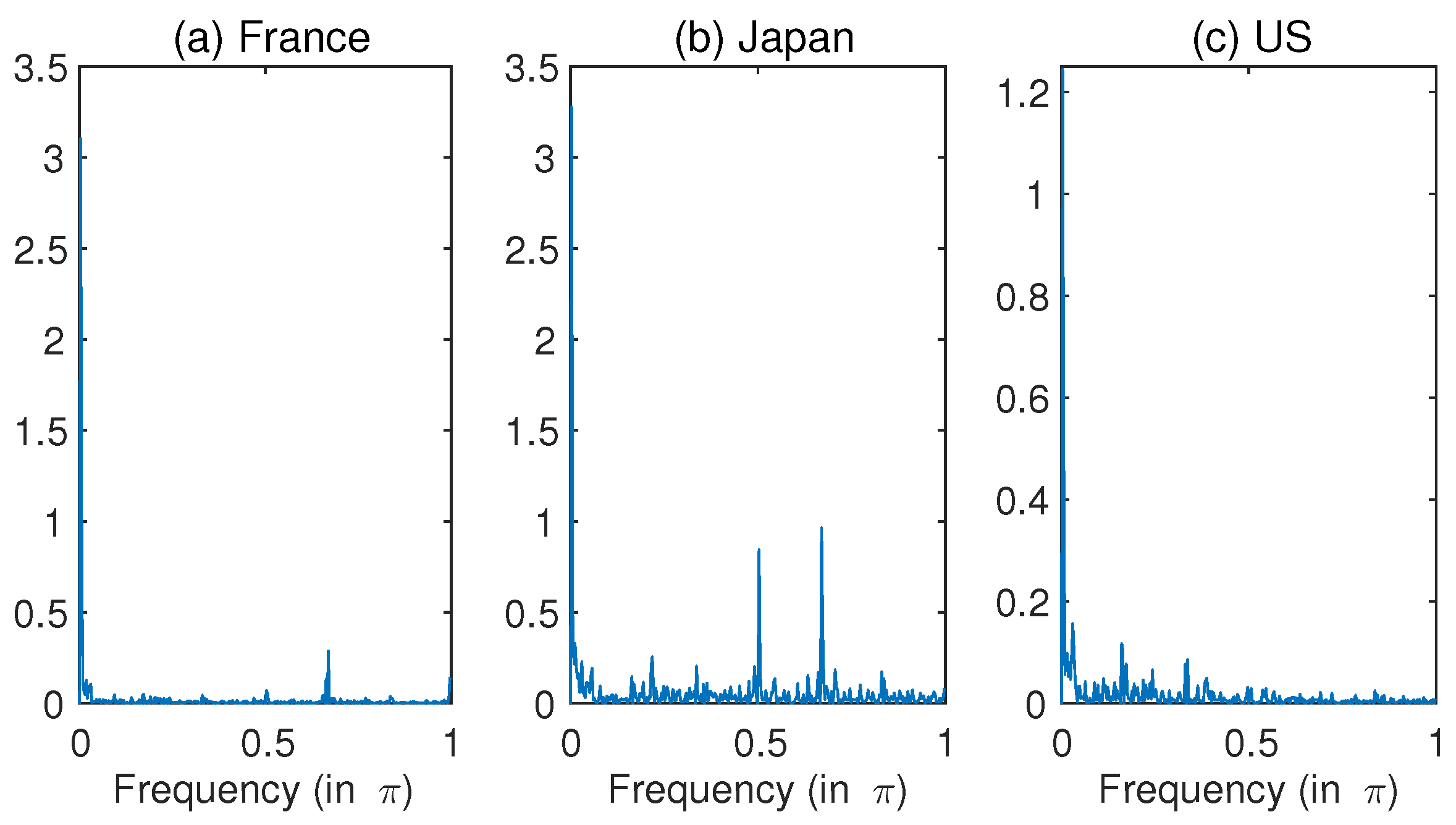
Table 2 shows the corresponding descriptive statistics. For seasonally-adjusted inflation rates,
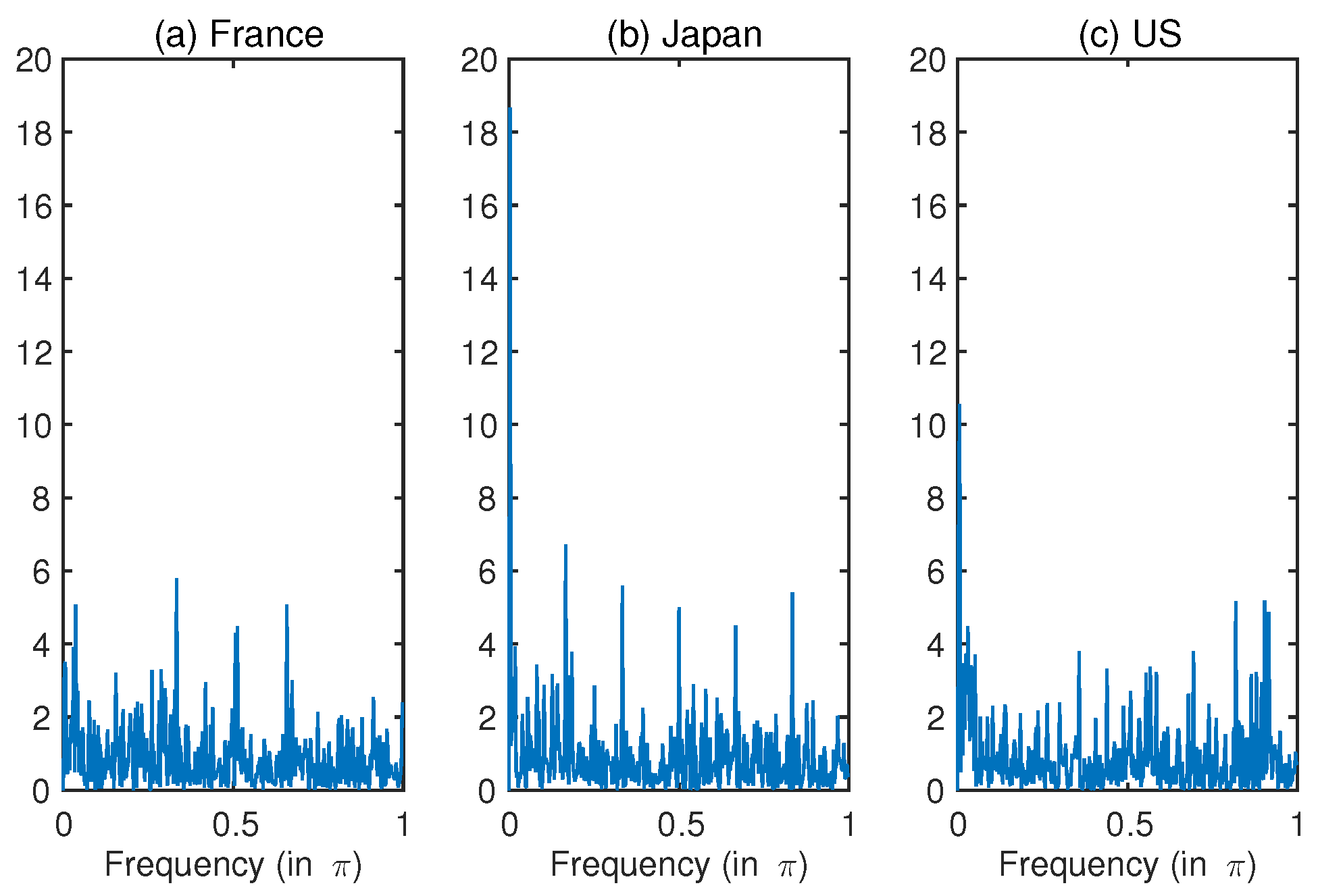
Figure 4 shows the estimated periodograms. As in
Figure 4, the highest peak is at
for all three countries. Apart from the pole, there are at least two small peaks. The second highest peak is at
for France and Japan, while the peak in the second mass is at
for the U.S. Although it is difficult to distinguish, the third highest peak for France is at
. Based on the ACF and spectral properties, we examine the reasons for these multiple peaks. The first candidate is time-dependent volatility as discussed in the previous section. The second one is the general GARMA process with multi-factors, and the third is a nested model of the multi-factor GARMA and the SV.
In this case, we estimate the three-factor GARMA-SV model given by:
based on (8) and (18) and using the MCL estimation technique. By the sample periodogram in
Figure 4, we expect that one of the three Gegenbauer frequencies is zero, corresponding to the highest peak at the point close to the origin. We do not report the higher orders of (
), as the estimates were insignificant (using the mean subtracted series following the recommendation of Chung [
28]). The estimates of
are located in (0.05, 0.2) and are significant at five percent, except for
for the U.S. series. For all three countries, the null hypothesis of
cannot be rejected. A positive value of
indicates that the Gegenbauer frequency is close to the origin, while a negative value implies that it is close to
π. Hence, the Gegenbauer frequency for U.S. data is close to the origin, while the estimates of (
) of the other two countries are close to
π. It is interesting to note that the estimates of
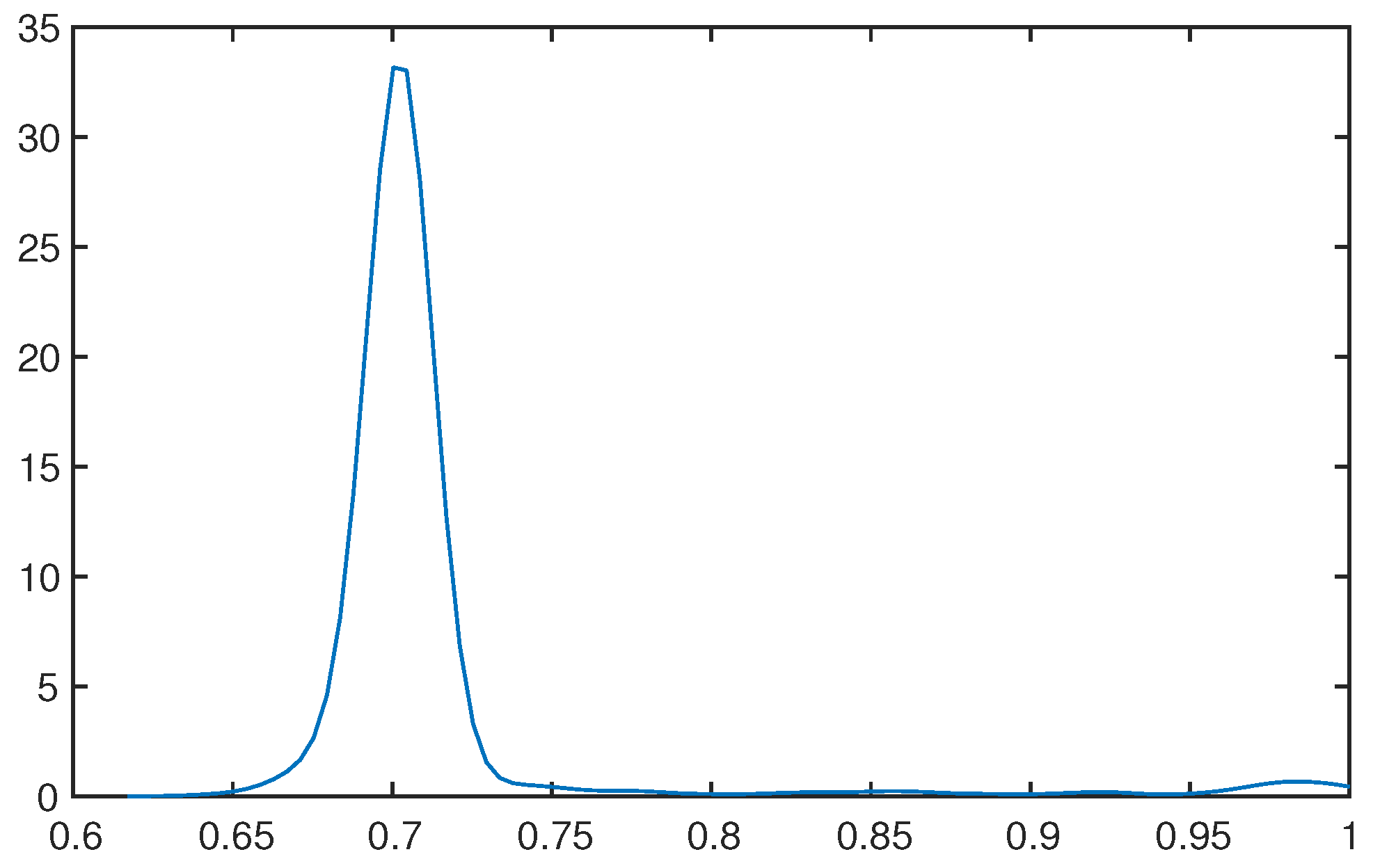
ρ are positive and significant, indicating the appropriateness of accommodating the time-dependent volatility structure in this multi-factor GARMA model. The empirical results support this three-factor GARMA-SV model for France and Japan, while the U.S. series favours the two-factor GARMA-SV model.
Since the estimates of
ρ are close to one for Japan and the U.S. series, we consider a GARMA model for the SV process,
. Using the MCL estimates from
Table 3, we obtain the residuals to satisfy
Now, we consider the interpretation of the parameter
. First of all, the behaviour of a periodic long-memory process is different from a periodic short memory process (for example, a seasonal ARMA). As shown by Chung [
28,
33], the
j-th autocovariance function for the GARMA process is approximated by
, where
K is a constant. Hence, the operator
produces a periodic long-memory with cycles of every
. For France, the values for
are 2.986 and 2.018, respectively. These results indicate that there are periodic long-range dependences with respect to every two and three months. The values of Japan are 2.986 and 3.976, implying the periodic long-memory with respect to every three and four months. For the U.S., the estimate for
is 5.946, producing the periodic long-memory with respect to every six months. As
is equal to one in three countries, there is no periodic long-memory for the first factor.
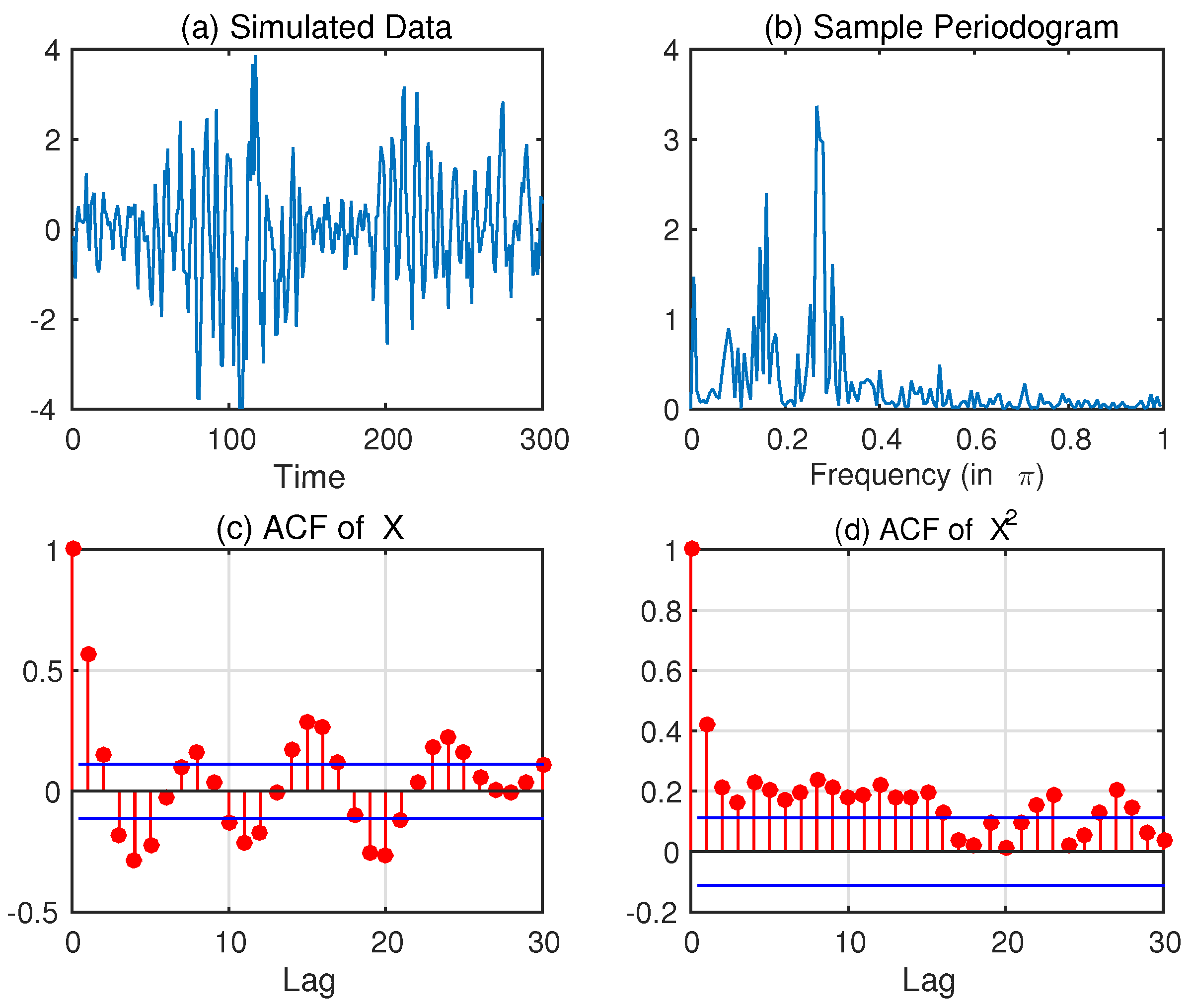
Figure 5 shows the periodograms for the log of the squared residuals,
, which can be considered as the proxy of log-volatility.
Figure 5 shows that there is a distinguished peak at zero frequency for the case of Japan and the U.S., implying that a short memory model model is adequate for France, while long-memory models are appropriate for the remaining two countries. Furthermore, Japan also has five other periodic peaks, implying a multiple periodic long-memory. For estimating the GARMA-SV model when
follows a GARMA model, the MCL technique requires a smoother simulation to be applied to the second GARMA process, which is an extension of the work of de Jong and Shephard [
43]. Another task is to reduce the computational time under the multiple grid-search method for finding optimal values of
’s in mean and volatility. We need to wait for further research for these problems.
In this section, we found that in addition to non-periodical long-range dependence, the empirical results indicate the existence of the periodic long memory under the time-dependent volatility.