A Method for Measuring Treatment Effects on the Treated without Randomization
Abstract
:1. Introduction
2. Modeling the Effect of a Treatment on the Treated in Non-Experimental Situations
2.1. Preparations
2.1.1. Notation
2.1.2. Potential Outcome Notation
2.1.3. Counterfactuals
2.1.4. Treatment Effects in a Pure Sense
2.1.5. The Purpose of the Paper
2.1.6. What is Causality?
- First, Basmann [11] (p. 99) revealed that common to all of the generally accepted meanings of “causality” is the notion that causality is a property of the real world and is not an algebraic property of the mathematical representations of parts of the real world. An insight that follows from this notion is that real-world relationships do not contain specification errors. This insight suggests that statistical causation requires deriving estimates within an environment free of specification errors. With regard to the definition of treatment effects, the notion requires that, to measure causal effects, we should calculate the difference between the real-world relations for the outcome of a treatment and the potential outcome of no treatment on the same individual. In what follows, we empirically implement this definition.
- Second, to show statistical causation, Skyrms [12] proved that positive statistical relevance needs to continue to hold when all relevant pre-existing conditions are controlled for. 11 Intuitively, the relevant pre-existing conditions can be thought of as all the factors that might affect a relationship but which cannot be captured (for example, omitted variables). For example, the typical empirical counterpart to household consumption function is derived from a utility function. We do not know how to measure the utility function, but it governs the actual structure of the consumption function. We control for such pre-existing conditions.
2.2. The Correctly Specified (or Misspecification-Free) Models of , , and
2.2.1. Mathematical Functions
2.2.2. Minimally Restricted Relations
2.2.3. Available Data for Estimation of (1)
2.2.4. Correctly Specified Models for and the Counterfactual for the Same Individual i
2.2.5. In What Way Are the Coefficients and Error Term of (5) Unique?
2.2.6. What Specification Errors is the TCE Free from?
2.2.7. Specification Errors and Omitted-Regressor Biases
2.2.8. The Available Data Are Not Adequate to Estimate TCE
2.3. Variable Coefficient Regression
2.3.1. Parameterization of the Variable Coefficient Regression
2.3.2. Identification of Model (14)
2.3.3. Identification of Model (12)
2.4. Estimation of Model (14) Under Assumptions I and II
2.5. Estimation of a Component of a Coefficient of (12) by Decomposition
2.5.1. Estimation of Treatment Effects
- Adopt a dynamic modelling approach of general to specific, nesting down from the large set of drivers to a parsimonious, smaller set.
- Adopt information criteria such as AIC, SBC, and pick the driver set which minimizes the criteria.
2.5.2. Some Intuition
2.5.3. Does Assumption III Make the Treatment Effect Theories Untestable?
2.5.4. The Number of Components of the Coefficients of (6)
2.5.5. Several Virtues of the Regressions in (12) and (13)
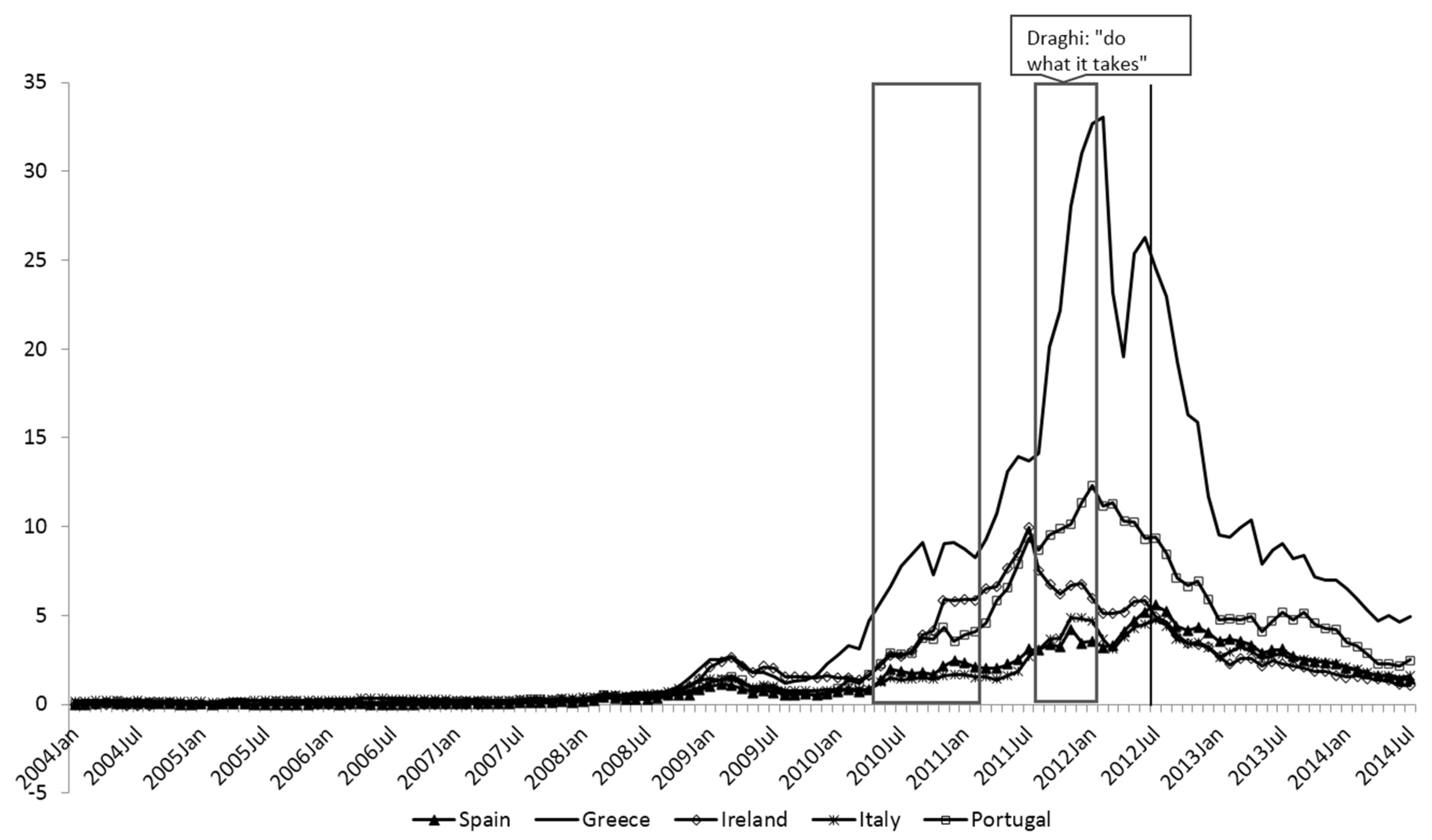
3. An Example Using the ECB’s Securities Market Program
Program Description
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix: Data Sources and Information
References
- W.H. Greene. Econometric Analysis, 7th ed. Upper Saddle River, NJ, USA: Pearson/Prentice Hall, 2012. [Google Scholar]
- J.M. Wooldridge. Introductory Econometrics: A Modern Approach. Mason, OH, USA: Thomson South-Western, 2013, pp. 438–443. [Google Scholar]
- P.W. Holland. “Statistics and Causal Inference.” J. Am. Stat. Assoc. 81 (1986): 945–960. [Google Scholar] [CrossRef]
- P.A.V.B. Swamy, J.S. Mehta, G.S. Tavlas, and S.G. Hall. “Small Area Estimation with Correctly Specified Linking Models.” In Recent Advances in Estimating Nonlinear Models With Applications in Economics and Finance. Edited by J. Ma and M. Wohar. New York, NY, USA: Springer, 2014. [Google Scholar]
- P.A.V.B. Swamy, J.S. Mehta, G.S. Tavlas, and S.G. Hall. “Two Applications of the Random Coefficient Procedure: Correcting for misspecifications in a small-area level model and resolving Simpson’s Paradox.” Econ. Model. 45 (2015): 93–98. [Google Scholar] [CrossRef]
- P.A.V.B. Swamy, G.S. Tavlas, and S.G. Hall. “On the Interpretation of Instrumental Variables in the Presence of Specification Errors.” Econometrics 3 (2015): 55–64. [Google Scholar] [CrossRef]
- J.W. Pratt, and R. Schlaifer. “On the Interpretation and Observation of Laws.” J. Econom. Ann. 39 (1988): 23–52. [Google Scholar] [CrossRef]
- D. Rubin. “Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies.” J. Educ. Psychol. 55 (1974): 688–701. [Google Scholar] [CrossRef]
- D. Rubin. “Bayesian Inference for Causal Effects.” Ann. Stat. 6 (1978): 34–58. [Google Scholar] [CrossRef]
- J. Pearl. “An Introduction to Causal Inference.” Int. J. Biostat. 6 (2010): 1–59. [Google Scholar] [CrossRef] [PubMed]
- R.L. Basmann. “Causality Tests and Observationally Equivalent Representations of Econometric Models.” J. Econom. 39 (1988): 69–104. [Google Scholar] [CrossRef]
- B. Skyrms. “Probability and Causation.” J. Econom. Ann. 39 (1988): 53–68. [Google Scholar] [CrossRef]
- A. Zellner. “Causality and Econometrics.” In Three Aspects of Policy and Policymaking. Edited by K. Brunner and A.H. Meltzer. Amsterdam, The Netherlands: North-Holland Publishing Company, 1979, pp. 9–54. [Google Scholar]
- J. Pearl. Causality: Models, Reasoning, and Inference. New York, NY, USA: Cambridge University Press, 2000. [Google Scholar]
- A.S. Goldberger. Functional Form and Utility: A Review of Consumer Demand Theory. Boulder, CO, USA: Westview Press, 1987. [Google Scholar]
- J.J. Heckman, and D. Schmierer. “Tests of Hypotheses Arising in the Correlated Random Coefficient Model.” Econ. Model. 27 (2010): 1355–1367. [Google Scholar] [CrossRef] [PubMed]
- A. Yatchew, and Z. Griliches. “Specification Error in Probit Models.” Rev. Econ. Stat. 66 (1984): 134–139. [Google Scholar] [CrossRef]
- C.R. Rao. Linear Statistical Inference and Its Applications, 2nd ed. New York, NY, USA: John Wiley & Sons, 1973. [Google Scholar]
- I. Chang, C. Hallahan, and P.A.V.B. Swamy. “Efficient Computation of Stochastic Coefficients Models.” In Computational Economics and Econometrics. Boston, MA, USA: Kluwer Academic Publishers, 1992, pp. 43–53. [Google Scholar]
- I. Chang, P.A.V.B. Swamy, C. Hallahan, and G.S. Tavlas. “A Computational Approach to Finding Causal Economic Laws.” Comput. Econ. 16 (2000): 105–136. [Google Scholar] [CrossRef]
- P.A.V.B. Swamy, G.S. Tavlas, S.G.F. Hall, and G. Hondroyiannis. “Estimation of Parameters in the Presence of Model Misspecification and Measurement Error.” Stud. Nonlinear Dyn. Econom. 14 (2010): 1–33. [Google Scholar] [CrossRef]
- S.G. Hall, G.S. Tavlas, and P.A.V.B. Swamy. “Time Varying Coefficient Models; A Proposal for Selecting the Coefficient Driver Sets.” Macroecon. Dyn., 2016. forthcoming. [Google Scholar] [CrossRef]
- S.G. Hall, P.A.V.B. Swamy, G. Tavlas, (Bank of Greece), and M.G. Tsionas. “Performance of the time-varying parameters model.” Unpublished work. 2016. [Google Scholar]
- E. George, D. Sun, and S. Ni. “Bayesian stochastic search for VAR model restrictions.” J. Econom. 142 (2008): 553–580. [Google Scholar] [CrossRef]
- M. Jochmann, G. Koop, and R.W. Strachan. “Bayesian forecasting using stochastic search variable selection in a VAR subject to breaks.” Int. J. Forecast. 26 (2010): 326–347. [Google Scholar] [CrossRef]
- P.A.V.B. Swamy, and J.S. Mehta. “Bayesian and non-Bayesian Analysis of Switching Regressions and a Random Coefficient Regression Model.” J. Am. Stat. Assoc. 70 (1975): 593–602. [Google Scholar]
- C.W.J. Granger. “Non-linear Models: Where Do We Go Next—Time Varying Parameter Models.” Stud. Nonlinear Dyn. Econom. 12 (2008): 1–10. [Google Scholar] [CrossRef]
- P. Cour-Thimann, and B. Winkler. The ECB’s Non-Standard Monetary Policy Measures: The Role of Institutional Factors and Financial Structure. Working Paper Series 1528; Frankfurt am Main, Germany: European Central Bank, 2013. [Google Scholar]
- M. De Pooter, R.F. Martin, and S. Pruitt. The Liquidity Effects of Official Bond Market Intervention. International Finance Discussion Papers; Washington, DC, USA: Board of Governors of the Federal Reserve System, 2015. [Google Scholar]
- F. Eser, and B. Schwaab. Assessing Asset Purchases within the ECB’s Securities Markets Programme. ECB Working Paper No. 1587; Frankfurt, Germany: European Central Bank, 2013. [Google Scholar]
- E. Ghysels, J. Idier, S. Manganelli, and O. Vergote. A High Frequency Assessment of the ECB Securities Markets Programme. ECB Working Paper, No. 1642; Frankfurt, Germany: European Central Bank, 2014. [Google Scholar]
- M. Draghi. “Speech by the President of the European Central Bank at the Global Investment Conference in London.” 26 July 2012. Available online: https://www.ecb.europa.eu/press/key/date/2012/html/sp120726.en.html (accessed on 22 January 2016).
- 2See Holland [3].
- 3For a short discussion on these issues, see Greene [1] (pp. 893–895).
- 4As we explain below, the coefficients and error term of a linear-in-variables and nonlinear-in-coefficients model are unique in the sense that they are invariant under the addition and subtraction of the coefficient of an omitted regressor times any included regressor on its right-hand side. Swamy, Mehta, Tavlas and Hall [4,5] showed that models with nonunique coefficients and error terms are misspecified.
- 5This is what Greene [1] (pp. 888–889) calls “the treatment effect in a pure sense.”
- 6See, for example, Swamy, Tavlas and Hall [6].
- 7Most empirical studies use a treatment dummy to derive the impact of the treatment; the dummy variable takes the value 1 for the treated individuals and 0 for the untreated individuals.
- 9Greene [1] (p. 888) pointed out that “The natural, ultimate objective of an analysis of a “treatment” or intervention would be the effect of treatment on the treated.”
- 10Greene [1] (p. 894) pointed out that the desired quantity is not necessarily the ATE, but ATET.
- 11Skyrms distinguished among different types of causation such as deterministic, probabilistic, and statistical. He argued that the answers to questions of probabilistic causation given by different statisticians depended on their conceptions of probability. Three major concepts of probability are: rational degree of belief, limiting relative frequency, and propensity or chance. Skyrms [12] (p. 59) recognized that not all would agree with the subjectivistic gloss he put on the causal approaches of Reichenbach, Granger, Suppes, Salman, Cartwright and others. As Skyrms pointed out, “statistical causation is positive statistical relevance which does not disappear when we control for all relevant pre-existing conditions.” We consider this definition of statistical causation here. Skyrms further clarified that “Within the Bayesian framework … “controlling for all relevant pre-existing conditions” comes to much the same as identifying the appropriate partition … which together with the presence or absence of the putative cause (or value of the causal variable) determines the chance of the effect.”
- 12The list of these misspecifications is given in Section 2.2.6 below.
- 13In his causal analyses, Pearl [14] used the Bayesian interpretation of probability in terms of degrees of belief about events, recursive models, and in many cases finitely additive probability functions. Pearl’s [14] (p. 176) Bayesian view of causality is that “[i]f something is real, then it cannot be causal because causality is a mental construct that is not well defined.” This view is not consistent with Basmann’s [11] view, which is also the view that we adopt in this paper.
- 14The principle of causal invariance (Basmann [11] (p. 73)): Causal relations and orderings are unique in the real world and they remain invariant with mere changes in the language we use to describe them. Examples of models that do not satisfy this principle are those that are built using stationarity producing transformations of observable variables (see Basmann [11] (p. 98)). A related principle is that causes must precede their effects in time. Pratt and Schlaifer [7] (pp. 24–25) pointed out an interesting exception to this principle which is: “Whether or not a cause must precede its effect, engineers who design machines that really work in the real world will continue to base their designs on a law which asserts that acceleration at time t is proportional to force at that same time t.” The reason why we consider real-world (misspecification-free) relationships is that they satisfy the principle of causal invariance. They do not disappear when we control for all relevant pre-existing conditions, see Skyrms [12] (p. 59). We build misspecification-free models with these properties. If we do not estimate − from the misspecification-free relations of and , then according to Basmann [11], our estimate of the treatment effect − will not be an estimate of the causal effect of a treatment on the treated ith individual.
- 15We do not treat measurement errors as random variables until we make some stochastic assumptions about them.
- 16The reason for assigning this label to them is that they are included as regressors in our regressions below.
- 17Data on are not available in some experiments like medical experiments. In these cases, what all we know is whether an individual is treated or not (see Greene [1] (pp. 893–894)). In these cases it is possible to obtain analytical expressions but not numerical measures for the treatment effects.
- 18The reason why we attach this label to them is that they are actually omitted from our regressions below.
- 19Unobserved treatment variable: In the absence of data on , the coefficient of a dummy variable is used to measure treatment effects, as in the Heckman and Schmierer’s (HS) [16] model. Greene [1] (pp. 251–254, 893) elaborated on this practice by commenting that though a treatment can be represented by a dummy variable, measurement of its effect cannot be done with multiple linear regression
- 20One result that can be derived from (6)–(9) is the following: Consider two competing models of the same dependent variable with unique coefficients and error terms. Let each of these models be written in the form of (6) and let some continuous regressors be common to these two models. Of the pair of coefficients on a common regressor in the two models, the one with smaller magnitudes of omitted-regressor and measurement-error biases will be closer to the common true partial derivative component of the pair. This correct conclusion could not be drawn from the J test of two separate families of hypotheses on a misspecified model (see Greene [1] (p. 136)).
- 21A proof of this statement follows from Pratt and Schlaifer’s [7] (p. 34) statement that “… some econometricians require that … (the included regressors) be independent of ‘the’ excluded variables themselves. We shall show … that this condition is meaningless unless the definite article is deleted and can then be satisfied only for certain “sufficient sets” of excluded variables …”
- 22A proof of this statement is given in Swamy et al. [4] (pp. 217–219).
- 23We call the coefficients of (12) “the random coefficients” but not “random parameters.” The reason is that there are only coefficients and no parameters in (12). We call the coefficients of (13) “the fixed parameters” to distinguish them from those of the fixed-coefficient versions of (12). We do not use the word “random parameters,” since it creates confusion between (12) and its fixed coefficient versions.
- 24The definition of coefficient drivers differs from the definition of instrumental variables. The latter variables do not explain variations in the coefficients of (12) as do coefficient drivers. The coefficient for any regressor in (12) is partly dependent on the coefficient drivers in (13). In instrumental variable estimation, first, the instrumental variables are used to transform both the dependent variable and the explanatory variables and then the transformed variables are used to estimate the coefficients to the regressors.
- 25The functional form of (13) is different from that of (8) or of (7) and (9). We will correct this mistake in Equation (21) below.
- 26A similar admissibility condition for covariates is given in Pearl [14] (p. 79). Pearl [14] (p. 99) also gives an equation that forms a connection between the opaque English phrase “the value that the coefficient vector of (12) would take in unit i, had = ( been = ” and the physical processes that transfer changes in into changes in .
- 27A clarification is called for here. In (12), the number of the vectors of K + 2 coefficients increases with the number of individuals in the cross-sectional sample. So many coefficients are clearly not consistently estimable. However, in (14) below, the number of unknown coefficients () is only (K + 2) × ( + 1). This number does not increase with . So, the trick that makes our estimation procedure yield a consistent estimator of is to include the same set of coefficient drivers across all the coefficient equations in (13) and impose appropriate zero restrictions on the elements of if different sets of coefficient drivers are needed to estimate different components of the coefficients of (12).
- 28Any variables that are highly correlated with will also be correlated with both the regression part, , and the random part, , of the dependent variable, , of Equation (14). Furthermore, this equation is the end result of the sequence of Equations (1)–(6), and (13) that is used to avoid specification errors (i)–(iv) of Section 2.2.6. These two sentences together prove that the avoidance of specification errors (i)–(iv) leads to the nonexistence of instrumental variables. There is no contradiction between this result and Heckman and Schmierer’s [16] (p. 1356) instrumental variables approach because in this paper, no use is made of their threshold crossing model which assumes separability between observables Z that affect choice and an unobservable V. Their instrumental variable is a function of Z.
- 30We consider below the cases where these quantities are unknown.
- 31Swamy and Mehta [26] originated the theorem stating that any nonlinear functional form can be exactly represented by a model that is linear in variables, but that has varying coefficients. The implication of this result is that, even if we do not know the correct functional form of a relationship, we can always represent this relationship as a varying-coefficient relationship and thus estimate it. Granger [27] subsequently confirmed this theorem.
- 32This bias depends on a linear specification. It also depends on a non-zero correlation between the omitted regressor and the included regressors.
- 33Asset purchase programs were a part of the ECB’s overall response to the two crises. For detailed review of the ECB’s responses, see Cour-Thimann and Winkler [28].
- 34We start our estimation well before the beginning of the SMP program as we believe the longer sample period is helpful in determining the other parameters of the model and hence gives us a more accurate set of parameters to remove the omitted variable bias. We choose to use monthly data as most of the fundamental driver variables are only available at a monthly frequency.
- 35NEWS is calculated from updates to forecasts of the general government balance found in the EC’s spring and autumn forecasts.
- 36It is difficult to make a comparison with the results of De Pooter, Martin and Pruitt [29] because they define their SMP variable as a percentage of outstanding debt rather than the absolute value of purchases. As far as we can discern, their result seems to yield a similar order of magnitude to our measure.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swamy, P.A.V.B.; Hall, S.G.; Tavlas, G.S.; Chang, I.-L.; Gibson, H.D.; Greene, W.H.; Mehta, J.S. A Method for Measuring Treatment Effects on the Treated without Randomization. Econometrics 2016, 4, 19. https://doi.org/10.3390/econometrics4020019
Swamy PAVB, Hall SG, Tavlas GS, Chang I-L, Gibson HD, Greene WH, Mehta JS. A Method for Measuring Treatment Effects on the Treated without Randomization. Econometrics. 2016; 4(2):19. https://doi.org/10.3390/econometrics4020019
Chicago/Turabian StyleSwamy, P.A.V.B., Stephen G. Hall, George S. Tavlas, I-Lok Chang, Heather D. Gibson, William H. Greene, and Jatinder S. Mehta. 2016. "A Method for Measuring Treatment Effects on the Treated without Randomization" Econometrics 4, no. 2: 19. https://doi.org/10.3390/econometrics4020019





