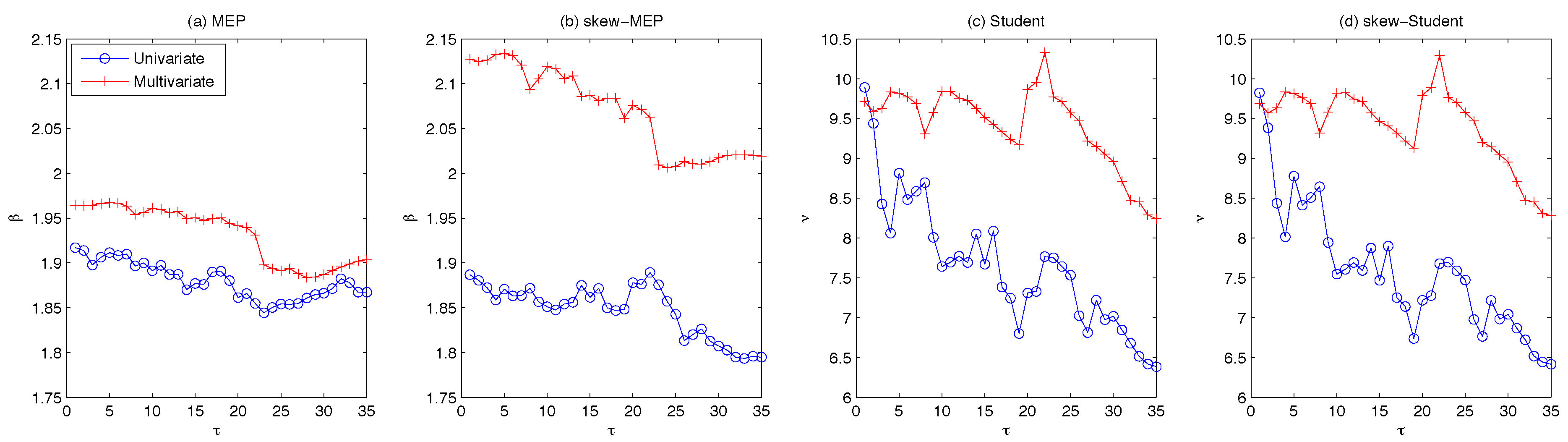
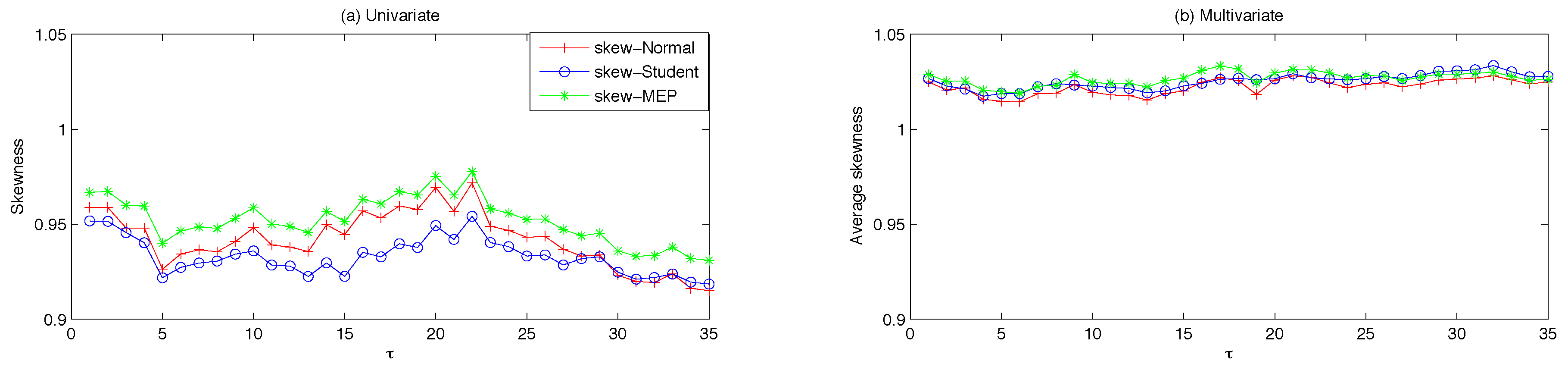
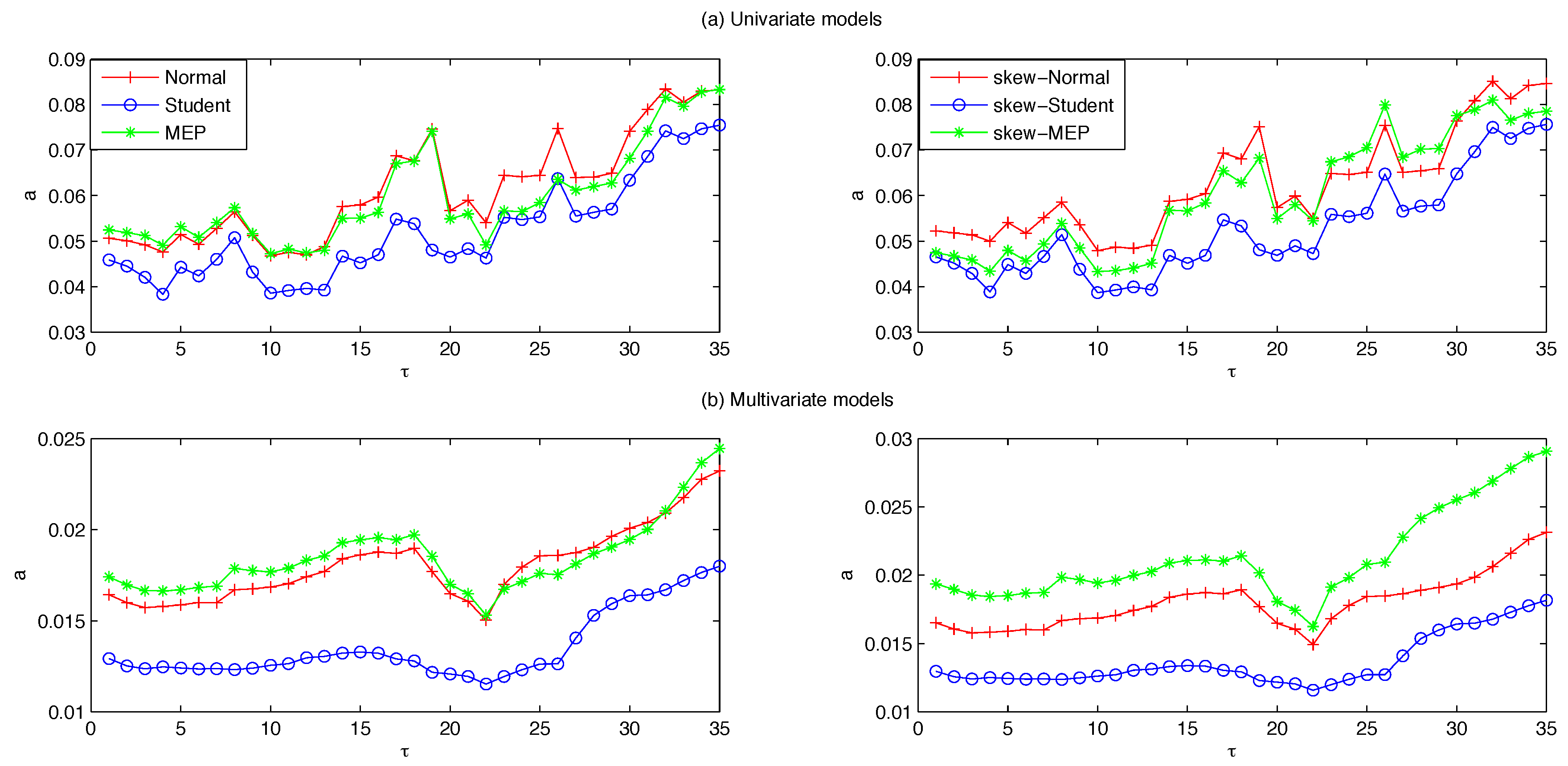
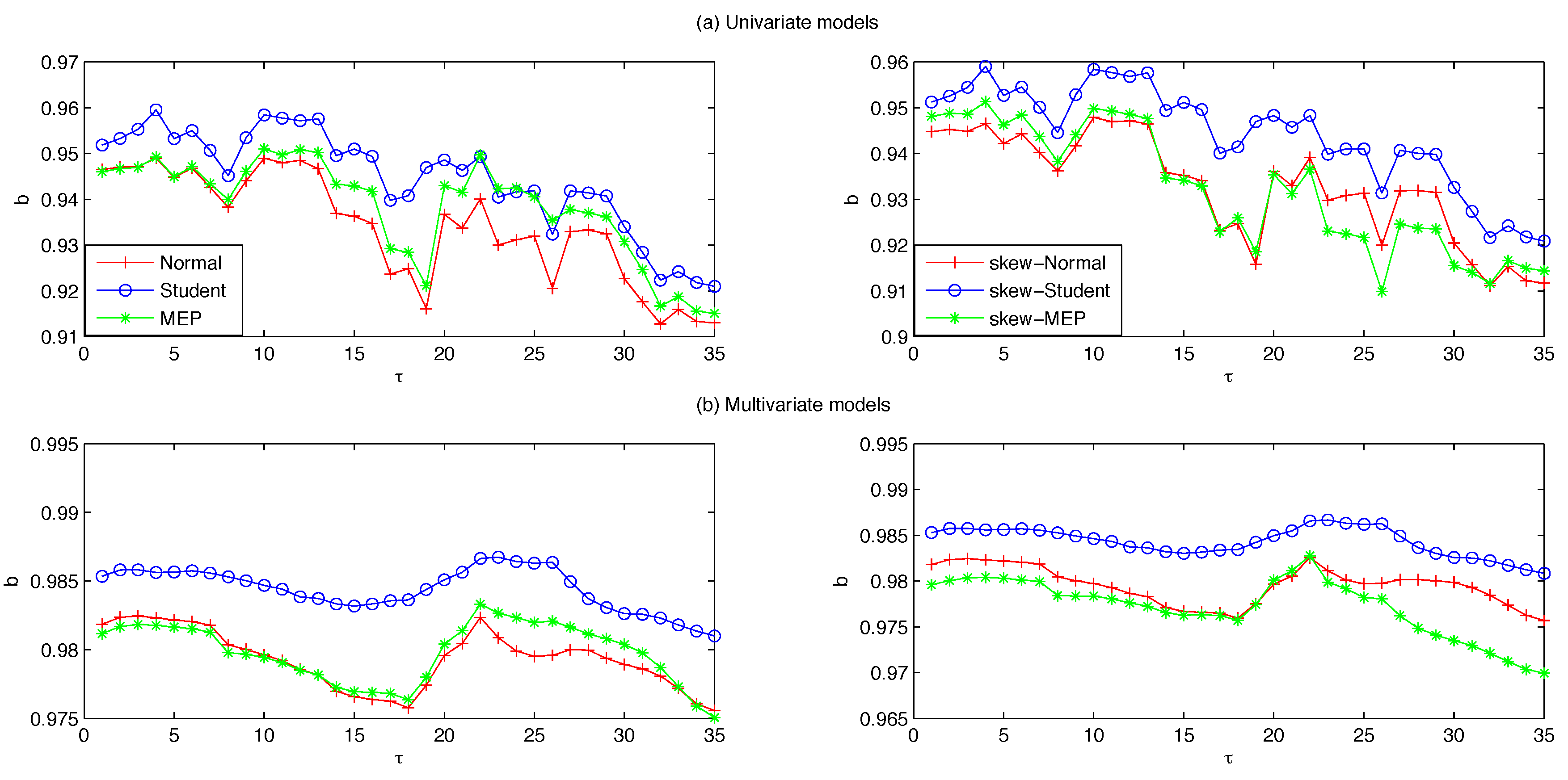
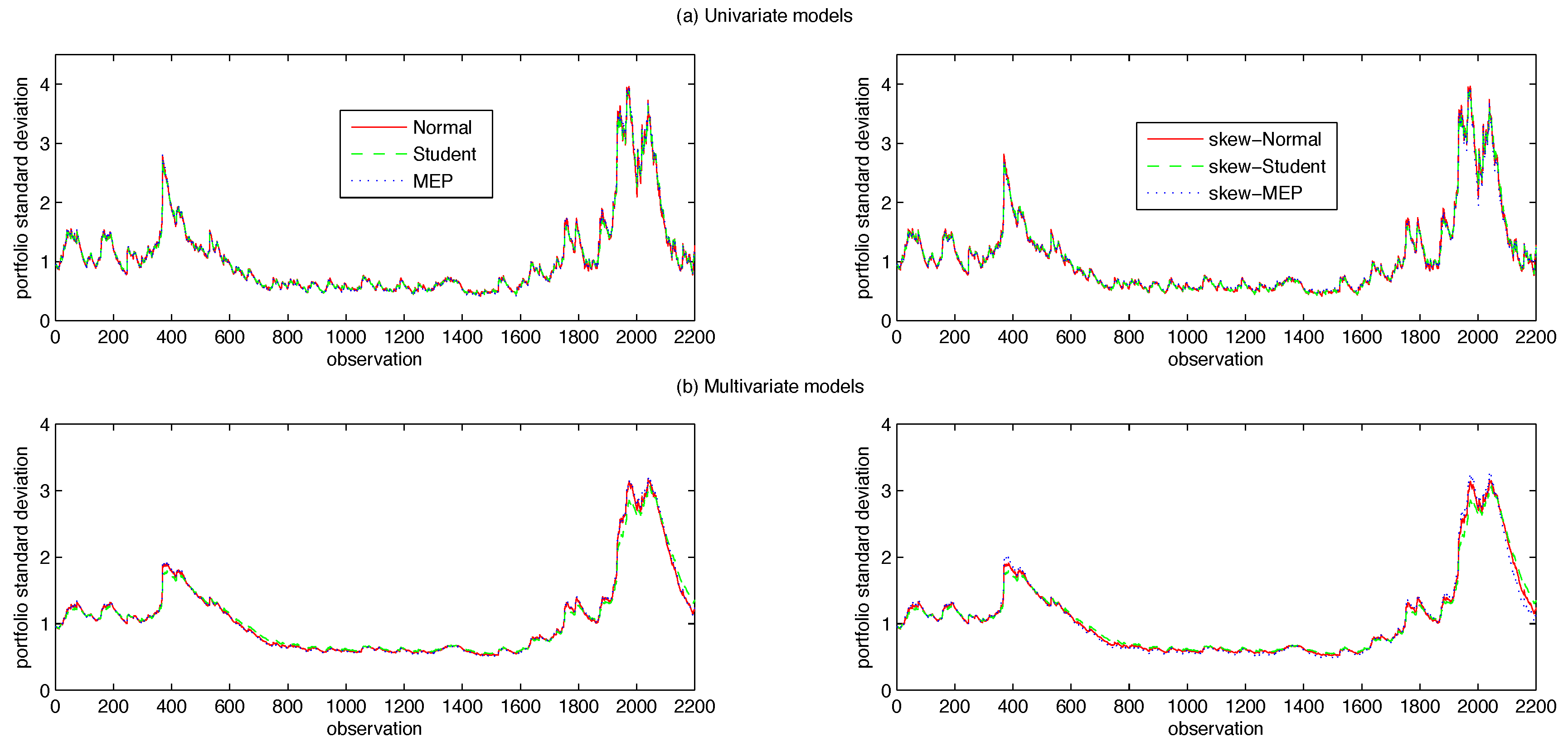
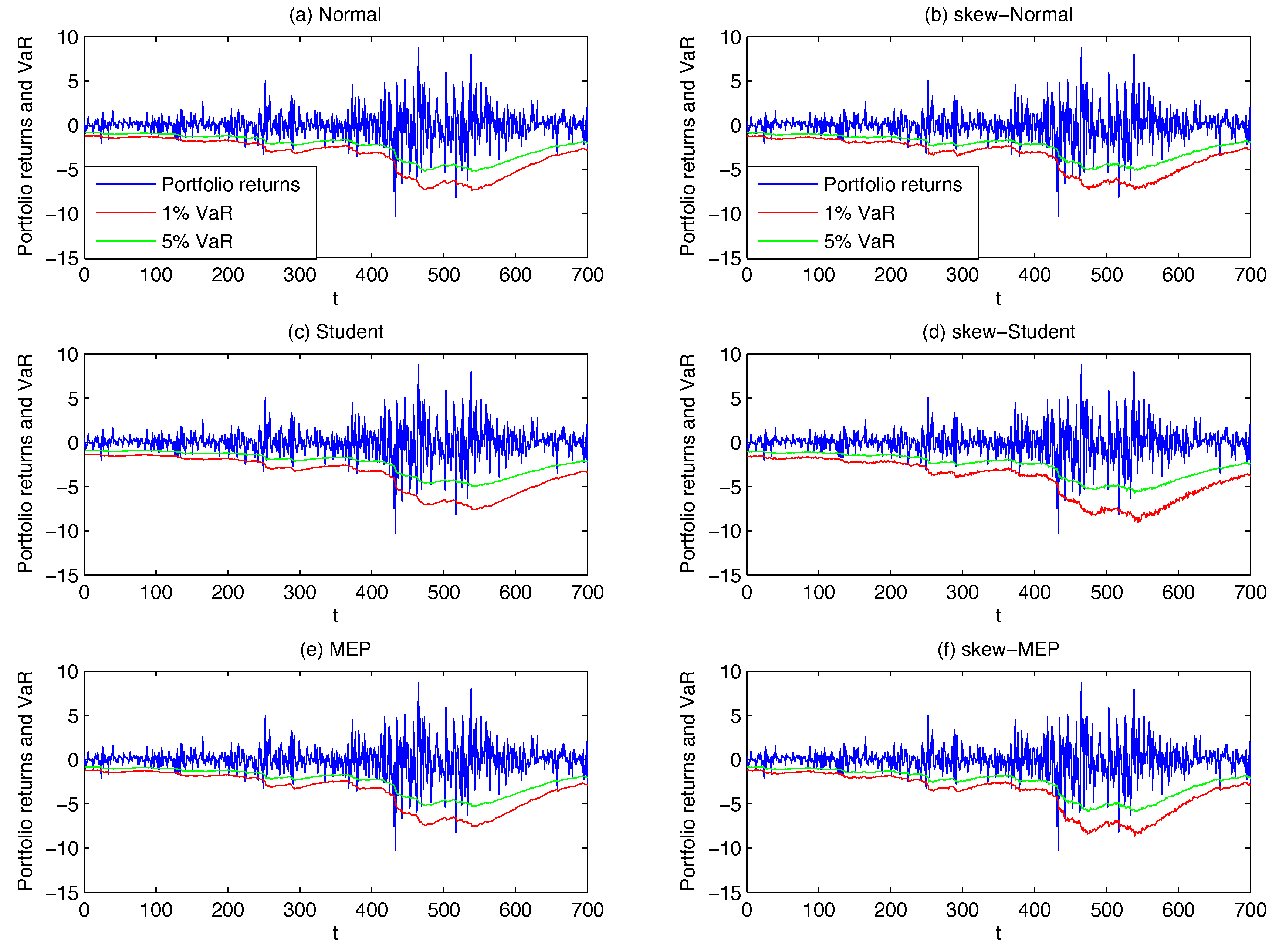
3.1. Data and Forecasting Scheme
Our dataset (used in the paper of Noureldin
et al. [
33])
5 comprises daily open-to-close returns of 10 stocks from the Dow Jones Industrial Average: Bank of America (BAC), JP Morgan (JPM), International Business Machines (IBM), Microsoft (MSFT), Exxon Mobil (XOM), Alcoa (AA), American Express (AXP), Du Pont (DD), General Electric (GE) and Coca Cola (KO). Each univariate vector of returns is calculated as
and covers a period of 2200 days, from February 2001 to November 2009. Univariate descriptive statistics over the period of interest are provided in
Table 1.
Table 1.
Univariate descriptive statistics.
Table 1.
Univariate descriptive statistics.
| Stock | Mean | Std.dev. | Skewness | Kurtosis | KS Test | JB Test |
|---|
| Estimation sample: 1 February 2001 to 23 January 2007 (1500 observations) |
| BAC | 0.09 | 1.09 | −0.18 | 7.45 | 0.00 | 0.00 |
| JPM | 0.00 | 1.68 | 0.90 | 31.02 | 0.00 | 0.00 |
| IBM | −0.04 | 1.24 | 0.01 | 5.96 | 0.01 | 0.00 |
| MSFT | −0.01 | 1.37 | 0.37 | 6.01 | 0.00 | 0.00 |
| XOM | −0.01 | 1.13 | 0.05 | 8.27 | 0.82 | 0.00 |
| AA | 0.01 | 1.59 | 0.14 | 4.74 | 0.00 | 0.00 |
| AXP | −0.02 | 1.44 | 0.33 | 7.73 | 0.00 | 0.00 |
| DD | 0.02 | 1.21 | 0.37 | 6.76 | 0.21 | 0.00 |
| GE | −0.01 | 1.34 | 0.13 | 7.90 | 0.02 | 0.00 |
| KO | 0.01 | 0.99 | 0.16 | 5.53 | 0.00 | 0.00 |
| Forecasting sample: 24 January 2007 to 30 October 2009 (700 observations) |
| BAC | −0.18 | 3.95 | 0.37 | 9.36 | 0.00 | 0.00 |
| JPM | 0.01 | 3.06 | 0.36 | 8.53 | 0.00 | 0.00 |
| IBM | 0.08 | 1.45 | −0.02 | 6.31 | 0.00 | 0.00 |
| MSFT | 0.02 | 1.60 | 0.08 | 5.90 | 0.00 | 0.00 |
| XOM | 0.03 | 1.61 | −0.39 | 11.31 | 0.00 | 0.00 |
| AA | −0.04 | 2.93 | −0.83 | 7.50 | 0.00 | 0.00 |
| AXP | 0.04 | 3.06 | 0.22 | 6.96 | 0.00 | 0.00 |
| DD | −0.04 | 1.89 | −0.12 | 5.70 | 0.00 | 0.00 |
| GE | 0.02 | 2.17 | 0.21 | 8.96 | 0.00 | 0.00 |
| KO | −0.03 | 1.22 | 0.07 | 7.68 | 0.06 | 0.00 |
| Full sample: 1 February 2001 to 30 October 2009 (2200 observations) |
| BAC | 0.01 | 2.40 | 0.33 | 21.72 | 0.00 | 0.00 |
| JPM | 0.00 | 2.21 | 0.57 | 16.90 | 0.00 | 0.00 |
| IBM | 0.00 | 1.31 | 0.02 | 6.24 | 0.02 | 0.00 |
| MSFT | 0.00 | 1.45 | 0.25 | 6.08 | 0.00 | 0.00 |
| XOM | 0.00 | 1.30 | −0.20 | 11.56 | 0.04 | 0.00 |
| AA | 0.00 | 2.11 | −0.69 | 9.95 | 0.00 | 0.00 |
| AXP | 0.00 | 2.09 | 0.32 | 11.23 | 0.00 | 0.00 |
| DD | 0.00 | 1.46 | 0.03 | 7.25 | 0.00 | 0.00 |
| GE | 0.00 | 1.65 | 0.22 | 10.85 | 0.00 | 0.00 |
| KO | 0.00 | 1.07 | 0.11 | 6.89 | 0.00 | 0.00 |
Across the three panels, the values of skewness and kurtosis show that the assets are far from being unconditionally normally distributed, thus supporting the conjecture that more flexible distributional assumptions can be conducive to enhanced model performance.
To this extent, one-step ahead forecasts of the conditional portfolio variance (in the univariate case) and of the conditional covariance matrix of returns (in the multivariate one) are recursively obtained as:
where
is the information set at time
t and
are defined as in Equations (
2) and (5), respectively. Using a rolling-fixed-window scheme, the parameters are estimated over a window length of 1500 observations and used to predict the conditional variance process for the following 20 days. Each time the window is shifted forward by 20 observations and the parameters are re-estimated over the new period in order to compute the next set of forecasts. We iterate this process until the end of the dataset for a total of 35 parameter estimates and 700 one-step ahead forecasts.
Table A1 in
Appendix B reports the complete list of windows and forecast horizons along with their corresponding calendar dates.
For each model, the portfolio VaR forecast at
α% confidence level is then obtained as
For the symmetric distributions in our analysis (normal, Student and MEP), one can easily compute the long VaR of the portfolio by applying Equation (
27) and the inverse of each CDF at
α%. However, for the non-symmetric distributions this is not straightforward. In order to bypass this complication, for each non-symmetric distribution we apply a simple Monte-Carlo simulation approach, as widely used in VaR computations. Namely, we draw
random vectors (numbers) from each symmetric multivariate (univariate) standardized distribution
and then we use the estimated skewness parameters to construct the corresponding skewed distribution
. By assuming
(
) as the true DGP, we obtain a set of 10,000 simulated returns over the period of interest. Finally, the simulated return distribution is used to derive the 5% and 1% quantiles for the one-step-ahead VaR.
3.2. Testing the Accuracy of VaR Forecasts
The models accuracy in predicting VaR is assessed using multiple statistical backtesting methods. A common starting point for this procedure is the so-called hit function, or indicator function, which is equal to
i.e., it takes the value one if the ex-post portfolio loss exceeds the VaR predicted at time
and the value zero otherwise. According to Christoffersen [
34], in order to be accurate, the hit sequence has to satisfy the two properties of correct failure rate and independence of exceptions. The former implies that the probability of realizing a VaR violation should be equal to
, while the latter further requires the violations to be independent of each other. These properties can be combined together into one single statement assessing that the hit function has to be an i.i.d. Bernoulli random variable with probability
p,
i.e.,
.
This represents the key foundation to many of the backtesting procedures developed in recent years and particularly to the accuracy tests being used in this paper. We focus on tests included in the following three categories:
Evaluation of the Frequency of Violations
Evaluation of the Independence of Violations
Evaluation of the Duration between Violations.
Their properties are briefly described below.
Frequency of Violations The first way of testing the VaR accuracy is to test the number or the frequency of margin exceedances. A test designed to this aim is the Kupiec test (Kupiec [
35]), also known as the Unconditional Coverage (UC) test. Its null hypothesis is simply that the percentage of violated VaR forecasts or failure rate
p is consistent with the given confidence level
α,
i.e.,
.
Denoting by
F the length of the forecasting period and with
v the number of violations occurred throughout this period, the log-likelihood ratio test statistic is defined as
where
is the maximum likelihood estimator under the alternative hypothesis. This ratio test statistic is asymptotically
distributed and the null hypothesis is rejected if the critical value at the
confidence level is exceeded.
A similar useful test is the TUFF (Time Until First Failure) test (Kupiec [
35]). Under the null, the probability of an exception is equal to the inverse probability of the VaR confidence level, namely
. Its basic assumptions are similar to those of the Kupiec test and the t-statistic under the null is obtained as
The TUFF statistic is also asymptotically
distributed.
Independence of Violations A limitation of the Kupiec test is that it is only concerned with the coverage of the VaR estimates without accounting for any clustering of the violations. This aspect is crucial for VaR practitioners, as large losses occurring in rapid succession are more likely to lead to disastrous events than individual exceptions.
The Independence test (IND) of Christoffersen [
34] uses the same likelihood ratio framework as the previous tests but is designed to explicitly detect clustering in the VaR violations. Under the null hypothesis of independence, the IND test assumes that the probability of an exceedance on a given day
t is not influenced by what happened the day before. Formally,
, where
denotes the probability of an
i event on day
being followed by a
j event on day
t.
The relevant IND test statistic can be derived as
where
is the number of violations with value
i at time
followed by
j at time
t. Under the null, the IND statistic is also asymptotically distributed as a
random variable.
Although the aforementioned test has received support in the literature, Christoffersen [
34] noted that it was not complete on its own. For this reason, he proposed a joint test, the Conditional Coverage (CC) test, which combines the properties of both UC and IND tests.
Formally, the CC ratio statistic can be proven to be the sum of the UC and the IND statistics:
where we added and subtracted the quantity
and substituted
for
. CC is also
distributed, but with two degrees of freedom since there are two separate statistics in the test. According to Campbell [
36], in some cases it is possible that a VaR model passes the joint test while still failing either the independence test or the unconditional coverage test. Thus it is advisable to run them separately even when the joint test yields a positive result.
A second test belonging to this class is the Regression-based test of Engle and Manganelli [
37], also known as Dynamic Quantile (DQ) test. Instead of directly considering the hit sequence, the test is based on its associated quantile process
which assumes the following values:
The idea of this approach is to regress current violations on past violations in order to test for different restrictions on the parameters of the model. That is, we estimate the linear regression model and then we test the joint hypothesis . This assumption coincides with the null of Christoffersen’s CC test. It is also possible to split the test and separately test the independence hypothesis and the unconditional coverage hypothesis, respectively as and . and are asymptotically distributed with respectively , K and one degrees of freedom.
Duration between Violations One of the drawbacks of Christoffersen’s CC test is that it is not capable of capturing dependence in all forms, since it only considers the dependence of observations between two successive days. To address this, Christofferson and Pelletier [
38] introduced the Duration-Based test of independence (DBI), which is an improved test for both independence and coverage. Its basic intuition is that if exceptions are completely independent of each other, then the upcoming VaR violations should be independent of the time that has elapsed since the occurrence of the last exceedance (Campbell [
36]). The duration (in days) between two exceptions is defined via the no-hit-duration
, where
is the day of
violation.
A correctly specified model should have an expected conditional duration of
days and the no-hit duration should have no memory. The authors construct the ratio statistic considering different distributions for the null and the alternative hypotheses, namely the exponential, since it is the only memory-free (continuous) random distribution, and the Weibull, which allows for duration dependence. The likelihood ratio statistic is derived as
which has a
distribution with one degree of freedom.
Under the null hypothesis of independent violations, and a is estimated via numerical maximization of . Whenever , the Weibull function has a decreasing path which corresponds to an excessive number of very long durations (very calm period) while corresponds to an excessive number of very short durations, namely very volatile periods.