A Spectral Model of Turnover Reduction
Abstract
:1. Introduction and Summary
2. Definitions
3. “Fixing” Covariance Matrix
A Simple Method
4. Spectral Model
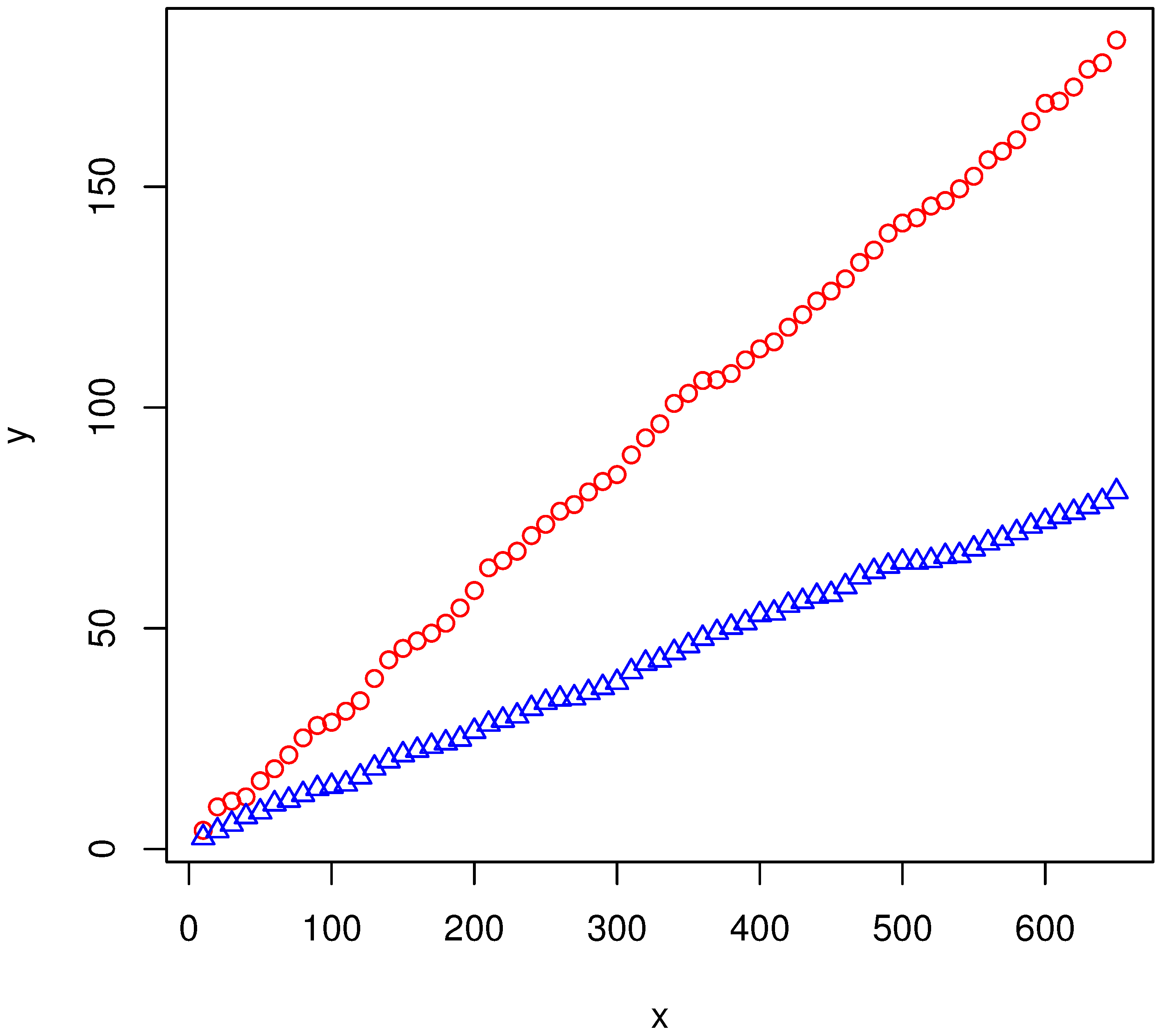
4.1. Caveats
4.2. Why Is All This Useful?
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Z. Kakushadze, and J.K.-S. Liew. “Is It Possible to OD on Alpha? ” J. Altern. Invest. (forthcoming). Available online: http://ssrn.com/abstract=2419415 (accessed on 25 February 2015). [CrossRef]
- C. Ackerman, R. McEnally, and D. Revenscraft. “The Performance of Hedge Funds: Risk, Return and Incentives.” J. Financ. 54 (1999): 833–874. [Google Scholar] [CrossRef]
- V. Agarwal, and N.Y. Naik. “On Taking the “Alternative” Route: The Risks, Rewards, and Performance Persistence of Hedge Funds.” J. Altern. Invest. 2 (2000): 6–23. [Google Scholar] [CrossRef]
- V. Agarwal, and N.Y. Naik. “Multi-Period Performance Persistence Analysis of Hedge Funds Source.” J. Financ. Quant. Anal. 35 (2000): 327–342. [Google Scholar] [CrossRef]
- G. Amin, and H. Kat. “Stocks, Bonds and Hedge Funds: Not a Free Lunch! ” J. Portf. Manag. 29 (2003): 113–120. [Google Scholar] [CrossRef]
- C.S. Asness, R.J. Krail, and J.M. Liew. “Do Hedge Funds Hedge? ” J. Portf. Manag. 28 (2001): 6–19. [Google Scholar] [CrossRef]
- C. Brooks, and H.M. Kat. “The Statistical Properties of Hedge Fund Index Returns and Their Implications for Investors.” J. Altern. Invest. 5 (2002): 26–44. [Google Scholar] [CrossRef]
- S.J. Brown, W. Goetzmann, and R.G. Ibbotson. “Offshore Hedge Funds: Survival and Performance, 1989–1995.” J. Bus. 72 (1999): 91–117. [Google Scholar] [CrossRef]
- N. Chan, M. Getmansky, S.M. Haas, and A.W. Lo. “Systemic Risk and Hedge Funds.” In The Risks of Financial Institutions. Edited by M. Carey and R.M. Stulz. Chicago, IL, USA: University of Chicago Press, 2006, pp. 235–338. [Google Scholar]
- F.R. Edwards, and M.O. Caglayan. “Hedge Fund and Commodity Fund Investments in Bull and Bear Markets.” J. Portf. Manag. 27 (2001): 97–108. [Google Scholar] [CrossRef]
- F.R. Edwards, and J. Liew. “Managed Commodity Funds.” J. Futures Mark. 19 (1999): 377–411. [Google Scholar] [CrossRef]
- F.R. Edwards, and J. Liew. “Hedge Funds versus Managed Futures as Asset Classes.” J. Deriv. 6 (1999): 45–64. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “A Primer on Hedge Funds.” J. Empir. Financ. 6 (1999): 309–331. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “Performance Characteristics of Hedge Funds and Commodity Funds: Natural vs. Spurious Biases.” J. Financ. Quant. Anal. 35 (2000): 291–307. [Google Scholar] [CrossRef]
- W. Fung, and D. Hsieh. “The Risk in Hedge Fund Strategies: Theory and Evidence from Trend Followers.” Rev. Financ. Stud. 14 (2001): 313–341. [Google Scholar] [CrossRef]
- D.-L. Kao. “Battle for Alphas: Hedge Funds versus Long-Only Portfolios.” Financ. Anal. J. 58 (2002): 16–36. [Google Scholar] [CrossRef]
- B. Liang. “On the Performance of Hedge Funds.” Financ. Anal. J. 55 (1999): 72–85. [Google Scholar] [CrossRef]
- B. Liang. “Hedge Funds: The Living and the Dead.” J. Financ. Quant. Anal. 35 (2000): 309–326. [Google Scholar] [CrossRef]
- B. Liang. “Hedge Fund Performance: 1990–1999.” Financ. Anal. J. 57 (2001): 11–18. [Google Scholar] [CrossRef]
- A.W. Lo. “Risk Management For Hedge Funds: Introduction and Overview.” Financ. Anal. J. 57 (2001): 16–33. [Google Scholar] [CrossRef]
- F.-É. Racicot, and R. Théoret. “The Procyclicality of Hedge Fund Alpha and Beta.” J. Deriv. Hedge Funds 19 (2013): 109–128. [Google Scholar] [CrossRef]
- T. Schneeweis, R. Spurgin, and D. McCarthy. “Survivor Bias in Commodity Trading Advisor Performance.” J. Futures Mark. 16 (1996): 757–772. [Google Scholar] [CrossRef]
- Z. Kakushadze. “Can Turnover Go to Zero? ” J. Deriv. Hedge Funds 20 (2014): 157–176. [Google Scholar] [CrossRef]
- Z. Kakushadze. “Combining Alpha Streams with Costs.” J. Risk 17 (2015): 57–78. [Google Scholar] [CrossRef]
- Z. Kakushadze. “Notes on Alpha Stream Optimization.” J. Invest. Strateg. 4 (2015): 37–81. [Google Scholar] [CrossRef]
- R. Rebonato, and P. Jäckel. “The most general methodology to create a valid correlation matrix for risk management and option pricing purposes.” Available online: http://ssrn.com/abstract=1969689 (accessed on 20 April 2014).
- Z. Kakushadze. “Factor Models for Alpha Streams.” J. Invest. Strateg. 4 (2014): 83–109. [Google Scholar] [CrossRef]
- G. ’t Hooft. “A Planar Diagram Theory For Strong Interactions.” Nuclear Phys. B 72 (1974): 461–473. [Google Scholar] [CrossRef]
- 1 Here “alpha” means a real-life (as opposed to “academic”) alpha, that is, any reasonable expected return on which one may wish to trade, that is, take risk. In fact, real-life alphas (e.g., momentum strategies) often have sizable exposure to risk. Furthermore, there is no “perfect” risk model w.r.t. which one would hypothetically neutralize risk exposure of a portfolio. Otherwise, there would only be mean-reversion caused by temporary trading imbalances, which is evidently not the case in real life. Different time horizons provide different alpha (trading) opportunities.
- 3 For the following discussion it is not important what the actual values of these weights are or how they are computed (e.g., via optimization, regression, etc.). We keep them arbitrary subject to the normalization condition . The weights can be negative (internal crossing).
- 4 The matrix is degenerate if and only if the matrix is degenerate: .
- 5 Actually, this assumes that there are no N/As in any of the alpha time series. If some or all alpha time series contain N/As in non-uniform manner and the correlation matrix is computed by omitting such pair-wise N/As, then the resulting correlation matrix may have negative eigenvalues that are not “small” in the sense used above, i.e., they are not zeros distorted by computational rounding. The deformation method we discuss above can be applied in this case as well. Non-positive-definiteness of the original (undeformed) correlation matrix typically is not a dominant effect in the first principal component (see below) and turnover reduction; however, in practice one would typically use a positive-definite (deformed) correlation matrix and the deformation can have a sizable effect—see Section 7 of [23] for illustrative empirical examples.
- 6 Here we are assuming that, if need be, the method reviewed in Subsection 3.1 has been applied and all . Furthermore, the basis of alphas is taken (i.e., the signs of are chosen) such that is maximized ( is the mean correlation). Thus, consider the case with uniform correlations , , studied in [1]. In this case, in the large N limit, the turnover reduction coefficient (see below) [1]. However, if we flip the signs of some alphas (and then we must also flip the signs of the corresponding weights ), which does not change the portfolio turnover, the mean correlation will no longer be equal ρ, hence the aforementioned choice of the basis for . We will discuss this point in more detail and give a precise prescription for fixing this basis below. For now we will just bear this in mind.
- 7 Note that is not suitable because T is not expected to have a peculiar behavior when is nearly degenerate. Furthermore, only the trace-based scalar invariant reproduces the special case discussed below. Also, see below why relative coefficients in (24) do not change the end result.
- 8 E.g., in the uniform correlation case where (), we have , while the rest of the eigenvectors have zero sums.
- 10 We emphasize the adjective “illustrative” for the reason that, because various hedge funds in this data do/did not all trade the same underlying instruments and also the corresponding time series are not 100% overlapping (some hedge funds are dead, some are newer than others, etc.), it would not necessarily be correct to assume that their trades could be crossed. Therefore, we use this data only to illustrate various properties of the correlation matrix, and not to directly draw any conclusions about turnover reduction had these alpha streams actually crossed their trades.
- 11 One may wish to use , their average or some other value between and .
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakushadze, Z. A Spectral Model of Turnover Reduction. Econometrics 2015, 3, 577-589. https://doi.org/10.3390/econometrics3030577
Kakushadze Z. A Spectral Model of Turnover Reduction. Econometrics. 2015; 3(3):577-589. https://doi.org/10.3390/econometrics3030577
Chicago/Turabian StyleKakushadze, Zura. 2015. "A Spectral Model of Turnover Reduction" Econometrics 3, no. 3: 577-589. https://doi.org/10.3390/econometrics3030577




