1. Introduction
The 21st century has seen substantial and growing interest in the analysis of dynamic covariances and correlations across investment instruments. In particular, there has been great emphasis paid to the analysis of financial assets (see [
1] and [
2], among others, and the references cited in the surveys by [
3] and [
4]). More recently, there has been growing interest in energy finance, particularly oil (see [
5], [
6], [
7] and [
8] among others).
In this research stream, the most widely-used representation is a variation of Multivariate Generalized AutoRegressive Conditional Heteroskedasticity (GARCH), namely Dynamic Conditional Correlation (DCC), as introduced by [
1]. The baseline representation has been extended in several directions, dealing with the parameterization (see [
2], [
6], and [
9], among others), the introduction of additional elements, such as asymmetry (see [
2] and [
10], among others), and the proposal of alternative estimation methods (see [
11] and [
12], among others).
Despite the growing interest in DCC and its central role in the estimation of dynamic correlations, several important issues relating to this representation seem to have been ignored in the financial econometrics literature. These important issues include the absence of any derivation of DCC and its mathematical properties, and a lack of any demonstration of the asymptotic properties of the estimated parameters (for a summary of these issues, see [
13]). In this respect, a useful contribution is [
14], who demonstrates the inconsistency of the two step estimator of the parameters of DCC. In fact, most published papers dealing with dynamic correlations simply do not discuss stationarity of the model, the regularity conditions, or the asymptotic properties of the estimators.
Another critical element of DCC is associated with the construction of the dynamic conditional correlations. In fact, the representation seems to provide estimated dynamic correlations as a bi-product of standardization, and not as a direct result of the equation governing the multivariate dynamics. This will be clarified below. An alternative representation which avoids this last criticism, but nevertheless has no discussion of the mathematical properties or demonstration of the asymptotic properties of the estimators, has been proposed by [
15]. However, this representation seems to have attracted considerably less interest in the literature.
It should be mentioned that many empirical applications involving DCC and related representations show that the impact of news can be rather limited, thereby making the estimated conditional correlations similar to those implied by simple BEKK models (see [
16] and [
17], at least in small cross-sectional problems (for further details, see [
9] and [
18]).
This paper highlights some critical issues associated with the use of the DCC and related representations to make potential users aware of the inherent problems they might encounter. The main message is not against the use of DCC, which is the most popular representation of dynamic conditional correlations, but is intended to be cautionary, so that users can understand and appreciate the limits of DCC. In fact, we suggest that DCC be regarded as a filter or as a diagnostic check, as in the Exponentially Weighted Moving Average approach adopted in the first versions of the [
19] methodology. When an equation has not been derived in a rigorous way, and for which we do not have any explicit details regarding the existence of moments, derivation and testability of the stationarity conditions, and demonstrated asymptotic properties of the estimators, it should not be considered as a model, but rather as a filter or a diagnostic check for estimating and forecasting dynamic conditional correlations. We will elaborate on this issue in the remainder of the paper after highlighting the critical aspects of the DCC framework.
The plan of the paper is to discuss ten things you should know about the DCC representation. These caveats are discussed in
Section 2. Some concluding remarks are given in
Section 3.
2. Ten Caveats about DCC
The DCC representation was introduced by [
1] to capture the empirically observed dynamic contemporaneous correlations of asset returns. The representation can be given as follows. Denote by
rt the vector containing the log-returns of
k assets. The density of the returns is characterized by the absence of serial correlation in the mean returns, and by the presence of time-varying second-order moments:
where
It−1 denotes the information set to time
t−1,
μ is the unconditional mean, which is generally equal, or very close, to zero, Σ
t is the dynamic conditional covariance matrix, and
D is a generic multivariate density function depending on the mean vector and dynamic conditional covariance matrix.
Following [
12], the covariance matrix can be decomposed into the product of dynamic conditional standard deviations and dynamic conditional correlations:
where
Dt =
diag(
σ1,
σ2,…,
σk),
diag(
a)is a matrix operator creating a diagonal matrix with the vector
a along the main diagonal, and
Rt is a dynamic correlation matrix. From Equations (1) and (2), the marginal density of each element of
rt has a time-varying conditional variance, and can be modeled, for example, as a univariate GARCH process.
The DCC representation focuses on the dynamic evolution of
Rt in Equation (2), and recovers that quantity by considering the dynamics of the conditional variance of the standardized residuals, which are defined as follows:
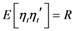
By construction, the standardized residuals have second-order unconditional moment equal to
with
R being the unconditional correlation, thereby motivating the focus on standardized residuals to recover the dynamics for the conditional correlations.
In practice, the standardized residuals can be used to verify empirically the existence of dynamics in the conditional correlations, for instance, by means of a rolling regression approach. Moreover, if the data generating process of the returns is given in Equations (1) and (2), the dynamic conditional covariance of the standardized residuals is given as:
Without distinguishing between the dynamic conditional covariance and dynamic conditional correlation matrices, [
1] presents the following equation based on the outer cross-products of the standardized residuals:
where Equation (6) has scalar parameters, as in the most common DCC representation,
![Econometrics 01 00115 i013]()
is assumed to be a positive definite matrix with unit elements along the main diagonal (which is alleged to be a conditional correlation matrix), the two scalar parameters satisfy a stability constraint of the form
α +
β < 1, and the sequence
Qt purportedly drives the dynamics of the conditional correlations.
However, as the matrix
Qt in Equation (6) does not satisfy the definition of a (dynamic) conditional correlation matrix, as in Equation (2), [
1] introduces the following standardization:
where
dg(
A) is a matrix operator returning a vector equal to the main diagonal of matrix A. (In discussing the equivalent of Equation (7) above, namely Equation (25) in [
1], a typographical error is present as the exponent is reported as −1 instead of −0.5.).
It is clear that Equation (7) is a simple standardization, suggesting that the primary statistic of interest, namely the dynamic conditional correlation matrix, can be computed from (6). However, to state the obvious, a dynamic conditional correlation matrix is a standardization of a dynamic conditional covariance matrix, but not every standardization, such as that in Equation (7), is consistent with a dynamic conditional correlation matrix. This lack of equivalence is even more obvious if it cannot be demonstrated (as distinct from being stated) that Equation (6) is a dynamic conditional correlation matrix. (A simple illustration would be to divide 10 elephants by 20 elephants, which is not a correlation despite being a fraction.) It should be clear that, as the second term on the right-hand side of Equation (6) is not a dynamic update of a conditional correlation matrix, the representation in Equation (6) cannot be a dynamic conditional correlation matrix.
Bearing these points in mind, the following caveats should be seriously considered before using the DCC representation.
2.1. DCC is Based on the Conditional Second-Order Moment of the Standardized Residuals, and Hence does not Directly Yield Conditional Correlations
The simple observation of Equation (6) recognizes the structure of the scalar BEKK model of dynamic conditional correlations (see [
16] and [
17]), pointing to an inherent contradiction in the DCC model. Combining Equations (1), (2), and (3) leads to:
Moreover, using Equation (7), this is equivalent to
However, if we consider the
Qt dynamic recurrence in Equation (6) as a BEKK model, then
Qt might be interpreted as the dynamic conditional covariance matrix of the innovation term, which is
ηt, and it thereby suggests that the following holds:
which is inconsistent with what is implied in Equations (1)–(3) and (5). Therefore, we note an implicit contradiction in the way the DCC correlation dynamics are derived.
In addition, a dynamic conditional correlation matrix may be obtained only through the standardization in Equation (7). However, we can also note an inconsistency between the dynamic conditional expectation reported in Equation (5) and the way in which the dynamic conditional correlation matrix is obtained in Equation (7). Such inconsistency causes further problems as Qt is not the conditional covariance of ηt, as shown in Equation (5), and is not the conditional correlation of ηt as it is just positive definite, but need not correspond to a dynamic conditional correlation matrix.
The last remark can easily be verified by visual inspection of the estimates of
Qt, which are typically not considered in empirical analysis. However, by using several datasets, it is straightforward to show that the elements of |
Qt| can be greater than 1 (see, for example, [
20]). As a consequence, it might be stated that the sequence
Qt is a convenient device for obtaining dynamic conditional correlations but, as it stands, has no proper interpretation as either a dynamic conditional covariance or dynamic conditional correlation matrix. This leads to another caveat about DCC.
2.2. DCC Is Stated Rather Than Derived
From the previous comments, it clearly emerges that DCC is a stated representation, but it is not a derived model that is based on the relationship between the innovations to returns and the standardized residuals. Moreover, the DCC representation does not satisfy the definition that relates dynamic conditional correlations to dynamic conditional covariances, as given in Equation (2). As such, the interpretation of DCC as a representation that may yield dynamic conditional correlations is inherently flawed. This quandary also begs the question as to whether DCC is actually a model, namely a set of assumptions, or alternatively as a representation with explicit and testable mathematical properties and derivable statistical properties.
A further motivation for the previous claim is inherently related to the construction of the conditional correlations within the DCC representation. Generally speaking, conditional correlations can be derived from a conditional covariance model by standardization of the covariances, namely
![Econometrics 01 00115 i014]()
. However, such a procedure cannot be applied to the DCC representation because the covariance is obtained as
![Econometrics 01 00115 i015]()
. Consequently, the traditional way of deriving correlations applies to the conditional matrix
Qt and not to the full conditional covariance. We conclude that we cannot derive conditional correlations in the usual way due to the presence of two standardizations rather than just one.
The above discussion also affects the many representations which are obtained as generalizations of the DCC representation including, among others, [
2], [
6] and [
14]. Moreover, this has further consequences for the model structure and the associated statistical properties.
2.3. DCC Has No Moments
This follows from the stated rather than derived properties of the representation (see [
20] for further details). Therefore, there is no connection between univariate models of conditional variance, such as ARCH ([
21]) and GARCH ([
22]), and multivariate models of conditional correlations. This is in marked contrast to the direct connection between the alternative univariate conditional volatility models and the BEKK multivariate model of dynamic conditional covariances (see [
16] and [
17]), and the direct connection between univariate conditional volatility models and the GARCC multivariate model of dynamic conditional correlations (see [
20]). Nevertheless, we observe that the financial econometrics literature includes several other models and approaches where the underlying stochastic component is characterized, for instance, by the known existence of lower-order moments while higher-order moments, or even the variance, might not exist. In any event, such approaches have been used extensively, with useful and interesting empirical results, within a risk management framework.
2.4. DCC Does Not Have Testable Regularity Conditions
This follows from point (3) above. In particular, [
1] (p. 342) refers to “reasonable regularity conditions” and “standard regularity conditions”, without stating them explicitly. The author of [
14] (pp. 10–11) assumes that the unstated regularity conditions, whatever they might be, are satisfied. Ann extension of the DCC representation to incorporate asymmetries is developed in [
2], but explicit regularity conditions are not provided. With no testable regularity conditions, such as log-moment or second moment conditions, the internal consistency of the model cannot be checked. There is, therefore, no evidence as to whether the purported estimates of dynamic conditional correlations have any connection to the definition of dynamic conditional correlations.
The absence of explicit regularity conditions and of explicit moment affects also the derivation of asymptotic properties of the parameter estimates. The author of [
1] suggests the following “two step” approach for estimating DCC parameters. Within a Quasi Maximum Likelihood framework, we have the following Gaussian log-likelihood for one observation of the returns
rt:
Following the decomposition in (2), we have:
where it is shown that the single observation likelihood can be decomposed into two terms, namely a function of the variance parameters only, Θ
V, and a function of both the variance and correlations parameters, Θ
V and Θ
C, respectively. Note that the first likelihood component is based on a correlation matrix set to the identity matrix, which is then used to recover the variance parameters only. The second likelihood component is used to estimate the correlation parameters, conditionally on the first stage likelihood estimated parameters (
![Econometrics 01 00115 i016]()
).
In [
1], it is suggested that the first likelihood component can be further decomposed into the sum of univariate likelihoods representing the marginal contribution of each return series, under the assumption of independence. This is a first simplification imposed to deal with the curse of dimensionality that generally affects multivariate GARCH models (see [
23] for further details). In addition, to simplify the computational burden associated with the maximization of the second stage likelihood
![Econometrics 01 00115 i017]()
, [
1] suggests replacing the matrix
Q with the sample correlation matrix of the standardized residuals
ηt, thereby introducing an intermediate “1.5” step.
The previously outlined approach entails a number of assumptions which are generally not satisfied by empirical data, as follows:
- -
Marginal variances are assumed to be independent, which rules out any form of spillovers or feedback across variances and shocks of the various assets. This is related to the general idea of having dependence across assets governed only by the correlations. However, this is not always the case, and shocks of different assets can affect the variance of a single asset.
- -
The sample correlation matrix is assumed to be an appropriate estimator for the matrix
![Econometrics 01 00115 i013]()
, which is not necessarily a correlation matrix.
- -
The approach is called “two step”, when in reality it is a “three step” procedure when sample correlations are used for
![Econometrics 01 00115 i013]()
, and is a proper “two step” procedure when the correlation likelihood
![Econometrics 01 00115 i018]()
is maximized with respect to the full parameter set Θ
C, and conditionally on the variance parameters Θ
V.
However, the possible incompatibility between the assumptions leading to the estimation approach described above do not prevent its use, which can be motivated and supported by its computational simplicity, an important issue of which users should be aware. Nevertheless, the asymptotic properties of the “two step” estimator are not discussed in [
1], apart from a reference to [
24], which remains an unpublished manuscript and does not, in fact, demonstrate any asymptotic properties for the DCC parameters.
We have the additional following caveat:
2.5. DCC Yields Inconsistent “Two Step” Estimators
The author of [
1] (p. 342) states that the standardized residuals in equation (6) are “a Martingale difference by construction” in suggesting how to estimate the parameters of DCC by resorting to standard ARMA methods. Moreover, the fact that the errors are a martingale difference sequence allows recovery of general results for multivariate GARCH processes and, in particular, those in [
17]. However, [
14] points out that the DCC representation cannot be interpreted as a linear multivariate GARCH, and this leads to the inconsistency of the “two step” DCC estimator discussed above. The inconsistency is governed by the fact that in equation (6) the matrix
Qt is not the expectation of the standardized residuals cross-products. Therefore, it is not possible to obtain a martingale difference by rewriting equation (6) in a companion VARMA form.
The primary merit of [
14] is in highlighting the inconsistency problem, but the proposed ‘solution’ still suffers from the same troubles afflicting the DCC representation of [
1]. In fact, [
14] discusses targeting and a modification to DCC to enable consistent estimation. However, he assumes that the estimators of the modified DCC representation are asymptotically normal under “standard” regularity conditions, without stating what the conditions might be. It has been shown in [
18] and [
23] that dynamic conditional correlations can be estimated consistently by using an indirect DCC representation based on the BEKK model, but asymptotic normality cannot be established.
2.6. DCC Has No Desirable Asymptotic Properties
In [
14], [
20] and [
23] it has been shown that the estimated parameters of the DCC representation under the standard two step approach have no asymptotic properties. Moreover, the asymptotic properties of the joint maximum likelihood estimator (for all parameters in one step) are not known. In their extension of DCC, [
2] do not establish any asymptotic properties. In a recent contribution, [
11] claim to prove consistency of the estimates of the DCC representation in Theorem 1, but the proof refers to pseudo-true parameters rather than the parameters of interest. In Theorem 2, the authors assume consistency of the estimated parameters of interest (such that the pseudo-true parameters are identical to the parameters of interest) in claiming a proof of asymptotic normality (see [
23] for further details).
It is clear that the availability of asymptotic properties is still an open question. As a consequence, the reliability of standard inferential procedures, such as statistical significance, or likelihood ratio testing across nested DCC representations, remains unknown, and should be considered only on the basis of appropriate simulation experiments.
2.7. DCC Is Not a Special Case of GARCC, Which Has Testable Regularity Conditions and Standard Asymptotic Properties
In [
20] the Generalized Autoregressive Conditional Correlation (GARCC) model is derived based on the relationship between the innovations to returns and the standardized residuals, using a vector random coefficient autoregressive process. The scalar and diagonal versions of BEKK are also shown to be special cases of a vector random coefficient autoregressive process, though not the Hadamard and full BEKK models. The GARCC model provides a motivation for dynamic conditional correlations that satisfy the definition of a conditional correlation matrix, and hence can be shown to produce dynamic conditional correlations. As an application of a vector random coefficient autoregressive process, the GARCC model also has testable regularity conditions, and the estimated parameters can be shown to be consistent and asymptotically normal.
2.8. DCC Is Not Dynamic Empirically and Variance Misspecification Impact Is Not Known
Are the purported dynamic conditional correlations real or apparent, and do they arise solely from the standardization of the dynamic conditional covariances? What is the impact of variance misspecification?
With respect to the first question, we refer to the parameter estimates which are generally observed in empirical studies, whereby
β is large and close to 1, while
α is typically small and less than 0.05. As a result, the conditionally dynamic matrix
Qt may ‘appear’ to be dynamic as both parameter estimates are statistically significant. However, the limited impact of the shocks, driven by the small estimate of
α, makes
Qt almost constant, with limited oscillations around the unconditional
Qt value of
![Econometrics 01 00115 i013]()
. In addition, such a limited dynamic effect might be amplified in the dynamic correlation matrix
Rt, as defined in (7), due to the presence of the standardization. This may well confuse the user of the DCC representation, who might not be aware that that the purported dynamics are spurious.
Moving to the second question, we give the underlying intuition starting from a classical example. In the context of the Box-Jenkins procedure, if an ARMA(1,1) is estimated when an ARMA(2,1) representation is correct, then the residuals might still show some AR dynamics. For instance, in the limiting case of real roots for the ARMA(2,1) model, if the roots of the estimated model correspond to those of the true model (such that the AR component captures precisely one of the two roots of the ARMA(2,1) model), then the residuals would still be an AR(1) process. Therefore, estimating the residuals with an AR filter could possibly capture the remaining dynamics.
Transposing the same argument into the GARCH framework, the conditional variance might be estimated as GARCH(1,1), but the correct model might have asymmetry, leverage, jumps, thresholds and/or higher time-varying moments. As a result, the parameter estimates might be biased. The standardized residuals, which are typically not checked for further conditional heteroskedasticity (as the common wisdom is that GARCH(1,1) should be sufficient), may have remaining heteroskedasticity, however mild. Fitting standardized residuals using a GARCH(1,1) model, which is the diagonal term of the DCC representation, will capture some dynamics. Even if the conditional correlations happen to be constant, the conditional covariances across the standardized residuals may appear to be dynamic because of the misspecification. Therefore, standardization does not filter out the dynamics in the covariances due to the biases in the initial GARCH(1,1) estimates. As a result, the conditional correlations may appear to be dynamic (with significant parameter estimates) due to misspecification in the first step. However, no research seems to have followed this line of research, and so it is not clear what the potential impact of the conditional variance misspecification might be on the conditional correlation dynamics.
2.9. DCC Cannot Be Distinguished Empirically from Diagonal BEKK in Small Systems
In [
18], it has been shown that the estimates of the dynamic conditional correlations from a scalar BEKK model—in effect an indirect DCC representation—are very similar to those from the DCC representation. This supports the argument that the DCC representation can mimic dynamic conditional correlations, at least for small financial portfolios. Theoretical arguments to support this claim are presented in [
9]. However, there is no empirical evidence of the similarities/dissimilarities between the dynamic correlations obtained from the DCC representation and those obtained, for instance, from a diagonal BEKK model. As a consequence, we cannot verify if the empirical fit provided by the DCC representation might be better than the fit obtained from a more general BEKK model in which the dependence across the conditional variance and covariances is taken into account. Clearly, the advantage of the DCC representation is in the ease of estimation, but mainly in large systems.
2.10. DCC May Be a Useful Filter or a Diagnostic Check, but It Is Not a Model
A significant problem in empirical practice is that many users seem to be under the misapprehension that DCC is a model when it is not. DCC has no obvious or desirable mathematical or statistical properties. Nevertheless, DCC may be a useful filter or a diagnostic check that can capture the dynamics in what are purported to be conditional ‘correlations’, even if they arise through possible model misspecification. In this context, the DCC filter may perform well empirically. In fact, the popularity of the DCC representation is motivated by two main elements, namely the ease in estimation, and the ability of the filter to capture the possible presence of dynamic correlations of conditional variance misspecification.
Consequently, the DCC filter may play a useful role in forecasting out-of-sample dynamic conditional covariances and correlations.
3. Conclusions
The paper discussed ten things potential users should know about the Dynamic Conditional Correlation (DCC) representation for estimating and forecasting time-varying conditional correlations. The reasons given for being cautious about the use of DCC included the following: DCC represents the dynamic conditional covariances of the standardized residuals, and hence does not yield dynamic conditional correlations; DCC is stated rather than derived; DCC has no moments; DCC does not have testable regularity conditions; DCC yields inconsistent two step estimators; DCC has no asymptotic properties; DCC is not a special case of GARCC, which has testable regularity conditions and standard asymptotic properties; DCC is not dynamic empirically as the effect of news is typically extremely small; DCC cannot be distinguished empirically from diagonal BEKK in small systems; and DCC may be a useful filter or a diagnostic check, but it is not a model.
The computational advantages of the DCC representation might become relevant when focusing on large systems. However, there is no empirical evidence on the comparison of conditional correlations obtained directly from the DCC representation and indirectly from the BEKK model in a large cross section of assets. As a result, we cannot verify if the use of the DCC filter provides conditional paths that are similar to those obtained from a viable alternative model. On the other hand, the BEKK model is more general as it allows for direct spillovers and feedback effects across conditional variance and covariances, as well as indirect spillovers and feedback effects across conditional correlations. The GARCC model is also a viable alternative as it satisfies the definition of a dynamic conditional correlation matrix, and also has demonstrable, as distinct from assumed, regularity conditions and asymptotic properties.
As DCC is presently the most popular representation of dynamic conditional correlations, potential users are strongly encouraged to understand and appreciate the limits of DCC in order to be able to use it as a sensible filter or as a diagnostic check for estimating and forecasting dynamic conditional correlations.
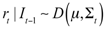
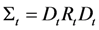

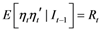
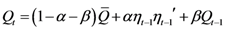
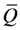 is assumed to be a positive definite matrix with unit elements along the main diagonal (which is alleged to be a conditional correlation matrix), the two scalar parameters satisfy a stability constraint of the form α + β < 1, and the sequence Qt purportedly drives the dynamics of the conditional correlations.
is assumed to be a positive definite matrix with unit elements along the main diagonal (which is alleged to be a conditional correlation matrix), the two scalar parameters satisfy a stability constraint of the form α + β < 1, and the sequence Qt purportedly drives the dynamics of the conditional correlations.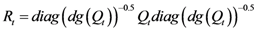
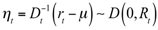
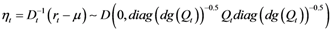
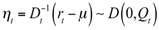
 . However, such a procedure cannot be applied to the DCC representation because the covariance is obtained as
. However, such a procedure cannot be applied to the DCC representation because the covariance is obtained as  . Consequently, the traditional way of deriving correlations applies to the conditional matrix Qt and not to the full conditional covariance. We conclude that we cannot derive conditional correlations in the usual way due to the presence of two standardizations rather than just one.
. Consequently, the traditional way of deriving correlations applies to the conditional matrix Qt and not to the full conditional covariance. We conclude that we cannot derive conditional correlations in the usual way due to the presence of two standardizations rather than just one.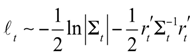
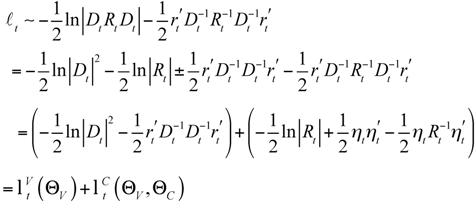
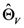 ).
). , [1] suggests replacing the matrix Q with the sample correlation matrix of the standardized residuals ηt, thereby introducing an intermediate “1.5” step.
, [1] suggests replacing the matrix Q with the sample correlation matrix of the standardized residuals ηt, thereby introducing an intermediate “1.5” step., which is not necessarily a correlation matrix.
, and is a proper “two step” procedure when the correlation likelihood
is maximized with respect to the full parameter set ΘC, and conditionally on the variance parameters ΘV.
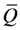 . In addition, such a limited dynamic effect might be amplified in the dynamic correlation matrix Rt, as defined in (7), due to the presence of the standardization. This may well confuse the user of the DCC representation, who might not be aware that that the purported dynamics are spurious.
. In addition, such a limited dynamic effect might be amplified in the dynamic correlation matrix Rt, as defined in (7), due to the presence of the standardization. This may well confuse the user of the DCC representation, who might not be aware that that the purported dynamics are spurious.




