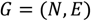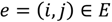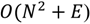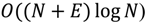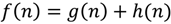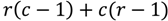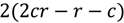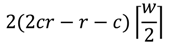2. GIS and Cost Rasters
In the context of geographical information systems (GIS), pathfinding can be performed using either the vector or the raster data structure, both having their respective strengths and weaknesses. In the vector data structure, each object is composed of a series of coordinate pairs. This data structure is very useful for finding paths in situations where the environment consists of entities with well-defined boundaries. However, most often the task of determining paths through off-network space is based on the idea of cost surface analysis where space is represented by discrete and regular cells specifically associated with the raster data structure. The main advantages of the raster structure are that, due to their regular composition, rasters are easy to handle and process, and are also well suited for representing continuous spaces [
11,
12,
13].
A raster-based representation of space can be transformed into a graph by treating the center point of each cell as a node, and connecting each such point to the center points of other cells. Since there are an infinite number of movement options in two-dimensional space, there are also multiple ways to approximate connectivity. The most commonly used connectivity pattern is to link a cell to its four orthogonal and four diagonal neighbors, amounting to eight movement angles [
14]. The neighborhood can, of course, be extended beyond the contiguous neighbors, allowing for more directions of movement but resulting in an increasingly dense graph [
15,
16]. If the cells of the raster are assigned with cost values (defining the cost of movement per distance unit through the cell), the cost of each step connecting the centers of two cells can be calculated according to the stretch of distance traveled through the underlying cells [
17].
The raster graph allows the same algorithms used commonly in transportation networks to be utilized in calculating paths through off-network space. Typically the classic algorithm originally proposed by Dijkstra [
18], or a variation of it, is used for this purpose. Dijkstra’s algorithm is well-known in the literature and can be found in almost any book on algorithms (see, for example, [
19]).
Dijkstra’s algorithm essentially solves the single-source least-cost paths problem on a weighted graph G; in other words, it produces a tree of least-cost paths from a start node s to all other nodes of G. The algorithm is initialized by assigning a tentative cost value c to all nodes: zero for s, and infinity for all other nodes. At the initial stage all nodes are also marked “open”, denoting that they have not yet been visited by the algorithm. The algorithm then repeatedly selects and “expands” the node with the smallest c among the “open” nodes. This means that the algorithm scans all unvisited neighbors of i, and checks if the combined value of ci and the cost of the edge connecting i and its neighbor j is smaller than the previously recorded tentative value cj. If this is the case, cj is updated with the new, smaller value. Once all the neighbors of i have been processed, i is marked “closed” and thus never visited again by the algorithm. The process is repeated until all nodes reachable from s have been visited, or if a path needs to be found between s and the destination node d only (rather than from s to all other nodes), it is sufficient to terminate the search as soon as d is reached. The path between the two nodes can be determined simply by backtracking the sequence of moves from d to s, which only requires that a pointer to the previous node be assigned to each node by the algorithm.
The running time of Dijkstra’s algorithm, in its most basic form, is
where
N and
E stand for the number of nodes and edges, respectively. However, when the algorithm is implemented with a priority queue for fast retrieval of the currently cheapest node, the running time is reduced to
assuming that the queue is implemented as a binary heap.
3. Strategies to Improve Raster-Based Pathfinding
There are two major drawbacks of raster-based pathfinding: one is the distortion inherently present in raster-based paths, and the other is the high computational effort needed to calculate the paths, especially when large rasters are concerned. The distortion, provoked by the neighborhood pattern used to create the raster graph, manifests itself as elongation and deviation error. The elongation error is due to the raster-based path unavoidably proceeding from one cell center to the center of one of the adjacent cells. Accordingly, there is a discrepancy between distance measured in the raster space and continuous space: the former tends to be greater than the latter. The deviation error, in turn, is the distance of the raster path from the corresponding continuous-space path. Considering the hypothetical case of a uniform cost raster, the deviation error is maximized when the path consists of an equal number of moves in orthogonal and diagonal directions, and when the orthogonal moves are made first followed by the diagonal moves [
15].
The use of larger neighborhoods is one conventional strategy to decrease the distortion in paths induced by the raster structure. Instead of the conventional eight-connected pattern, larger patterns embracing 16, 32 or even more neighbors have been used [
14,
15,
16,
20]. Even though distortion can be decreased in this manner, it comes with the cost of increasingly dense graphs and associated computational expense. Another way of addressing the problem is to correct the calculated paths by replacing the distorted segments of the path with straight lines, whenever possible [
20,
21]. This results in more intuition, and also more useful paths.
The other major drawback of raster-based pathfinding—high computational cost—is a general challenge concerning all kinds of graph search problems. However, the problem is aggravated for raster-based graphs due to their high density. A raster typically needs to have a relatively high resolution in order to provide an adequately accurate representation of the environment. As each cell is treated as a node, this translates into a large number of nodes in the graph. In contrast, for graphs representing transportation networks, a relatively small number of nodes are needed to represent the network, each node being typically connected to two or three nodes only.
Although Dijkstra’s algorithm is rarely used in its basic form without employing more efficient internal data structures, finding a path with Dijkstra’s algorithm is nevertheless computationally demanding, especially with large graphs. The computational efficiency of pathfinding can be improved with heuristic strategies, which can be classified into three categories: limiting the search area, decomposing the search problem, and using an “abstraction” problem-solving strategy [
22]. The idea behind limiting the search area is to make use of some knowledge about the start and destination locations to constrain the search to a least-cost path within a certain area. This addresses one of the main disadvantages of Dijkstra’s algorithm, that is, that it propagates the search in all directions instead of the actual direction of the destination. The A* algorithm, originally proposed by Hart
et al. [
23], is typically used to address this problem. Dijkstra and A* are effectively similar, with the exception that the latter performs an informed search based on a heuristic evaluation function. The function is denoted as
where
g(n) gives the path cost from
s to
n, and
h(n) is the estimated cost to get from
n to
d [
24]. If the heuristic estimate employed by the algorithm is admissible, signifying that the distance from
n to
d is never overestimated, the algorithm is guaranteed to find an optimum path [
25]. A* is considered to be the best choice in its class of algorithms: no other optimal algorithm is guaranteed to expand fewer nodes than A*. However, this does not always guarantee fast search, because for most problems, the number of nodes within the search space is still exponential in the length of the path [
24].
Both Dijkstra and A* are deterministic algorithms that follow specific rules in their operation, and thus their behavior is completely predictable [
26]. As an alternative to these methods, stochastic methods employing probabilistic search rules have been used to solve pathfinding problems. For example, ant colony optimization (ACO), inspired by the behavior of ants [
27], has been used to find optimal paths on terrain images [
28] and in indoor environments [
29]. Genetic algorithms (GA), drawing on the principles of natural selection [
30], have also been used to address shortest path [
31], corridor location [
32] and re-routing problems [
33]. According to a performance evaluation of Dijkstra, A* and GA [
26], the use of a stochastic search method can be a more efficient choice compared to the deterministic methods, especially for large-scale pathfinding problems. However, due to the tractability and predictability of the deterministic methods, it is likely that especially A* will remain a popular choice for pathfinding, provided that techniques improving its performance can be utilized.
Bidirectional search, which belongs to the category of techniques aimed at decomposing the search problem, is one available option for limiting the search effort of the A* algorithm. In this technique, two searches are run simultaneously: one from
s towards
d, and one in the opposite direction. An optimum path is found once these two searches meet each other somewhere in the middle. The rationale for employing bidirectional rather than unidirectional search is that whereas a search tree grows exponentially by its depth, the combined number of processed nodes by two smaller searches can be, at least in principle, less than the number of nodes processed by a single large search [
34,
35,
36]. The challenge with bidirectional search is that there is no guarantee an optimum path between
s and
d has been found when the two search frontiers meet. The search frontiers may therefore have to significantly overlap each other, resulting in performance inferior to conventional unidirectional search. While several solutions have been proposed to provide improved efficiency compared to more conventional bidirectional search [
36,
37,
38], their utility has not been extensively tested with real-world datasets [
22].
Although the graph search process can be trimmed using the techniques described above, they do not always provide a satisfactory solution to the computational challenge posed by large graphs. Therefore, instead of attempting to modify the search algorithm itself, an alternative way to seek improved performance is to decrease the size of the graph. This may involve creating an abstraction of the problem, thereby retaining only the essential features of the problem and discarding the irrelevant details. For rasters and raster graphs, there are several standard techniques that may be used to create an abstraction. The most straightforward way is to reduce the resolution of the raster by means of resampling, and then use the coarse raster to construct the raster graph. While this may indeed result in a dramatic reduction in the size of the raster graph and computation time, its obvious drawback is the loss of information and detail. One problem in particular is related to obstacles and narrow passageways surrounded by obstacles, which may be lost completely at coarsened resolutions. As a consequence, the pathfinding procedure may fail to find any path (even if one exists in reality), or may propose a path through an inaccessible region. This problem can be addressed by transforming the raster into a quadtree representation [
39] in which a group of cells is subdivided, step by step, into four smaller groups until each quadrant corresponds to a uniform block of cells. Compared to using the original raster for pathfinding, a quadtree-based search for an optimum path may be substantially faster, as the number of cells (nodes) is potentially considerably lower in the quadtree representation [
40]. However, this approach may yield suboptimal results when the cells are large, requiring the postprocessing of paths, the use of “framed” quadtrees, or alternative node placement strategies [
16,
20,
41].
A commonly applied solution for creating abstractions, especially in the context of transportation networks, is to exploit hierarchies. One option is to utilize the natural hierarchies present in transportation networks. By favoring primary roads and disregarding irrelevant local details, computation time can be reduced significantly. A hierarchy may also refer to a series of successive abstractions of the network that are specifically created for pathfinding purposes. There are many mechanisms for creating such abstractions, as explained in a review by Sturtevant and Jansen [
42]. While certain techniques, such as clique-based hierarchy, are best suited for general graphs where the topological relationships of the nodes are explicitly defined, the so-called sector-based hierarchy is particularly useful for raster graphs, where the topological relationships are implicit and portray a regular structure.
Hierarchical Pathfinding A* (HPA*), proposed by Botea
et al. [
43] and further improved by Jansen and Buro [
44] and Harabor and Botea [
45], is a pathfinding method that incorporates two heuristic strategies (the A* algorithm and an abstraction strategy) to improve the computational performance of raster-based pathfinding. The fundamental idea of creating an abstraction in the HPA* method is based on dividing a raster into a set of
blocks of equal size (or, as Li
et al. [
46] propose, into irregular-sized blocks based on decision tree). This initial phase is illustrated in
Figure 1a. Then, for each border between two adjacent blocks, the obstacle-free segments along the border are identified (
Figure 1b). These segments are the
entrances between the blocks. Movement through an entrance is only allowed via
transitions, which are defined for each entrance according to a predetermined transition placement scheme. A transition consists of two nodes, each placed on one side of the border between two adjacent blocks. An edge is drawn between these border nodes, connecting the blocks together (
Figure 1c). Edges of this type are called “inter-edges”. Another type of edges, “intra-edges”, are defined between all pairs of border nodes within each block by calculating the least-cost paths between them using eight-connectivity (
Figure 1d). The border nodes, together with the two kinds of edges, constitute the graph at the level of the block partition. Obviously, before using the graph to calculate a path between locations
s and
d (which may be located anywhere on the raster) these locations need to be temporarily connected to the graph. This is done by calculating least-cost paths from
s to the border nodes of the block containing
s and repeating the same procedure for
d as well (
Figure 1e). Finally, a path between
s and
d can be calculated on the graph using the A* algorithm (
Figure 1f).
The utility of HPA* is that a great deal of computation can be done in the preprocessing stage (phases a–d in
Figure 1), making the actual pathfinding task much faster. When a path is requested between locations
s and
d, all that is needed is to temporarily connect them to the precalculated graph by making small Dijkstra searches on the original cost raster within the blocks containing
s and
d, and then calculate a path between them on the graph using A*.
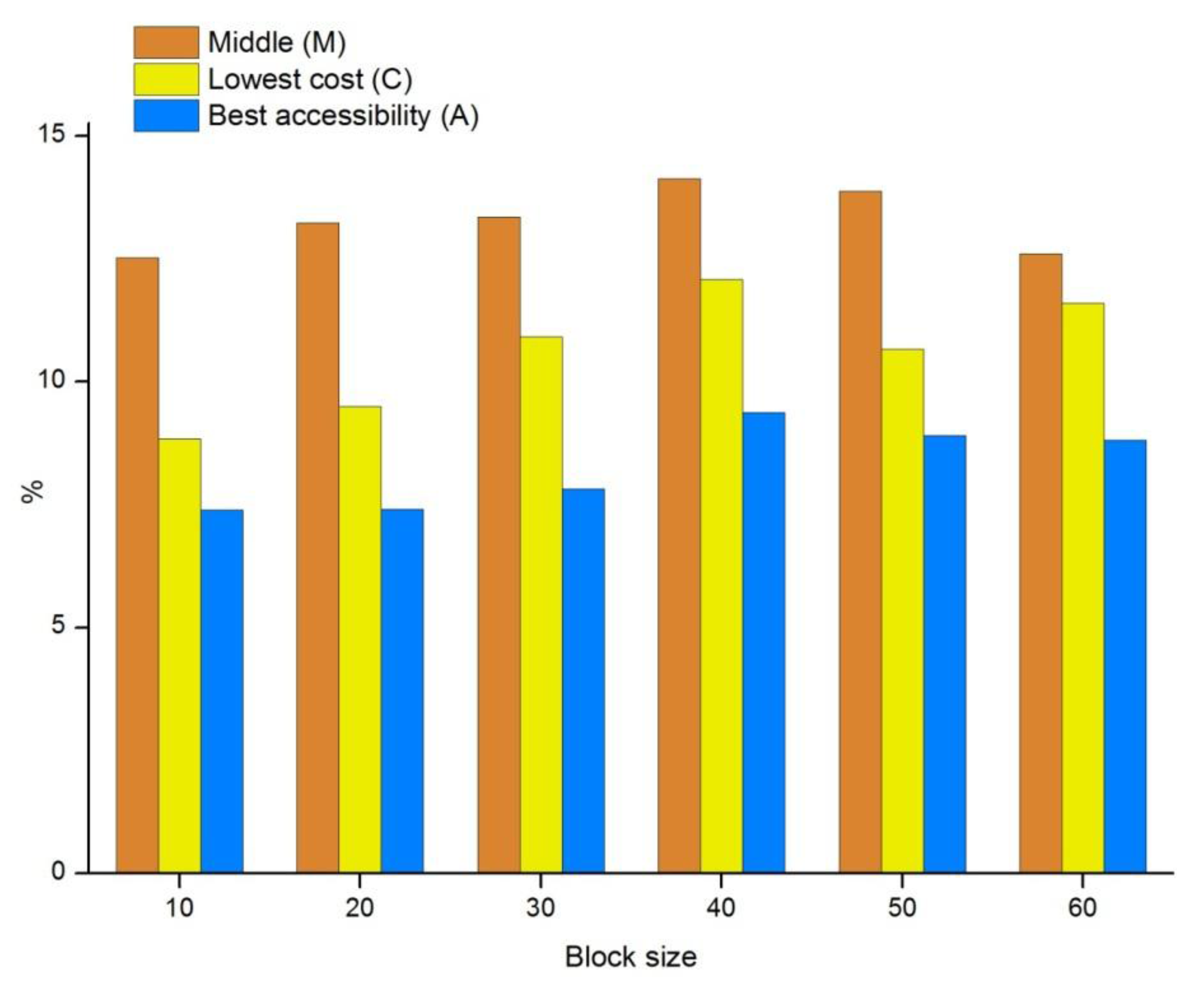
The overall computational effort of the pathfinding phase is determined by the block size. A large block size translates to a light-weight graph with a relatively small number of nodes. This saves time in the pathfinding phase, but the drawback of large block size is the increased effort needed to connect s and d to the graph. Conversely, small block size reduces the time needed to connect the locations to the graph, but the graph itself will contain more nodes, thus increasing computational cost. In order to address this problem of trade-off, a multi-level graph can be constructed. The benefit of a multi-level graph is that it allows paths to be calculated quickly by taking advantage of high abstraction levels, while providing a base level of small blocks that prevents the need for making large searches on the original raster to connect s and d to the graph.
In addition to block size, the placement pattern of transitions is an important parameter affecting the quality of the paths produced by the method. In their study, Botea
et al. [
43] suggest placing the transition in the middle of an entrance, if the width of the entrance is less than six cells. Otherwise, two transitions are defined, one on each end of the entrance. It is important to realize that this placement pattern is intended to be used for binary rasters consisting only of free space with uniform passage cost and impassable obstacles. For rasters of this kind, the positioning of the transitions is not a highly critical factor, as the calculated paths can be corrected later by replacing the unnecessarily curved parts of the paths with straight shortcut lines, provided that the shortcuts do not intersect any obstacles. However, most real-world datasets involve a wide spectrum of traversability conditions which cannot be reduced to two classes. In such a case, a transition placement strategy based on the presumption of a binary division of space may not be very useful. This is true firstly because without taking into account the underlying traversal cost, the transition may end up being located at a position rarely used by any truly optimal path. Secondly, due to the varying cost of the cells, the paths generally cannot be improved by replacing curved parts of the path with straight shortcuts in the postprocessing phase. In other words, the transitions should be placed at the most appropriate locations in the first place, as the alignment of the path cannot be efficiently improved later.
Figure 1.
The scheme of the HPA* method: (a) dividing the cost raster into blocks, (b) identifying the entrances along the block borders, (c) determining a transition (inter-edge) to represent each entrance, (d) connecting the transition nodes within each block (intra-edges), (e) connecting s (start) and d (destination) temporarily to the graph, and (f) finding a path between s and d.
Figure 1.
The scheme of the HPA* method: (a) dividing the cost raster into blocks, (b) identifying the entrances along the block borders, (c) determining a transition (inter-edge) to represent each entrance, (d) connecting the transition nodes within each block (intra-edges), (e) connecting s (start) and d (destination) temporarily to the graph, and (f) finding a path between s and d.
Although the HPA* method, and raster-based pathfinding in general, has been widely studied in the literature, most of the research has been carried out in the fields of robotics, operations research and computer games. In these fields, the emphasis is usually on obstacle avoidance problems in restricted environments, whereas in geography and GIS the pathfinding typically involves varied traversal cost and large geographical areas. However, the standard raster-based pathfinding method, regardless of its limitations, is usually used in GIS without considering any alternative methods.
Motivated by the apparent lack of research, the intended contribution of this study is to propose an improvement to the HPA* algorithm which allows the transitions to be placed in a more informed manner than has been proposed in previous studies. The entire proposed algorithm is then implemented in GIS and tested and evaluated with actual data. The contribution of this study should be of particular interest for geography and GIS, and related application areas where paths need to be optimized in terms of varying traversal cost.
4. Implemented Method
Experimental implementation of the HPA* method was made for this study using the C# programming language and the ArcObjects components of the ArcGIS software. The basic HPA* algorithm, along with its pseudocode, has been described in detail in [
43] and will not be reiterated here. The major parts of the implemented method, and the contribution made by this work, are described below.
4.1. Transition Placement Strategies
As described above, transitions play an important role in the HPA* method. Since access from one block to another is only allowed through transitions, and since paths between any start and destination must “share” them, transitions greatly affect the quality of paths. Three different strategies for placing a transition on an entrance in the HPA* method are considered in this study. These strategies are based on the idea of placing a transition either in the middle of an entrance, at the position of lowest cost, or at the position of best accessibility and will be referred to as one-letter acronyms, as M, C, and A, respectively.
The M strategy is directly adopted from Botea
et al. [
43]. Despite being simplistic, it has certain advantages. The first advantage is its tractability: no complicated assessment of cell costs needs to be performed. Secondly, a transition placed in the middle of an entrance can be relatively efficient in minimizing the potential error, especially when the underlying cost is uniform over the whole width of the entrance.
The flaw of the M strategy lies in the fact that optimal paths tend to favor areas of low traversal cost, particularly corridors of low cost. The M strategy does not take this into account, and therefore there is a high chance that the location of the transition deviates from locations where the truly optimum paths cross the block border. In contrast, the C strategy aims at placing the transition at the position of the lowest traversal cost along an entrance. This procedure is not significantly more complicated than the M method as only the costs of the cells on the two sides of the entrance need to be evaluated. This simplicity is, again, also its disadvantage. The position of lowest transition cost along the border may only be an isolated case or part of a local cluster of low-cost cells rather than a larger area or corridor of low traversal cost. Particularly problematic are local clusters of low-cost cells near either end of an entrance, as this may force the paths to make unnecessary twists and thus impair path quality.
The limitations of the M and C strategies can be addressed by the third transition placement strategy presented here, namely the strategy based on determining the location of best accessibility (A). The objective of the A strategy is to more accurately predict where paths passing from a block to an adjacent block will cross an entrance between the two. Here, accessibility generally refers to the overall cost of movement between a transition candidate on the border between two blocks and the other borders of the blocks. There are different ways of assessing the accessibility of a transition candidate. One of the most straightforward options would be to calculate least-cost paths from both nodes comprising the transitions to the border cells of their respective blocks and then use this information to determine an accessibility score. The problem with this approach is that locations in the middle of the block border tend to naturally receive high accessibility scores, and as a consequence the transition placement pattern of A resembles that of M, resulting in a fundamentally similar abstraction. Therefore, a different strategy needs to be adopted to determine accessibility scores. The idea is to estimate where least-cost paths passing from one block to another most likely cross the border between the two. To determine this, least-cost paths are calculated between the cells of “opposite” block edges for each pair of adjacent blocks sharing a common border. This is illustrated in
Figure 2 for a case of horizontally adjacent blocks,
B1 and
B2, with the size of 4 × 4 cells. The procedure is performed between all pairs of cells along borders
b1upper and
b2lower,
b1lower and
b2upper, and
b1left and
b2right, excluding the cells assigned the role of a potential transition node. Once all the paths connecting the cells at the opposite borders of the blocks are calculated, the accessibility score is determined for each potential transition node by summing up the number of paths crossing each node. The transition will be created between those nodes that have the highest combined accessibility score. If two or more potential transitions along the same entrance happen to have an identical score, the centermost of these candidates serves as the transition.
Figure 2.
The principle used to determine accessibility scores. For illustration purposes, paths are shown only between the border cell at the top left corner of the first block and cells along the opposite, lower border of the neighboring block. The calculated score indicates the potential transitions which will most likely be shared by different paths, and the transition is placed at the position of the highest score (in the case of a tie, the centermost candidate is chosen).
Figure 2.
The principle used to determine accessibility scores. For illustration purposes, paths are shown only between the border cell at the top left corner of the first block and cells along the opposite, lower border of the neighboring block. The calculated score indicates the potential transitions which will most likely be shared by different paths, and the transition is placed at the position of the highest score (in the case of a tie, the centermost candidate is chosen).
4.2. Hierarchical Abstraction
In addition to the placement of transitions, the operation of the method is mostly dependent on the choice of block size and the number of hierarchical levels above the base level. The implemented method receives both of these parameters as user input. First, the raster is divided into blocks according to the specified base block size (e.g., 20 × 20 cells). Using this division, transitions are placed on the entrances between adjacent blocks and the graph is constructed.
If the hierarchy consists only of the base level L1, this is all that needs to be done in the preprocessing phase. When more than one hierarchical level is requested, the levels are constructed according to the quadtree structure such that each block at a higher level consists of four blocks at one level below. For example, with a base block size of 20 × 20 cells and the number of levels set to three, the block size of the levels L1, L2 and L3 would be 20 × 20, 40 × 40, and 80 × 80 cells, respectively. The higher levels are always constructed on top of the graph defined at the base level, sharing the same nodes and edges. However, the intra-edges of larger blocks are constructed by concatenating the lower-level edges to constitute direct connections between their border nodes. This procedure guarantees that while generating higher-level abstractions, path quality is not affected by the number of hierarchical levels defined above the base level. It is worth noting that the quadtree structure used here is by no means the only conceivable option to construct the succession of hierarchies. The quadtree structure was chosen since it is well-known in the literature and easy to implement and manage, but there are no compelling reasons to restrict the hierarchical structure specifically to this structure.
If the hierarchy consists only of the base level L1, this is all that needs to be done in the preprocessing phase. When more than one hierarchical level is requested, the levels are constructed according to the quadtree structure such that each block at a higher level consists of four blocks at one level below. For example, with a base block size of 20 × 20 cells and the number of levels set to three, the block size of the levels L1, L1 and L1 would be 20 × 20, 40 × 40, and 80 × 80 cells, respectively. The higher levels are always constructed on top of the graph defined at the base level, sharing the same nodes and edges. However, the intra-edges of larger blocks are constructed by concatenating the lower-level edges to constitute direct connections between their border nodes. This procedure guarantees that while generating higher-level abstractions, path quality is not affected by the number of hierarchical levels defined above the base level. It is worth noting that the quadtree structure used here is by no means the only conceivable option to construct the succession of hierarchies. The quadtree structure was chosen since it is well-known in the literature and easy to implement and manage, but there are no compelling reasons to restrict the hierarchical structure specifically to this structure.
Besides the base block size and the number of levels, the user may also determine any number of transitions for an entrance by defining the maximum number of cells that can be represented by a single transition. For each entrance, the width of the entrance is divided by this value and the ceiling of the quotient is used to divide the entrance into segments of equal width. A transition is then placed separately for each segment, according to the chosen transition placement strategy.
4.3. Graph Search
Analogous to finding a route through a large road network, the most reasonable way of finding the path with the HPA* method is to utilize the highest level of the hierarchy to the maximum extent possible. This allows the method to discard most of the nodes and edges at the lower levels, completing the calculation more quickly. On the basis of this principle, the pathfinding procedure has been implemented as follows.
The algorithm constructs a temporary graph Gt which contains only those parts of the original hierarchy of graphs that are necessary for finding a path between two given locations s and d. First, the highest level of the hierarchy serves as the basis for Gt (here the highest level Ll is included in the temporary graph completely, but in the case of very large areas and graphs, the extent to which the highest level abstraction is included in Gt should be delimited according to some criteria). Secondly, the block containing s at level Ll (Bo) is identified. The subgraphs associated with the four blocks from level Ll-1, which are contained in Bo, are added to Gt. The process is successively continued downwards throughout the hierarchy until the base level (L1) is reached. At the base level, s is connected to Gt by calculating least-cost paths using Dijkstra’s algorithm through the original cost raster to the border nodes of the base level block containing s. The same procedure is of course performed for d as well. This effectively means that only two small searches on the original cost raster are needed to connect s and d to the base level Ll, and from that level, they are connected to successively higher levels of the hierarchy.
Once the graph structure Gt has been completed, calculating a path between s and d is a simple matter of running the A* algorithm on Gt. In this implementation, the function of the estimated distance that is used to guide the A* search in the general direction of the destination node is based on the product of the Euclidean distance between n and d, and the lowest unit cost value cmin present in the cost raster. The graph search can be done both unidirectionally and bidirectionally; however, since initial tests indicated that no improvement was gained by using the bidirectional search technique, only unidirectional search was included in the final implementation. The algorithm was implemented with a priority queue using a binary heap.
7. Discussion
While the HPA* method can provide a considerable computational advantage for pathfinding on large cost rasters, it also involves certain disadvantages that need to be considered. The main criticism of the method is the deviation of the paths from the true optimum, which is an unavoidable result of the abstraction. Even when this error is not very large, it adds to the error inherently present in raster-based paths. The error could be decreased by allowing more transitions per entrance, and thereby gain a more accurate representation of the movement options. Again, this comes at the price of increased computational cost in the pathfinding phase, which may be prohibitive in applications requiring immediate response.
An additional source of error stems from the fact that the transitions only allow block borders to be crossed in an orthogonal fashion. However, this is only a matter of implementation, as diagonal transitions could be taken account of, for example, by employing a node placement pattern in which nodes are placed on cell borders rather than cell centers [
16,
20]. By using this procedure, a transition would consist of only a single node located on the border between two blocks, offering more flexibility as to the directions in which the border can be crossed. This would also provide computational advantage by decreasing the number of nodes in the abstraction. However, the counterweight of this option would be a more complex preprocessing phase.
There are some additional aspects concerning the described method, or its implementation, that could be done differently. In this case, as well as in the implementation of the original authors of the HPA* method, the higher level abstractions are built on the base level abstraction. There are two important advantages to this. Firstly, the construction of the higher level abstractions can be done quickly, and secondly, the results always remain the same irrespective of the number of hierarchical levels used. However, it could be possible to define transitions (and the intra-edges) independently for each level of abstraction. This would provide more flexibility in the placement of transitions, which in turn could improve path quality, especially at very high levels of abstraction. In fact, this procedure was tested at an early phase of the study with fairly promising results but was subsequently abandoned due to impractically long preprocessing time. An additional issue would be the consistency of the results, since the results would always depend on the number of abstraction levels used.
Another modification of the method might be to retain only a single transition per entrance at all levels. In the implemented method, all the transitions defined at the base level are transferred to higher levels as long as they correspond to the boundaries of the higher level blocks. However, this exceeds what is needed to ensure connectivity at higher levels. By redefining entrances at each level, and selecting only a single transition from the lower level to represent the entrance at the higher level, the size of the graph could be reduced significantly. An experiment with this procedure was done as well. The computational effort was indeed reduced, but as a negative effect, the error increased to an unacceptably high level of 15%–40%. A path calculated in this way could be refined in a postprocessing phase by successively recalculating the path at lower level abstractions using the crossed higher level blocks as a “mask” delimiting the search at the lower level. While the path can be refined in this manner, the computational expense incurred by the postprocessing phase cancels out any advantage gained by the sparcification of the graph.