1. Introduction
A typical approach to land-use and land-cover change (LUCC) modeling is to investigate how different variables relate to historic land transitions, and to then use those relationships to build models to project future land transitions [
1,
2]. Moreover, in general the spatially-explicit models of LUCC begin with a digital map of an initial time and then simulate transitions in order to produce a prediction map for a subsequent time [
3]. Upon seeing the prediction results, questions may arise about the accuracy of the base maps, the performance of the model and whether this predicted map represents the real scenario [
4]. In this regard, it is necessary to quantify the map errors, the amount of differences among the maps and to validate the models used for prediction.
With the growth of high-resolution spatial modeling, geographic information systems (GIS) and remote sensing the need for map comparison methods increases. Good comparison methods are needed to perform calibration and validation of spatial results in a structured manner [
5]. The importance of map comparison methods is recognized and has growing interest among researchers [
6,
7]. In general maps are compared for a number of reasons: (1) to compare maps generated by models under different scenarios and assumptions, (2) to detect temporal/spatial changes, (3) to calibrate/validate land-use models, (4) to perform uncertainty and sensitivity analyses and (5) to assess map accuracy. In fact, map comparison may be seen as finding a goodness-of-fit measure [
8].
There has been tremendous interest in validation of simulation models that predict changes over time [
9,
10]. However, there is usually less than perfect agreement between the change predicted by the model and the change observed in the reference maps, which is no surprise, since scientists usually do not anticipate that a model’s prediction will be perfect. Furthermore, scientists rarely believe that the data are perfect. Therefore, a natural question is, “What accounts for the most important disagreements between the prediction and the data: (1) error in the prediction map, or (2) error in the reference maps?” [
11]. If precise information on accuracy and error structure is available, then there could be a method to incorporate information concerning data quality into measures of model validation [
12,
13].
Assessing model performance is a continuous challenge for modelers of landscape dynamics. A common approach is historical validation where a predicted map is compared to an actual map [
14]. However, many types of land-use models simulate land-use changes starting from an original land-use map, such as Markov models, cellular automata, logistic regression models, neural networks,
etc. Since most locations do no change their land use over the length of a typical simulation period, the similarity between the simulated land-use map and the actual land-use map will be high for most calibrated models [
15]. Therefore, to rigorously assess the accuracy of the simulated land-use map, a meaningful reference level is required [
16].
The evaluation of spatial similarities and land use change between two raster maps is traditionally based on pixel-by-pixel comparison techniques. This kind of change detection procedure is called the post-classification comparisons [
17]. A problem with this traditional approach is that, because they are based on a pixel-by-pixel comparison, they do not necessarily capture the qualitative similarities between the two maps. This problem becomes important when map comparisons (e.g., of actual and predicted land use) are used to evaluate the output of predictive spatial models such as cellular automata based land use models [
18]. The lack of appropriate comparison techniques, specially, the ones that can handle qualitative comparisons of complex land use maps for the purpose of evaluating model output, is currently a major problem in the area of predictive simulation modeling [
19].
Recently, numerous map comparison methods have been proposed that take into account the spatial relation between cells, as opposed to simple cell-by-cell overlap [
20]. These new methods consider, for example, proximity [
21], the presence of recognizable structures,
i.e., features [
22], moving windows [
23] or wavelet decomposition [
24]. Others have evaluated model performance based on metrics summarizing the whole landscape [
25,
26].
This is how different methods have been introduced and new software packages are being developed, for the sake of map comparison/validation of models that predict LUCC change from a map of initial time to a map of a subsequent time [
2]. This paper addresses these issues and illustrates some methods through a case study from Khulna, Bangladesh to validate the predicted maps. The main objective of this paper is to find out whether the simulation is giving any abrupt result or not and to compare among the different model validation techniques. Therefore, in this paper, we will discuss the advantages and disadvantages of some commonly-used map comparison techniques to assess the agreement between the simulated maps and the actual land-cover maps.
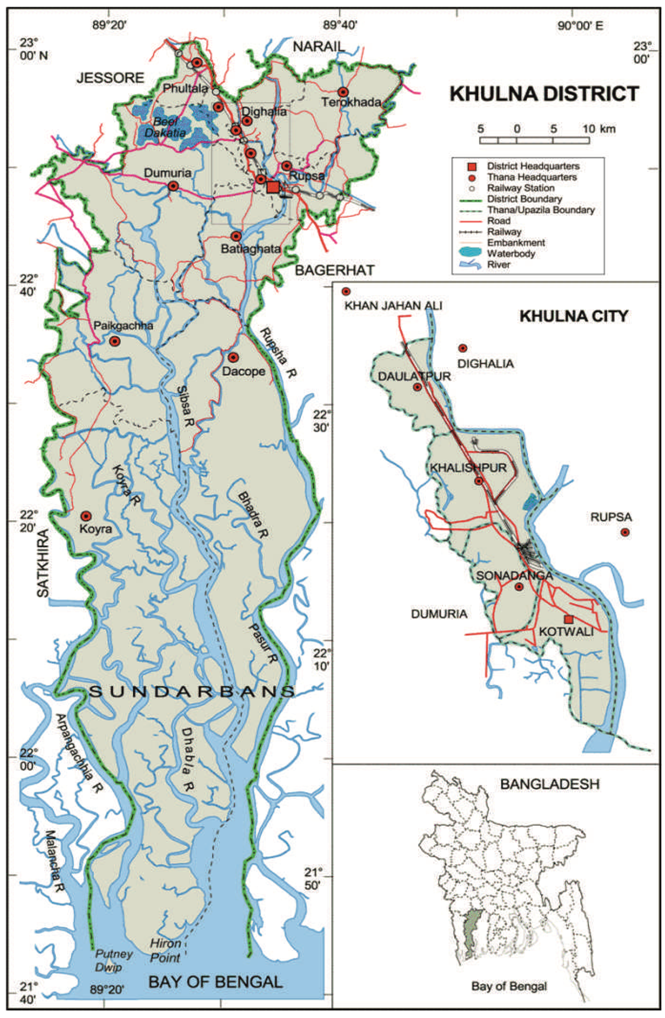
Figure 1.
Location of Khulna City in Bangladesh. Source: Banglapedia, National Encyclopedia of Bangladesh, 2012.
Figure 1.
Location of Khulna City in Bangladesh. Source: Banglapedia, National Encyclopedia of Bangladesh, 2012.
4. Conclusions
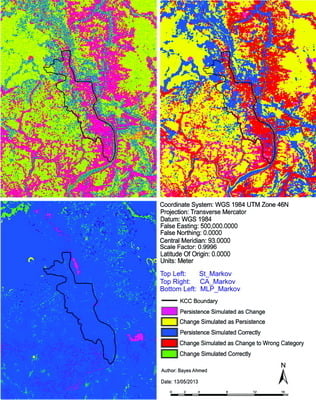
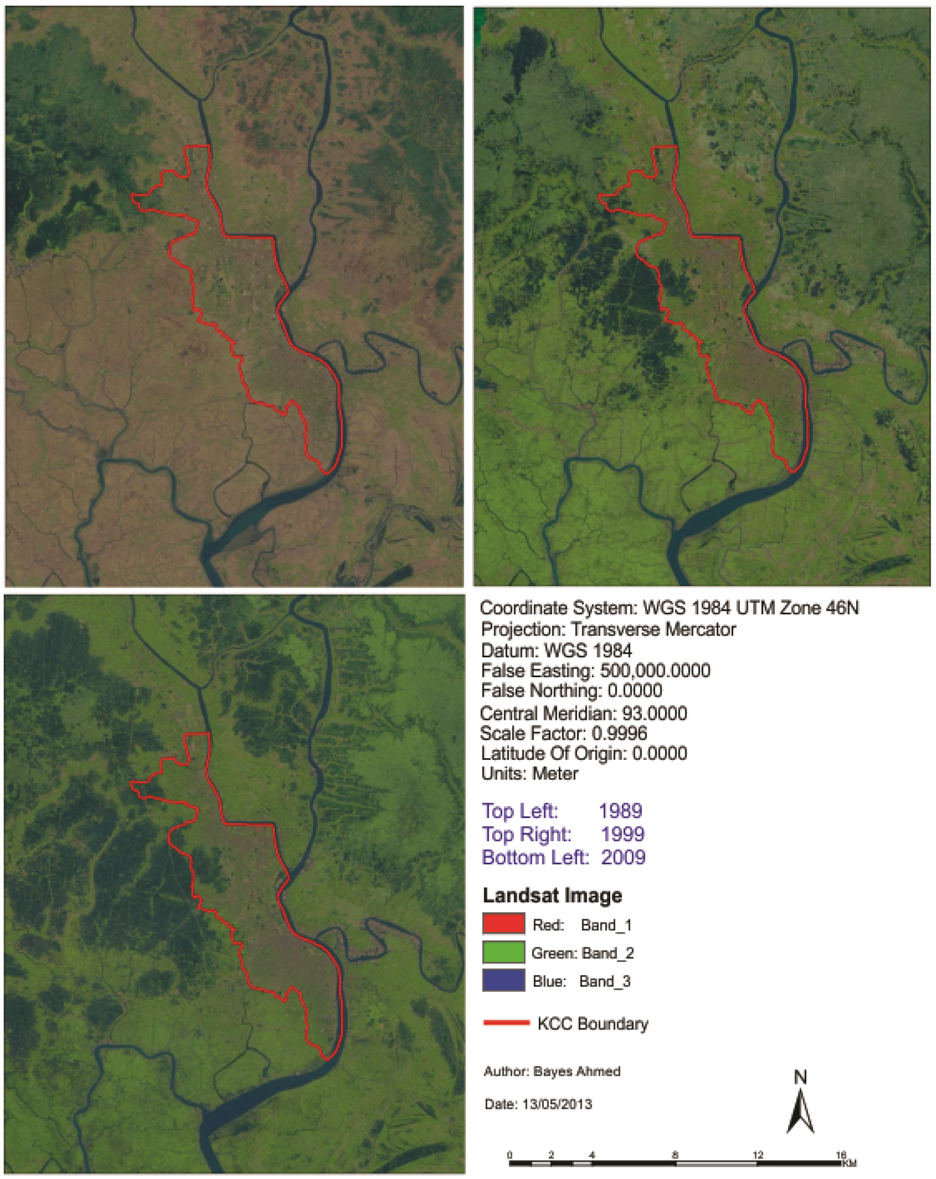
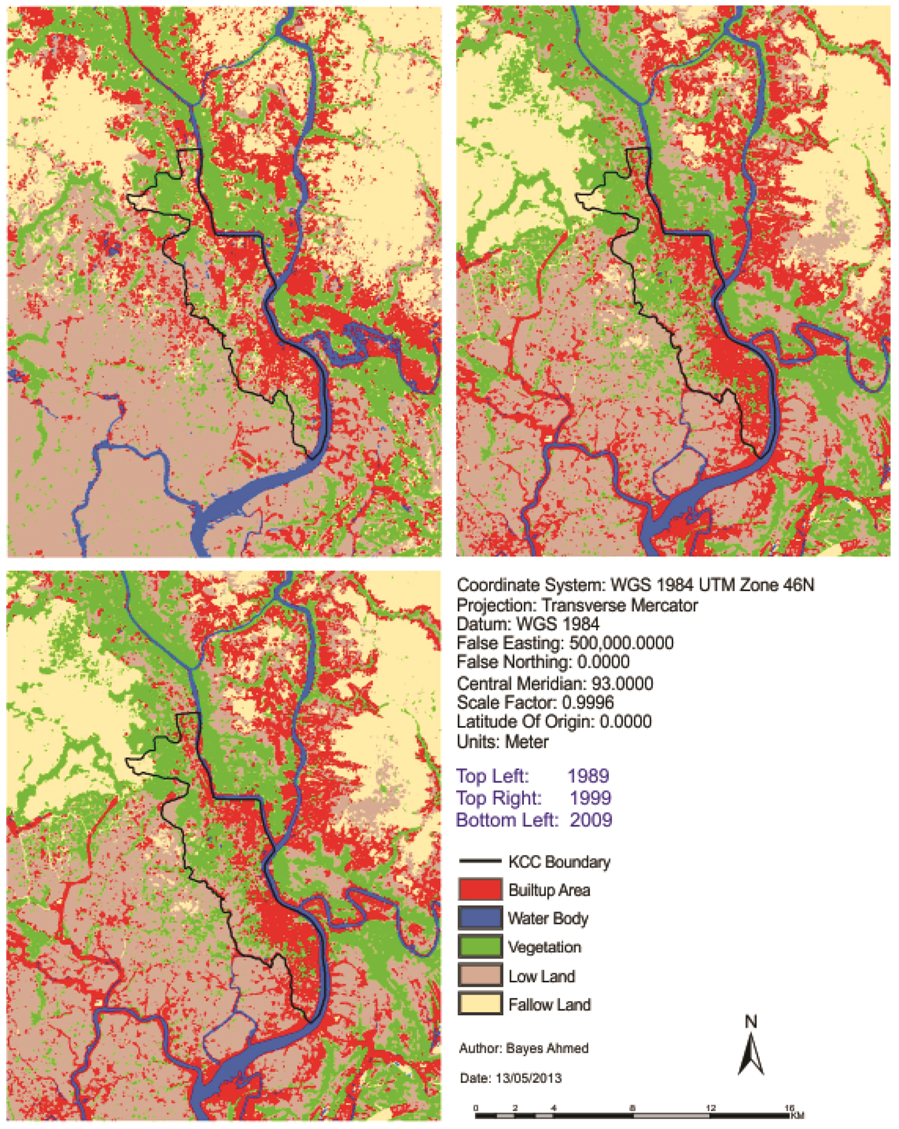
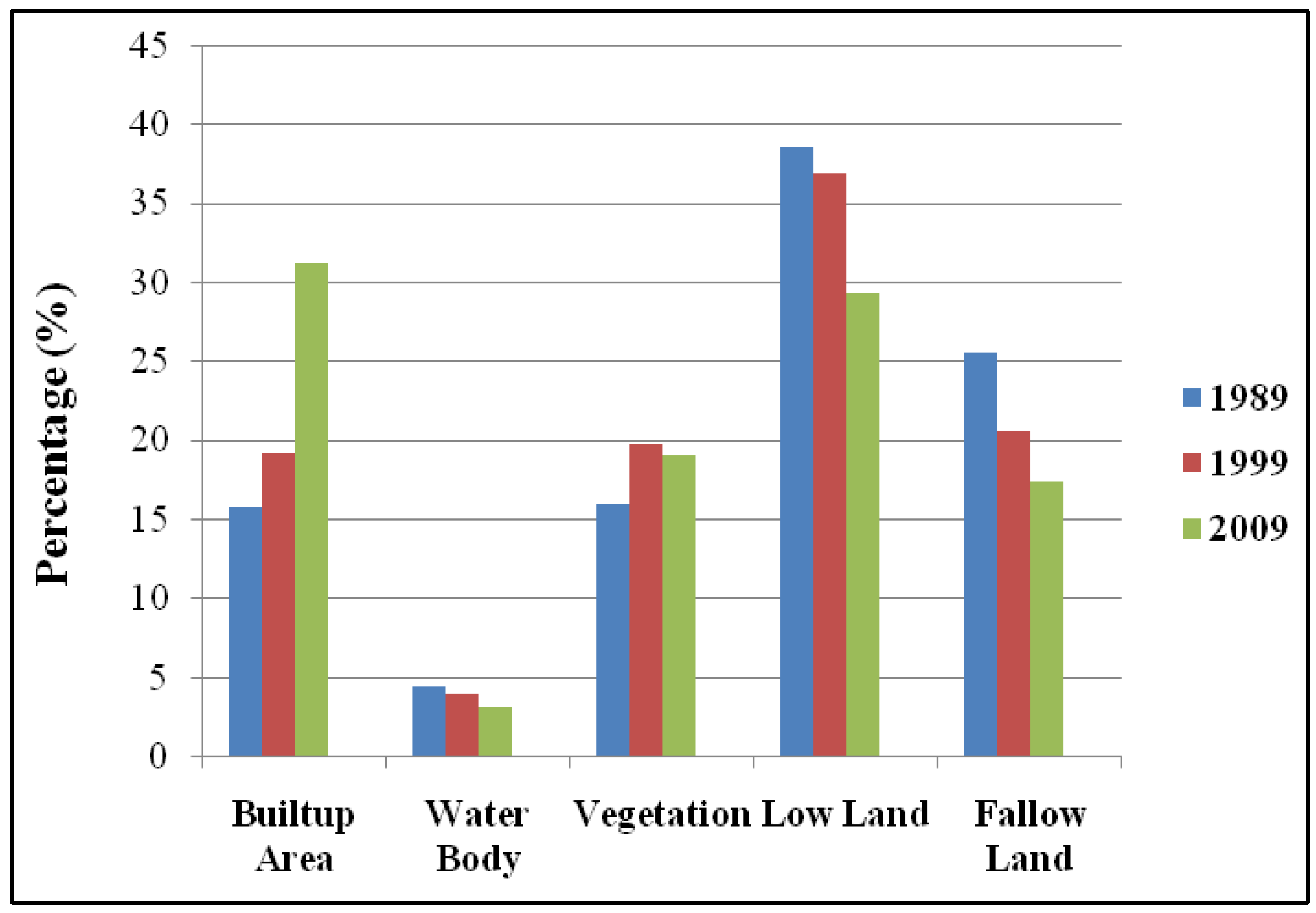
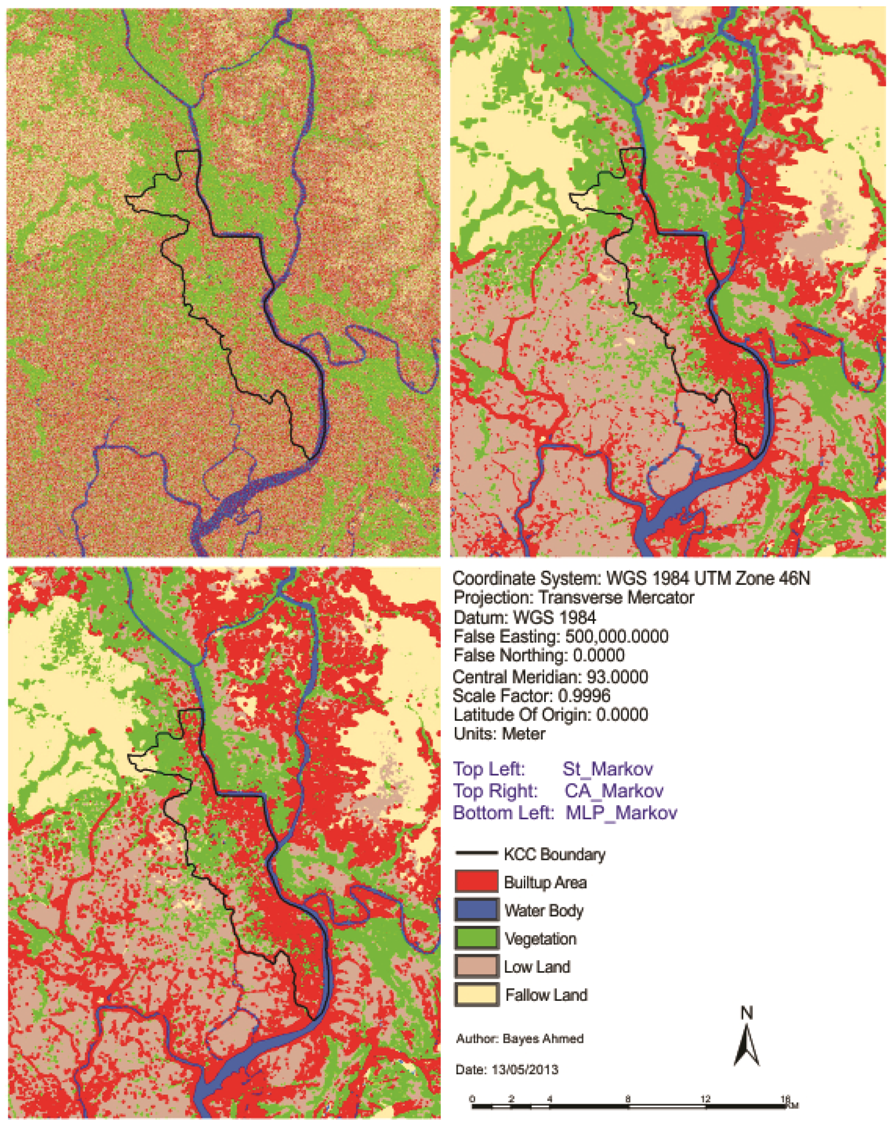
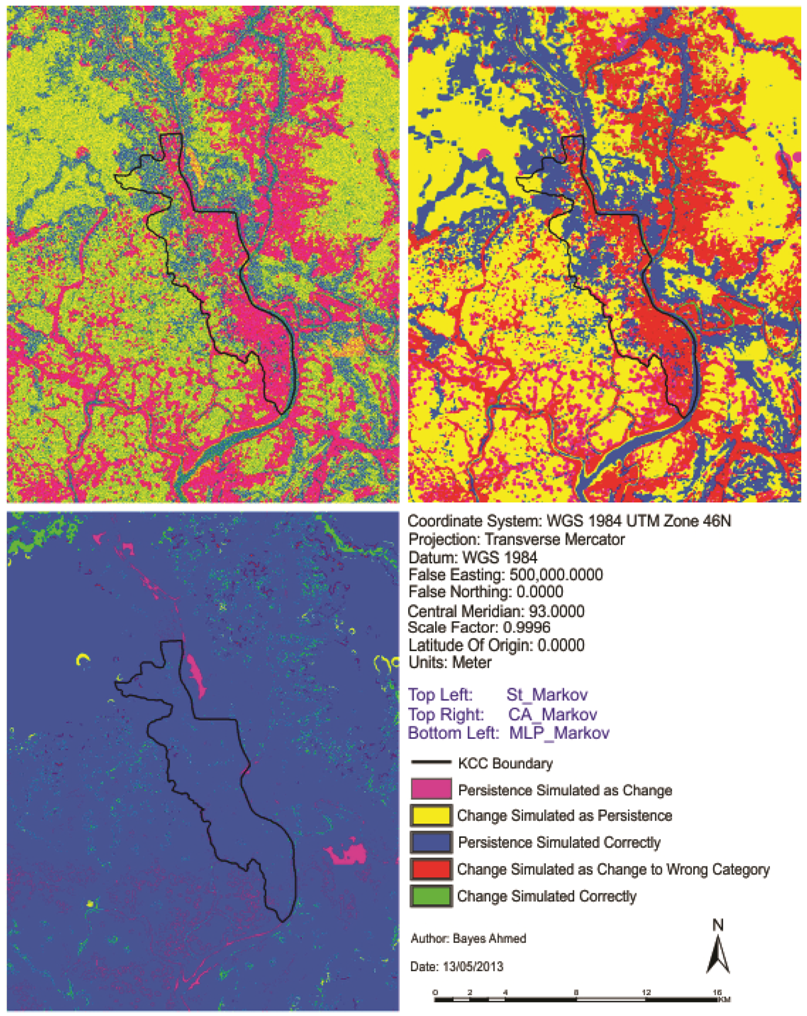
At the beginning of this paper, a fisher supervised classification method is applied to prepare the base maps of Khulna City with five land cover classes. After performing accuracy assessment and quantifying map errors, it is found that the errors in the maps are not much larger than the amount of land change between the two points in time (1989–1999 and 1999–2009). Later, being persistent with the inherent changing characteristics, three different methods are implemented to simulate the land cover maps of Khulna City (2009). The methods are named as “Stochastic Markov (St_Markov)”, “Cellular Automata Markov (CA_Markov)” and “Multi Layer Perceptron Markov (MLP_Markov)” model.
Then different model validation techniques like per category method, kappa statistics, components of agreement and disagreement, three map comparison and fuzzy method are applied. A comparative analysis, in terms of concerned advantages and disadvantages, on the validation techniques has also been discussed. Fuzzy set theory is found best able to distinguish areas of minor spatial errors from major spatial errors. In all cases, it is found that “MLP_Markov” is giving the best results among the three modeling techniques. This is how, it is possible to compare different models and choose which modeling technique is giving better results.
In order to compare the predicted change to the observed change and to perform validation for predictive land change models; it is recommended that scientists should use Kappa, three map comparison and fuzzy method based on the outcome of this paper.
Our hope might be realized if the error in the base maps is reduced to the point where the error becomes smaller than apparent change in land. This paper will help the researchers deciding whether the most important errors are in the model or in the data. Moreover, it is our belief that this kind of research has a high potential to contribute towards learning about the different available validation techniques and to choose the right one by the researchers working on different case studies.
We have designed this article in such an order so that it produces helpful information for other scientists whose goals are to validate a model’s performance and to set an agenda for future research.
5. Future Research
For any kind of model validation or map comparison, the accuracy of the base maps is very important. However, maintaining accuracy of the base maps is difficult due to lack of availability of historical data or verification of the older maps. Moreover, there are different image classification (e.g., supervised, unsupervised, object-based, hybrid, etc.) methods, which can give different results. Even the use of different filtering techniques (e.g., median, mode, mean, Gaussian), filter size, classifier (e.g., hard, soft, segmentation) and reclassification methods can give variant results. The spatial and temporal resolution of the remotely sensed images can also put impact while identifying training sites for signature development. All these factors can play important role in assessing the accuracy of maps or model validation purposes. This is why future research can be conducted incorporating all these relevant issues.
There are many available map comparison techniques. Each has its own advantages and disadvantages. Therefore, it is very important to distinguish which technique is suitable for a particular context or case study. This can be another dimension for future research. Finally, future research must address the spatial dependency between the maps to be compared.
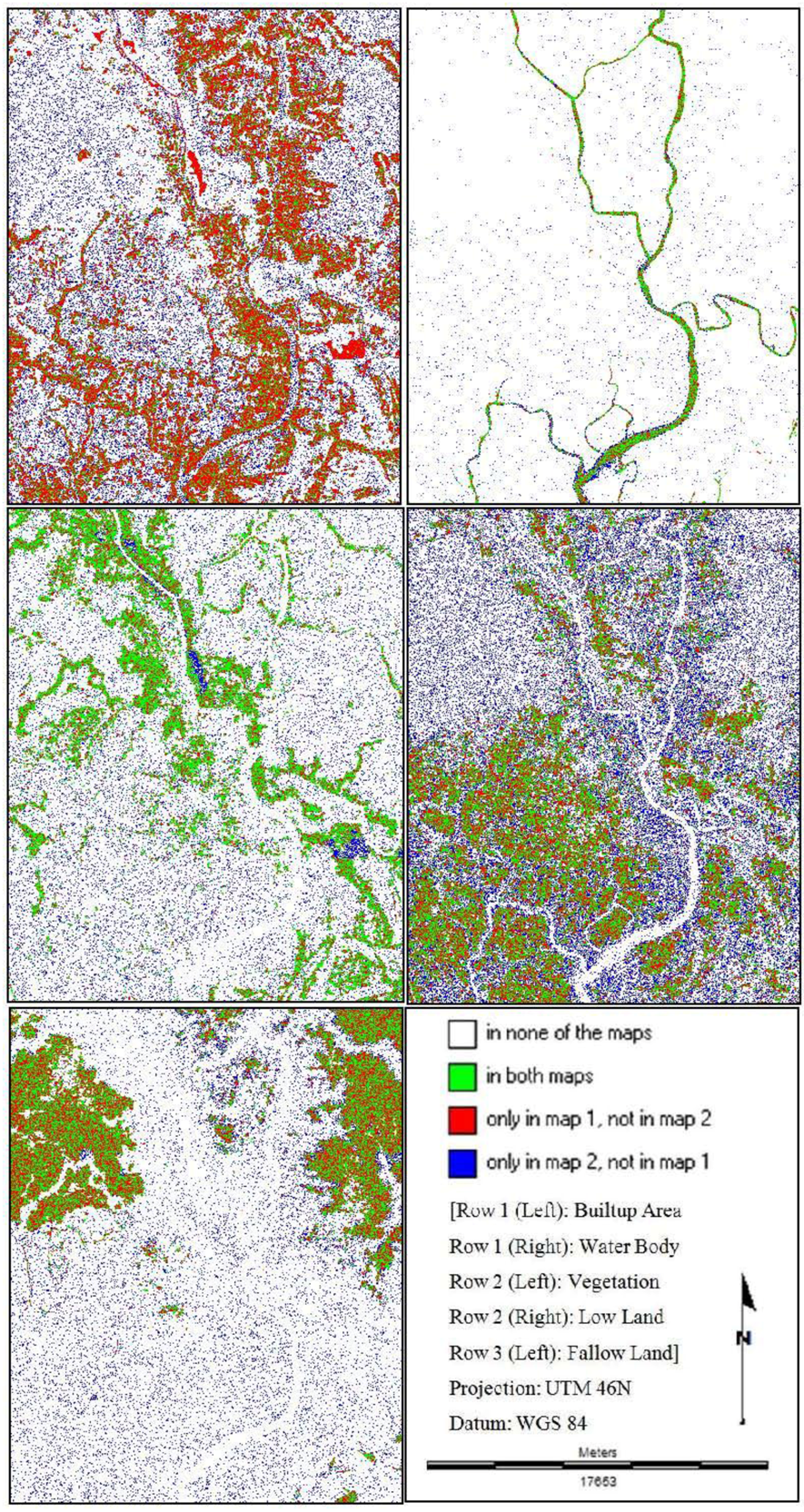

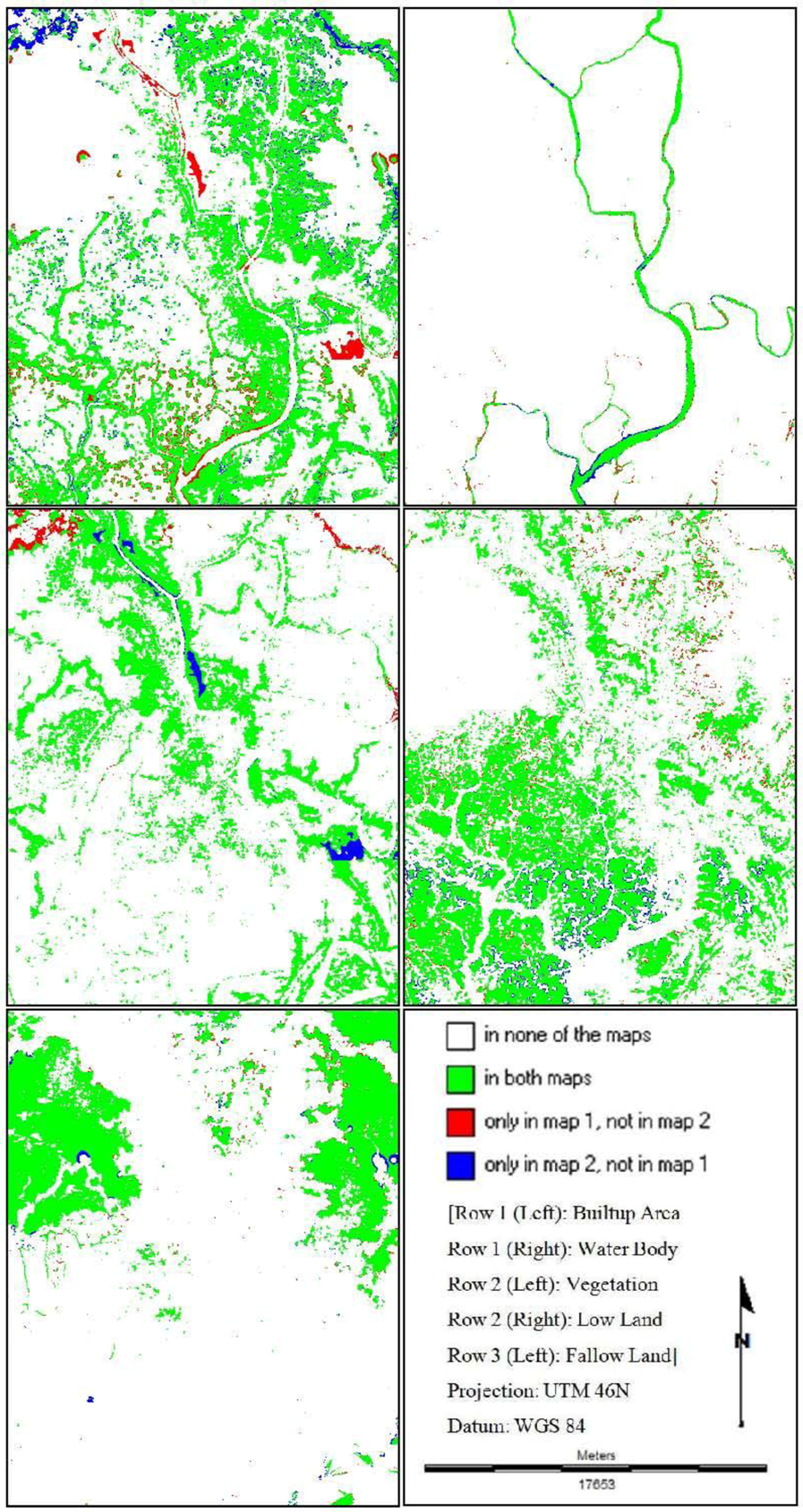
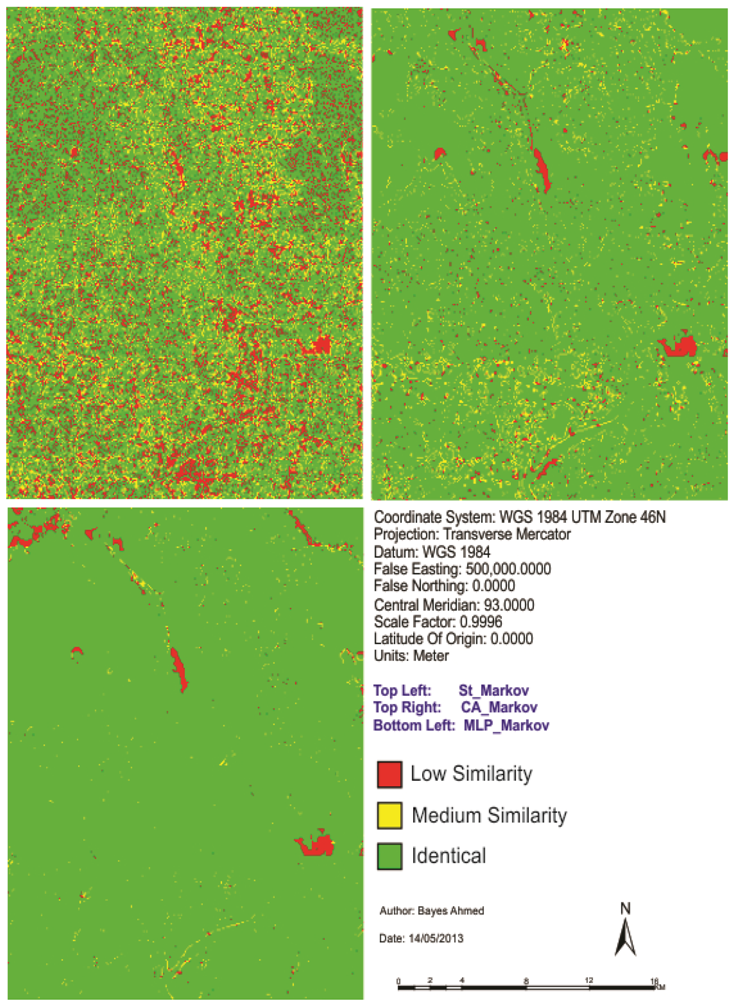
 Fuzzy Kappa (KFuzzy)
Fuzzy Kappa (KFuzzy)