2.1. Classical Doppler Broadening: Non Relativistic Case
Often the emission (or absorption) of radiation by a particle (atom, ion, etc.) occurs during the movement. By the Doppler effect, the observed frequency in the observer (at rest) frame (see
Figure 1) is different from the frequency emitted in the atom frame. The mean particle velocity at thermodynamic equilibrium is related to the temperature of the medium. Hence the broadening of the statistical Doppler effect is related to the distribution of the velocities of the emitter at the temperature T of the medium and the mass
m of the emitter.
One can assume a motionless observer, looking at an emitting atom moving with a velocity
in a direction forming an angle
with the direction of observation (Ox) (see
Figure 1), records a shifted angular frequency
with respect to the angular eigenfrequency
of the emitter assumed to be stationary. This angular frequency is given by
where
c is the velocity of the light in vacuum. The normalized intensity (normalized to one) of the line at the angular frequency
is given by the average over the normalized Maxwell distribution (normalized to one).
of the Dirac delta distribution as the following
Using the integral representation of the Dirac delta distribution (
u is the integration variable whose unit is the second)
We find the normalized intensity (normalized to one) as
where
,
is the Boltzmann constant and
m is the emitter mass. This is the formula of the intensity of the line in the non relativistic case. It is symmetric (Gaussian) around the central angular frequency
. We note that the integrals in Formula (6) are strongly convergent because we deal with purely Gaussian integrals. The full width at the half maximum (FWHM) is given by the well known formula (in angular frequency unit)
where
M is the mass of the emitter in atomic mass unit whereas
T is the temperature in Kelvin.
2.2. Relativistic Doppler Broadening
When an observer at a rest, recording the emitted radiation from a moving atom (or ion) with relativistic velocity
, they find that the angular frequency of this radiation is equal to [
6]:
where
and
is the angular eigenfrequency and
is the angle between the velocity of the emitter and the observation direction (
) (see
Figure 1). By using the normalized Juttner-Maxwell distribution (normalized to one) [
7]
where
and
is the modified Bessel function of order two, we obtained the normalized relativistic intensity (normalized to one) of the line profile
Here, we have introduced the integral over the spherical angles that makes the emitter velocity with the fixed frame axis (see
Figure 1). We have replaced the Dirac delta distribution by its integral representation by integrating over the variable
u. Replacing the Juttner-Maxwell distribution
given by (11) and
given by (8) in Formula (14), we reach a more suitable expression of the relativistic intensity of the line profile
or after integration on
between zero and
;
Finally, the integration over
u, allows us to get the relativistic intensity of the line profile
where
if
and
if
and
is the reduced angular frequency. We can manage the formula to be more suitable for the numerical treatment:
if we put
, (
is given by formula (12)) we find
We note that the integral in the last formula is convergent because we deal with the integral in distribution sense [
8].
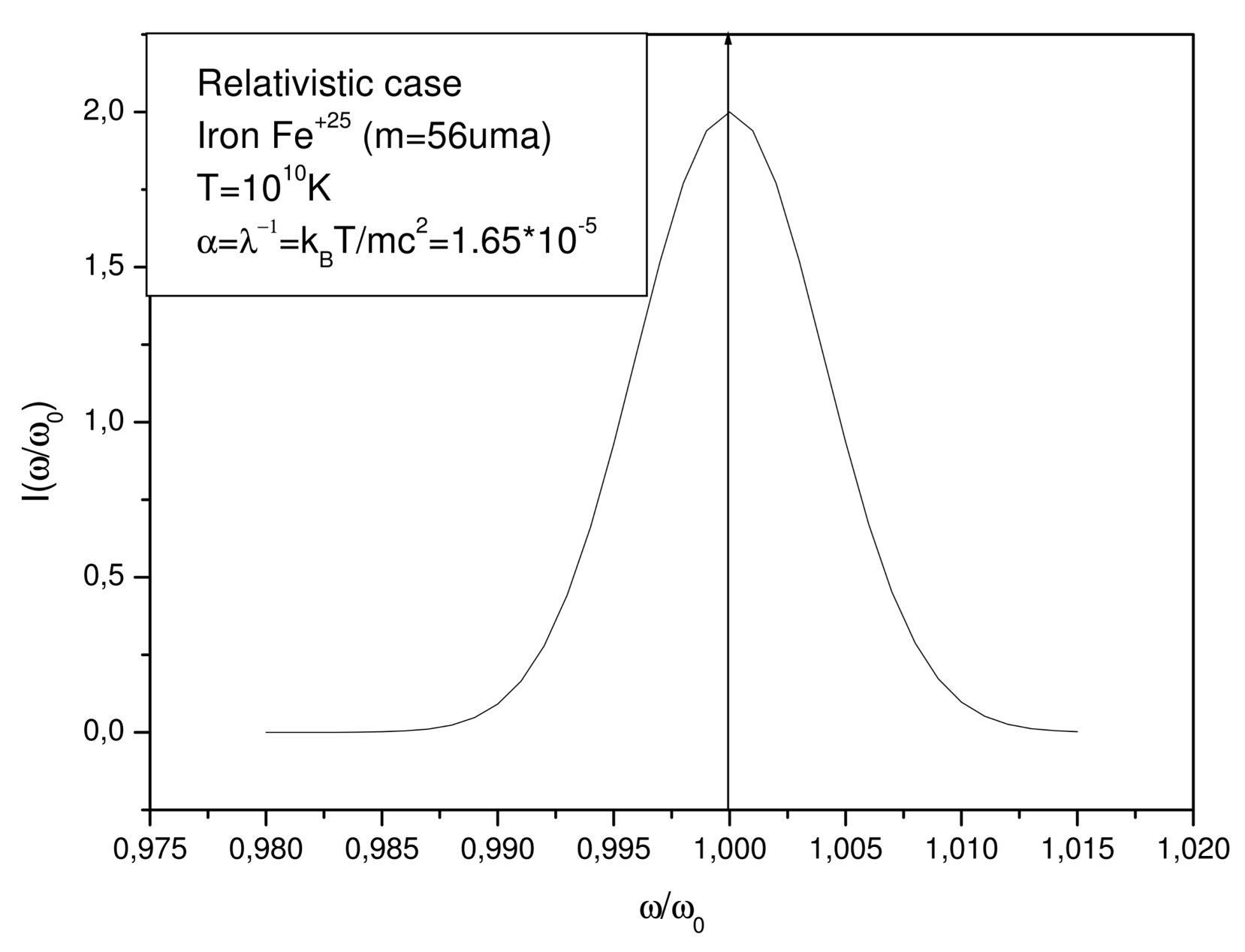
Unlike the classical Doppler effect, the relativistic one has a property: an asymmetric broadening as it is shown clearly in the following table corresponding to the temperatures in the range
–
K. We remark also that in the relativistic case, as in the classical case, the central frequency is unchanged (see
Figure 2). The maximum value of the intensity is at
both for classical and relativistic case but the maximum value of the relativistic case is smaller than the maximum of the classical case (the asymmetry at
) is negative, see
Figure 3.
We mention that in the
Table 1, we have denoted by
the value of the reduced angular frequency at the left and the right of the peak of the line (centred at
).
and
are chosen to be symmetrical with respect the centre of the line at
and giving intensities very close to the half of the maximum of the intensity. Strictly speaking, we have considered
and
with g = 0.00045 for
, 0.00075 for
, 0.00085 for
(produced in nuclear reactions) and 0.00095 for
(it is synthesized in laboratories for use in nuclear reactions). As we see in this table, the value of the intensity at the right
is greater than the intensity at the left
. This remark shows clearly that the line profile has an asymmetry as defined by [
9] (see the definition at the last line in the above table). Another feature in this study is that we have not specified the line profile, because we have used the reduced angular frequency
: for each specific line (specific transition), we must multiply
(the x-axis) by the corresponding angular eigenfrequency
to obtain the intensity
. If we define the asymmetry as [
10]
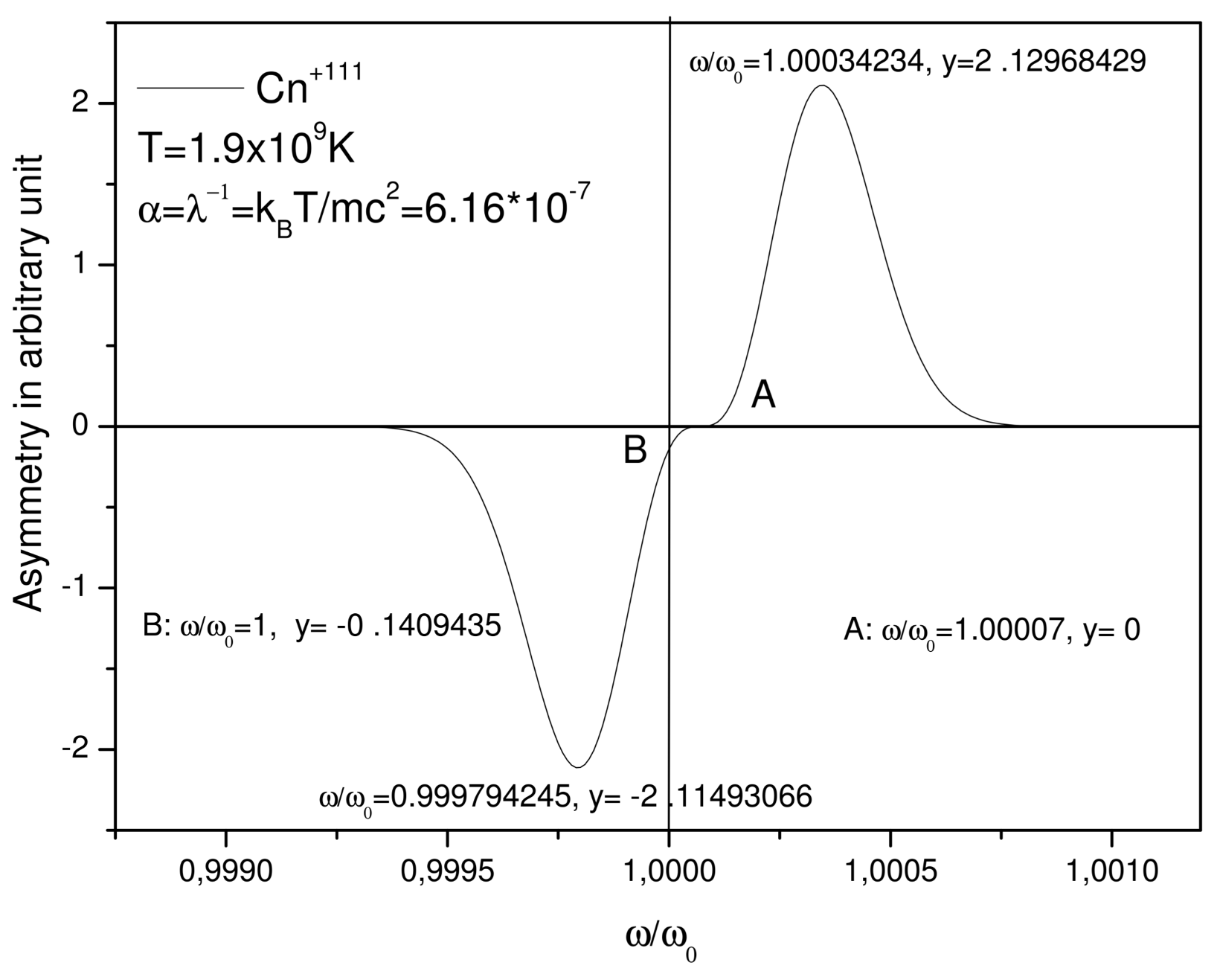
which is the difference between the normalized relativistic intensity given by (18) and the normalized classical intensity given by (6), we obtain the following figure representing the asymmetry for
at 1.9 × 10
K.
In
Figure 3, we see clearly that, in the left of
, the intensity of the relativistic profile is lower than of the classical profile, whereas it is higher in the right of
. It can be seen clearly in this figure that the asymmetry is a function of (
) and that means that for any line, the asymmetry is as indicated in this figure. To obtain the asymmetry, for a specific line centred at
, we must multiply
by
. The same remark holds for
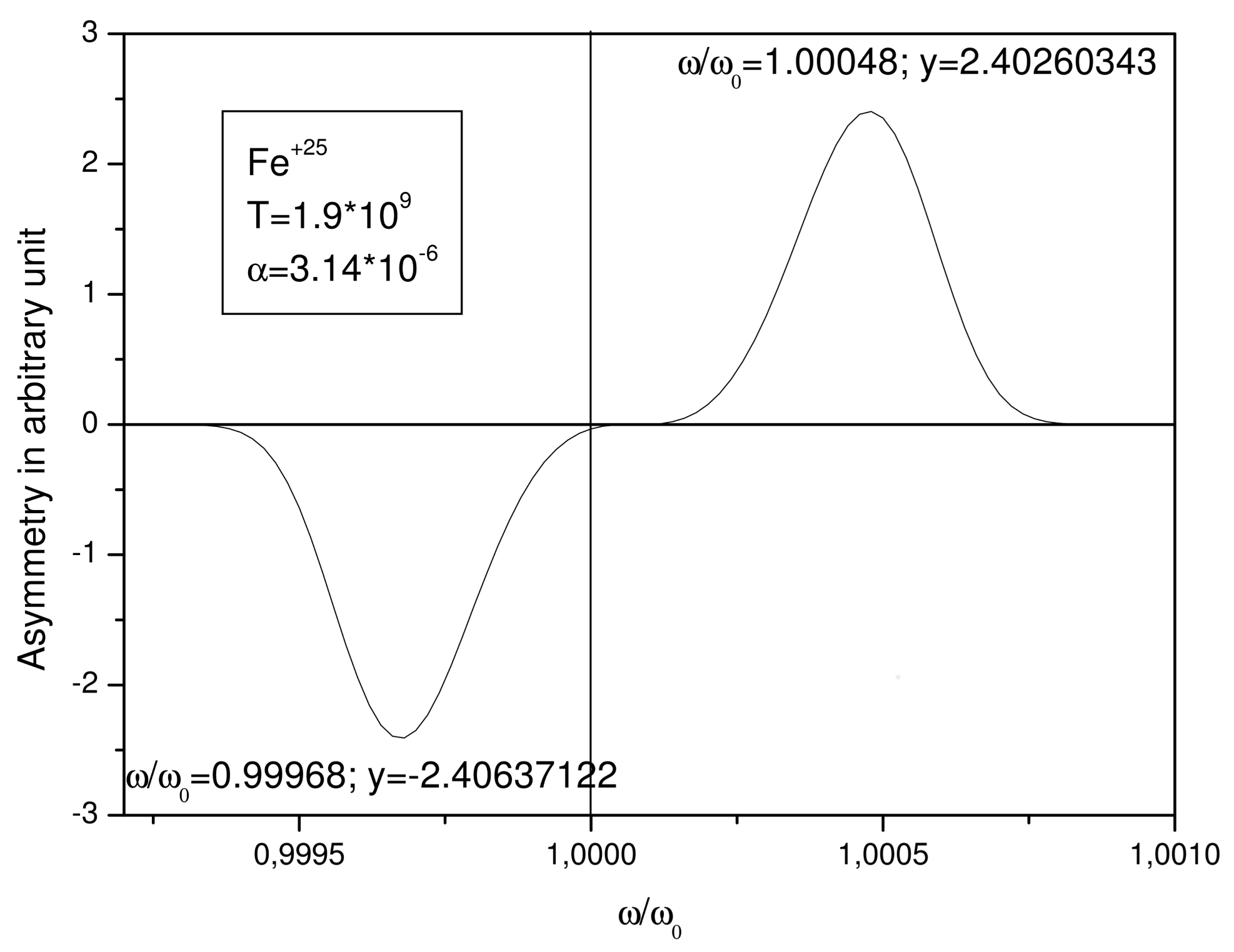
Figure 4 for the hydrogen-like Iron, but with a more pronounced asymmetry since the maximum of the asymmetry is equal to 2.40 for the iron (Fe
) whereas for the Copernicium (Cn
) is equal to 2.12.