Charged ρ Meson Condensate in Neutron Stars within RMF Models
Abstract
:1. Introduction
2. Description of the Model
3. Charged Condensate
4. Numerical Results
4.1. Inclusion of the Condensate
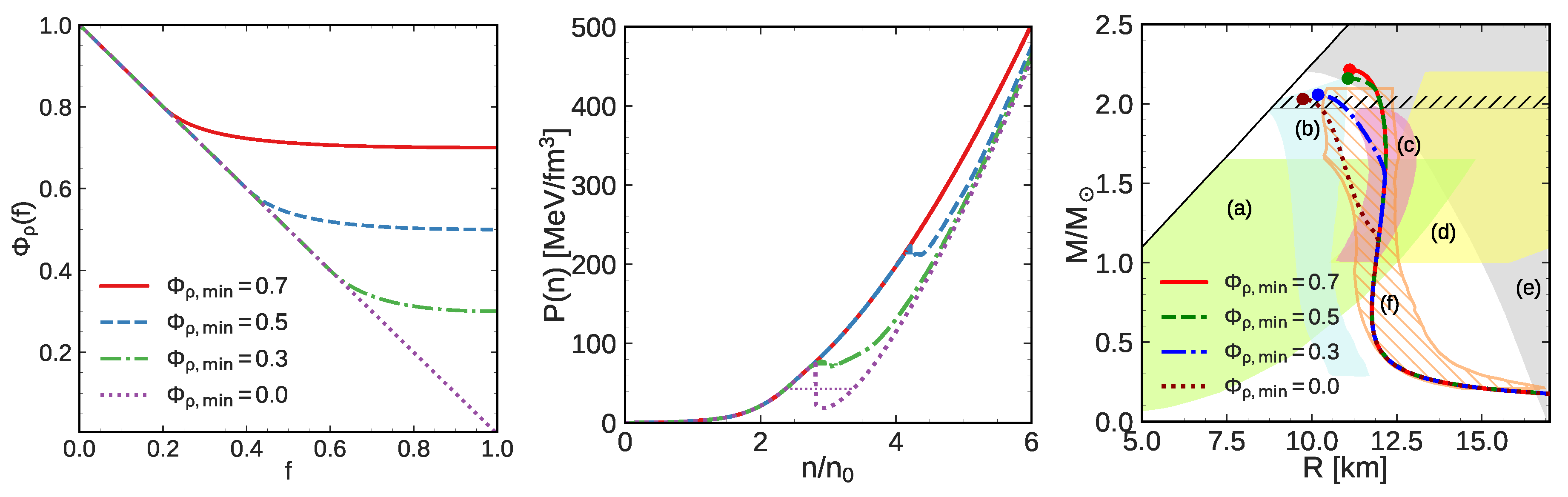
4.2. Variation of the -Meson Effective Mass
4.3. Variation of the
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| EoS | Equation of state |
| NS | Neutron star |
| RMF | Relativistic mean-field |
| ISM | Isospin-symmetric matter |
| BEM | Beta-equilibrium matter |
| PT | Phase transition |
References
- Klahn, T.; Klähn, T.; Blaschke, D.; Typel, S.; Van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, A.; Ho, A.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Bassa, C.; Dhillon, V.S.; Hessels, J.W.T.; Kaspi, V.M.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef] [PubMed]
- Schaffner-Bielich, J. Hypernuclear Physics for Neutron Stars. Nucl. Phys. A 2008, 804, 309–321. [Google Scholar] [CrossRef]
- Voskresensky, D.N. On the possibility of the condensation of the charged rho meson field in dense isospin asymmetric baryon matter. Phys. Lett. B 1997, 392, 262–266. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Delta isobars in relativistic mean-field models with sigma-scaled hadron masses and couplings. Nucl. Phys. A 2017, 961, 106–141. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Charged ρ-meson condensation in neutron stars. Nucl. Phys. A 2018, 970, 291–315. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic mean-field models with effective hadron masses and coupling constants, and rho- condensation. Nucl. Phys. A 2005, 759, 373–413. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic Mean-Field Models with Scaled Hadron Masses and Couplings: Hyperons and Maximum Neutron Star Mass. Nucl. Phys. A 2016, 950, 64–109. [Google Scholar] [CrossRef]
- Riek, F.; Lutz, M.F.M.; Korpa, C.L. Photoabsorption off nuclei with self consistent vertex corrections. Phys. Rev. C 2009, 80, 024902. [Google Scholar] [CrossRef]
- Ohnishi, A.; Kawamoto, N.; Miura, K. Brown-Rho Scaling in the Strong Coupling Lattice QCD. Mod. Phys. Lett. A 2008, 23, 2459–2464. [Google Scholar] [CrossRef]
- Brown, G.E.; Rho, M. Double decimation and sliding vacua in the nuclear many body system. Phys. Rept. 2004, 396, 1–39. [Google Scholar] [CrossRef]
- Paeng, W.G.; Kuo, T.T.S.; Lee, H.K.; Ma, Y.L.; Rho, M. Scale-invariant hidden local symmetry, topology change, and dense baryonic matter. II. Phys. Rev. D 2017, 96, 014031. [Google Scholar] [CrossRef]
- Van Straaten, S.; Ford, E.C.; van der Klis, M.; Méndez, M.; Kaaret, P. Relations between timing features and colors in the x-ray binary 4u 0614+09. Astrophys. J. 2000, 540, 1049–1061. [Google Scholar] [CrossRef]
- Ozel, F.; Psaltis, D.; Guver, T.; Baym, G.; Heinke, C.; Guillot, S. The Dense Matter Equation of State from Neutron Star Radius and Mass Measurement. Astrophys. J. 2016, 820, 28. [Google Scholar] [CrossRef]
- Suleimanov, V.F.; Poutanen, J.; Nättilä, J.; Kajava, J.J.E.; Revnivtsev, M.G.; Werner, K. The direct cooling tail method for X-ray burst analysis to constrain neutron star masses and radii. Mon. Not. Roy. Astron. Soc. 2017, 466, 906–913. [Google Scholar] [CrossRef]
- Bogdanov, S. The Nearest Millisecond Pulsar Revisited with XMM-Newton: Improved Mass-Radius Constraints for PSR J0437-4715. Astrophys. J. 2013, 762, 96. [Google Scholar] [CrossRef]
- Trümper, J.E.; Burwitz, V.; Haberl, F.; Zavlin, V.E. The puzzles of RX J1856.5-3754: Neutron star or quark star? Nucl. Phys. B (Proc. Suppl.) 2004, 132, 560–565. [Google Scholar] [CrossRef]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Neutron Star Masses and Radii from Quiescent Low-Mass X-ray Binaries. Astrophys. J. 2014, 784, 123. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. Neutron Star Radii, Universal Relations, and the Role of Prior Distributions. Eur. Phys. J. A 2016, 52, 18. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Making a soft relativistic mean-field equation of state stiffer at high density. Phys. Rev. C 2015, 92, 052801. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Delta isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Charged ρ Meson Condensate in Neutron Stars within RMF Models. Universe 2018, 4, 1. https://doi.org/10.3390/universe4010001
Maslov KA, Kolomeitsev EE, Voskresensky DN. Charged ρ Meson Condensate in Neutron Stars within RMF Models. Universe. 2018; 4(1):1. https://doi.org/10.3390/universe4010001
Chicago/Turabian StyleMaslov, Konstantin A., Evgeni E. Kolomeitsev, and Dmitry N. Voskresensky. 2018. "Charged ρ Meson Condensate in Neutron Stars within RMF Models" Universe 4, no. 1: 1. https://doi.org/10.3390/universe4010001





