Constraining ƒ(R) Gravity by the Large-Scale Structure
Abstract
:1. Introduction
2. f(R) Gravity
2.1. Chameleon Models
2.2. Analytical f(R) Gravity Models and Yukawa-Like Gravitational Potentials
3. Constraining f(R) Gravity Models Using Clusters of Galaxies
| Model | Reference | |||||
|---|---|---|---|---|---|---|
| Arnaud et al. 2010 | 1.177 | 1.051 | 5.4905 | 0.3081 | 8.403 | [114] |
| Sayers et al. 2013 | 1.18 | 0.86 | 3.67 | 0.67 | 4.29 | [115] |
| Planck et al. 2013 | 1.81 | 1.33 | 4.13 | 0.31 | 6.41 | [116] |
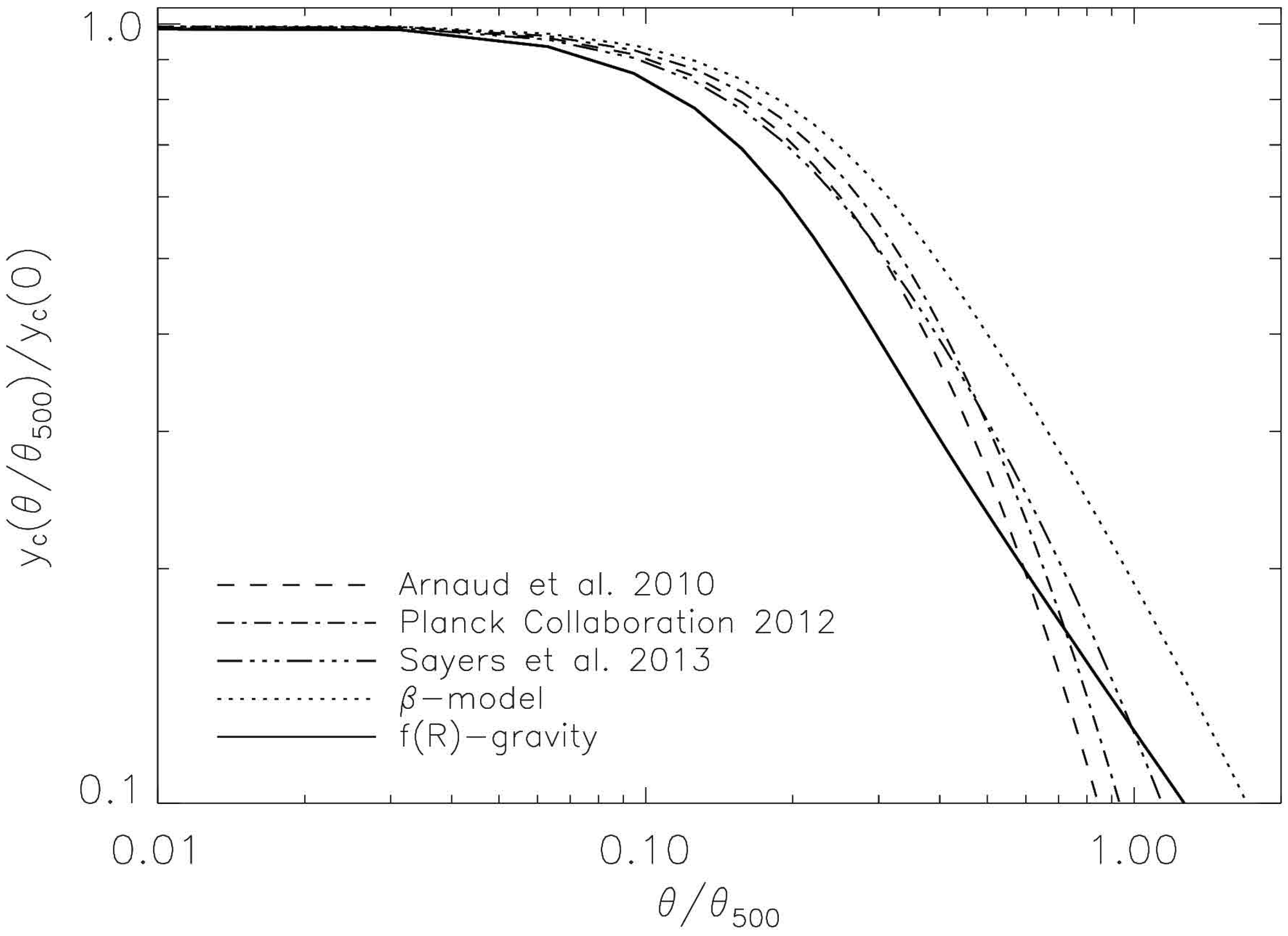
3.1. Pressure Profile from Yukawa-Like Gravitational Potential
3.1.1. Data and Results
| Parameterization | δ | γ | L | ζ |
|---|---|---|---|---|
| (A) | - | |||
| (B) | - |
| 68% CL | 95% CL | 68% CL | 95% CL | |
|---|---|---|---|---|
| δ | < | < | < | < |
| γ | > | > | > | > |
| < | < | < 12 | < 19 |


3.2. Chameleon Gravity: Hydrostatic and Weak Lensing Mass Profile of Galaxy Cluster
3.2.1. Data and Results

4. N-Body Hydrodynamical Simulations in f(R) Gravity
5. Constraining the Expansion History of the Universe in f(R) Gravity

6. Testing Gravity Using the Cosmic Microwave Background Data

7. Discussion and Future Perspectives
Acknowledgments
Conflicts of Interest
References
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements of the Cosmological Parameters Omega and Lambda from the First Seven Supernovae at z ≥ 0.35. Astrophys. J. 1997, 483, 565. [Google Scholar]
- Riess, A.G.; Strolger, L.-G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z > 1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar]
- Pope, A.C.; Matsubara, T.; Szalay, A.S.; Blanton, M.R.; Eisenstein, D.J.; Gray, J.; Jain, B.; Bahcall, N.A.; Brinkmann, J.; Budavari, T.; et al. Cosmological Parameters from Eigenmode Analysis of Sloan Digital Sky Survey Galaxy Redshifts. Astrophys. J. 2004, 607, 655. [Google Scholar] [CrossRef]
- Percival, W.J.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; Collins, C.; Couch, W.; Dalton, G.; et al. The 2dF Galaxy Redshift Survey: The power spectrum and the matter content of the Universe. Mon. Not. R. Astron. Soc. 2001, 327, 1297–1306. [Google Scholar] [CrossRef]
- Tegmark, M.; Blanton, M.R.; Strauss, M.A.; Hoyle, F.; Schlegel, D.; Scoccimarro, R.; Vogeley, M.S.; Weinberg, D.H.; Zehavi, I.; Berlind, A.; et al. The Three-Dimensional Power Spectrum of Galaxies from the Sloan Digital Sky Survey. Astrophys. J. 2004, 606, 702. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2013 Results. XV. CMB power spectra and likelihood. Astron. Astrophys. 2013, 571, A15. [Google Scholar]
- Planck Collaboration. Planck 2013 Results. XX. Cosmology from Sunyaev? Zeldovich cluster counts. Astron. Astrophys. 2013, 571, A20. [Google Scholar]
- Planck Collaboration. Planck 2013 Results. XXIII: Isotropy and statistics of the CMB. Astron. Astrophys. 2013, 571, A23. [Google Scholar]
- Planck Collaboration. Planck Results. I. Overview of products and scientific results. 5 February 2015; arXiv:1502.01582v1. [Google Scholar]
- Planck Collaboration. Planck Results. XIII. Cosmological parameters. 6 February 2015; arXiv:1502.01589v1. [Google Scholar]
- Planck Collaboration. Planck Results. XIV. Dark energy and modified gravity. 5 February 2015; arXiv:1502.01590v1. [Google Scholar]
- Planck Collaboration. Planck Results. XVII. Primordial non-Gaussianity. 5 February 2015; arXiv:1502.01592v1. [Google Scholar]
- Planck Collaboration. Planck Results. XVIII. Background geometry and topology of the Universe. 5 February 2015; arXiv:1502.01593v1. [Google Scholar]
- Planck Collaboration. PPlanck 2015 results. XX. Constraints on inflation. 7 February 2015; arXiv:1502.02114v1. [Google Scholar]
- Planck Collaboration. Planck Results. XXI. The integrated Sachs-Wolfe effect. 5 February 2015; arXiv:1502.01595v1. [Google Scholar]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2011, 418, 1707–1724. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S; Odintsov, S.D. Unified cosmic history in modified gravity: from F(R) theory to Lorentz non- invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar]
- Capozziello, S.; Francaviglia, M. Extended theories of gravity and their cosmological and astrophysical applications. Gen. Relativ. Gravit. 2008, 40, 357–420. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Faraoni, V. A Bird’s eye view of f(R)-gravity. 2 October 2009; arXiv:0909.4672v2 [gr-qc]. [Google Scholar]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413–462. [Google Scholar] [CrossRef]
- Lobo, F.S.N. The Dark side of gravity: Modified theories of gravity. 10 July 2008; arXiv:0807.1640 [gr-qc]. [Google Scholar]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Available online: http://www.emis.ams.org/journals/ LRG/Articles/lrr-2010-3/download/lrr-2010-3Color.pdf (accessed on 22 July 2015).
- Sotiriou, T.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. F(R) theories of gravitation. Scholarpedia 2015, 10, 31422. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Odintsov, S.D.; Stabile, A. Hydrostatic equilibrium and stellar structure in f(R) gravity. Phys. Rev. D 2012, 83, 064004. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; de Martino, I.; Formisano, M.; Odintsov, S.D. Jeans analysis of self-gravitating systems in f(R) gravity. Phys. Rev. D 2012, 85, 044022. [Google Scholar] [CrossRef]
- Arbuzova, E.V.; Dolgov, A.D.; Reverberi, L. Jeans instability in classical and modified gravity. Phys. Lett. B 2014, 739, 279–284. [Google Scholar] [CrossRef]
- Farinelli, R.; De Laurentis, M.; Capozziello, S.; Odintsov, S.D. Numerical solutions of the modified Lane-Emden equation in f(R)-gravity. Mon. Not. R. Astron. Soc. 2014, 440, 2909–2915. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Magnetic neutron stars in f(R) gravity. Astrophys. Space Sci. 2015, 355, 333–341. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Extreme neutron stars from Extended Theories of Gravity. J. Cosmol. Astropart. Phys. 2015. [Google Scholar] [CrossRef] [PubMed]
- De Laurentis, M.; de Martino, I. Testing f(R)-theories using the first time derivative of the orbital period of the binary pulsars. Mon. Not. R. Astron. Soc. 2013, 431, 741–748. [Google Scholar] [CrossRef]
- De Laurentis, M.; de Martino, I. Probing the physical and mathematical structure of f(R) gravity by PSR J0348 + 0432. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550040. [Google Scholar]
- De Laurentis, M.; Capozziello, S. Quadrupolar gravitational radiation as a test-bed for f(R)-gravity. Astropart. Phys. 2011, 35, 257–265. [Google Scholar] [CrossRef]
- De Laurentis, M.; de Rosa, R.; Garufi, F; Milano, L. Testing gravitational theories using eccentric eclipsing detached binaries. Mon. Not. R. Astron. Soc. 2012, 424, 2371–2379. [Google Scholar]
- Bogdanos, C.; Capozziello, S.; De Laurentis, M.; Nesseris, S. Massive, massless and ghost modes of gravitational waves from higher-order gravity. Astropart. Phys. 2010, 34, 236–244. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013. [Google Scholar] [CrossRef] [PubMed]
- Clifton, T.; Barrow, J.D. Observational Constraints on the Completeness of Space near Astrophysical Objects. Phys. Rev. D 2010, 81, 063006. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. The Power of General Relativity. Phys. Rev. D 2005, 72, 103005. [Google Scholar] [CrossRef]
- Antoniadis, J. Gravitational Radiation from Compact Binary Pulsars. Astrophys. Space Sci. Proc. 2014, 40, 1–22. [Google Scholar]
- Berry, C.P.L.; Gair, J.R. Linearized f(R) Gravity: Gravitational Radiation & Solar System Tests. Phys.Rev. D 2011, 83, 104022. [Google Scholar]
- Cardone, V.; Capozziello, S. Systematic biases on galaxy halos parameters from Yukawa-like gravitational potentials. Mon. Not. R. Astron. Soc. 2011, 414, 1301–1313. [Google Scholar] [CrossRef]
- Napolitano, N.R.; Capozziello, S.; Romanowsky, A.J.; Capaccioli, M.; Tortora, C. esting Yukawa-like Potentials from f(R)-gravity in Elliptical Galaxies. Astrophys. J. 2012, 748, 87. [Google Scholar] [CrossRef]
- Capozziello, S.; de Filippis, E.; Salzano, V. Modelling clusters of galaxies by f(R) gravity. Mon. Not. R. Astron. Soc. 2009, 394, 947–959. [Google Scholar] [CrossRef]
- Schmidt, F.; Vikhlinin, A.; Hu, W. Cluster constraints on f(R) gravity. Phys. Rev. D 2009, 80, 083505. [Google Scholar] [CrossRef]
- Ferraro, S.; Schmidt, F.; Hu, W. Cluster abundance in f(R) gravity models. Phys. Rev. D 2011, 83, 063503. [Google Scholar] [CrossRef]
- De Martino, I.; De Laurentis, M.; Atrio-Barandela, F.; Capozziello, S. Constraining f(R) gravity with Planck data on galaxy cluster. Mon. Not. R. Astron. Soc. 2014, 442, 921–928. [Google Scholar] [CrossRef]
- Terukina, A.; Yamamoto, K. Gas Density Profile in Dark Matter Halo in Chameleon Cosmology. Phys. Rev. D 2012, 86, 103503. [Google Scholar] [CrossRef]
- Terukina, A.; Lombriser, L.; Yamamoto, K.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing chameleon gravity with the Coma cluster. J. Cosmol. Astropart. Phys. 2014. [Google Scholar] [CrossRef]
- Wilcox, H.; Bacon, D.; Nichol, R.C.; Rooney, P.J.; Terukina, A.; Romer, A.K.; Koyama, K.; Zhao, G.-B.; Hood, R.; Mann, R.G.; et al. The XMM Cluster Survey: Testing chameleon gravity using the profiles of clusters. 15 July 2015; arXiv:1504.03937. [Google Scholar]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2013. [Google Scholar] [CrossRef]
- Jennings, E.; Baugh, C.M.; Li, B.; Zhao, G.-B.; Koyama, K. Redshift-space distortions in f(R) gravity. Mon. Not. R. Astron. Soc. 2012, 425, 2128–2143. [Google Scholar] [CrossRef]
- Zhao, G.-B.; Li, B.; Koyama, K. N-body simulations for f(R) gravity using a self-adaptive particle-mesh code. Phys. Rev. D 2011, 83, 044007. [Google Scholar] [CrossRef]
- Puchwein, E.; Baldi, M.; Springel, V. Modified-Gravity-GADGET: A new code for cosmological hydrodynamical simulations of modified gravity models. Mon. Not. R. Astron. Soc. 2013, 436, 348–360. [Google Scholar] [CrossRef]
- Arnold, C.; Puchwein, E.; Springel, V. The Lyman alpha forest in f(R) modified gravity. Mon. Not. R. Astron. Soc. 2015, 448, 2275–2283. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M.; Silvestri, A.; Frusciante, N. EFTCAMB/EFTCosmoMC: Massive neutrinos in dark cosmologies. Phys. Rev. D 2015, 91, 063524. [Google Scholar] [CrossRef]
- Marchini, A.; Melchiorri, A.; Salvatelli, V.; Pagano, L. Constraints on modified gravity from the Atacama Cosmology Telescope and the South Pole Telescope. Phys. Rev. D 2013, 87, 083527. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Accelerating cosmology in modified gravity: From convenient F(R) or string-inspired theory to bimetric F(R) gravity. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1460006. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Carloni, S.; Troisi, A.; Dunsby, P.K.S. Some remarks on the dynamical systems approach to fourth order gravity. Gen. Rel. Grav. 2009, 41, 1757–1776. [Google Scholar] [CrossRef]
- Carloni, S.; Dunsby, P.K.S.; Capozzielllo, S.; Troisi, A. Cosmological dynamics of Rn gravity. Class. Quant. Grav 2005, 22, 4839–4868. [Google Scholar] [CrossRef]
- Abdelwahab, M.; Goswami, M.; Dunsby, P.K.S. Cosmological dynamics of fourth order gravity: A compact view. Phys. Rev. D 2008, 85, 083511. [Google Scholar]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Born-Infeld gravity in Weitzenbock spacetime. Phys. Rev. D 2008, 78, 124019. [Google Scholar] [CrossRef]
- Setare, M.R.; Houndjo, M.J.S. Finite-time future singularity models in f(T) gravity and the effects of viscosity. Can. J. Phys. 2013, 90, 260–267. [Google Scholar] [CrossRef]
- Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Solar system constraints on f(T) gravity. Phys. Rev. D 2011, 83, 023508. [Google Scholar]
- Liu, D.; Reboucas, M.J. Energy conditions bounds on f(T) gravity. Phys. Rev. D 2012, 86, 083515. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.Q.; Lee, C.C.; Luo, L.W. Equation of state for dark energy in f(T) gravity. J. Cosmol. Astropart. Phys. 2011. [Google Scholar] [CrossRef]
- Setare, M.R.; Houndjo, M.J.S. Finite-time future singularities models in f(T) gravity and the effects of viscosity. Can. J. Phys. 2013, 91, 260–267. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Universe Acceleration in Modified Gravities: F(R) and F(T) cases. In Proceedings of the KMI International Symposium 2013, Nagoya, Japan, 11–13 December 2013.
- Li, B.; Sotiriou, T.P.; Barrow, J.D. Large-scale Structure in f(T) Gravity. Phys. Rev. D 2011, 83, 104017. [Google Scholar] [CrossRef]
- Basilakos, S.; Capozziello, S.; De Laurentis, M.; Paliathanasis, A.; Tsamparlis, M. Noether symmetries and analytical solutions in f(T) cosmology: A complete study. Phys. Rev. D 2013, 88, 103526. [Google Scholar] [CrossRef]
- Zheng, R.; Huang, Q. Growth factor in f(T) gravity. J. Cosmol. Astropart. Phys. 2011. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, S.; Saridakis, E.N. f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmo. Astropart. Phys. 2011. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Li, B.; Barrow, J.D. Generalizations of teleparallel gravity and local Lorentz symmetry. Phys. Rev. D 2011, 83, 104030. [Google Scholar] [CrossRef]
- Yang, R.J. Conformal transformation in f(T) theories. Europhys. Lett. 2011, 93, 60001. [Google Scholar] [CrossRef]
- Maluf, J.W.; Faria, F.F. Conformally invariant teleparallel theories of gravity. Phys. Rev. D 2012, 85, 027502. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; De Laurentis, M.; Nojiri, S.; Sáez-Gómez, D. No further gravitational wave modes in F(T) gravity. Phys. Lett. B 2013, 727, 194–198. [Google Scholar] [CrossRef]
- Geng, C.Q.; Lee, C.C.; Saridakis, E.N.; Wu, Y.P. Teleparallel. Dark Energy. Phys. Lett. B 2011, 704, 384–387. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Myrzakulov, R. Noether Symmetry Approach for teleparallel-curvature cosmology. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550095. [Google Scholar] [CrossRef]
- Myrzakulov, R. FRW Cosmology in F(R,T) gravity. Eur. Phys. J. C 2012. [Google Scholar] [CrossRef]
- Sharif, M.; Rani, S.; Myrzakulov, R. Analysis of F(R,T) Gravity Models Through Energy Conditions. Eur. Phys. J. Plus 2013. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastiani, L.; Zerbini, S. Some aspects of generalized modified gravity models. Int. J. Mod. Phys. D 2013, 22, 1330017. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss-Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. From Inflation to Dark Energy in the Non-Minimal Modified Gravity. J. Phys. Conf. Ser. 2007, 66, 012005. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sami, M. Dark energy cosmology from higher-order, string-inspired gravity and its reconstruction. Phys. Rev. D 2006, 74, 046004. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D.; Mota, D.F. The Cosmology of Modified Gauss-Bonnet Gravity. Phys. Rev. D 2007, 76, 044027. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Toporensky, A.; Tretyakov, P. Reconstruction and deceleration-acceleration transitions in modified gravity. Gen. Relativ. Gravit. 2010, 42, 1997–2008. [Google Scholar] [CrossRef] [Green Version]
- De Laurentis, M.; Lopez-Revelles, A.J. Newtonian, Post Newtonian and Parameterized Post Newtonian limits of f(R,G) gravity. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1450082. [Google Scholar] [CrossRef]
- De Laurentis, M. Topological invariant quintessence. Mod. Phys. Lett. A 2015, 30, 1550069. [Google Scholar] [CrossRef]
- De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in F(R,G) gravity. Phys. Rev. D 2015, 91, 083531. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon Fields: Awaiting Surprises for Tests of Gravity in Space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a runaway dilaton. Phys. Rev. D 2002, 65, 023508. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Symmetron Fields: Screening Long-Range Forces Through Local Symmetry Restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef]
- Vainshtein, A. A New Strategy for Solving Two Cosmological Constant Problems in Hadron Physics. Phys. Lett. B 1972. [Google Scholar] [CrossRef]
- Deffayet, C.; Dvali, G.; Gabadadze, G.; Vainshtein, A.I. Accelerated Universe from Gravity Leaking to Extra Dimensions. Phys. Rev. D 2002, 65, 044026. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157163. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f(R)-gravity viewpoint. Ann. Phys. 2012, 524, 545–578. [Google Scholar] [CrossRef]
- Capozziello, S.; Tsujikawa, S. Solar system and equivalence principle constraints on f(R) gravity by the chameleon approach. Phys. Rev. D 2008, 77, 107501. [Google Scholar] [CrossRef]
- Sunyaev, R.; Zeldovich, Y. The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies. Comments Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Sunyaev, R.; Zeldovich, Y. The velocity of clusters of galaxies relative to the microwave background: The possibility of its measurement. Mon. Not. R. Astron. Soc. 1980, 190, 413–420. [Google Scholar] [CrossRef]
- Fixsen, D.J. The Temperature of the Cosmic Microwave Background. Astrophys. J. 2009. [Google Scholar] [CrossRef]
- Cavaliere, A.; Fusco-Femiano, R. X-rays from hot plasma in clusters of galaxies. Astron. Astrophys. 1976, 49, 137–144. [Google Scholar]
- Cavaliere, A.; Fusco-Femiano, R. The Distribution of Hot Gas in Clusters of Galaxies. Astron. Astrophys. 1978, 70, 677–684. [Google Scholar]
- Jones, C.; Forman, W. The structure of clusters of galaxies observed with Einstein. Astrophys. J. 1984, 276, 38–55. [Google Scholar] [CrossRef]
- Atrio-Barandela, F.; Kashlinsky, A.; Kocevski, D.; Ebeling, H. Measurement of the Electron-Pressure Profile of Galaxy Clusters in 3 Year Wilkinson Microwave Anisotropy Probe (WMAP) Data. Astrophys. J. 2008. [Google Scholar] [CrossRef]
- Nagai, D.; Kravtsov, A.V.; Vikhlinin, A. Effects of Galaxy Formation on Thermodynamics of the Intracluster Medium. Astrophys. J. 2007. [Google Scholar] [CrossRef]
- Arnaud, M.; Pratt, G.W.; Piffaretti, R.; Böhringer, H.; Croston, J.H.; Pointecouteau, E. The universal galaxy cluster pressure profile from a representative sample of nearby systems (REXCESS) and the YSZ – M500 relation. Astron. Astrophys. 2010, 517, A92. [Google Scholar] [CrossRef]
- Sayers, J.; Czakon, N.G.; Mantz, A.; Golwala, S.R.; Ameglio, S.; Downes, T.P.; Koch, P.M.; Lin, K.-Y.; Maughan, B.J.; Molnar, S.M.; et al. Sunyaev-Ze’dovich-measured Pressure Profiles from the Bolocam X-Ray/SZ Galaxy Cluster Sample. Astrophys. J. 2013. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck Intermediate Results V: Pressure profiles of galaxy clusters from the Sunyaev-Zeldovich effect. Astron. Astrophys. 2013, 550, A131. [Google Scholar]
- Allen, S.W.; Evrard, A.E.; Mantz, A.B. Cosmological Parameters from Observations of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2011, 49, 409. [Google Scholar] [CrossRef]
- Mana, A.; Giannantonio, T.; Weller, J.; Hoyle, B.; Hütsi, G.; Sartoris, B. Combining clustering and abundances of galaxy clusters to test cosmology and primordial non-Gaussianity. Mon. Not. R. Astron. Soc. 2013, 434, 684–695. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. 5 February 2015; arXiv:1502.01597. [Google Scholar]
- Sartoris, B.; Biviano, A.; Fedeli, C.; Bartlett, J.G.; Borgani, S.; Costanzi, M.; Giocoli, C.; Moscardini, L.; Weller, J.; Ascaso, B.; et al. Next Generation Cosmology: Constraints from the Euclid Galaxy Cluster Survey. 8 May 2015; arXiv:150502165. [Google Scholar]
- De Martino, I.; Atrio-Barandela, F.; da Silva, A.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Measuring the Redshift Dependence of the Cosmic Microwave Background Monopole Temperature with Planck Data. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- De Martino, I.; Génova-Santos, R.; Atrio-Barandela, F.; da Silva, A.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Constraining the redshift evolution of the Cosmic Microwave Background black-body temperature with PLANCK data. 6 June 2015; arXiv:1502.06707v2. [Google Scholar]
- Hand, N.; Appel, J.W.; Battaglia, N.; Bond, J.R.; Das, S.; Devlin, M.J.; Dunkley, J.; Dünner, R.; Essinger-Hileman, T.; Fowler, J.W.; et al. The Atacama Cosmology Telescope: Detection of Sunyaev-Ze’dovich Decrement in Groups and Clusters Associated with Luminous Red Galaxies. Astrophys. J. 2011. [Google Scholar] [CrossRef]
- Sehgal, N.; Trac, H.; Acquaviva, V.; Ade, P.A.R.; Aguirre, P.; Amiri, M.; Appel, J.W.; Barrientos, L.F.; Battistelli, E.S.; Bond, J.R.; et al. The Atacama Cosmology Telescope: Cosmology from Galaxy Clusters Detected via the Sunyaev-Ze’dovich Effect. Astrophys. J. 2011. [Google Scholar] [CrossRef]
- Hasselfield, M.; Hilton, M.; Marriage, T.A.; Addison, G.E.; Barrientos, L.F.; Battaglia, N.; Battistelli, E.S.; Bond, J.R.; Crichton, D.; Das, S.; et al. The Atacama Cosmology Telescope: Sunyaev-Ze’dovich selected galaxy clusters at 148 GHz from three seasons of data. J. Cosmol. Astropart. Phys. 2013. [Google Scholar] [CrossRef] [PubMed]
- Menanteau, F.; Sifón, C.; Barrientos, L.F.; Battaglia, N.; Bond, J.R.; Crichton, D.; Das, S.; Devlin, M.J.; Dicker, S.; Dünner, R.; et al. The Atacama Cosmology Telescope: Physical Properties of Sunyaev-Ze’dovich Effect Clusters on the Celestial Equator. Astrophys. J. 2013. [Google Scholar] [CrossRef]
- Staniszewski, Z.; Ade, P.A.R.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; Cho, H.-M.; Crawford, T.M.; Crites, A.T.; et al. Galaxy Clusters Discovered with a Sunyaev-Ze’dovich Effect Survey. Astrophys. J. 2009. [Google Scholar] [CrossRef]
- Vanderlinde, K.; Crawford, T.M.; de Haan, T.; Dudley, J.P.; Shaw, L.; Ade, P.A.R.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Brodwin, M.; et al. Galaxy Clusters Selected with the Sunyaev-Zel’dovich Effect from 2008 South Pole Telescope Observations. Astrophys. J. 2010. [Google Scholar] [CrossRef]
- Williamson, R.; Benson, B.A.; High, F.W.; Vanderlinde, K.; Ade, P.A.R.; Aird, K.A.; Andersson, K.; Armstrong, R.; Ashby, M.L.N.; Bautz, M.; et al. A Sunyaev-Ze’dovich-selected Sample of the Most Massive Galaxy Clusters in the 2500 deg2 South Pole Telescope Survey. Astrophys. J. 2011. [Google Scholar] [CrossRef]
- Benson, B.A.; de Haan, T.; Dudley, J.P.; Reichardt, C.L.; Aird, K.A.; Andersson, K.; Armstrong, R.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; et al. Cosmological Constraints from Sunyaev-Ze’dovich-selected Clusters with X-Ray Observations in the First 178 deg2 of the South Pole Telescope Survey. Astrophys. J. 2013. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck intermediate results. X: Physics of the hot gas in the Coma cluster. Astron. Astrophys. 2013, 554, A140. [Google Scholar]
- Planck Collaboration. Planck 2015 results. XXII. A map of the thermal Sunyaev-Zeldovich effect. Astron. Astrophys. 5 February 2015; arXiv:1502.01596. [Google Scholar]
- Planck Collaboration. Planck 2015 results. XXVII. The Second Planck Catalogue of Sunyaev-Zeldovich Sources. 5 February 2015; arXiv:1502.01598. [Google Scholar]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. 2011. [Google Scholar] [CrossRef]
- Fusco-Femiano, R.; Lapi, A.; Cavaliere, A. The Planck Sunyaev-Ze’dovich versus the X-Ray View of the Coma Cluster. Astrophys. J. 2013. [Google Scholar] [CrossRef]
- Kocevski, D.D.; Ebeling, H. On the Origin of the Local Group’s Peculiar Velocity. Astrophys. J. 2006. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2013 results. XII. Component separation. Astron. Astrophys. Astron. Astrophys. 2014, 571, A12. [Google Scholar]
- Battaglia, N.; Bond, J.R.; Pfrommer, C.; Sievers, J.L. On the Cluster Physics of Sunyaev-Ze’dovich and X-Ray Surveys. I. The Influence of Feedback, Non-thermal Pressure, and Cluster Shapes on Y-M Scaling Relations. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- Shaw, L.D.; Nagai, D.; Bhattacharya, S.; Lau, E.T. Impact of Cluster Physics on the Sunyaev-Ze’dovich Power Spectrum. Astrophys. J. 2010. [Google Scholar] [CrossRef]
- Lombriser, L.; Koyama, K.; Zhao, G.-B.; Li, B. Chameleon f(R) gravity in the virialized cluster. Phys. Rev. D 2012, 85, 124054. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997. [Google Scholar] [CrossRef]
- Snowden, S.L.; Mushotzky, R.F.; Kuntz, K.D.; Davis, D.S. A catalog of galaxy clusters observed by XMM-Newton. Astron. Astrophys. 2008, 478, 615–658. [Google Scholar] [CrossRef]
- Wik, D.R.; Sarazin, C.L.; Finoguenov, A.; Matsushita, K.; Nakazawa, K.; Clarke, T.E. A Suzaku Search for Nonthermal Emission at Hard X-Ray Energies in the Coma Cluster. Astrophys. J. 2009. [Google Scholar] [CrossRef]
- Churazov, E.; Vikhlinin, A.; Zhuravleva, I.; Schekochihin, A.; Parrish, I.; Sunyaev, R.; Forman, W.; Böhringer, H.; Randall, S. X-ray surface brightness and gas density fluctuations in the Coma cluster. Mon. Not. R. Astron. Soc. 2012, 421, 1123–1135. [Google Scholar] [CrossRef]
- Okabe, N.; Okura, Y.; Futamase, T. Weak-lensing Mass Measurements of Substructures in Coma Cluster with Subaru/Suprime-cam. Astrophys. J. 2010. [Google Scholar] [CrossRef]
- Heymans, C.; van Waerbeke, L.; Miller, L.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Simon, P.; Bonnett, C.; et al. CFHTLenS: The Canada-France-Hawaii Telescope Lensing Survey. Mon. Not. R. Astron. Soc. 2012, 427, 146–166. [Google Scholar] [CrossRef]
- Baldi, M. Dark Energy simulations. Phys. Dark Univ. 2012, 1, 162. [Google Scholar] [CrossRef]
- Oyaizu, H. Nonlinear evolution of f(R) cosmologies. I. Methodology. Phys. Rev. D 2009, 78, 123523. [Google Scholar]
- Khoury, J.; Wyman, M. N-body simulations of DGP and degravitation theories. Phys. Rev. D 2009, 80, 064023. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.-B.; Teyssier, R.; Koyama, K. ECOSMOG: An Efficient COde for Simulating MOdified Gravity. J. Cosmol. Astropart. Phys. 2012. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.-C.; Li, B.; Shaw, D.J. Nonlinear structure formation with the environmentally dependent dilaton. Phys. Rev. D 2011, 83, 104026. [Google Scholar] [CrossRef]
- Davis, A.-C.; Li, B.; Mota, D.F.; Winther, H.A. Structure Formation in the Symmetron Model. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- Llinare, C.; Mota, D.F. Releasing Scalar Fields: Cosmological Simulations of Scalar-Tensor Theories for Gravity Beyond the Static Approximation. Phys. Rev. Lett. 2013, 110, 161101. [Google Scholar] [CrossRef]
- Schmidt, F.; Lima, M.V.; Oyaizu, H.; Hu, W. Nonlinear evolution of f(R) cosmologies. III. Halo statistics. Phys. Rev. D 2009, 79, 083515. [Google Scholar]
- Lee, J.; Zhao, G.-B.; Li, B.; Koyama, K. Modified Gravity Spins up Galactic Halos. Astrophys. J. 2013. [Google Scholar] [CrossRef]
- Lam, T.Y.; Nishimichi, T.; Schmidt, F.; Takada, M. Testing Gravity with the Stacked Phase Space around Galaxy Clusters. Phys. Rev. Lett. 2012, 109, 051301. [Google Scholar] [CrossRef]
- Llinares, C.; Mota, D.F. Shape of Clusters of Galaxies as a Probe of Screening Mechanisms in Modified Gravity. Phys. Rev. Lett. 2010, 110, 151104. [Google Scholar] [CrossRef]
- Zhao, H.; Macció, A.V.; Li, B.; Hoekstra, H.; Feix, M. Structure Formation by Fifth Force: Power Spectrum from N-Body Simulations. Astrophys. J. 2010. [Google Scholar] [CrossRef]
- Winther, H.A.; Mota, D.F.; Li, B. Environment Dependence of Dark Matter Halos in Symmetron Modified Gravity. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.-B.; Koyama, K. Haloes and voids in f(R) gravity. Mon. Not. R. Astron. Soc. 2012, 421, 3481–3487. [Google Scholar] [CrossRef] [Green Version]
- Puchwein, E.; Bartelmann, M.; Dolag, K.; Meneghetti, M. The impact of gas physics on strong cluster lensing. Astron. Astrophys. 2005, 442, 405–412. [Google Scholar] [CrossRef]
- Puchwein, E.; Sijacki, D.; Springel, V. Simulations of AGN Feedback in Galaxy Clusters and Groups: Impact on Gas Fractions and the LX – T Scaling Relation. Astrophys. J. 2008, 687, L53. [Google Scholar] [CrossRef]
- Stanek, R.; Rudd, D.; Evrard, A.E. The effect of gas physics on the halo mass function. Mon. Not. R. Astron. Soc. 2009, 394, L11–L15. [Google Scholar] [CrossRef]
- Van Daalen, M.P.; Schaye, J.; Booth, C.M.; Dalla Vecchia, C. The effects of galaxy formation on the matter power spectrum: A challenge for precision cosmology. Mon. Not. R. Astron. Soc. 2011, 415, 3649–3665. [Google Scholar] [CrossRef]
- Semboloni, E.; Hoekstra, H.; Schaye, J.; van Daalen, M.P.; McCarthy, I.G. Quantifying the effect of baryon physics on weak lensing tomography. Mon. Not. R. Astron. Soc. 2011, 417, 2020–2035. [Google Scholar] [CrossRef]
- Casarini, L.; Macció, A.V.; Bonometto, S.A.; Stinson, G.S. High-accuracy power spectra including baryonic physics in dynamical Dark Energy models. Mon. Not. R. Astron. Soc. 2014, 412, 911–920. [Google Scholar] [CrossRef]
- Viel, M.; Haehnelt, M.G.; Springel, V. The effect of neutrinos on the matter distribution as probed by the intergalactic medium. J. Cosmol. Astropart. Phys. 2010. [Google Scholar] [CrossRef]
- Baldi, M.; Villaescusa-Navarro, F.; Viel, M.; Puchwein, E.; Springel, V.; Moscardini, L. Cosmic degeneracies—I. Joint N-body simulations of modified gravity and massive neutrinos Mon. Not. R. Astron. Soc. 2014, 440, 75–88. [Google Scholar]
- Arnold, C.; Puchwein, E.; Springel, V. Scaling relations and mass bias in hydrodynamical f(R) gravity simulations of galaxy clusters. Mon. Not. R. Astron. Soc. 2014, 440, 833–842. [Google Scholar] [CrossRef]
- Starobinsky, A.A. How to determine an effective potential for a variable cosmological term. JETP Lett. 1998, 68, 757–763. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Karagiannakis, N.; Park, M. Dark Energy and Equation of State Oscillations with Collisional Matter Fluid in Exponential Modified Gravity. Phys. Rev. D 2015, 91, 064029. [Google Scholar] [CrossRef]
- Gong, Y. Growth factor parametrization and modified gravity. Phys. Rev. D 2008, 78, 123010. [Google Scholar] [CrossRef]
- Hwang, J.C. Perturbations of the Robertson-Walker space—Multicomponent sources and generalized gravity. Astrophys. J. 1991, 375, 443–462. [Google Scholar] [CrossRef]
- Boisseau, B.; Esposito-Farese, G.; Polarski, D.; Starobinsky, A.A. Reconstruction of a Scalar-Tensor Theory of Gravity in an Accelerating Universe. Phys. Rev. Lett. 2000. [Google Scholar] [CrossRef]
- Tsujikawa, S. Matter density perturbations and effective gravitational constant in modified gravity models of dark energy. Phys. Rev. D 2007, 76, 023514. [Google Scholar] [CrossRef]
- López-Revelles, A.J. Growth of matter perturbations for realistic f(R) models. Phys. Rev. D 2013, 87, 024021. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, C.; Huang, Q.G.; Li, M.; Li, S.; Li, X.D.; Wang, S. Testing modified gravity models with recent cosmological observations. Sci. China Phys. Mech. Astron. 2012, 55, 2244–2258. [Google Scholar] [CrossRef]
- Gannouji, R.; Moraes, B.; Polarski, D. The growth of matter perturbations in f(R) models. J. Cosmol. Astropart. Phys. 2009. [Google Scholar] [CrossRef]
- Fu, X.; Wu, P.; Yu, H. The growth of linear perturbations in the DGP model. Phys. Lett. B 2009, 677, 12–15. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Uddin, K.; Tavakol, R. Density perturbations in f(R) gravity theories in metric and Palatini formalisms. Phys. Rev. D 2008, 77, 043007. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H.R. Gauge-ready formulation of the cosmological kinetic theory in generalized gravity theories. Phys. Rev. D 2002, 65, 023512. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Peculiar Velocity Field in the Local Supercluster. Astrophys. J. 1976, 205, 318–328. [Google Scholar] [CrossRef]
- Lahav, O.; Lilje, P.B.; Primack, J.R.; Rees, M.J. Dynamical effects of the cosmological constant. Mon. Not. R. Astron. Soc. 1991, 251, 128–136. [Google Scholar] [CrossRef]
- Polarski, D.; Gannouji, R. On the growth of linear perturbations. Phys. Lett. B 2008, 660, 439–443. [Google Scholar] [CrossRef]
- Linder, E.V. Cosmic growth history and expansion history. Phys. Rev. D 2005, 72, 043529. [Google Scholar] [CrossRef]
- Wang, L.-M.; Steinhardt, P.J. Cluster Abundance Constraints for Cosmological Models with a Time-varying, Spatially Inhomogeneous Energy Component with Negative Pressure. Astrophys. J. 1998. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–139. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Huterer, D.; Kirkby, D.; Bean, R.; Connolly, A.; Dawson, K.; Dodelson, S.; Evrard, A.; Jain, B.; Jarvis, M.; Linder, E.; et al. Growth of cosmic structure: Probing dark energy beyond expansion. Astropart. Phys. 2015, 63, 23–41. [Google Scholar] [CrossRef]
- LSST Science Collaboration. LSST Science Book; Version 2.0.; 1 December 2009. [Google Scholar]
- Hu, W.; White, M. Acoustic Signatures in the Cosmic Microwave Background. Astrophys. J. 1996. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a Cosmological Model and Angular Variations of the Microwave Background. Astrophys. J. 1967, 147, 73–90. [Google Scholar] [CrossRef]
- Kofman, L.A.; Starobinskii, A.A. Effect of the Cosmological Constant on Large scale Anisotropies in the Microwave Background. Sov. Astron. Lett. 1985, 11, 271–274. [Google Scholar]
- Acquaviva, V.; Baccigalupi, C. Dark energy records in lensed cosmic microwave background. Phys. Rev. D 2006, 74, 103510. [Google Scholar] [CrossRef]
- Carbone, C.; Baldi, M.; Pettorino, V.; Baccigalupi, C. Maps of CMB lensing deflection from N-body simulations in Coupled Dark Energy Cosmologies. J. Cosmol. Astropart. Phys. 2013. [Google Scholar] [CrossRef] [PubMed]
- Peebles, P.J.E. Tests of cosmological models constrained by inflation. Astrophys. J. 1984, 284, 439. [Google Scholar] [CrossRef]
- Barrow, J.D.; Saich, P. Growth of large-scale structure with a cosmological constant. Mon. Not. R. Astron. Soc. 1993, 262, 717–725. [Google Scholar] [CrossRef]
- Kunz, M.; Corasaniti, P.-S.; Parkinson, D.; Copeland, E. J. Model-independent dark energy test with sigma(8) using results from the Wilkinson microwave anisotropy probe. Phys. Rev. D 2004, 70, 041301. [Google Scholar] [CrossRef]
- Baldi, M.; Pettorino, V. High-z massive clusters as a test for dynamical coupled dark energy. Mon. Not. R. Astron. Soc. 2011, 412, L1–L5. [Google Scholar] [CrossRef]
- Amendola, L.; Ballesteros, G.; Pettorino, V. Effects of modified gravity on B-mode polarization. Phys. Rev. D 2014, 90, 043009. [Google Scholar] [CrossRef]
- Raveri, M.; Baccigalupi, C.; Silvestri, A.; Zhou, S.-Y. Measuring the speed of cosmological gravitational waves. Phys. Rev. D 2015, 91, 061501. [Google Scholar] [CrossRef]
- Abebe, A.; Abdelwahab, M.; de la Cruz-Dombriz, A.; Dunsby, P.K.S. Covariant gauge-invariant perturbations in multifluid f(R) gravity. Class. Quant. Grav. 2012, 29, 130511. [Google Scholar] [CrossRef]
- Abebe, A.; de la Cruz-Dombriz, A.; Dunsby, P.K.S. Large Scale Structure Constraints for a Class of f(R) Theories of Gravity. Phys. Rev. D 2013, 88, 044050. [Google Scholar] [CrossRef]
- Carloni, S.; Dunsby, P.K.S.; Troisi, A. The Evolution of density perturbations in f(R) gravity. Phys. Rev. D 2008, 77, 024024. [Google Scholar] [CrossRef]
- Ananda, K.N.; Carloni, S.; Dunsby, P.K.S. A detailed analysis of structure growth in f(R) theories of gravity. Class. Quant. Grav. 2009, 26, 235018. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.; Brandenberger, R.H. Theory of cosmological perturbations Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Saltas, I.D.; Sawicki, I.; Amendola, L.; Kunz, M. Anisotropic Stress as a Signature of Nonstandard Propagation of Gravitational Waves. Phys. Rev. Lett. 2014, 113, 191101. [Google Scholar] [CrossRef]
- Lewis, A; Challinor, A.; Lasenby, A. Efficient Computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473–476. [Google Scholar]
- Zhao, G.B.; Pogosian, L.; Silvestri, A.; Zylberberg, J. Searching for modified growth patterns with tomographic surveys. Phys. Rev. D 2009, 79, 083513. [Google Scholar] [CrossRef]
- Bertschinger, E.; Zukin, P. Distinguishing modified gravity from dark energy. Phys. Rev. D 2008, 78, 024015. [Google Scholar] [CrossRef]
- The Dark Energy Survey Collaboration. The Dark Energy Survey. 12 October 2005; arXiv:astro-ph/0510346. [Google Scholar]
- Ivezic, Z.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; Angel, R.; Angeli, G.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. 29 August 2014; arXiv:0805.2366. [Google Scholar]
- Cheung, C.; Fitzpatrick, A.L.; Kaplan, J.; Senatore, L.; Creminelli, P. The effective field theory of inflation. J. High Energy Phys. 2008. [Google Scholar] [CrossRef]
- Gubitosi, G.; Piazza, F.; Vernizzi, F. The Effective Field Theory of Dark Energy. J. Cosmol. Astropart. Phys. 2013. [Google Scholar] [CrossRef]
- Bloomfield, J.; Flanagan, É.; Flanagan, ÉÉ.; Park, M.; Watson, S. Dark energy or modified gravity? An effective field theory approach. J. Cosmol. Astropart. Phys. 2013. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M.; Frusciante, N.; Silvestri, A. EFTCAMB/EFTCosmoMC: Numerical Notes v1.0. 21 October 2014; arXiv:1405.3590. [Google Scholar]
- Song, Y.-S.; Peiris, H.; Hu, W. Cosmological constraints on f(R) acceleration models. Phys. Rev. D 2007, 76, 063517. [Google Scholar] [CrossRef]
- Schmidt, F. Weak lensing probes of modified gravity. Phys. Rev. D 2008, 78, 043002. [Google Scholar] [CrossRef]
- Song, Y.S.; Hu, W.; Sawicki, I. Large scale structure of f(R) gravity. Phys. Rev. D 2007, 75, 044004. [Google Scholar] [CrossRef]
- Lixin, X. FRCAMB: An f(R) Code for Anisotropies in the Microwave Background. 10 June 2015; arXiv:1506.03232v1. [Google Scholar]
- Spergel, D.; Gehrels, N.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; et al. Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. 13 March 2015; arXiv:1506.03232v1arXiv:1503.03757. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.-L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. 14 October 2011; arXiv:1110.3193. [Google Scholar]
- Schlegel, D.; Abdalla, F.; Abraham, T.; Ahn, C.; Allende Prieto, C.; Annis, J.; Aubourg, E.; Azzaro, M.; Baltay, S.M.; Bailey., C.; et al. The Big Boss Experiment. 9 June 2011; arXiv:1106.1706. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martino, I.; De Laurentis, M.; Capozziello, S. Constraining ƒ(R) Gravity by the Large-Scale Structure. Universe 2015, 1, 123-157. https://doi.org/10.3390/universe1020123
De Martino I, De Laurentis M, Capozziello S. Constraining ƒ(R) Gravity by the Large-Scale Structure. Universe. 2015; 1(2):123-157. https://doi.org/10.3390/universe1020123
Chicago/Turabian StyleDe Martino, Ivan, Mariafelicia De Laurentis, and Salvatore Capozziello. 2015. "Constraining ƒ(R) Gravity by the Large-Scale Structure" Universe 1, no. 2: 123-157. https://doi.org/10.3390/universe1020123







