Counting and Correcting Thermodynamically Infeasible Flux Cycles in Genome-Scale Metabolic Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials: Metabolic Network Reconstructions
2.2. Methods
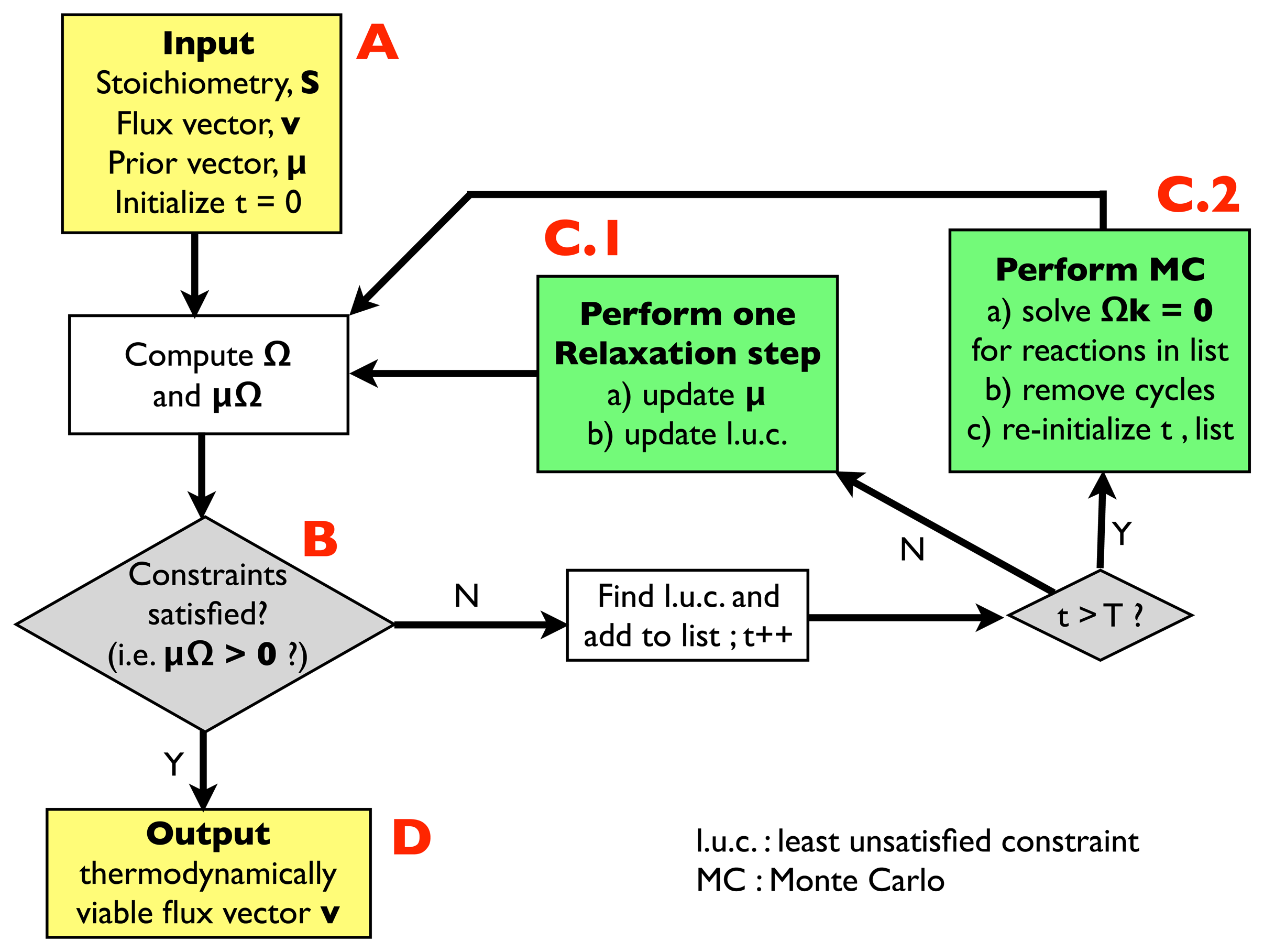
2.2.1. Algorithm for Thermodynamic Analysis: Structure
- (A)
- Input: the input information includes a stoichiometric matrix, S, a flux vector, v (e.g., a solution of FBA) and a prior vector, μ, of chemical potentials. Initialize an integer variable, t, at t = 0 (relaxation steps) and an empty list.
- (B)
- Compute the matrix, Ω, and evaluate the thermodynamic constraints (2), i.e., compute μΩ. If they are satisfied, i.e., if μΩ > 0, go to (D); otherwise, register the least unsatisfied constraint (l.u.c.), i.e., the value of the index, r, for which the corresponding components of the vector, μΩ, is smallest (more negative). Insert it into the list, and increase the t variable by 1; if t < T, with T, a pre-defined large parameter, go to (C.1); otherwise, go to (C.2).
- (C.1)
- Update the vector, μ, by performing a single step of the relaxation algorithm described in Section 2.2.2.; update the list by inserting the new l.u.c. and go back to (B).
- (C.2)
- Perform a Monte Carlo computation, as described in Section 2.2.3., in order to find a solution of system Equation (3), namely Ωk = 0, including only the reactions appearing in the list. Once a solution is found, correct the associated cycle as described in Section 2.2.4. and 2.2.5. ; re-initialize t, empty the list and go back to (B).
- (D)
- Output: a thermodynamically feasible flux vector.
2.2.2. Checking Thermodynamic Viability by Relaxation
2.2.3. Identifying Loops by Monte Carlo
2.2.4. Correcting the Flux Configuration: Local Strategy
 1 ∩
1 ∩
 2, where:
2, where:
 1 and
1 and
 2, are then given by:
2, are then given by:
2.2.5. Correcting the Flux Configuration: Global Strategy
- If at least one of the fluxes is zero, this reaction cannot be involved in any cycle. In particular, na is not associated with a loop.
- If all fluxes are non-zero, the vector ka cannot have a definite sign (positive or negative), since the sum of its entries, namely Equation (17), weighted with some positive coefficients, is zero.
 = {r1, r2, …}. We shall instead denote by
the set of irreversible reactions for which υr = 0 in v*. Clearly, v* also minimizes Qp subject to the stronger constraints υr = 0 for r ∈
= {r1, r2, …}. We shall instead denote by
the set of irreversible reactions for which υr = 0 in v*. Clearly, v* also minimizes Qp subject to the stronger constraints υr = 0 for r ∈
 0 and υr > 0 for r ∈
0 and υr > 0 for r ∈
 \
\  0. Given this, one can now proceed along the same lines as before, because, for any vector na in the null space of Sint:
0. Given this, one can now proceed along the same lines as before, because, for any vector na in the null space of Sint:
- If some reaction, r, for which is forced to have zero flux, since r ∈
0, then na is not associated with a cycle;
- Otherwise, we can demonstrate that na does not correspond to a cycle by taking the partial derivative of Qp(v* + Lana) as done above.
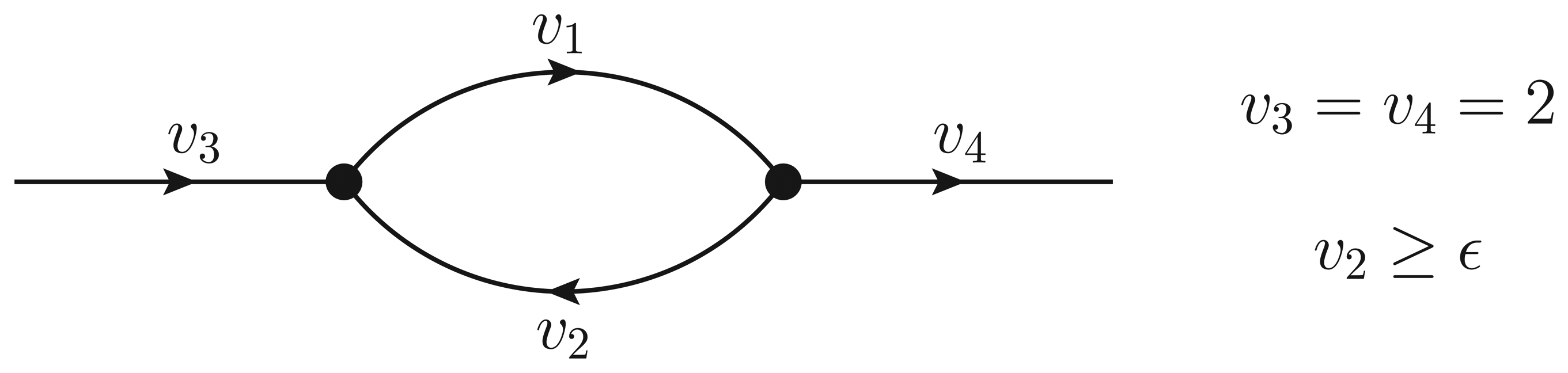
- If ϵ < − 1, then υ2 > ϵ and the Qp minimization yields v* = (1,−1);
- If − 1 ≤ ϵ ≤ 0, then υ2 = ϵ, but the flux configuration v* = (1 − ϵ, ϵ) is still feasible (in particular, the configuration is feasible for ϵ = 0);
- If ϵ > 0, then υ2 = ϵ, and the optimal flux configuration is not feasible.
3. Results
3.1. A Test: Identifying Infeasible Loops in the E. Coli Network iAF1260
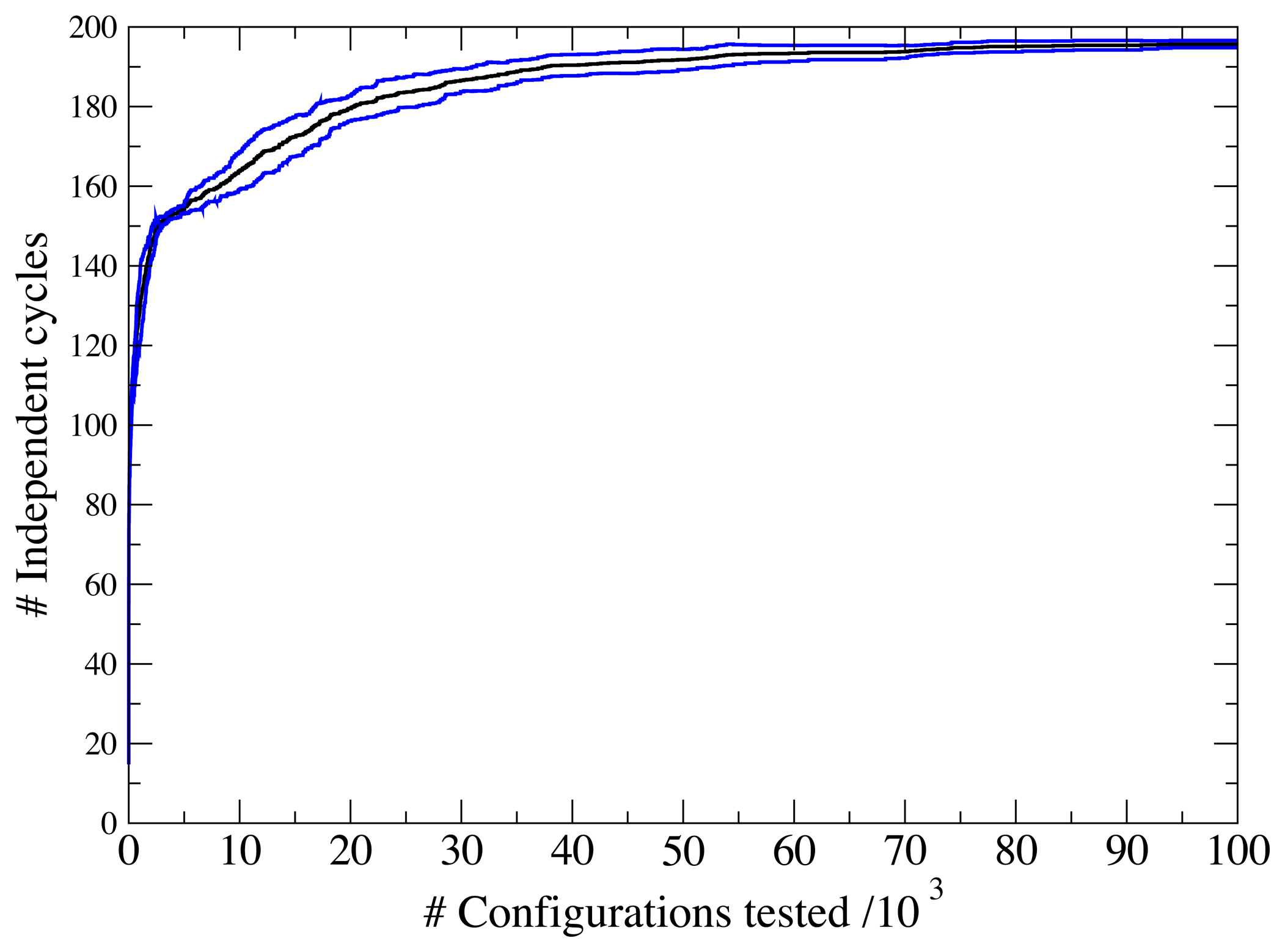
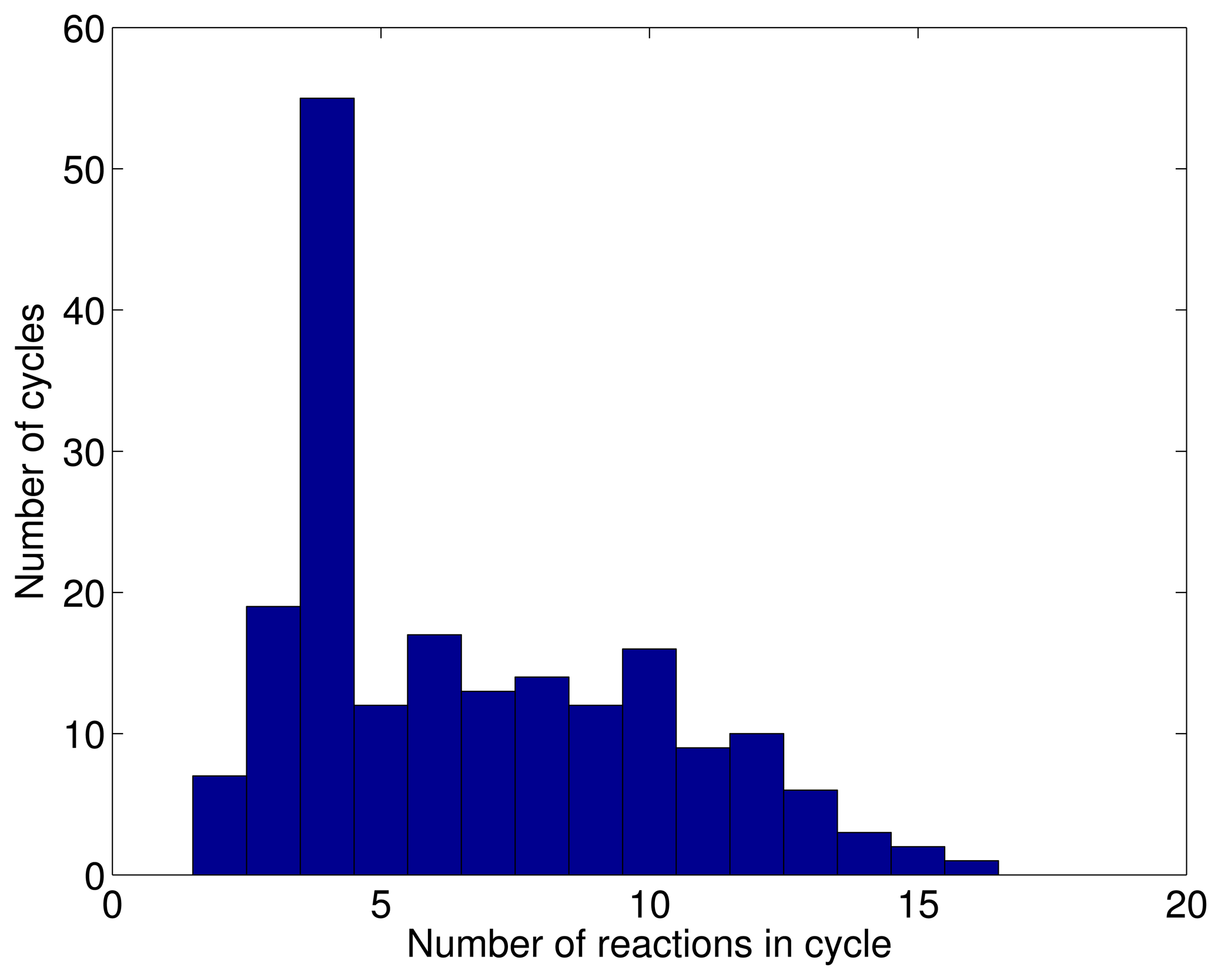
3.2. Inconsistencies in the FBA Solution for the Overall Human Reactome Recon-2
3.3. Correcting Infeasible Loops in FBA Solutions for Cell-Type Specific Human Metabolic Networks
4. Discussions
| Cell type | N | M | NFBA | MFBA | # cycles | Nlocal | Mlocal | Nglobal | Mglobal | qFBA,local | qFBA,global | qlocal,global | ΔG sign |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bile duct | 2,076 | 1,445 | 1,009 | 743 | 215 | 516 | 554 | 367 | 476 | 0.706 | 0.559 | 0.781 | + |
| Cer. cortex | 2,169 | 1,494 | 1,231 | 898 | 358 | 818 | 767 | 257 | 320 | 0.750 | 0.448 | 0.629 | + |
| Cerv. ut. | 1,774 | 1,171 | 1,046 | 780 | 194 | 562 | 620 | 339 | 380 | 0.666 | 0.480 | 0.735 | - |
| Gall blad. | 3,073 | 2,159 | 1,666 | 1,284 | 385 | 1,514 | 1,227 | 254 | 356 | 0.751 | 0.471 | 0.521 | + |
| Kidney | 3,176 | 2,212 | 1,695 | 1,285 | 414 | 1,423 | 1,196 | 142 | 449 | 0.759 | 0.469 | 0.551 | + |
| Lung macroph.. | 2,810 | 1,991 | 1,313 | 960 | 223 | 817 | 779 | 606 | 587 | 0.765 | 0.681 | 0.849 | - |
| Pancreas | 2,821 | 1,951 | 1,319 | 948 | 409 | 814 | 797 | 225 | 534 | 0.756 | 0.534 | 0.701 | + |
| Rectum | 2,976 | 2,041 | 1,328 | 1,135 | 406 | 989 | 1017 | 259 | 399 | 0.765 | 0.560 | 0.670 | - |
| Small int. | 3,179 | 2,213 | 1,385 | 1,192 | 405 | 836 | 1023 | 185 | 206 | 0.776 | 0.578 | 0.745 | + |
| Smooth muscle | 1,806 | 1,222 | 1,042 | 796 | 184 | 579 | 607 | 314 | 320 | 0.677 | 0.501 | 0.747 | + |
| Tonsil ger. | 2,126 | 1,421 | 1,178 | 884 | 405 | 881 | 764 | 357 | 412 | 0.667 | 0.503 | 0.644 | - |
| Tonsil sqam. | 2,573 | 1,718 | 1,719 | 1,250 | 423 | 1,455 | 1,188 | 301 | 403 | 0.718 | 0.334 | 0.430 | + |
| Urot. blad. | 2,874 | 1,965 | 1,597 | 1,308 | 219 | 1,111 | 1,158 | 148 | 686 | 0.760 | 0.450 | 0.613 | + |
| Uterus post-m. | 2,773 | 1,973 | 1,266 | 1,095 | 305 | 736 | 927 | 303 | 389 | 0.763 | 0.578 | 0.757 | + |
| Uterus pre-m. | 2,793 | 1,982 | 1,376 | 1,157 | 208 | 924 | 1022 | 259 | 582 | 0.785 | 0.507 | 0.658 | + |
Acknowledgments
Conflicts of Interest
References
- Price, N.; Famili, I.; Beard, D.; Palsson, B. Extreme pathways and kirchhoff's second law. Biophys. J. 2002, 83, 2879–2882. [Google Scholar]
- Soh, K.; Hatzimanikatis, V. Network thermodynamics in the post-genomic era. Curr. Opin. Microbiol. 2010, 13, 350–357. [Google Scholar]
- Beard, D.; Babson, E.; Curtis, E.; Qian, H. Thermodynamic constraints for biochemical networks. J. Theor. Biol. 2004, 228, 327–333. [Google Scholar]
- Hoppe, A.; Hoffmann, S.; Holzhutter, H. Including metabolite concentrations into flux balance analysis: Thermodynamic realizability as a constraint on flux distributions in metabolic networks. BMC Syst. Biol. 2007, 1, 23:1–23:12. [Google Scholar]
- Qian, H.; Beard, D. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem. 2005, 114, 213–220. [Google Scholar]
- Beard, D.; Liang, S.; Qian, H. Energy balance for analysis of complex metabolic networks. Biophys. J. 2002, 83, 79–86. [Google Scholar]
- Palsson, B.O. Systems Biology: Properties of Reconstructed Networks; Cambridge University Press: Cambridge, NY, USA, 2006. [Google Scholar]
- Bowden, A.C. Fundamentals of Enzyme Kinetics; Wiley-Blackwell: Weinheim, Germany, 2013. [Google Scholar]
- Ge, H.; Qian, M.; Qian, H. Stochastic theory of nonequilibrium steady states. Part II: Applications in chemical biophysics. Phys. Rep. 2012, 510, 87–118. [Google Scholar]
- Frey, E.; Kroy, K. Brownian motion: A paradigm of soft matter and biological physics. Ann. Phys. 2005, 14, 20–50. [Google Scholar]
- Beg, Q.; Vazquez, A.; Ernst, J.; de Menezes, M.; Bar-Joseph, Z.; Barabási, A.L.; Oltvai, Z.N. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. USA 2007, 104, 12663–12668. [Google Scholar]
- De Martino, A.; Marinari, E. The solution space of metabolic networks: Producibility, robustness and fluctuations. J. Phys. Conf. Ser. 2010, 233, 012019. [Google Scholar]
- Schrijver, A. Theory of Linear and Integer Programming; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Orth, J.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar]
- Segrè, D.; Vitkup, D.; Church, G. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar]
- Jankowski, M.; Henry, C.; Broadbelt, L.; Hatzimanikatis, V. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 2008, 95, 1487–1499. [Google Scholar]
- Fleming, R.; Thiele, I.; Nasheuer, H. Quantitative assignment of reaction directionality in constraint-based models of metabolism: Application to Escherichia coli. Biophys. Chem. 2009, 145, 47–56. [Google Scholar]
- Kummel, A.; Panke, S.; Heinemann, M. Systematic assignment of thermodynamic constraints in metabolic network models. BMC Bioinforma. 2006, 7, 512:1–512:12. [Google Scholar]
- Alberty, R.A. Thermodynamics of Biochemical Reactions; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Schellenberger, J.; Lewis, N.; Palsson, B.O. Elimination of thermodynamically infeasible loops in steady-state metabolic models. Biophys. J. 2011, 100, 544–553. [Google Scholar]
- Henry, C.; Broadbelt, L.; Hatzimanikatis, V. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar]
- Müller, A.; Brockmayr, A. Fast thermodynamically constrained flux variability analysis. Bioinformatics 2013, 29, 903–909. [Google Scholar]
- Beard, D.A.; Qian, H. Chemical Biophysics; Cambridge University Press: Cambridge, NY, USA, 2008. [Google Scholar]
- De Martino, D.; Figliuzzi, M.; de Martino, A.; Marinari, E. A scalable algorithm to explore the gibbs energy landscape of genome-scale metabolic networks. PLoS Comp. Biol. 2012, 8, e1002562. [Google Scholar]
- De Martino, D. Thermodynamics of biochemical networks and duality theorems. Phys. Rev. E 2013, 87, 053108. [Google Scholar]
- Johnson, D.B. Finding all the elemtary circuits of a directed graph. SIAM J. Comput. 1975, 4, 77–84. [Google Scholar]
- Wright, J.; Wagner, A. Exhaustive identification of steady state cycles in large stoichiometric networks. BMC Syst. Biol. 2008, 2, 61:1–61:9. [Google Scholar]
- Wiback, S.; Famili, I.; Greenberg, H.; Palsson, B.O. Monte Carlo sampling can be used to determine the size and shape of the steady-state flux space. J. Theor. Biol. 2004, 228, 437–447. [Google Scholar]
- Price, N.; Schellenberger, J.; Palsson, B.O. Uniform sampling of steady-state flux spaces: Means to design experiments and to interpret enzymopathies. Biophys. J. 2004, 87, 2172–2186. [Google Scholar]
- Mezard, M.; Montanari, A. Information, Physics, and Computation; Oxford University Press: Oxford, NY, USA, 2009. [Google Scholar]
- Feist, A.; Henry, C.; Reed, J.; Krummenacker, M.; Joyce, A.; Karp, P.; Broadbelt, L.; Hatzimanikatis, V.; Palsson, B.O. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121:1–121:18. [Google Scholar]
- Thiele, I.; Swainston, N.; Fleming, R.M.T.; Hoppe, A.; Sahoo, S.; Aurich, M.K.; Haraldsdottir, H.; Mo, M.L.; Rolfsson, O.; Stobbe, M.D.; et al. A community-driven global reconstruction of human metabolism. Nat. Biotechnol. 2013, 31, 419–425. [Google Scholar] [Green Version]
- Schellenberger, J.; Que, R.; Fleming, R.M.T.; Thiele, I.; Orth, J.D.; Feist, A.M.; Zielinski, D.C.; Bordbar, A.; Lewis, N.E.; Rahmanian, S.; et al. Quantitative prediction of cellular metabolism with constraint-based models: The COBRA Toolbox v2.0. Nat. Protoc. 2011, 6, 1290–1307. [Google Scholar]
- Shlomi, T.; Cabili, M.N.; Herrgård, M.J.; Palsson, B.O.; Ruppin, E. Network-based prediction of human tissue-specific metabolism. Nat. Biotechnol. 2008, 26, 1003–1010. [Google Scholar]
- Krauth, W.; Mezard, M. Learning algorithms with optimal stability in neural networks. J. Phys. A 1987, 20, L745–L752. [Google Scholar]
- Binder, K.; Heermann, D.W. Monte Carlo Simulation in Statistical Physics; Springer: Heidelberg, Germany, 2002. [Google Scholar]
- De Martino, A.; de Martino, D.; Mulet, R.; Uguzzoni, G. Reaction networks as systems for resource allocation: A variational principle for their non-equilibrium steady states. PLoS One 2012, 7, e39849. [Google Scholar]
- Schilling, C.H.; Letscher, D.; Palsson, B.O. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 2000, 203, 229–248. [Google Scholar]
- Mahadevan, R.; Schilling, C. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar]
Supplementary Files
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Martino, D.; Capuani, F.; Mori, M.; De Martino, A.; Marinari, E. Counting and Correcting Thermodynamically Infeasible Flux Cycles in Genome-Scale Metabolic Networks. Metabolites 2013, 3, 946-966. https://doi.org/10.3390/metabo3040946
De Martino D, Capuani F, Mori M, De Martino A, Marinari E. Counting and Correcting Thermodynamically Infeasible Flux Cycles in Genome-Scale Metabolic Networks. Metabolites. 2013; 3(4):946-966. https://doi.org/10.3390/metabo3040946
Chicago/Turabian StyleDe Martino, Daniele, Fabrizio Capuani, Matteo Mori, Andrea De Martino, and Enzo Marinari. 2013. "Counting and Correcting Thermodynamically Infeasible Flux Cycles in Genome-Scale Metabolic Networks" Metabolites 3, no. 4: 946-966. https://doi.org/10.3390/metabo3040946




