Theoretical Analysis of Vibration Frequency of Graphene Sheets Used as Nanomechanical Mass Sensor
Abstract
:1. Introduction
2. Experimental Approach
2.1. Nonlocal Elasticity Theory
2.2. Single-Layer Graphene Sheets
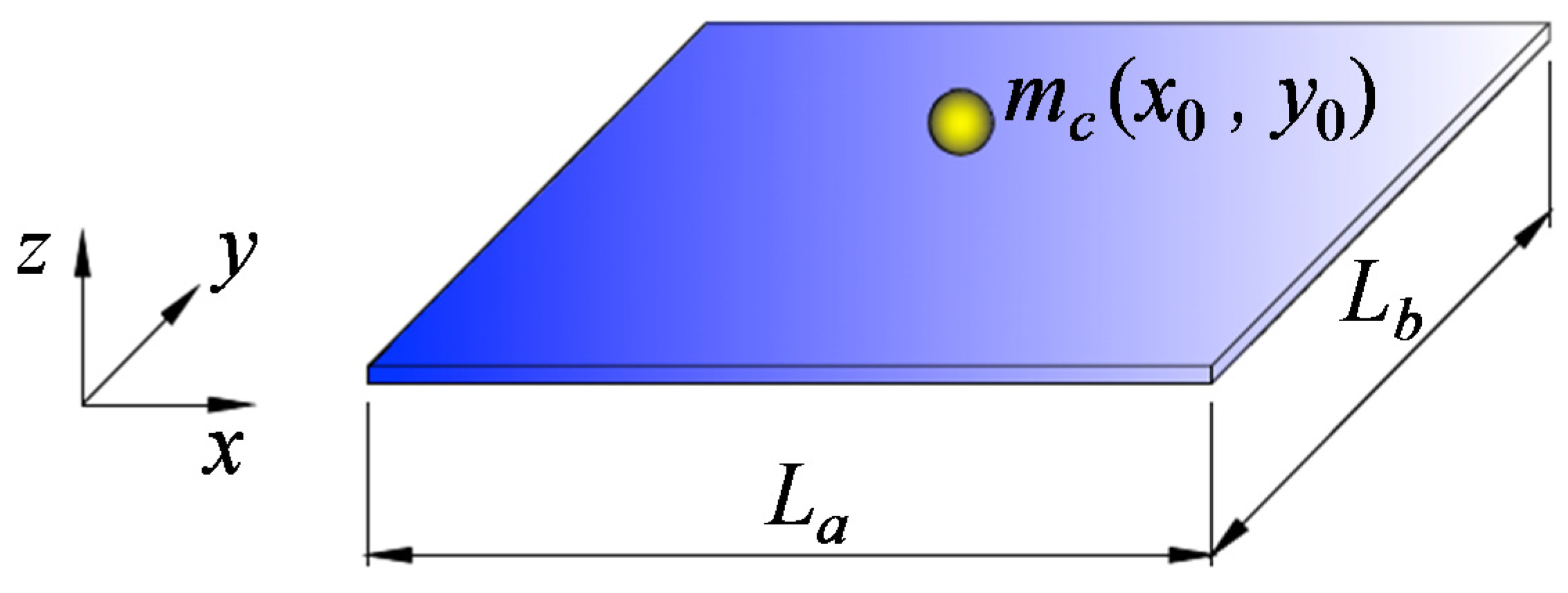
2.3. Double-Layer Graphene Sheets
3. Analytical Results and Discussion
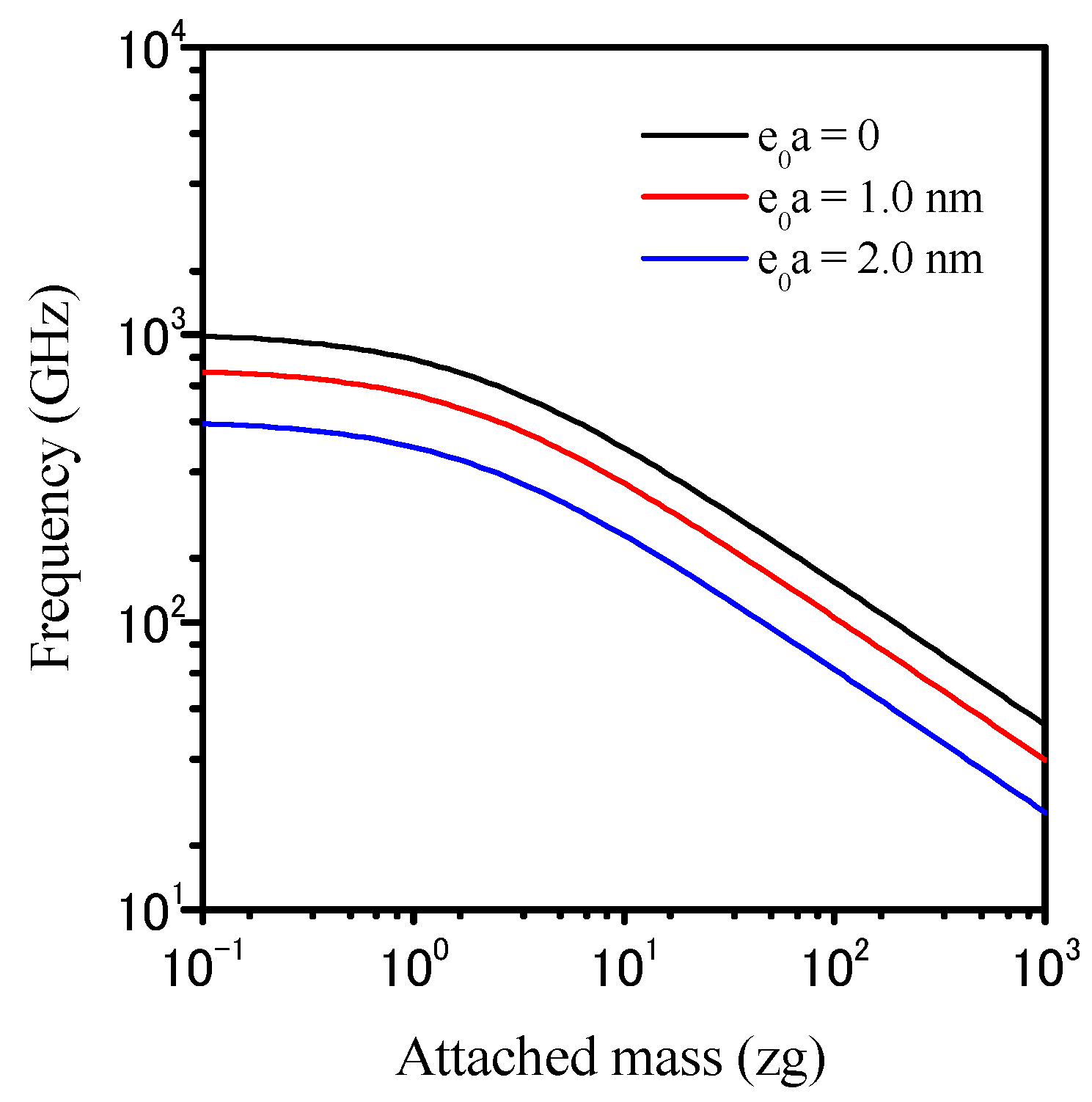
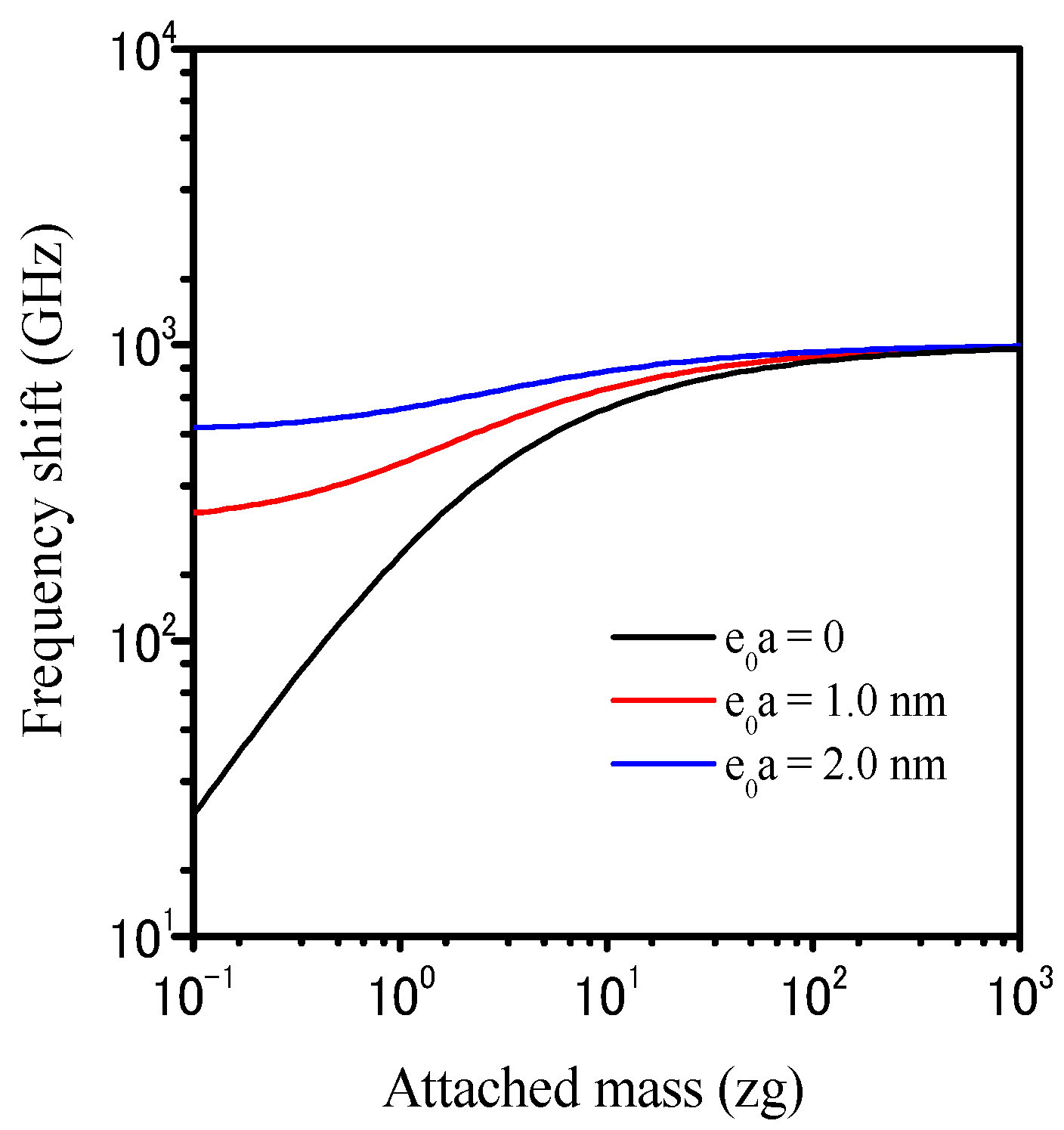
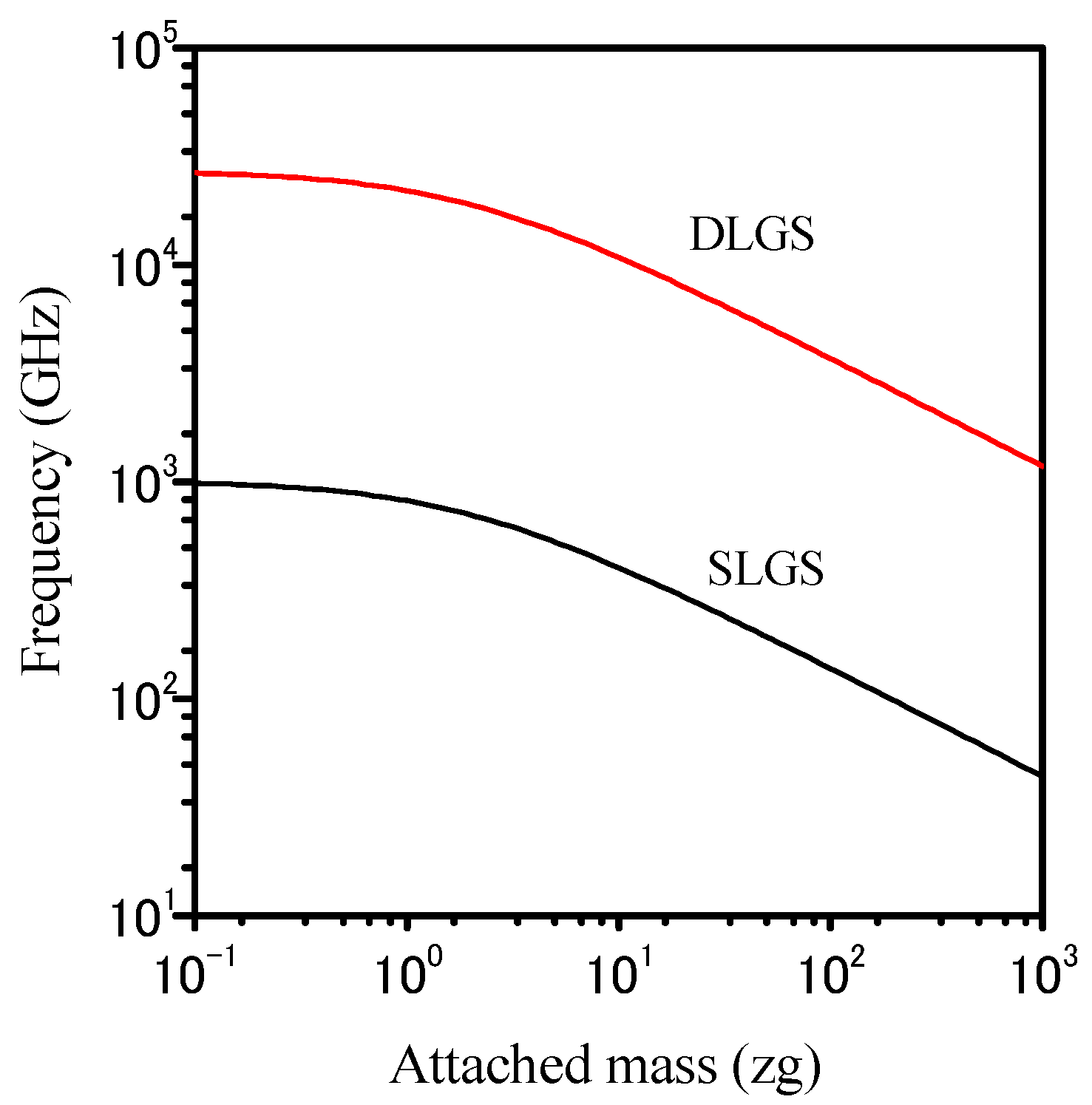
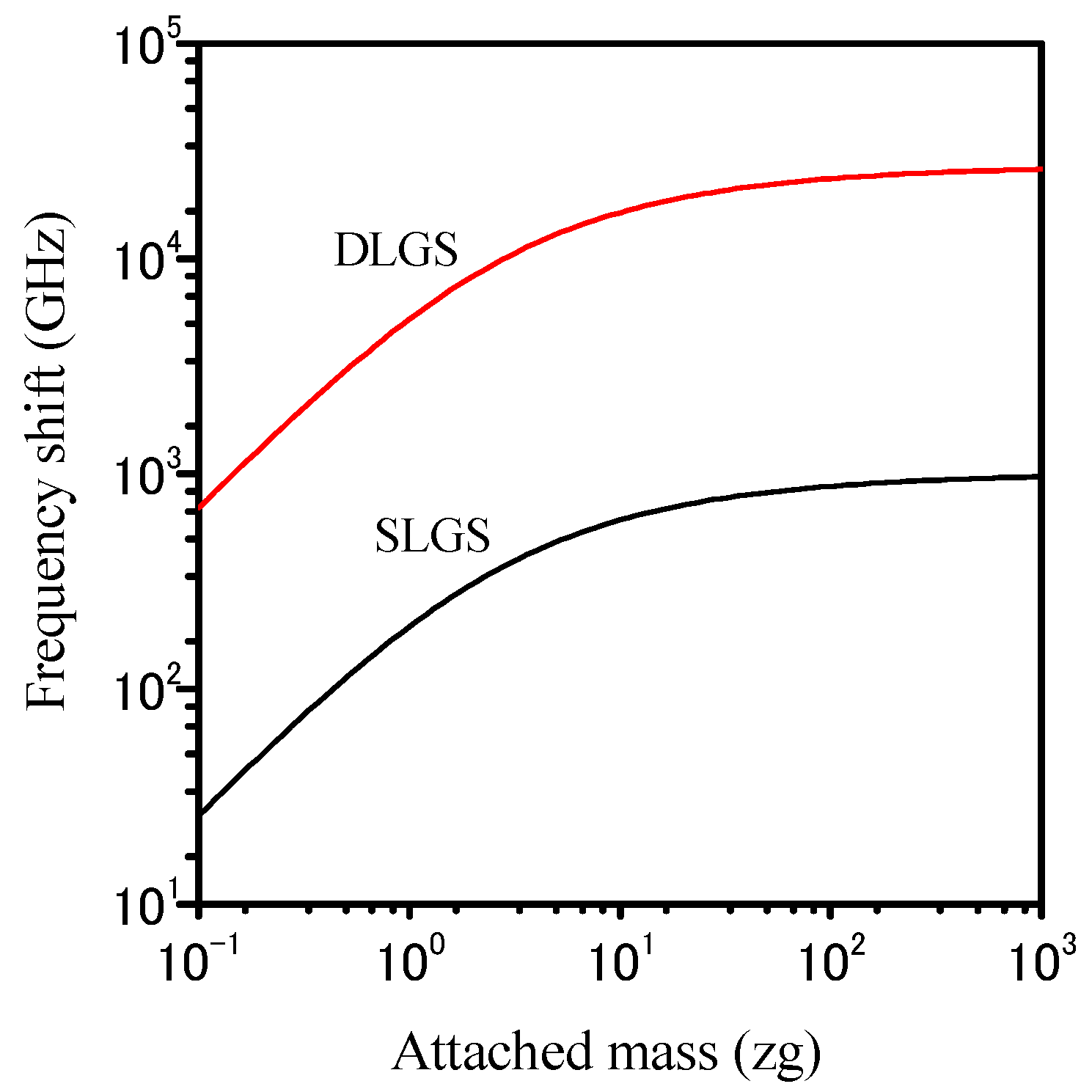
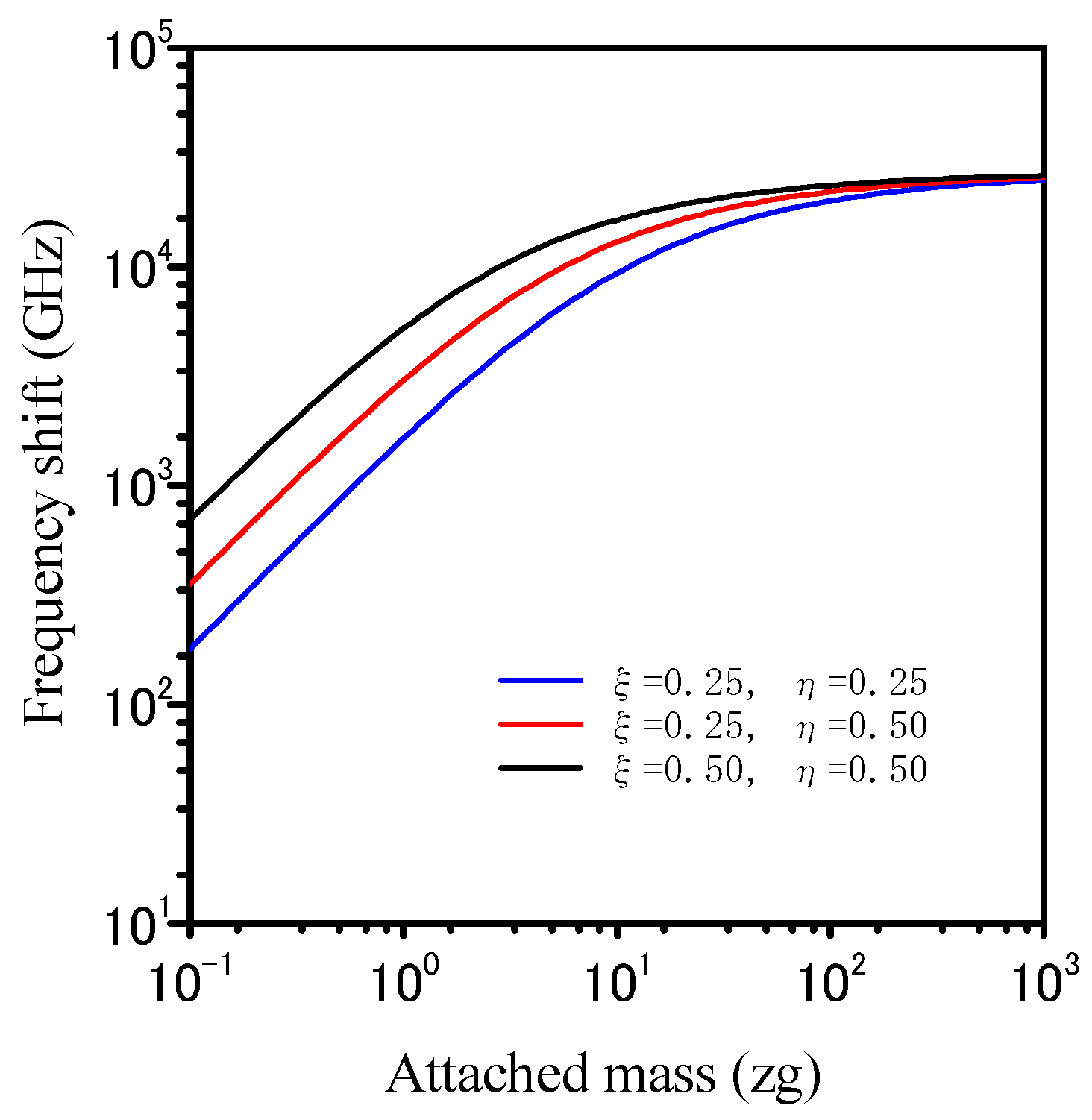
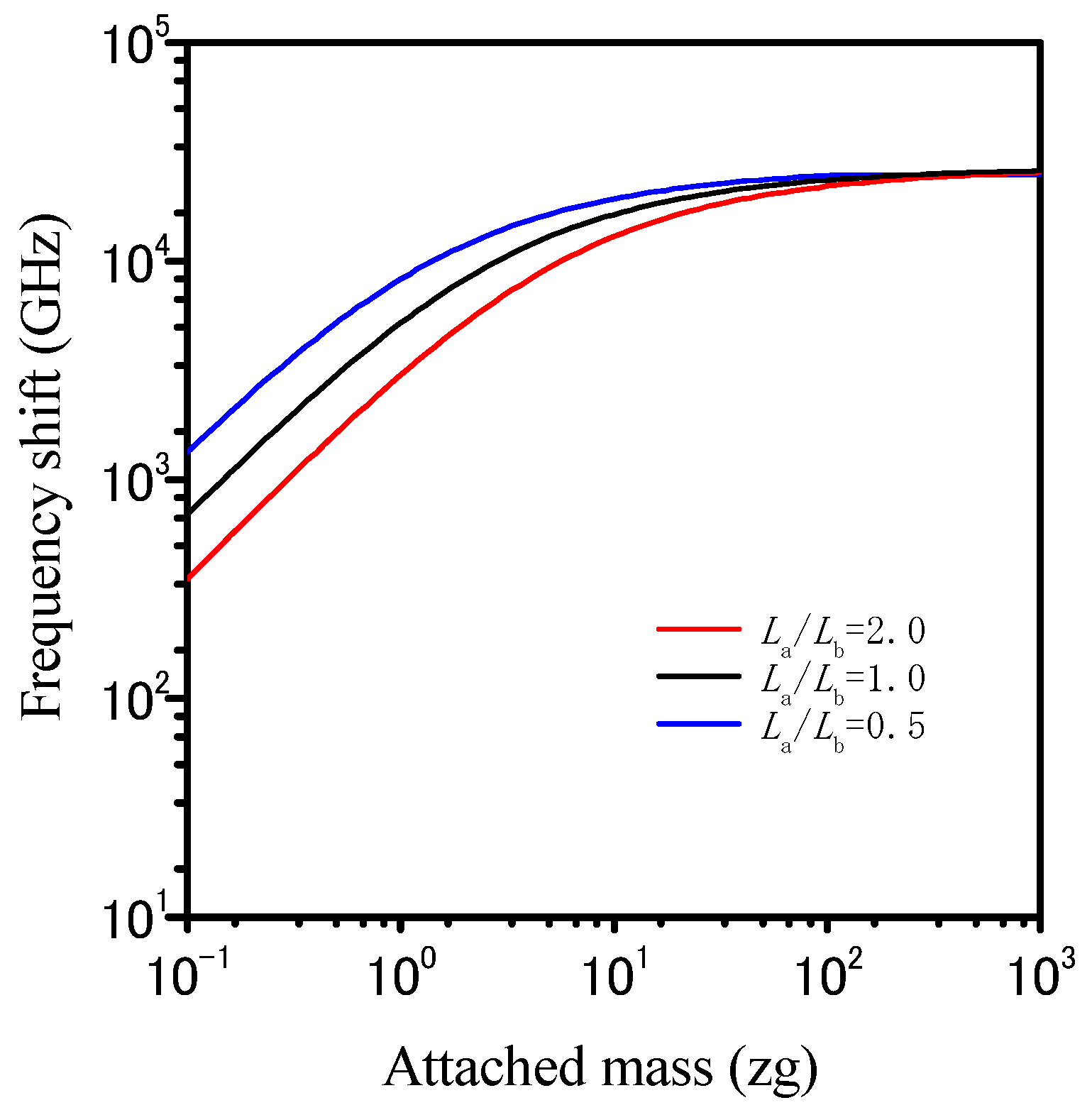
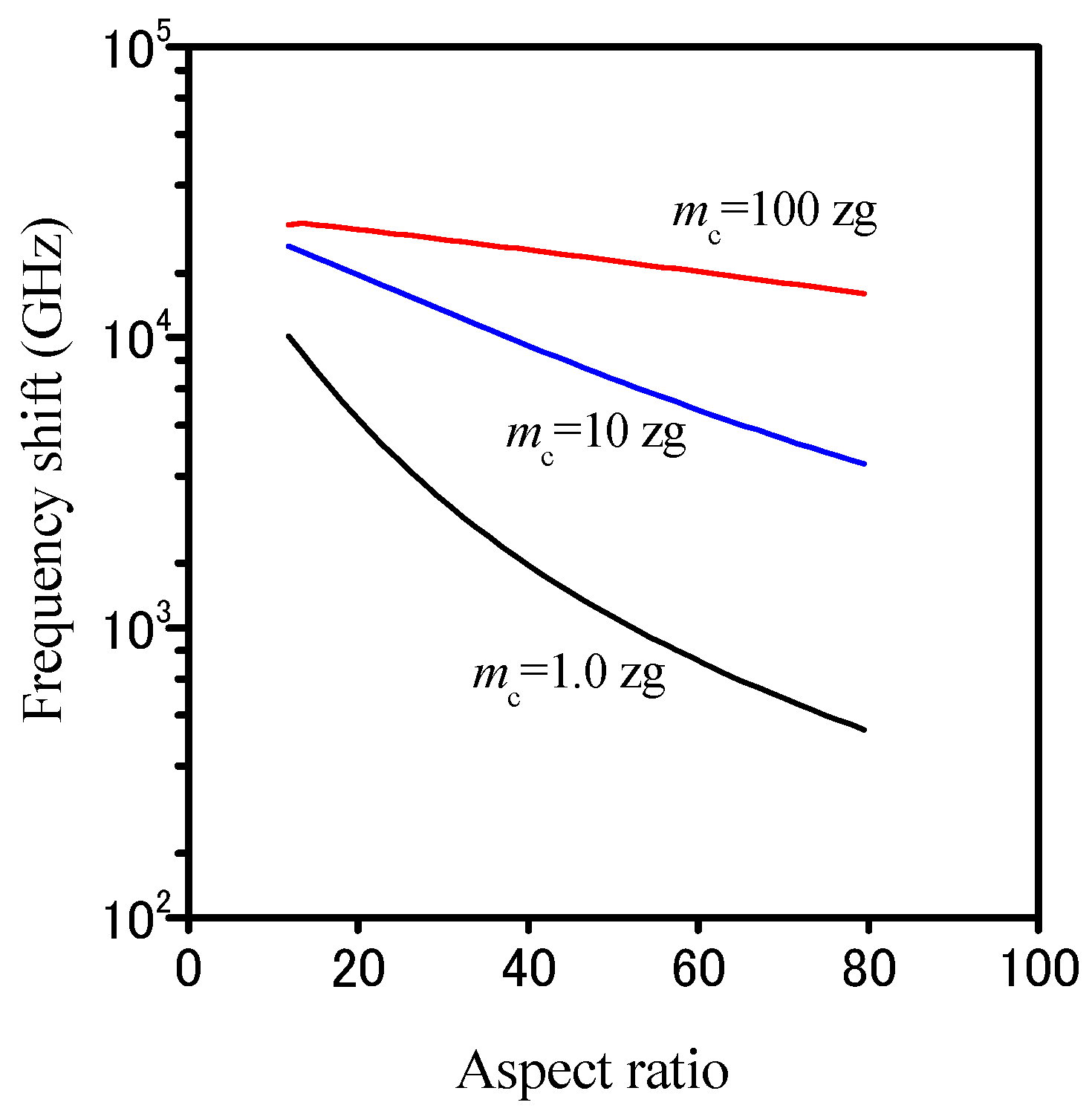
4. Conclusions
Conflicts of Interest
References
- Frank, I.W.; Tanenbaum, D.M.; van der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Cheng, H.M. The fabrication, properties, and uses of graphene/polymer composites. Macromol. Chem. Phys. 2012, 213, 1060–1077. [Google Scholar] [CrossRef]
- Chen, C.; Rosenblatt, S.; Bolotin, K.I.; Kalb, W.; Kim, P.; Kymissis, I.; Stormer, H.L.; Heinz, T.F.; Hone, J. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhi, L.; Mullen, K. Transparent, conductive graphene electrodes for dye-sensitized solar cells. Nano Lett. 2008, 8, 323–327. [Google Scholar] [CrossRef] [PubMed]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on grapheme. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arash, B.; Jiang, J.W.; Rabczuk, T. A review on nanomechanical resonators and their applications in sensors and molecular transportation. Appl. Phys. Rev. 2015, 2, 021301. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.; Rabczuk, T. MoS2 Nanoresonators: Intrinsically better than graphene? Nanoscale 2014, 6, 3618–3625. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.W.; Wang, B.S.; Park, H.; Rabczuk, T. Adsorbate migration effects on continuous and discontinuous temperature-dependent transitions in the quality factors of graphene nanoresonators. Nanotechnology 2014, 25, 025501. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.W.; Park, H.; Rabczuk, T. Preserving the Q-factors of ZnO nanoresonators via polar surface reconstruction. Nanotechnology 2013, 24, 405705. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Enhancing the mass sensitivity of graphene nanoresonators via nonlinear oscillations: The elective strain mechanism. Nanotechnology 2012, 23, 47550. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Arash, B. A review on applications of carbon nanotubes and graphenes as nano-resonator sensors. Comput. Mater. Sci. 2014, 82, 350–360. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. Detection of gas atoms with carbon nanotubes. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Huang, X.M.H.; Roukes, M.L. Ultrasensitive nanoelectromechanical mass detection. Appl. Phys. Lett. 2004, 84, 4469–4471. [Google Scholar] [CrossRef]
- Chaste, J.; Eichler, A.; Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Eichler, A.; Moser, J.; Chaste, J.; Zdrojek, M.; Wilson-Rae, I.; Bachtold, A. Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene. Nat. Nanotechnol. 2011, 6, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Pang, W.; Yan, L.; Zhang, H.; Yu, H.Y.; Kim, E.S.; Tang, W.C. Femtogram mass sensing platform based on lateral extensional mode piezoelectric resonator. Appl. Phys. Lett. 2006, 88, 243503. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.S.; Gao, Y.; Yang, X.; Chen, H.Z. Unique synthesis of graphene-based materials for clean energy and biological sensing applications. Chin. Sci. Bull. 2012, 57, 3000–3009. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.C.; Liu, Y.Q. Controllable synthesis of graphene and its applications. Adv. Mater. 2010, 22, 3225–3241. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.S.; Zhao, Y; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.H.; Kim, P.; Choi, J.Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.W.; Flege, J.I.; Sutter, E.A. Epitaxial graphene on ruthenium. Nat. Mater. 2008, 7, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Arghavan, S.; Singh, A.V. Effects of van der Waals interactions on the nonlinear vibration of multi-layered graphene sheets. J. Phys. D: Appl. Phys. 2012, 45, 455305. [Google Scholar] [CrossRef]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the electronic structure of bilayer grapheme. Science 2006, 313, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Virojanadara, C.; Yakimova, R.; Zakharov, A.A.; Johansson, L.I. Large homogeneous mono-/bi-layer graphene on 6h-sic(0001) and buffer layer elimination. J. Phys. D Appl. Phys. 2010, 43, 374010. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, T.T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer grapheme. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Dai, Y.; Ye, Y.; Luo, J.X.; Shi, Z.J.; Dai, L.; Qin, G.G. Bilayer graphene anode for small molecular organic electroluminescence. J. Phys. D Appl. Phys. 2012, 45, 245103. [Google Scholar] [CrossRef]
- Popov, A.M.; Lebedeva, I.V.; Knizhnik, A.A.; Lozovik, Y.E.; Potapkin, B.V. Structure, energetic and tribological properties, and possible applications in nems of argon-separated double-layer grapheme. J. Phys. Chem. C 2013, 117, 11428–11435. [Google Scholar] [CrossRef]
- Popov, A.M.; Lebedeva, I.V.; Knizhnik, A.A.; Lozovik, Y.E.; Potapkin, B.V.; Poklonski, N.A.; Siahlo, A.I.; Vyrko, S.A. AA stacking, tribological and electronic properties of double-layer graphene with krypton spacer. J. Chem. Phys. 2013, 139, 154705. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; He, X.; Kitipornchai, S.; Zhang, H. Geometrical nonlinear free vibration of multi-layered graphene sheets. J. Phys. D Appl. Phys. 2011, 44, 135401. [Google Scholar] [CrossRef]
- Shi, J.X.; Ni, Q.Q.; Lei, X.W.; Natsuki, T. Nonlocal vibration of embedded double-layer graphene nanoribbons in in-phase and anti-phase modes. Phys. E 2012, 44, 1136–1141. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.X.; Ni, Q.Q. Vibration analysis of circular double-layered graphene sheets. J. Appl. Phys. 2012, 111, 044310. [Google Scholar] [CrossRef]
- Hill, E.W.; Vijayaraghavan, A.; Novoselov, K. Graphene sensors. IEEE Sens. J. 2011, 11, 3161–3170. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q.; Duan, W.H. Detection of gas atoms via vibration of graphenes. Phys. Lett. A 2011, 375, 2411–2415. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Enhancing the mass sensitivity of graphene nanoresonators via nonlinear oscillations: The effective strain mechanism. Nanotechnology 2012, 23, 475501. [Google Scholar] [CrossRef] [PubMed]
- Sakhaee-Pour, A.; Ahmadiana, M.T.; Vafaib, A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun. 2008, 145, 168–172. [Google Scholar] [CrossRef]
- Lei, X.W.; Natsuki, T.; Shi, J.X.; Ni, Q.Q. Vibration analysis of circular double-layered graphene sheets. J. Appl. Phys. 2013, 113, 154313. [Google Scholar] [CrossRef]
- Dai, M.D.; Kim, C.W.; Eom, K. Nonlinear vibration behavior of graphene resonators and their applications in sensitive mass detection. Nanoscale Res. Lett. 2012, 7, 449. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.B.; Tang, H.L.; Li, D.K.; Tang, G.J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal kirchhoff plate theory. Comp. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Lee, H.L.; Yang, Y.C.; Chang, W.J. Mass Detection Using a Graphene-Based Nanomechanical Resonator. Jpn. J. Appl. Phys. 2013, 52, 025101. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using double-layered graphene sheets resonators. J. Appl. Phys. 2013, 114, 094307. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, P.Q.; Lee, H.P.; Wang, C.M.; Reddy, J.N. Non-local elastic plate theories. Proc. R. Soc. A 2007, 463, 3225–3240. [Google Scholar] [CrossRef]
- Polizzotto, C. Nonlocal elasticity and related variational principles. Inter. J. Solid. Struc. 2001, 38, 7359–7380. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput. Mater. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Kitipornchai, S.; He, X.Q.; Liew, K.M. Continuum model for the vibration of multilayered graphene sheets. Phys. Rev. B 2005, 72, 075443. [Google Scholar] [CrossRef]
- Shi, J.X.; Natsuki, T.; Lei, X.W.; Ni, Q.Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Narendar, S.; Gopalakrishnan, S. Nonlocal scale effects on wave propagation in multi-walled carbon nanotubes. Comput. Mater. Sci. 2009, 47, 526–538. [Google Scholar] [CrossRef]
- Amiriana, B.; Hosseini-Arab, R.; Moosavia, H. Thermo-mechanical vibration of short carbon nanotubes embedded in pasternak foundation based on nonlocal elasticity theory. Shock. Vib. 2013, 20, 821–832. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natsuki, T. Theoretical Analysis of Vibration Frequency of Graphene Sheets Used as Nanomechanical Mass Sensor. Electronics 2015, 4, 723-738. https://doi.org/10.3390/electronics4040723
Natsuki T. Theoretical Analysis of Vibration Frequency of Graphene Sheets Used as Nanomechanical Mass Sensor. Electronics. 2015; 4(4):723-738. https://doi.org/10.3390/electronics4040723
Chicago/Turabian StyleNatsuki, Toshiaki. 2015. "Theoretical Analysis of Vibration Frequency of Graphene Sheets Used as Nanomechanical Mass Sensor" Electronics 4, no. 4: 723-738. https://doi.org/10.3390/electronics4040723




