The Effects of Different Electron-Phonon Couplings on the Spectral and Transport Properties of Small Molecule Single-Crystal Organic Semiconductors
Abstract
:1. Introduction
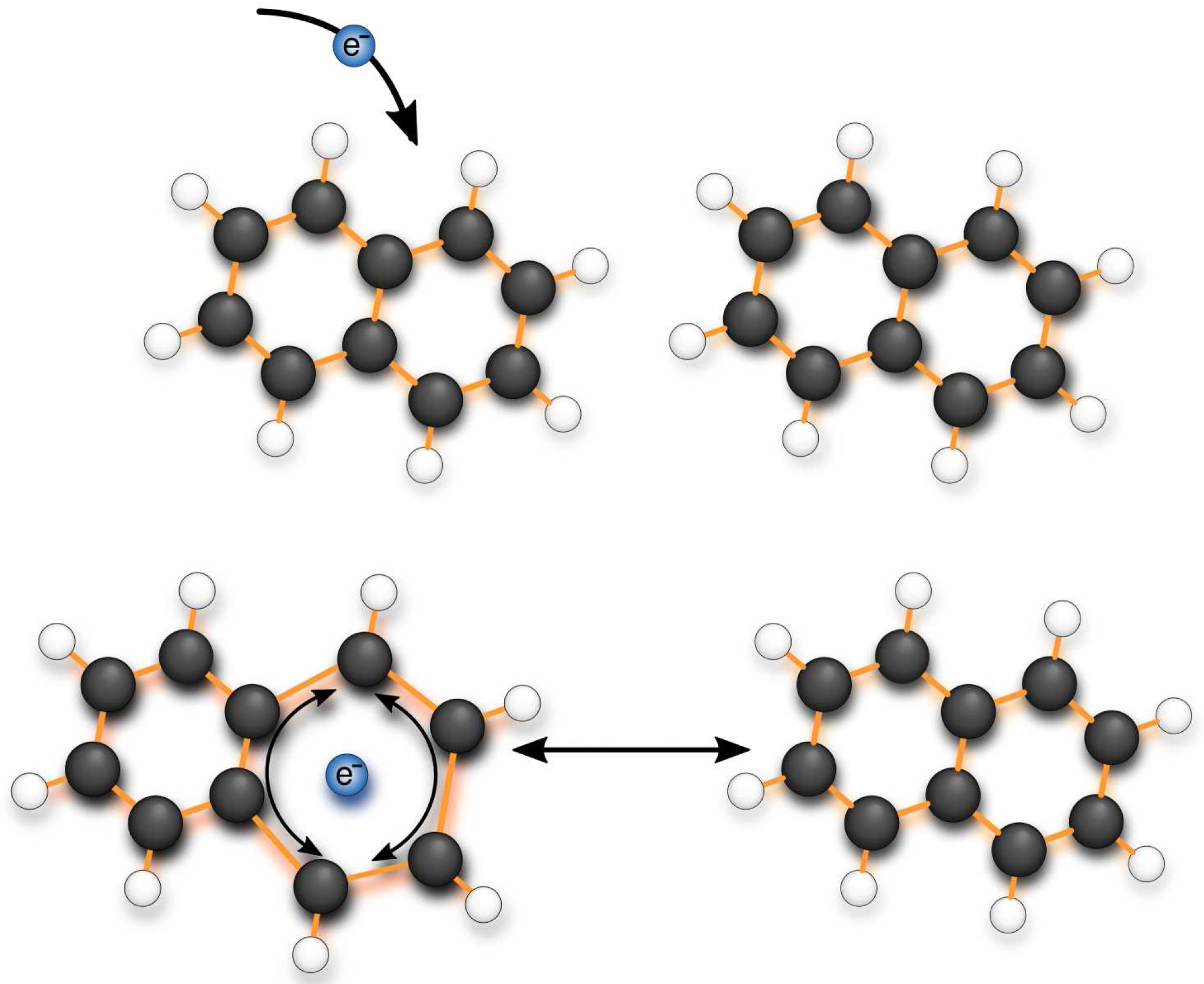
2. Effects of Low-Frequency Vibrational Modes
2.1. Band Anisotropy
2.2. Inter-Molecular Vibrational Modes
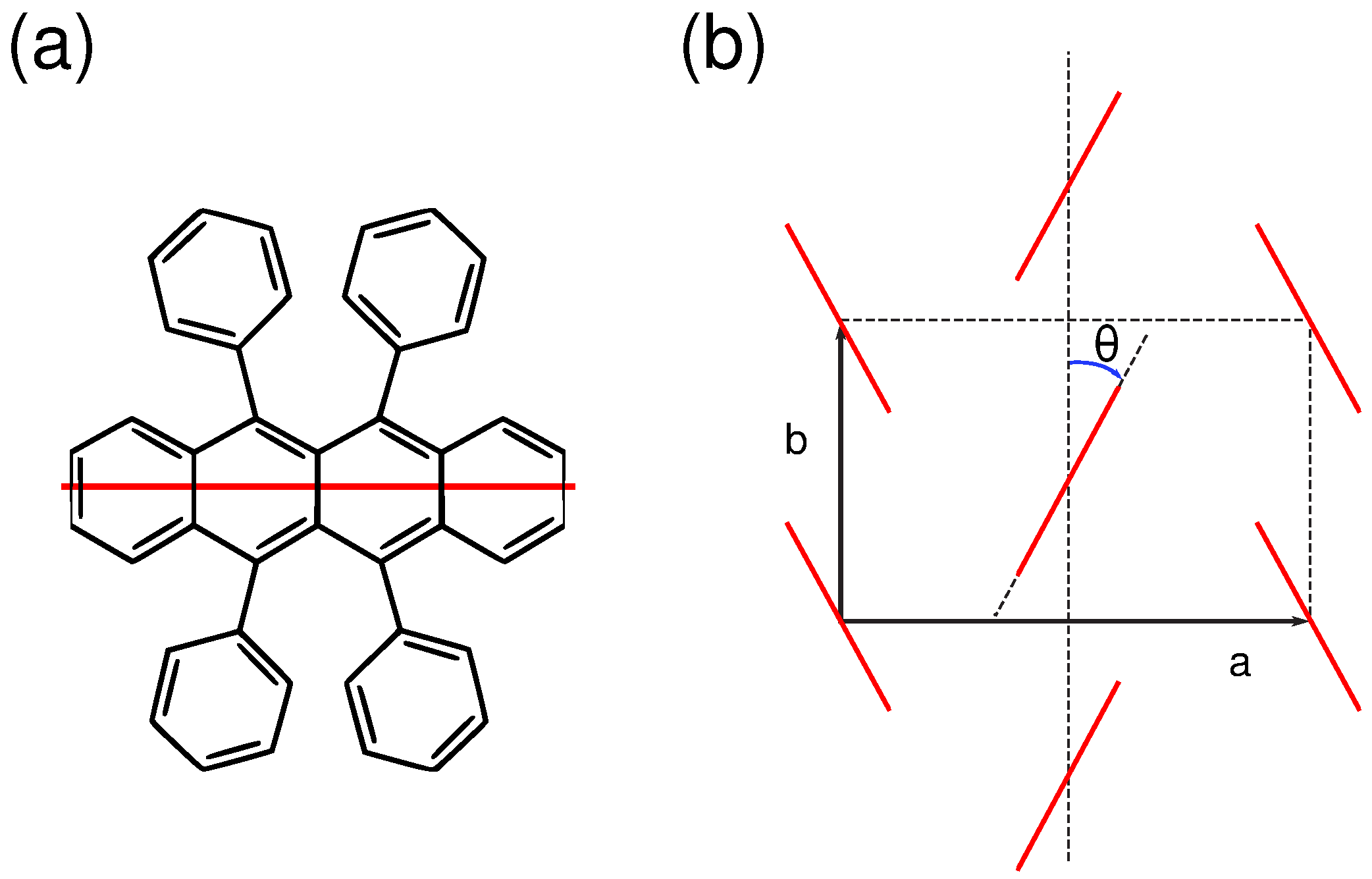
2.3. Calculation Method
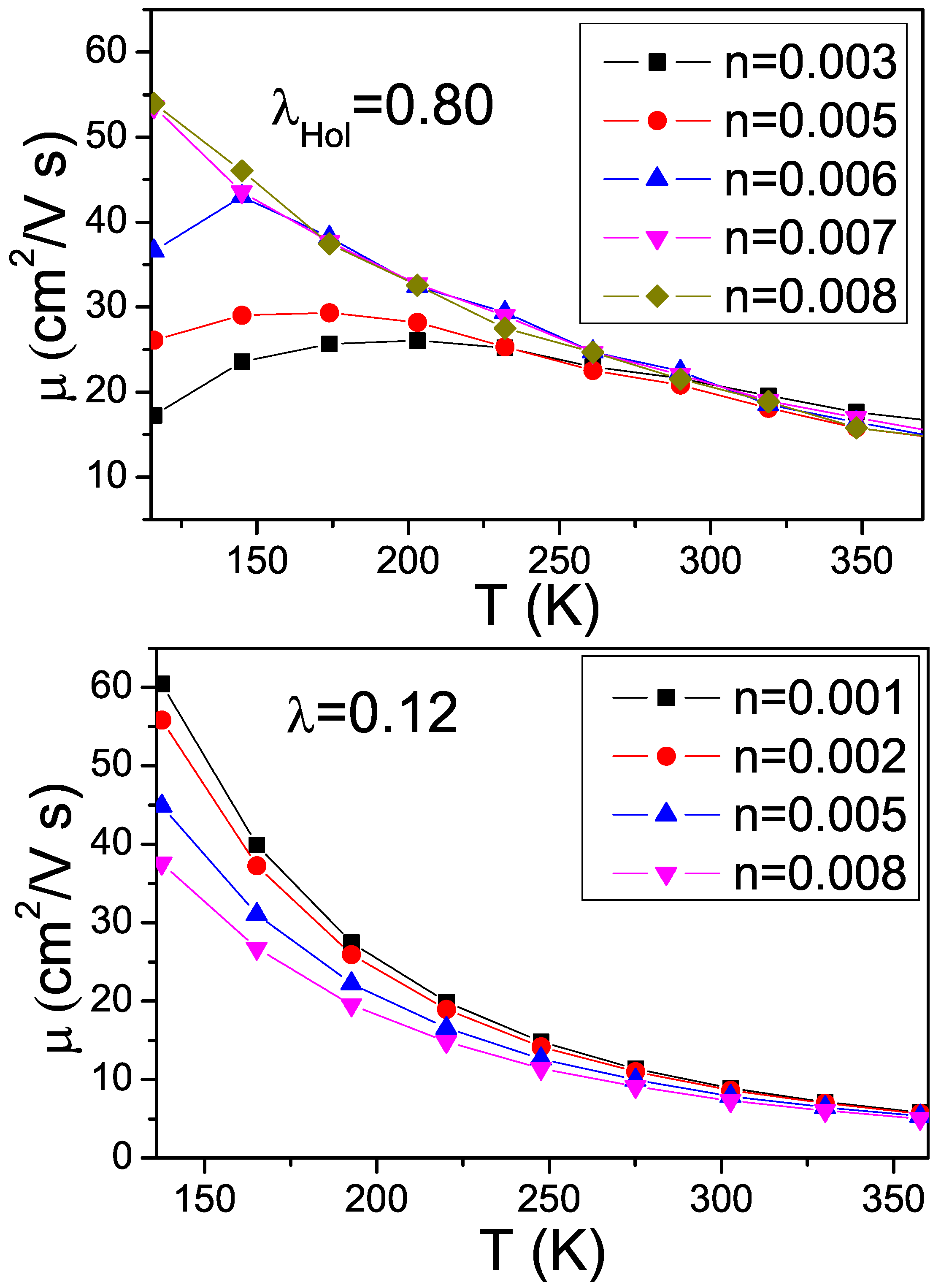
2.4. Results about Spectral and Transport Properties
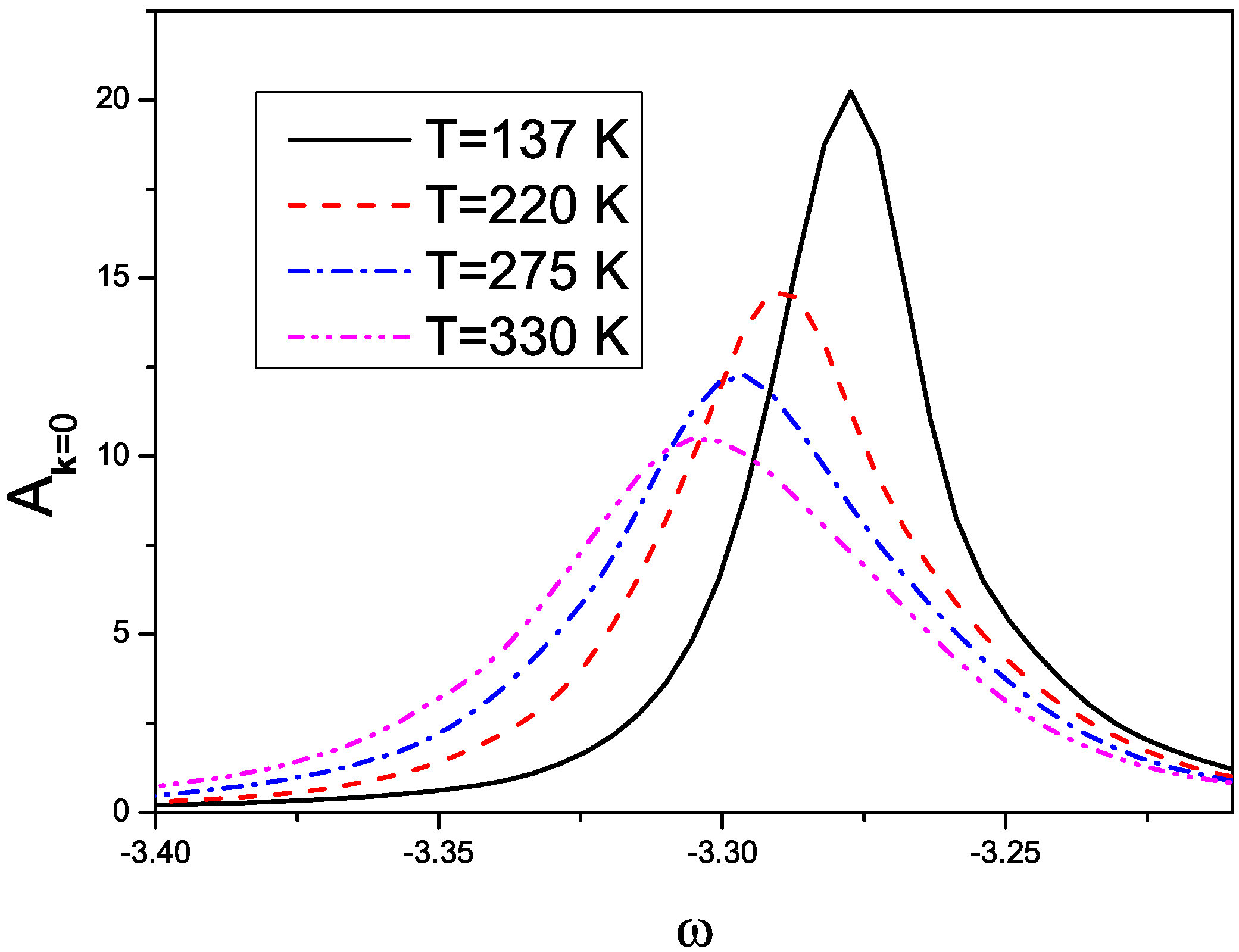
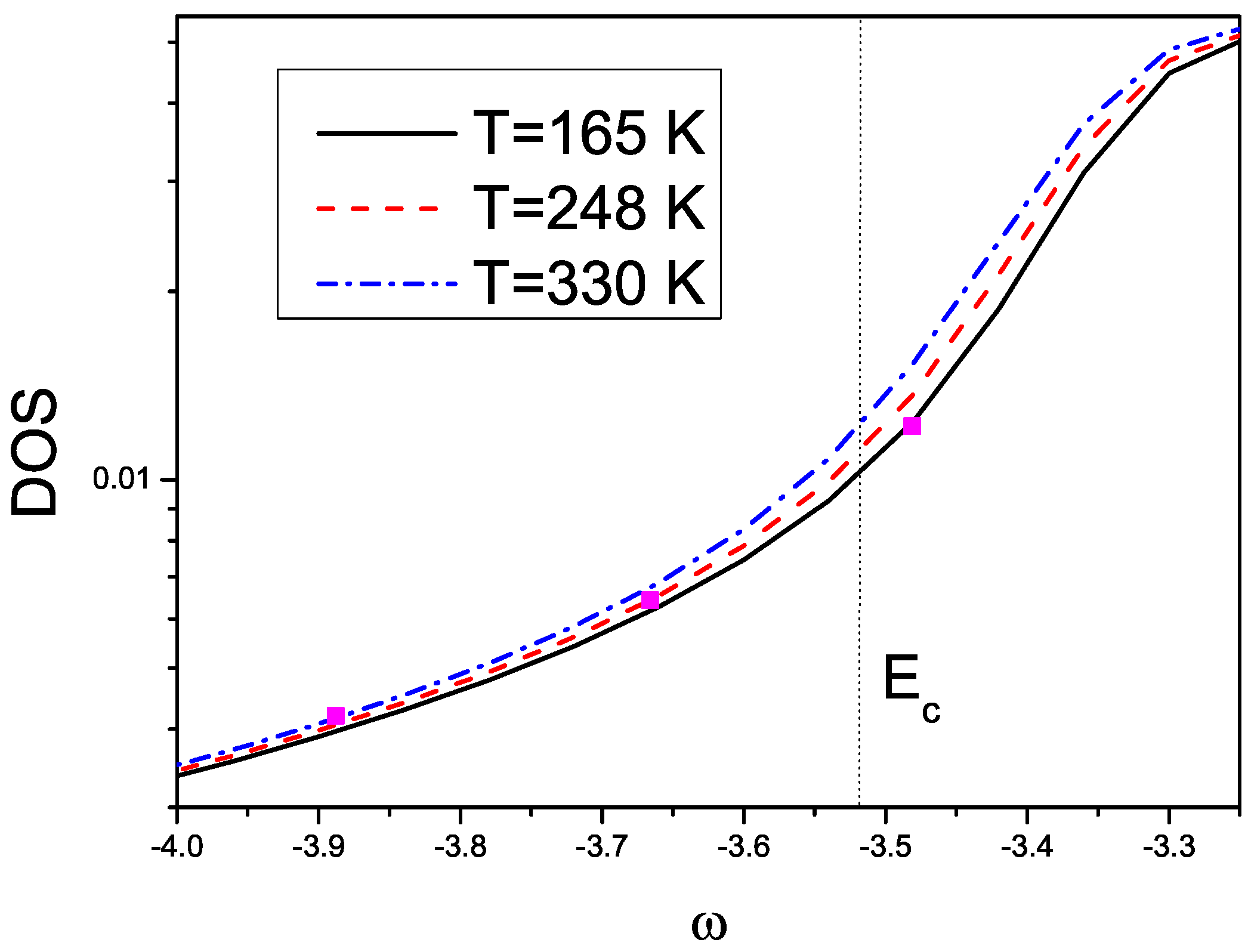
3. Effects of Combined Low Frequency Inter-Molecular and High Frequency Intra-Molecular Vibrational Modes
3.1. Model Hamiltonian
3.2. Calculation Method
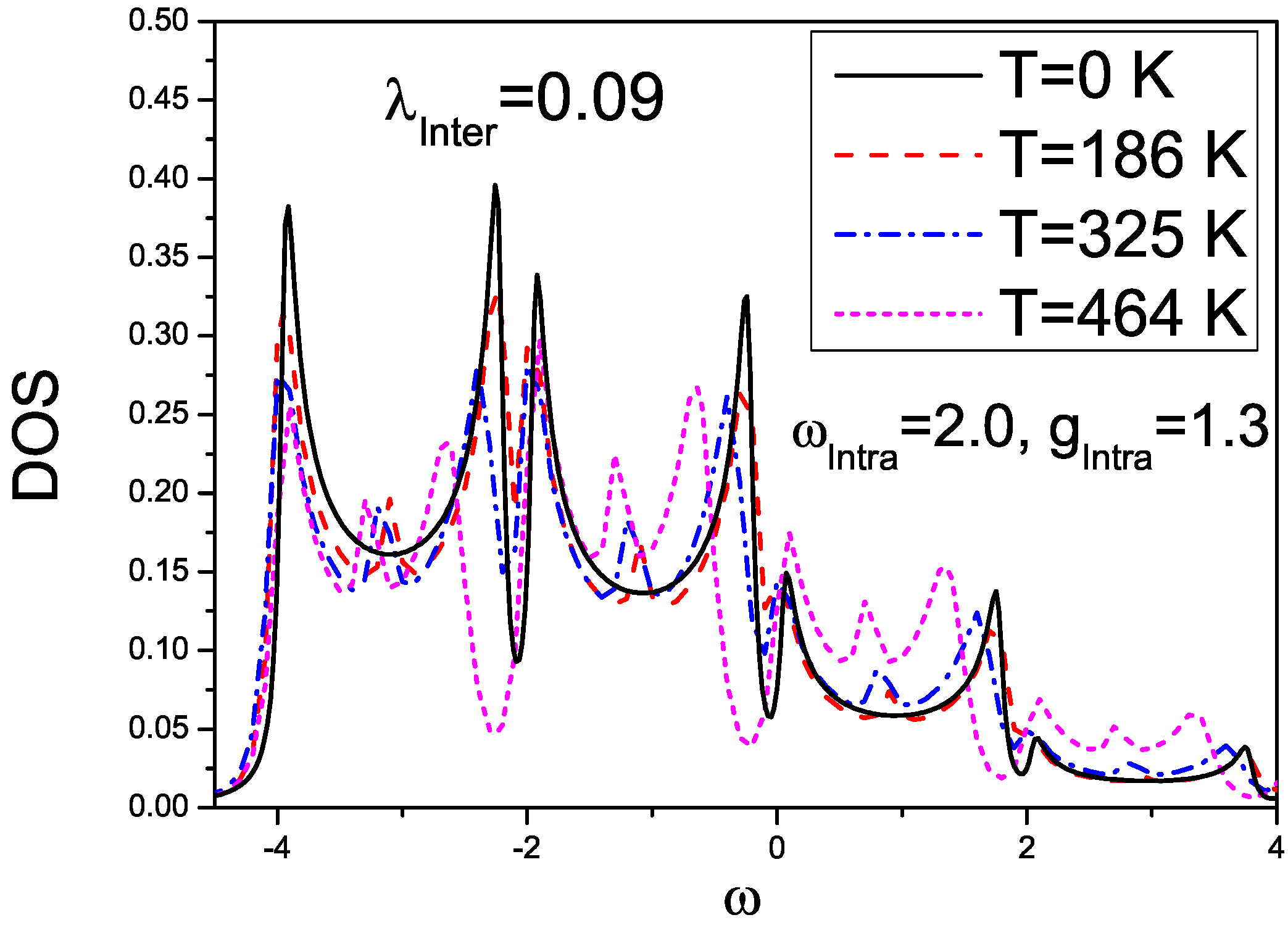
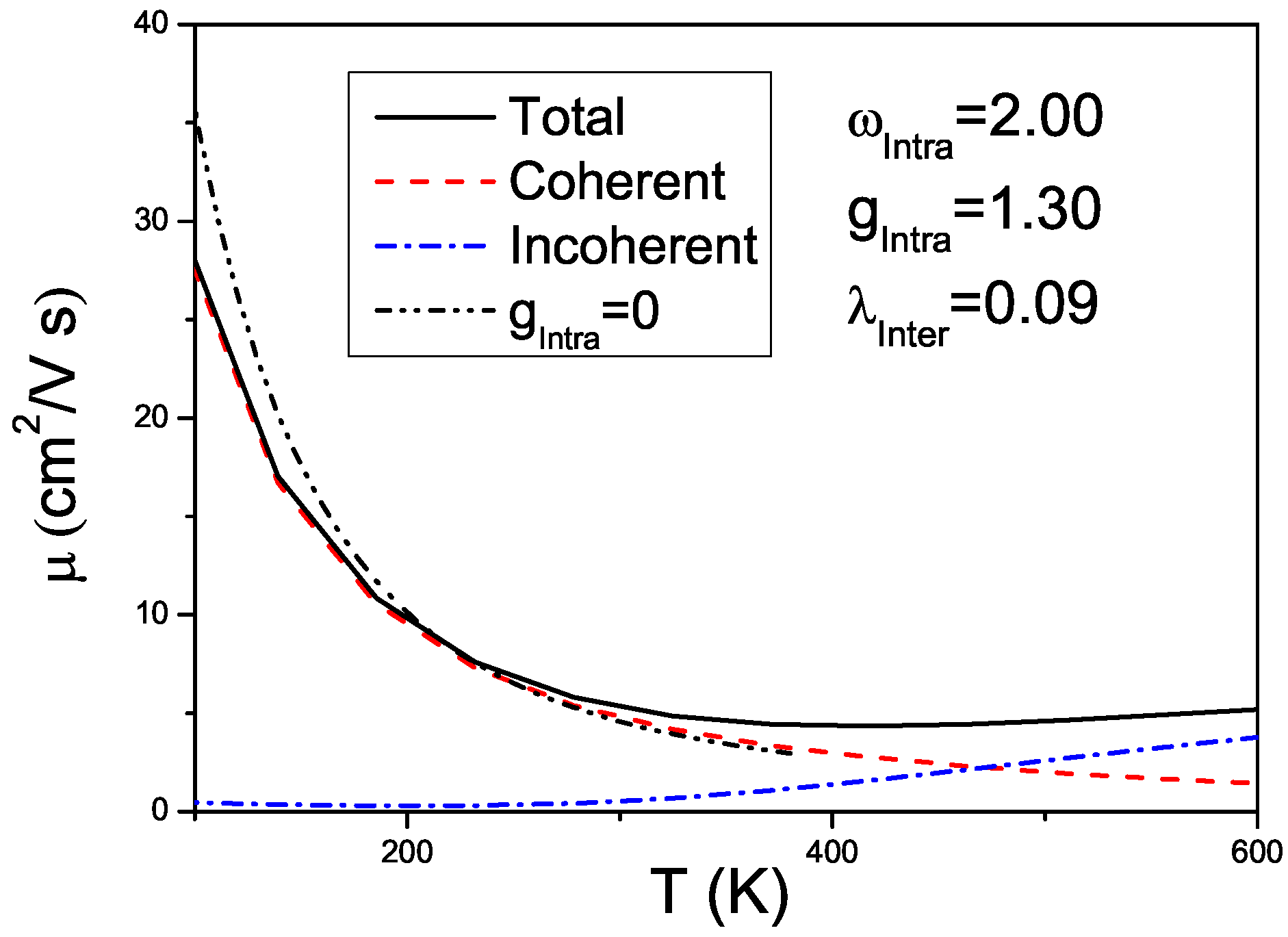
3.3. Results on Spectral and Transport Properties
4. Effects of Gates Made of Polarizable Dielectrics and Disorder
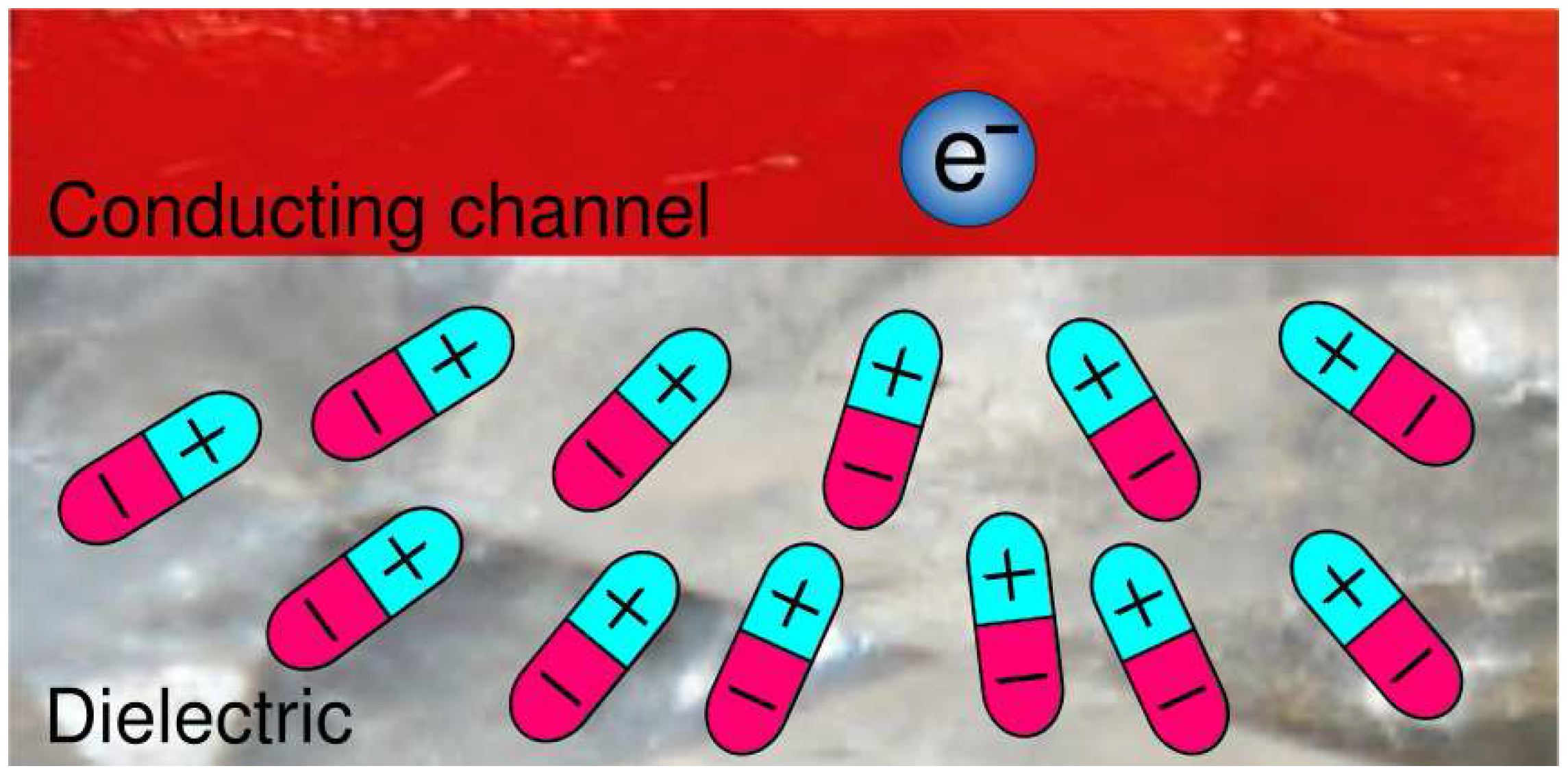
4.1. Model Hamiltonian
4.2. Results about Transport Properties
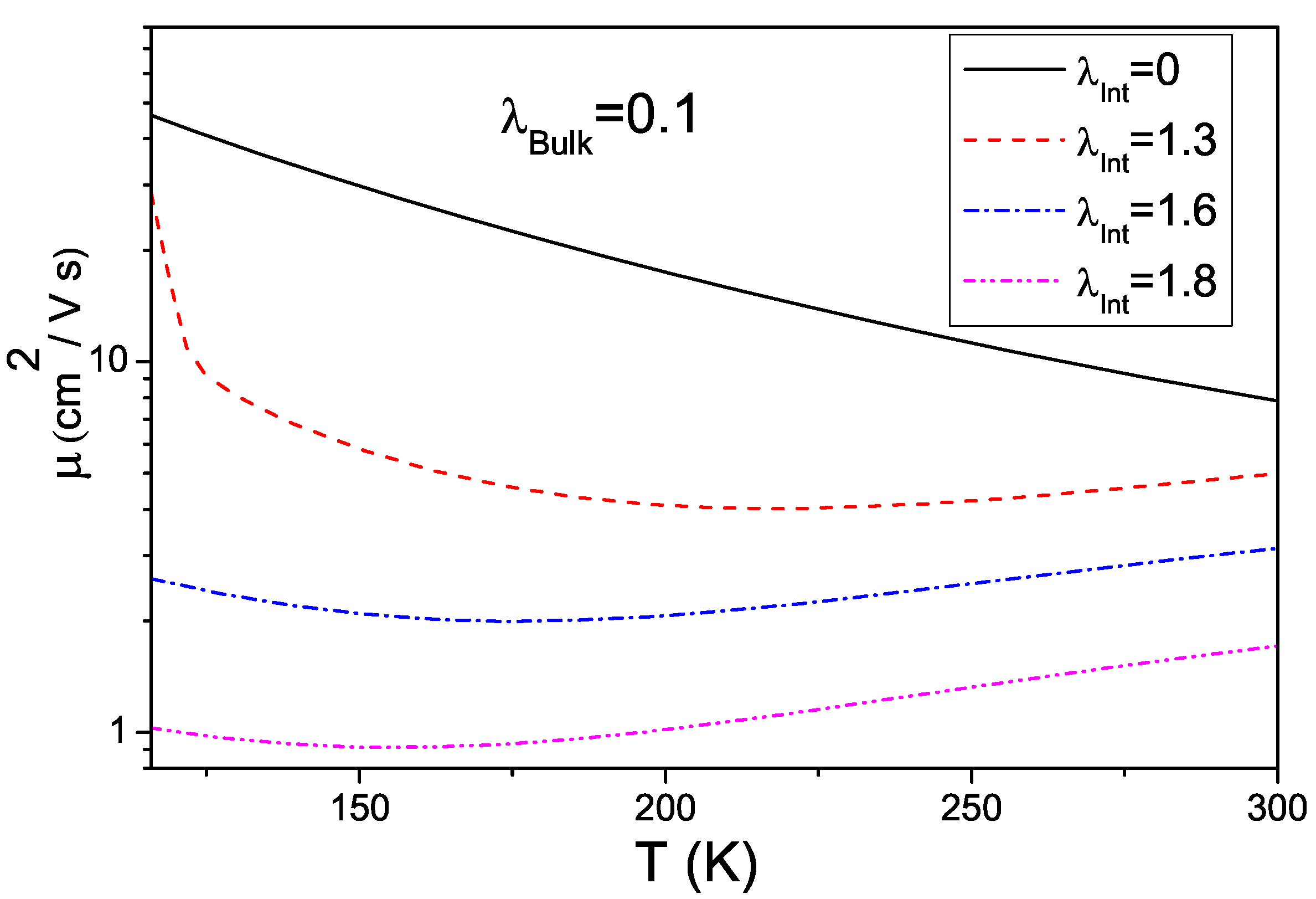
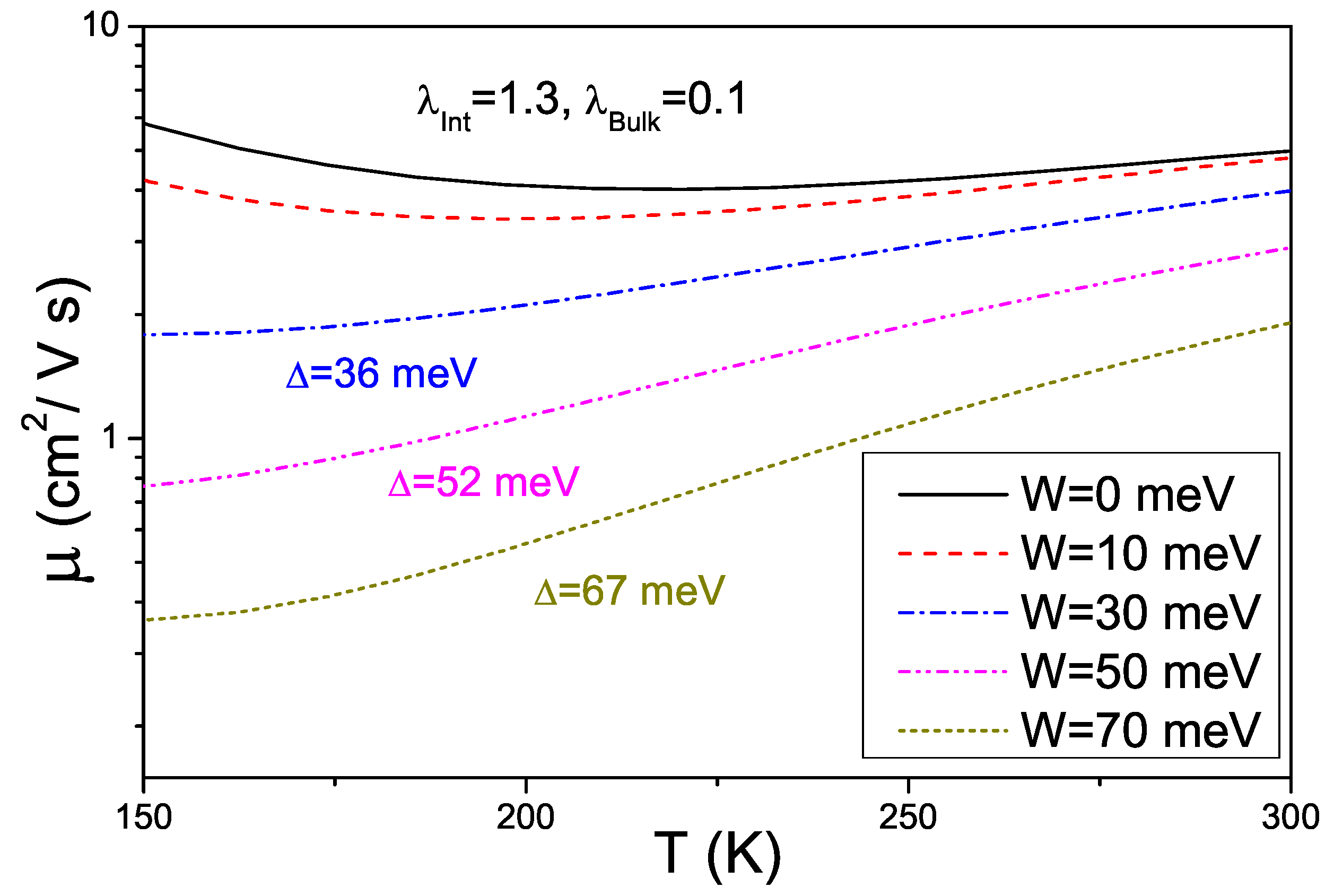
4.3. Interplay between Electron-Phonon Coupling and Disorder Strength
5. Conclusions
Conflicts of Interest
References
- Hasegawa, T.; Takeya, J. Organic field-effect transistors using single crystals. Sci. Technol. Adv. Mater. 2009, 10, 024314–024329. [Google Scholar] [CrossRef]
- Gershenson, M.E.; Podzorov, V.; Morpurgo, A.F. Colloquium: Electronic transport in single-crystal organic transistors. Rev. Mod. Phys. 2006, 78, 973–989. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Silbey, R.J.; Filho, D.A.; Calbert, J.P.; Cornil, J.; Bredas, J.L. Three-dimensional band structure and bandlike mobility in oligoacene single crystals: A theoretical investigation. J. Chem. Phys. 2003, 118, 3764–3774. [Google Scholar] [CrossRef]
- Coropceanu, V.; Cornil, J.; Filho, D.A.d.; Olivier, Y.; Silbey, R.; Bredas, J.-L. Charge Transport in Organic Semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.C.; Silbey, R.J. A unified theory for charge-carrier transport in organic crystals. J. Chem. Phys. 2008, 128, 114713. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Charge transport in organic crystals: interplay of band transport, hopping and electron-phonon scattering. New J. Phys. 2010, 12, 023011. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Devreese, J.T. Advances in Polaron Physics; Springer Verlag: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Warta, W.; Karl, N. Hot holes in naphthalene: High, electric-field-dependent mobilities. Phys. Rev. B 1985, 32, 1172–1182. [Google Scholar] [CrossRef]
- Karl, N. XIth Molecular Crystal Symposium; Lugano, Switzerland, 1985; p. 135. [Google Scholar]
- Karl, N. Charge carrier transport in organic semiconductors. Synth. Met. 2003, 133–134, 649–657. [Google Scholar] [CrossRef]
- Stassen, A.F.; de Boer, R.W.I.; Iosad, N.N.; Morpurgo, A.F. Influence of the gate dielectric on the mobility of rubrene single-crystal field-effect transistors. App. Phys. Lett. 2004, 85, 3899–3901. [Google Scholar] [CrossRef]
- Hulea, I.N.; Fratini, S.; Xie, H.; Mulder, C.L.; Iossad, N.N.; Rastelli, G.; Ciuchi, S.; Morpurgo, A.F. Tunable Frohlich polarons in organic single-crystal transistors. Nat. Mater. 2006, 5, 982–986. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Miwa, K.; Seki, S.; Takeya, J. A comparative study of organic single-crystal transistors gated with various ionic-liquid electrolytes. App. Phys. Lett. 2009, 94, 063301. [Google Scholar] [CrossRef]
- Fratini, S.; Xie, H.; Hulea, I.N.; Ciuchi, S.; Morpurgo, A.F. Current saturation and Coulomb interactions in organic single-crystal transistors. New J. Phys. 2008, 10, 033031. [Google Scholar] [CrossRef]
- Ding, H.; Reese, C.; Makinen, A.J.; Bao, Z.; Gao, Y. Band structure measurement of organic single crystal with angle-resolved photoemission. Appl. Phys. Lett. 2010, 96, 222106. [Google Scholar] [CrossRef]
- Machida, S.I.; Nakayama, Y.; Duhm, S.; Xin, Q.; Funakoshi, A.; Ogawa, N.; Kera, S.; Ueno, N.; Ishii, H. Highest-Occupied-Molecular-Orbital Band Dispersion of Rubrene Single Crystals as Observed by Angle-Resolved Ultraviolet Photoelectron Spectroscopy. Phys. Rev. Lett. 2010, 104, 156401. [Google Scholar] [CrossRef] [PubMed]
- Hatch, R.C.; Huber, D.L.; Höchst, H. Electron-Phonon Coupling in Crystalline Pentacene Films. Phys. Rev. Lett. 2010, 104, 047601. [Google Scholar] [CrossRef] [PubMed]
- Marumoto, K.; Kuroda, S.; Takenobu, T.; Iwasa, Y. Spatial Extent of Wave Functions of Gate-Induced Hole Carriers in Pentacene Field-Effect Devices as Investigated by Electron Spin Resonance. Phys. Rev. Lett. 2006, 97, 256603. [Google Scholar] [CrossRef] [PubMed]
- Marumoto, K.; Arai, N.; Goto, H.; Kijima, M.; Murakami, K.; Tominari, Y.; Takeya, J.; Shimoi, Y.; Tanaka, H.; Kuroda, S.; et al. Microscopic mechanisms behind the high mobility in rubrene single-crystal transistors as revealed by field-induced electron spin resonance. Phys. Rev. B 2011, 83, 075302. [Google Scholar] [CrossRef]
- Laarhoven, H.A.V.; Flipse, C.F.J.; Koeberg, M.; Bonn, M.; Hendry, E.; Orlandi, G.; Jurchescu, O.D.; Palstra, T.T.M.; Troisi, A. On the mechanism of charge transport in pentacene. J. Chem. Phys. 2008, 129, 044704. [Google Scholar] [CrossRef] [PubMed]
- Sakanoue, T.; Sirringhaus, H. Band-like temperature dependence of mobility in a solution-processed organic semiconductor. Nat. Mater. 2010, 9, 736–740. [Google Scholar] [CrossRef] [PubMed]
- Troisi, A.; Orlandi, G. Charge-Transport Regime of Crystalline Organic Semiconductors: Diffusion Limited by Thermal Off-Diagonal Electronic Disorder. Phys. Rev. Lett. 2006, 96, 086601. [Google Scholar] [CrossRef] [PubMed]
- Sanchez Carrera, R.S.; Paramonov, P.; Day, G.M.; Coropceanu, V.; Bredas, J.-L. Interaction of Charge Carriers with Lattice Vibrations in Oligoacene Crystals from Naphthalene to Pentacene. J. Am. Chem. Soc. 2010, 132, 14437–14446. [Google Scholar] [CrossRef] [PubMed]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. [Google Scholar] [CrossRef]
- Troisi, A. Prediction of the Absolute Charge Mobility of Molecular Semiconductors: The Case of Rubrene. Adv. Mat. 2007, 19, 2000–2004. [Google Scholar] [CrossRef]
- Troisi, A. Dynamic disorder in molecular semiconductors: Charge transport in two dimensions. J. Chem. Phys. 2011, 134, 034702. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Coropceanu, V.; Bredas, J.-L. Nonlocal electron-phonon coupling in organic semiconductor crystals: The role of acoustic lattice vibrations. J. Chem. Phys. 2013, 138, 204713. [Google Scholar] [CrossRef] [PubMed]
- Fratini, S.; Ciuchi, S. Bandlike Motion and Mobility Saturation in Organic Molecular Semiconductors. Phys. Rev. Lett. 2009, 103, 266601. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Cataudella, V.; de Filippis, G.; Perroni, C.A. Transport properties and optical conductivity of the adiabatic Su-Schrieffer-Heeger model: A showcase study for rubrene-based field effect transistors. Phys. Rev. B 2011, 83, 165203. [Google Scholar] [CrossRef]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Theory of charge transport in organic crystals: Beyond Holstein’s small-polaron model. Phys. Rev. B 2009, 79, 235206. [Google Scholar] [CrossRef]
- Perroni, C.A.; Nocera, A.; Ramaglia, V.M.; Cataudella, V. Spectral, optical, and transport properties of the adiabatic anisotropic Holstein model: Application to slightly doped organic semiconductors. Phys. Rev. B 2011, 83, 245107. [Google Scholar] [CrossRef]
- Gargiulo, F.; Perroni, C.A.; Ramaglia, V.M.; Cataudella, V. Electronic transport within a quasi-two-dimensional model for rubrene single-crystal field effect transistors. Phys. Rev. B 2011, 84, 245204. [Google Scholar] [CrossRef]
- Hannewald, K.; Bobbert, P.A. Ab initio theory of charge-carrier conduction in ultrapure organic crystals. Appl. Phys. Lett. 2004, 85, 1535–1537. [Google Scholar] [CrossRef]
- Hannewald, K.; Stojanović, V.M.; Schellekens, J.M.T.; Bobbert, P.A. Theory of polaron bandwidth narrowing in organic molecular crystals. Phys. Rev. B 2004, 69, 075211. [Google Scholar] [CrossRef]
- Perroni, C.A.; Ramaglia, V.M.; Cataudella, V. Effects of electron coupling to intramolecular and intermolecular vibrational modes on the transport properties of single-crystal organic semiconductors. Phys. Rev. B 2011, 84, 014303. [Google Scholar] [CrossRef]
- Perroni, C.A.; Cataudella, V. Interplay between electron-phonon coupling and disorder strength on the transport properties of organic semiconductors. Phys. Rev. B 2012, 85, 155205. [Google Scholar] [CrossRef]
- Perroni, C.A.; Cataudella, V. Bipolaron formation in organic semiconductors at the interface with dielectric gates. Europhys. Lett. 2012, 98, 47004. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part I. The molecular-crystal model. Ann. Phys. 1959, 8, 325–342. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part II. The small polaron. Ann. Phys. 1959, 8, 343–389. [Google Scholar] [CrossRef]
- Shehu, A.; Quiroga, S.D.; D’Angelo, P.; Albonetti, C.; Borgatti, F.; Murgia, M.; Scorzoni, A.; Stoliar, P.; Biscarini, F. Layered Distribution of Charge Carriers in Organic Thin Film Transistors. Phys. Rev. Lett. 2010, 104, 246602. [Google Scholar] [CrossRef] [PubMed]
- Girlando, A.; Grisanti, L.; Masino, M. Peierls and Holstein carrier-phonon coupling in crystalline rubrene. Phys. Rev. B 2010, 82, 035208. [Google Scholar] [CrossRef]
- Venuti, E.; Billotti, I.; della Valle, R.G.; Brillante, A.; Ranzieri, P.; Masino, M.; Girlando, A. Polarized Raman Spectra of a Rubrene Single Crystal. J. Phys. Chem. C 2008, 112, 17416–17422. [Google Scholar] [CrossRef]
- Nocera, A.; Perroni, C.A.; Ramaglia, V.M.; Cataudella, V. Stochastic dynamics for a single vibrational mode in molecular junctions. Phys. Rev. B 2011, 83, 115420. [Google Scholar] [CrossRef]
- Nocera, A.; Perroni, C.A.; Ramaglia, V.M.; Cataudella, V. Probing nonlinear mechanical effects through electronic currents: The case of a nanomechanical resonator acting as an electronic transistor. Phys. Rev. B 2012, 86, 035420. [Google Scholar] [CrossRef]
- Nocera, A.; Perroni, C.A.; Ramaglia, V.M.; Cantele, G.; Cataudella, V. Magnetic effects on nonlinear mechanical properties of a suspended carbon nanotube. Phys. Rev. B 2013, 87, 155435. [Google Scholar] [CrossRef]
- Perroni, C.A.; Nocera, A.; Cataudella, V. Single-parameter charge pumping in carbon nanotube resonators at low frequency. Europhys. Lett. 2013, 103, 58001. [Google Scholar] [CrossRef]
- Perroni, C.A.; Romeo, F.; Nocera, A.; Ramaglia, V.M.; Citro, R.; Cataudella, V. Noise-assisted Thouless pump in elastically deformable molecular junctions. arXiv:1307.6834v1 [cond-mat.mes-hall]. 2013. [Google Scholar]
- Mahan, G.D. Many-Particle Physics, 2nd ed.; Plenum Press: New York, NY, USA, 1990. [Google Scholar]
- Economou, E.N. Green’s Functions in Quantum Physics; Springer Verlag: Berlin, Germany, 1983. [Google Scholar]
- Perroni, C.A.; Piegari, E.; Capone, M.; Cataudella, V. Polaron formation for nonlocal electron-phonon coupling: A variational wave-function study. Phys. Rev. B 2004, 69, 174301. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Calandra, M.; Han, J.E. Colloquium: Saturation of electrical resistivity. Rev. Mod. Phys. 2003, 75, 1085–1099. [Google Scholar] [CrossRef]
- Hannewald, K.; Bobbert, P.A. Anisotropy effects in phonon-assisted charge-carrier transport in organic molecular crystals. Phys. Rev. B 2004, 69, 075212. [Google Scholar] [CrossRef]
- Ishii, H.; Kobayashi, N.; Hirose, K. Strong anisotropy of momentum-relaxation time induced by intermolecular vibrations of single-crystal organic semiconductors. Phys. Rev. B 2013, 88, 205208. [Google Scholar] [CrossRef]
- Piegari, E.; Perroni, C.A.; Cataudella, V. Signatures of polaron formation in systems with local and non-local electron-phonon couplings. Eur. Phys. J. B 2005, 44, 415–421. [Google Scholar] [CrossRef]
- Ciuchi, S.; Fratini, S. Band Dispersion and Electronic Lifetimes in Crystalline Organic Semiconductors. Phys. Rev. Lett. 2011, 106, 166403. [Google Scholar] [CrossRef] [PubMed]
- Lang, I.J.; Firsov, Y.A. Kinetic Theory of Semiconductors with Low Mobility. Sov. Phys. JETP 1963, 16, 1301. [Google Scholar]
- Iorio, A.; Perroni, C.A.; Ramaglia, V.M.; Cataudella, V. Electron-lattice and strain effects in manganite heterostructures: The case of a single interface. Phys. Rev. B 2011, 83, 085107. [Google Scholar] [CrossRef]
- Vukmirovic, N.; Bruder, C.; Stojanović, V.M. Electron-Phonon Coupling in Crystalline Organic Semiconductors: Microscopic Evidence for Nonpolaronic Charge Carriers. Phys. Rev. Lett. 2012, 109, 126407. [Google Scholar] [CrossRef] [PubMed]
- Kirova, N.; Bussac, M.-N. Self-trapping of electrons at the field-effect junction of a molecular crystal. Phys. Rev. B 2003, 68, 235312. [Google Scholar] [CrossRef]
- Li, Y.; Coropceanu, V.; Bredas, J.-L. Thermal Narrowing of the Electronic Bandwidths in Organic Molecular Semiconductors: Impact of the Crystal Thermal Expansion. J. Phys. Chem. Lett. 2012, 3, 3325–3329. [Google Scholar] [CrossRef]
- Ortmann, F.; Hannewald, K.; Bechstedt, F. Ab initio description and visualization of charge transport in durene crystals. App. Phys. Lett. 2008, 93, 222105. [Google Scholar] [CrossRef]
- Ortmann, F.; Hannewald, K.; Bechstedt, F. Charge Transport in Guanine-Based Materials. J. Phys. Chem. B 2009, 113, 7367–7371. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Perroni, C.A.; Gargiulo, F.; Nocera, A.; Ramaglia, V.M.; Cataudella, V. The Effects of Different Electron-Phonon Couplings on the Spectral and Transport Properties of Small Molecule Single-Crystal Organic Semiconductors. Electronics 2014, 3, 165-189. https://doi.org/10.3390/electronics3010165
Perroni CA, Gargiulo F, Nocera A, Ramaglia VM, Cataudella V. The Effects of Different Electron-Phonon Couplings on the Spectral and Transport Properties of Small Molecule Single-Crystal Organic Semiconductors. Electronics. 2014; 3(1):165-189. https://doi.org/10.3390/electronics3010165
Chicago/Turabian StylePerroni, Carmine Antonio, Fernando Gargiulo, Alberto Nocera, Vincenzo Marigliano Ramaglia, and Vittorio Cataudella. 2014. "The Effects of Different Electron-Phonon Couplings on the Spectral and Transport Properties of Small Molecule Single-Crystal Organic Semiconductors" Electronics 3, no. 1: 165-189. https://doi.org/10.3390/electronics3010165



