A Markov-Switching Vector Autoregressive Stochastic Wind Generator for Multiple Spatial and Temporal Scales

Abstract

Despite recent efforts to record wind at finer spatial and temporal scales, stochastic realizations of wind are still important for many purposes and particularly for wind energy grid integration and reliability studies. Most instances of wind generation in the literature focus on simulating only wind speed, or power, or only the wind vector at a particular location and sampling frequency. In this work, we introduce a Markov-switching vector autoregressive (MSVAR) model, and we demonstrate its flexibility in simulating wind vectors for 10-min, hourly and daily time series and for individual, locally-averaged and regionally-averaged time series. In addition, we demonstrate how the model can be used to simulate wind vectors at multiple locations simultaneously for an hourly time step. The parameter estimation and simulation algorithm are presented along with a validation of the important statistical properties of each simulation scenario. We find the MSVAR to be very flexible in characterizing a wide range of properties in the wind vector, and we conclude with a discussion of extensions of this model and modeling choices that may be investigated for further improvements.

1. Introduction

Long, realistic simulated time series of wind have many potential uses. They are a crucial component in erosion modeling [1], hurricane modeling [2], ocean surface wind modeling for climate research [3], climate impact studies [4], ocean transport and sea state modeling [5], wind insurance risk [6], power production and wind turbine performance [7] and building energy simulations [8]. However, a very important application is for wind energy integration studies in which utilities must balance uncertain loads and supplies and must plan for the dispatch and transmission of electricity [9,10]. Balancing authorities must test how increasing the amount of wind in their portfolio will impact their system, how to best allocate spinning reserves and how extreme events may be handled [11,12,13].

Historically, very long series of wind measured at short temporal frequencies of an hour or less have not been readily available, so models for generating such series have been developed specifically for this purpose. As the spatial and temporal distribution of measurement stations for winds increase, these real data can feed into synthetic system experiments, but synthetic data are still needed for constructing experiments based on hypotheses related to changing features of the data generation process. In this paper, we introduce a model for synthetic generation of both wind speed and direction (via the horizontal and vertical components of wind, u and v) and assess how well its generated wind captures the statistical properties of observed wind at various spatial and temporal scales both at individual locations and across multiple locations. However, first, we note differences between wind forecasting models and wind generators, put wind generators in the broader context of stochastic weather generators and, finally, review Markov-chain models as they have been applied for generating wind.

Many forecasting models have been developed to forecast wind for system integration (see [14] and [15] for overviews). In some instances, forecasting models and synthetic weather generator models for wind are interchangeable. For example, a time series model that can be used for either forecasting or wind speed generation is built in [16]. However, most forecasting models for wind tend to focus on only either wind speed or wind power (e.g., [17,18,19,20]), and some very good advanced forecasting models (e.g., [17,18]) would not translate into stochastic weather generators due to their conditioning on the wind at off-site locations.

It is perhaps most appropriate to view wind simulation in the context of stochastic weather generators. Stochastic weather generators are statistical models whose realizations statistically match observed weather patterns. Most focus in the weather generation literature is on precipitation and minimum and maximum temperature [21]. Within the stochastic weather generation literature, wind is playing an increasingly important role. The classic model in [22] was extended to include daily mean wind speed using a square root transformation to normality in [23]. A model that approximates a gamma distribution for the skewness of wind while simultaneously simulating many other weather quantities is used in [24]. Hourly mean wind speeds with sea level pressure are simulated in a resampling framework in [25]. A multivariate closed-skew normal to capture the skewness of wind within a full weather generator is proposed in [26]. All of these approaches focus on modeling the asymmetry and kurtosis in wind, which are crucial features, along with other weather variables. Wind direction is rarely simulated, even though it is known to have an impact on wind power production [19].

In models wherein wind is the primary focus, Markov chain models have a long history. First- and second-order Markov chains have been used to model wind speed or the wind vector [27,28,29]. Birth and death Markov chain models have been tested [30]. The effect of the number of wind speed categories on the resulting generated series has been investigated [31]. A cyclic time-variant Markov model has been introduced to capture diurnal variability [32]. Finally, some argue that Markov chain models to generate synthetic wind speed series should not be used for time steps under one hour [33].

In most instances, the model fitting is relatively basic, with wind speed categorized into ranges before fitting Markov models, even in more recent work, such as [34]. Most models focus primarily on simulating wind speed or wind power for one temporal sampling frequency, with a few exceptions that model the wind vector [29,32,35]. Some more advanced approaches that use Markov-switching autoregressive [36] or vector autoregressive models have been proposed [20] with the underlying assumption that many locations tend to observe one of a few prevailing wind regimes, and characteristics within these regimes may differ dramatically [37,38].

Recently, more research has begun to focus on capturing the spatial dependence of wind. In a classic paper, the long-range dependence of the space-time structure of wind over Ireland was examined [39]. A second-order Markov chain model to simulate wind power at two sites simultaneously was developed [40]. An autoregressive framework with temporally varying coefficients for wind vector fields to capture temporal nonstationarity was used [41]. Continuing the modeling of wind vector fields, a Gaussian linear state-space model, capturing the intricate non-separable behavior of the process, was implemented by [42].

In this work, we simulate both speed and direction with a Markov-switching vector autoregressive (MSVAR) model fit to the corresponding u and v components. This model was first introduced with respect to wind generation in [38], and here, the simulation algorithm is generalized to capture seasonality in addition to diurnal cycles, and a nonparametric transformation of the components to normality captures the skewness and kurtosis. Since end user applications require variable temporal and spatial resolutions of simulations, we evaluate the MSVAR model’s flexibility in reproducing wind statistics at various spatial and temporal scales and at multiple locations simultaneously. Developing stochastic models that can replicate multiple scale statistics can be quite difficult, but the MSVAR model does well in replicating the variability observed at these scales when fit separately to each scale.

The remainder of this paper is organized as follows: in Section 2, we describe our wind generation model, parameter estimation and simulation algorithm. Then, we describe the data that we base our simulation scenarios on, along with the scenarios themselves. We evaluate the performance of the MSVAR model simulations in Section 4, focusing on their ability to capture the temporal and spatial autocorrelations, non-Gaussian distributions and the correlation between the u and v components. Finally, we conclude with a discussion of future work in Section 5.

2. Stochastic Wind Generator Model

In this section, we introduce the stochastic model to generate a synthetic wind vector. We match moments within subsets of the data to identify reasonable parameter estimates for the model and explain our detrending, transformation and clustering approaches.

2.1. Markov-Switching Vector Autoregressive Model

In [38], a model for generating the wind vector at a single location is introduced, but they only simulate hourly wind vectors averaged across a large region for a given month. Here, we extend that model to simulate wind vectors across an entire year for either 10-min, hourly or daily time steps and also at multiple locations. We let ${\mathbf{y}}_t$ be the $(2·p)\times 1$ vector of the wind u and v components of p locations at time $t=1,2,\dots ,n$, so ${\mathbf{y}}_t={(u_{t,1},v_{t,1},u_{t,2},v_{t,2},\dots ,u_{t,p},v_{t,p})}^T$. The steps we take are:

• The original $u_{t,j}$ and $v_{t,j}$ components for $t=1,\dots ,n$ and $j=1,\dots ,p$ do not follow a Gaussian distribution, so they are first each transformed to normality with a Gaussian copula as follows:

  (a)

  The empirical cumulative distribution function (ecdf) of each component of ${\mathbf{y}}_t$ is obtained with:

  $${\widehat{F}}_{u_j}\left(a\right)=\frac{1}{n}\sum _{t=1}^n{\mathrm{𝟙}}_{[u_{t,j}<a]}$$

  (1)

  and similarly for $v_{t,j}$, where $\mathrm{𝟙}$ is the indicator function that is unity, if the set condition holds, and is zero otherwise.

  (b)

  The transformed values of $u_{t,j}$, denoted $u_{t,j}^{\prime }$, are $u_{t,j}^{\prime }={\Phi }^{-1}({\widehat{F}}_{u_j}(u_{t,j}))$, and similarly for $v_{t,j}$, where ${\Phi }^{-1}(·)$ is the inverse of the standard normal cumulative distribution function.

• Then, we remove the seasonality and diurnal variability from the transformed $u_{t,j}$ and $v_{t,j}$ components of ${\mathbf{y}}_t$ individually using a generalized additive model (GAM) [43] with:

  $$u_{t,j}^{\prime }={\beta }_0+s\left(m_t\right)+s\left(d_t\right)+s\left(h_t\right)+{ϵ}_{t,j}$$

  (2)

  where $m_t$ is the month of the year, $d_t$ is the day of the year and $h_t$ is the hour of the day for observation t, and similarly for $v_{t,j}^{\prime }$. The function $s(·)$ is a penalized regression spline, which is the default in the R mgcv package [44]. Define detrended residuals as $u_{t,j}^r=u_{t,j}^{\prime }-{\widehat{u}}_{t,j}^{\prime }$ and $v_{t,j}^r=v_{t,j}^{\prime }-{\widehat{v}}_{t,j}^{\prime }$, and the corresponding detrended vector is ${\mathbf{y}}_t^r={(u_{t,1}^r,v_{t,1}^r,u_{t,2}^r,v_{t,2}^r,\dots ,u_{t,p}^r,v_{t,p}^r)}^T$. The diurnal wind cycle can have a substantial impact on sizing and modeling integrated renewable systems, so it is important to model it properly [32,45,46], but note that the term $s\left(h_t\right)$ is removed from Equation (2) when fitting a trend for the daily averages.
• Depending on the number of locations wherein it is desired to simulate the wind vector, we take one of two approaches to choosing the number of “regimes” in the Markov-switching model.

  $p=1$

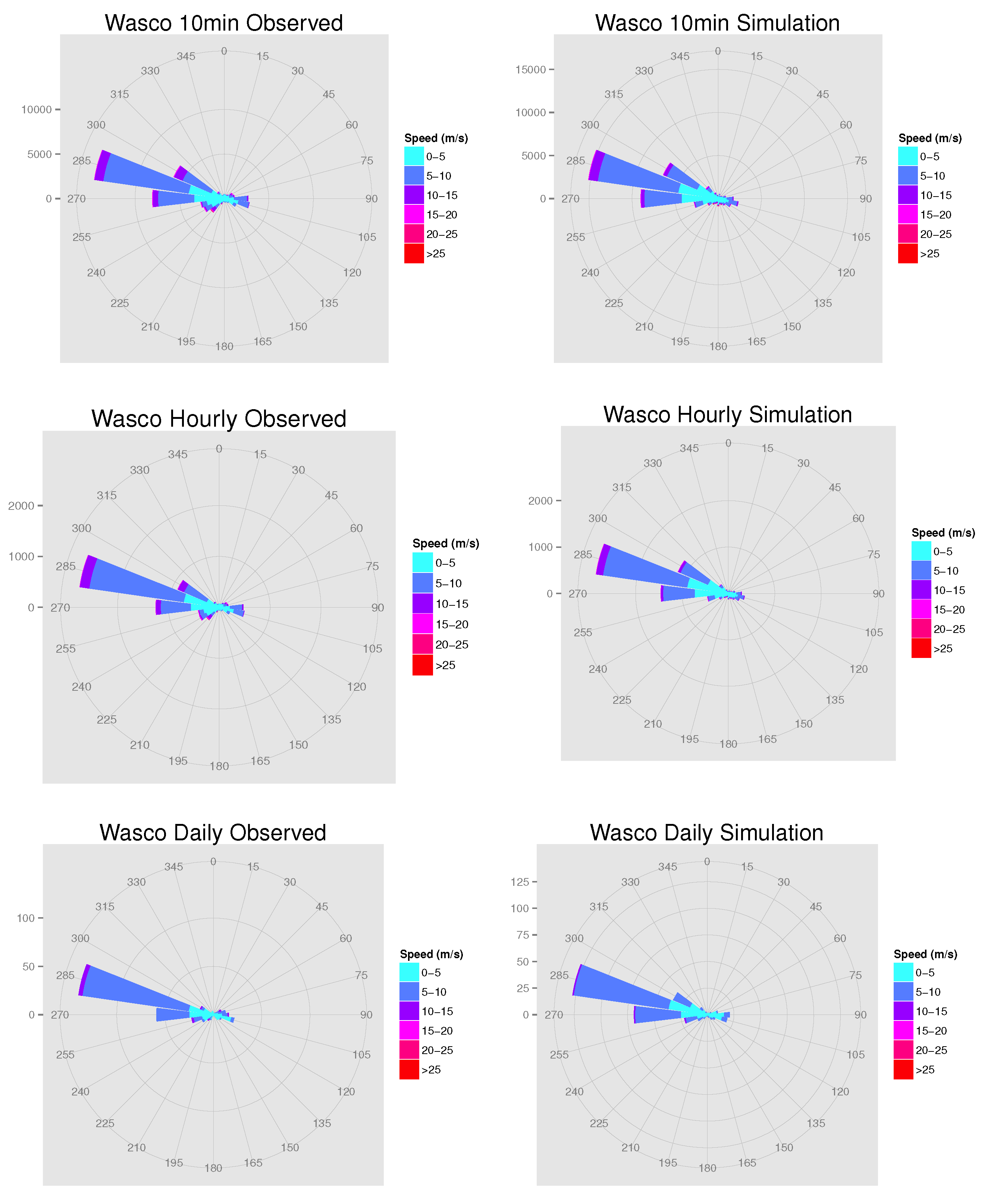
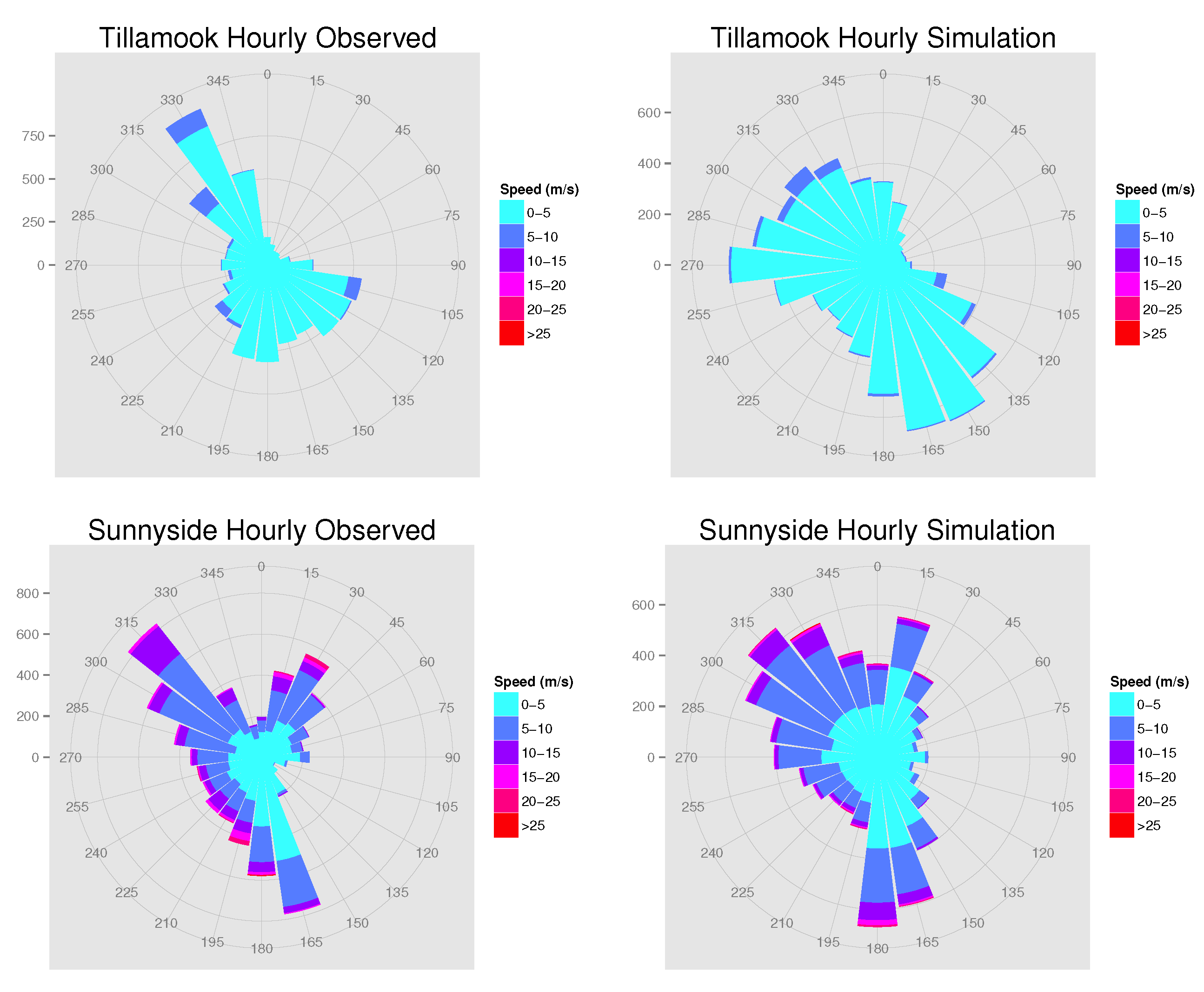
  : Plot the wind rose of the observed wind speed and direction. Let the number of modes in the joint distribution of speed and direction be the number of regimes.

  $p>1$

  : Average the observed wind speed and wind directions across all p sites at each time t. Plot the wind rose of the averaged speed and directions, and let the number of regimes equal the number of modes in the joint distribution. Note that the circular mean of directions is taken whenever an average of directions is required [47].

• Given the number of regimes, K, we must classify the observations belonging to each one. We do this with an unconstrained Gaussian mixture model (GMM) clustering approach [48] applied to the observed transformed u and v components, $u_{t,j}^{\prime }$ and $v_{t,j}^{\prime }$. Here, the components of the mixture model are assumed to be multivariate normal distributions with means ${\mu }_k$, covariance matrices ${\Sigma }_k$ and mixing proportions ${\tau }_k$ for $k=1,\dots ,K$. The GMM is able to model ellipsoidal clusters of any size and orientation. We use the mclust package in R to perform the clustering [49], but we note here that clustering the 10-min data, which has 52,560 observations, fails, due to the size of the dataset. Thus, we cluster the hourly data and apply each hour’s cluster assignment to all 10-min observations within the corresponding hour. Secondly, when $p>1$, we construct two sets of regimes based on the following sets of values:

  (a)

  the mean of the transformed u and v components across all p locations, defined as ${\overline{u}}_t^{\prime }=\frac{1}{p}{\sum }_{j=1}^p{u}_{t,j}^{\prime }$ and ${\overline{v}}_t^{\prime }=\frac{1}{p}{\sum }_{j=1}^p{v}_{t,j}^{\prime }$ for $t=1,\dots ,n$; and

  (b)

  the transformed u and v components of all p locations, ${\mathbf{y}}_t^{\prime }={(u_{t,1}^{\prime },v_{t,1}^{\prime },u_{t,2}^{\prime },v_{t,2}^{\prime },\dots ,u_{t,p}^{\prime },v_{t,p}^{\prime })}^T.$

• Use the subsets of observations identified in Step 4 to obtain least-squares estimates of the parameters in Equation (3), the Markov-switching autoregressive model (MSVAR) of order one:

  $${\mathbf{y}}_t^r={\mathbf{A}}_{r_t}{\mathbf{y}}_{t-1}^r+ϵ\left(r_t\right);ϵ\left(r_t\right)\sim N(0,{\Sigma }_{r_t})$$

  (3)

  where the lag-one autoregressive matrix ${\mathbf{A}}_{r_t}$ and innovation covariance matrix ${\Sigma }_{r_t}$ depend on the regime, $r_t\in \{1,2,\dots ,K\}$. We let $\left\{r_t\right\}$ be a Markov chain on finite space, $\{1,2,\dots ,K\}$, that indicates the regime at time t. The regime-switching process is defined by a transition probability matrix $\mathbf{P}=\left\{p_{jk}\right\}$, $j,k=1,2,\dots ,K$, where $p_{jk}=P(r_{t+1}=k|r_t=j)$, and ${\sum }_k{p}_{jk}=1$ for all j.
• The transition probability matrix, $\mathbf{P}$, is estimated using the identified clusters and the observed proportion of instances in which the cluster assignments switch,

  $${\widehat{p}}_{jk}=\frac{{\sum }_{t=1}^n{\mathrm{𝟙}}_{[r_{t+1}=k|r_t=j]}}{{\sum }_{t=1}^n{\mathrm{𝟙}}_{[r_t=j]}}.$$

  (4)

  The coefficient matrices, ${\mathbf{A}}_{r_t}$, are estimated using least-squares with the lm command in R based on the observations with regime $r_t$. We note that the eigenvalues of ${\mathbf{A}}_{r_t}$ must be positive in order for the VAR model to be stable; we did not encounter any difficulties in estimating these coefficients with the lm command, but any issues in estimation can be dealt with by using a constrained least squares estimation of ${\mathbf{A}}_{r_t}$. The variability matrix, ${\Sigma }_{r_t}$, is estimated with the standard covariance estimator of the residuals of the model within each regime.
• Given the parameter estimates of ${\mathbf{A}}_{r_t}$, ${\Sigma }_{r_t}$ and $\mathbf{P}$ from Step 6, simulate a new set of values, denoted ${\tilde{\mathbf{y}}}_t^r$, from Equation (3).
• Add back the estimated trend from Equation (2) to obtain:

  $${\tilde{\mathbf{y}}}_t^{\prime }={\tilde{\mathbf{y}}}_t^r+{({\widehat{u}}_{t,1}^{\prime },{\widehat{v}}_{t,1}^{\prime },{\widehat{u}}_{t,2}^{\prime },{\widehat{v}}_{t,2}^{\prime },\dots ,{\widehat{u}}_{t,p}^{\prime },{\widehat{v}}_{t,p}^{\prime })}^T.$$

  (5)
• Transform the ${\tilde{\mathbf{y}}}_t^{\prime }$ back into the original units by:

  $${\tilde{u}}_{t,j}={\widehat{F}}_{u_j}^{-1}(\Phi \left({\tilde{u}}_{t,j}^{\prime }\right))$$

  (6)

  and similarly for ${\tilde{v}}_{t,j}$ to obtain ${\tilde{\mathbf{y}}}_t$. Now, we have a simulated set of u and v components at p locations.
• As a final step, we convert the u and v components of ${\tilde{\mathbf{y}}}_t$ into speed and direction, as these are usually more interpretable quantities upon which to perform validation.

3. Simulation Scenarios

In this section, we describe the data that the wind generation is based on and then outline the scenarios for which we will generate wind.

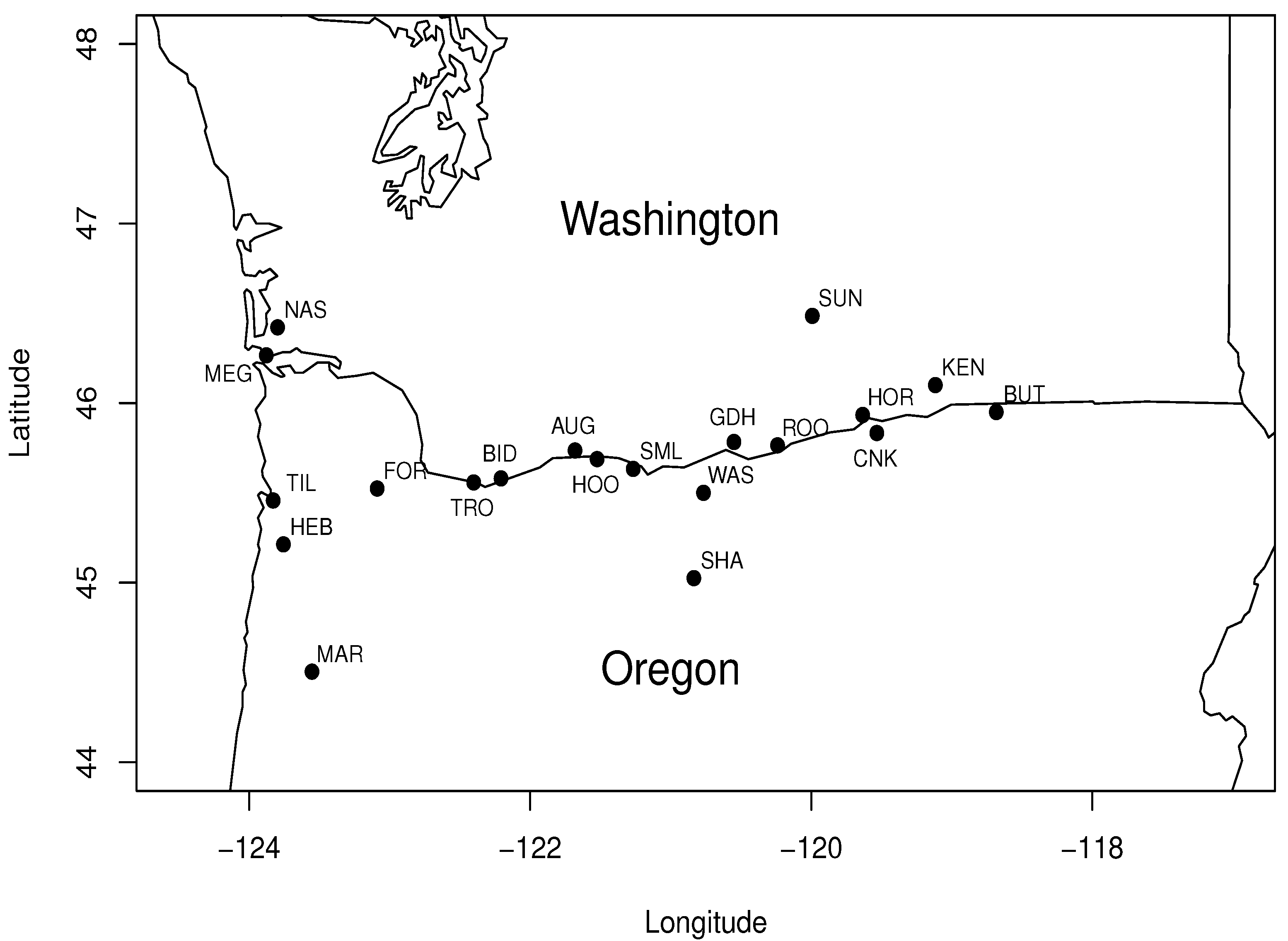
3.1. Data Description

The Bonneville Power Administration (BPA) maintains and archives data from twenty meteorological towers along the border between Oregon and Washington, and it can be accessed at [50]. The tower sites are plotted in Figure 1 with their acronyms. Full names are given in Table 1. The sites are quite spatially diverse, with those along the coastline exhibiting very distinct behavior from those farther inland. In addition, most of the sites are located along the Columbia River Gorge that channels wind within its canyon, and the domain is also split by the Cascade mountains that run from the north to the south through central Washington and Oregon. Hood River lies to the west, and Sevenmile Hill is to the east of the crest of the mountains. In the western region, the climate is wet and maritime, and to the east, it is dry. Substantial east-west pressure gradients develop across the mountains, and this geography has been exploited in several wind forecasting models [17,18,51,52].

Figure 1. Plot of the locations of the twenty meteorological towers.

Figure 1. Plot of the locations of the twenty meteorological towers.

Table 1. Summary of location names and the number of missing observations for each temporal aggregation level. Note that the 10-min, hourly and daily data have 52,560, 8,760 and 365 observations in a year, respectively.

Acronym	Name	10-min	Hourly	Daily
AUG	Augspurger	1,422	236	9
BID	Biddle Butte	0	0	0
BUT	Butler Grade	2,690	444	14
CNK	Chinook	2,687	444	14
FOR	Forest Grove	0	0	0
GDH	Goodnoe Hills	2,687	444	14
HOO	Hood River	0	0	0
HOR	Horse Heaven	0	0	0
KEN	Kennewick	0	0	0
MAR	Mary’s Peak	4,081	673	23
MEG	Megler	0	0	0
HEB	Mt. Hebo	2,148	351	12
NAS	Naselle Ridge	201	30	0
ROO	Roosevelt	281	46	1
SML	Seven Mile Hill	2,687	444	14
SHA	Shaniko	199	32	0
SUN	Sunnyside	0	0	0
TIL	Tillamook	0	0	0
TRO	Troutdale	0	0	0
WAS	Wasco	0	0	0

Table 1. Summary of location names and the number of missing observations for each temporal aggregation level. Note that the 10-min, hourly and daily data have 52,560, 8,760 and 365 observations in a year, respectively.

Acronym	Name	10-min	Hourly	Daily
AUG	Augspurger	1,422	236	9
BID	Biddle Butte	0	0	0
BUT	Butler Grade	2,690	444	14
CNK	Chinook	2,687	444	14
FOR	Forest Grove	0	0	0
GDH	Goodnoe Hills	2,687	444	14
HOO	Hood River	0	0	0
HOR	Horse Heaven	0	0	0
KEN	Kennewick	0	0	0
MAR	Mary’s Peak	4,081	673	23
MEG	Megler	0	0	0
HEB	Mt. Hebo	2,148	351	12
NAS	Naselle Ridge	201	30	0
ROO	Roosevelt	281	46	1
SML	Seven Mile Hill	2,687	444	14
SHA	Shaniko	199	32	0
SUN	Sunnyside	0	0	0
TIL	Tillamook	0	0	0
TRO	Troutdale	0	0	0
WAS	Wasco	0	0	0

Here, we use the 2013 data, which is reported at all towers in 5-min averages. Wind speeds are reported here in meters per second, and wind direction is measured with $0^{\circ }$ as north and progressing clockwise around the circle. No quality control is necessary for any of the towers in 2013, but for some locations, there is a substantial amount of missing data, as noted in Table 1. We do not use the raw 5-min averages, but aggregate these into 10-min, hourly and daily averages. Ten of the locations have no missing data for any of the timescales, and for the rest, the number of missing observations is reduced as the aggregation increases. Nevertheless, to avoid imputation, we focus mainly on those locations with no missing data.

3.2. Spatial and Temporal Scales

The wind at individual sites can be far more variable than when wind is averaged over a larger region. The same is true for temporal scale: as larger time windows are used to construct averages, the wind becomes less noisy. For this reason, we want to test the ability of the MSVAR model algorithm to replicate the variability of wind at different spatial and temporal scales.

In terms of spatial scales, we simulate wind vectors for individual tower locations, “local” locations, which are the averages of two or three nearby stations, and a “region-wide” average across all 20 locations. To ensure that our results are robust to our choices of location, we simulate at the following three individual locations: Sunnyside, Tillamook and Wasco. In addition, for the local averages, we select three sets of nearby locations that are representative of the different behaviors in the region and name them “coast”, “east” and “west”. They are each comprised of the following towers:

• Coastal: Tillamook and Mt. Hebo;
• East of Cascades: Kennewick, Butler and Horse Heaven;
• West of Cascades: Biddle Butte and Troutdale.

Finally, for the region-wide average, we use all 20 towers, and in those cases that a tower has missing values, they are dropped from the average.

Each of these spatial scales may be important for different reasons. A wind farm operator may be interested in the behavior of only one wind farm at one location or a small subset of locations. The balancing authority, on the other hand, is interested in the average amount of energy produced by all wind farms within its borders, so a region-wide average would be more important. The wind at an individual location or averaged across a local group could also be important in diagnosing problems in transmission from those sites or if they are producing an unexpected amount of electricity.

For the temporal scales, 10-min, hourly and daily averages are taken for each of the spatial scales. Table 2 summarizes the number of bivariate time series (i.e., ${\mathbf{y}}_t$ is $2\times 1$) that we model for each combination of spatial and temporal scale, resulting in a total of 21 scenarios. The 10-min averages are used for load balancing; hourly averages are used for dispatch and transmission modeling; and daily averages are used for day-ahead trading. The three temporal scales that we model here are also important for regulation, load following and unit commitment, respectively [9].

Table 2. Number of bivariate time series for each spatial and temporal scale for which the model is used to simulate data.

Temporal	Spatial Scales
Scales	Individual	Local	Regional
10-min	3	3	1
Hourly	3	3	1
Daily	3	3	1

Table 2. Number of bivariate time series for each spatial and temporal scale for which the model is used to simulate data.

Temporal	Spatial Scales
Scales	Individual	Local	Regional
10-min	3	3	1
Hourly	3	3	1
Daily	3	3	1

3.3. Spatial Locations

While the number of parameters that are required to estimate in the MSVAR model grows quickly as the number of locations, p, increases, for a moderate number of locations, the model should still be able to simulate the wind vector at multiple locations simultaneously. We test two additional such scenarios at the hourly time step with four and ten locations. With four locations, $p=4$, and ${\mathbf{y}}_t$ is $8\times 1$; and we model Forest Grove, Troutdale, Biddle Butte and Hood River. None of these locations have any missing values, and they are all located along the Columbia River Gorge to the west of the Cascades.

For the ten locations, we take all ten towers that have no missing data. Therefore, $p=10$, and ${\mathbf{y}}_t$ is $20\times 1$. These towers are distributed across the entire domain with coastal sites (Megler and Tillamook); sites west of the Cascades and near the Gorge (Forest Grove, Troutdale, Biddle Butte and Hood River); east of the Cascades and far from the Gorge (Sunnyside); and east of the Cascades near the Gorge (Wasco, Horse Heaven and Kennewick).

4. Validation

The validation of a stochastic weather generator in general depends on the features that are most important to the end user, and many different characteristics of the simulated data could be investigated. For example, the ability of a model to duplicate the length of stormy and calm periods is investigated in [36]. For each of the simulation scenarios outlined in Section 3, we are interested in replicating the following features of the observed data:

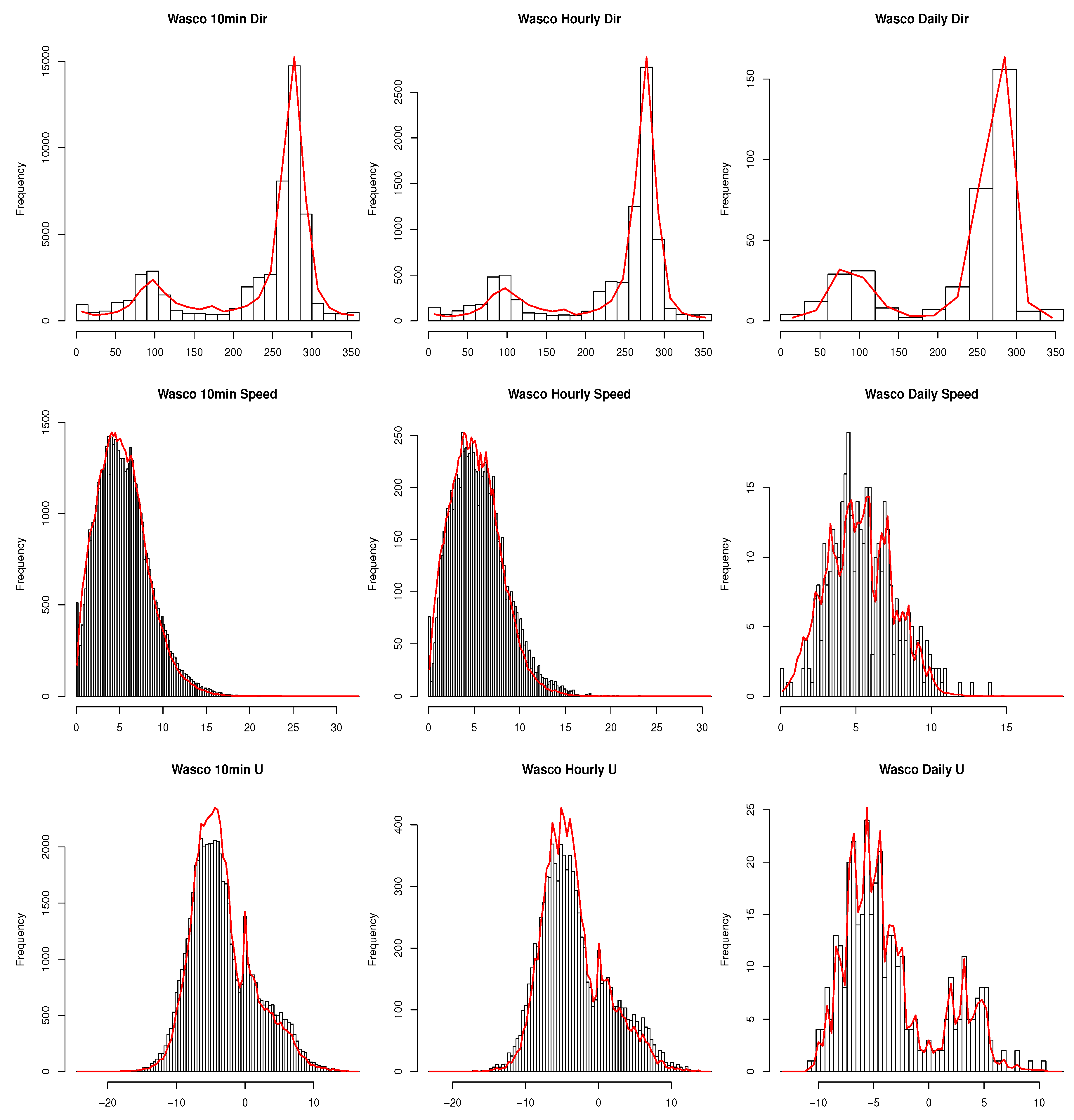
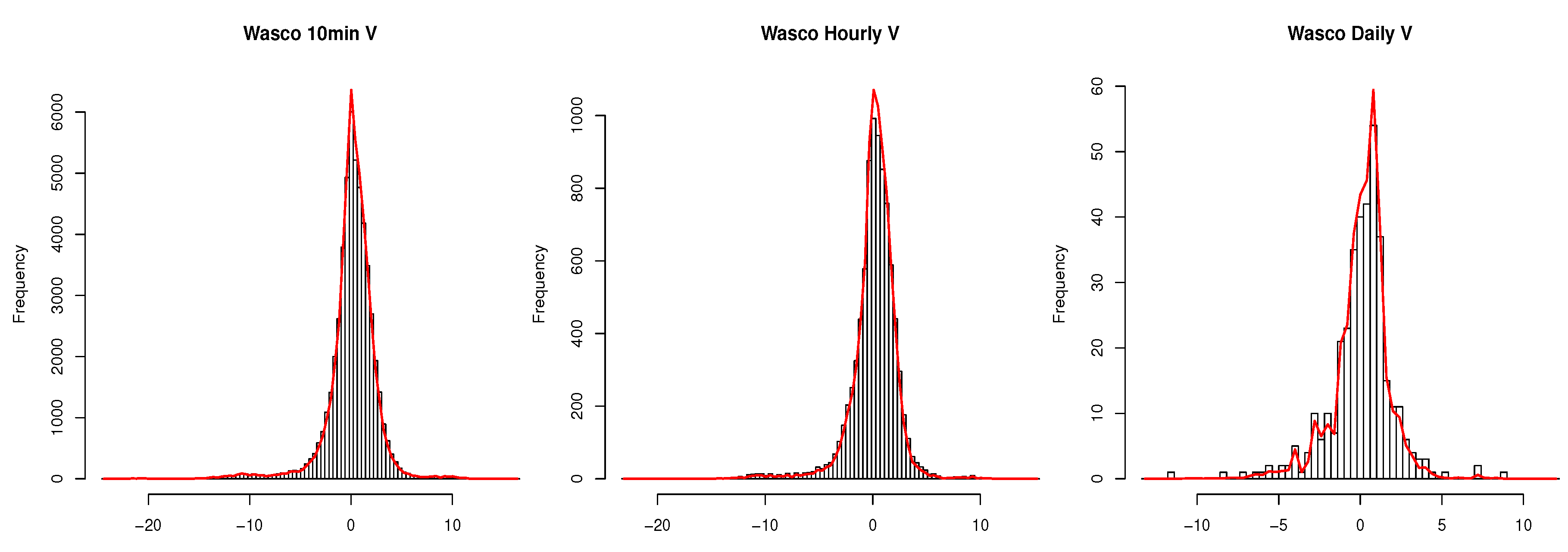
• the distribution of speed, direction, u and v;
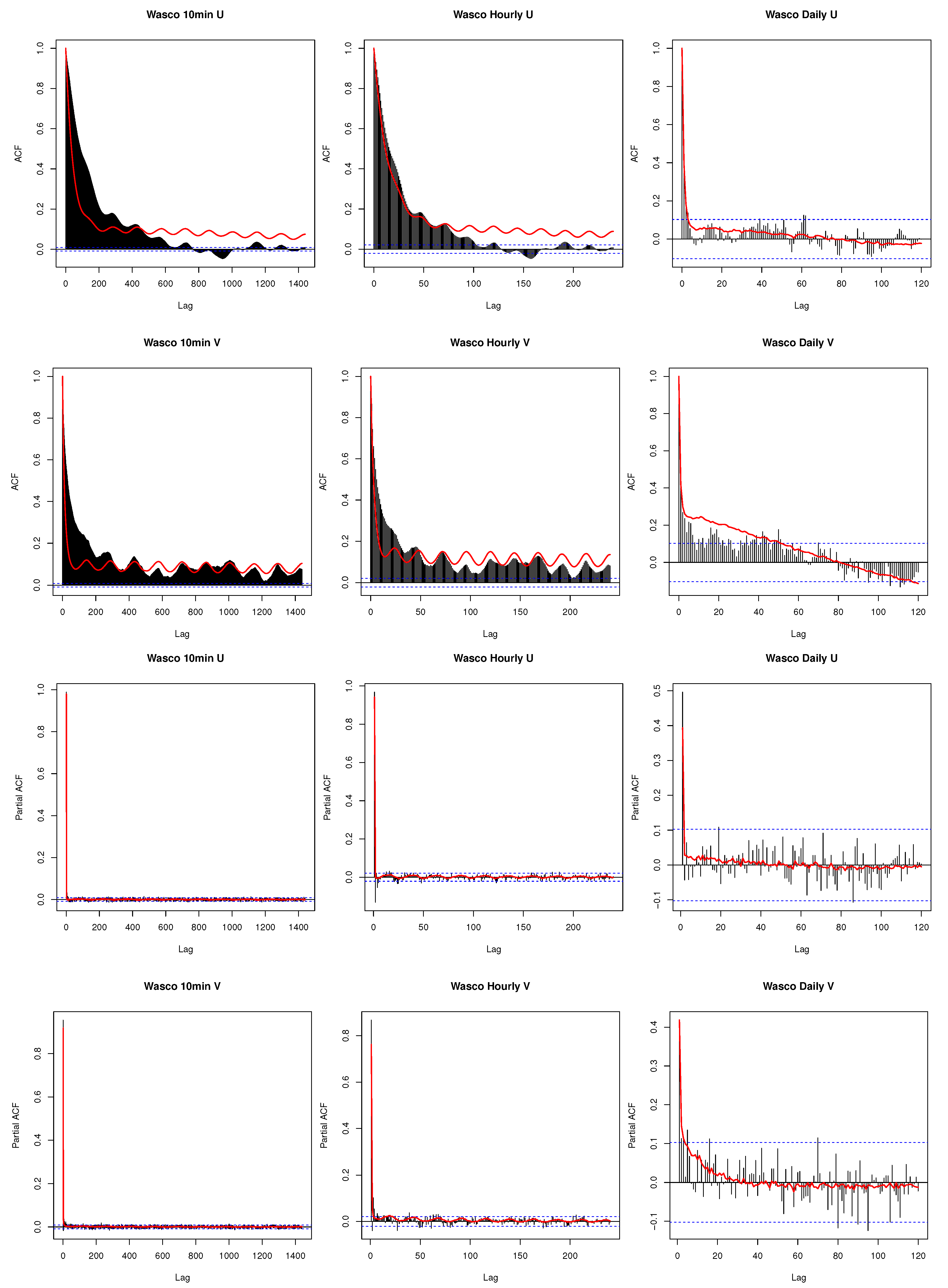
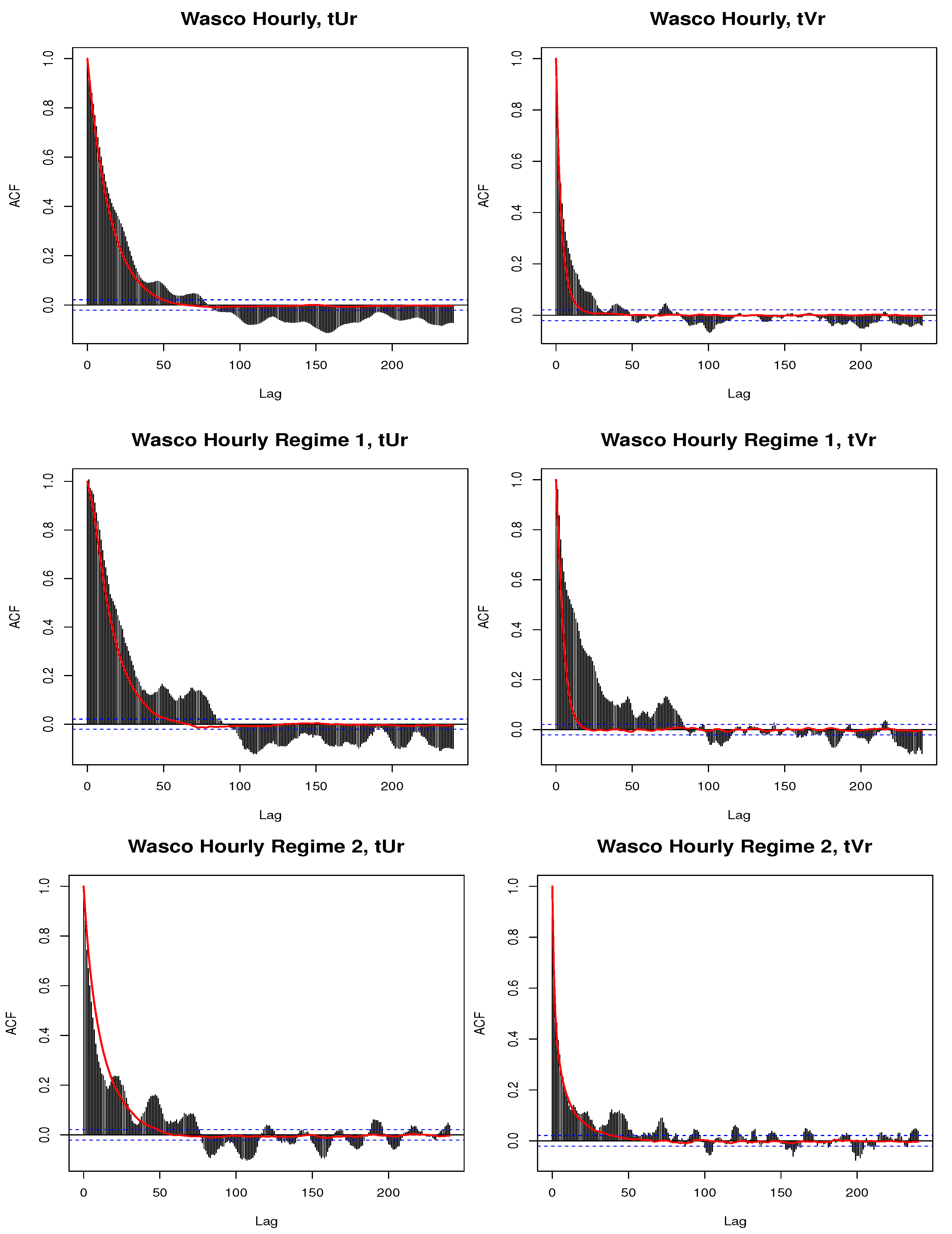
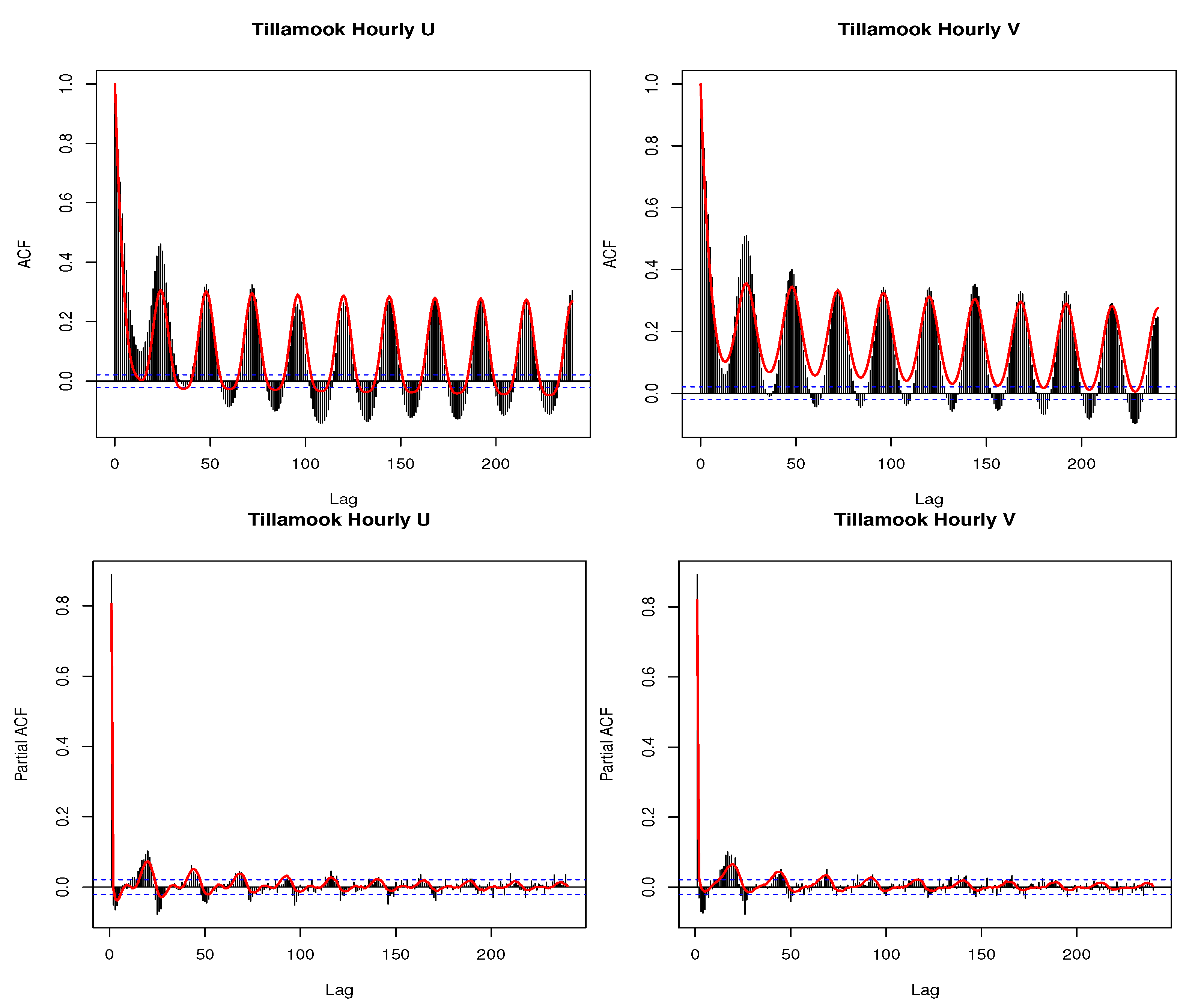
• the temporal autocorrelation of the u and v components;
• the diurnal variability of the u and v components;
• the joint distribution of speed and direction; and
• the correlation between the u and v components.

In addition, for the scenarios in which the wind vector is simulated at more than one location simultaneously, we are interested in capturing a sixth feature: the spatial correlations among the u and v components. To assess the ability of the MSVAR model to capture these features, we simulated 100 realizations under each of the 23 scenarios (the 21 scenarios outlined in Table 2, plus the two sets of spatial locations) and construct the following:

• histograms of speed, direction, u and v of the observed data with the average count per bin taken across all 100 simulations overlaid;
• autocorrelation (ACF) and partial autocorrelation (PACF) plots of the observed u and v components with the average ACF and PACF for each lag taken over the 100 simulations overlaid (e.g., the average of 100 lag-1 autocorrelations is taken to obtain the plotted value), and diurnal variability can also be assessed with the ACF plots;
• wind roses of the observed speed and direction and wind roses of the average number of simulated observations across all 100 simulations occurring in each speed and direction bin;
• the observed correlation between the u and v components and the average correlation between the u and v components across all 100 simulations; and
• a heat map of the spatial correlations among the observed u and v components and a heat map of the average of the spatial correlations across all 100 simulations.

Of course, we cannot show all of the figures and results here, but we describe a full set for one scenario and then examples wherein the MSVAR achieves its best and worst performance. The full graphical validation for every scenario is available in the Appendix.

4.1. Spatial and Temporal Scales

First, we take one individual location, Wasco, and Figure 2 to Figure 4 demonstrate the types of plots that we produce to evaluate the quality of the simulation. In Figure 2, the histograms of the observed direction, speed, u and v are produced. For each bin, the average count of observations across the 100 simulations is taken, and this average count is overlaid with the red curve. With the exception of the high count of observed zero wind speeds, the distributions of all of the variables in the simulation are extremely close on average to the observed. The asymmetry in the wind speeds is captured for the 10-min and hourly averages, but the asymmetry in the observed distribution diminishes for the daily averages, and this feature is also well-modeled in the simulation. Even the bi-modality in the distribution of the u component is captured.

Figure 2. Histograms of observed direction, speed, u and v (first, second, third and fourth rows) for 10-min, hourly and daily time resolutions (left, center and right columns) for Wasco. The average simulated count for each variable is given by each overlaid red curve.

Figure 2. Histograms of observed direction, speed, u and v (first, second, third and fourth rows) for 10-min, hourly and daily time resolutions (left, center and right columns) for Wasco. The average simulated count for each variable is given by each overlaid red curve.

In Figure 3, we plot the autocorrelation function (ACF) and partial autocorrelation function (PACF) plots for the u and v components. For each lag, the average ACF and PACF across the 100 simulated datasets are computed, and this is overlaid in red on top of the observed values. The PACF’s drop to zero almost immediately for all temporal scales for both u and v, and the simulation matches this. In the ACFs, on the other hand, the simulated average ACFs for the 10-min scale drop too quickly and persist at a level that is too high for the u component. At the hourly averaged time scale, the u component’s temporal dependence is easily captured for approximately the first 60 h and then is too high. We note that if such simulated data are used in a grid integration study and the strength of the temporal dependence is too strong, then the simulated data are too smooth. This, in turn, could cause too few reserves to be held online. However, the impact that such mismatches in the statistical properties of the simulated data may have on grid integration studies is beyond the scope of the current work. The ACFs for the daily averages are relatively well represented in the simulation. The diurnal cycle can be observed in the ACF plots by the cyclical peaks, especially for the v component, and the simulation is able to match this behavior on average.

Figure 4 shows the observed wind rose in the left column, and the average number of observations within each combination of speed and direction bin across all 100 simulations is plotted in the right column. From this, we see that the directions match quite precisely those of the observed data, and the slightly higher winds that are observed coming from the west are duplicated in the simulation.

The parameter estimates of the MSVAR(1) for Wasco are also informative. We assume that there are regimes wherein the spatial and/or temporal patterns are distinct, and the detrending step ignores the regimes and removes a trend across all observations regardless of regime. Thus, the estimates of ${\mathbf{A}}_{r_t}$ and ${\Sigma }_{r_t}$ should be significantly different from each other across regimes. In Table 3, we report the parameter estimates for Wasco at the 10-min, hourly and daily temporal scales, and significant differences exist between ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ for each time scale (results not shown). In addition, for each time scale, these coefficients are significantly different from zero. The differences between ${\widehat{\mathbf{A}}}_1$ and ${\widehat{\mathbf{A}}}_2$ increase as the temporal aggregation increases, and this pattern is similar for the other simulation scenarios and for the estimates of ${\Sigma }_1$ and ${\Sigma }_2$, as well. For example, at the daily scale, the strength of the relationship between the residual transformed u and v components is much stronger in the second regime, as evidenced by the higher off-diagonal elements of ${\widehat{\mathbf{A}}}_2$ and ${\widehat{\Sigma }}_2$, and their temporal dependence is also much stronger in the second regime given the higher diagonal elements of ${\widehat{\mathbf{A}}}_2$.

Figure 3. Observed autocorrelation functions (ACFs) (top two rows) and and partial autocorrelation functions (PACFs) (bottom two rows) of u and v with 10-min, hourly and daily in the left, center and right columns, respectively, for Wasco. The average simulated correlation for each variable is given by each overlaid red curve.

Figure 3. Observed autocorrelation functions (ACFs) (top two rows) and and partial autocorrelation functions (PACFs) (bottom two rows) of u and v with 10-min, hourly and daily in the left, center and right columns, respectively, for Wasco. The average simulated correlation for each variable is given by each overlaid red curve.

Figure 4. Wind roses of speed and direction for the observed (left) and the average across the 100 simulations (right) at Wasco.

Figure 4. Wind roses of speed and direction for the observed (left) and the average across the 100 simulations (right) at Wasco.

Table 3. Estimated coefficient and covariance matrices for the Wasco simulation scenarios.

Time Scale	${\widehat{A}}_1$		${\widehat{A}}_2$		${\widehat{\Sigma }}_1$		${\widehat{\Sigma }}_2$
10-min	0.99	0.01	0.96	−0.10	0.03	0.00	0.04	−0.02
	0.01	0.95	0.00	0.81	0.00	0.10	−0.02	0.15
Hourly	0.97	0.07	0.89	−0.34	0.08	0.02	0.08	−0.05
	0.04	0.85	−0.02	0.49	0.02	0.32	−0.05	0.24
Daily	0.36	−0.07	0.61	0.47	0.62	−0.08	0.80	0.49
	0.03	0.19	0.28	0.46	−0.08	0.49	0.49	0.70

Table 3. Estimated coefficient and covariance matrices for the Wasco simulation scenarios.

Time Scale	${\widehat{A}}_1$		${\widehat{A}}_2$		${\widehat{\Sigma }}_1$		${\widehat{\Sigma }}_2$
10-min	0.99	0.01	0.96	−0.10	0.03	0.00	0.04	−0.02
	0.01	0.95	0.00	0.81	0.00	0.10	−0.02	0.15
Hourly	0.97	0.07	0.89	−0.34	0.08	0.02	0.08	−0.05
	0.04	0.85	−0.02	0.49	0.02	0.32	−0.05	0.24
Daily	0.36	−0.07	0.61	0.47	0.62	−0.08	0.80	0.49
	0.03	0.19	0.28	0.46	−0.08	0.49	0.49	0.70

At the hourly scale, the temporal dependence between the residual transformed u and v components is weaker for the second regime than the first regime, as evidenced by the lower diagonal elements of ${\widehat{\mathbf{A}}}_2$. In fact, this can also be observed in Figure 5, which shows the ACF plot of the transformed, detrended u and v components for the hourly Wasco scenario for the overall dataset and then split by the two regimes. It is clear that the observed temporal autocorrelation is different between the two identified regimes when compared with the overall ACF. In addition, the average of the temporal dependence for the transformed residuals across the 100 simulations is overlaid both overall and within each regime. Within each regime, the MSVAR(1) model is able to properly capture the broad features of the temporal dependence, except for the transformed v residuals in Regime 1. Using a higher order lag for the VAR part of the model within this regime could help to solve this problem.

Figure 5. ACF of the detrended, transformed residuals of u and v for the hourly Wasco scenario for the overall series (top row) and each of the two regimes (second and third rows).

Figure 5. ACF of the detrended, transformed residuals of u and v for the hourly Wasco scenario for the overall series (top row) and each of the two regimes (second and third rows).

Finally, we will note a few interesting aspects of the simulations at the other two locations. At Tillamook, the diurnal pattern in the winds is much stronger than at Wasco, but the MSVAR models this pattern quite nicely; see Figure 6. Except for some small negative autocorrelations, the MSVAR average temporal correlation is very close to the observed. In this case, some of the observed partial autocorrelations are significantly different from zero, and the simulated data matches this well on average. Tillamook and Sunnyside both have a more complex array of wind directions than does Wasco, as shown in Figure 7. The primary modes of wind direction are captured in the simulation, but the wind directions are more variable in the simulation than in the observed data.

Figure 6. Observed ACFs (top row) and PACFs (bottom row) of hourly u and v for Tillamook. The average simulated correlation for each variable is given by each overlaid red curve.

Figure 6. Observed ACFs (top row) and PACFs (bottom row) of hourly u and v for Tillamook. The average simulated correlation for each variable is given by each overlaid red curve.

Figure 7. Wind roses of hourly direction and speed for the observed (left) and average across the 100 simulations (right) at Tillamook (top) and Sunnyside (bottom).

Figure 7. Wind roses of hourly direction and speed for the observed (left) and average across the 100 simulations (right) at Tillamook (top) and Sunnyside (bottom).

For the averages of two to three local sites, many of the same conclusions are reached as with the individual sites, even though the distributions of speed and direction are different for these cases. For the sites west of the Cascades, some very non-normal and strongly left-skewed behavior is present in the wind speed and u component, but this is well-modeled in the simulation. The temporal dependence in the west is quite strong at the 10-min and hourly scale, and the MSVAR does not quite achieve this strength in the temporal dependence. On the other hand, for the regional average, the MSVAR overestimates the temporal dependence on average at the 10-min and hourly scales. However, the joint distribution of wind speed and wind direction is quite close to the observed, and the correlations between the u and v components at all temporal scales are captured quite closely by the MSVAR model. This regional average is an important spatial scale at which to model across all temporal scales for a utility’s load balancing, dispatch and trading, and the MSVAR excels at modeling all three of these scenarios.

Table 4 reports the correlations between the observed u and v components and the average across the 100 simulations for each of the 21 scenarios depicted in Table 2. The overall correlation between u and v is not well represented by the MSVAR at some individual locations, such as Wasco, but it generally improves with temporal and spatial aggregation. This is not too surprising, since with a Markov-switching model, the correlations between u and v are expected to differ among the regimes, so measuring an overall correlation masks the more linear association within the identified regimes. In addition, the correlation is computed based on observations that have not been transformed or detrended, so correlation may not even be the best way to quantify the relationship between u and v. Yet, ultimately, the correlations are of less importance than the joint distribution of wind speed and direction, which can be assessed in the wind roses.

Table 4. Observed overall correlations between the u and v components for the simulation scenarios summarized in Table 2 and the corresponding average simulated correlations.

Temporal	Spatial	Observed Overall Corr.	Simulated Overall Corr.
	Tillamook	−0.37	−0.42
	Sunnyside	−0.03	−0.17
	Wasco	0.02	−0.23
10-min	Coast	−0.11	−0.10
	East	0.55	0.42
	West	0.19	0.21
	Region	0.24	0.21
	Tillamook	−0.39	−0.47
	Sunnyside	−0.01	−0.28
	Wasco	0.02	−0.30
Hourly	Coast	−0.10	−0.09
	East	0.56	0.42
	West	0.19	0.18
	Region	0.23	0.10
	Tillamook	−0.25	−0.14
	Sunnyside	0.19	0.15
	Wasco	0.14	−0.13
Daily	Coast	−0.06	−0.06
	East	0.58	0.39
	West	0.21	0.05
	Region	0.28	0.40

Table 4. Observed overall correlations between the u and v components for the simulation scenarios summarized in Table 2 and the corresponding average simulated correlations.

Temporal	Spatial	Observed Overall Corr.	Simulated Overall Corr.
	Tillamook	−0.37	−0.42
	Sunnyside	−0.03	−0.17
	Wasco	0.02	−0.23
10-min	Coast	−0.11	−0.10
	East	0.55	0.42
	West	0.19	0.21
	Region	0.24	0.21
	Tillamook	−0.39	−0.47
	Sunnyside	−0.01	−0.28
	Wasco	0.02	−0.30
Hourly	Coast	−0.10	−0.09
	East	0.56	0.42
	West	0.19	0.18
	Region	0.23	0.10
	Tillamook	−0.25	−0.14
	Sunnyside	0.19	0.15
	Wasco	0.14	−0.13
Daily	Coast	−0.06	−0.06
	East	0.58	0.39
	West	0.21	0.05
	Region	0.28	0.40

4.2. Spatial Locations

Figure 8 shows the spatial correlation of the observed u and v components for the sets of four and ten locations along with the average across 100 simulations when the regimes are defined based on the u and v components at all of the locations. Note that the scale for the difference in observed and simulated correlation is only different for the v component for the ten sites in the bottom right plot of Figure 8. Results with regimes defined based on the average of the transformed u and v components across the locations are similar, but slightly worse. For the four locations, the MSVAR model captures the spatial correlations of both the u and v components very well. For the ten locations, the spatial correlations among the u components are replicated well, but there is a distinct group of locations among the v components to the west of the Cascades that deviate more strongly from the observed. It is likely that the correlations among locations on either side of the crest of the Cascade mountains are so distant, that they are more difficult to capture simultaneously in the MSVAR model. Figure 9 shows a similar plot, but for wind speed. Again, the more the locations, the more difficult it becomes to capture all of the correlations, but the simulated correlations are all within 0.30 of the observed, on average; and the spatial pattern in the observed wind speed correlations is captured in the simulation, regardless of the number of sites.

Figure 8. Observed correlation of u and v across space for the set of four sites (top two rows) and the set of 10 sites (bottom two rows) in the left column. In the middle column are the average simulated correlations for both u and v for the second regime definition in Step 4(b). The last column shows the difference between the observed and average simulated correlations. The sites are organized from west to east along the horizontal axis.

Figure 8. Observed correlation of u and v across space for the set of four sites (top two rows) and the set of 10 sites (bottom two rows) in the left column. In the middle column are the average simulated correlations for both u and v for the second regime definition in Step 4(b). The last column shows the difference between the observed and average simulated correlations. The sites are organized from west to east along the horizontal axis.

Figure 9. Observed correlation of speed across space for the set of four sites (top row) and the set of 10 sites ( bottom row) in the left column. In the middle column are the average simulated correlations for the speed for the second regime definition in Step 4(b). The last column shows the difference between the observed and average simulated correlations. The sites are organized from west to east along the horizontal axis.

Figure 9. Observed correlation of speed across space for the set of four sites (top row) and the set of 10 sites ( bottom row) in the left column. In the middle column are the average simulated correlations for the speed for the second regime definition in Step 4(b). The last column shows the difference between the observed and average simulated correlations. The sites are organized from west to east along the horizontal axis.

Focusing on the distribution of the speed and direction of each location individually, the features are replicated remarkably well, even though the locations have very different behavior. Figure 10 shows the wind roses of the observed and average simulated wind for the four sites that are common to both spatial simulations. The winds at Forest Grove are generally from the north or the south; Troutdale and Biddle Butte winds are almost equally split between the east and west; and Hood River winds are primarily from the west. Biddle Butte has higher wind speeds from the east than the west. All of these features are replicated in the simulated data, but they are a bit more precise in the simulation of the four sites simultaneously. As might be expected, once ten sites are simulated simultaneously, some specificity in simulating individual sites is lost. In addition, some of the sites in the set of 10 locations that have complex wind directions are more difficult to duplicate than others; for example, the wind directions of Megler, Sunnyside and Horse Heaven have greater spread in the simulated data than in the observed.

Figure 10. The left column is the observed distribution of wind speed and direction; the center column is the average across all 100 simulations of four sites simulated simultaneously based on the second regime definition in Step 4(b); and the right column is the average across all 100 simulations of these four sites for the 10 sites simulated simultaneously based on the second regime definition.

Figure 10. The left column is the observed distribution of wind speed and direction; the center column is the average across all 100 simulations of four sites simulated simultaneously based on the second regime definition in Step 4(b); and the right column is the average across all 100 simulations of these four sites for the 10 sites simulated simultaneously based on the second regime definition.

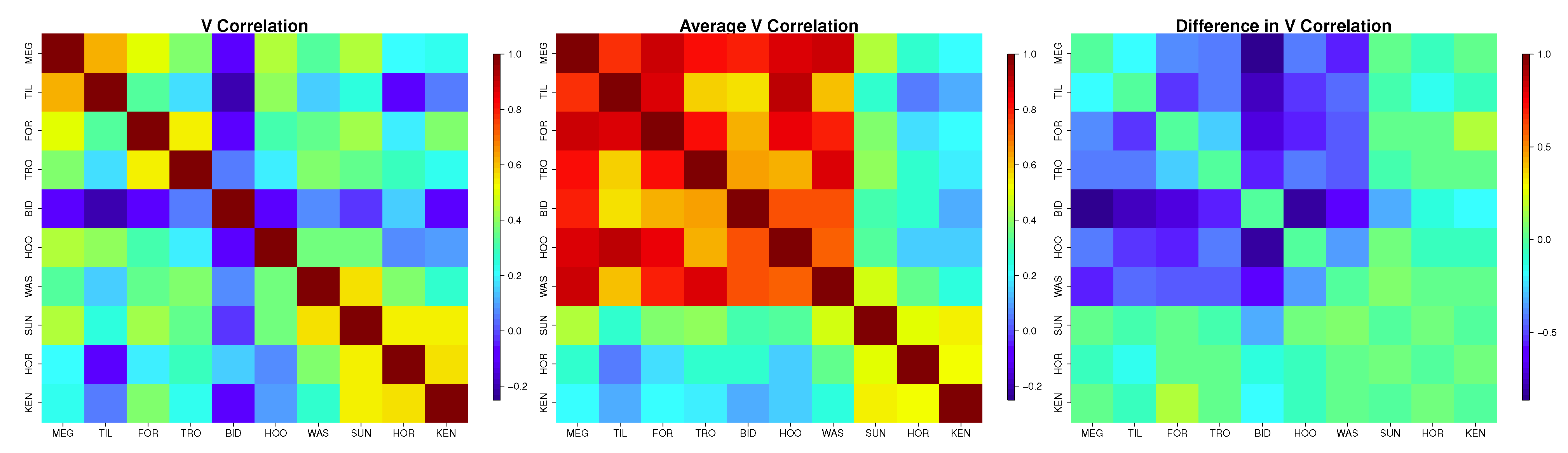
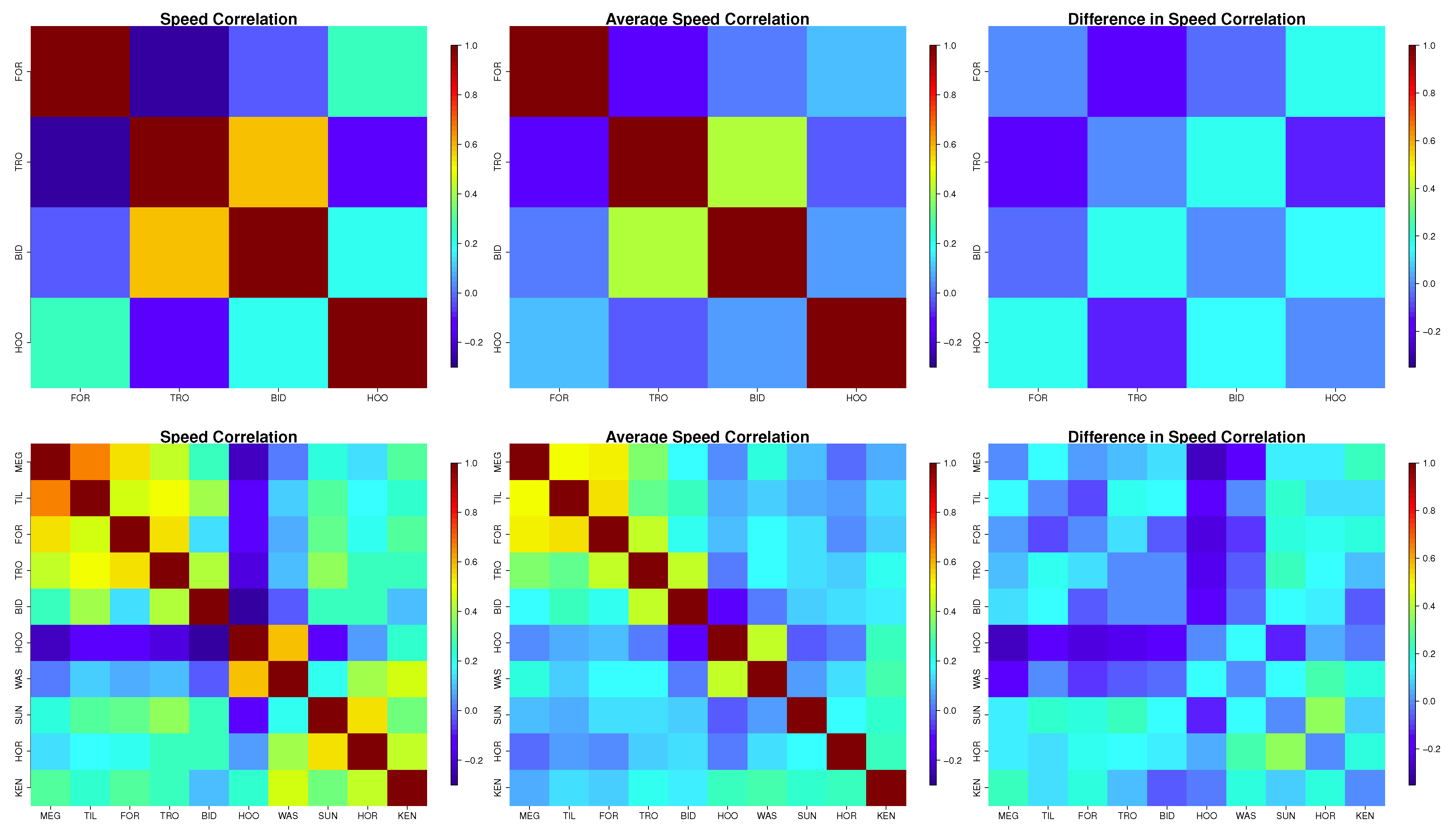
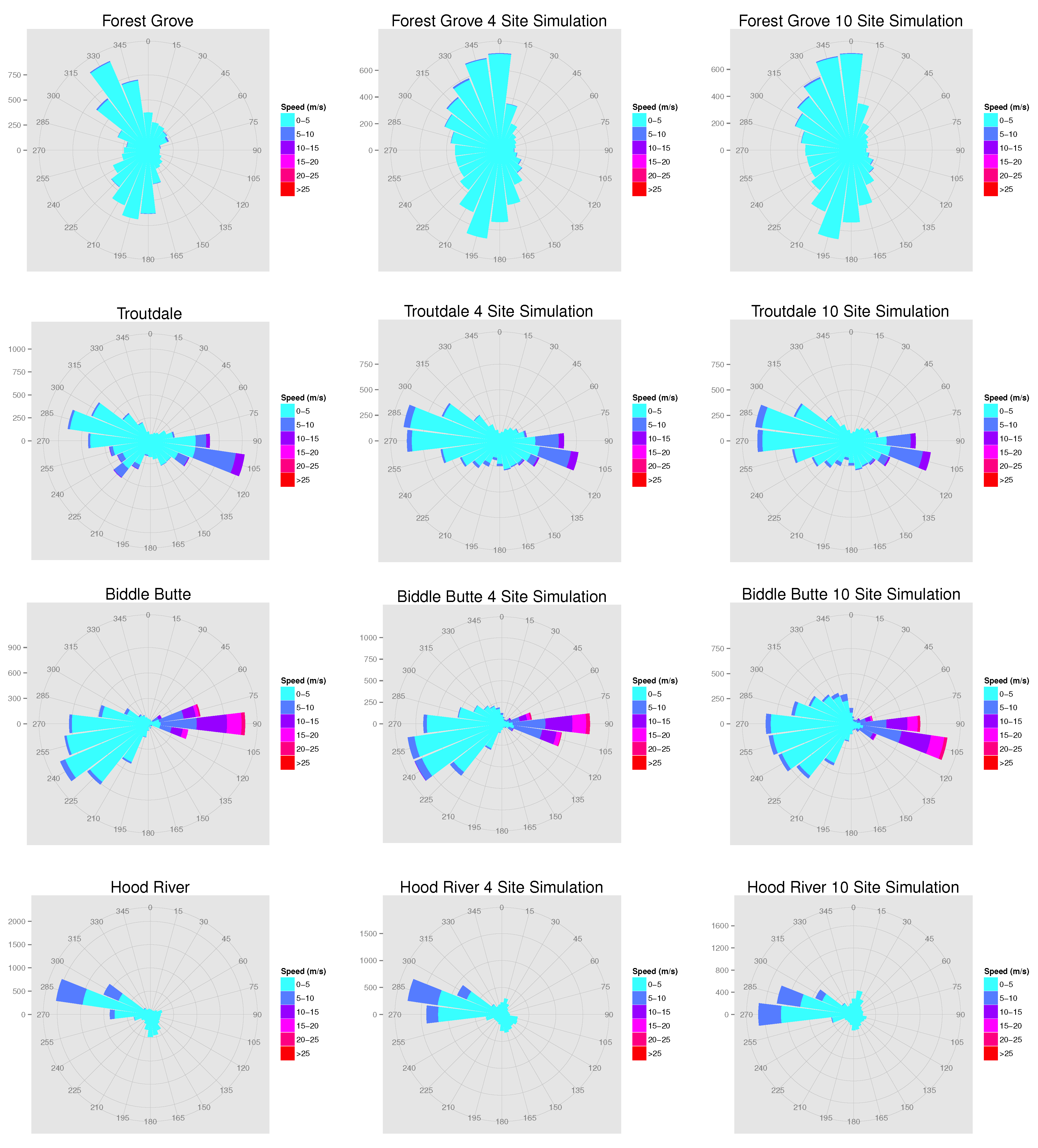
5. Discussion

The MSVAR model and the algorithm described here demonstrate very good potential for generating realizations of the wind vector for various temporal and spatial scales. Most promising is its ability to simultaneously simulate at multiple locations and to maintain the proper spatial relationships. Within regimes, the temporal dependencies in the observed data differ, and while not shown here, the spatial dependencies among locations also differ by regime [38]. The Markov-switching part of the model does relatively well in capturing these differences, but some improvement could be realized by allowing the number of lags within regimes to differ. In addition, when the wind directions are complex, the model does not perform as well as when the wind directions are nearly dichotomous, and improving the measure of association between the u and v components at individual locations is important, since both speed and direction jointly impact wind power. Additional validation may be performed, as well, such as comparing the distribution of wind speed and direction across seasons or between daytime and nighttime hours and evaluating the frequency and severity of high wind events.

Future modifications to improve the model include investigating the impact of the following on the simulated wind: the number of regimes selected; increasing the number of lags in the MSVAR; joint transformation of the u and v components to normality; and different detrending techniques. The marginal improvement gained, if any, of adding additional regimes and lags should be investigated, as well as having a single regime and a single lag. As the number of regimes and lags increase, the number of observations available to estimate the parameters within each regime decreases, so the benefit of adding regimes and lags must be clear. The joint transformation of u and v to normality cannot be treated with the same nonparametric approach that we have used here for the individual components, since quantiles in the multivariate setting are not well defined. We may need to resort to parametric models, such as the multivariate skew-t distribution [53], which has some history and utility in modeling winds [18]. In addition, it is possible that the diurnal patterns or the seasonal variability differs across a year, and such features can be incorporated into the trend.

In this work, we have fit a separate MSVAR model to each timescale and spatial aggregation level. It may also be useful to consider simulating wind at multiple individual locations and then averaging the individual time series to see if the averaged simulated behavior is similar to the average behavior of the observed series, so different models need not be fit for scenarios, such as “east”, “west” and “coastal”. Similar experiments in time can be performed wherein simulated 10-min data are averaged to the hourly and daily timescales and compared to the observed data at the corresponding timescale. The benefit would be that only one model would need to be fit as opposed to a separate model for each timescale.