Calculating MIPS 2.0
Abstract
:1. Introduction
2. Methodology
2.1. Sequential MIPS
2.1.2. Spreadsheet-Based Calculation Tool
2.1.3. Features of GaBi LCA Software
2.2. Matrix Formulation
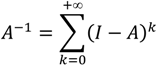
2.3. LCA Databases
2.3.1. Abiotic Raw Materials (MI Abiotic)
| Description of the material | Common terminology | MFA/MIPS terminology | Ecoinvent LCI terminology |
|---|---|---|---|
| Material removed to get access to reserve, i.e., metal containing ores | Overburden, interburden | Unused extraction | N.A. |
| The metal containing material | Run of mine, gross ore, crude ore | Used extraction | N.A. |
| The pure metal | Net ore or metal content | Metal component of used extraction | Elementary flow |
| Elementary flows in ecoinvent 2.2 | Allocation factor [%] | Allocated used extraction [kg/kg elementary flow] | Unused extraction coeff. [kg/kg used extraction] | MI abiotic factor [kg/kg elementary flow] | ||
|---|---|---|---|---|---|---|
| Case | Unit | |||||
| A | Granite, in ground | [kg] | 100 | 1.00 | 0.01* (world average) | 1.01 = 1.00 × (1 + 0.01) |
| B | Nickel, 1.98% in silicates, 1.04% in crude ore, in ground | [kg] | 100 | 96.15 = 1/0.0104 | 0.60** (world average) | 153.75 = 96.15 × (1 + 0.60) |
| C | Silver, Ag 4.6E−5%, Au 1.3E−4%, in ore, in ground | [kg] | 0.26 = 4.6E−5/(4.6E−5 + 1.3E−4) | 568,181.82 = 0.26*1/4.6E−7 | 1.25 (Peru) | 1,278,409.09 = 568,181.82 × (1 + 1.25) |
| C | Copper, Cu 0.38%, Au 9.7E−4%, Ag 9.7E−4%, Zn 0.63%, Pb 0.014%, in ore, in ground | [kg] | 0.37 = 0.38/(0.38 + 2 × 9.7E−4 + 0.63 + 0.014) | 97.47 = 0.37 × 1/0.0038 | 2*** (Sweden) | 292.41 = 97.47 × (1 + 2) |
| D | Cadmium, 0.30% in sulfide, Cd 0.18%, Pb, Zn, Ag, In, in ground | [kg] | 0 (Cd is always a by-product) | 1.00 (by-product’s own mass) | N.A. | 1.00 (by-product’s own mass) |
Case A: Non-Metallic Minerals
Case B: Single-Metal Metallic Ores
Case C: Multiple-Metals Metallic Ores
Case D: By-Products
2.3.2. Biotic Raw Materials (MI Biotic)
| Elementary flows in ecoinvent 2.2 | Unit |
|---|---|
| Wood, hard, standing | [m3] |
| Wood, primary forest, standing | [m3] |
| Wood, soft, standing | [m3] |
| Wood, unspecified, standing | [m3] |
| Carbon dioxide, in air | [kg] |
2.3.3. Water (MI Water)
| Elementary flows in ecoinvent 2.2 | Unit | Water depletion, GLO (H) [m3/m3] | MIT water factor [kg/m3] |
|---|---|---|---|
| Volume occupied, reservoir | [m3] | 0 | 0 |
| Water, cooling, unspecified natural origin | [m3] | 0 | 1000 |
| Water, lake | [m3] | 1 | 1000 |
| Water, river | [m3] | 1 | 1000 |
| Water, salt, ocean | [m3] | 0 | 1025 |
| Water, salt, sole | [m3] | 0 | 1007–1200 |
| Water, turbine use, unspecified natural origin | [m3] | 0 | 0 |
| Water, unspecified natural origin | [m3] | 1 | 1000 |
| Water, well, in ground | [m3] | 1 | 1000 |
2.3.4. Earth Movement in Agriculture and Silviculture (MI Soil)
2.3.5. Air (MI Air)
2.3.6. Import MIT Characterization Factors into LCA Software
2.3.7. Import MIT Characterization Factors into Numerical Computation Software
- Technology matrix (A) of processes × processes;
- Intervention matrix (B) of elementary flows × processes;
- Characterization matrix (C) of impact categories × elementary flows.
- Add an empty row to the characterization matrix C;
- Fill this new row with the MIT abiotic characterization factors in the columns corresponding to the elementary flows of the category “Resource, in ground”.
2.4. Enhancing Algorithms
2.4.1. Structural Path Analysis and Accumulative Structural Path Analysis
- Pre-calculation: direct C ∙ B and total C ∙ B ∙ A−1 MI abiotic for one unit of each process in the technology matrix A (“total” means life cycle-wide here);
- Build a final demand vector (f) to model the product system;
- Use the results of step 1 to calculate the reference total MI abiotic associated with the product system defined in step 2: C ∙ B ∙ A−1 ∙ f;
- Choose a disaggregation criterion (e.g., 5%), contribution threshold to MI abiotic under which processes are not further disaggregated;
- For each element in the final demand vector (or in the vectors built in step 10 after the first round), store relevant information (e.g., process name, parent process name, disaggregation path length, etc.), and scale the direct and total MI abiotic results calculated in step 1 with the demand level defined in step 2 (or step 10 after the first round);
- Divide each of the total MI abiotic results obtained in step 5 by the reference calculated in step 3. Each resulting relative contribution to total MI abiotic of the product system is compared to the disaggregation criterion. If the contribution is smaller than the disaggregation criterion, this branch of the process chain is flagged and will not be further disaggregated;
- Divide each of the direct MI abiotic results obtained in step 5 by the reference calculated in step 3. Each resulting relative contribution to total MI abiotic of the product system is compared to the disaggregation criterion. If the contribution is higher than the disaggregation criterion, go to step 8, otherwise jump to step 10;
- If the direct contribution of a given process to the total MI abiotic of the product system is higher than the disaggregation criterion, we want to find out which elementary flows contribute the most. Each non-zero element in the corresponding process column of the intervention matrix B is first scaled with the demand level defined in step 2 (or step 10 after the first round). This result is then converted into an MI abiotic value by multiplication with the MI abiotic characterization factor from matrix C corresponding to this elementary flow;
- Divide the MI abiotic results from each of the elementary flows obtained in step 8 by the reference calculated in step 3. Store the result. The resulting relative contributions to total MI abiotic of the product system can be compared to the disaggregation criterion but, whatever the ratio, no further disaggregation is possible because we have already reached the elementary flow level;
- All processes that have been tested in steps 5 to 9, and not flagged in step 6, are to be disaggregated one level deeper down the process chain. A vector is created for each of these now “parent processes”, gathering the flows from their “children processes”. The flows are scaled according to the corresponding coefficient of the technology matrix A and the demand of the parent process. Take these vectors and go back to step 5;
2.4.2. Dynamic MIPS
- Technology matrix A and corresponding matrix of meta-data A_meta containing at least a list of the processes in matrix A with a unique ID and their position in matrix A (i.e., row or column number, which should be the same);
- Intervention matrix B and corresponding matrix of meta-data B_meta containing at least a list of the elementary flows in matrix B with a unique ID and their row number in matrix B;
- Characterization matrix C and corresponding matrix of meta-data C_meta containing at least a list of the impact categories in matrix C with a unique ID and their row number in matrix C.
- In the numerical calculation software, replicate the matrices A, B, and C, and vector f to cover each time step of the time series and rename the replicates accordingly (e.g., A_2020 for matrix A(t) in year 2020);
- Write a routine to automatically export spreadsheets as separate text files. Although numerical calculation software have read/write functions for usual spreadsheet programs such as Microsoft Excel, compatibility issues may arise. Using dedicated read/write functions for text files helps avoiding such issues;
- 3.
- Create a spreadsheet for each process that should be dynamic. The first row after the headers should contain at least the unique ID of this output process. Each subsequent row corresponds to an intermediary input or elementary flow that should be modified in matrix A or B, respectively. Flows that do not vary need not be listed. Each row should contain a code identifying the type of flow, the flow unique ID, and time series of the quantities needed for one unit of output process;
- 4.
- Save the spreadsheets as text files (see step 2);
- 5.
- Read each text file into the numerical calculation software. Start by matching the unique ID of the output process with the meta-data in matrix A_meta, which gives its column number (cj) in matrices A and B;
- 6.
- Then read each subsequent row. If it refers to an intermediary input, match its unique ID with the meta-data in matrix A_meta. If it refers to an elementary flow, match its unique ID with the meta-data in matrix B_meta. In both cases it also gives the row number (ri) in matrix A or B of the process or elementary flow, respectively, that should be modified. For each time step t of the time series, replace the value at the coordinate (ri; cj) of the corresponding matrix A(t) or B(t) (replicates generated in step 1) with the quantity stored in the text file;
- 7.
- Create a spreadsheet for each characterization method that should be dynamic. The first row after the headers should contain at least the unique ID of the impact category. Each subsequent row corresponds to an elementary flow whose characterization factor should be modified in matrix C. Factors that do not vary need not be listed. Each row should contain the flow unique ID and time series of the characterization factor;
- 8.
- Save the spreadsheets as text files (see step 2);
- 9.
- Read each text file into the numerical calculation software. Start by matching the unique ID of the characterization method with the meta-data in matrix C_meta, which gives its row number (ri) in matrix C;
- 10.
- Then read each subsequent row. Match each unique ID with the meta-data in matrix B_meta. It gives the column number (cj) in matrix C of the elementary flow whose characterization factor should be modified. For each time step t of the time series, replace the value at the coordinate (ri; cj) of the corresponding matrix C(t) (replicates generated in step 1) with the quantity stored in the text file;
- 11.
- Create a spreadsheet for the functional unit vector. The first row after the headers should contain a code that identifies it as a functional unit vector. Subsequent rows should contain the unique ID of each process making up the functional unit with time series of the quantities needed for one functional unit;
- 12.
- Save the spreadsheet as text file (see step 2);
- 13.
- Read the text file into the numerical calculation software;
- 14.
- Match each row’s unique ID with the meta-data in matrix A_meta. It gives the row number (ri) in vector f of the process whose quantity should be modified. For each time step t of the time series, replace the value at the coordinate (ri) of the corresponding vector f(t) (replicates generated in step 1) with the quantity stored in the text file;
- 15.
- Compute Equation (4) for each time step of the time series, save and export the results.
2.4.3. Hybrid MIPS
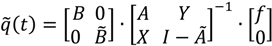
3. Results and Discussion
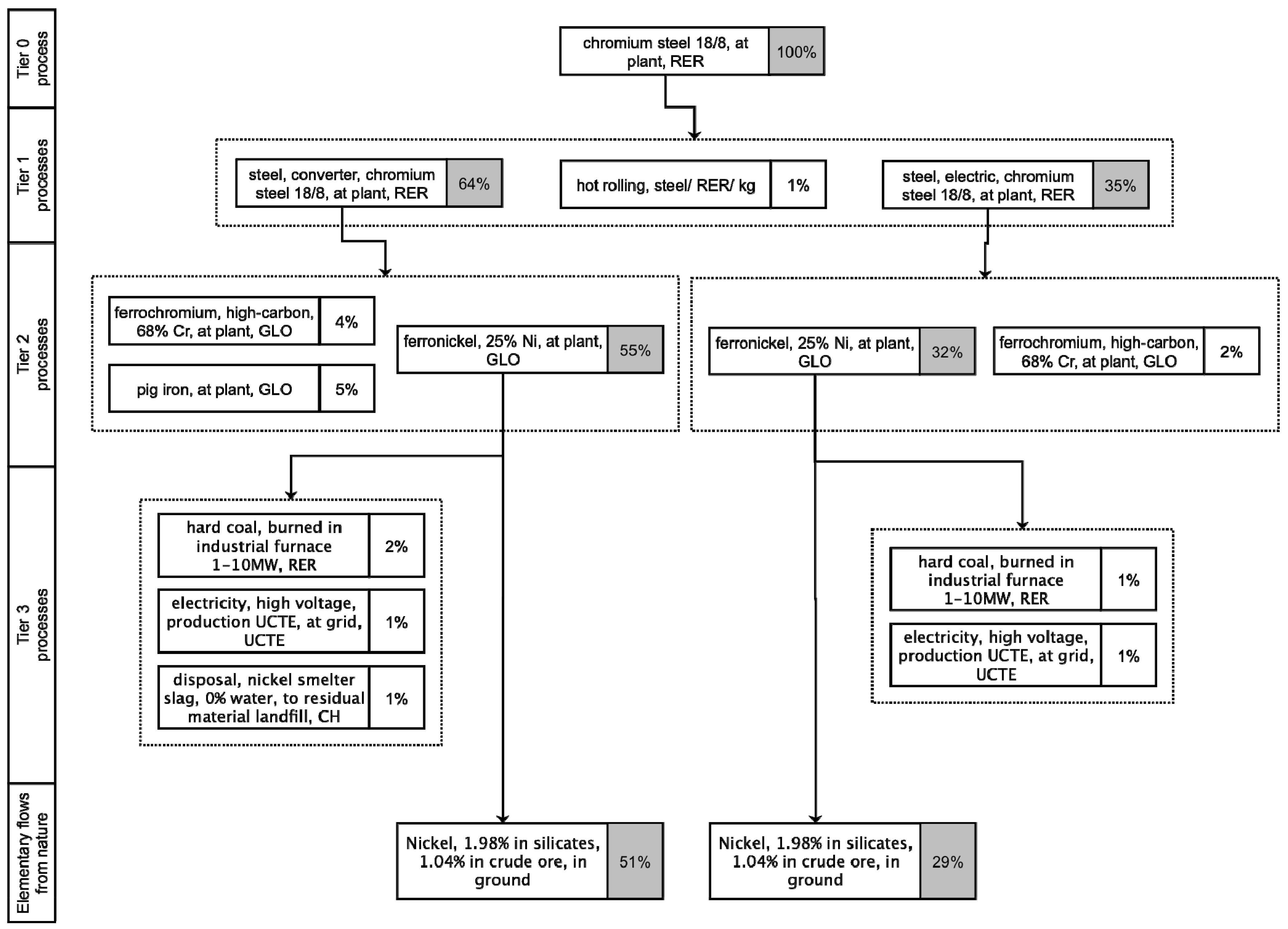
3.1. Application of Structural Path Analysis
3.2. Application of Midpoint MI Abiotic Characterization Method

3.3. Application of Dynamic MIPS

3.4. Application of Tiered Hybrid MIPS-IOA

 is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension
is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension  is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD.
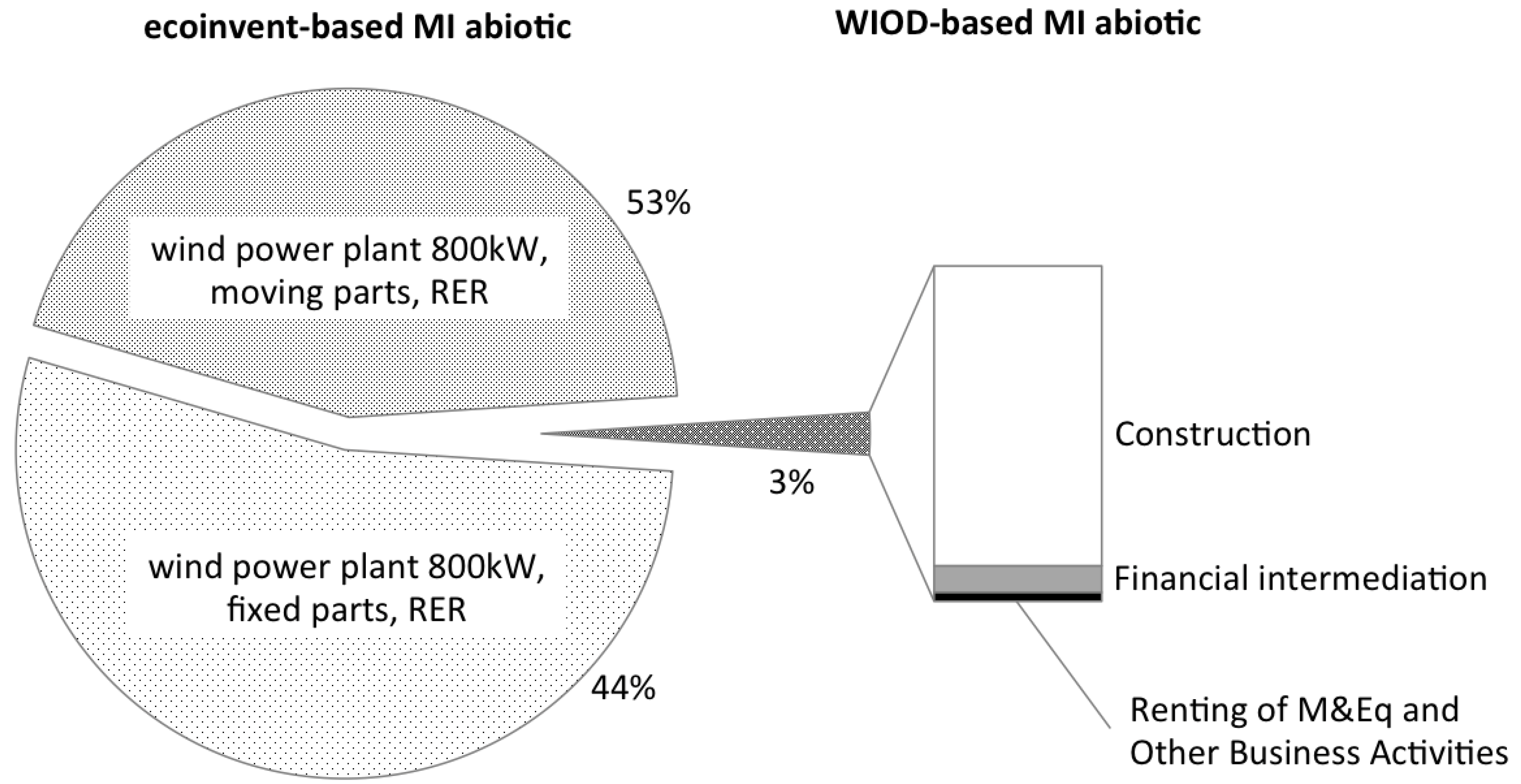
is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD. contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.
contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.| Components of installed capital costs | NREL cost modeling [$/kW] | included in ecoinvent model | included in IOA model + WIOD industry |
|---|---|---|---|
| Direct capital cost | |||
| Turbine | 1212 | yes | no |
| Foundations | 57 | yes | no |
| Electrical interface and connections | 154 | yes | no |
| Indirect capital costs | |||
| Turbine transportation | 40 | yes | no |
| Roads and civil work | 85 | no | yes—Construction |
| Turbine assembly and installation | 59 | yes | no |
| Engineering and permits | 24 | no | yes—Renting of M&Eq and Other Business Activities |
| Soft costs | |||
| Contingencies | 100 | no | no |
| Market price adjustment | 362 | no | no |
| Financing cost | 63 | no | yes—Financial Intermediation |
3.5. Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Schmidt-Bleek, F. Wieviel Umwelt braucht der Mensch? MIPS—Das Maß für ökologisches Wirtschaften, 1st ed.; Birkhäuser Verlag: Basel, Switzerland, 1993. [Google Scholar]
- Schmidt-Bleek, F. Das MIPS-Konzept, 1st ed.; Droemer-Knaur-Verlag: Munich, Germany, 1998. [Google Scholar]
- Vigon, B.W.; Tolle, D.A.; Cornaby, B.W.; Latham, H.C.; Harrison, C.L.; Boguski, T.L. Life Cycle Assessment: Inventory Guidelines and Principles; EPA/600/R-92/245; U.S. Environmental Protection Agency: Washington, DC, USA, 1993. [Google Scholar]
- Guinée, J.B.; Gorrée, M.; Heijungs, R.; Huppes, G.; Kleijn, R.; de Koning, A.; van Oers, L.; Wegener Sleeswijk, A.; Suh, S.; Udo de Haes, H.A.; et al. I: LCA in perspective. IIa: Guide. IIb: Operational annex. III: Scientific background. In Handbook on Life Cycle Assessment. Operational Guide to the ISO Standards; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2002. [Google Scholar]
- Bringezu, S.; Schütz, H.; Moll, S. Rationale for and interpretation of economy-wide materials flow analysis and derived indicators. J. Ind. Ecol. 2003, 7, 43–64. [Google Scholar] [CrossRef]
- MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/en/projects/topics-online/mips/ (accessed on 23 July 2013).
- Frischknecht, R.; Jungbluth, N.; Althaus, H.J.; Doka, G.; Dones, R.; Heck, T.; Hellweg, S.; Hischier, R.; Nemecek, T.; Rebitzer, G.; et al. Overview and Methodology—Data v2.0 (2007); ecoinvent Report No. 1; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- Ritthoff, M.; Rohn, H.; Liedtke, C. Calculating MIPS—Resource Productivity of Products and Services; Wuppertal Spezial 27e; Wuppertal Institute for Climate, Environment and Energy: Wuppertal, Germany, 2002. [Google Scholar]
- MIPS Calculation Sheet. MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/uploads/tx_wupperinst/MIPS_calculation-sheet.xls (accessed on 23 July 2013).
- Material Intensity Factors. MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/uploads/tx_wupperinst/MIT_2011.pdf (accessed on 23 July 2013).
- GaBi Software Homepage. Available online: http://www.gabi-software.com/international/index/ (accessed on 23 July 2013).
- Heijungs, R. A generic method for the identification of options for cleaner products. Ecol. Econ. 1994, 10, 69–81. [Google Scholar] [CrossRef]
- Suh, S.; Huppes, G. Methods for life cycle inventory of a product. J. Clean. Prod. 2005, 13, 687–697. [Google Scholar] [CrossRef]
- Suh, S.; Heijungs, R. Power series expansion and structural analysis for life cycle assessment. Int. J. Life Cycle Assess. 2007, 12, 381–390. [Google Scholar]
- Bourgault, G.; Lesage, P.; Samson, R. Systematic disaggregation: A hybrid LCI computation algorithm enhancing interpretation phase in LCA. Int. J. Life Cycle Assess. 2012, 17, 774–786. [Google Scholar] [CrossRef]
- Weisz, H.; Krausmann, F.; Eisenmenger, N.; Schütz, H.; Haas, W.; Schaffartzik, A. Economy—Wide Material Flow Accounting—“A Compilation Guide”; Eurostat: Luxembourg, 2007. [Google Scholar]
- WRI Materials Flows Database. Available online: http://www.wri.org/publication/material-flow-accounts#database (accessed on 23 July 2013).
- Wernick, I.K.; Irwin, F.H. Material Flows Accounts—A Tool for Making Environmental Policy; WRI Report; World Resource Institute: Washington, DC, USA, 2005. [Google Scholar]
- Bundesanstalt für Geowissenschaften und Rohstoffe (BGR). Nickel—Geologisches Jahrbuch; Spezial Heft No. 7; BGR: Hannover, Germany, 1999. [Google Scholar]
- Adriaanse, A.; Bringezu, S.; Hammond, A.; Moriguchi, Y.; Rodenburg, E.; Rogich, D.; Schütz, H. Resource Flows : The Material Basis of Industrial Economies; World Resource Institute: Washington, DC, USA, 1997. [Google Scholar]
- Nemecek, T.; Kägi, T. Life Cycle Inventories of Agricultural Production Systems—Data v2.0 (2007); Ecoinvent Report No. 15; Swiss Centre for Life Cycle Inventories: Zürich, Switzerland, 2007. [Google Scholar]
- Werner, F.; Althaus, H.J.; Künniger, T.; Richter, K.; Jungbluth, N. Life Cycle Inventories of Wood as Fuels and Construction Material—Data v2.0 (2007); Ecoinvent Report No. 9; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- Goedkoop, M.; Heijungs, R.; Huijbregts, M.; de Schryver, A.; Struijs, J.; van Zelm, R. ReCiPe 2008—A Life Cycle Impact Assessment Method Which Comprises Harmonised Category Indicators at the Midpoint and the Endpoint Level—Report I: Characterisation; Ministry of Housing, Spatial Planning and Environment (VROM): The Hague, The Netherlands, 2009. [Google Scholar]
- OpenLCA Home Page. Available online: http://www.openlca.org (accessed on 23 July 2013).
- Scilab Home Page. Available online: http://www.scilab.org (accessed on 23 July 2013).
- Lenzen, M. A guide for compiling inventories in hybrid life-cycle assessments: Some Australian results. J. Clean. Prod. 2002, 10, 545–572. [Google Scholar] [CrossRef]
- Peters, G.P.; Hertwich, E.G. Structural analysis of international trade: Environmental impacts of Norway. Econ. Sys. Res. 2006, 18, 155–181. [Google Scholar] [CrossRef]
- Defourny, J.; Thorbecke, E. Structural path analysis and multiplier decomposition within a social accounting matrix framework. Econ. J. 1984, 94, 111–136. [Google Scholar] [CrossRef]
- Pehnt, M. Dynamic life cycle assessment (LCA) of renewable energy technologies. Renew. Energy 2006, 31, 55–71. [Google Scholar] [CrossRef]
- Zhai, P.; Williams, E.D. Dynamic hybrid life cycle assessment of energy and carbon of multicrystalline silicon photovoltaic systems. Environ. Sci. Technol. 2010, 44, 7950–7955. [Google Scholar] [CrossRef]
- Collinge, W.O.; Landis, A.E.; Jones, A.K.; Schaefer, L.A.; Bilec, M.M. Dynamic life cycle assessment: Framework and application to an institutional building. Int. J. Life Cycle Assess. 2013, 18, 538–552. [Google Scholar] [CrossRef]
- Suh, S. Input-output and hybrid life cycle assessment. Int. J. Life Cycle Assess. 2003, 8, 257. [Google Scholar] [CrossRef]
- Suh, S.; Lenzen, M.; Treloar, G.J.; Hondo, H.; Horvath, A.; Huppes, G.; Jolliet, O.; Klann, U.; Krewitt, W.; Moriguchi, Y.; et al. System boundary selection in life-cycle inventories using hybrid approaches. Environ. Sci. Technol. 2004, 38, 657–664. [Google Scholar] [CrossRef]
- Suh, S.; Nakamura, S. Five years in the area of input-output and hybrid LCA. Int. J. Life Cycle Assess. 2007, 12, 351–352. [Google Scholar]
- Finnveden, G.; Hauschild, M.Z.; Ekvall, T.; Guinée, J.; Heijungs, R.; Hellweg, S.; Koehler, A.; Pennington, D.; Suh, S. Recent developments in life cycle assessment. J. Environ. Manag. 2009, 91, 1–21. [Google Scholar] [CrossRef]
- Rowley, H.; Lundie, S.; Peters, G. A hybrid life cycle assessment model for comparison with conventional methodologies in Australia. Int. J. Life Cycle Assess. 2009, 14, 508–516. [Google Scholar] [CrossRef]
- Suh, S. Functions, commodities and environmental impacts in an ecological-economic model. Ecol. Econ. 2004, 48, 451–467. [Google Scholar] [CrossRef]
- Classen, M.; Althaus, H.J.; Blaser, S.; Scharnhorst, W.; Tuchschmid, M.; Jungbluth, N.; Emmenegger, M.F. Life Cycle Inventories of Metals—Data v2.0 (2007); Ecoinvent Report No. 10; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- World Wide Fund for Nature (WWF). Modell Deutschland—Klimaschutz bis 2050: Vom Ziel her denken; Final Report; WWF Germany: Berlin, Germany, 2009. [Google Scholar]
- The WIOD-Database. World input-output tables and international supply and use tables. Available online: http://www.wiod.org/protected3/data/wiot_analytic/wiot09_row_apr12.xlsx (accessed on 23 July 2013).
- Timmer, M.; Erumban, A.A.; Gouma, R.; Los, B.; Temurshoev, U.; de Vries, G.J.; Arto, I.; Andreoni, V.; Genty, A.; Neuwahl, F.; et al. The World Input-Output Database (WIOD): Contents, Sources and Methods; University of Groningen: Groningen, The Netherlands, 2012. [Google Scholar]
- Materials use-All countries; Environmental Accounts; The WIOD-Database. Available online: http://www.wiod.org/protected3/data/materials/mat_may12.zip (accessed on 23 July 2013).
- Burger, P.; Bauer, C. Teil XIII—Windkraft—Data v2.0 (2007); Ecoinvent Report No. 6-XIII; Swiss Centre for Life Cycle Inventories: Villigen, Switzerland, 2007. [Google Scholar]
- Tegen, S.; Hand, M.; Maples, B.; Lantz, E.; Schwabe, P.; Smith, A. 2010 Cost of Wind Energy Review; Technical Report NREL/TP-5000-52920; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Wiedemann, T.O.; Suh, S.; Kuishuang, F.; Lenzen, M.; Acquaye, A.; Scott, K.; Barrett, J.R. Application of hybrid life cycle approaches to emerging energy technologies—The case of wind power in the UK. Environ. Sci. Technol. 2011, 45, 5900–5907. [Google Scholar] [CrossRef]
- Williams, E.D.; Weber, C.L.; Hawkins, T.R. Hybrid framework for managing uncertainty in life cycle inventories. J. Ind. Ecol. 2009, 13, 928–944. [Google Scholar] [CrossRef]
- Mudd, G.M. The Sustainability of Mining in Australia: Key Production Trends and Their Environmental Implications for the Future; Research Report No. RR5; Department of Civil Engineering, Monash University and Mineral Policy Institute: Melbourne, Australia, 2009. [Google Scholar]
- Exiobase Homepage. Available online: http://www.exiobase.eu (accessed on 23 July 2013).
- Access workbooks by country; ESA 95 Supply Use and Input-Output tables; Eurostat. Available online: http://epp.eurostat.ec.europa.eu/portal/page/portal/esa95_supply_use_input_tables/data/workbooks (accessed on 23 July 2013).
- Material flow accounts. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=env_ac_mfa&lang=en (accessed on 23 July 2013).
- Watson, D.; Acosta Fernandez, J.; Wittmer, D.; Gravgard Pedersen, O. Environmental Pressures from European Consumption and Production : A Study in Integrated Environmental and Economic Analysis; EEA Technical Report No. 2/2013; European Environment Agency: Copenhagen, Denmark, 2013. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Saurat, M.; Ritthoff, M. Calculating MIPS 2.0. Resources 2013, 2, 581-607. https://doi.org/10.3390/resources2040581
Saurat M, Ritthoff M. Calculating MIPS 2.0. Resources. 2013; 2(4):581-607. https://doi.org/10.3390/resources2040581
Chicago/Turabian StyleSaurat, Mathieu, and Michael Ritthoff. 2013. "Calculating MIPS 2.0" Resources 2, no. 4: 581-607. https://doi.org/10.3390/resources2040581





