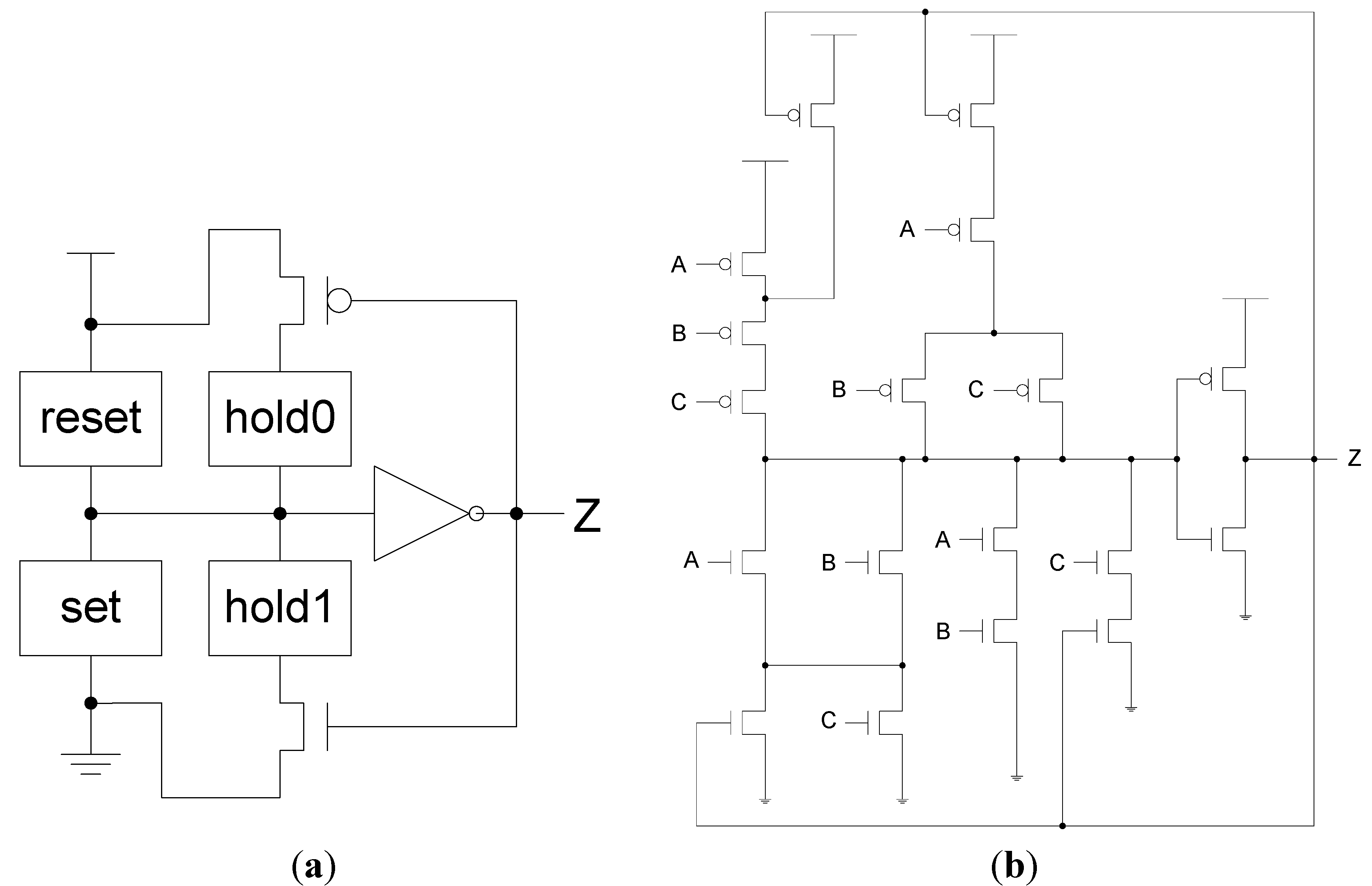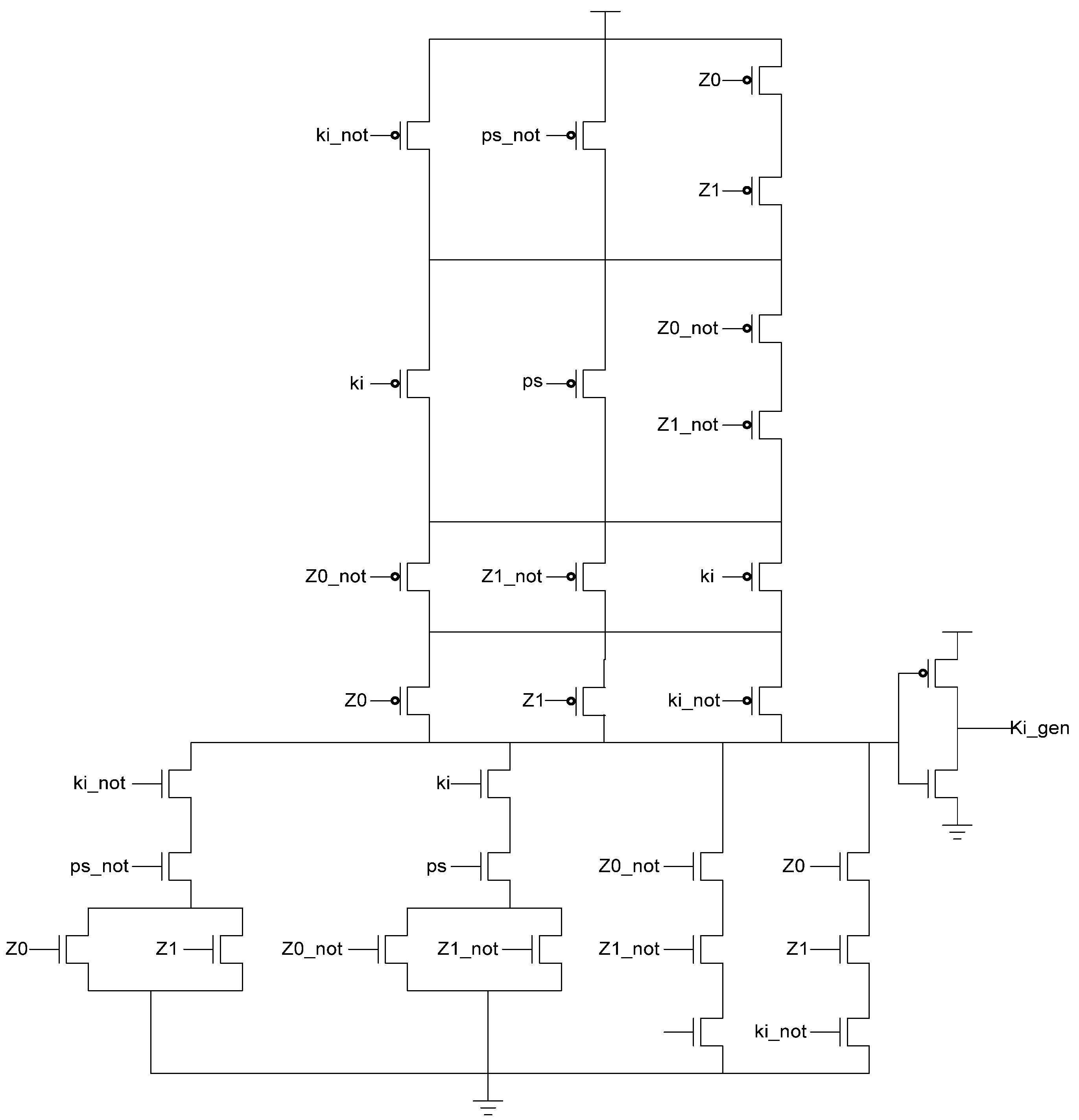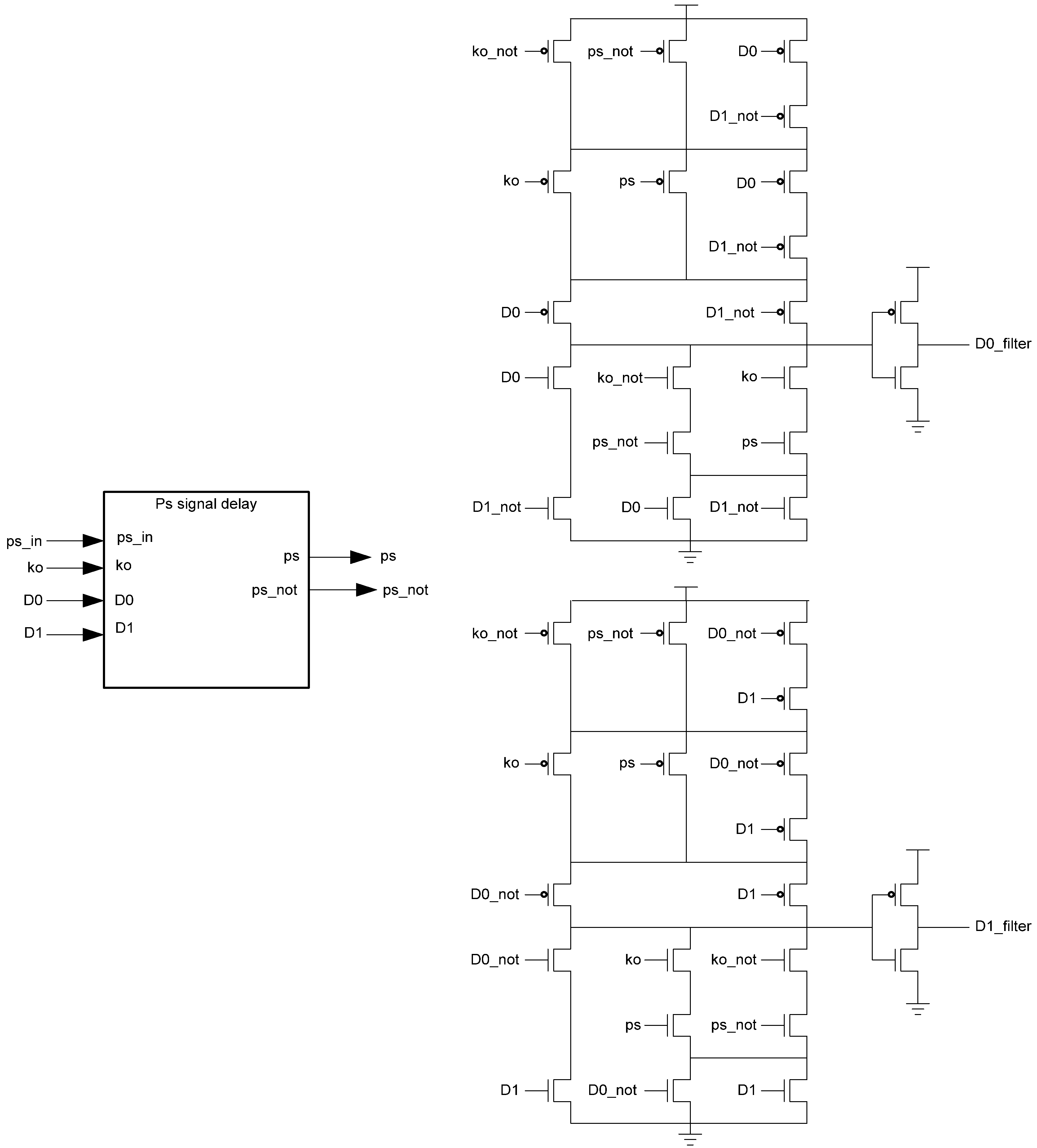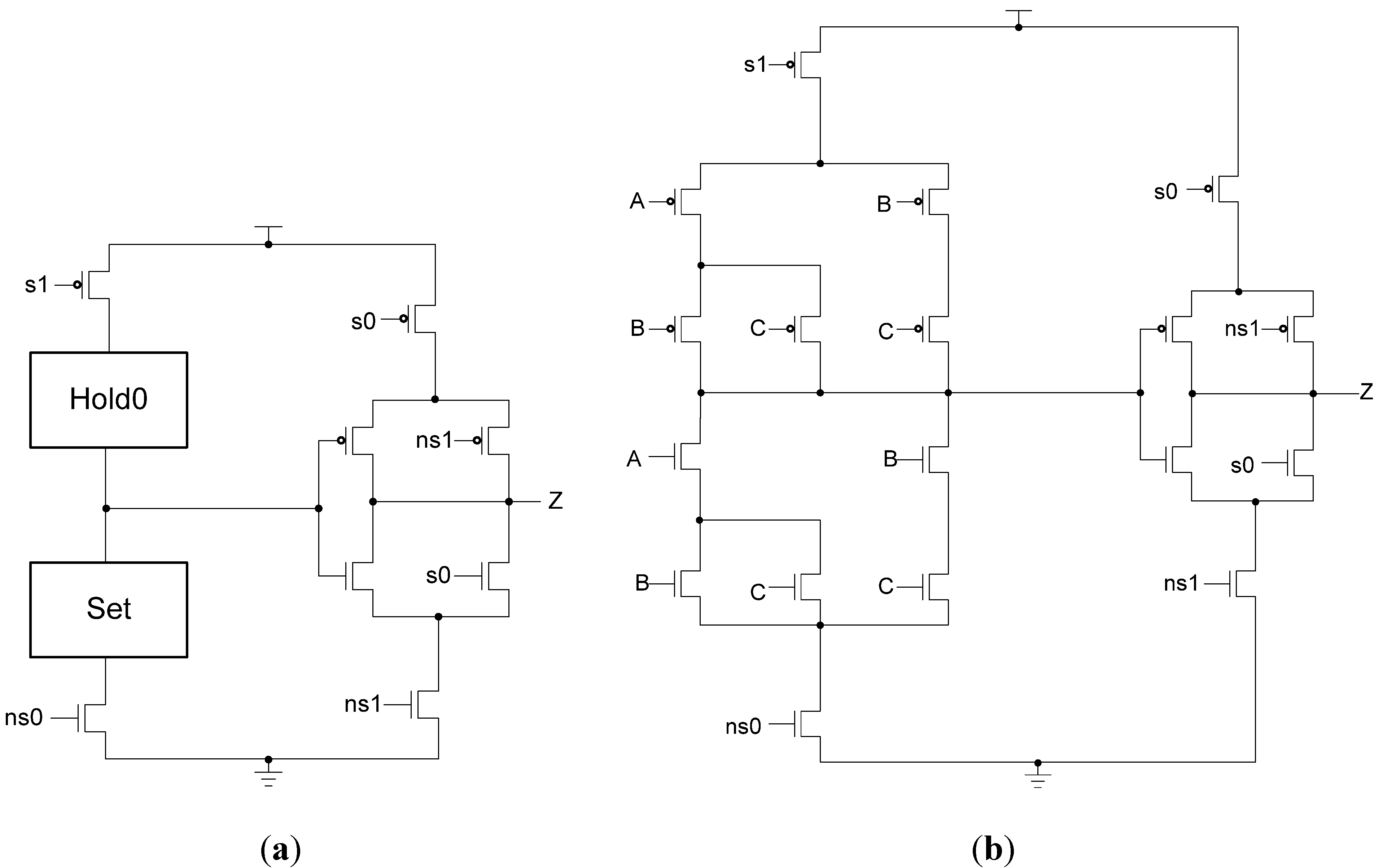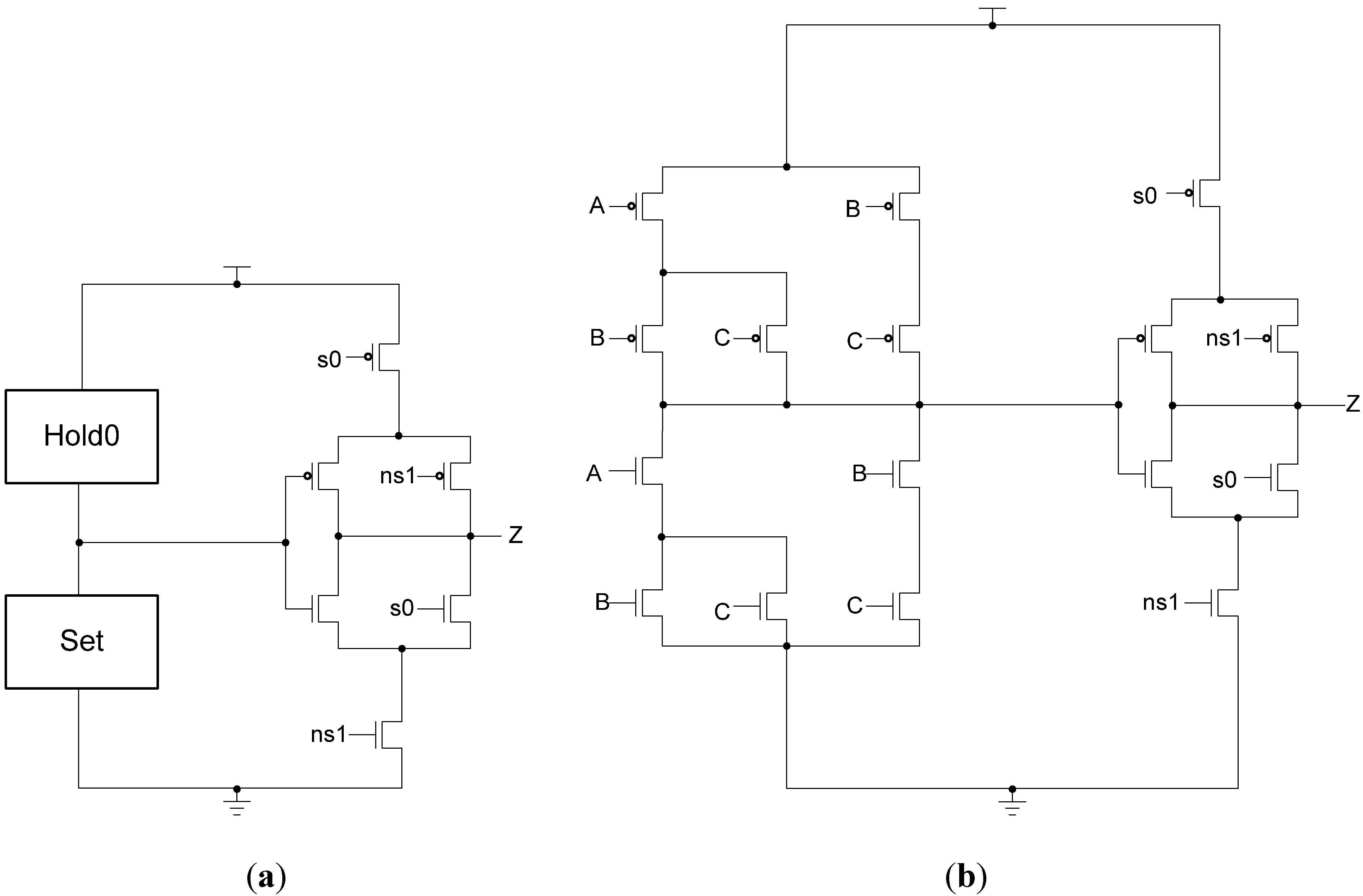2.1. NULL Convention Logic (NCL)
NCL [
38] is a commonly used delay-insensitive (DI) asynchronous logic design style, which utilizes a multi-rail one-hot scheme, such as dual-rail, to encode data. A dual-rail signal,
D, consists of two wires or rails,
D0 and
D1, which may assume any value from the set {DATA0, DATA1, NULL}, as depicted in
Table 1. The DATA0 state corresponds to a Boolean logic 0, the DATA1 state corresponds to a Boolean logic 1, and the NULL state corresponds to the empty set (meaning that the value of
D is not yet available). The two rails are mutually exclusive, such that both rails can never be asserted simultaneously; this state is defined as an illegal state.
Table 1.
Dual-rail signal.
Table 1.
Dual-rail signal.
| State | D0 | D1 |
|---|
| NULL | 0 | 0 |
| DATA0 | 1 | 0 |
| DATA1 | 0 | 1 |
| Illegal | 1 | 1 |
NCL circuits are comprised of 27 fundamental gates, which constitute the set of all functions consisting of four or fewer variables [
43]. Since each rail of an NCL signal is considered a separate variable, a four variable function is not the same as a function of four literals, which would consist of eight variables for dual-rail logic (e.g., a literal includes both a variable and its complement,
F and
F’, whereas NCL rails are never complemented, such that a dual-rail NCL signal,
F, consists of two variables,
F1 and
F0, where
F0 is equivalent to
F’). The primary type of threshold gate, shown in
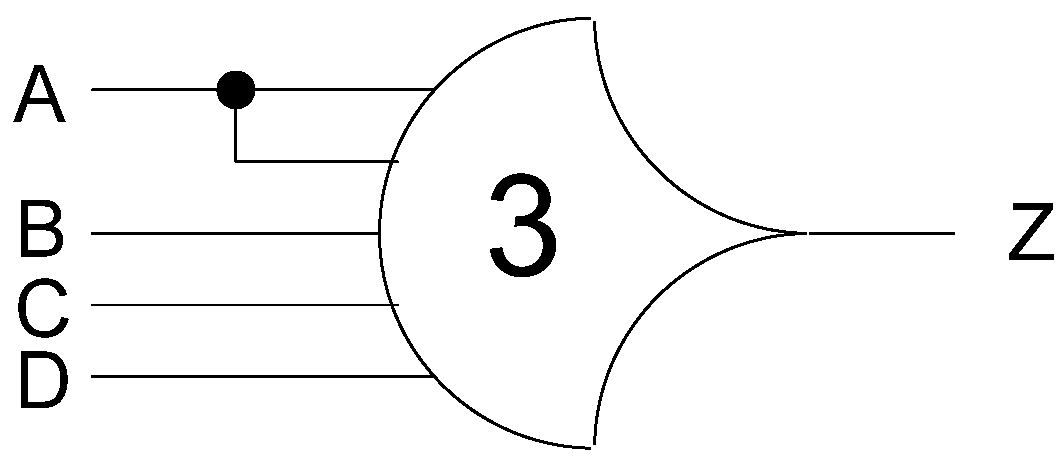
Figure 1, is the THmn gate, where 1 ≤
m ≤
n. THmn gates have
n inputs. At least
m of the
n inputs must be asserted before the output will become asserted. In a THmn gate, each of the
n inputs is connected to the rounded portion of the gate; the output emanates from the pointed end of the gate; and the gate’s threshold value,
m, is written inside of the gate.
Figure 1.
THmn threshold gate.
Figure 1.
THmn threshold gate.
Another type of threshold gate is referred to as a weighted threshold gate, denoted as THmn
w,
w1,
w2, …,
wR. Weighted threshold gates have an integer value,
m ≥
wR > 1, applied to input
R. Here, 1 ≤
R <
n; where
n is the number of inputs;
m is the gate’s threshold; and
w1,
w2, …,
wR, each >1, are the integer weights of input1, input2, …, input
R, respectively. For example, consider the TH34W2 gate, whose
n = 4 inputs are labeled
A,
B,
C, and
D, shown in
Figure 2. The weight of input
A,
W(
A), is therefore 2. Since the gate’s threshold,
m, is 3, this implies that in order for the output to be asserted, either inputs
B,
C, and
D must all be asserted, or input
A must be asserted along with any other input,
B,
C, or
D.
Figure 2.
TH34w2 threshold gate: Z = AB + AC + AD + BCD.
Figure 2.
TH34w2 threshold gate: Z = AB + AC + AD + BCD.
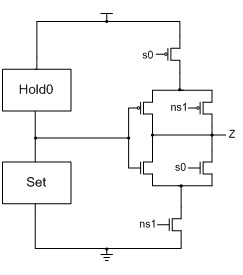
NCL threshold gates are designed with hysteresis state-holding capability, such that after the output is asserted, all inputs must be deasserted before the output will be deasserted. Hysteresis ensures a complete transition of inputs back to NULL before asserting the output associated with the next wavefront of input data. Therefore, a THnn gate is equivalent to an n-input C-element (
i.e., when all inputs are asserted the output is asserted; the output then remains asserted until all inputs are deasserted, at which time the output becomes deasserted) [
44]; and a TH1n gate is equivalent to an n-input OR gate. NCL threshold gates may also include a reset input to initialize the output. Circuit diagrams designate resettable gates by either a
d or an
n appearing inside the gate, along with the gate’s threshold.
d denotes the gate as being reset to logic 1;
n, to logic 0. These resettable gates are used in the design of DI registers.
To achieve hysteresis state-holding capability, NCL gates have both
set and
hold equations, where the
set equation determines when the gate will become asserted and the
hold equation determines when the gate will remain asserted once it has been asserted. The
set equation determines the gate’s functionality as one of the 27 NCL gates [
43], whereas the
hold1 equation is simply all inputs ORed together. The general equation for an NCL gate with output
Z is:
Z =
set + (
Z- ×
hold1), where
Z- is the previous output value and
Z is the new value.
To implement an NCL gate using CMOS technology, an equation for the complement of
Z is also required, which in general form is:
Z’ =
reset + (
Z-’ ×
hold0), where
reset is the complement of
hold1 (
i.e., the complement of each input, ANDed together) and
hold0 is the complement of
set, such that the gate output is deasserted when all inputs are deasserted, and then remains deasserted while the gate’s
set condition is false. The new output value,
Z, depends on the previous output value,
Z-, which requires internal gate feedback, as shown in
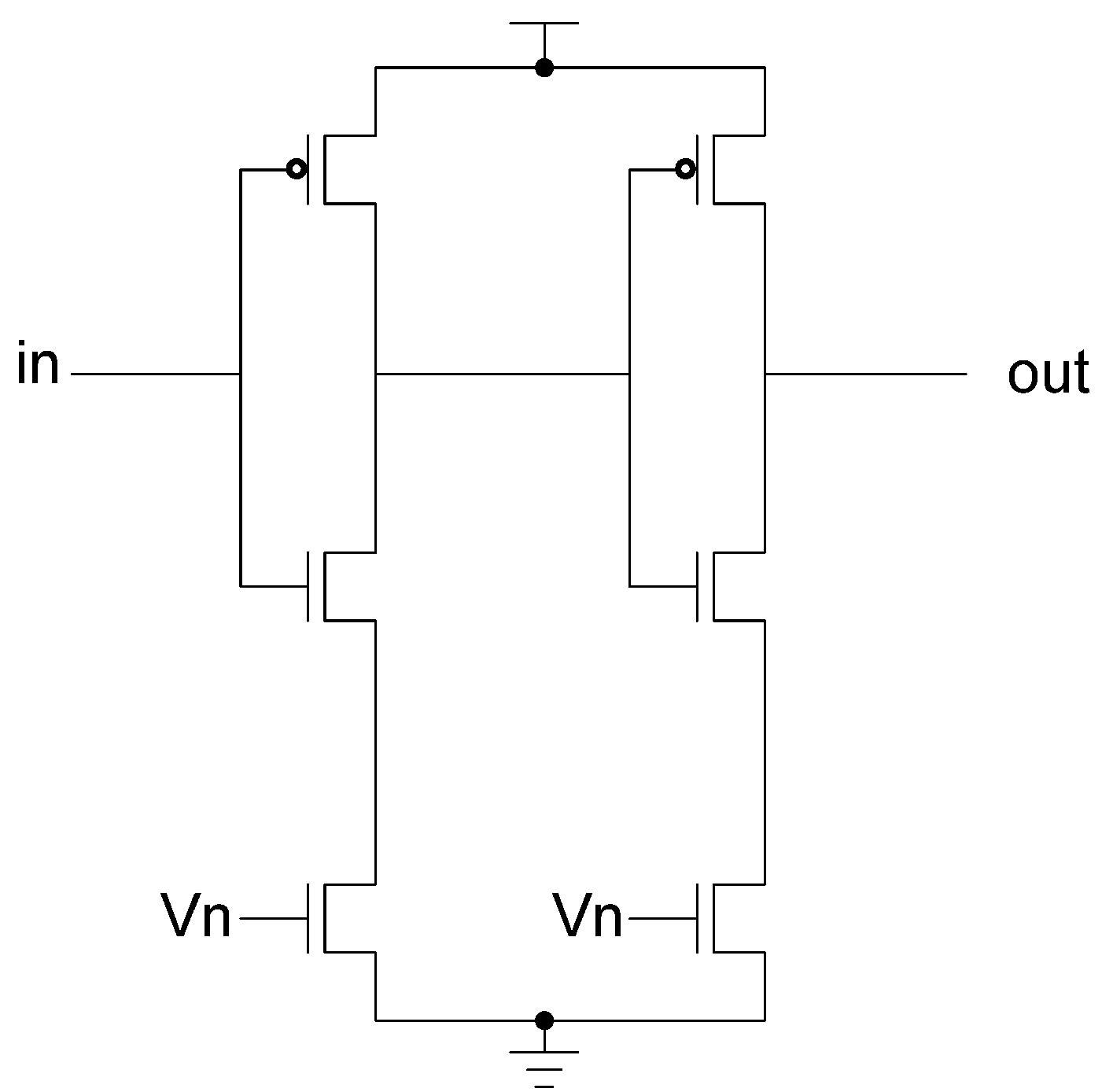
Figure 3, for a static implementation [
43].
Figure 3.
(a) Static NULL Convention Logic (NCL) gate structure; (b) Static NCL TH23 implementation.
Figure 3.
(a) Static NULL Convention Logic (NCL) gate structure; (b) Static NCL TH23 implementation.
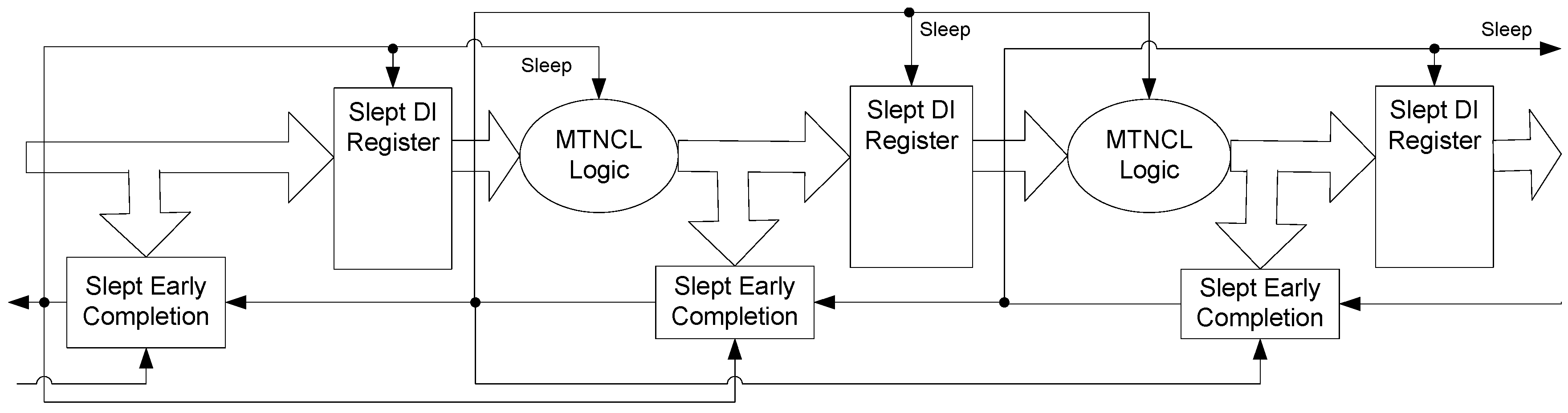
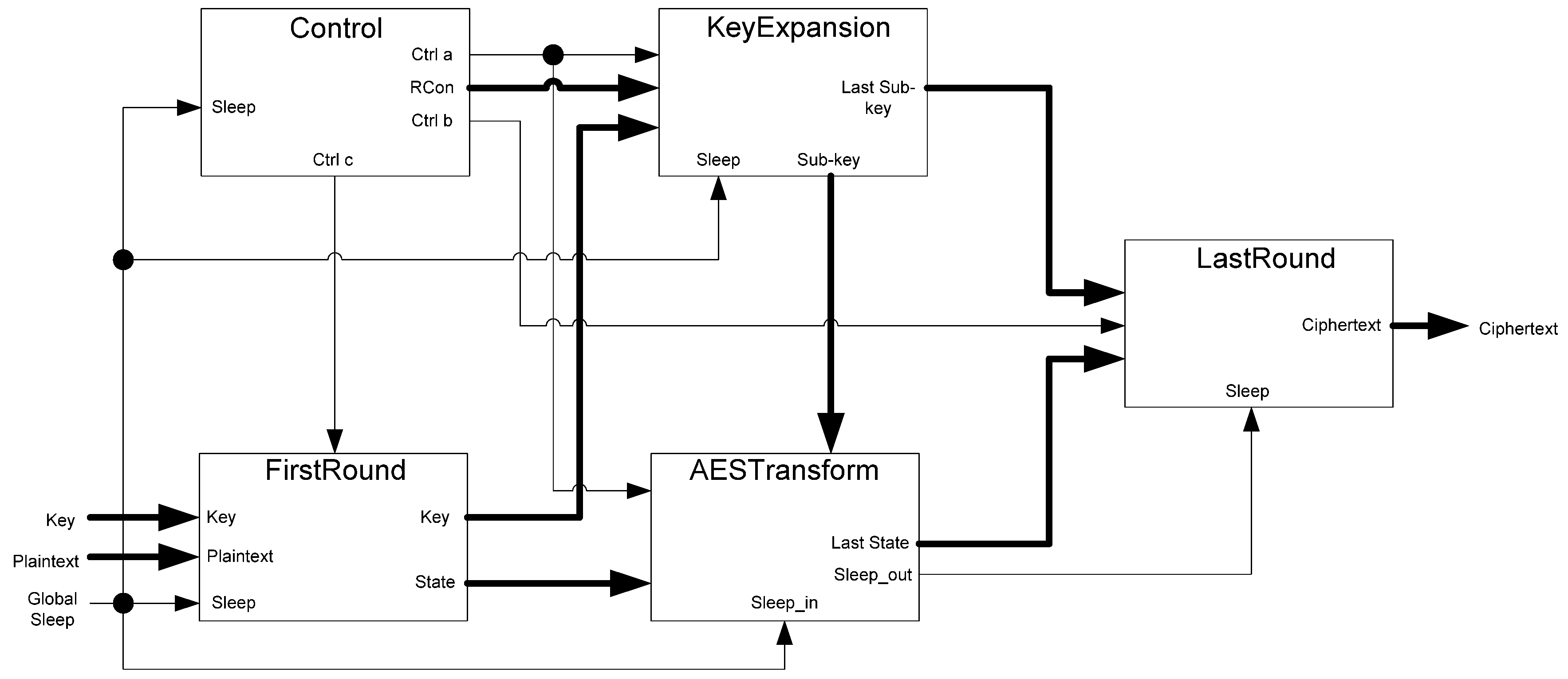
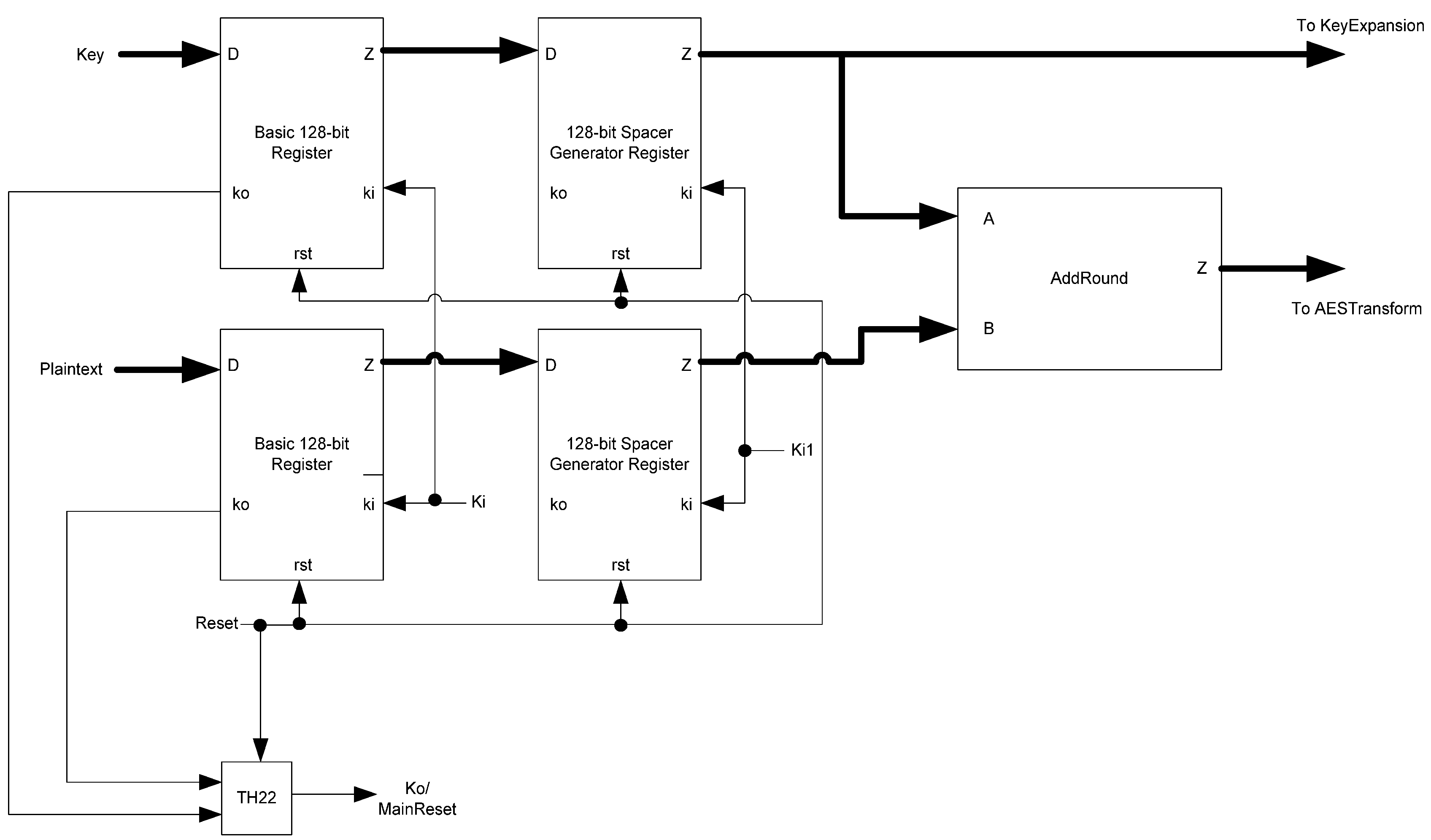
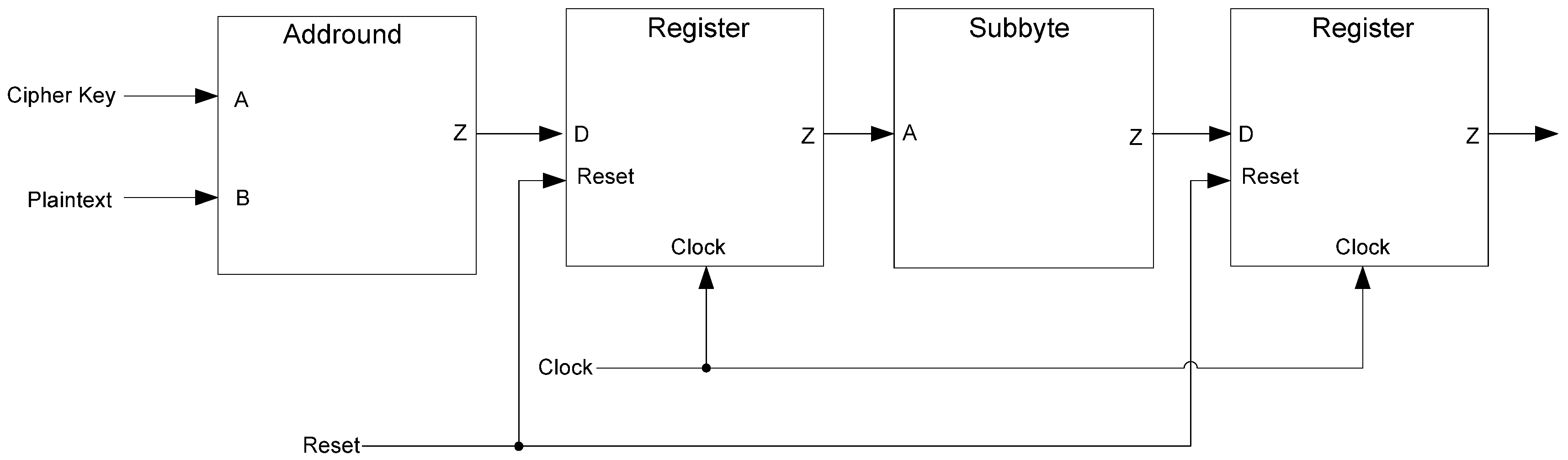
The framework for NCL systems consist of DI combinational logic sandwiched between DI registers, as shown in
Figure 4, which is very similar to synchronous systems. NCL systems contain at least two DI registers, one at both the input and at the output. Two adjacent register stages interact through their request and acknowledge signals,
Ki and
Ko, respectively, to prevent the current DATA wavefront from overwriting the previous DATA wavefront, by ensuring that the two DATA wavefronts are always separated by a NULL wavefront. The acknowledge signals are combined in the Completion Detection circuitry [
43] to produce the request signal(s) to the previous register stage. NCL registration is realized through cascaded arrangements of single-bit dual-rail registers, shown in
Figure 5, which pass a DATA value at the input only when
Ki is request for data (rfd) (
i.e., logic 1) and likewise pass NULL only when
Ki is request for null (rfn) (
i.e., logic 0). They also contain a NOR gate to generate
Ko, which is rfn when the register output is DATA and rfd when the register output is NULL.
Figure 4.
NCL system framework: input wavefronts are controlled by local handshaking signals and Completion Detection instead of by a global clock signal. Feedback requires at least three DI registers in the feedback loop to prevent deadlock.
Figure 4.
NCL system framework: input wavefronts are controlled by local handshaking signals and Completion Detection instead of by a global clock signal. Feedback requires at least three DI registers in the feedback loop to prevent deadlock.
Figure 5.
Single-bit dual-rail register.
Figure 5.
Single-bit dual-rail register.
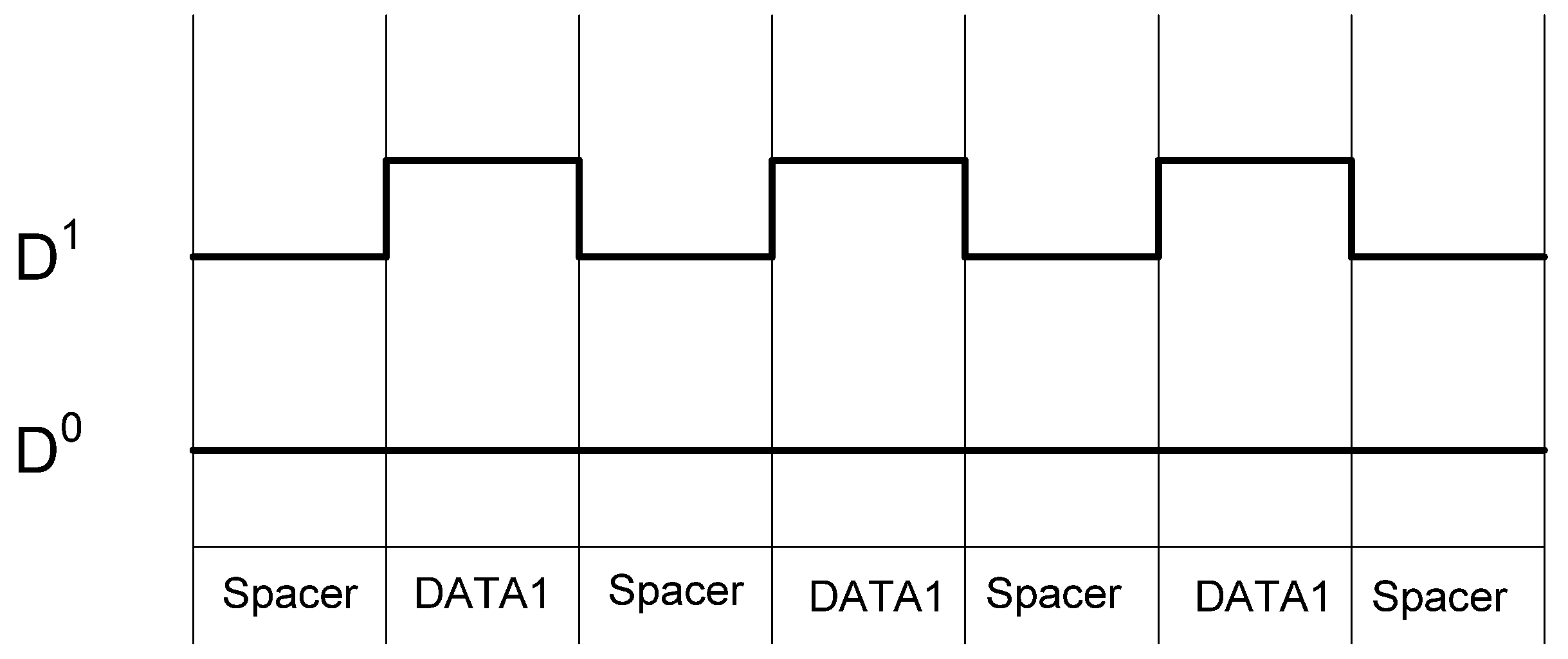
The NCL dual-rail encoding style decouples the relationship between the data being processed and the side-channel characteristics of the circuit, particularly power consumption, giving NCL circuits increased resistance to power related side-channel attacks over synchronous circuits. However, while the overall switching activity of a data bit may be balanced regardless of data, the individual encoding rails are not balanced, as illustrated in
Figure 6. Furthermore, if the two rails are driving different capacitance, which is always the case in a large circuit, then attackers may be able to distinguish between the rails, allowing attackers to determine a relationship between the processed data and the circuit’s side-channels.
Figure 6.
NCL switching activity for passing consecutive DATA1s.
Figure 6.
NCL switching activity for passing consecutive DATA1s.
2.3. Dual-Spacer Dual-Rail DelayInsensitive Logic (D3L)
D
3L is an extension of the NCL logic style that utilizes a dual-spacer protocol, as opposed to NCL’s single spacer protocol [
41]. The motivation for this is the elimination of imbalanced switching activity on the two encoding wires of a data bit. By balancing this switching activity, data is further decoupled from the power consumption of the circuit, providing increased robustness against power analysis attacks.
Table 2 shows the D
3L encoding scheme. Like NCL, the DATA and NULL states remain the same. However, the NULL state is now called the All-Zero Spacer (AZS); and the former illegal state, where both rails are asserted, is now the All-One Spacer (AOS). The AZS and AOS are alternated between spacer cycles, implementing a dual-spacer protocol. As a result, the switching activity over a complete set of data/spacer cycles is balanced on both rails, as shown in
Figure 9.
Table 2.
D3L encoding scheme.
Table 2.
D3L encoding scheme.
| State | D0 | D1 |
|---|
| All-Zero Spacer (AZS) | 0 | 0 |
| Data0 | 1 | 0 |
| Data1 | 0 | 1 |
| All-One Spacer (AOS) | 1 | 1 |
Figure 9.
D3L switching activity for passing consecutive DATA1s.
Figure 9.
D3L switching activity for passing consecutive DATA1s.
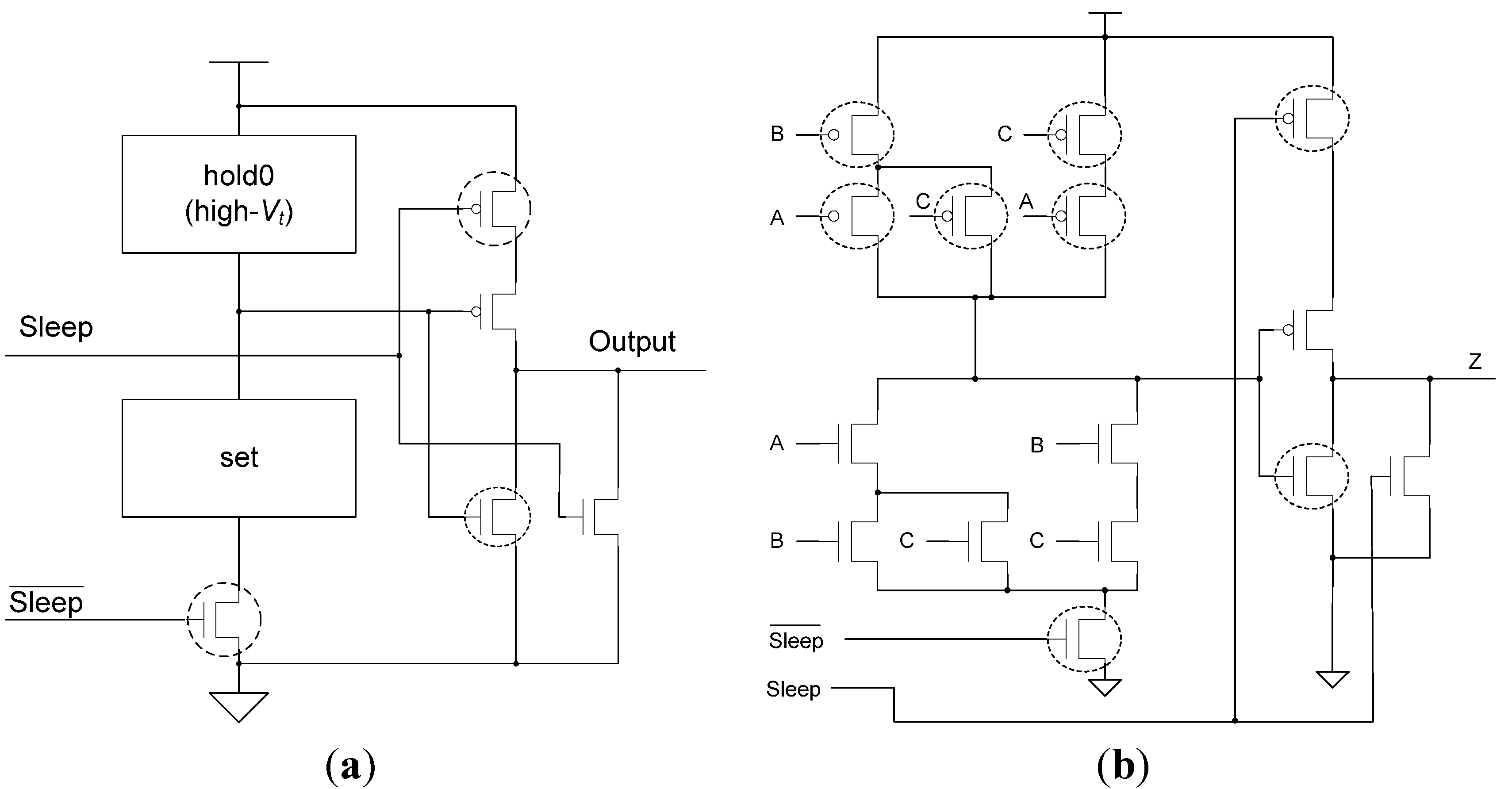
The D
3L threshold gates are modified versions of the NCL threshold gates. As such, the complete set of 27 NCL functions is implemented in D
3L. While NCL gates use hysteresis, D
3L gates are unable to do so to accommodate the dual-spacer protocol. As such, D
3L threshold gates are smaller than NCL threshold gates due to the omission of the hysteresis transistors. The removal of hysteresis, however, means that D
3L gates are unable to guarantee input completeness. Instead, the NCL_X technique [
45] is used to provide input-completeness. This technique adds additional logic to D
3L functions that check the inputs and outputs of each function to create a completion signal. Since the spacer cycles in D
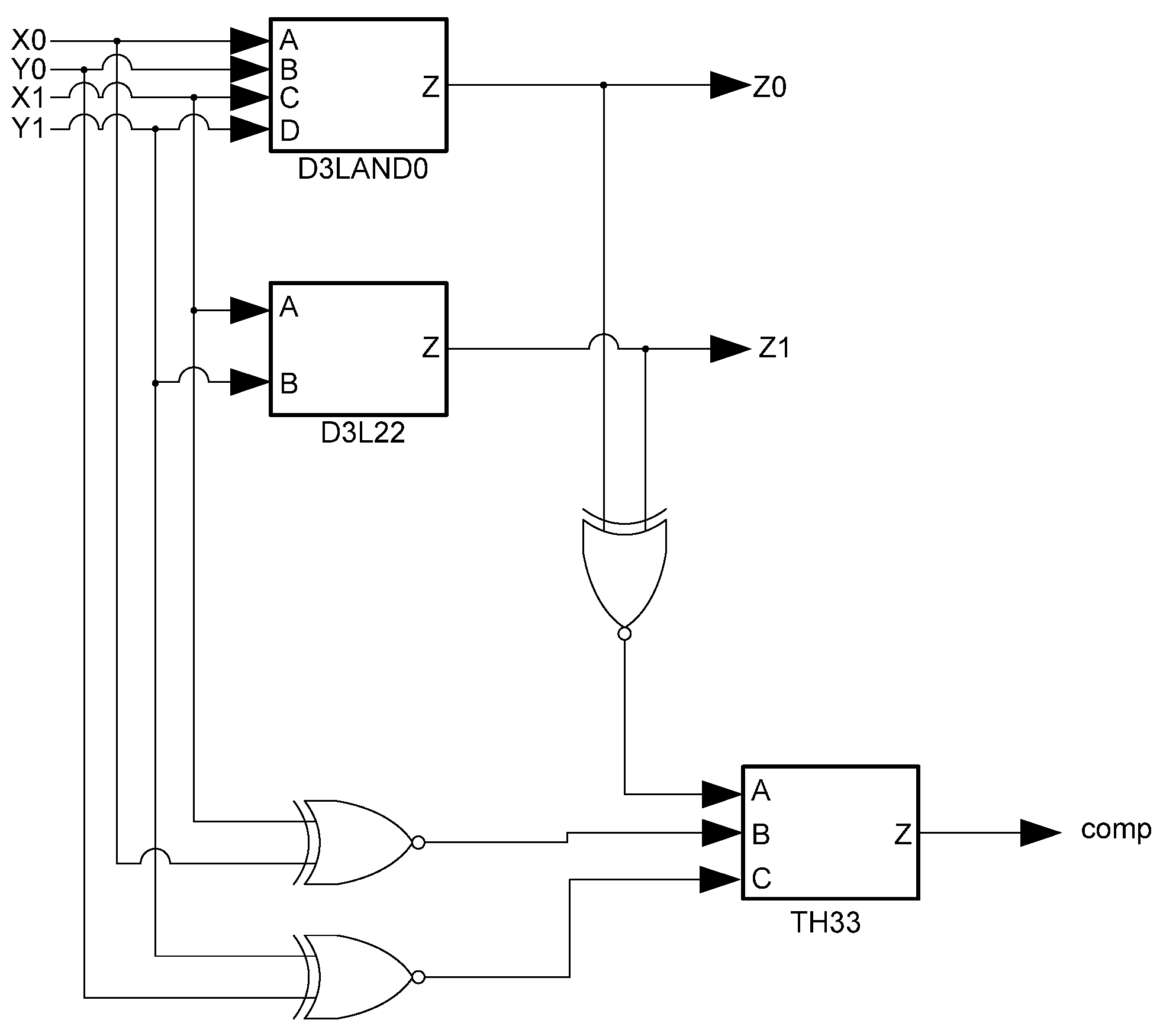
3L occur when data rails are the same, an XNOR gate can be used to detect them. The outputs from these XNOR gates are input to the completion component, along with the usual handshaking signals, to ensure that the logic is ready for the next wavefront. A downside to this technique, however, is the overhead incurred by adding large amounts of XNOR and threshold gates to the design to ensure input-completeness. An input-complete D
3L AND function is shown in
Figure 10.
Figure 10.
D3L input-complete AND function.
Figure 10.
D3L input-complete AND function.
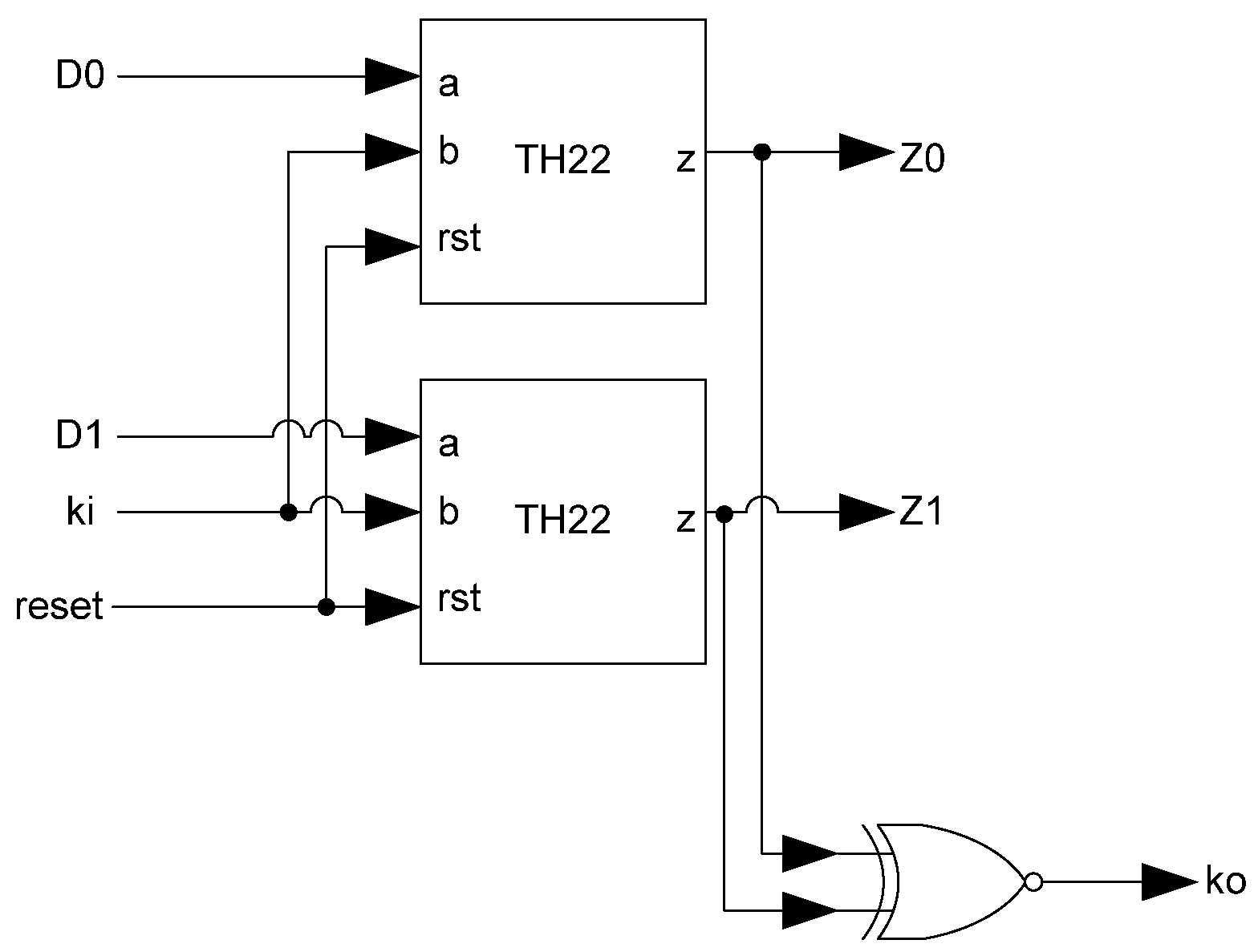
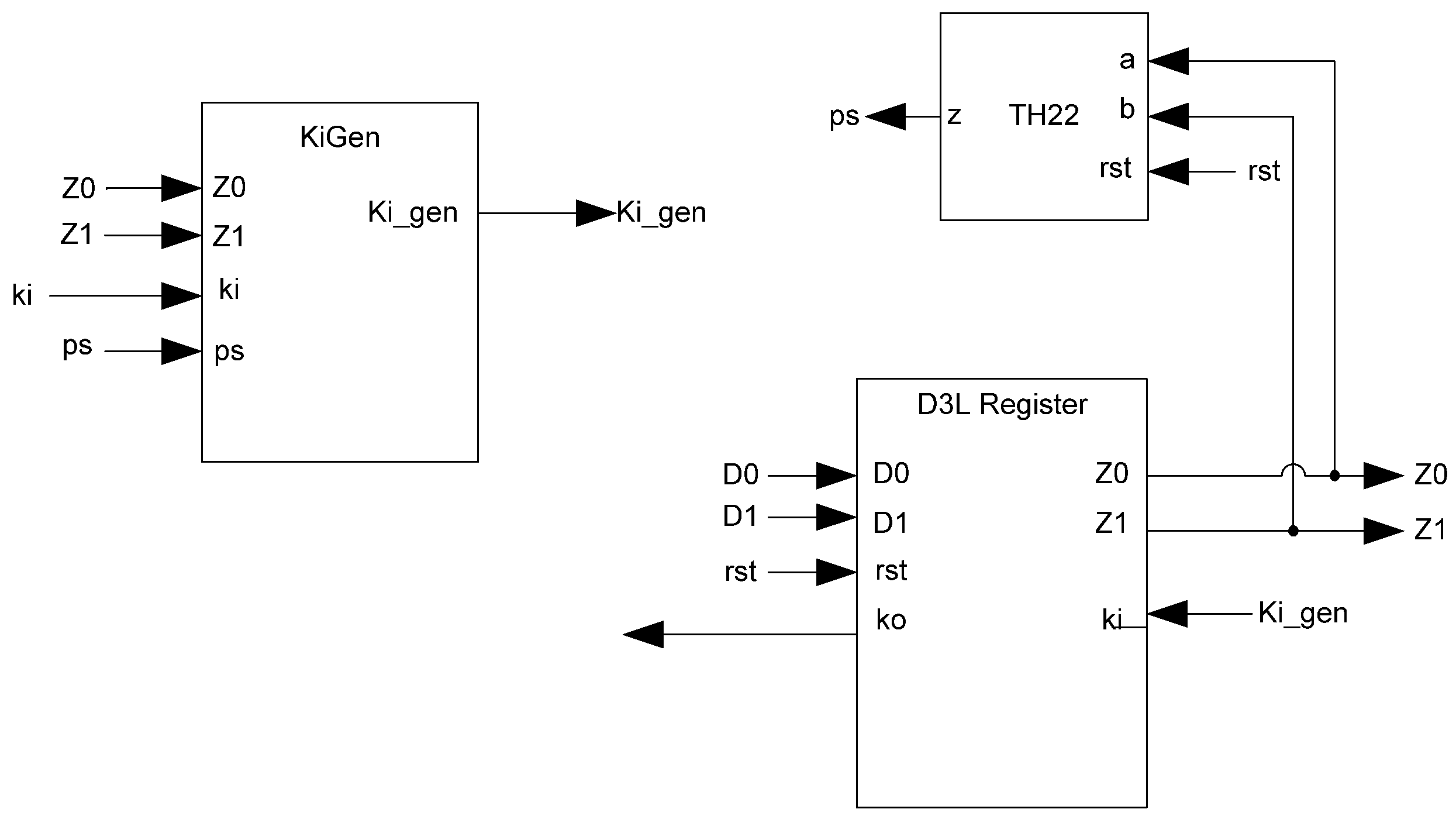
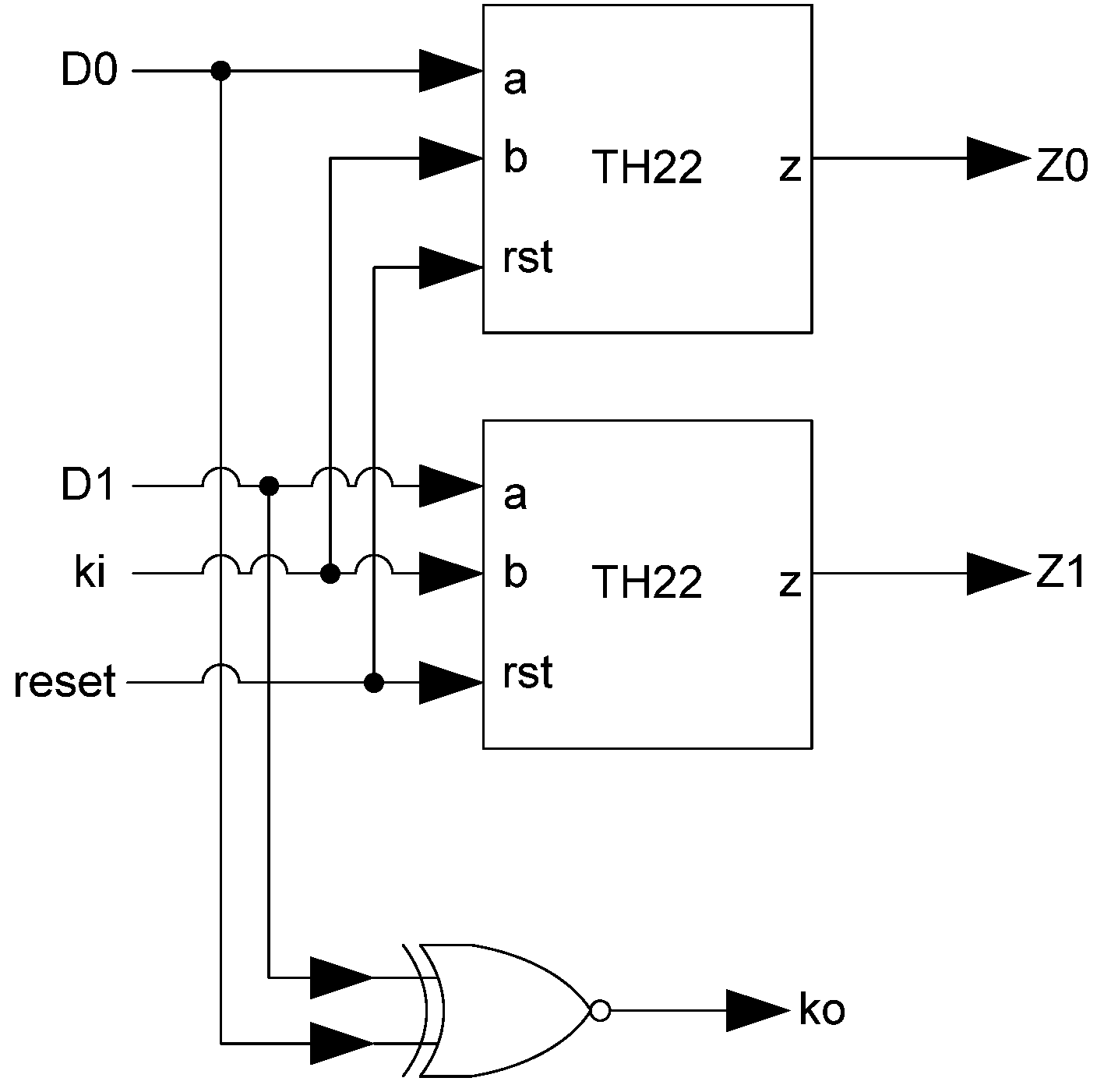
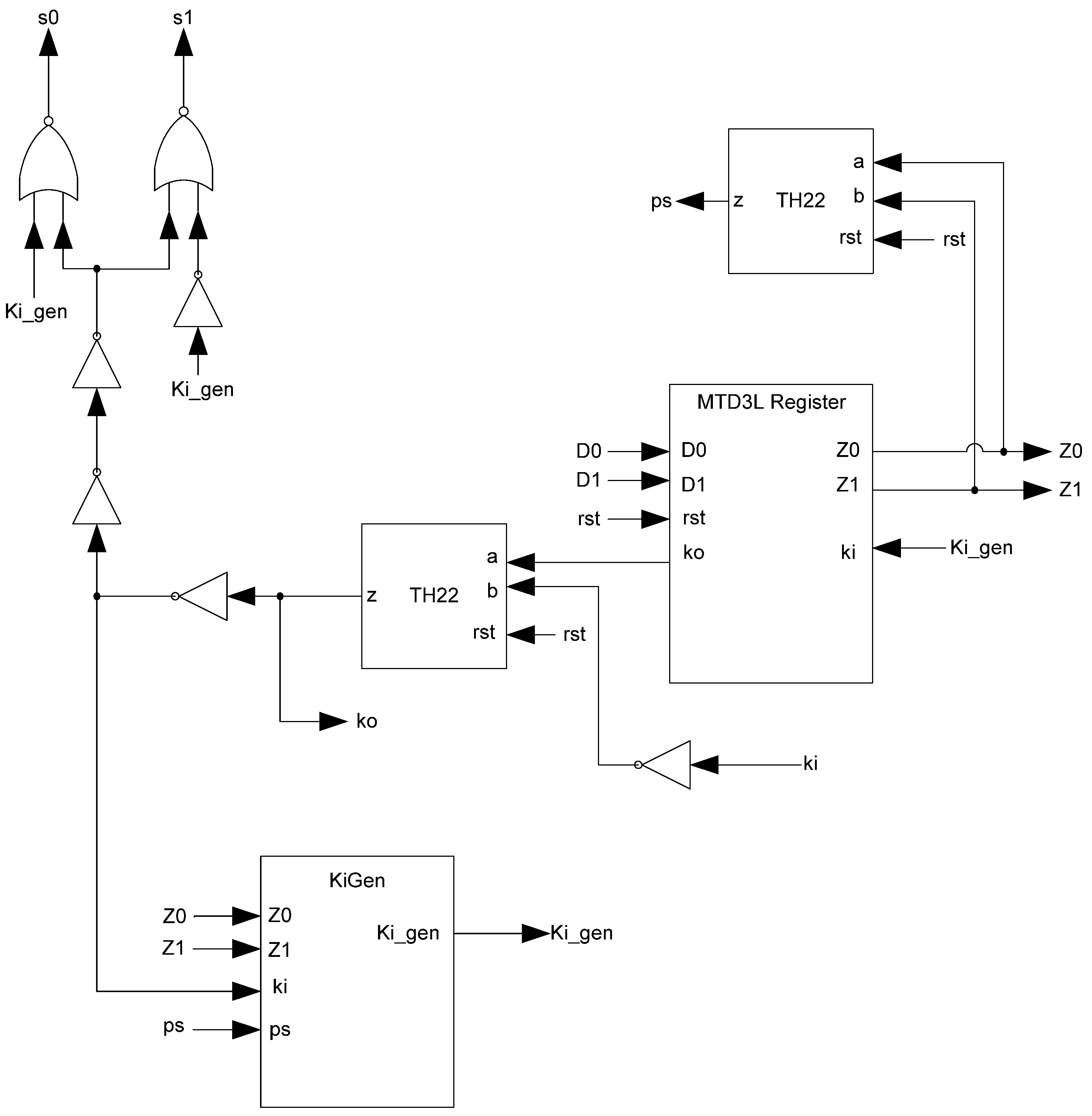
The basic D
3L Register, shown in
Figure 11, is a modified NCL register. It consists of two TH22 gates which are resettable to the desired value. An XNOR gate facilitates
Ko generation by checking the relative values of the register’s outputs. As mentioned previously, the XNOR gate is required to detect both AZS and AOS.
Additional logic is required to facilitate the dual-spacer protocol. NCL registers require a NULL input before they are able to accept new data. They will not recognize an all-one spacer. To fix this, extra logic capable of recognizing the all-one spacer is used to control the register’s
Ki input. This Ki Generator has four inputs: the early completion
Ki,
ps (previous spacer), and the two dual-rail outputs of the register. The value of
ps is generated by a resettable TH22 gate. This value is logic 0 for an AZS and logic 1 for an AOS. The ps gate and the register must be reset to the same value. If the register is reset to DATA then the ps gate is reset to logic 0. The Ki Generator’s output follows the Boolean equation Ki_gen =
Ki ps (Z0+Z1)+ Ki ps (
Z0+
Z1)+
Z0 Z1 Ki+Z0 Z1
Ki resulting from the truth table shown in
Table 3, yielding the transistor level implementation shown in
Figure 12. If an AOS is needed then the value of
Ki_gen will be changed to logic 1 allowing the register to latch it. Once the next data value arrives,
Ki_gen will switch to logic 0. As a result, one of the register’s TH22 gates will have two low inputs which will change its output to logic 0, latching the data. A complete D
3L register is shown in
Figure 13.
Table 3.
Ki Generator (KiGen) truth table.
Table 3.
Ki Generator (KiGen) truth table.
| Row | Z0 | Z1 | Ki | ps | Ki_gen |
|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 | 1 | 1 |
| 5 | 0 | 1 | 0 | 0 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 0 | 0 |
| 8 | 0 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 0 | 1 |
| 10 | 1 | 0 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 0 | 0 |
| 12 | 1 | 0 | 1 | 1 | 1 |
| 13 | 1 | 1 | 0 | 0 | 1 |
| 14 | 1 | 1 | 0 | 1 | 1 |
| 15 | 1 | 1 | 1 | 0 | 0 |
| 16 | 1 | 1 | 1 | 1 | 0 |
Figure 12.
KiGen transistor diagram.
Figure 12.
KiGen transistor diagram.
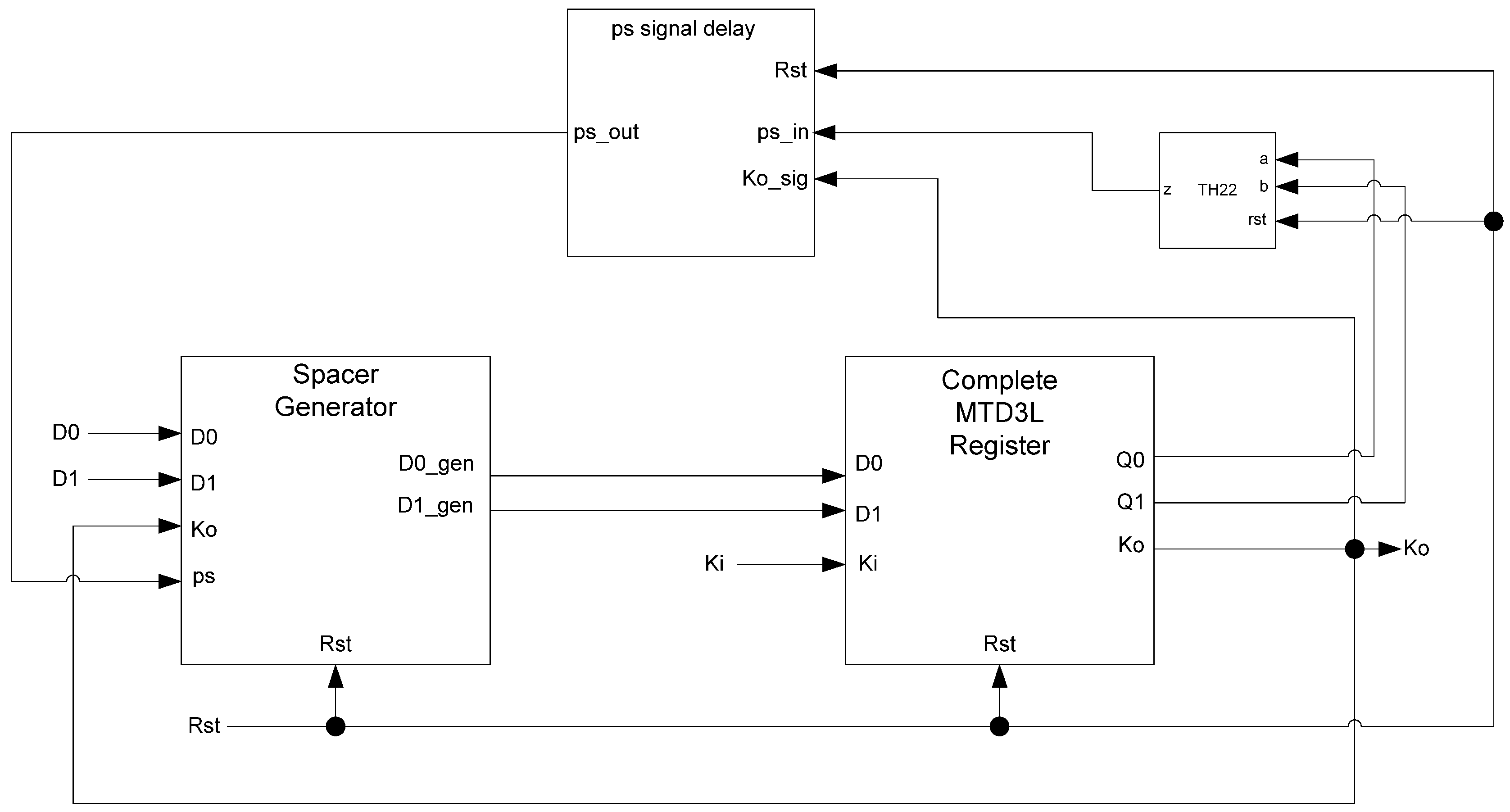
Figure 13.
Complete D3L register.
Figure 13.
Complete D3L register.
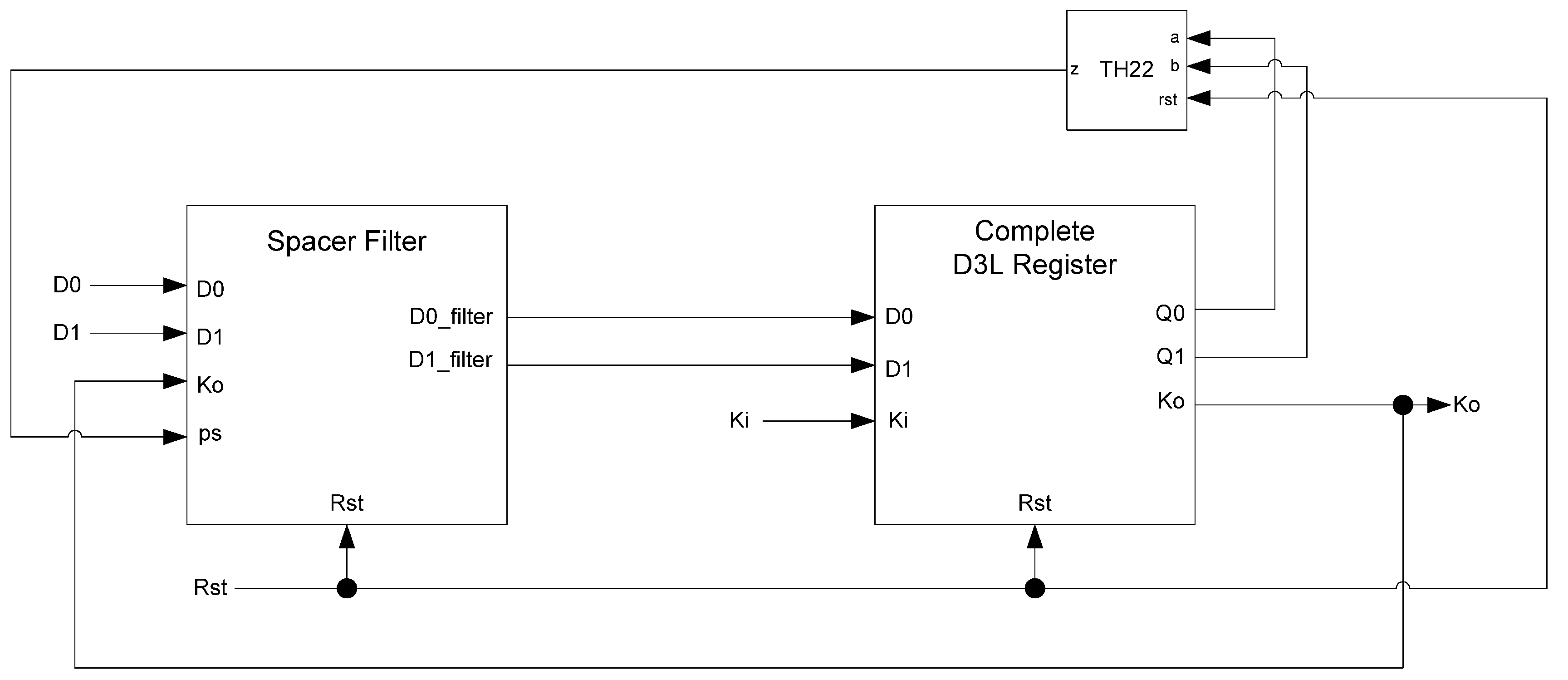
While the D
3L register is capable of handling the dual-spacer protocol, it is insufficient to implement ring register configurations. This is because a basic D
3L register is incapable of generating alternating spacers. Instead, the same spacer would pass through the ring twice causing deadlock. To solve this, a D
3L filter register is required for generating alternating spacers, which consists of a basic D
3L register with a spacer filter operating on the register’s inputs. The spacer filter monitors the dual-rail input, the previous spacer, and the
Ko from the register to ensure that spacers are alternated as they pass through. In a typical ring register configuration, the first two registers would be normal D
3L registers reset to NULL and a filter register reset to DATA0 or DATA1. When the filter register receives an AZS or AOS it outputs the alternate spacer. This ensures that the same spacer does not pass through the ring twice.
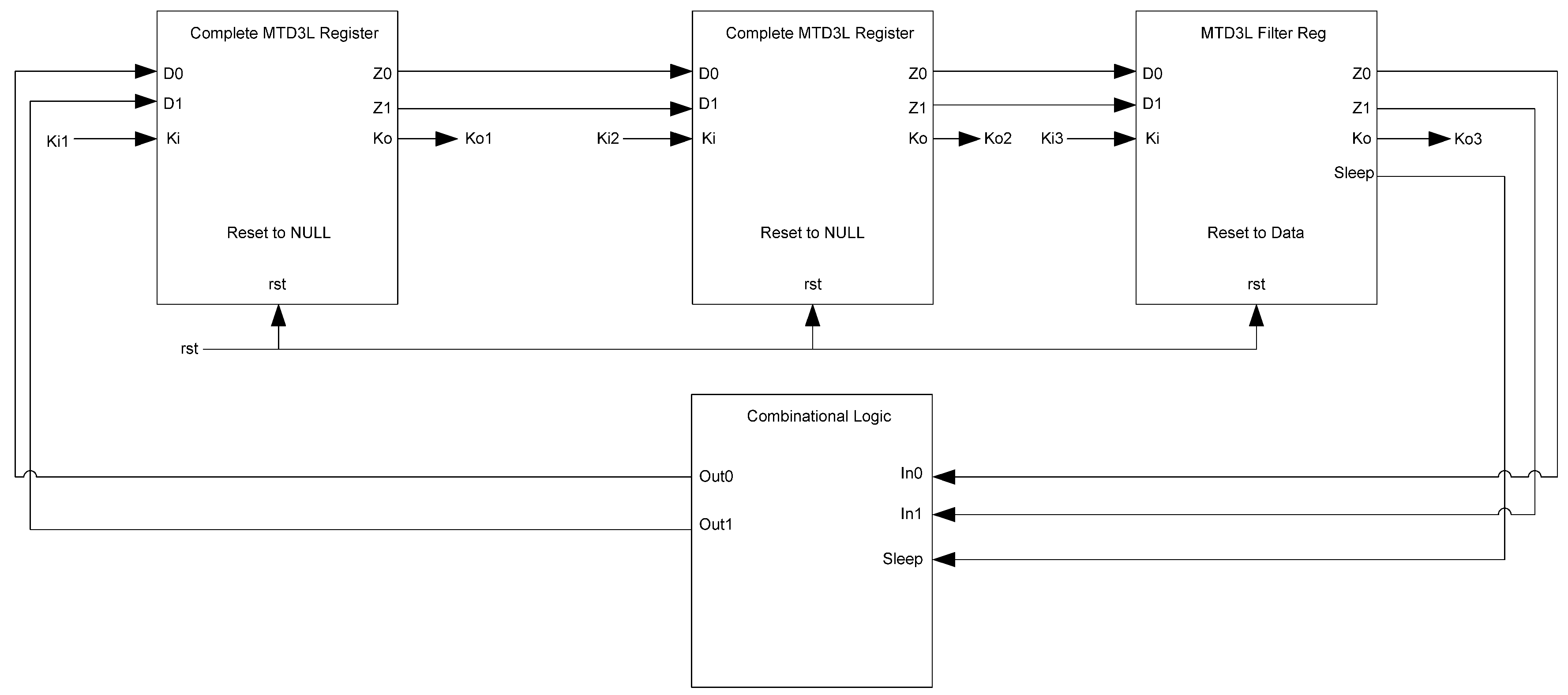
Figure 14 shows the D
3L filter register diagram, while
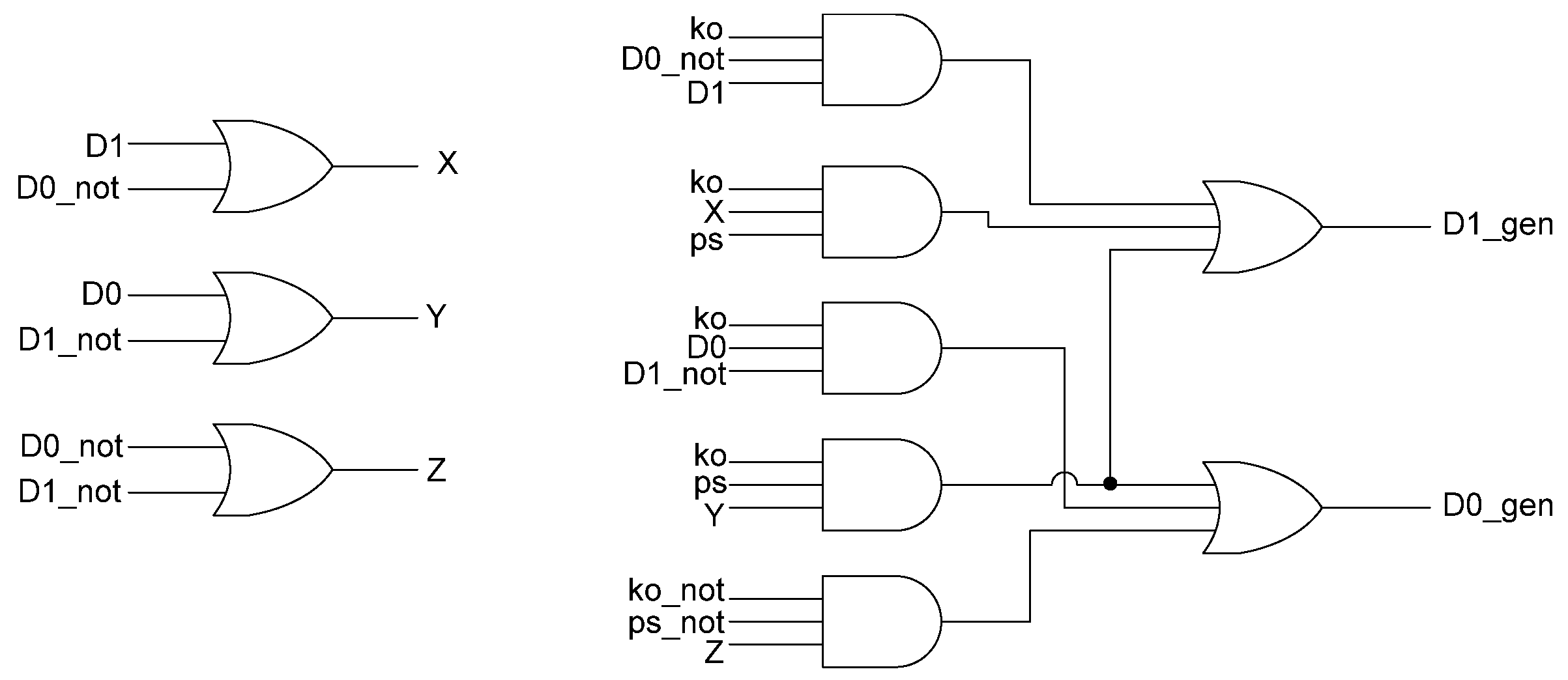
Figure 15 shows the transistor level schematic of the spacer filter, whose outputs are based on the following equations:
Figure 14.
D3L filter register.
Figure 14.
D3L filter register.
Figure 15.
Spacer filter transistor level diagram.
Figure 15.
Spacer filter transistor level diagram.
The PS signal delay component used in the spacer filter, shown in
Figure 16, prevents
ps from changing unless the register’s
Ko is logic 1,
i.e., requesting DATA. This ensures that the value of
ps is only changed once the register receives the spacer.
Figure 16.
PS signal delay component.
Figure 16.
PS signal delay component.
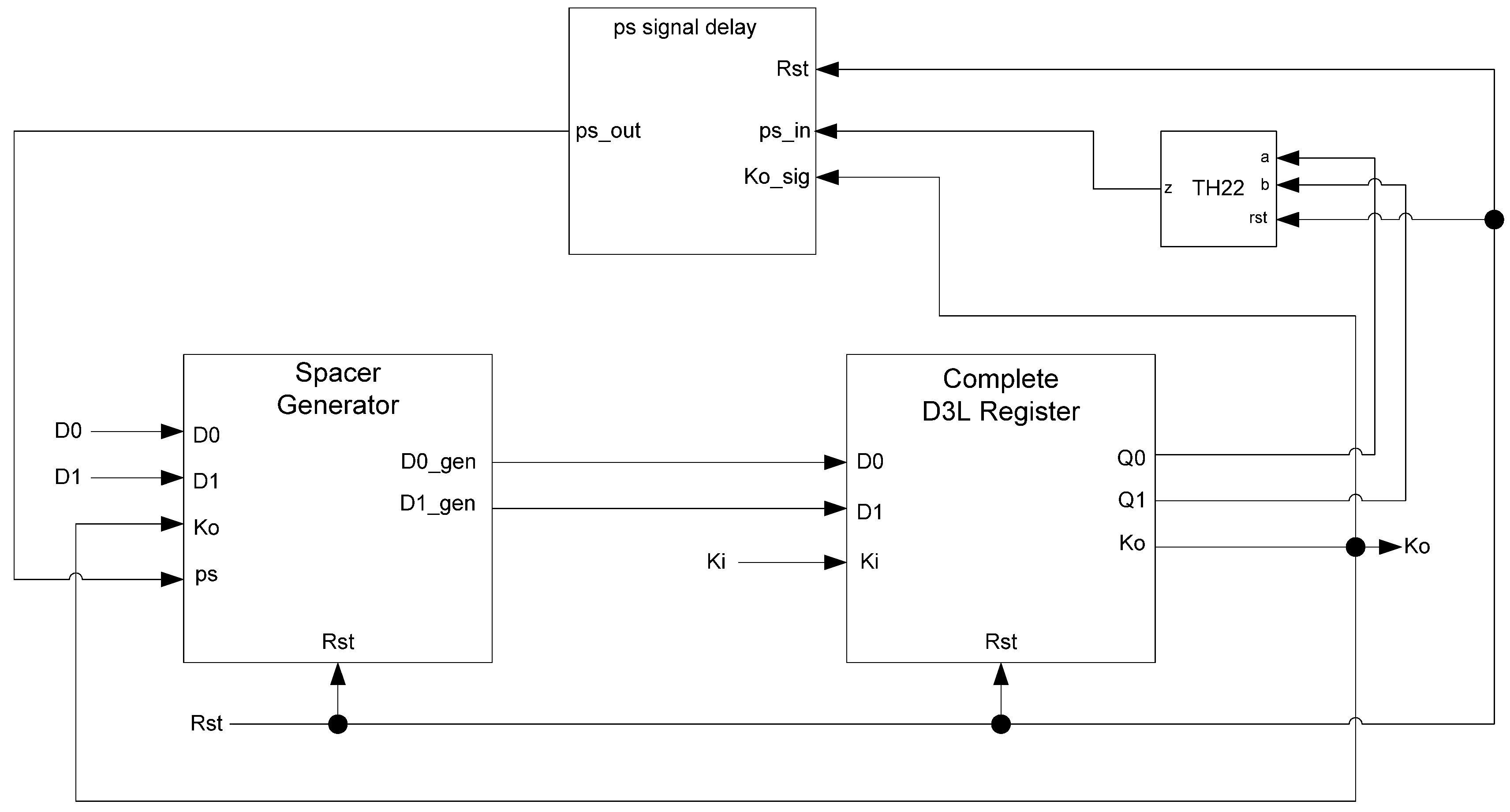
In situations where a component needs many cycles to output data but does not have input provided for each cycle, the component will not be able to receive the spacers it needs as input. Instead, a spacer generator register is used to generate these spacers for the component. A spacer generator register is a basic D
3L register with a spacer generator sitting between it and its inputs. The spacer generator keeps track of the previous spacer and generates the alternate spacer when requested regardless of the dual-rail input it receives. For example, if the previous spacer was an AZS and the register requests a spacer, the spacer generator will generate an AOS. The next time a spacer is requested, it generates an AZS.
Figure 17 shows the D
3L spacer generator register; and
Figure 18 shows the circuit diagram for the spacer generator component. The outputs of the spacer generator are given by the following equations:
Figure 17.
D3L spacer generator register.
Figure 17.
D3L spacer generator register.
Figure 18.
Spacer generator circuit diagram.
Figure 18.
Spacer generator circuit diagram.