A Low Power CMOS Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT Calculation
Abstract
:1. Introduction
2. Proposed Low Power Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT
2.1. Traditional CMOS Imaging System with 2D-DCT Calculation

2.2. Proposed Low Power Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT Calculation
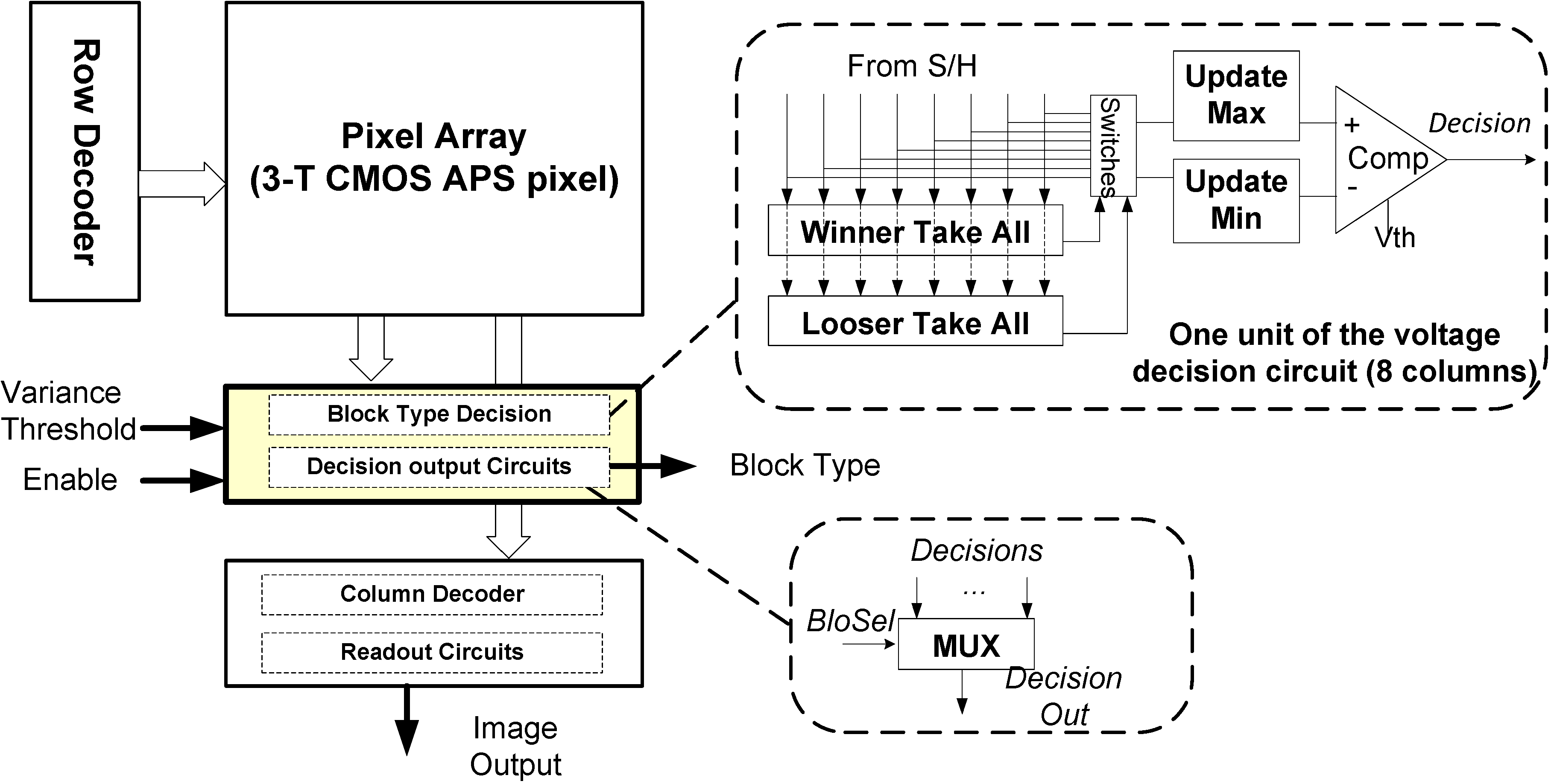
2.2.1. Architecture of the Proposed Low Power Imaging System

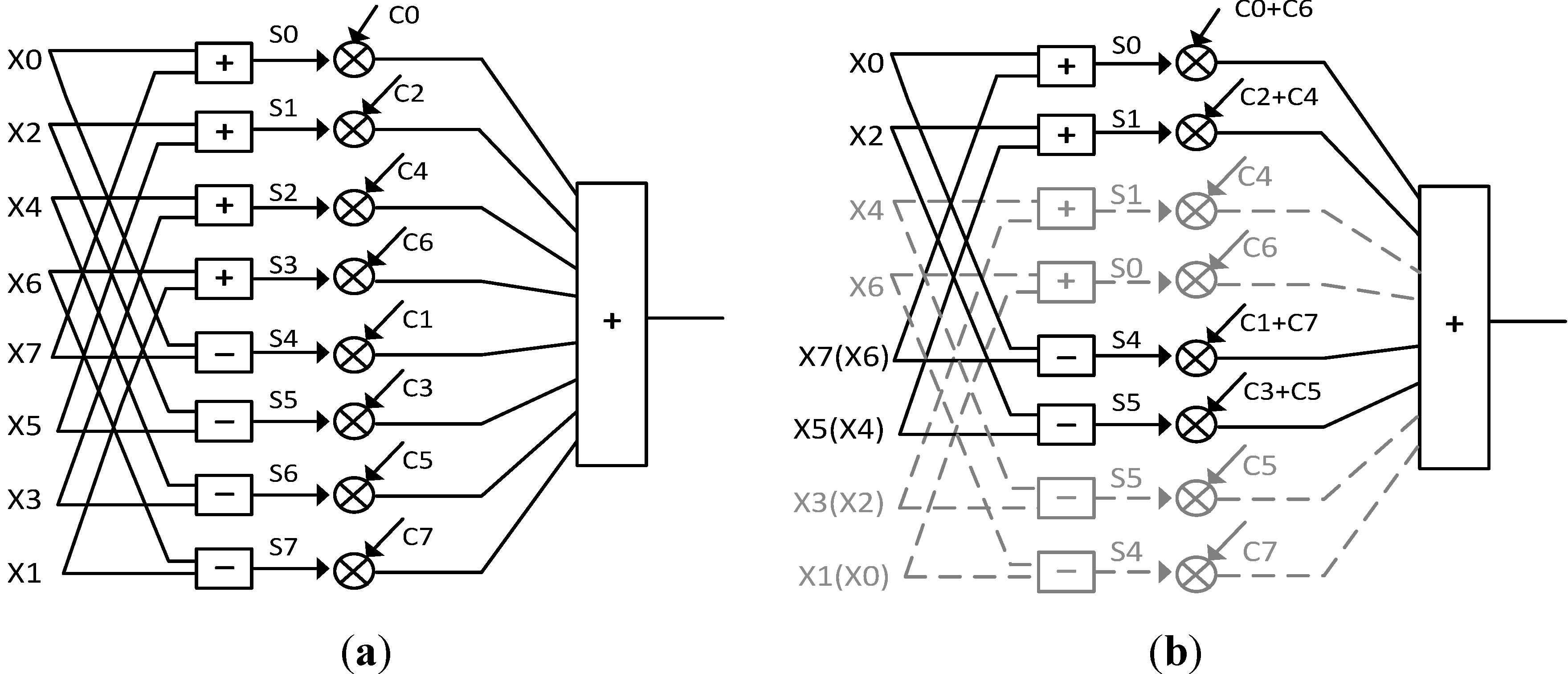
2.2.2. Adaptive Complexity Compression

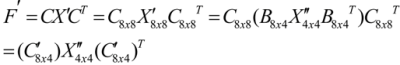
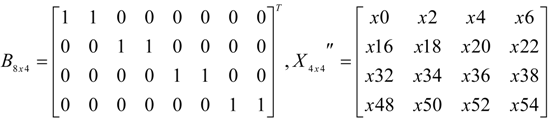 , C'8x4 = C8x8B8x4, and the subscriptions indicate the sizes of the matrixes.
, C'8x4 = C8x8B8x4, and the subscriptions indicate the sizes of the matrixes.3. Implementation of the Low Power Imaging System and Results
3.1. Image Sensor for Smart Image Capture with Block Type Decision Block

| Technology | TSMC 0.18 µm |
|---|---|
| Voltage supply | 1.8 V |
| Pixel array size | 128 × 128 |
| Pitch width | 5 µm |
| Chip size | 2 mm × 2 mm |
| Fill factor | 26% |
| Estimated power (whole chip) | 0.5 mW @ 30 FPS |
| Estimated power (decision logic) | 7 µW @ 30 FPS |
3.2. Image Sensor for Smart Image Capture with Block Type Decision Block Adaptive Complexity 2D-DCT Calculation
3.2.1. Adaptive Data Format
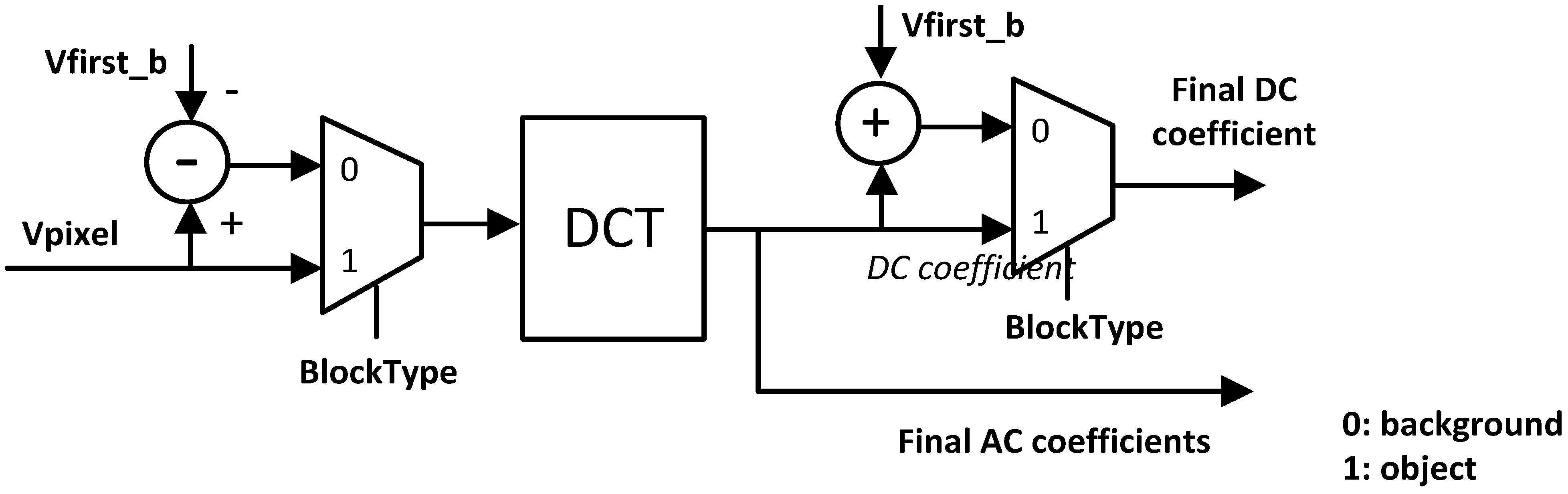
3.2.2. Adaptive Spatial Resolution
3.3. Performance


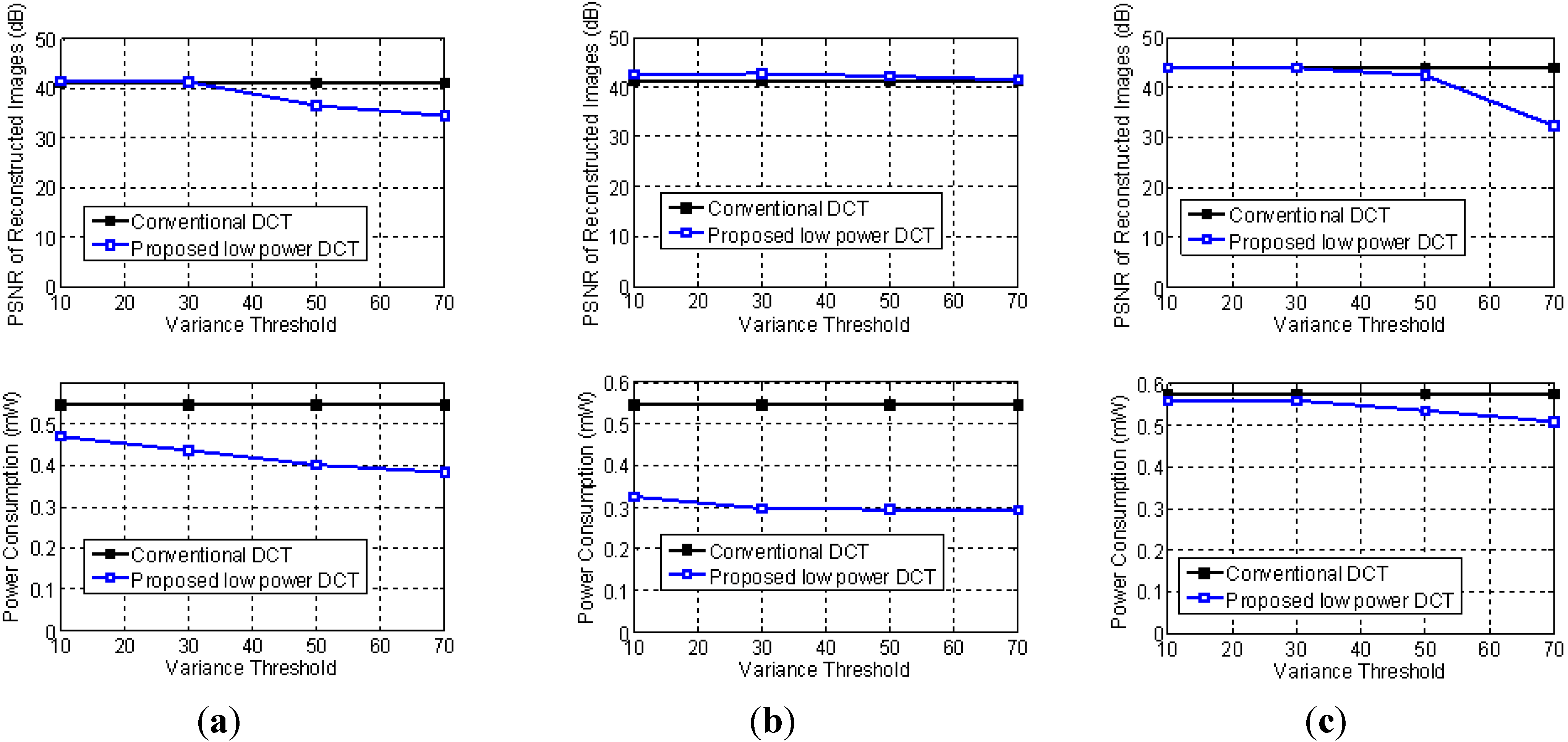
| Images | Background ratio (th = 30) | Percentage of power saving | Extra image quality degradation |
|---|---|---|---|
| Garden | 0.8% | 0.5% | None |
| Cameraman | 50% | 24% | None |
| Plane | 90% | 46% | None |
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Yadid-Pecht, O.; Etienne-Cummings, R. CMOS Imagers: From Phototransduction to Image Processing; Kluwer: Norwell, MA, USA, 2004. [Google Scholar]
- Fish, A.; Yadid-Pecht, O. Low-Power “Smart” CMOS Image Sensors. In Proceedings of the IEEE International Symposium on Circuits and Systems, Washington DC, USA, 18–21 May 2008; pp. 1408–1411.
- Xu, C.; Zhang, W.; Ki, W. A 1.0 V VDD CMOS active-pixel sensor with complementary pixel architecture and pulsewidth modulation fabricated with a 0.25 µm CMOS process. IEEE J. Solid-State Circuits 2002, 37, 1853–1859. [Google Scholar] [CrossRef]
- Shen, C.; Xu, C.; Huang, R.; Zhang, W.; Ko, P.K.; Chan, M. A New APS Architecture on SOI Substrate for Low Voltage Operation. In Proceedings of the 9th International Symposium on IC Technology, Systems & Applications, Singapore, 3–5 September 2001; pp. 275–278.
- Fish, A.; Hamami, S.; Yadid-Pecht, O. CMOS image sensors with self-powered generation capability. IEEE Trans. Circuits Syst. II 2006, 53, 131–135. [Google Scholar]
- Shi, C.; Law, M.K.; Bermak, A. A novel asynchronous pixel for an energy harvesting CMOS image sensor. IEEE Trans. VLSI Syst. 2011, 19, 118–129. [Google Scholar] [CrossRef]
- Gao, Q.; Yadid-Pecht, O. Dual VDD Block Based CMOS Image Sensor–Preliminary Evaluation. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–19 May 2011; pp. 1820–1823.
- Gao, Q.; Yadid-Pecht, O. A low power block based CMOS image sensor with dual VDD. IEEE Sens. J. 2012, 12, 747–755. [Google Scholar] [CrossRef]
- Loeffler, C.; Lightenberg, A.; Moschytz, G.S. Practical Fast 1-D DCT Algorithms with 11-Multiplications. In Proceedings of the International Conference on AcousticsSpeechand Signal Processing-89, Glasgow, UK, 23–26 May 1989; Volume 2, pp. 988–991.
- Thoudam, V.P.S.; Bhaumik, B.; Chatterjee, S. Ultra Low Power Implementation of 2-D DCT for Image/Video Compression. In Proceedings of International Conference on Computer Applications & Industrial Electronics (ICCAIE 2010), Kuala Lumpur, Malaysia, 5–7 December 2010; pp. 532–536.
- Sun, C.-C.; Ruan, S.-J.; Heyne, B.; Goetze, J. Low-power and high-quality Cordic-based Loeffler DCT for signal processing. Circuits Devices Syst. IET 2007, 1, 453–461. [Google Scholar] [CrossRef]
- Tran, T.D. The binDCT: Fast multiplierless approximation of the DCT. IEEE Signal Process. Lett. 2000, 7, 141–144. [Google Scholar] [CrossRef]
- Sung, T.-Y.; Shieh, Y.-S.; Yu, C.-W.; Hsin, H.-C. High-Efficiency and Low-Power Architectures for 2-D DCT and IDCT Based on CORDIC Rotation. In Proceedings of the 7th International Conference on Parallel and Distributed ComputingApplications and Technologies, Taipei, Taiwan, 4–7 December 2006; pp. 191–196.
- Jeong, H.; Kim, J.; Cho, W.-K. Low-power multiplierless DCT architecture using image data correlation. IEEE Trans. Consum. Electron. 2004, 50, 262–267. [Google Scholar] [CrossRef]
- Xanthopoulos, T.; Chandrakasan, A.P. A low-power DCT core using adaptive bitwidth and arithmetic activity exploiting signal correlations and quantization. IEEE J. Solid-State Circuits 2000, 35, 740–750. [Google Scholar] [CrossRef]
- Pillai, L. Video Compression Using DCT; Xilinx: San Jose, CA, USA, 2002. [Google Scholar]
- Loeve, M. Probability Theory, Graduate Texts in Mathematics, 4th ed.; Springer-Verlag: Berlin, Germany, 1977. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, Q.; Yadid-Pecht, O. A Low Power CMOS Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT Calculation. J. Low Power Electron. Appl. 2013, 3, 267-278. https://doi.org/10.3390/jlpea3030267
Gao Q, Yadid-Pecht O. A Low Power CMOS Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT Calculation. Journal of Low Power Electronics and Applications. 2013; 3(3):267-278. https://doi.org/10.3390/jlpea3030267
Chicago/Turabian StyleGao, Qing, and Orly Yadid-Pecht. 2013. "A Low Power CMOS Imaging System with Smart Image Capture and Adaptive Complexity 2D-DCT Calculation" Journal of Low Power Electronics and Applications 3, no. 3: 267-278. https://doi.org/10.3390/jlpea3030267




