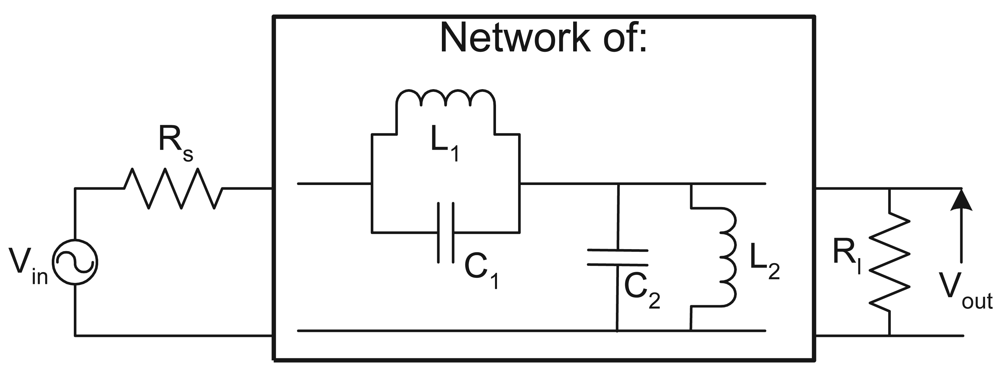
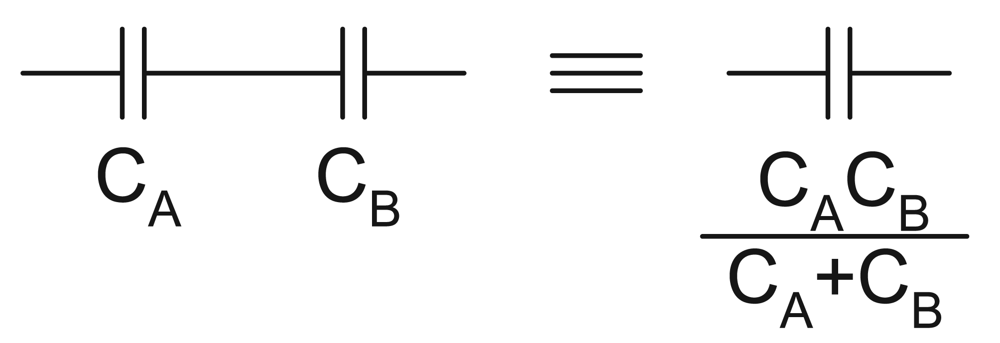3.1. y Parameter Generation
Based upon classical synthesis procedures [
9,
12,
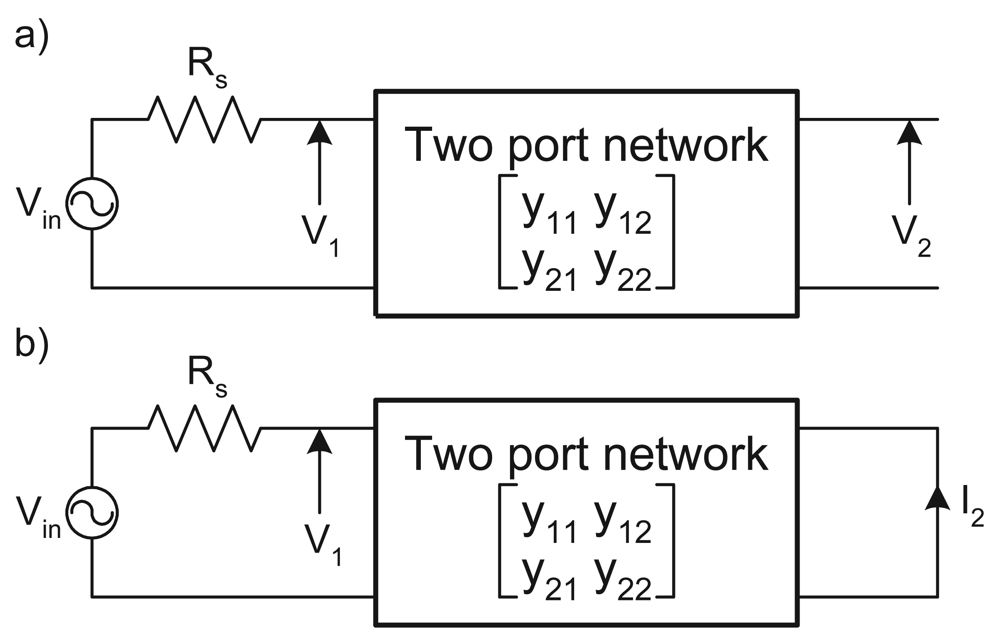
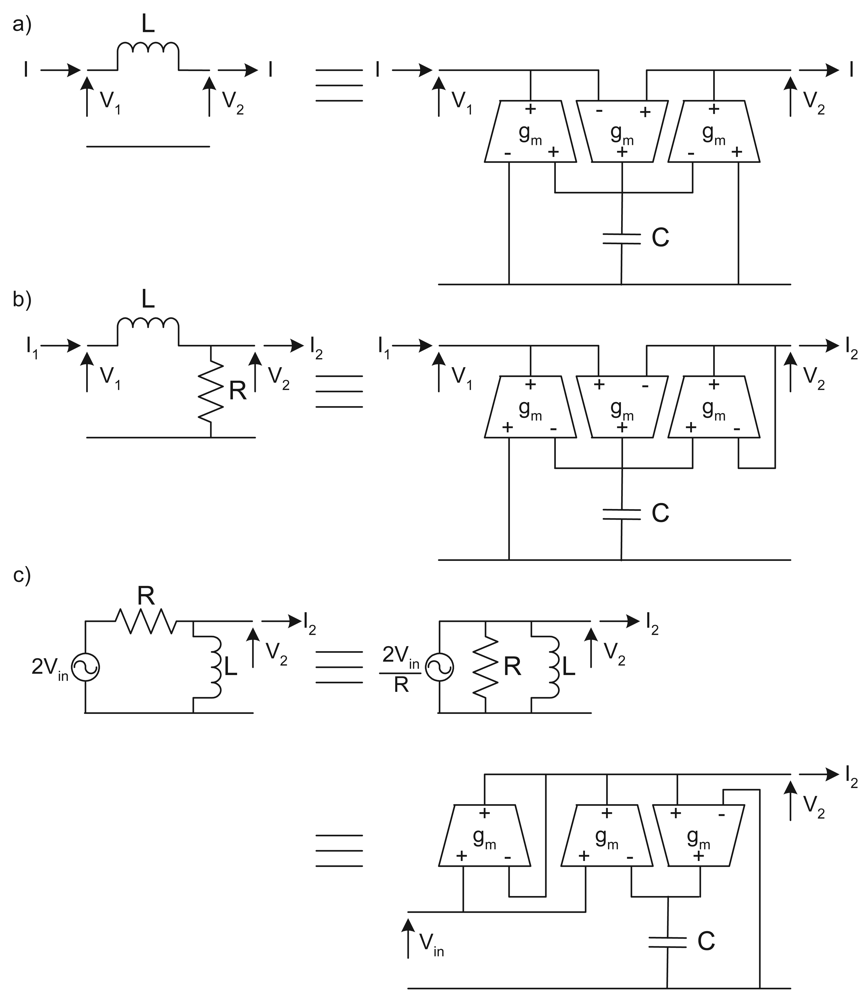
13] the starting point for the generation of a doubly terminated LC ladder network is the generation of a suitable singly terminated network as illustrated in
Figure 2. For both cases in
Figure 2 the input is
Vin(
s) and in case (a) the output is a voltage, while in case (b) the output is a current, but otherwise the two set-ups are identical. Considering case (b) (case (a) is similar but in terms of the
z parameters) the input voltage to output transfer function is given by
For simplicity a design is considered for the case
Rs= 1 Ω. From this prototype the end component values can then be scaled to match the wanted terminating resistor, see Section 6. The obtained
A(
s) is thus of the form
In comparison, the wanted transfer function,
(2), is of the form
where
N(
s) is an even function and D(s) is a strictly Hurwitz polynomial. Separating
D(
s) into its odd (
Do(
s)) and even (
De(
s)) parts
Comparing
(18) and
(21) it is thus seen that
and
From this, analytic forms for the required
y parameters can easily be found. If the wanted transfer function is
where
| a | = | 6.88 × 10−3 |
| b | = | 2.34 × 10−8 |
| c | = | 1.34 × 10−6 |
| d | = | 3.70 × 10−5 |
| e | = | 6.79 × 10−4 |
| f | = | 8.67 × 10−3 |
| g | = | 0.075 |
| h | = | 0.4 |
the required
y12 and
y11 are then
where
| a′ | = | a/h |
| = | 1.72 × 10−2 |
| b′ | = | b/h |
| = | 5.85 × 10−6 |
| d′ | = | d/h |
| = | 9.25 × 10−5 |
| f′ | = | f/h |
| = | 2.17 × 10−2 |
From
(18), for a singly terminated network the form of
y22 is not significant.
3.2. Transmission Zero Realisation
The design procedure now proceeds by examining the form of y11 and y12. y11 has a private pole (one that is not present in y12), given by hs. This results in a transmission zero at s = 0. y12 has six transmission zeros: one at s = 0 due to the numerator a′s; and five at s → ∞ due to the difference in order between the numerator and denominator.
The key to LC ladder synthesis is realising the correct positions of all of these zeros using suitable arrangements of components and then choosing the values of the components so that y11 is numerically satisfied. The realised y12 can then differ by at most a constant gain factor from the wanted y12, which corresponds to the LC ladder matching the wanted filter shape, but not necessarily the gain. However, this can be readily compensated for by the presence of an ideal transformer, amplifier, or simply compensating for the expected values in the next part of any end system.
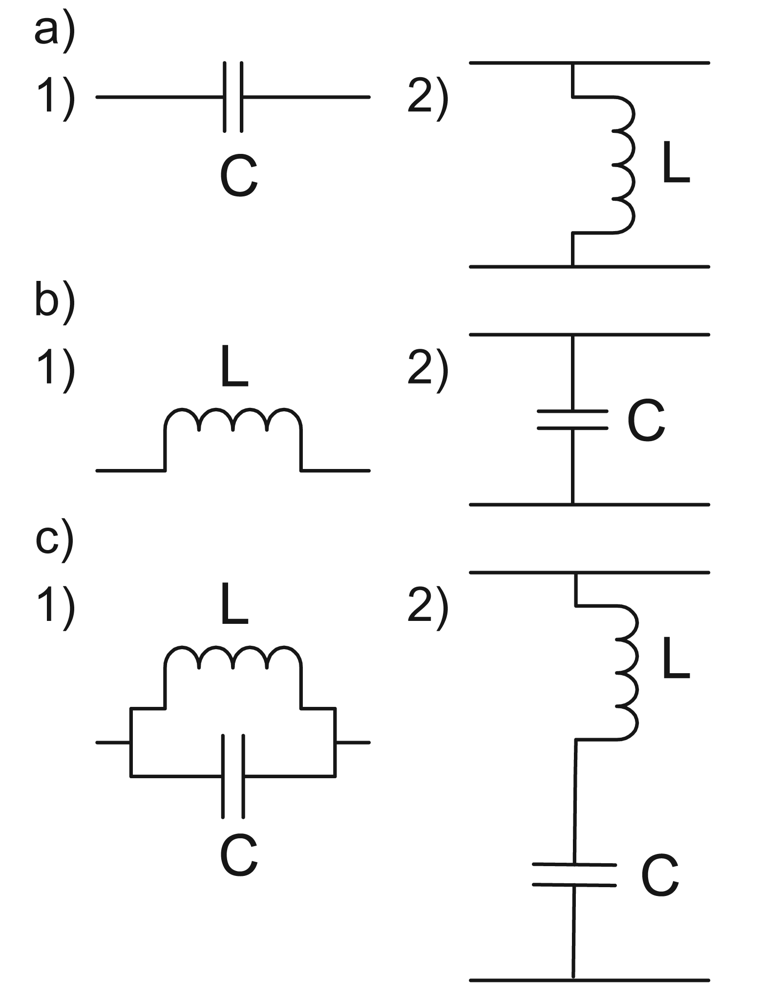
A transmission zero at the origin can be realised by one of the arrangements in
Figure 3a—a series capacitor or a shunt inductor. A transmission zero at infinity corresponds to one of the elements in
Figure 3b—a series inductor or a shunt capacitor. For completeness, although it is not required in the example here, it is possible to realise zeros at arbitrary frequencies through the use of one of the elements in
Figure 3c which realise a zero at
ω = (
LC)
−1/2. Also, it is possible to shift the position of zeros through the use of a partial pole removals [
12], but this is not explored further here.
To realise the network it is simply a matter of arranging the potential elements from
Figure 3 so that all of the transmission zeros are provided and the combinations of elements do not
cancel out. For example, in principle two transmission zeros at
s = 0 could be realised by a cascade of capacitors as illustrated in
Figure 4. In practice of course this is not possible, the two capacitors in series are equivalent to just one capacitor of a different value and so only one transmission zero is realised.
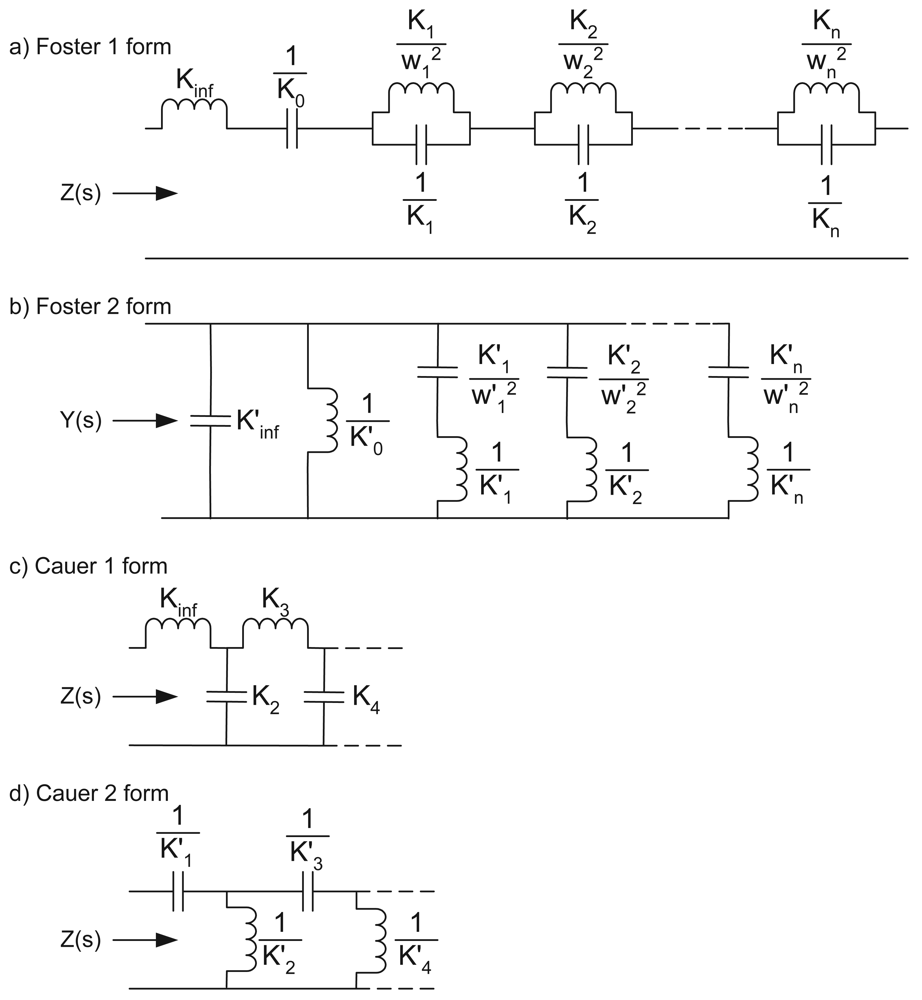
Ideally combinations of the networks illustrated in
Figure 5 are used to order the elements to give the required poles. These networks correspond to Foster 1, Foster 2, Cauer 1 and Cauer 2 realisations and are used as the resulting component values can be readily found by simple manipulations of the wanted immittance function. For a Foster 1 realisation the component values are given by the partial fraction expansion
while for the Foster 2 form the values are given by the alternative partial fraction expansion
For the Cauer 1 realisation the component values are given by a continued fraction expansion around infinity
and the Cauer 2 values are given by a continued fraction expansion around zero
Unfortunately, due to the arrangements of zeros needed a Cauer based network does not give a satisfactory result (see Section 3.4). We utalise an alternative method based upon the solution of non-linear simultaneous equations to provide the wanted network.
3.3. Network Synthesis
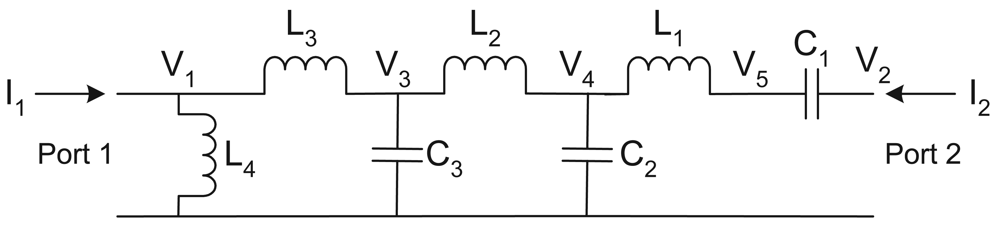
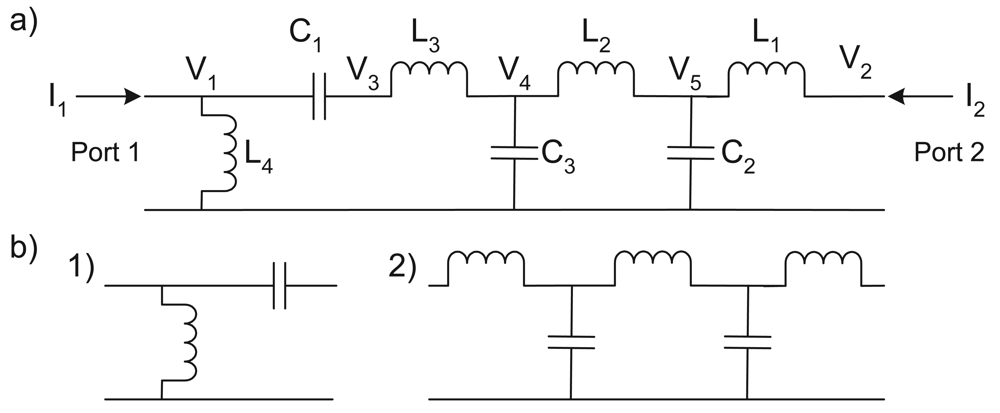
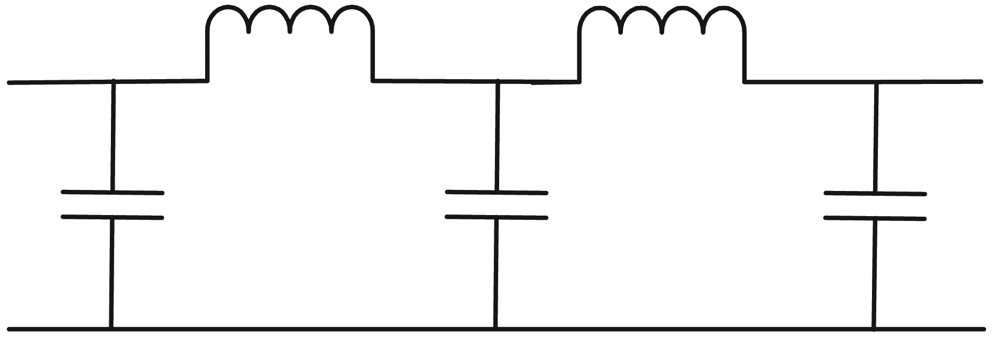
It is clearly seen that the network to be synthesised needs two elements from
Figure 3a to realise the transmission zeros at the origin and five elements from
Figure 3b for the transmission zeros at infinity. Furthermore one of the zeros at the origin must be private to
y11 and so must be realised at port one of the network, not in the middle. A network that satisfies these requirements without any elements cancelling is given in
Figure 6. This has the nodal matrix
(31) and the
y parameters
(32),
(33).
From these it can be seen that
y11 and
y12 are indeed of the correct form (have the same structure in terms of the number of poles and zeros). It is noted that due to the series connection of an inductor and capacitor to port two of the network, for the derived
y parameters to be valid it is necessary to draw a current through this branch of the circuit. The transfer function implemented thus has to be of the form in
Figure 2b.
From
(32) and
(33), and introducing
βL3 =
L4 to allow the equations to be written in a more compact form, the coefficients of the implemented
y parameters can be extracted as
Comparing the coefficients of
(25),
(26), to
(34)–
(41) a series of multiplicative simultaneous equations are thus formed. To find the required component values it is simply a matter of solving this set of equations:
Note that there are only seven component parameters, but eight equations. An exact solution is thus not possible. In general, the first equation,
(42), corresponds only to the passband gain of the filter. By ignoring this equation, it is possible to solve for the other equations. Again, this gives the wanted filter shape and the passband gain can be corrected for elsewhere as discussed previously.
The multiplicative simultaneous equations are readily solved using the M
aple or M
atlabfsolve
tool for the solution of non-linear simultaneous equations. Based on convergence issues however, (and due to the potential presence of local and global solutions) an initial guess at the component values needs to be provided. Based upon this different solutions may be found and it is not guaranteed that all the component values will be found exactly, or will be positive.
If a starting guess that gives only positive component values cannot be found it is possible instead to view the solution of the equations as a constrained minimisation problem which can be solved via the
fmincon
function. In brief, the equations to be solved,
(42)–
(49), are rearranged into a cost function. Typically this is of the form of a sum of the square of the residuals:
where
x represents each simultaneous equation (
b–
h) and each equation is a function of the component values
Alternative cost functions, such as using l1 and Huber norms, rather than the l2 norm, are also possible and could be used if desired, as could any desired optimisation technique. Ideally F(x) = 0, and it cannot be negative, so the optimisation problem is now simply a matter of minimising F(x) subject to the constraint that 0 < x < ∞ for all of the arguments of x.
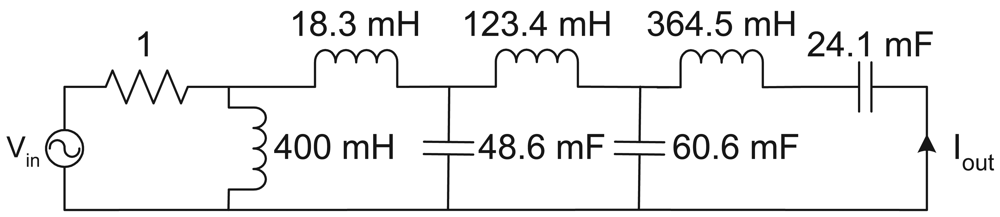
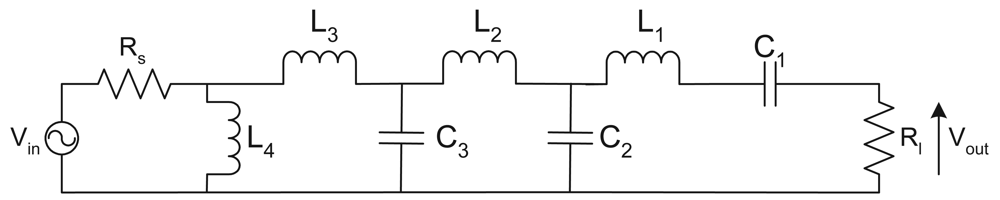
Solving these equations for the singly terminated LC ladder gives the required component values. The best approximation found is given by
| C1 | = | 24.1 mF |
| C2 | = | 60.6 mF |
| C3 | = | 48.6 mF |
| L1 | = | 364.5 mH |
| L2 | = | 123.4 mH |
| L3 | = | 18.3 mH |
| L4 | = | 400 mH |
which gives a network with a centre frequency gain 1.4 times the wanted gain, which would need to be compensated for elsewhere. The full form of the singly terminated LC ladder filter is thus shown in
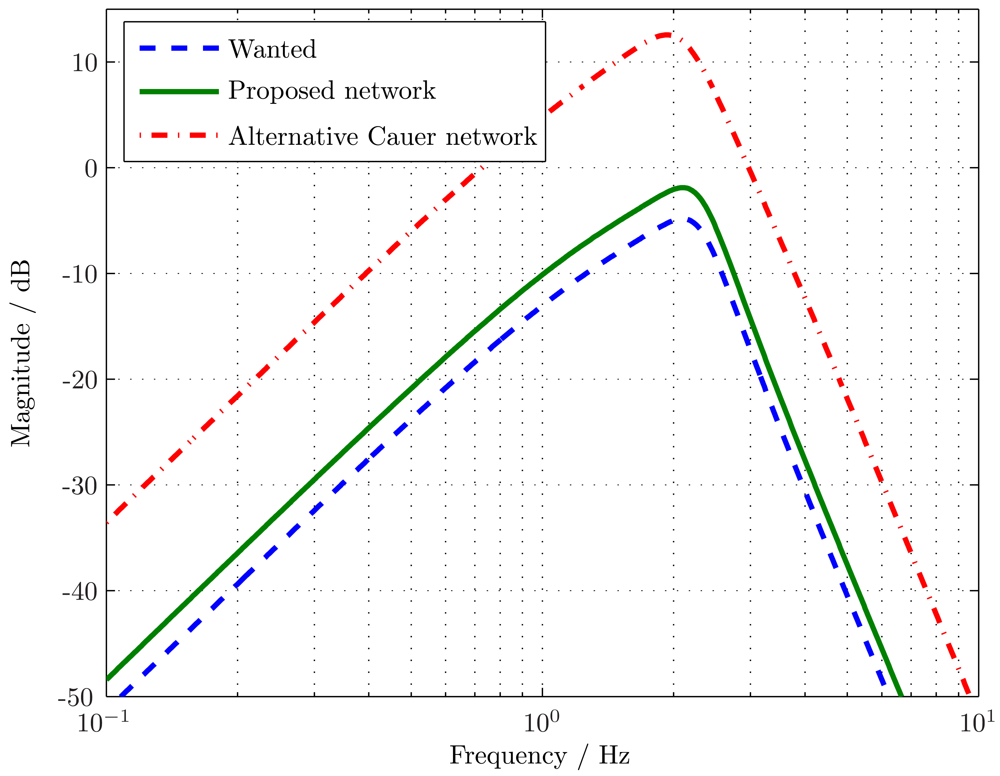
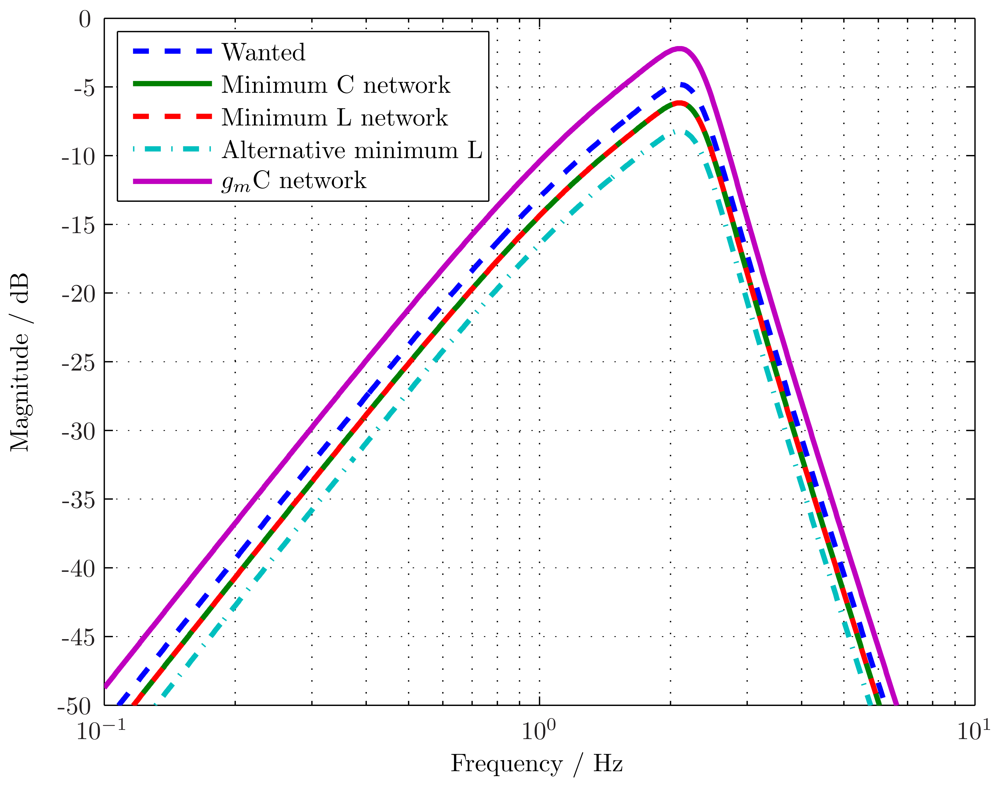
Figure 7 where it is noted that the input signal is voltage mode while the output signal is current mode. The resulting Bode magnitude response is shown in
Figure 8. The 1.4 gain factor between the wanted and implemented responses is clearly seen, as is the correct response shape.
3.4. Alternative Networks
At this point it is noted that the alternative network illustrated in
Figure 9a is also a viable singly terminated one which gives the wanted transfer function form when the load is a short circuit and it is driven by a Thevenin source with resistance of 1 Ω. This network is readily seen as the cascade of a 2nd order Cauer high pass section which provides two transmission zeros at
s = 0 and a 5th order Cauer low pass section which provides five zeros at
s → ∞. (For ease of comparison the prototype Cauer stages are illustrated in
Figure 9b and
Figure 9c.)
The Cauer network from
Figure 9a in theory gives the same response as the original network from
Figure 6 and being simply a cascade of simpler elements perhaps has a more obvious design procedure. The original network from
Figure 6 is essentially derived from the fact that a shunt inductor is required at port 1 to give
y11 the private pole that it requires, but the series capacitor realising the second transmission zero at
s = 0 is free to be placed anywhere in the network, that is, in series with any of the floating inductors.
All of these networks (with the series capacitor in series with each different inductor) will give the correct
form of the transfer function, but the simultaneous equations that need to be solved to derive the component values will be slightly different in each case. Indeed, for the case illustrated in
Figure 9a no exact solution to the simultaneous equations has been found. The best solution found has component values:
| C1 | = | 133.3 mF |
| C2 | = | 68.5 mF |
| C3 | = | 504.1 mF |
| L1 | = | 400 mH |
| L2 | = | 18.3 mH |
| L3 | = | 48.3 mH |
| L4 | = | 13.4 mH |
The resulting Bode magnitude plot is also shown in
Figure 8. Here it is noticed that the curvature of the magnitude response just below the passband is not the same as that for the wanted
T(
s) or that provided by the network of
Figure 6. It is thus concluded that although the Cauer based network is feasible, and has a clearer design process, it is a less desirable arrangement. In principle, all of the different singly terminated networks could be generated and a further optimisation procedure used to select between networks, for example selecting the network with the most dynamic range [
17], or the least component spread.