Optimization Method for Developing Spectral Controlling Cosmetics: Application for Thermal Barrier Cosmetic

Abstract

In this paper, a method of optimizing a thermal barrier cosmetic and spectral selective cosmetic by controlling the particle size and material is proposed as a countermeasure to heatstroke. The radiative properties of single cosmetic particles of a wide range of particle sizes and wavelengths in non-absorbing air were calculated in this study based on the Mie theory. Al₂O₃, TiO₂, Au, and Ag were used as the material of the cosmetic particle. The radiative property of a particle cloud in dependent scattering was calculated. The radiative transfer in the cosmetic layer was analyzed, and the spectral reflectance of the cosmetic layer on the human skin was calculated. A new parameter was defined to quantitatively evaluate the performance of the thermal barrier cosmetic and spectral selective cosmetic. For the thermal barrier cosmetic, the Al₂O₃ particle was determined to be suitable, and its size was optimized. For the spectral selective cosmetic, the Au particle was likewise determined to be suitable, and its size was optimized. Our cosmetics satisfied both aesthetic and thermal concerns.

1. Introduction

As the problem of global warming has increased, a greater number of heat strokes have been reported. A heatstroke occurs when the summation of the metabolic heat and external heat exceeds an acceptable heat limit of a person. The most significant external heat source that causes a heatstroke is sunlight, especially during outdoor physical activities, such as sports. A thermal barrier cosmetic is therefore proposed in this paper as a countermeasure to heatstroke.

People in outdoor environments are exposed to a considerable amount of sunlight. The solar energy that reaches the Earth’s surface through a range from 300 nm to 2500 nm is divided into three parts (air mass = 1.5): respective ultraviolet (UV) (5%), visible (VIS) (43%), and near-infrared (NIR) (52%) regions [1]. People absorb large amounts of solar irradiation from the VIS and NIR regions. This absorption increases the body temperature and causes heatstroke.

Cosmetics have a close relation with the light spectrum. Sunscreen was developed to protect human skin from UV light [2]. Depending on the action mechanism, sunscreens can be classified into: physical blockers (i.e., those that reflect the light) and chemical absorbers (i.e., those that absorb the UVA and/or UVB sunlight, subsequently converting it into other forms of energy, preferably at a high rate and yield) [3]. Regarding chemical absorbers, Shaath introduced a simplified qualitative approach suitable for the prediction of the direction of the wavelength shifts in the UV absorption spectrum of a sunscreen chemical [3]. In addition, regarding physical blockers, Popov et al. studied the alteration of the optical properties of the superficial layer of human skin at the UV range by the application of nanoparticles of titanium dioxide (TiO₂), silicon (Si), and zinc oxide (ZnO) [4]. Their theoretical study revealed the optimal sizes of the nanoparticles to minimize the light transmittance of UV wavelengths. However, there is a concern that physical blockers may also contribute to electron transfer reactions and sensitize reactive singlet oxygen. Furthermore, in the VIS region, cosmetics are used to control skin aesthetics. By mimicking the manner in which light interacts with Morpho butterfly scales, while using synthetic materials to form periodic nanostructures, L’Oreal has created a photonic cosmetic product that contains no chemical pigments [5]. Moreover, Yamada et al. numerically investigated radiation transfer in skin by the Monte Carlo method to design and produce cosmetics [6]. Nakamura et al. developed a numerical model to clarify the optical characteristics of the human skin surface and the interaction between the cosmetic particles and human skin [7]. Although NIR radiation comprises 52% of the energy of sunlight, no cosmetics exist that control NIR radiation. Meanwhile, Gonome et al. developed a spectral selective coating pigmented by nano/microparticles to reflect NIR light for industrial use [8,9]. Álvarez-Docio et al. also developed CoAl₂O₄ pigments for NIR light reflection and discussed the effects of the morphology and dispersion of the particles [10]. These spectral selections by means of a scattering medium are also useful for cosmetics.

In this study, two types of thermal barrier cosmetics were theoretically designed. One type—the thermal barrier cosmetic (TBC)—is intended to block all solar heat. Accordingly, the cosmetic reflects sunlight in all solar spectral regions. The other type—the spectral selective cosmetic (SSC)—is intended to maintain the appearance of natural skin, while simultaneously blocking solar heat. Therefore, the reflectance of the cosmetic layer in the VIS region should be similar to that of human skin, and the reflectance in the NIR region should be high.

In the theoretical design of the proposed thermal barrier cosmetics, the radiative property of a single cosmetic particle was calculated. Al₂O₃, TiO₂, Au, and Ag were selected to comprise the material of the cosmetic particle. From these data, the radiative property of a particle cloud in dependent scattering was calculated. Finally, the radiative transfer in the cosmetic layer was calculated, and the effects of the particle sizes and materials on the spectral properties of the cosmetic layer were examined.

2. Materials and Methods

2.1. Complex Refractive Index

The scattering and absorption of radiation by a single homogeneous spherical particle in a non-absorbing medium can be obtained by solving Maxwell’s equations. The radiative properties of a single spherical particle of diameter d_p, interacting with an electromagnetic wave of wavelength λ, are governed by two independent non-dimensional parameters, namely the complex refractive index of the particle m = n − ik and the size parameter x = πd_p/λ, as described in the Mie scattering theory [11].

Figure 1 shows the spectral distribution of real and imaginary parts of the complex index of refraction of Al₂O₃, TiO₂, Au, and Ag in the range of 0.3–2.5 μm, respectively [12]. The imaginary part of Al₂O₃ is almost zero in all spectral regions, and the line is behind the axis. Using the spectral complex refractive index, the radiative properties of a single particle were calculated.

2.2. Radiative Properties of Single Particles

According to the Mie theory, the radiative properties of the particle, such as the extinction efficiency factor Q_ext and scattering efficiency factor Q_sca, can be calculated using the following equations [13]:

$$Q_{\mathrm{sca}}=\frac{2}{x^2}{\displaystyle \sum _{k=1}^{\infty }(2k+1)({\left|a_n\right|}^2+{\left|b_n\right|}^2)}$$

(1)

$$Q_{\mathrm{ext}}=\frac{2}{x^2}{\displaystyle \sum _{k=1}^{\infty }(2k+1)Re\left[a_n+b_n\right]}$$

(2)

where a_n and b_n are the Mie scattering coefficients. The medium is assumed to be non-absorbing with a refractive index equal to 1.0. The particle size varies from 0.01 to 10 μm and is logarithmically divided into 100 data points. The radiation interacting with a particle may be scattered from its original direction at angle θ. With the use of the direction cosine μ = cosθ, the scattering phase function Φ(μ) can be calculated.

2.3. Radiative Properties of a Particle Cloud

2.3.1. Independent Scattering

A large collection of particles must be considered in radiative heat transfer through the cosmetic layer. If the scattering is independent, then the effects of a large number of particles are simply expressed as their summation. For simplicity, it is often assumed that a particle cloud consists of spheres that are equally large. The fraction of energy scattered by all particles per unit length along the direction of the incoming beam is equal to the scattering cross-section summed over all the particles. If n_p is the number of particles per unit volume, and all particles have a uniform diameter d_p, then the following is true:

$${\mathsf{\sigma }}_{s,\mathsf{\lambda },mono}=\mathsf{\pi }{\left(\frac{d_p}{2}\right)}^2{Q}_{\mathrm{sca}}{n}_p,{\mathsf{\beta }}_{\mathsf{\lambda },mono}=\mathsf{\pi }{\left(\frac{d_p}{2}\right)}^2{Q}_{\mathrm{ext}}{n}_p$$

(3)

where σ_s and β are the scattering and extinction coefficients, respectively. Because the phase function in a cloud of uniform particles is the same for each particle, it is also the same for the particle cloud. In this case, the total volume of particles per unit volume or volume fraction can be calculated using the following equation:

$$f_v=\frac{1}{6}\mathsf{\pi }{d}_p^3{n}_p$$

(4)

2.3.2. Dependent Scattering

In a dense cosmetic layer where particles touch, radiation transfer cannot be treated as scattering by separate particles [14]. This effect is referred to as dependent scattering. The relation between independent and dependent scattering is given by following equation [15]:

$${\mathsf{\beta }}_d={\gamma \mathsf{\beta }}_i,{\mathsf{\sigma }}_d={\gamma \mathsf{\sigma }}_i$$

(5)

where scaling factor γ is introduced,

$$\gamma =\frac{1}{1-f_v}$$

(6)

here, subscripts i and d indicate independent and dependent scattering, respectively.

A considerable difference arises in the dense cosmetic layer on account of dependent scattering, which is actually a mutual influence of scattering particles. Dependent scattering has no effect on the phase function [16]. Dependent scattering is assumed in our calculations.

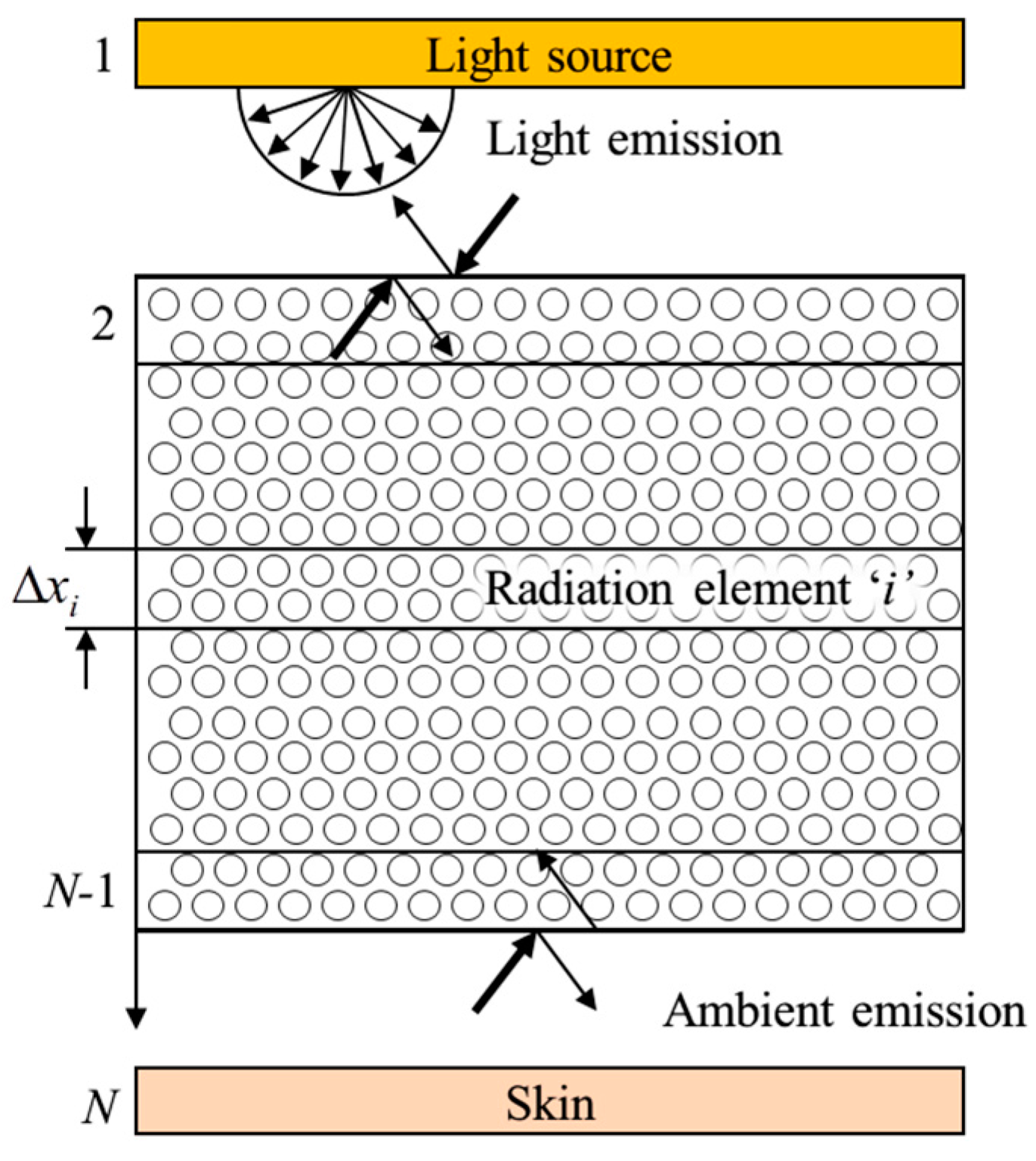
2.4. Radiative Transfer Analysis

To calculate the radiative transfer in the cosmetic layer, the cosmetic layer is handled as a participating medium in a one-dimensional plane parallel system, as shown in Figure 2. The radiative transfer in this system can be expressed using the one-dimensional radiative transfer equation (RTE):

$$\frac{1}{{\mathsf{\beta }}_{\mathsf{\lambda }}}\frac{d{I}_{\mathsf{\lambda }}(r,s)}{dS}=-I_{\mathsf{\lambda }}(r,s)+\frac{{\mathsf{\omega }}_{\mathsf{\lambda }}}{4\mathsf{\pi }}{\displaystyle {\int }_{4\mathsf{\pi }}{I}_{\mathsf{\lambda }}(r,s^{\prime }){\Phi }_{\mathsf{\lambda }}(s^{\prime }\to s)d\Omega }$$

(7)

where I (W m⁻² (sr)⁻¹) is the radiative intensity, r is a positional vector, s is a directional vector, S (m) denotes a path, and Ω (sr) represents a solid angle. Additionally, ω is the single scattering albedo and is defined as ω = σ_s/β, which gives the relative importance of scattering.

To solve the RTE, a radiation element method by means of the ray emission model (REM²) [17] is used. REM² can be applied to anisotropic media with specular and/or diffuse surface boundaries under arbitrary thermal conditions. A one-dimensional plane-parallel system is considered as the analytical model used in REM². Figure 2 shows the analytical model. In this calculation, the dispersed state is assumed to be mono-dispersed. Actually, the particles can make an agglomeration state, and the particle size distribution can change. It affects the spectral radiative properties of the particle cloud [18,19]. However, the effect of agglomeration was neglected to simplify the calculation. Elements 1 and N are taken as boundary elements. The S₁₂ approximation of Fiveland was used for direction division [12]. A refractive index 1 of air is assumed for all elements. Cosmetics are made of particles and a medium. The medium vaporizes on the skin; then, the cosmetic layer makes the particle layer dense. Therefore, in our calculation, the medium is assumed to be air. However, as indicated in the introduction, there are potential complications of the model due to other processes such as electron or triplet energy transfer in real application. These potential complications are also neglected to simplify the calculation. Solar irradiation enters from element 1. Spectral solar irradiation is evaluated using Bird’s model [20]. The basement is human skin, the reflectance of which was measured by Cooksey et al. [21]. The spectral reflectance of human skin is shown in Figure 3.

2.5. Evaluation Parameter

The performance parameter of the cosmetic for solar reflectance in the solar spectrum region is proposed as follows:

$${\mathsf{\rho }}_{TSR}=\frac{{\displaystyle {\int }_{0.30}^{2.50}\mathsf{\rho }(\mathsf{\lambda })I(\mathsf{\lambda })d\mathsf{\lambda }}}{{\displaystyle {\int }_{0.30}^{2.50}I(\mathsf{\lambda })d\mathsf{\lambda }}}$$

(8)

where I(λ) is the solar irradiation and ρ(λ) is the spectral reflectance of the cosmetic layer. This parameter is mainly used for designing TBC and should be high to reflect solar irradiation. A parameter is used to evaluate the maintenance of the visual performance of the cosmetic layer by considering the spectral eye sensitivity. It is defined as follows:

$$D_{VIS}=\frac{{\displaystyle {\int }_{0.38}^{0.78}\left|\mathsf{\rho }\left(\mathsf{\lambda }\right)-{\mathsf{\rho }}_{skin}(\mathsf{\lambda })\right|\eta (\mathsf{\lambda })I(\mathsf{\lambda })d\mathsf{\lambda }}}{{\displaystyle {\int }_{0.38}^{0.78}I(\mathsf{\lambda })d\mathsf{\lambda }}}$$

(9)

where η(λ) is the normalized standard luminous efficiency [12]. This parameter should be low for the SSC concept. To design SSC, which maintains the skin’s visual appearance and reflects sunlight, the optimization parameter R is defined as follows:

$$R=\frac{{\mathsf{\rho }}_{TSR}}{D_{VIS}}$$

(10)

To achieve an optimized cosmetic, parameter R should be maximized.

3. Results and Discussion

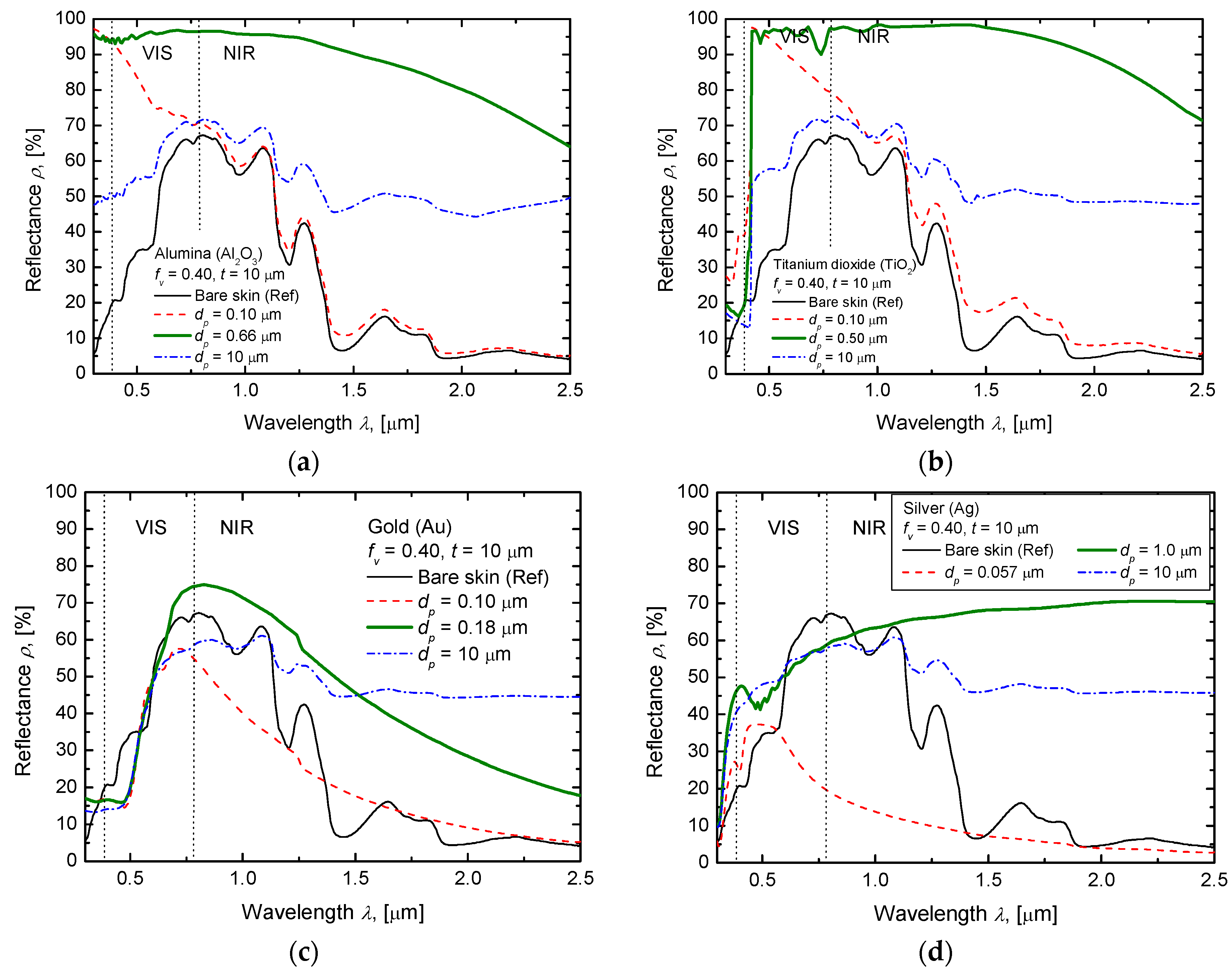
3.1. Spectral Reflectance

Figure 3 shows the calculated spectral reflectance of the cosmetic layer on human skin when the volume fraction of the cosmetic particle is 0.40 and the cosmetic layer thickness is 10 μm. The materials of the cosmetic particle are Al₂O₃, TiO₂, Au, and Ag. For Al₂O₃ and TiO₂ cosmetics, when the particle diameter is 0.10 μm, the spectral reflectance peak is in the VIS region, and the spectral reflectance decreases with the wavelength increment. When the particle diameter is an optimum one (Al₂O₃: d_p = 0.66 μm, TiO₂: d_p = 0.50 μm), the spectral reflectance is approximately 95% of the solar spectrum region. When the particle diameter is 10 μm, the spectral reflectance increases and comprises approximately 50% of the NIR region.

These spectral reflectances indicate that Al₂O₃ and TiO₂ are suitable for TBC. For the Au cosmetic, the spectral reflectance is lower than the ones of bare human skin when the particle diameter is 0.1 μm. When the particle diameter is 0.18 μm, the spectral reflectance is higher than those of bare human skin in the NIR spectrum region. At the same time, the cosmetic spectral reflectance is similar to that of bare human skin in the VIS region. In the spectrum over 1.5 μm, the spectral reflectance of the cosmetic with d_p = 10 µm is higher than those with d_p = 0.18 µm. However, the solar irradiation in that spectral region is not considerably high; therefore, the thermal barrier performance may not be high. For the Ag cosmetic, the spectral reflectance is lower than the ones of bare human skin when the particle diameter is 0.057 μm. However, the cosmetic spectral reflectance is similar to that of bare human skin in the short-VIS region. When the particle diameter is over 1.0 μm, the spectral reflectance is higher than those of bare human skin in the NIR spectrum region. However, the cosmetic spectral reflectance is not similar to that of bare human skin in the VIS region. These spectral reflectances indicate that Au and Ag are suitable for SSC.

3.2. Evaluation Parameter

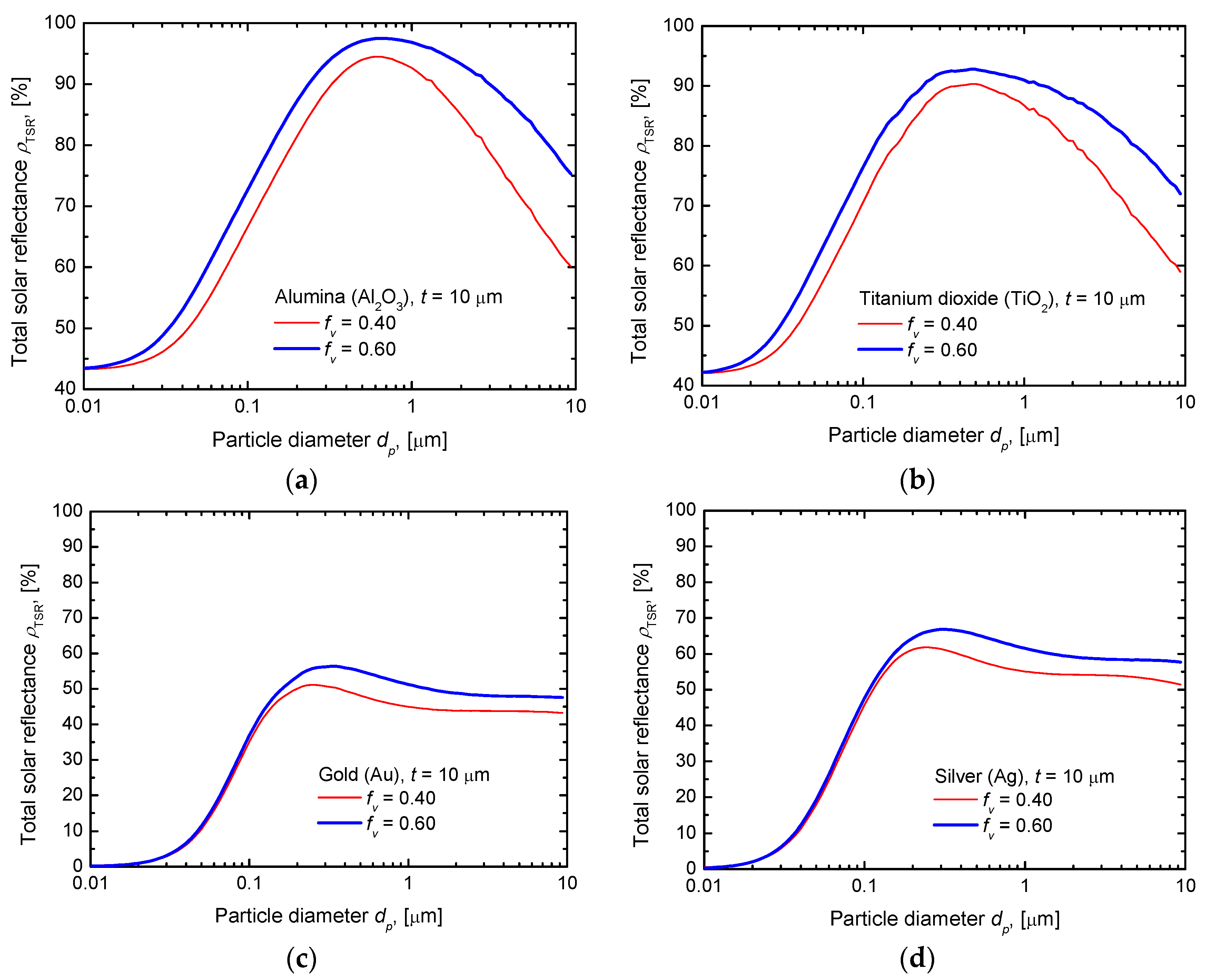
3.2.1. Total Solar Reflectance

To quantitatively evaluate the thermal barrier performance, the total solar reflectance is calculated according to Equation (8). Figure 4 shows the effect of the particle diameter on the total solar reflectance. For all cosmetics, the total solar reflectance increases with the increasing particle size until it reaches its maximum value. Therefore, when the material of the cosmetic is Al₂O₃, the optimum particle for TBC is 0.614 and 0.658 µm when the volume fraction f_v is 0.40 and 0.60, respectively.

When the material of the cosmetic is TiO₂, the optimum particle for TBC is 0.498 and 0.464 µm when the volume fraction f_v is 0.40 and 0.60, respectively. When the material of the cosmetic is Au, the optimum particle for TBC is 0.248 and 0.327 µm when the volume fraction f_v is 0.40 and 0.60, respectively. When the material of the cosmetic is Ag, the optimum particle for TBC is 0.248 and 0.305 µm when the volume fraction f_v is 0.40 and 0.60, respectively. When the volume fraction is 0.40, the maximum total solar reflectance is 94.5%, 90.3%, 51.2%, and 61.8% for Al₂O₃, TiO₂, Au, and Ag, respectively. Al₂O₃ and TiO₂ are so high that they are suitable for TBC, especially Al₂O₃. For a large particle diameter, a further increase in the particle diameter decreases the total solar reflectance, and the total solar reflectance converges to its limit value. Finally, we conclude that the Al₂O₃ particle with d_p = 0.614 µm is the optimum particle for TBC.

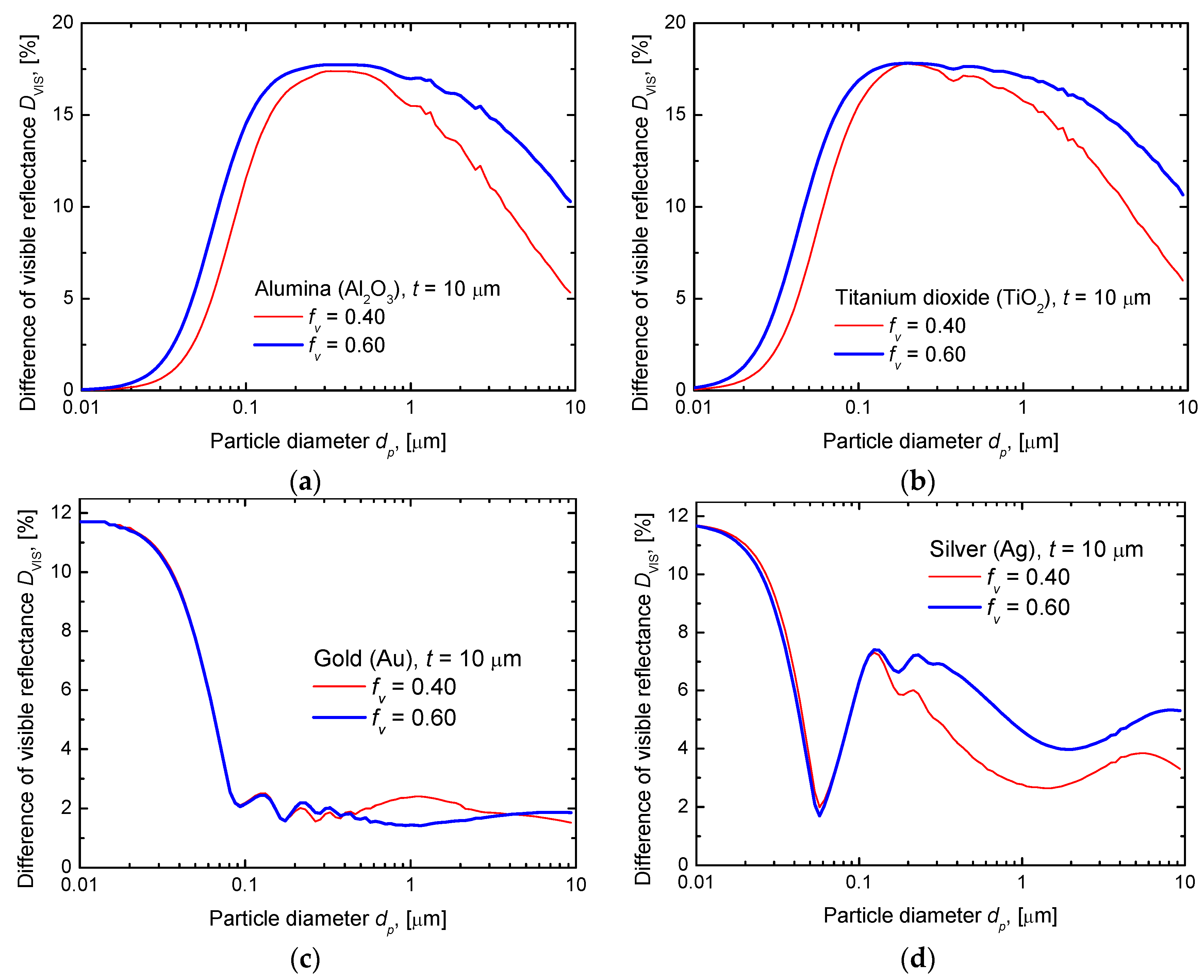
3.2.2. Difference of Visible Reflectance

To quantitatively evaluate the performance in maintaining the visual quality of skin, the difference of the visible reflectance is calculated according to Equation (9). Figure 5 shows the effect of the particle diameter on the difference of the visible reflectance. For Al₂O₃ and TiO₂ cosmetics, the difference increases with particle size until it reaches its maximum value. A further increase in particle diameter decreases the difference. To design SSC, the difference should be low; then, the particle diameter is small. However, the total solar reflectance is low when the particle diameter is small, as shown in Figure 4. This result indicates that Al₂O₃ and TiO₂ are not suitable for SSC.

For the Au cosmetics, the difference decreases with the increasing of the particle size until it reaches its minimum value. A further increase in the particle diameter makes the difference almost the same. The difference of visible reflectance is the lowest in the cosmetic with 9.32 µm diameter particles in a 0.40-volume fraction and with 1.14 μm diameter particles in a 0.60-volume fraction. When the difference is small, the total solar reflectance is also high, as shown in Figure 4c. For the Ag cosmetics, the difference decreases with the increasing of the particle size until it reaches its minimum value. A further increase in the particle diameter makes the difference high. The difference of visible reflectance is the lowest in the cosmetic with 0.057 µm diameter particles in a 0.40-volume and a 0.60-volume fraction. However, when the difference is small, the total solar reflectance is low, as shown in Figure 4d. These results indicate that Au is suitable for SSC.

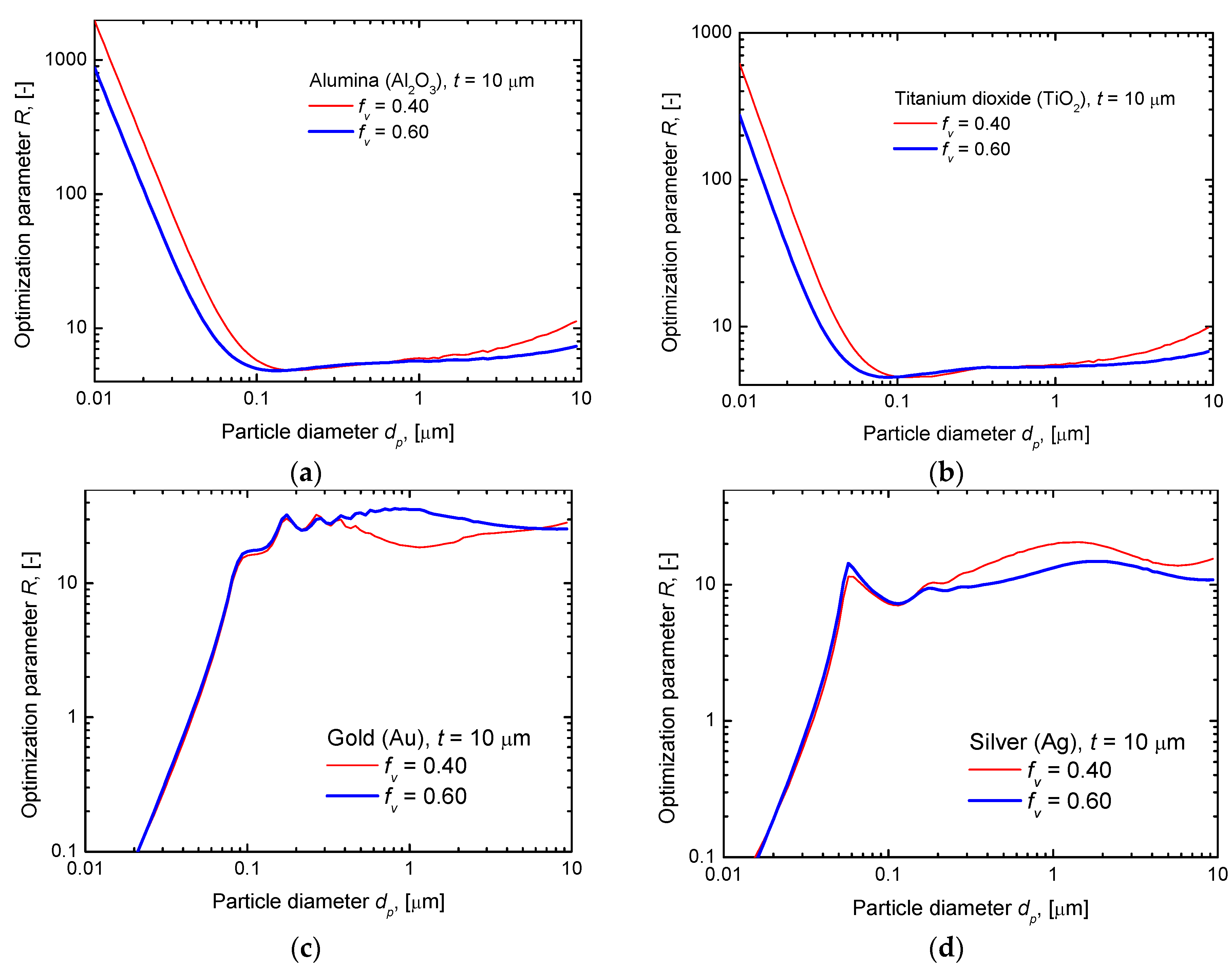
3.2.3. Optimization Parameter

To quantitatively evaluate the spectral selective performance, optimization parameter R was calculated according to Equation (10). Figure 6 shows the effect of the particle diameter on R. For Al₂O₃ and TiO₂ cosmetics, the optimization parameter decreases with the increasing of the particle size until it reaches its minimum value. A further increase in the particle diameter increases the optimization parameter. When the optimization parameter is high, the particle diameter is low. The higher optimization parameter corresponds to the smaller particle regime, in which the total solar reflectance is lower Therefore, these cosmetics cannot be used as SSC. However, the difference of the visible reflectance is so small that the optimization parameter becomes high.

For the Au and Ag cosmetics, the optimization parameter increases with increasing the particle size until it reaches its maximum value. A further increase in the particle diameter makes the optimization parameter almost the same. For the Au cosmetics, when the particle diameter is 0.18 μm, the optimization parameter is approximately 31, regardless of the volume fraction. For the Ag cosmetics, when the particle diameter is 0.057 μm, the optimization parameter is approximately 14, regardless of the volume fraction. Therefore, we conclude that the Au particle with d_p = 0.18 µm is the optimum one for SSC. This result shows that the ratio of energy in VIS and NIR regions can help the theoretical design of the spectral selective cosmetic.

4. Conclusions

In this paper, a method of optimizing the thermal barrier cosmetic and spectral selective cosmetic by controlling the particle size and material was proposed. The radiative properties of single cosmetic particles of a wide range of particle sizes and wavelengths in non-absorbing air were calculated based on the Mie theory. Al₂O₃, TiO₂, Au, and Ag were used as the material of the cosmetic particle. The radiative property of a particle cloud in dependent scattering was calculated. The radiative transfer in the cosmetic layer was analyzed by REM², and the spectral reflectance of the cosmetic layer on the human skin was calculated. To quantitatively evaluate the spectral selective performance, the three evaluation parameters were defined and the effects of the particle sizes and materials on the spectral properties of the cosmetic layer were discussed.

The spectral reflectance of the cosmetic layer on the human skin was calculated. The new parameter was defined to evaluate the performance of the thermal barrier cosmetic and spectral selective cosmetic. For the thermal barrier cosmetic, the optimum particle was determined to be the Al₂O₃ particle with d_p = 0.614 µm. For the spectral selective cosmetic, the optimum particle was determined to be the Au particle with d_p = 0.18 µm. In fact, the cosmetic design should be performed with consideration of the skin sweat gland size, particle mass, and particle cost. However, our optimization method can partly enable the cosmetic design to control the spectral property of the cosmetic. We hope that our designed cosmetic will have beneficial applications, such as helping prevent heatstroke in athletes and workers in outdoor environments.