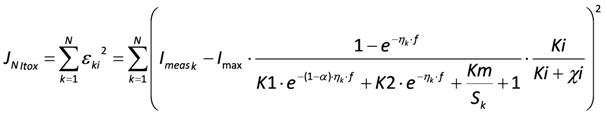1. Introduction
Electrochemically active microorganisms in a microbial fuel cell (MFC) oxidize organic material to carbon dioxide, protons and electrons. In the absence of a soluble electron acceptor they donate the electron to a solid electron acceptor, the anode. An electron acceptor at the second electrode, the cathode, is reduced so that the electrons flow through the electrical circuit and thus produce an electrical current. The rate of degradation of organic material is proportional to the current. Therefore, the current is a measure for the metabolic activity of the bacteria in the microbial fuel cell.
The MFC has many applications such as a renewable source for energy production, bio-electrochemical production of chemicals or as a BOD sensor in water [
1,
2,
3,
4]. This paper, however, focuses on the use of an MFC as sensor for toxic chemicals in water.
The MFC produces a constant current under constant conditions. However, when a toxic component enters the anodic compartment of the MFC, the bacteria are affected by the toxic component, resulting in a change of current. This change is often seen as a decrease in current [
2,
5]. The MFC can therefore be used as a senor for toxic components in water.
In research on MFCs, the cells are typically characterized by polarization curves [
6,
7,
8]. When the anode potential is varied, the resulting current gives information related to the energetic losses in the system and the metabolic state of the bacteria. At a certain potential the current will be zero. This zero-current potential mainly depends on the oxidation potential of the organic material, the substrate. The difference between this zero-current potential and the actual anode potential is called the anodic overpotential. This anodic overpotential determines the energy that bacteria can gain from the oxidation of the substrate and the corresponding donation of electrons to the anode. A polarization curve thus shows the dependency of the current on the anodic overpotential.
The Butler Volmer Monod (BVM) model was developed to describe polarization curves of the MFC under nontoxic conditions [
9]. Under toxic conditions one of the extended BVM models can be used [
10]. These models are based on biochemical and electrochemical kinetics. The extended BVM models also include enzyme inhibition kinetics. Theoretically, it is possible to distinguish between four types of toxic inhibitions.
(1) Overall inhibition of the bacteria, where the toxic component acts as an irreversible inhibitor. This gives the following model
In the following, this model is referred to as “Itox”.
(2) Inhibition effect on the ratio between electrochemical and biochemical rate constant. This gives the following model:
where, for example, the toxic component acts as an electron acceptor. This model is referred to as “IK1”.
(3) Inhibition effect on the ratio between the forward and backward reaction rate constant of substrate oxidation. This gives the following model:
and is referred to as ‘IK2’
(4) Competition between substrate and toxic component to bind to the redox complex. This gives
and is referred to as ‘IKm’.
In these models I (mA) is the current, Imax (mA) is the maximum current determined by maximum enzymatic rates of microorganisms, η (V) is the overpotential, K1 (−) is a lumped parameter describing the ratio between biochemical and electrochemical rate constants, K2 (−) is a lumped parameter describing the forward over backward biochemical rate constants, Km (mol/L) is the substrate affinity constant, and S (mol/L) the substrate concentration. Furthermore, f = F/RT with F (C/mol) being the Faraday’s constant, R (J/mol/K) the gas constant and T (K) temperature. Ki is the inhibition constant of component i and χi is the concentration of toxic component i.
Ki is the inhibition constant that shows how toxic the component is for the bacteria and thus how sensitive the sensor is for the toxic component. Hence, a low value for
Ki gives a very sensitive sensor. For each of these inhibition mechanisms the polarization curves look different. Furthermore, for each of the mechanisms it is possible to determine at which overpotential the current changes most when a toxic component enters the cell [
10]. As yet, no experimental data on polarization curves in the presence of toxic components are available in the literature. In this study, we investigate whether it is possible to fit one of the models (1–4) to the polarization curves when toxic components are present in the system. Furthermore, we study if it is possible to distinguish between different types of toxic components based on the different enzyme inhibition kinetics.
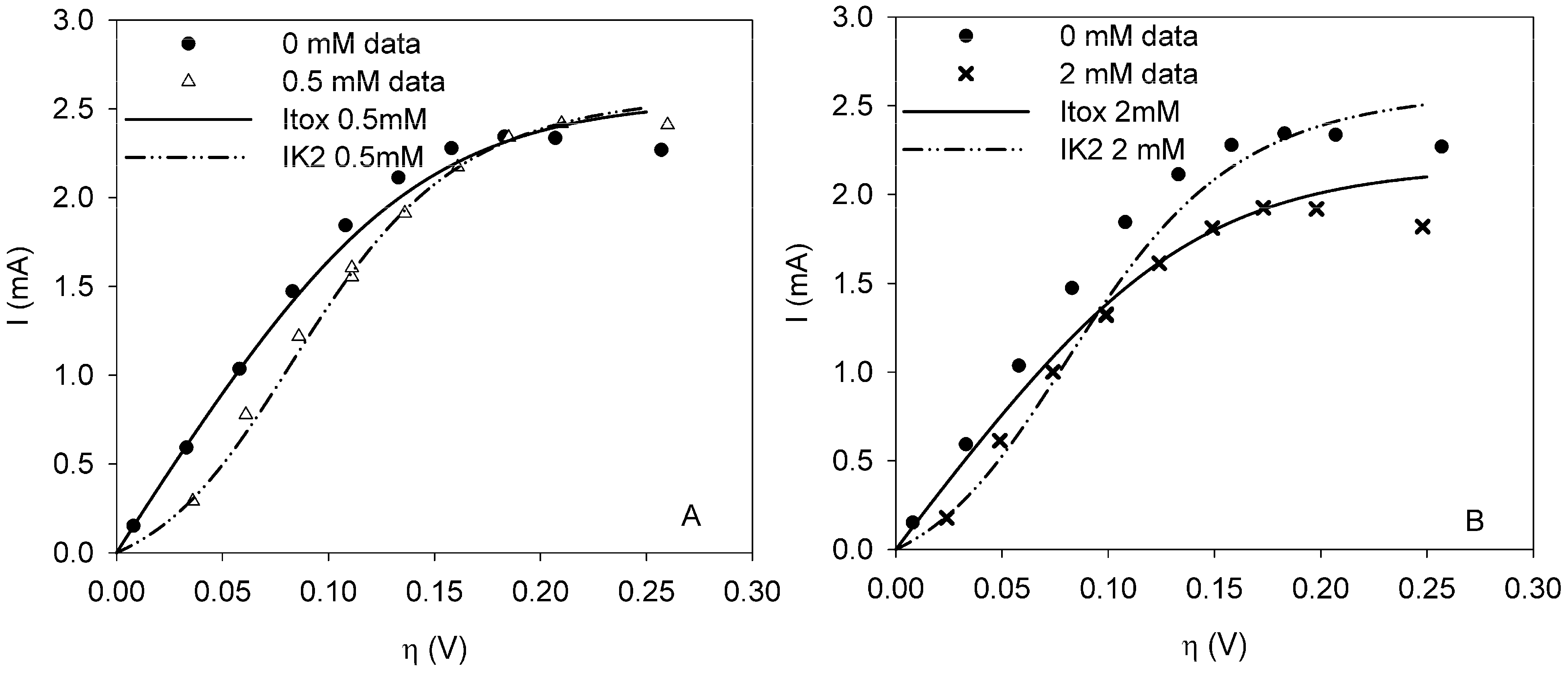
First, polarization curves under non-toxic and toxic condition using four components at three different concentrations were experimentally determined. These polarization curves were then compared with the model responses (1–4), describing the four types of toxic inhibitions.
4. Conclusions
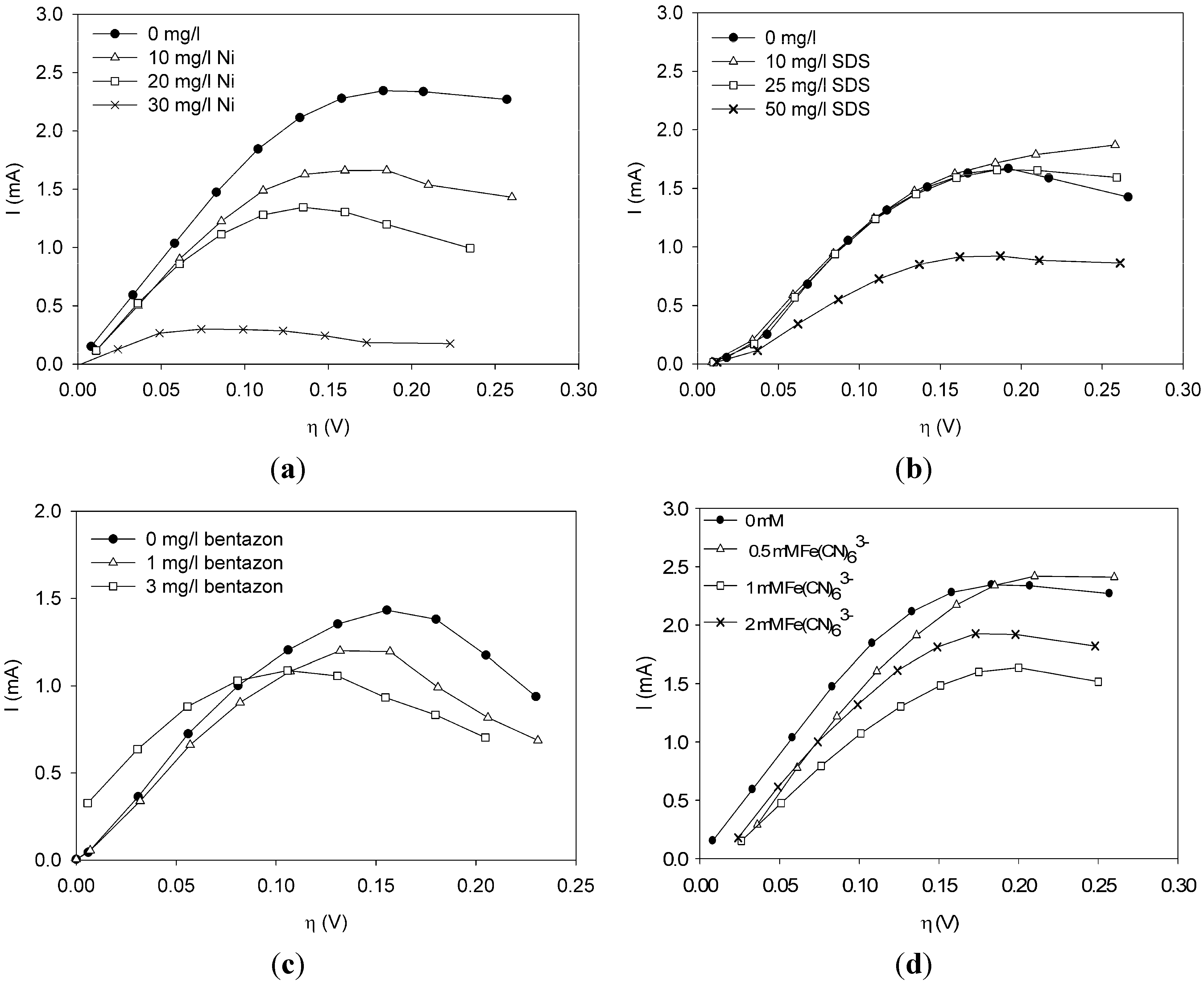
This paper shows for the first time the effect of toxic components on polarization curves in an MFC-based biosensor. From experimentally determined polarization curves, it is clear that toxic components have an effect on the electrochemically active bacteria in the cell, which is seen as a shift in the polarization curve. The way the polarization curve changes depends on the type of components and their concentration. There is a dose-response relationship for all the tested components, meaning that current decreases more when the concentration of toxic component is higher. This paper shows that dose-response relationships can be visualized when polarization curves are made. As seen for nickel and SDS, a higher concentration leads to a lower current at all overpotentials.
It was possible to fit the extended BVM models (1–4) to the polarization curves related to all the components used. Comparing the sum of squared errors for each fit, it is clear that the model Itox fits best for nickel and SDS and bentazon. For potassiumferricyanide it seems that combined effects play a role. At low concentrations, only one type of kinetic inhibition plays a role (model IK2). When the concentration increases, however, model Itox, representing the overall inhibition of the cell, gives a better fit.
The results show that the extended BVM model can be used to distinguish between different types of kinetic inhibitions although in most cases the same type of inhibition was observed, i.e., the inhibition of the whole organisms (model Itox). The extended BVM-model can determine the type of kinetic inhibition of a component, but the model may need to be improved for combined effects or for a concentration effect.
The value of the inhibition constant Ki can be determined. The value of Ki tells something about the sensitivity of the sensor for the measured component. This is important to know when deciding whether the sensor is suitable for a specific application.
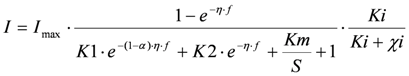


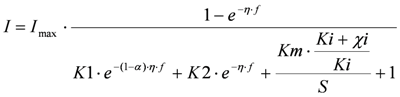
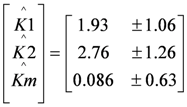
 and
and  the models were then fitted to the polarization curve related to the case with 20 mg/L nickel in the sensor. The value of Km could not be estimated accurately because of
the models were then fitted to the polarization curve related to the case with 20 mg/L nickel in the sensor. The value of Km could not be estimated accurately because of  ~0.1 mM and S = 5 mM, S >> Km and leading to Km/S << 1 in Equation (1). Moderate toxicity levels such that
~0.1 mM and S = 5 mM, S >> Km and leading to Km/S << 1 in Equation (1). Moderate toxicity levels such that  fiting the data to model IKm (Equation (4)) will result in inaccurate estimates of Ki and are thus not considered here. For the three remaining types of toxic inhibition, the values as shown in Table 1 were found:
fiting the data to model IKm (Equation (4)) will result in inaccurate estimates of Ki and are thus not considered here. For the three remaining types of toxic inhibition, the values as shown in Table 1 were found: 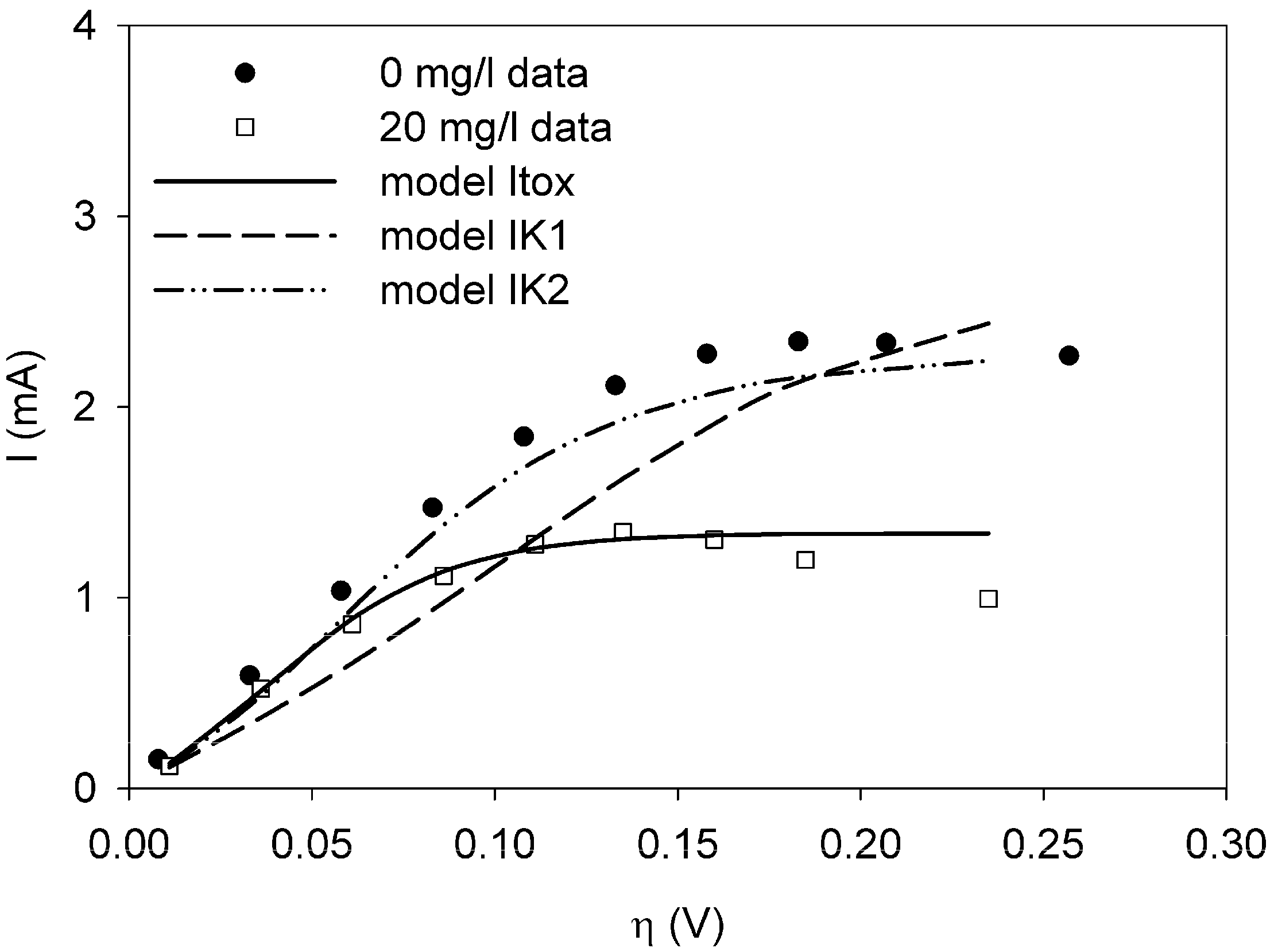
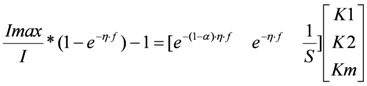
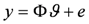
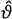 is given by
is given by
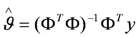
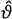 the estimate of [K1 K2 Km]T. The Nx3-dimensional regressor matrix
the estimate of [K1 K2 Km]T. The Nx3-dimensional regressor matrix contains the N values of the overpotential at which the current is measured and the estimated substrate concentration S in the biofilm.
contains the N values of the overpotential at which the current is measured and the estimated substrate concentration S in the biofilm. containing the measured current (I*) at each overpotential.
containing the measured current (I*) at each overpotential. 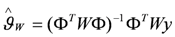

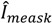 the k-th measurement of the current and
the k-th measurement of the current and 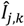 the estimated current at measurement index k using the estimated parameter values of K1, K2 and Km. Index j denotes the model type (Itox, IK1, IK2, or IKm) with the corresponding equation to calculate the estimated current.
the estimated current at measurement index k using the estimated parameter values of K1, K2 and Km. Index j denotes the model type (Itox, IK1, IK2, or IKm) with the corresponding equation to calculate the estimated current.