Thermal Conductivity of a Nanoscale Yttrium Iron Garnet Thin-Film Prepared by the Sol-Gel Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
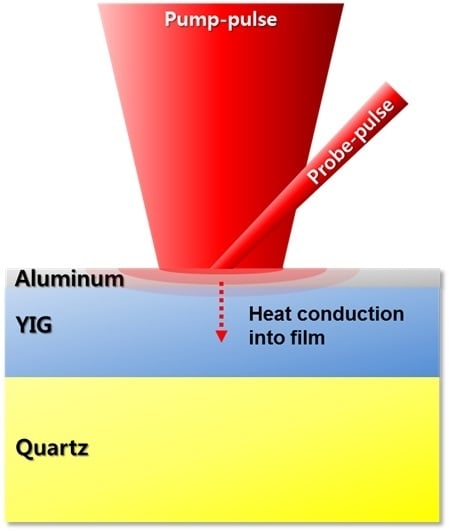
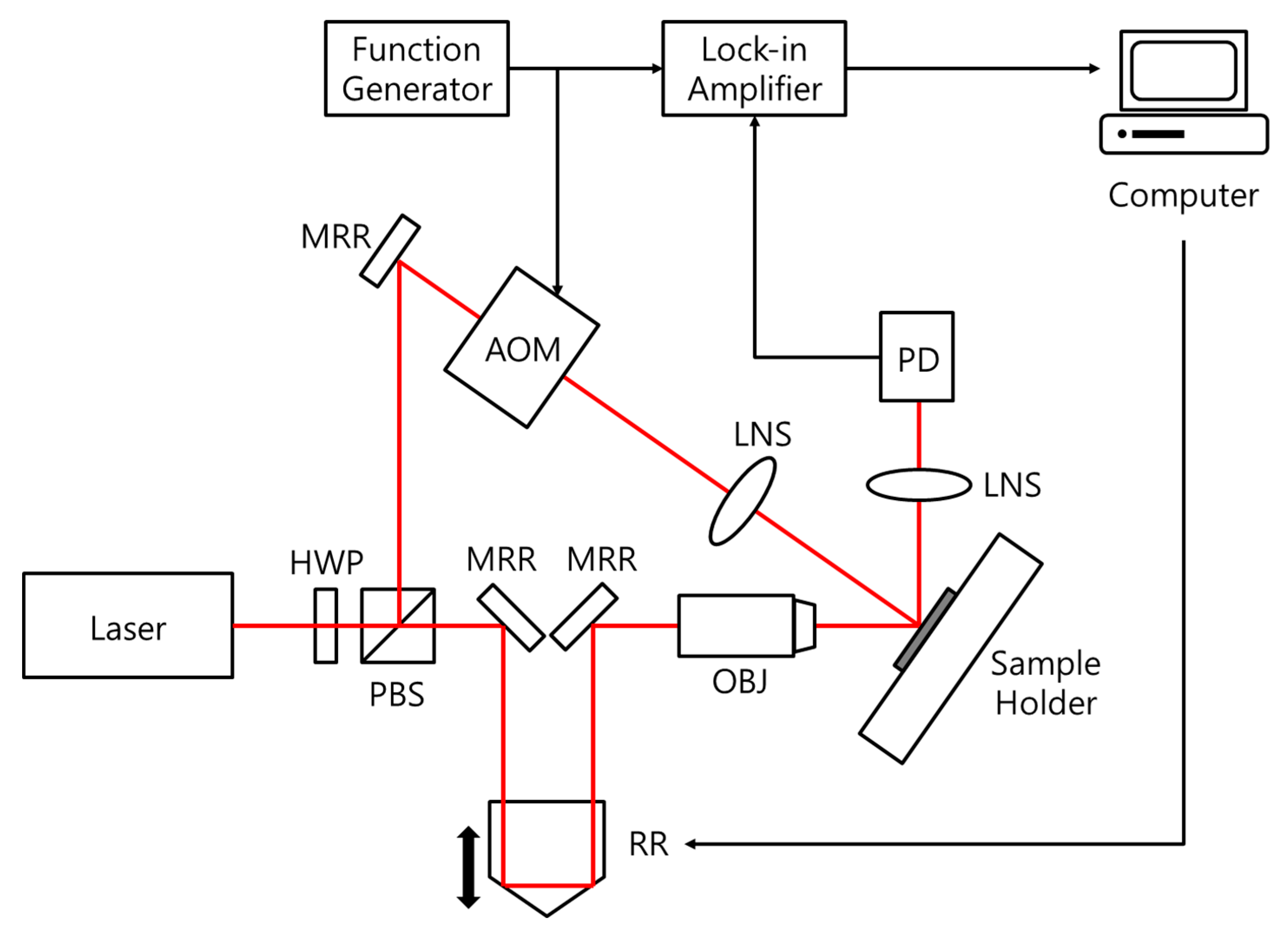
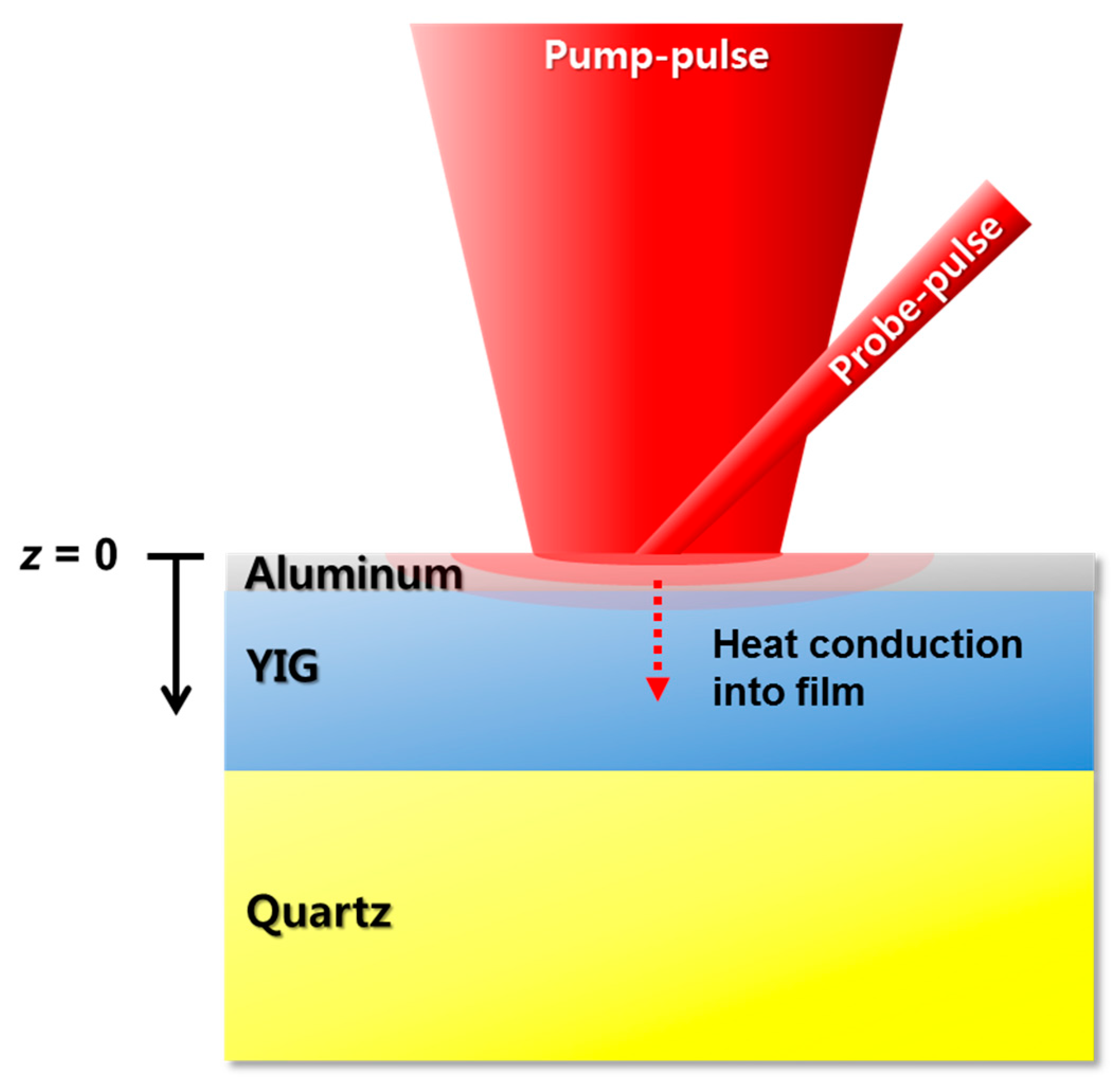
2.2. Ultrafast Pump-Probe Technique
3. Theory and Calculation
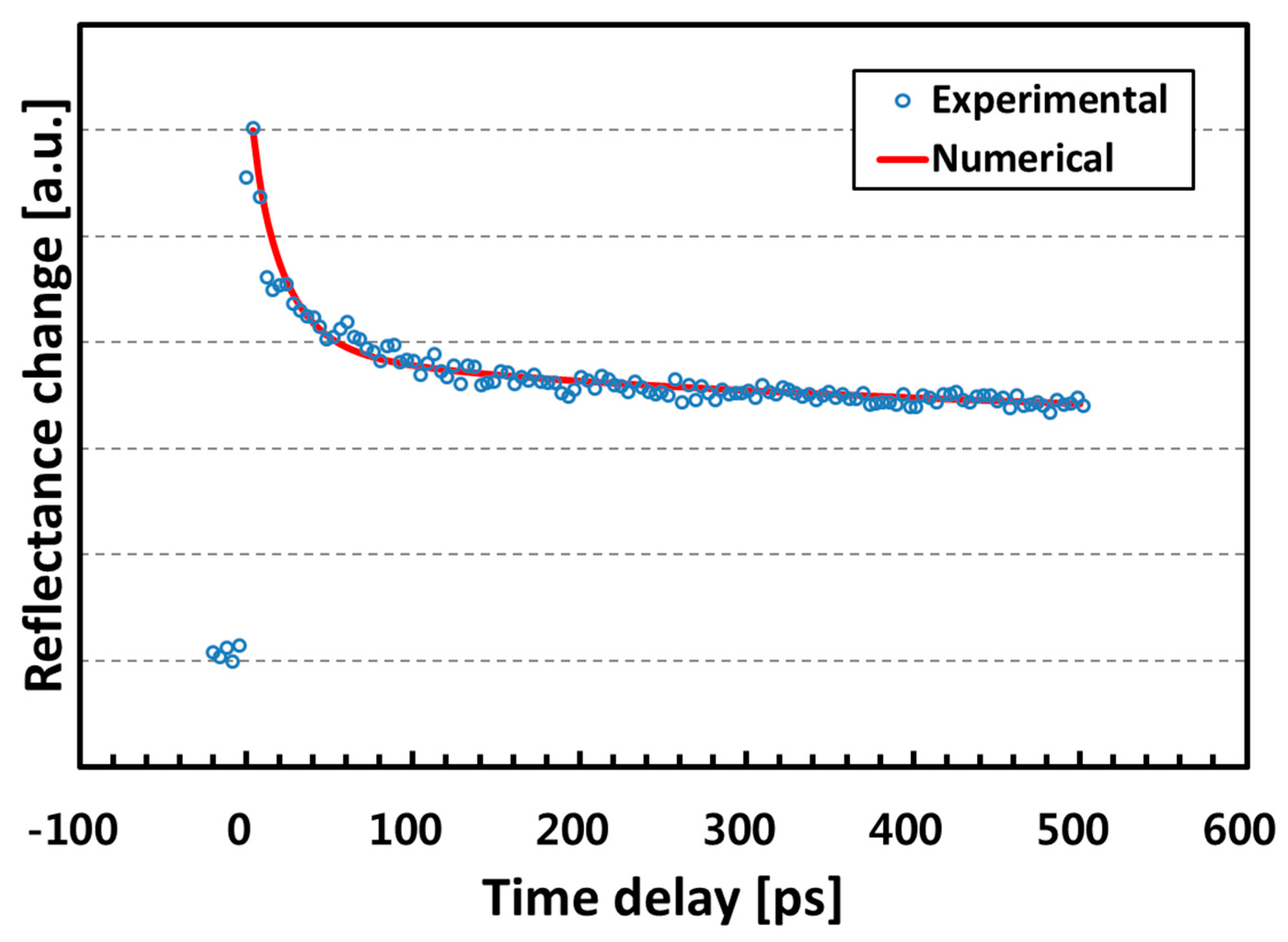
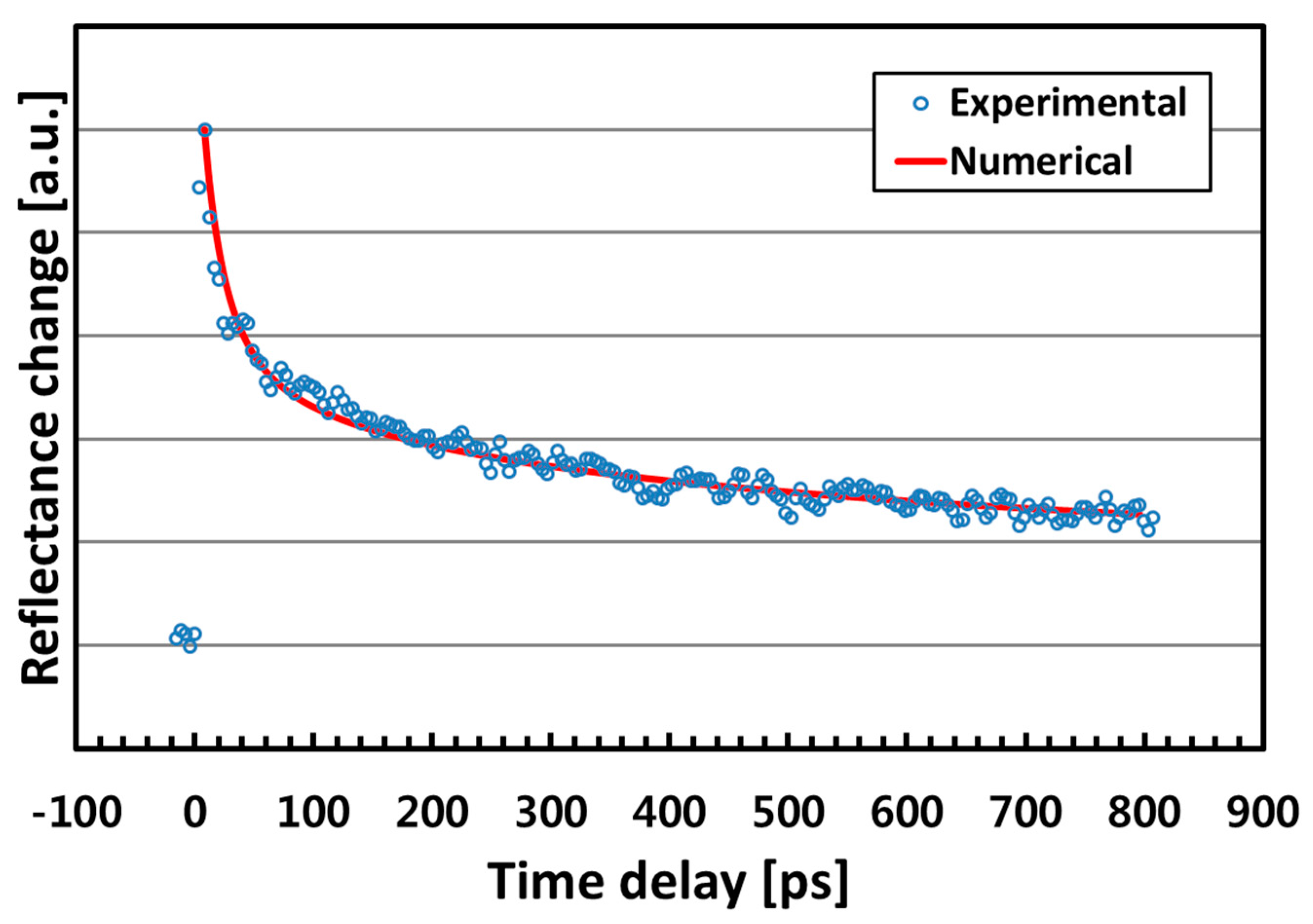
4. Results and Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kaya, A.; Atalay, S.; Gencer, H.; Kaya, O.; Kolat, V.; Izgi, T. YIG film for magnetic field sensor. Acta Phys. Pol. A 2015, 127, 937–939. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, C.; Ji, R.; Fang, C.; Zeng, Y. Low-temperature synthesis and microstructure-property study of single-phase yttrium iron garnet (YIG) nanocrystals via a rapid chemical coprecipitation. Mater. Chem. Phys. 2011, 125, 646–651. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, H.; Liu, Y.; Wen, Q.; Jia, L. The magnetic and dielectric properties of microwave sintered yttrium iron garnet (YIG). Mater. Lett. 2008, 62, 2647–2650. [Google Scholar] [CrossRef]
- Uchida, K.-I.; Kikkawa, T.; Miura, A.; Shiomi, J.; Saitoh, E. Quantitative temperature dependence of longitudinal spin seebeck effect at high temperatures. Phys. Rev. X 2014, 4, 041023. [Google Scholar] [CrossRef]
- Boudiar, T.; Payet-Gervy, B.; Blanc-Mignon, M.-F.; Rousseau, J.-J.; Le Berre, M.; Joisten, H. Magneto-optical properties of yttrium iron garnet (YIG) thin films elaborated by radio frequency sputtering. J. Magn. Magn. Mater. 2004, 284, 77–85. [Google Scholar] [CrossRef]
- Euler, C.; Hołuj, P.; Langner, T.; Kehlberger, A.; Vasyuchka, V.; Kläui, M.; Jakob, G. Thermal conductance of thin film YIG determined using bayesian statistics. Phys. Rev. B 2015, 92, 094406. [Google Scholar] [CrossRef]
- Ravi, B.; Gandhi, A.S.; Guo, X.; Margolies, J.; Sampath, S. Liquid precursor plasma spraying of functional materials: A case study for yttrium aluminum garnet (YAG). J. Therm. Spray Technol. 2008, 17, 82–90. [Google Scholar] [CrossRef]
- Shaiboub, R.; Ibrahim, N.B.Y.; Abdullah, M.; Abdulhade, F. The physical properties of erbium-doped yttrium iron garnet films prepared by sol-gel method. J. Nanomater. 2012, 2012, 2. [Google Scholar] [CrossRef]
- Aldbea, F.W.; Ahmad, N.; Ibrahim, N.; Yahya, M. Effect of increasing ph value on the structural, optical and magnetic properties of yttrium iron garnet films prepared by a sol-gel method. J. Sol-Gel Sci. Technol. 2014, 71, 31–37. [Google Scholar] [CrossRef]
- Opuchovic, O.; Beganskiene, A.; Kareiva, A. Sol-gel derived Tb3Fe5O12 and Y3Fe5O12 garnets: Synthesis, phase purity, micro-structure and improved design of morphology. J. Alloys Compd. 2015, 647, 189–197. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, X.; Wei, X.; Zhang, L.; Yao, X. Preparation and annealing process of Y3Fe5O12 by sol-gel method. Ferroelectrics 2001, 264, 249–254. [Google Scholar]
- Musa, M.A.; Osman, N.H.; Hassan, J.; Zangina, T. Structural and magnetic properties of yttrium iron garnet (YIG) and yttrium aluminum iron garnet (YALG) nanoferrite via sol-gel synthesis. Results Phys. 2017, 7, 1135–1142. [Google Scholar] [CrossRef]
- Pramanik, N.C.; Fujii, T.; Nakanishi, M.; Takada, J. Development of nanograined hexagonal barium ferrite thin films by sol-gel technique. Mater. Lett. 2005, 59, 468–472. [Google Scholar] [CrossRef]
- Lopez, O.; Amy-Klein, A.; Lours, M.; Chardonnet, C.; Santarelli, G. High-resolution microwave frequency dissemination on an 86-km urban optical link. Appl. Phys. B Lasers Opt. 2010, 98, 723–727. [Google Scholar] [CrossRef] [Green Version]
- Olson, F.; Yaeger, J. Microwave delay techniques using YIG. IEEE Trans. Microw. Theory Tech. 1965, 13, 63–69. [Google Scholar] [CrossRef]
- Kato, H.; Inoue, M. Reflection-mode operation of one-dimensional magnetophotonic crystals for use in film-based magneto-optical isolator devices. J. Appl. Phys. 2002, 91, 7017–7019. [Google Scholar] [CrossRef]
- An, K.; Olsson, K.S.; Weathers, A.; Sullivan, S.; Chen, X.; Li, X.; Marshall, L.G.; Ma, X.; Klimovich, N.; Zhou, J. Magnons and phonons optically driven out of local equilibrium in a magnetic insulator. Phys. Rev. lett. 2016, 117, 107202. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.Y.; Alwi, H.A.; Huang, Q.; Abd-Shukor, R.; Tsai, C.; Wang, H.; Kim, K.; Naugle, D.; Krishnaswamy, S. Thermal diffusivity measurement of YBa2Cu3O7−x thin film with a picosecond thermoreflectance technique. Phys. C Supercond. 2010, 470, 365–368. [Google Scholar] [CrossRef]
- Richardson, C.; Ehrlich, M.; Wagner, J. Interferometric detection of ultrafast thermoelastic transients in thin films: Theory with supporting experiment. J. Opt. Soc. Am. B 1999, 16, 1007–1015. [Google Scholar] [CrossRef]
- Zhang, F.; Krishnaswamy, S.; Lilley, C.M. Bulk-wave and guided-wave photoacoustic evaluation of the mechanical properties of aluminum/silicon nitride double-layer thin films. Ultrasonics 2006, 45, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag. 2016, 138, 040802. [Google Scholar] [CrossRef]
- Capinski, W.; Maris, H.; Ruf, T.; Cardona, M.; Ploog, K.; Katzer, D. Thermal-conductivity measurements of GaAs/AlAs superlattices using a picosecond optical pump-and-probe technique. Phys. Rev. B 1999, 59, 8105–8113. [Google Scholar] [CrossRef]
- Stevens, R.J.; Smith, A.N.; Norris, P.M. Measurement of thermal boundary conductance of a series of metal-dielectric interfaces by the transient thermoreflectance technique. J. Heat Transf. 2005, 127, 315–322. [Google Scholar] [CrossRef]
- Miklós, A.; Bozóki, Z.; Lörincz, A. Picosecond transient reflectance of thin metal films. J. Appl. Phys. 1989, 66, 2968–2972. [Google Scholar] [CrossRef]
- Volkov, Y.A.; Palatnik, L.; Pugachev, A. Investigation of the thermal properties of thin aluminum. Sov. J. Exp. Theor. Phys. 1976, 43, 1171. [Google Scholar]
- Stops, D. Size effect on thermal conductivity in thin aluminium films. Thin Solid Films 1980, 67, L43–L46. [Google Scholar] [CrossRef]
- Stojanovic, N.; Yun, J.; Washington, E.B.; Berg, J.M.; Holtz, M.W.; Temkin, H. Thin-film thermal conductivity measurement using microelectrothermal test structures and finite-element-model-based data analysis. J. Microelectromech. Syst. 2007, 16, 1269–1275. [Google Scholar] [CrossRef]
- Schmidt, A.J.; Cheaito, R.; Chiesa, M. Characterization of thin metal films via frequency-domain thermoreflectance. J. Appl. Phys. 2010, 107, 024908. [Google Scholar] [CrossRef]
- Thomsen, C.; Grahn, H.T.; Maris, H.J.; Tauc, J. Surface generation and detection of phonons by picosecond light pulses. Phys. Rev. B 1986, 34, 4129. [Google Scholar] [CrossRef]
- Clark, A.; Strakna, R. Elastic constants of single-crystal YIG. J. Appl. Phys. 1961, 32, 1172–1173. [Google Scholar] [CrossRef]
- Weber, M.J. Handbook of Optical Materials; CRC Press: Boca Raton, FL, USA, 2002; Volume 19. [Google Scholar]
- Miura, A.; Kikkawa, T.; Iguchi, R.; Uchida, K.-I.; Saitoh, E.; Shiomi, J. Probing length-scale separation of thermal and spin currents by nanostructuring YIG. Phys. Rev. Mater. 2017, 1, 014601. [Google Scholar] [CrossRef]
- Slack, G.A.; Oliver, D. Thermal conductivity of garnets and phonon scattering by rare-earth ions. Phys. Rev. B 1971, 4, 592. [Google Scholar] [CrossRef]
- Bertolotti, M.; Liakhou, G.; Li Voti, R.; Paoloni, S.; Sibilia, C.; Sparvieri, N. A cryostatic setup for the low-temperature measurement of thermal diffusivity with the photothermal method. Rev. Sci. Instrum. 1995, 66, 5598–5602. [Google Scholar] [CrossRef]
- Padture, N.P.; Klemens, P.G. Low thermal conductivity in garnets. J. Am. Ceram. Soc. 1997, 80, 1018–1020. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Lattice constant (Å) | 12.354 |
| Crystal size (nm) | 24 |
| Saturation magnetization (emu/g) | 6.1 |
| Coercivity (Oe) | 38 |
| Material | Aluminum | YIG | Quartz |
|---|---|---|---|
| Density (kg/m3) | 2700 | 5170 | 2203 |
| Specific heat (J/kg·K) | 900 | 590 | 740 |
| Refractive index | 2.23 | - | - |
| Extinction coefficient | 7.60 | - | - |
| Optical reflectivity | 0.88 | - | - |
| Reference | Sample Thickness (μm) | Deposition Technique | Characterization Technique | Measurement Temperature (K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|---|---|
| Present study | 0.250 | Sol-gel | Ultrafast pump-probe | 300 | 11.0 |
| [6] | 0.190 | Pulsed laser deposition | 3ω method | 275 | 9.0 |
| [4] | 1.0 × 103 | Liquid phase epitaxy | Laser flash method | 300 | 8.0 |
| [17] | 2.5 × 103 | Traveling solvent floating zone | Steady-state method | 300 | 8.8 |
| [33] | 11.3 × 103 | PbO–PbF2 flux | Steady-state method | 300 | 7.4 |
| [35] | 12.7 × 103 | Sintering | Laser flash method | 296 | 6.0 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.Y. Thermal Conductivity of a Nanoscale Yttrium Iron Garnet Thin-Film Prepared by the Sol-Gel Process. Nanomaterials 2017, 7, 247. https://doi.org/10.3390/nano7090247
Kim YY. Thermal Conductivity of a Nanoscale Yttrium Iron Garnet Thin-Film Prepared by the Sol-Gel Process. Nanomaterials. 2017; 7(9):247. https://doi.org/10.3390/nano7090247
Chicago/Turabian StyleKim, Yun Young. 2017. "Thermal Conductivity of a Nanoscale Yttrium Iron Garnet Thin-Film Prepared by the Sol-Gel Process" Nanomaterials 7, no. 9: 247. https://doi.org/10.3390/nano7090247