On the Performance of the Cache Coding Protocol
Abstract
:1. Introduction
2. System Model
3. Heuristic
3.1. Source Coding
3.2. Unrestricted Coding
3.3. Cache Coding
- The probability of receiving a packet by a relay node or is . As we need n packets in each relay node, the expected number of transmissions from S to and until the relays decode the whole generation is equal to .
- Until and decode the whole generation, they forward the packets received from S. As each relay node receives n packets until decoding the whole generation, each relay node forwards n coded packets received from S. Thus, the expected number of transmissions from and to D until both and have decoded the whole generation is equal to .
- The expected number of transmissions from and to D after they have decoded the whole generation requires us to determine the expected number of linearly independent packets received by D before and have decoded the whole generation. Before the relay nodes decode the whole generation, the expected number of packets received by D from is equal to . Meanwhile, the expected number of packets received by D only from is equal to . Hence, the expected number of linearly independent packets in D, before the relay nodes decode the whole generation, is equal to . In order to decode the whole generation, D needs a total of n linearly independent packets; hence, after and have decoded the whole generation, D must receive another linearly dependent packets. Since the probability of receiving a packet by D from and the probability of receiving a packet by D from is , the expected number of transmissions from and to D after they have decoded the whole generation is equal to .
4. Absorbing Markov Chain Model
4.1. Transition Probabilities
- andNo single relay node has decoded the data or decodes the data after receiving the new coded packet. Thus, both relays receive the coded packet and forward the received packet to D. Thus,In this case, for example, consider the probability where , and . This case is the union of three possibilities.
- and receive from S. D receives from both and . In this case, all receptions are successful, so the probability of this incident is equal to .
- and receive from S. D receives only from . In this case, three of four receptions are successful, so the probability of this incident is equal to
- and receive from S. D receives only from . In this case, three of four receptions are successful, so the probability of this incident is equal to .
- and or and .In this case, if one the relay node with DoFs equal to receives a new packet, it decodes the generation completely and starts to send recoded data to D. However, the other relay node still forwards the received coded packet. Thus,In this case, for example, consider the probability where , and . This case occurs when and both receive a packet from S and D receives a packet from both and . Therefore, all four transmissions must be successful; hence, this incident must have a probability of .
- andIn this case, recodes and sends data to D, while forwards the received coded packets. Even if receives a new packet and decodes data completely (the case ), it recodes data and sends a recoded packet to the destination, which is different from the packet sent by . The difference between this case and Case 2 is the fact that sends a recoded packet to D whether or not it receives a packet from S. However, this event does not occur in Case 2. Thus,In this case, consider the probability where , and . If , this incident occurs when receives a packet from S, and also D receives a packet from either or . Each of these incidents have a probability of . Hence, the total probability is equal to .
- Case 4 : andIn this case, recodes and sends data to D, while forwards the received coded packets. Even if receives a new packet and decodes data completely (the case ), it recodes data and sends a recoded packet to the destination, which is different from the packet sent by . The difference between this case and Case 2 is the fact that sends a recoded packet to D whether or not it receives a packet from S. However, this event does not occur in Case 2. The probabilities in this case are identical to the previous case. Thus,
- Case 5 : andIn this case, both and have decoded the data. Therefore, S will not transmit any longer to or , while and will recode the decoded data and send different coded packets to D.
4.2. Cost of Transitions
- S sends a packet unless the DoF of both and is equal to n.
- and send a packet when their DoF is equal to n or they receive a packet from S.
- and
- and or and
- and
- and
- and
4.3. Performance Analysis Using the Markov Chain
4.3.1. Calculation of the Number of Transitions
4.3.2. Calculation of the Number of Transmissions in All Links
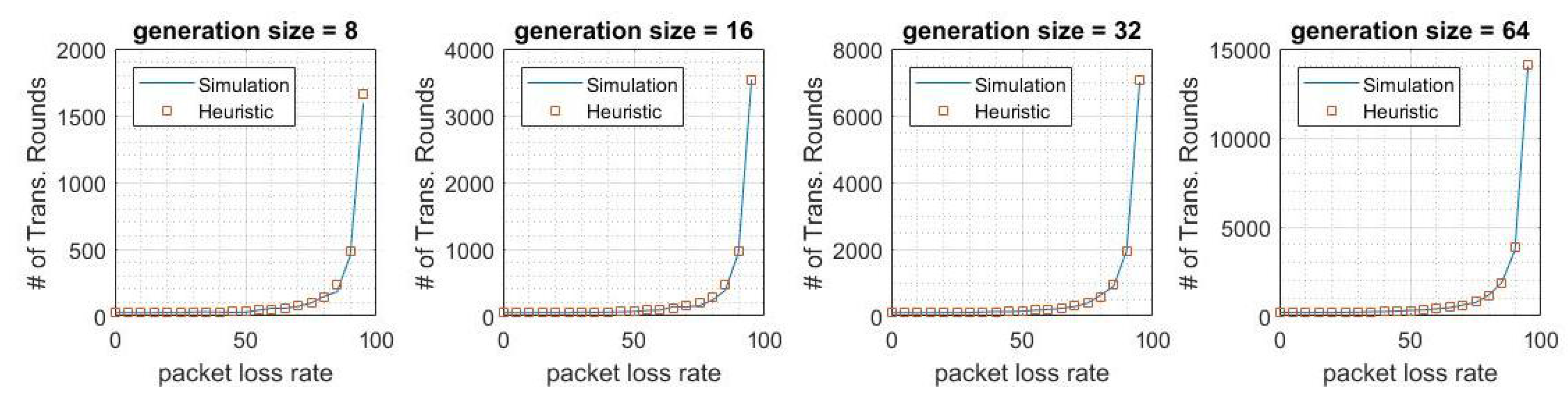
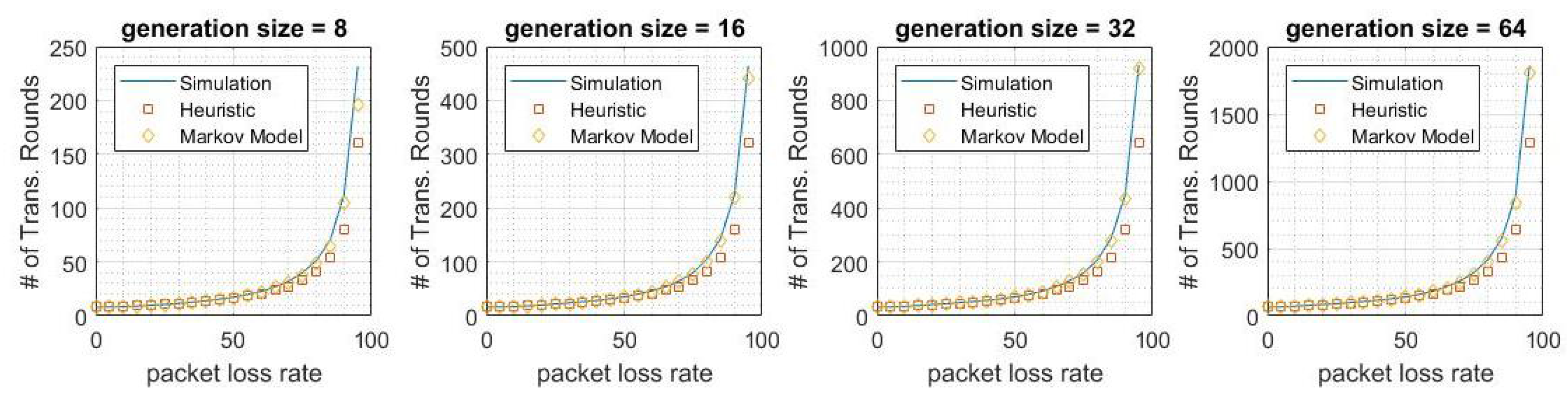
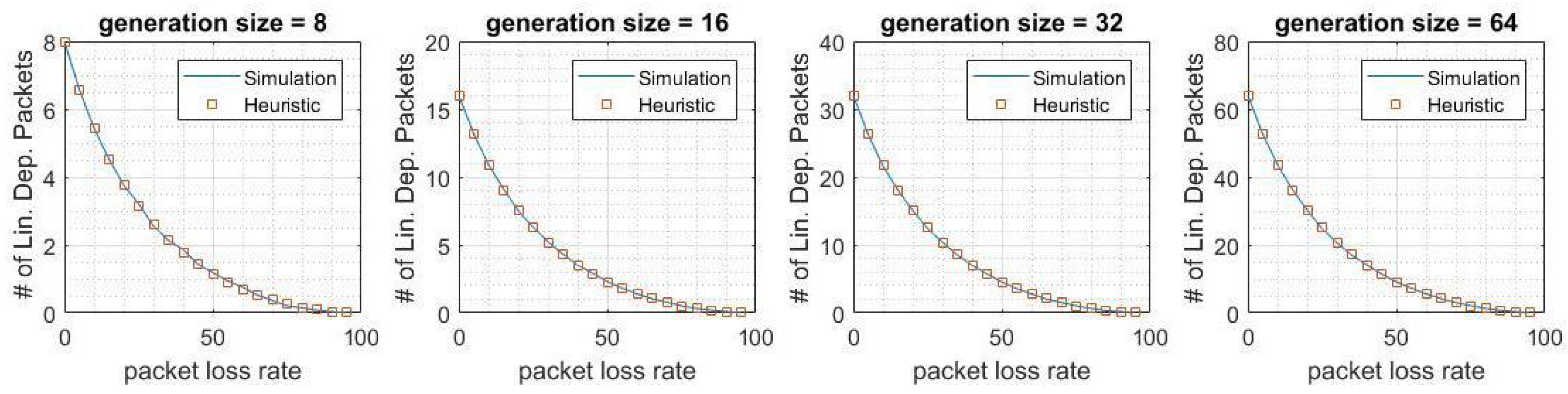
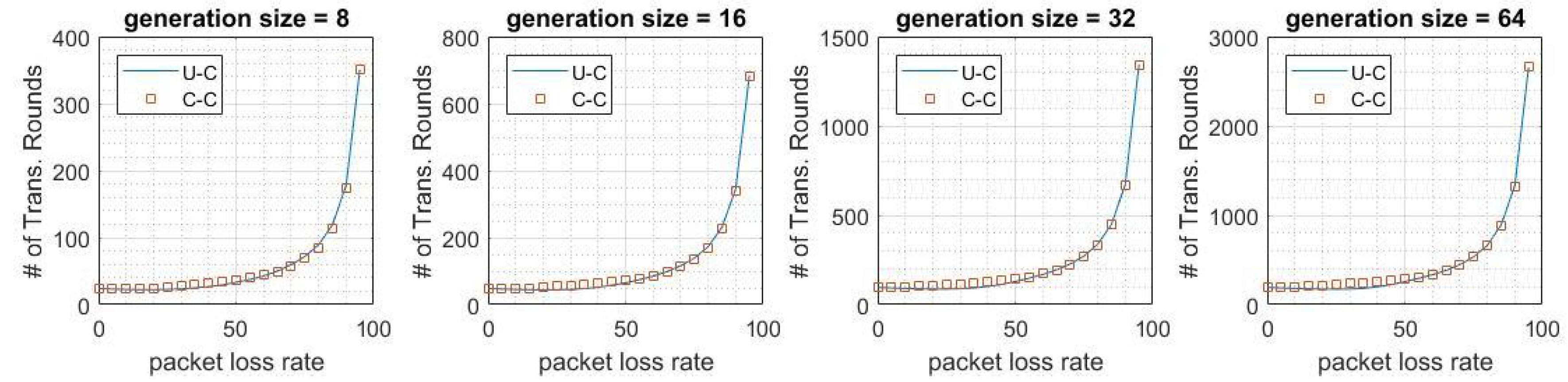
5. Results
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, C.; Fang, Y.; Zhu, X. Throughput-Delay Tradeoffs in Large-Scale MANETs with Network Coding. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 199–207. [Google Scholar]
- Ahlswede, R.; Cai, N.; Yeng, R.W. Network information flow. IEEE Trans. Inform. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Koetter, R.; Medard, M. An algebraic approach to network coding. IEEE ACM Trans. Netw. 2003, 46, 782–795. [Google Scholar] [CrossRef]
- Ho, T.; Medrad, M.; Koetter, D.; Karager, D.R. A Random Linear Network Coding Approach to Multicast. IEEE Trans. Inform. Theory 2006, 11, 4413–4430. [Google Scholar] [CrossRef]
- Joy, J.; Yu-Ting, Y.; Perez, V.; Lu, D.; Gerla, M. A new approach to coding in content-based MANETs. In Proceedings of the 2014 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 3–6 February 2014; pp. 173–177. [Google Scholar]
- Esfahani, A.; Mantas, G.; Rodriguez, J.; Neves, J.C. An efficient homomorphic MAC-based scheme against data and tag pollution attacks in network coding-enabled wireless networks. Int. J. Inf. Secur. 2017, 16, 4413–4430. [Google Scholar] [CrossRef]
- Lee, S.H.; Gerla, M.; Krawczyk, H.; Lee, K.W.; Quaglia, E. Performance evaluation of secure network coding using homomorphic signature. In Proceedings of the International Symposium on Network Coding, Beijing, China, 25–27 July 2011; pp. 1–6. [Google Scholar]
- Gennaro, R.; Katz, J.; Krawczyk, H.; Rabin, T. Secure network coding over the integers. In Proceedings of the 13th International Conference on Practice and Theory in Public Key Cryptography, Paris, France, 26–28 May 2010; pp. 142–160. [Google Scholar]
- Agrawal, S.; Boneh, D. Homomorphic MACs: MAC-Based Integrity for Network Coding. In Proceedings of the 7th Applied Cryptography and Network Security, (ACNS 2009), Paris, France, 2–5 June 2009; pp. 292–305. [Google Scholar]
- Dong, J.; Curtmola, R.; Nita-Rotaru, C. Practical defenses against pollution attacks in intra-flow network coding for wireless mesh networks. In Proceedings of the Second ACM Conference on Wireless Network Security, Zurich, Switzerland, 16–19 March 2009; pp. 111–122. [Google Scholar]
- Lucani, D.E.; Médard, M.; Stojanovic, M. Broadcasting in time-division duplexing: A random linear network coding approach. In Proceedings of the Network Coding, Theory, and Applications, 2009, (NetCod’09), Lausanne, Switzerland, 15–16 June 2009; pp. 62–67. [Google Scholar]
- Khamfroush, H.; Pahlevani, P.; Lucani, D.E.; Hundeboll, M. On the coded packet relay network in the presence of neighbors: Benefits of speaking in a crowded room. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 1928–1933. [Google Scholar]
- Khamfroush, H.; Lucani, D.E.; Pahlevani, P.; Barros, J. On optimal policies for network-coded cooperation: Theory and implementation. IEEE J. Sel. Area Commun. 2015, 33, 199–212. [Google Scholar] [CrossRef]
- Khamfroush, H.; Lucani, D.E.; Barros, J.; Pahlevani, P. Network-Coded Cooperation over Time-Varying Channels. IEEE Trans. Commun. 2014, 62, 4413–4425. [Google Scholar] [CrossRef]
- Kemeny, J.G.; Snell, J.L. Finite Markov Chains; D. Van Nostrand: New York, NY, USA, 1960. [Google Scholar]
- Garrido, P.; Lucani, D.E.; Agüero, R. Markov chain model for the decoding probability of sparse network coding. IEEE Trans. Commun. 2017, 65, 1675–1685. [Google Scholar] [CrossRef]
- Lucani, D.E.; Medard, M.; Stojanovic, M. On coding for delay—Network coding for time-division duplexing. IEEE Trans. Inform. Theory 2012, 58, 2330–2348. [Google Scholar] [CrossRef]
- Pedersen, M.V.; Heide, J.; Fitzek, F.H. Kodo: An open and research oriented network coding library. In Proceedings of the International Conference on Research in Networking, Valencia, Spain, 9–13 May 2011; pp. 145–152. [Google Scholar]





| Generation Size | Error = 0.5 | Error = 0.75 | ||||
|---|---|---|---|---|---|---|
| Simulation | Heuristic | Markov | Simulation | Heuristic | Markov | |
| 8 | 10.469500 | 10.854200 | 10.387300 | 40.071900 | 32.562500 | 37.576200 |
| 16 | 21.913100 | 21.708300 | 21.261800 | 79.952000 | 65.125000 | 76.481200 |
| 32 | 44.574400 | 43.416700 | 43.685100 | 158.715000 | 130.250000 | 152.631800 |
| 64 | 89.816200 | 86.833300 | 84.539200 | 322.970000 | 260.500000 | 308.481900 |
| Generation Size | Error = 0.5 | Error = 0.75 | ||||
|---|---|---|---|---|---|---|
| Simulation | Heuristic | Markov | Simulation | Heuristic | Markov | |
| 8 | 26.373600 | 27.333300 | 26.527300 | 69.231800 | 66.000000 | 68.246300 |
| 16 | 54.644400 | 54.666700 | 54.638100 | 135.878000 | 132.000000 | 134.491700 |
| 32 | 112.070000 | 109.333000 | 111.984200 | 268.762000 | 264.000000 | 265.871200 |
| 64 | 226.947000 | 218.667000 | 223.247100 | 534.164000 | 528.000000 | 528.796300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maboudi, B.; Sehat, H.; Pahlevani, P.; Lucani, D.E. On the Performance of the Cache Coding Protocol. Information 2018, 9, 62. https://doi.org/10.3390/info9030062
Maboudi B, Sehat H, Pahlevani P, Lucani DE. On the Performance of the Cache Coding Protocol. Information. 2018; 9(3):62. https://doi.org/10.3390/info9030062
Chicago/Turabian StyleMaboudi, Behnaz, Hadi Sehat, Peyman Pahlevani, and Daniel E. Lucani. 2018. "On the Performance of the Cache Coding Protocol" Information 9, no. 3: 62. https://doi.org/10.3390/info9030062





