Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate

Abstract

Handling uncertainty in an appropriate manner during the real operation of a cyber-physical system (CPS) is critical. Uncertain production scheduling as a part of CPS uncertainty issues should attract more attention. In this paper, a Mixed Integer Nonlinear Programming (MINLP) uncertain model for batch process is formulated based on a unit-specific event-based continuous-time modeling method. Utility uncertainty and uncertain relationship between production rate and utility supply are described by fuzzy theory. The uncertain scheduling model is converted into deterministic model by mathematical method. Through one numerical example, the accuracy and practicability of the proposed model is proved. Fuzzy scheduling model can supply valuable decision options for enterprise managers to make decision more accurate and practical. The impact and selection of some key parameters of fuzzy scheduling model are elaborated.

1. Introduction

A cyber-physical system (CPS) was identified as a key research area by the US National Science Foundation (NSF) and was listed as the number one research priority by the US President’s Council of Advisors on Science and Technology [1]. In recent years, CPS is attracting much attention and is being considered as an emerging technology. It has wide potential applications in defense [2,3], transportation [4], industrial automation [5], energy [6,7], health care [1,8] and agriculture [9,10], etc. Cyber-physical systems (CPS) can be viewed as a new generation of systems with integrated control, communication and computational capabilities [1]. It combines computation and communication capabilities with the physical world [11].

Uncertainty is intrinsic in most technical systems, including CPS. CPS generally functions in an inherently complex and unpredictable physical environment. A major difficulty with CPS is that it must be designed and operated in the presence of uncertainty [12]. Therefore, handling uncertainty in an appropriate manner during the real operation of CPS is critical. In CPS, physical components are inserted by sensors and actuators. Sensors have the abilities of self-calibration, dynamic parameter setting, Ethernet-based communication and self-adaptation [13]. So CPS has enough capability to detect uncertainties in itself or from external environment.

For a manufacturing enterprise, the real operation of CPS is just the execution of production scheduling. So the uncertainty problem of production scheduling is a part of the CPS uncertainty issue. Uncertainties in manufacturing are various, which include demand uncertainty, processing time uncertainty, utility uncertainty, due date uncertainty, equipment failure and the absence of employee. For the uncertain scheduling problem of batch process, some research results have been obtained. Guillen, et al. [14] proposed a multistage stochastic optimization model to address the scheduling of supply chains with embedded multipurpose batch chemical plants under demand uncertainty. Zhu, et al. [15] proposed a robust optimization approach for the short-term scheduling of batch plants under demand uncertainty where the uncertain parameters can be described by a normal distribution function. Ierapetritou [16] developed a strategy to quantify scheduling robustness in the face of uncertainty, to increase scheduling flexibility, and to improve system performance when unexpected events occur during scheduling execution. Xu, et al. [17] established a scheduling mathematical model for multi-product batch processes under finite intermediate storage policy with uncertain processing time based on fuzzy programming theory.

Nowadays, most studies mainly deal with uncertainties of demand and processing time in production scheduling. Research on utility uncertainty is rare, and the supply amount of utility is assumed to be constant. In fact, utility disturbance is an important uncertain factor to the production process. In the production process, utilities such as steam, cooling water and electricity, are supplied to areas or product lines to support the normal operation of equipment. Sometimes, these utilities are shared by different areas. However, the utility supply is affected seriously by the energy system, and the energy system is also disturbed by many uncertainty factors. So, utility disturbances usually occur, which will affect the normal running of machines, make the scheduling decision infeasible, even leads to the shutdown of the product line [18,19,20]. Consequently, dealing with utility uncertainty well in production scheduling is vital to enterprise competitiveness. Moreover, the production rate is closely related to the utility supply. The relationship between them is roughly assumed to be linear in most studies, which is unable to reflect the actual production situation. So building the uncertain relationship between the production rate and the utility supply is another key point for production scheduling.

For the above two uncertainties, it is time-consuming and material-consuming to establish a mechanism model [21]. Existing methods to describe uncertainty include chance constraint programming, fuzzy theory and scenario trees [22,23]. Chance constraint programming needs a large amount of historical data to analyze the distribution function of uncertainty [24]. The scenario trees method adds many constraints, enables a large programming model scale, and has a computation time too long to meet requirements [25]. If the historical data of uncertainty is insufficient or difficult to acquire, then fuzzy theory is an effective means.

In this paper, a MINLP uncertain scheduling model for batch process is formulated based on unit-specific event-based continuous-time (USEBCT) modeling method. Fuzzy method is utilized to describe the uncertainty of utility supply. For the uncertain relationship between the production rate and the utility supply, firstly establish the linear function in deterministic scheduling model, and then use fuzzy method to represent the coefficient of linear function. The uncertain scheduling model is converted into deterministic model by mathematical method. Through one numerical example, the accuracy and practicability of the proposed model are proved.

This paper is organized as follows: Section 2 describes the problem definition of short scheduling for batch process. Section 3 formulates the deterministic scheduling model. Section 4 details the fuzzy scheduling model and the defuzzification method. A numerical example and roles of proposed model are given in Section 5. Conclusions are presented in Section 6.

2. Problem State

The short-term scheduling problem for batch processes is stated as follows. Given (i) the production recipe (i.e., the amount of the materials required for the production of each product); (ii) the available units, their capacity limits and utility; (iii) the available storage capacity for each of the materials; and (iv) the time horizon under consideration, then the objective is to determine (i) the optimal sequence of tasks taking place in each unit; (ii) the amount of material being processed at each time in each unit; and (iii) the processing time of each task in each unit.

Some assumptions in this paper are given as follows: (i) the switching time between different tasks is neglected [26]; (ii) raw materials are sufficient and supplied at the beginning of the scheduling horizon [27]; (iii) intermediates and final products are only from producing [28,29,30].

3. Deterministic Scheduling Model Based on USEBCT Modeling Method

The USEBCT model is proposed by Ierapetritou and Floudas [31]. The USEBCT model permits event to happen at any moment in the scheduling horizon. The duration time of every event is varying. The scale of mathematical programming is smaller, and the computation time is shorter, so compared with discrete-time model, USEBCT model is more actual and accurate in describing the production situation.

3.1. Basic Concepts of USEBCT Model

(1)

Event: time measurement, each event has one start time and finish time;

(2)

State: raw materials, intermediates and final products;

(3)

Task: action of producing or consuming one state;

(4)

Unit: machines in which the task can be performed.

3.2. Deterministic Scheduling Model

The proposed deterministic scheduling model is formulated based on the model framework proposed by Vooradi and Shaik (V&S model) [26]. For the reason of computation time, $\Delta n$ is set to be zero. Moreover, material balances, duration constraints, tightening constraints and utility constraints are modified according to the requirements of modeling.

(1) Allocation constraints

$${\displaystyle \sum _{i\in I_j}w(i,n)}\le 1,\hspace{1em}\forall j\in J,n\in N.$$

(1)

In every unit, at the most one task can be active at each event as given by constraint (1), in which $w(i,n)$ is binary variable. If task $i$ is active at event $n$, $w(i,n)=1$, else $w(i,n)=0$.

(2) Capacity constraints

$$B_i{}^{\min }\times w(i,n) \le b(i,n) \le B_i{}^{\max }\times w(i,n), \forall i \in I, n \in N.$$

(2)

Constraint (2) limits the size of one batch. If task $i$ is active at event $n$, then the decision variable of processed material $b(i,n)$ is forced in the range of the minimum and maximum batch sizes. Otherwise, $b(i,n)$ is forced to be zero.

(3) Material balances

When $n=1$,

$$ST(s,n)=S{T}_s^0+{\displaystyle \sum _{i\in I_s^c}{\rho }^{\mathrm{c}}{}_{is}}b(i,n),\hspace{0.17em} \forall s\in S^{\mathrm{R}}, S^{\mathrm{I}}, n=1.$$

(3)

$$ST(s,n) = S{T}_s^0, \hspace{0.17em}\forall s\in S^{\mathrm{P}}, n=1.$$

(4)

When $n>1$,

$$ST(s,n) = ST(s,n - 1) + {\displaystyle \sum _{i\in I_s^c}{\rho }^{\mathrm{c}}{}_{is}}b(i,n), \forall s\in S^{\mathrm{R}}, n\in N, n>1.$$

(5)

$$ST(s,n)=ST(s,n-1) + {\displaystyle \sum _{i\in I_s^{\mathrm{p}}}{\rho }^{\mathrm{p}}{}_{is}b(i,n-1}) + {\displaystyle \sum _{i\in I_s^c}{\rho }^{\mathrm{c}}{}_{is}}b(i,n),\hspace{0.17em} \forall s\in S^{\mathrm{I}}, n\in N, n>1.$$

(6)

$$ST(s,n)=ST(s,n-1) + {\displaystyle \sum _{i\in I_s^{\mathrm{p}}}{\rho }^{\mathrm{p}}{}_{is}}b(i,n-1), \forall s\in S^{\mathrm{P}}, n\in N, n>1.$$

(7)

Constraints (3) and (4) are material balances of raw materials, intermediates and products at initial event. Constraints (5)–(7) are material balances of the above three states at the later events. If n is equal to 1, the amount of states (raw material or intermediate) at event n is equal to the initial value, and decreased by any amounts consumed at event n, as given by constraint (3). The amount of final product at event n is calculated as initial value, as given by constraint (4).

If $n>1$, the amount of a state at current event is adjusted by any amounts produced by tasks that ends at the previous event and adjusted by any amounts consumed by the tasks that starts at the current event, as given by constraint (5) to constraint (7).

(4) Duration constraints

In order to formulate the relationship between consumption of utility and production rate, the variable $P(i,n)$ is introduced to represent the production rate of task $i$ at event $n$. The finish time of task $i$ at event $n$ is equal to the start time plus duration time of the task, which is calculated by $b(i,n)/P(i,n)$.

$$T^{\mathrm{f}}(i,n) = T^{\mathrm{s}}(i,n) + \frac{b(i,n)}{P(i,n)}, \forall i\in I, n\in N.$$

(8)

$$P(i,n)=P_i^{\min }+{\displaystyle \sum _{u\in U_i}{c}_{ui}\cdot u(u,i,n)},\hspace{1em}\forall i\in I, n\in N.$$

(9)

In constraint (9), production rate $P(i,n)$ is formulated by the summery of minimum production rate, which maintains the equipment running, and linear function of consumption of utility. The parameter $c_{ui}$ is assumed as a constant number in deterministic model. However the relationship between consumption of utility and production rate is not linear simply. In fuzzy model, the parameter $c_{ui}$ is defined as a fuzzy number to describe the uncertain relationship between consumption of utility and production rate as given by constraint (25).

(5) Sequencing constraints

① Same task in the same unit

In constraint (10), the start time of task $i$ at event $n+1$ should be greater than or equal to the finish time of the same task at event $n$.

$$T^{\mathrm{s}}(i,n+1)\ge T^{\mathrm{f}}(i,n), \forall i\in I, n\in N, n<N.$$

(10)

② Different tasks in the same unit

$$T^{\mathrm{s}}(i,n+1)\ge T^{\mathrm{f}}(i{}^{\prime },n), \forall i,i{}^{\prime }\in I_j, i\ne i{}^{\prime }, j\in J, n\in N, n<N.$$

(11)

The constraint (11) is written for two different tasks performed in the same unit at event $n$ and $n+1$, respectively. If task $i$ is active at event $n+1$, the start time of task $i$ must be greater than or equal to the finish time of previous task $i{}^{\prime }$.

③ Different tasks in different units

$$\begin{array}{l}{T}^{\mathrm{s}}(i,n+1)\ge T^{\mathrm{f}}(i{}^{\prime },n)-M(1-w(i{}^{\prime },n)),\forall s,i,i{}^{\prime },j,j{}^{\prime }, n\in N, n<N i\in I_j,\\ i{}^{\prime }\in I_{j{}^{\prime }}, i\ne i{}^{\prime }, j\ne j{}^{\prime }, i\in I_s^{\mathrm{c}}, i{}^{\prime }\in I_s^{\mathrm{p}}.\end{array}$$

(12)

According to the production recipe, for different tasks that produce or consume the same state, the start time of the consuming task at the next event is enforced to be later than the finish time of the producing task at the current event as given by constraint (12). Otherwise, the constraint is relaxed and the two times are not related.

(6) Tightening constraints

$${\displaystyle \sum _{i\in I_j}{\displaystyle \sum _{n\in N}\frac{b(i,n)}{P(i,n)}}}\le Hm,\hspace{1em}\forall j\in J$$

(13)

The sum of the durations of all tasks suitable in each unit should be less than the scheduling horizon as given by constraint (13).

(7) Utility constraints

$$u(u,i,n)={\delta }_{iu}\cdot b(i,n), \forall u\in U, i\in I_u, n\in N.$$

(14)

$$u(u,i,n) \le U_{ui}^{\max }, \forall u\in U, i\in I_u, n\in N.$$

(15)

The consumption of utility is a linear function of amount of processed material, which is given by constraint (14). The consumption of utility is limited by the total supply amount of utility. Constraint (15) expresses that the consumption of utility $u$ at event $n$ should not be greater than the maximum supply. The maximum supply amount of utility $U_{ui}^{\max }$ is another uncertain parameter and assumed as a constant number in deterministic model. But the supply amount of utility is affected seriously by energy system, and the energy system is also disturbed by lots of uncertain factors. So, utility disturbances usually occur. In fuzzy model, the parameter $U_{ui}^{\max }$ is defined as a fuzzy number to describe the uncertain utility supply as given by constraint (26).

Constraint (16) is similar to that for same task in the same unit written for each utility. The start time of consuming utility $u$ at event $n+1$ should not be earlier than that at event $n$.

$$T_u^{\mathrm{s}}(u,n+1) \ge T_u^{\mathrm{s}}(u,n), \forall u\in U, n\in N, n<N.$$

(16)

To account for the utility consumption over different tasks, constraints (17) and (18) enforce the start time of all suitable tasks that consume the same utility to be equal to $T_u^{\mathrm{s}}(u,n)$, if the task is active at event $n$.

$$T_u^{\mathrm{s}}(u,n)\ge T^{\mathrm{s}}(i,n)-M(1-w(i,n)), \forall u\in U, i\in I_u, n\in N.$$

(17)

$$T_u^{\mathrm{s}}(u,n)\le T^{\mathrm{s}}(i,n)+M(1-w(i,n)), \forall u\in U, i\in I_u, n\in N.$$

(18)

If $w(i,n)=1$, constraints (17) and (18) can be rewritten by $T_u^{\mathrm{s}}(u,n)\ge T^{\mathrm{s}}(i,n)$ and $T_u^{\mathrm{s}}(u,n)\le T^{\mathrm{s}}(i,n)$, which is equivalent to $T_u^{\mathrm{s}}(u,n)=T^{\mathrm{s}}(i,n)$. If $w(i,n)=0$, constraints (17) and (18) are relaxed.

$$T^{\mathrm{f}}(i,n-1) \le T_u^{\mathrm{s}}(u,n)+M(1-w(i,n-1)), \forall u\in U, i\in I_u, n\in N, n>1.$$

(19)

In constraint (19), the finish times of all suitable tasks that consume a utility at previous event are enforced to occur before, if the task is active. Otherwise, constraint (19) is relaxed.

(8) Storage constraints

$$ST(s,n)\le S{T}_s^{\max }, \forall s\in S^{\mathrm{dfis}}, n\in N.$$

(20)

$$\begin{array}{l}{T}^{\mathrm{f}}(i{}^{\prime },n)\ge T^{\mathrm{s}}(i,n)-M(1-w(i{}^{\prime },n)),\forall s\in S^{\mathrm{dfis}},j,j{}^{\prime }\in J, n<N, i\in I_j,\\ i{}^{\prime }\in I_{j{}^{\prime }}, i\ne i{}^{\prime }, j\ne j{}^{\prime }, i\in I_s^c, i{}^{\prime }\in I_s^{\mathrm{p}}.\end{array}$$

(21)

Infinite storage and dedicated finite intermediate storage policies are considered in this work. Constraint (20) expresses the limit of storage capacity. For handling dedicated finite intermediate storage case, constraint (21) along with constraint (12) is used to avoid real time storage violations without the need for considering storage as a separate task.

If constraints (12) and (21) are not relaxed, constraint (22) is workable. In constraint (22), the finish time of producing task at event $n$ should be greater than or equal to the start time of consuming task at the same event, and less than or equal to the start time of consuming task at event $n+1$.

$$T^{\mathrm{s}}(i,n)\le T^{\mathrm{f}}(i{}^{\prime },n)\le T^{\mathrm{s}}(i,n+1)$$

(22)

(9) Bounds on variables

$$\begin{array}{l}{T}_u^{\mathrm{s}}(u,n)=0,\hspace{1em}n=1,\forall u\in U;T_u^{\mathrm{s}}(u,n)\le Hm,\hspace{1em}\forall n\in N, u\in U;\\ T^{\mathrm{s}}(i,n)\le Hm,\hspace{1em}{T}^{\mathrm{f}}(i,n)\le Hm, \forall i\in I, n\in N.\end{array}$$

(23)

Constraint (23) initials the consumption time of utility at the first event, and limits all the start and finish times of tasks to be within the scheduling horizon.

(10) Objective function

$$\mathrm{Max} \hspace{0.17em}profit={\displaystyle \sum _{s\in S^{\mathrm{P}}}{\mathrm{P}}_s{\displaystyle \sum _{n=N}(ST(s,n) +}} {\displaystyle \sum _{i\in I_s^{\mathrm{P}}}{\rho }_{is}^{\mathrm{P}}\cdot b(i,n)})$$

(24)

The objective function is the maximization of profit, and the total amount of the final products produced by the end of last event is calculated by constraint (24).

4. Fuzzy Scheduling Model and Defuzzification

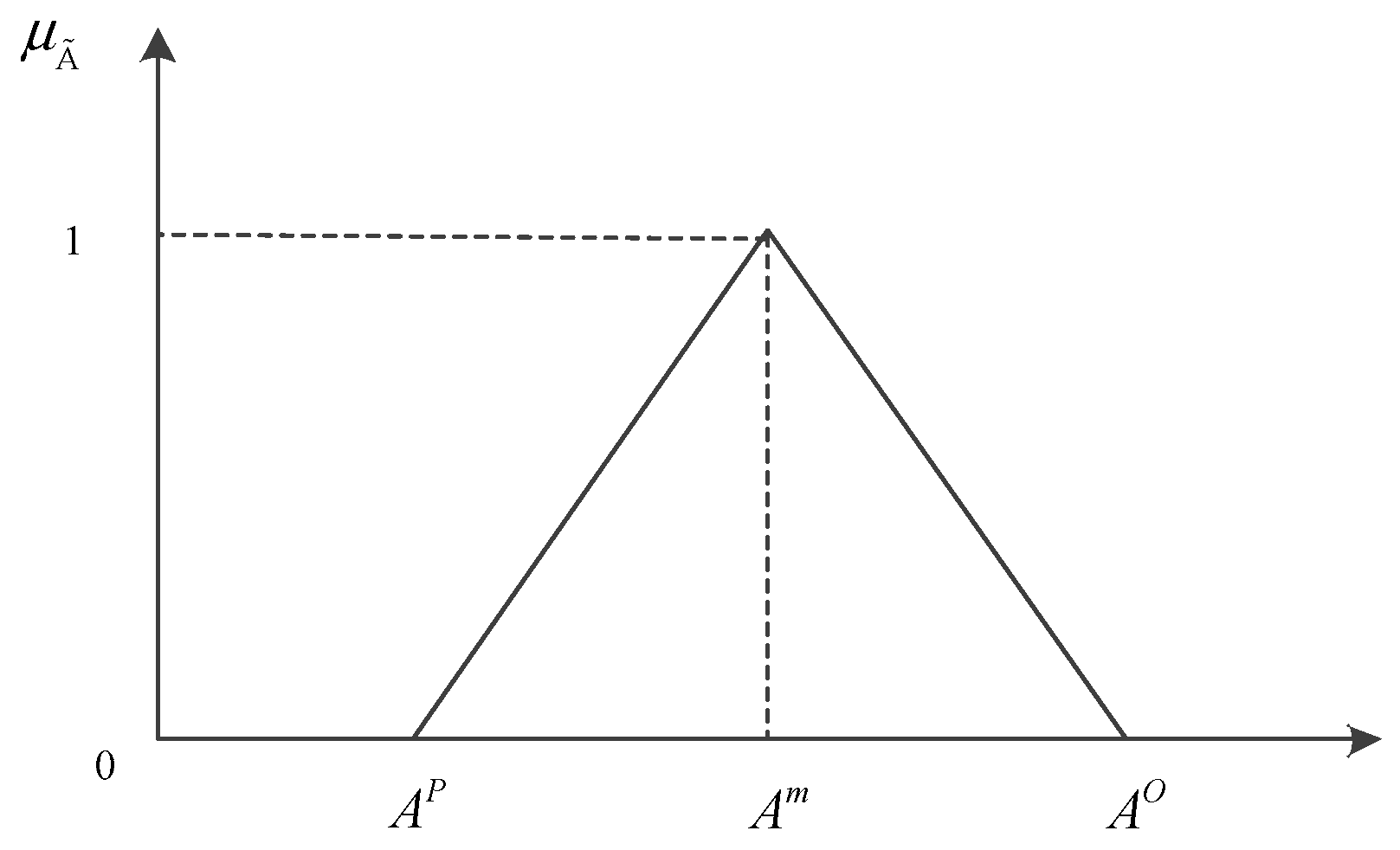
4.1. Uncertainty Description

Coefficient ${\tilde{c}}_{ui}$ and maximum supply amount of utility ${\tilde{U}}_{ui}^{\max }$ are fuzzy numbers, as given by constraints (25) and (26). The two fuzzy numbers are described by triangular possibility distributions. This description of fuzzy numbers has been extensively used in literatures due to their various advantages (e.g., Lai and Hwang, 1992 [32], 1993 [33], Liang, 2006 [34] and 2008 [35]). The simplicity in required data acquisition and simplicity in related fuzzy computations are the most important advantages [36,37,38]. These advantages are our main motivation in using the triangular fuzzy numbers for modeling the imprecise data in our problem. Figure 1 presents the triangular possibility distribution of fuzzy number $\tilde{A}=(A^P, A^m, A^o)$, where $A^P$, $A^m$ and $A^o$ are the most pessimistic value, the most possible value, and the most optimistic value. The triangular possibility distribution of $\tilde{A}$ is defined as Equation (27).

$$P(i,n)=P_i^{\min }+{\displaystyle \sum _{u\in U_i}{\tilde{c}}_{ui}\cdot u(u,i,n)}, \forall i\in I, n\in N.$$

(25)

$$u(u,i,n)\le {\tilde{U}}_{ui}^{\max }, \forall u\in U, i\in I_u$$

(26)

$${\mu }_{\tilde{\mathrm{A}}}=\{\begin{array}{l}\frac{A-A^P}{A^m-A^P}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}^P\le A\le A^m\\ \frac{A^O-A}{A^O-A^m}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}^m<A\le A^O\\ \\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\mathrm{otherwise}\end{array}$$

(27)

$$U=[D_{\min }-D_1,D_{\max }+D_2]$$

(28)

$$D_1=0.2\times \left|D_{\min }-D_{mf}\right|$$

(29)

$$D_2=0.2\times \left|D_{\max }-D_{mf}\right|$$

(30)

The universe U of fuzzy number is defined as Equation (28) according to Basyigit and Ulu [39], where $D_{\min }$ is the minimum value in statistical data of fuzzy number, $D_{\max }$ is the maximum value in statistical data of fuzzy number. $D_1$ and $D_2$ are defined as Equation (29) and (30) according to the experience of engineering. $D_{mf}$ is the value of which the frequency of occurrence is the most in statistical data of fuzzy number.

Typically, the three prominent values, i.e., the most pessimistic, the most possible, and the most optimistic values for fuzzy numbers are estimated by decision maker [32,37,40]. In this paper, the three prominent values are defined according to determining method of universe [39] and the experience of engineering. The most pessimistic value $A^P$ is equal to the left boundary of universe. The most possible value $A^m$ is equal to $D_{mf}$. The most optimistic value $A^O$ is equal to the right boundary of universe. These relationships are given by Equations (31) to (33).

$$A^P=D_{\min }-D_1$$

(31)

$$A^m=D_{mf}$$

(32)

$$A^O=D_{\max }+D_2$$

(33)

The deterministic scheduling model is replaced by the following fuzzy scheduling model:

Objective function: (24)

Constraints: (1)–(8), (10)–(14), (16)–(23)

   (25), deterministic constraint (9) is replaced by fuzzy constraint (25)

   (26), deterministic constraint (15) is replaced by fuzzy constraint (26).

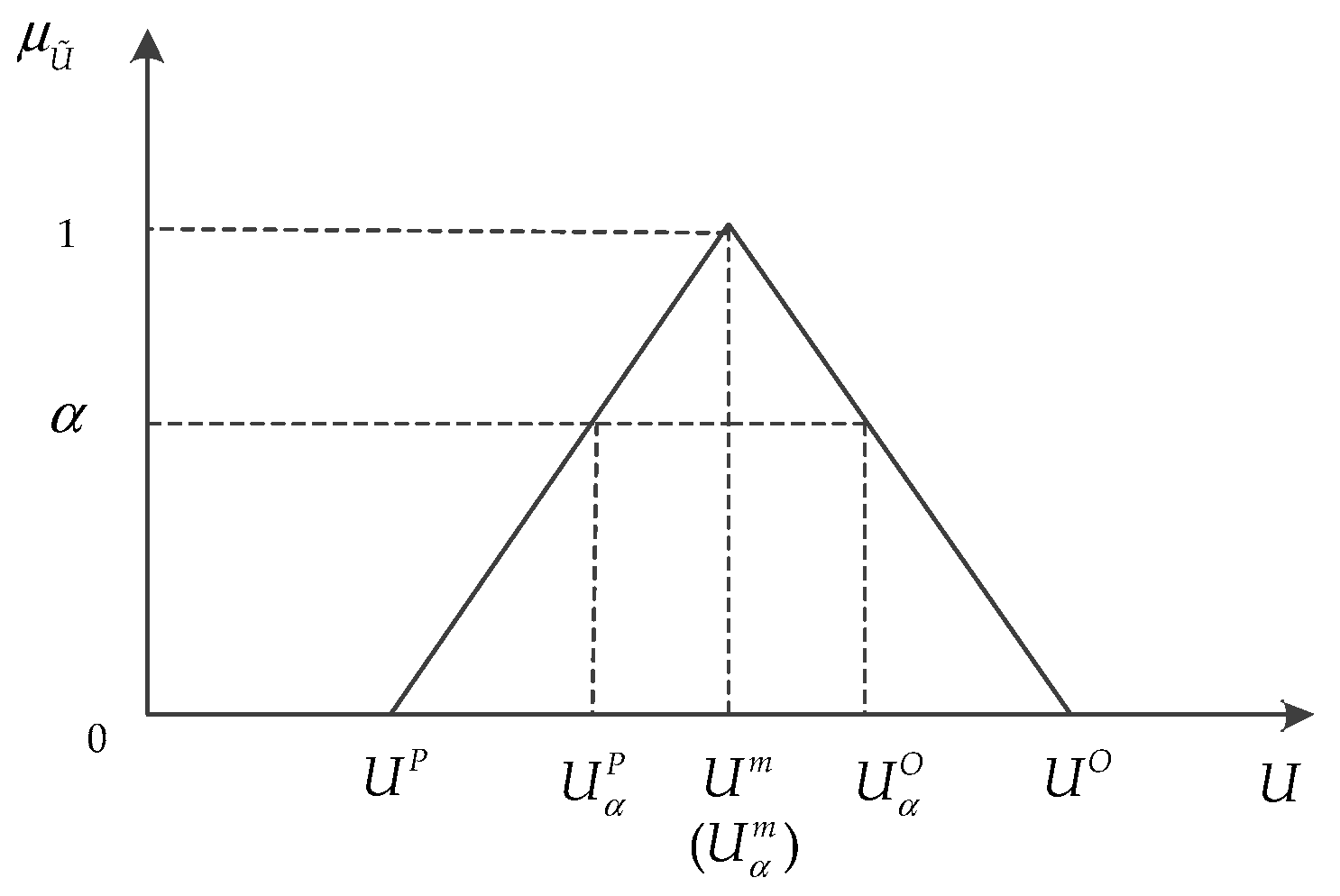
4.2. Defuzzification of Fuzzy Scheduling Model

Defuzzification is a process whereby the fuzzy scheduling model is converted into a deterministic scheduling model. Constraint (25) can be converted into inequality constraints. All the fuzzy numbers are on one side of inequality constraints, so fuzzy numbers ranking problem is not involved. We apply the well-known weighted average method. This approach seems to be the simplest and most reliable defuzzification method in converting the fuzzy constraints into their deterministic ones [35,37,38,41]. In this regard, we also need to determine a minimal acceptable possibility level $\alpha$, which denotes the minimum acceptable possibility level of occurrence for the corresponding imprecise/fuzzy data. So, the equivalent deterministic constraints can be represented as follows:

$$P(i,n)\ge P_i^{\min }+{\displaystyle \sum _{u\in U_i}(w_a{C}_{\alpha }^P+w_b{C}_{\alpha }^m+}{w}_c{C}_{\alpha }^O)\cdot u(u,i,n),\hspace{1em}\forall i\in I, n\in N.$$

(34)

$$P(i,n)\le P_i^{\min }+{\displaystyle \sum _{u\in U_i}(w_a{C}_{\alpha }^P+w_b{C}_{\alpha }^m}+w_c{C}_{\alpha }^O)\cdot u(u,i,n),\hspace{1em}\forall i\in I, n\in N.$$

(35)

$$u(u,i,n)\le w_a{U}_{\alpha }^P+w_b{U}_{\alpha }^m+w_c{U}_{\alpha }^O, \forall u\in U, i\in I_u, n\in N$$

(36)

where $w_a+w_b+w_c=1$, and $w_a$, $w_b$ and $w_c$ represent the weights of the most pessimistic, the most possible and the most optimistic value of the related fuzzy numbers, respectively. In practice, the suitable values for these weights as well as $\alpha$ are usually determined subjectively by the experience and knowledge of the decision maker. Based on the most likely value concept proposed by Lai and Hwang [32] and considering several relevant works [42,43], we set these parameters to: $w_a$ = 1/6, $w_b$ = 4/6, $w_c$ = 1/6 in numerical experiments. $C_{\alpha }^P$, $U_{\alpha }^P$, $C_{\alpha }^m$, $U_{\alpha }^m$, $C_{\alpha }^O$, $U_{\alpha }^O$ are boundary points of $\alpha$-cut fuzzy set. Take ${\tilde{U}}_{ui}^{\max }$ as example, boundary points calculated by (37) to (39). The relationships among them are illustrated in Figure 2.

$$U_{\alpha }^P=U^P+\alpha (U^m-U^P)$$

(37)

$$U_{\alpha }^m=U^m$$

(38)

$$U_{\alpha }^O=U^O-\alpha (U^O-U^m)$$

(39)

Equivalent deterministic model through defuzzification is reformulated as follows:

Objective function: (24)

Constraints: (1)–(8), (10)–(14), (16)–(23) and (34)–(36).

5. Case Study

Numerical example is introduced firstly by Maravelias and Grossmann [44] and has been studied in several studies [31,45]. As shown in Figure 3, this example involves four tasks in three units processing seven states. The corresponding data is given in

Table 1. Data of production capability and coefficients of utility consumption.

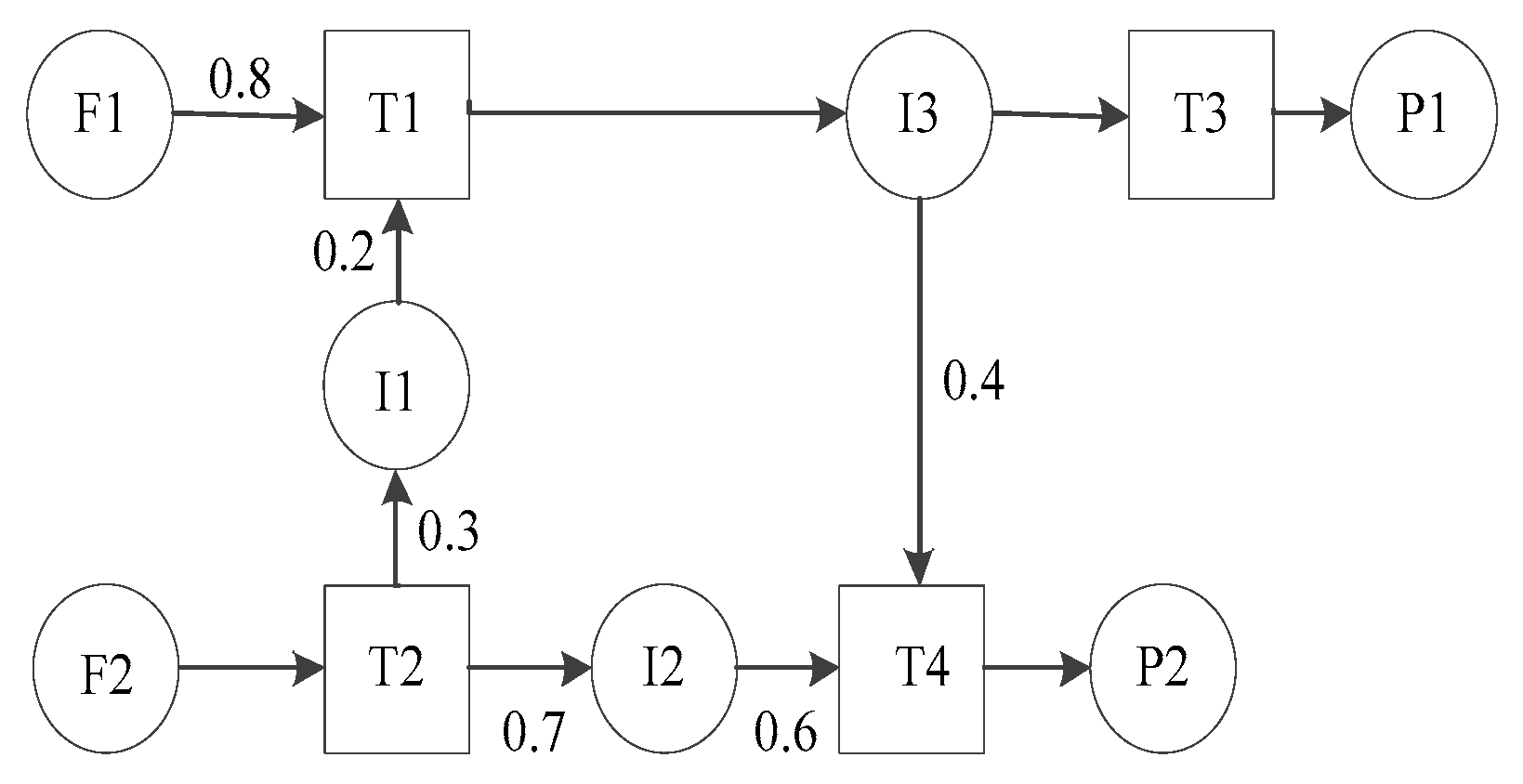
	${\mathit{B}}^{\mathbf{min}}$	${\mathit{B}}^{\mathbf{max}}$	Task 1 (R1)	Task 2 (R2)	Task 3 (R3)	Task 4 (R4)
			${\mathit{\delta }}_{\mathit{i}\mathit{H}\mathit{S}}$	${\mathit{\delta }}_{\mathit{i}\mathit{C}\mathit{W}}$	${\mathit{\delta }}_{\mathit{i}\mathit{H}\mathit{S}}$	${\mathit{\delta }}_{\mathit{i}\mathit{C}\mathit{W}}$
RI1	40	80	0.25	0.3	-	-
RI2	25	50	0.25	0.3	-	-
RII	40	80	-	-	0.2	0.5

$B^{\min }$, $B^{\max }$ in kg, ${\delta }_{iHS}$ in kg per kg of batch.

and

Table 2. Data related States.

	F1	F2	I1	I2	I3	P1	P2
STsmax	1000	1000	200	100	500	1000	1000
STs0	400	400	0	0	0	0	0
Prices	0	0	0	0	0	30	40

ST_s^max (kg), ST_s⁰ (kg) in kg, Price_s in $/kg.

. There are two types of reactors available for the process (type I and II) with different number of corresponding units available: two reactors (RI1 and RI2) of type I, while one reactor (RII) of type II. Reactions R1 and R2 require type I reactor, while reactions R3 and R4 require type II reactor. Furthermore, reactions R1 and R3 require heat, provided by steam (HS) produced in limited amounts in the plant, while reactions R2 and R4 are exothermic and require cooling water (CW), also available in limited amounts. Due to safety reasons and temperature restrictions, the heat integration of the process is not possible.

The minimum batch-size for all tasks is the half of maximum capacities of units. Finite storage policy for intermediates and unlimited storage policy for the raw materials, final products, are applied. Numerical example is solved using Lingo 11.0 (Lindo Systems, Chicago, IL, USA) with a 2.20 GHz computer. Scheduling horizon is seven hours, and event number is set to 5. A better optimization solution cannot be found by larger event numbers. The data of fuzzy numbers are given in

Table 3. Data of fuzzy number ${\tilde{c}}_{ui}$

		Task 1		Task 2		Task 3	Task 4
		RI1	RI2	RI1	RI2	RII	RII
three prominent values		(0.8 1 1.3)	(0.4 0.6 0.7)	(0.55 0.6 0.62)	(0.4 0.5 0.6)	(1.9 2 2.2)	(0.9 1 1.2)
actual data	event 1	0.92	0.65	0.60	0.45	1.95	0.95
	event 2	0.90	0.60	0.61	0.50	2.10	1.00
	event 3	0.98	0.62	0.60	0.50	2.00	0.98
	event 4	1.00	0.58	0.59	0.51	1.98	1.10
	event 5	1.15	0.50	0.58	0.55	2.00	1.00

and

Table 4. Data of fuzzy number ${\tilde{U}}_{ui}^{\max }$ .

		Task 1		Task 2		Task 3	Task 4
		RI1	RI2	RI1	RI2	RII	RII
three prominent values		(23 24 25)	(20 24 27)	(27 30 35)	(28 30 31)	(22 24 27)	(29 30 33)
actual data	event 1	23.5	25.5	32.5	30.0	25.4	29.7
	event 2	24.0	23.0	31.2	30.5	23.6	31.5
	event 3	23.8	24.0	28.5	30.0	24.0	29.6
	event 4	24.5	22.0	30.0	29.4	24.0	30.0
	event 5	24.0	24.7	29.6	29.0	23.0	30.8

. Three prominent values (most pessimistic value, most possible value, and most optimistic value) of fuzzy numbers are in parentheses.

In order to demonstrate the advantages of proposed fuzzy mode, we input a set of actual data into the deterministic model. The results based on the actual data are viewed as a criterion for comparing the accuracy of deterministic model and fuzzy model. Actual data of fuzzy number ${\tilde{c}}_{ui}$ and ${\tilde{U}}_{ui}^{\max }$ are given in Table 3 and Table 4.

.

Results based on actual data, of deterministic model and fuzzy model are compared in

Table 5. Optimization results of deterministic model and fuzzy model.

Results Based on Actual Data		Deterministic Model		Fuzzy Model
Objective Function ($)	Completion Time (h)	Objective Function ($)	Completion Time (h)	$\mathit{\alpha }$	Objective Function ($)	Completion Time (h)
5448	11.20	5400	12.30	0.5	5426.25	11.42
				0.6	5421.00	12.10
				0.7	5415.75	12.19
				0.8	5410.50	11.37

. In this numerical example, $w_a$ = 1/6, $w_b$ = 4/6, $w_c$ = 1/6. The objective function (maximization of profit) based on actual data is 5448$. The corresponding completion time is 11.20 h, which is the sum of processing time of three machine units (RI1, RI2 and RII).

The objective function of deterministic model is 5400$.The completion time of deterministic model is 12.30 h. For fuzzy model, the objective function ranges from 5426.25$ to 5410.50$, correspondingly, $\alpha$ varies from 0.5 to 0.8. Completion time also varies depending on different $\alpha$. In order to compare the optimization results better, deviations of deterministic and fuzzy models as well as average values of deviations for fuzzy model are given in

Table 6. Deviation analysis.

Deterministic Model		Fuzzy Model
Objective Function ($)	Completion Time (h)	$\mathit{\alpha }$	Objective Function ($)	Completion Time (h)
0.88%	9.82%	0.5	0.40%	1.96%
		0.6	0.50%	8.04%
		0.7	0.59%	8.84%
		0.8	0.69%	1.52%
		average value	0.545%	5.09%

. Based on data in Table 5, taking results of actual data as criterion, the deviations of deterministic model and fuzzy model are calculated by formula $\frac{\left|x-a\right|}{a}$, where $x$ is the measured data and $a$ is truth-value. Results of deterministic and fuzzy models are used as measured data. Results based on actual data are used as truth-value.

In the deterministic scheduling model, some uncertain parameters like ${\tilde{U}}_{ui}^{\max }$ and ${\tilde{c}}_{ui}$ are assumed as constant numbers. In the fuzzy scheduling model, these uncertain parameters are defined as fuzzy numbers, which considers the uncertainties in scheduling problem. Actual data of these uncertain parameters are fluctuant, but not constant. Results based on actual data are optimized through the collected data from actual operating condition, which can reflect the practical situation of production line. So the results closer to that based on actual data should be more practical. For accuracy, in this paper, we view the results based on actual data as the truth-value to evaluate the accuracy of deterministic model and fuzzy model, because it is fairer than just comparing the results of deterministic model and fuzzy model. Consequently, the results closer to that based on actual data should be more accurate. As shown in Table 6, the average values of deviations in terms of objective function and completion time about fuzzy model are 0.545% and 5.09%, which are all smaller than that of deterministic model. It means that the results of fuzzy model are closer to results based on actual data. So the proposed fuzzy model is more practical and accurate than deterministic model.

Fuzzy scheduling model can supply valuable decision options for enterprise managers to make decision more accurate and practical. Decision maker can adjust the acceptable possibility level $\alpha$, according to risks taken by enterprises, and then obtain more accurate and practical scheduling results. The smaller $\alpha$ decider chooses, the higher risks are taken by enterprise, but the profit will be greater and the scheduling results will be more far away from that of deterministic model. In contrast, the larger $\alpha$ decider chooses, the lower risks are taken by enterprise, but the profit will be less and the scheduling results will be closer to that of deterministic model. In addition to objective function and completion time, Gantt charts for deterministic model and fuzzy model are illustrated in Figure 4 and Figure 5.

It is noteworthy that the membership function of fuzzy number is vital for the quality of fuzzy scheduling results. If membership function is not symmetry and tends to the superior side, the objective function of fuzzy model will be better than that of deterministic model, and vice versa. So one precise membership function analyzed by historical data, is an important support for the accuracy of optimization results of fuzzy scheduling model. Some parameters, for example acceptable possibility level $\alpha$ and weights $w_a$, $w_b$ and $w_c$, also have important impact on optimization result of fuzzy model. However these parameters only affect optimization result on quantitative value but not on the quality as membership function. With the increasing of acceptable possibility level $\alpha$, the optimization result gets close to that of deterministic model. That is because the greater the acceptable possibility level is, the more the fuzzy number is close to the most possible value. The selection of $\alpha$ depends on decision maker. If decision maker doesn’t want to take too much risk, the acceptable possibility level should be greater, and vice versa. Weights $w_a$, $w_b$ and $w_c$, represent the inclination extent to most pessimistic value, the most possible value, and the most optimistic value in membership function. The three weights are usually selected by experience.

6. Conclusions

In this paper, a MINLP uncertain model for batch process is formulated based on the unit-specific event-based continuous-time modeling method. Utility uncertainty and uncertain relationship between production rate and utility supply are described by fuzzy theory. The uncertain scheduling model is converted into deterministic model by mathematical method. The accuracy and practicability of the proposed model is proved through one numerical example. Fuzzy scheduling model can supply valuable decision options for enterprise managers to make decision more accurate and practical. The impact and selection of some key parameters of fuzzy scheduling model are elaborated.