Interval Type-2 Fuzzy Model Based on Inverse Controller Design for the Outlet Temperature Control System of Ethylene Cracking Furnace
Abstract
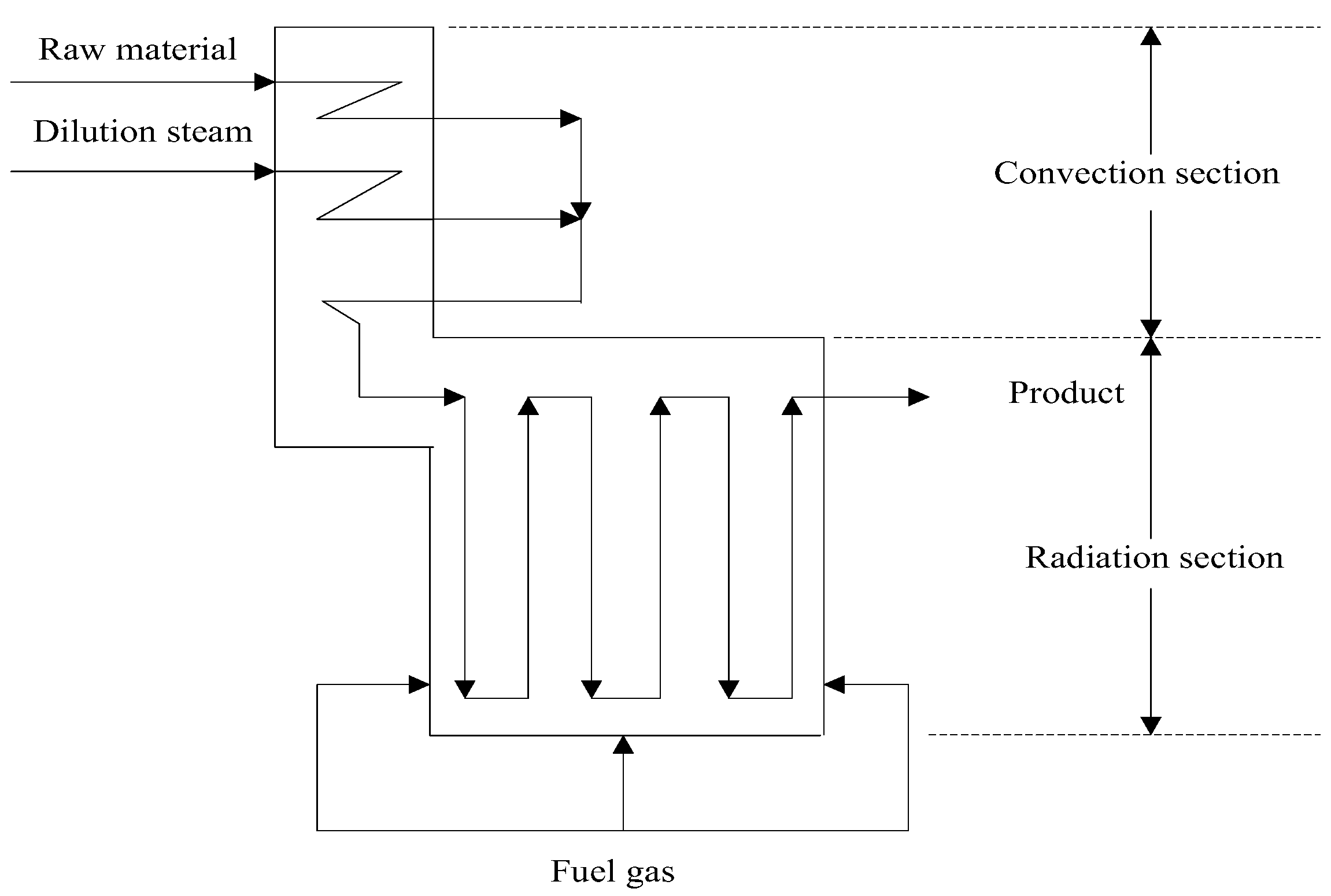
:1. Introduction
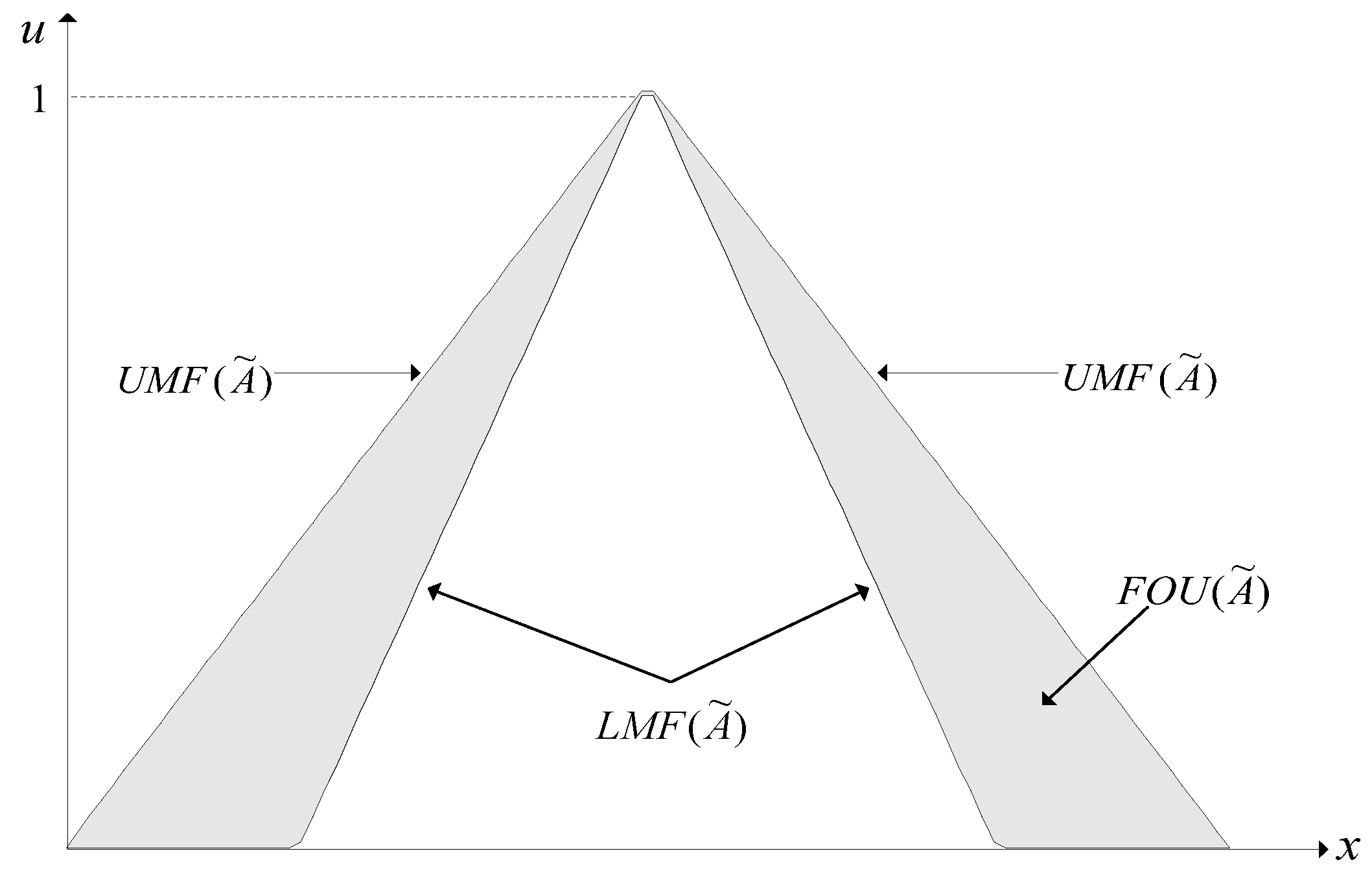
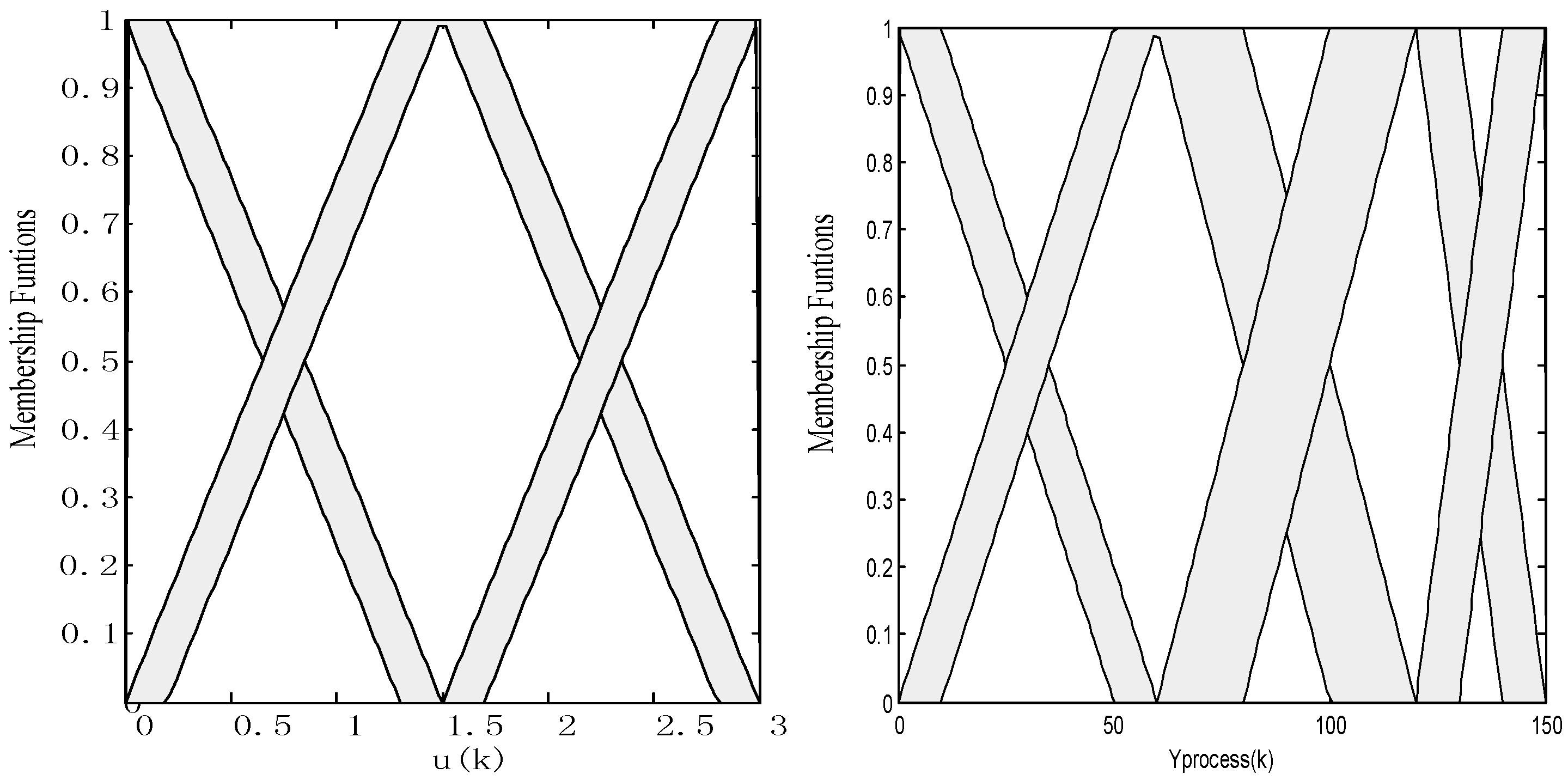
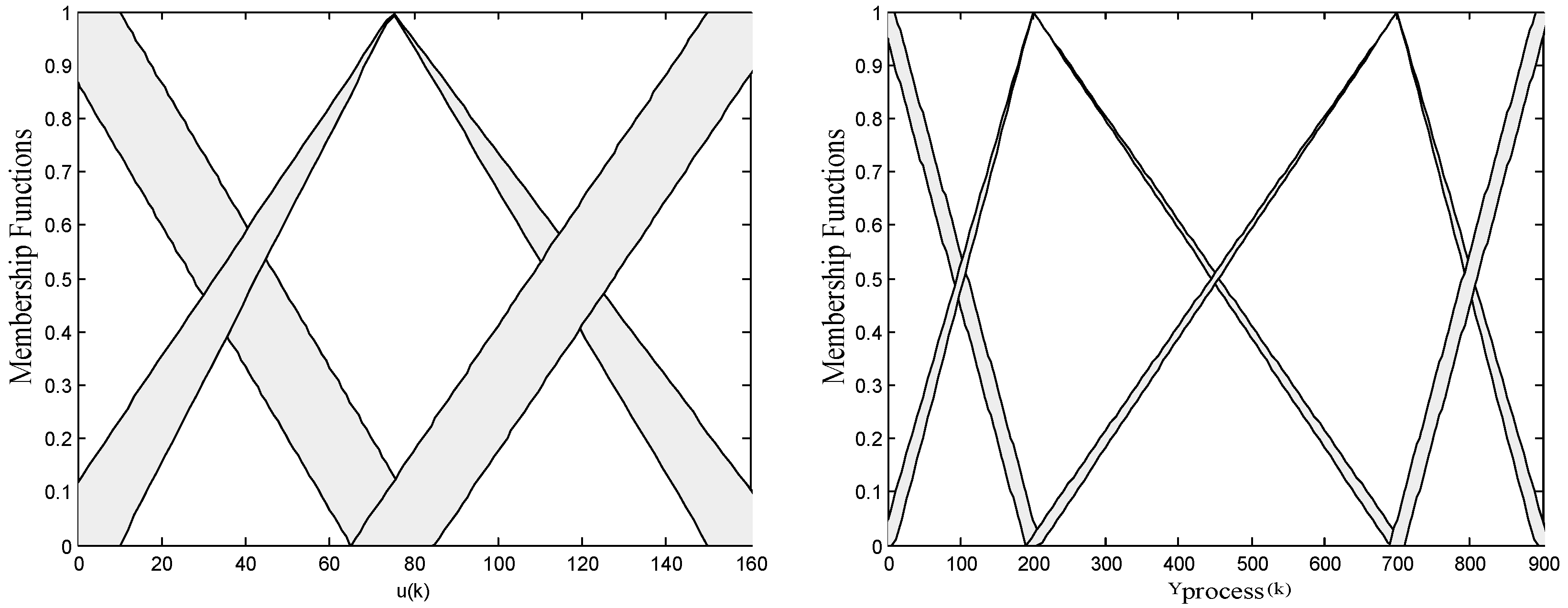
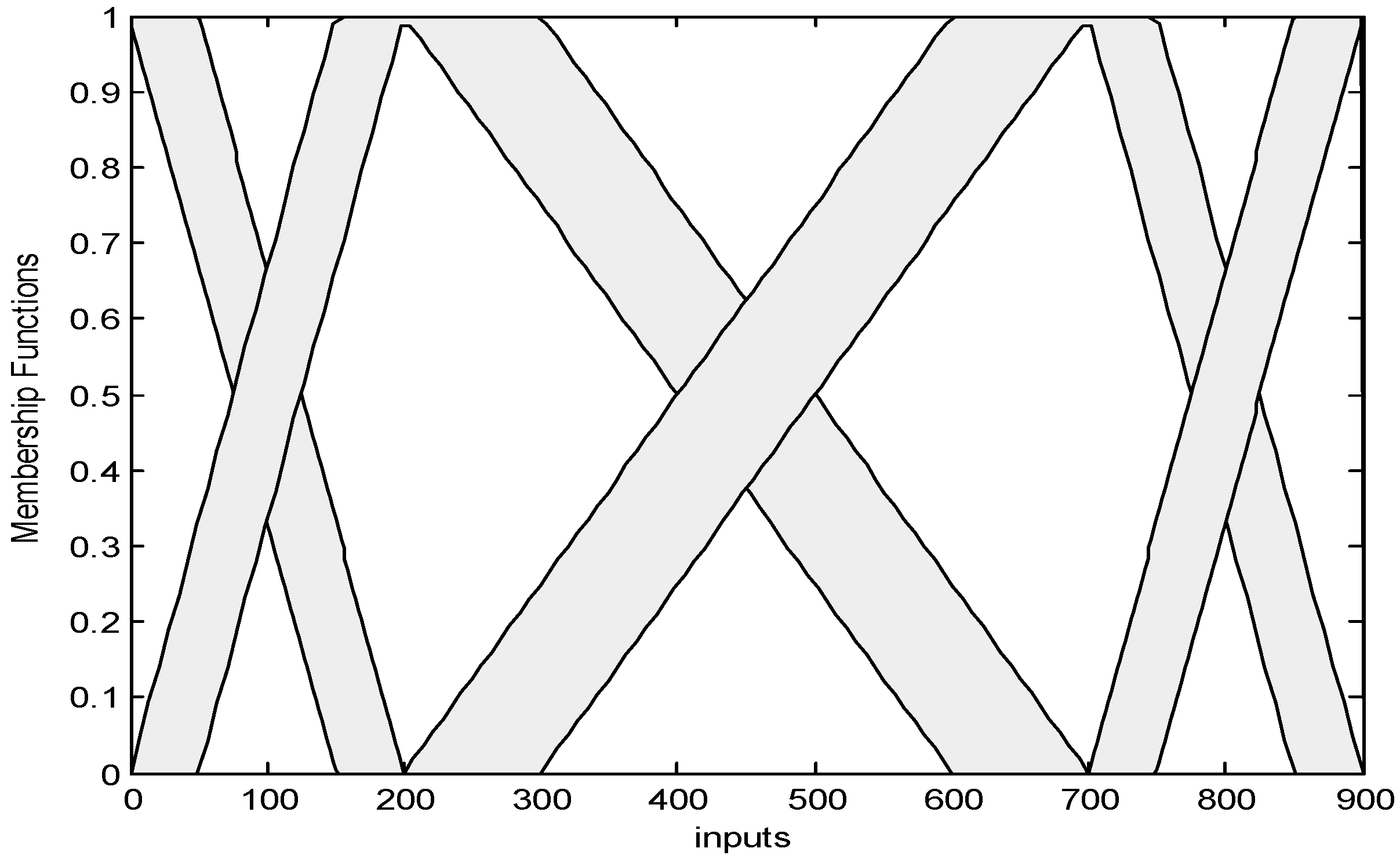
2. Interval Type-2 Fuzzy Set and Model
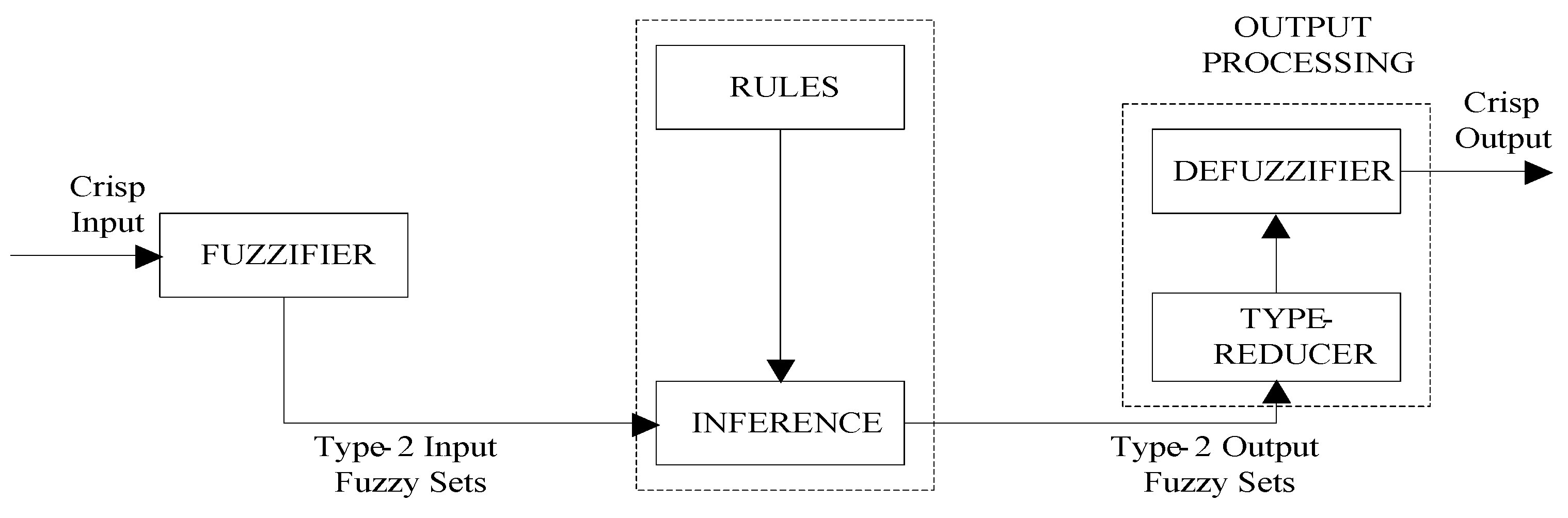
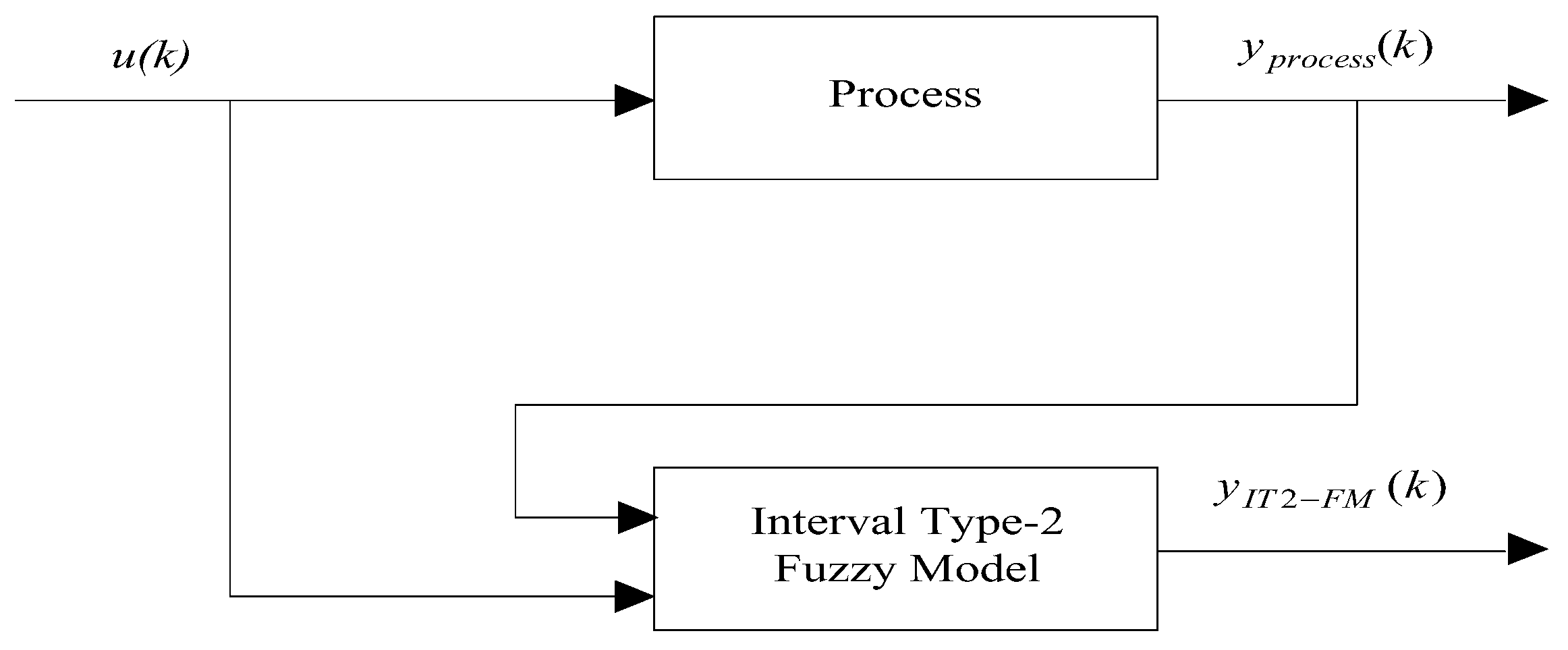
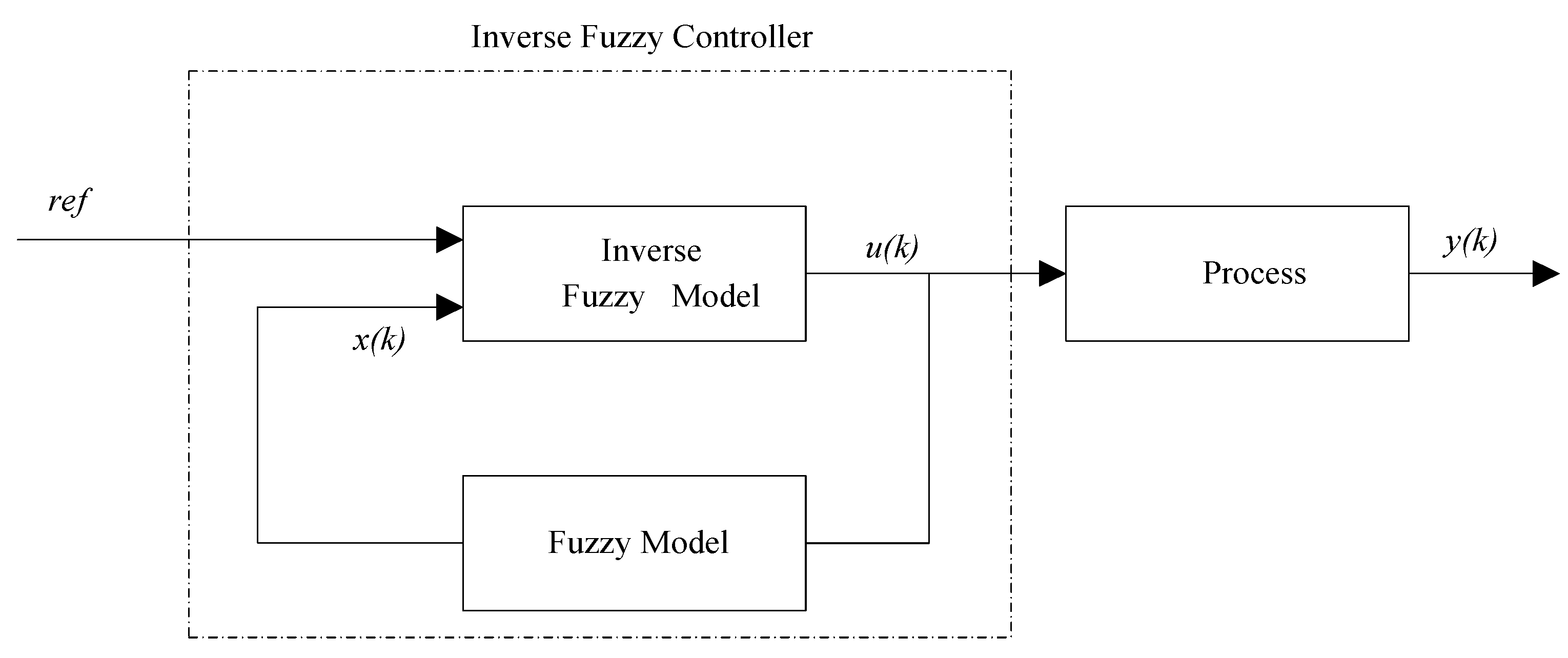
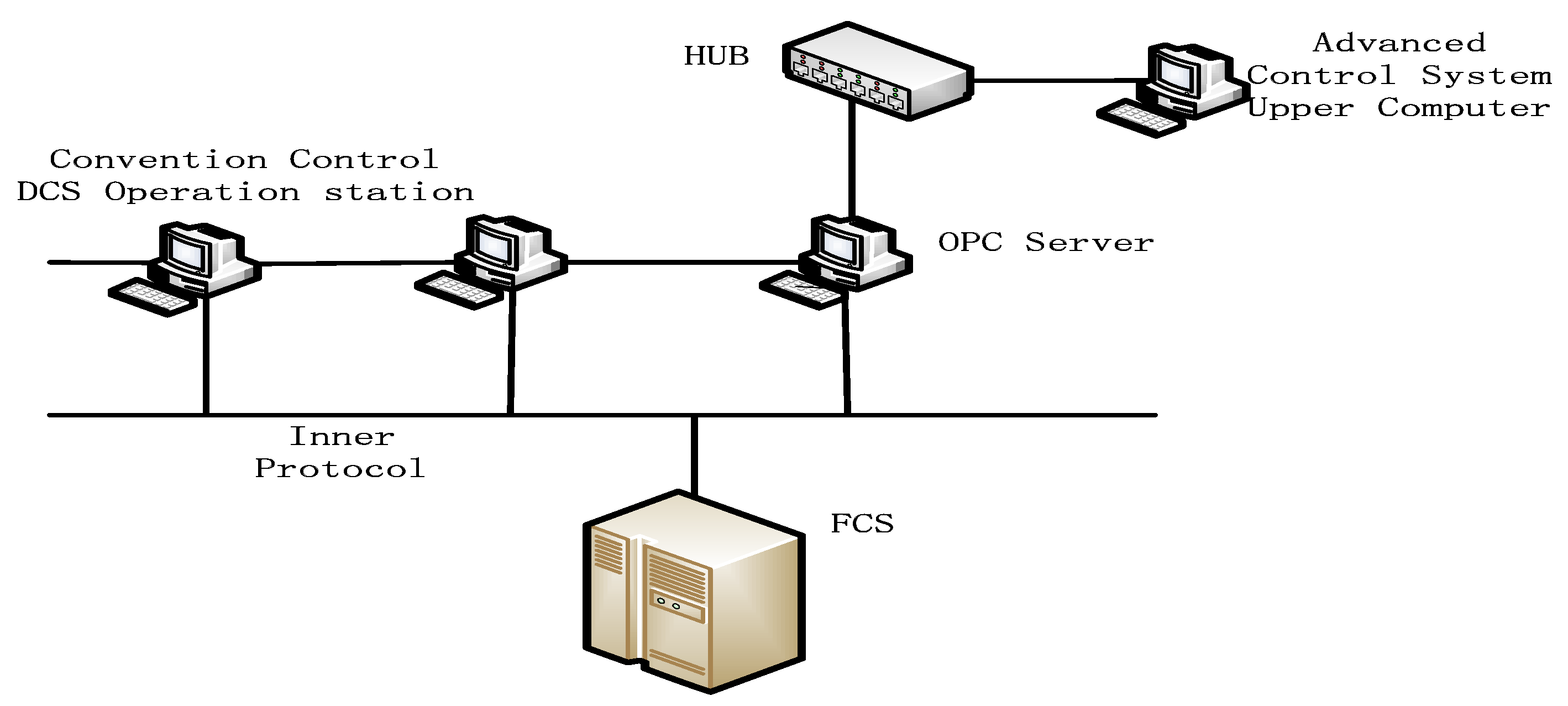
3. Approach Structure of the Interval Type-2 Fuzzy Model
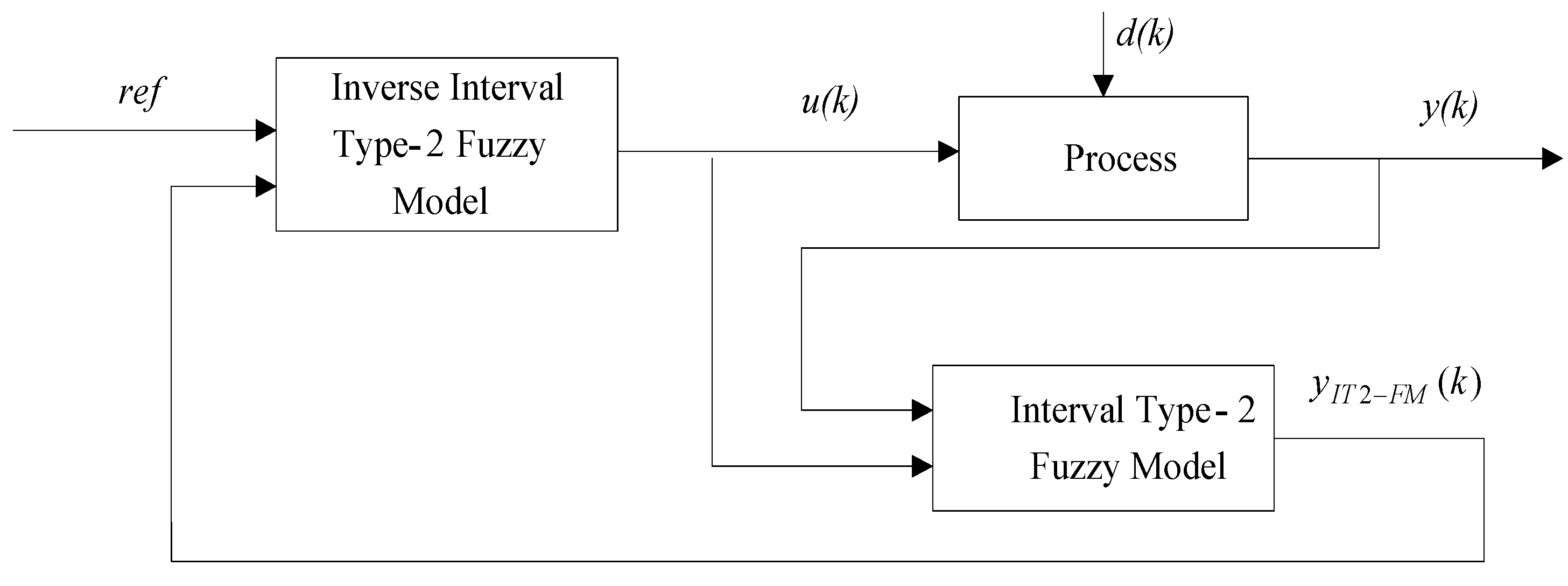
4. Inverse Interval Type-2 Fuzzy Controller Design
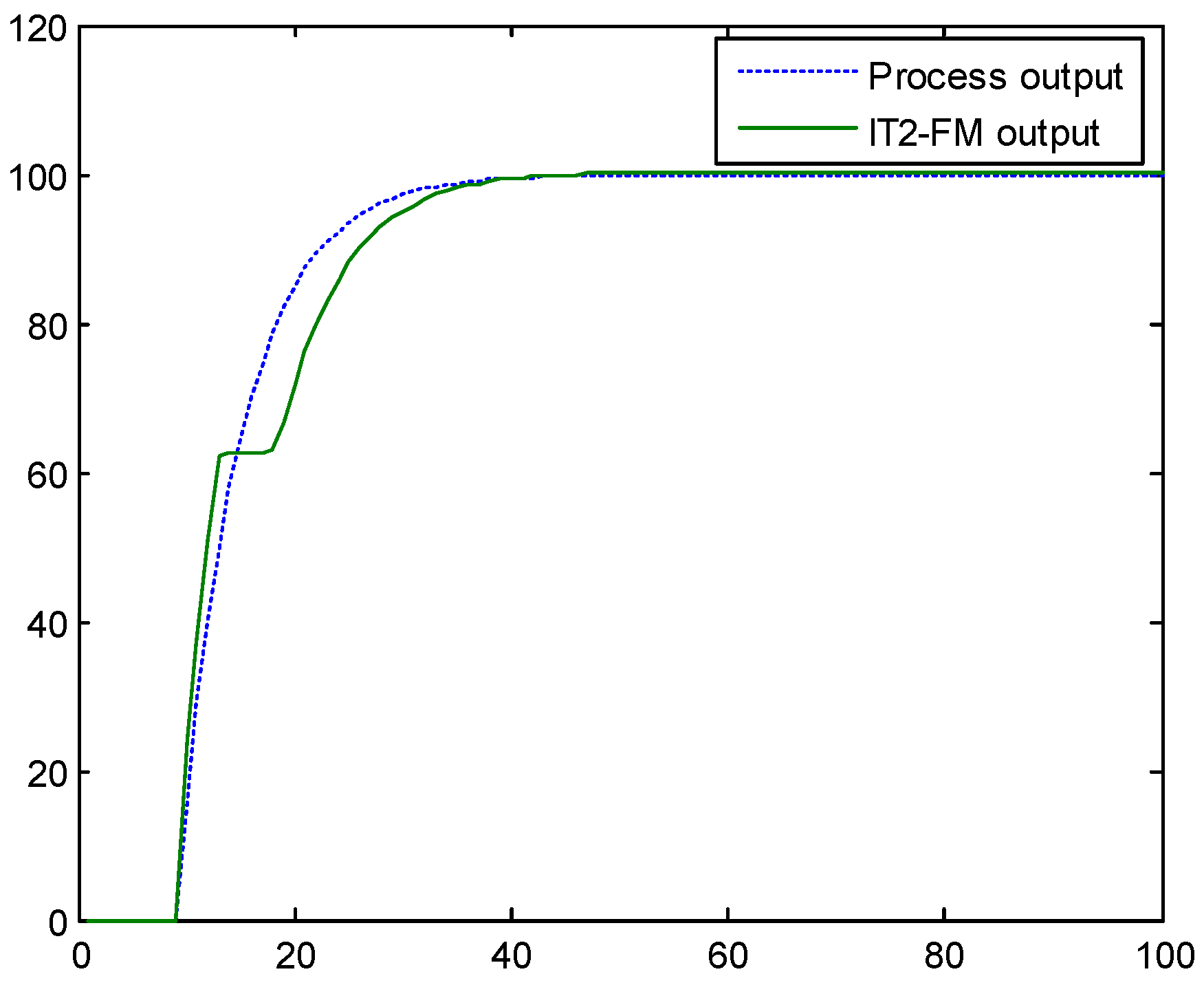
5. Simulation Studies
5.1. Performance Comparison of Type-1 and Interval Type-2 Fuzzy Approach Models
- (1)
- Root mean square error (RMSE), which is described as the following formula:
- (2)
- Variance accounted for (VAF) [4], which is described as the following formula:
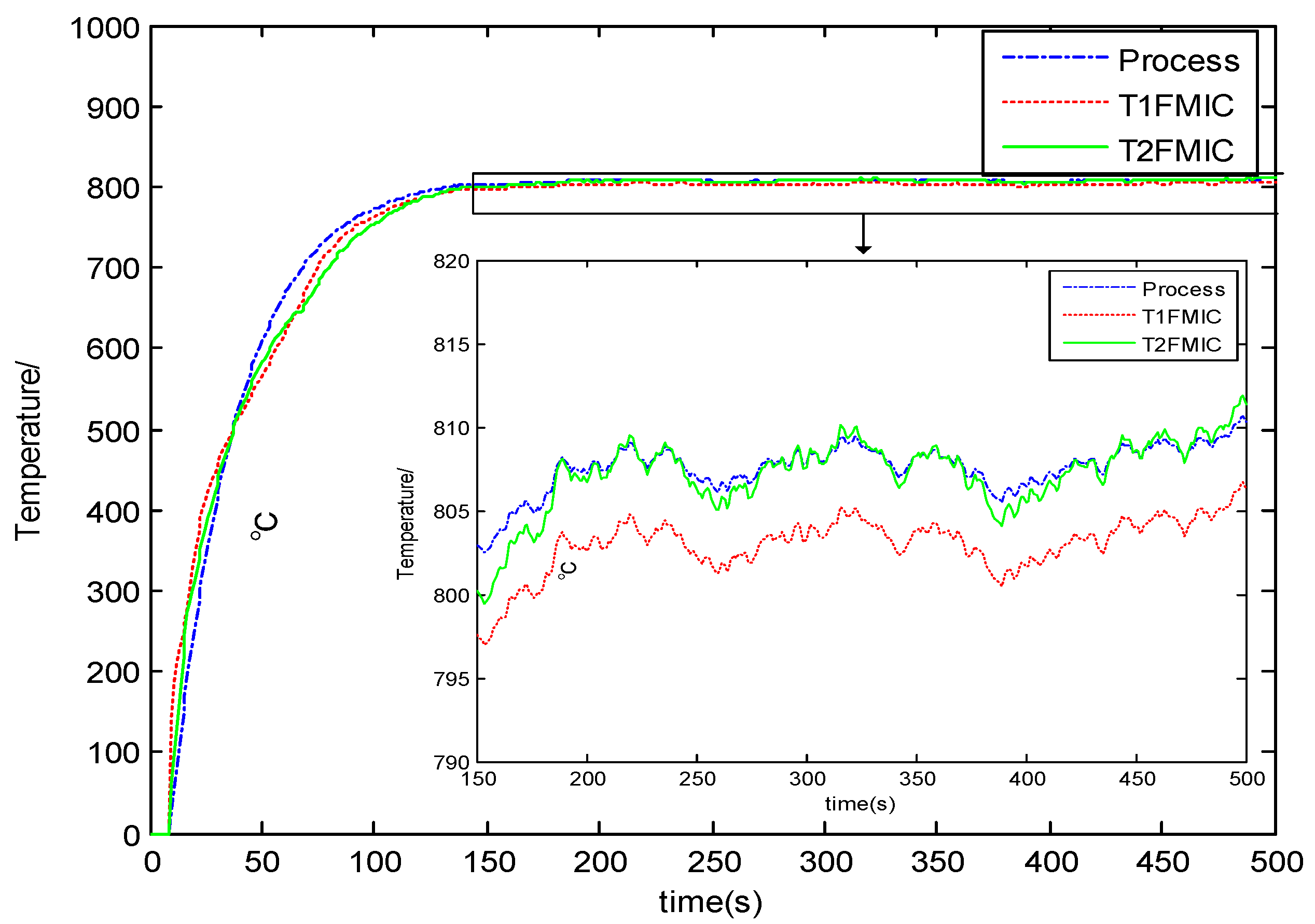
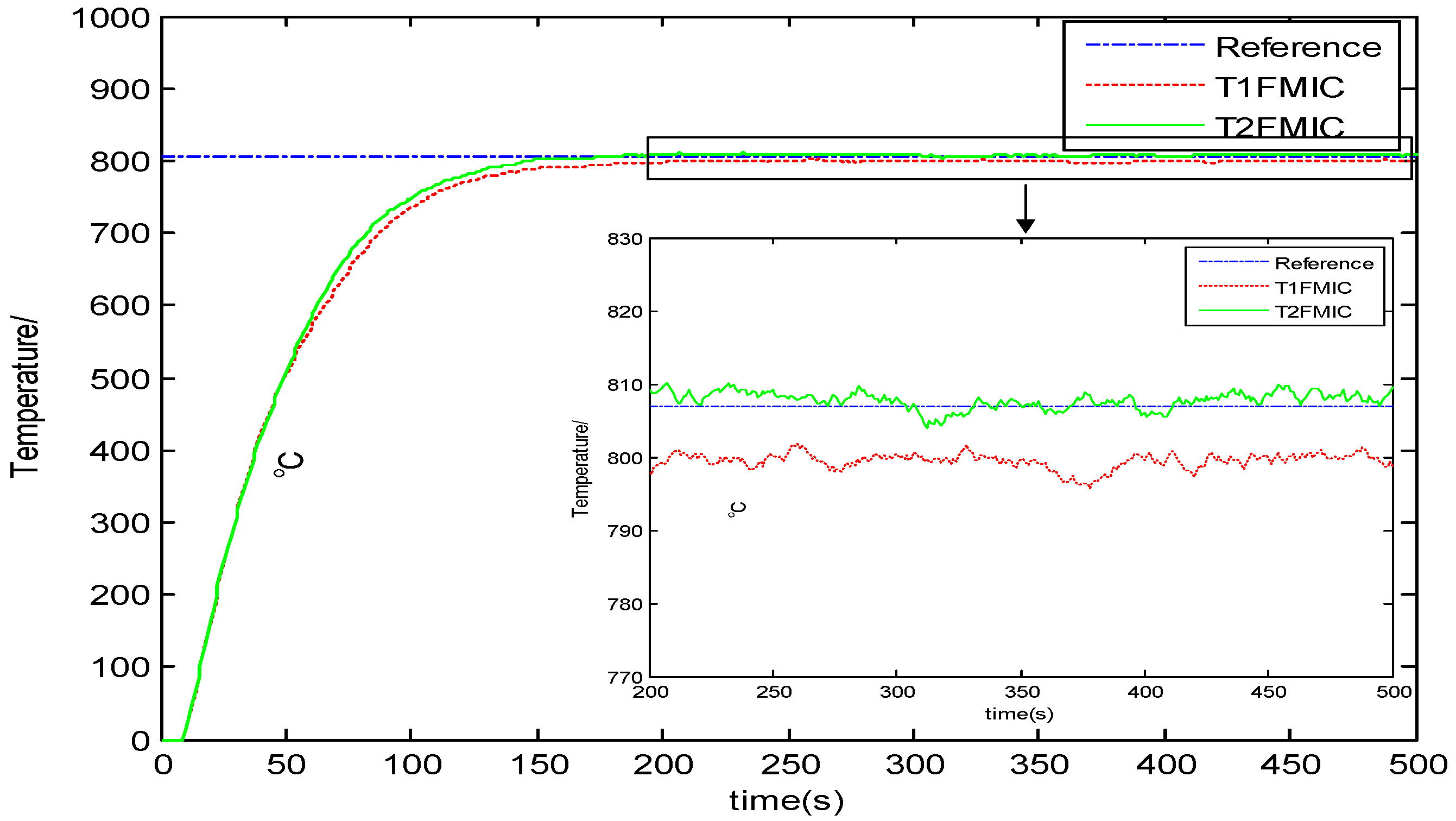
5.2. Control Performance Evaluation of the T1-FMIC and IT2-FMIC Strategies for the Outlet Temperature of the Ethylene Cracking Furnace
- (1)
- Integral of the square error (ISE), which is described as:
- (2)
- Integral of the absolute error (IAE), which is described as:
- (3)
- Integral of the time-weighted absolute error (ITAE), which is defined as:
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, P.; Li, Q.A.; Lei, R.X. Development and application of advanced process control system for the ethylene cracking heaters. Chem. Ind. Eng. 2011, 62, 2216–2220. [Google Scholar]
- Li, P.; Li, T.; Cao, J.T. Advanced Process Control of an Ethylene Cracking Furnace. Meas. Control 2015, 48, 50–53. [Google Scholar] [CrossRef]
- Kumbasar, T. A simple design method for interval type-2 fuzzy pid controllers. Soft. Comput. 2014, 18, 1293–1304. [Google Scholar] [CrossRef]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Interval type-2 fuzzy inverse controller design in nonlinear IMC structure. Eng. Appl. Artif. Intell. 2011, 24, 996–1005. [Google Scholar] [CrossRef]
- Galluzzo, M.; Cosenza, B.; Matharu, A. Control of a Nonlinear Continous Bioreactor with Bifurcation by a Type-2 Fuzzy Logic Controller. Comput. Chem. Eng. 2008, 32, 2986–2993. [Google Scholar] [CrossRef]
- Martinez, R.; Castillo, O.; Aguilar, L.T. Optimization of Interval Type-2 Fuzzy Logic Controllers for a Perturbed Autonomous Wheeled Mobile Robot Using Genetic Algorithms. Inf. Sci. 2009, 179, 2158–2174. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Castillo, O.; Castro, J.R. Generalized type-2 fuzzy systems for controlling a mobile robot and a performance comparison with interval type-2 and type-1 fuzzy systems. Expert Syst. Appl. 2015, 42, 5904–5914. [Google Scholar] [CrossRef]
- Wu, D.; Tan, W.W. Genetic Learning and Performance Evaluation of Interval Type-2 Fuzzy Logic Controllers. Eng. Appl. Artif. Intell. 2006, 19, 829–841. [Google Scholar] [CrossRef]
- Li, T.; Cao, J.T.; Li, P. Research of ethylene cracking furnace temperature control method based on IT2FIM. Chin. Comput. Appl. Chem. 2015, 32, 683–687. [Google Scholar]
- Shahnazi, R. Observer-based adaptive interval type-2 fuzzy control of uncertain MIMO nonlinear systems with unknown asymmeteric saturation actuators. Inf. Sci. 2016, 171, 1053–1065. [Google Scholar]
- Castillo, O.; Cervantes, L.; Soria, J.; Sanchez, M.; Castro, J.R. A generalized type-2 fuzzy granular approach with applications to aerospace. Inf. Sci. 2016, 354, 165–177. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Castillo, O.; Castro, J.R. Information granule formation via the concept of uncertainty-based information with interval type-2 fuzzy sets representation and Takagi-Sugeno-Kang consequents optimized with Cuckoo search. Appl. Soft Comput. 2015, 27, 602–609. [Google Scholar] [CrossRef]
- Cervantes, L.; Castillo, O. Type-2 fuzzy logic aggregation of multiple fuzzy controllers for airplane flight control. Inf. Sci. 2015, 324, 247–256. [Google Scholar] [CrossRef]
- Olivas, F.; Valdez, F.; Castillo, O.; Gonzalez, C.I.; Martinez, G.; Melin, P. Ant colony optimization with dynamic parameter adaptation based on interval type-2 fuzzy logic systems. Appl. Soft Comput. 2017, 53, 74–87. [Google Scholar] [CrossRef]
- Tai, K.; EI-Sayed, A.R.; Biglarbegian, M.; Gonzalez, C.I.; Castillo, O.; Mahmud, S. Review of recent type-2 fuzzy controller applications. Algorithms 2016, 9, 39. [Google Scholar] [CrossRef]
- Caraveo, C.; Valdez, F.; Castillo, O. Optimization of fuzzy controller design using a new bee colony algorithm with fuzzy dynamic parameter adaptation. Appl. Soft Comput. 2016, 43, 131–142. [Google Scholar] [CrossRef]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Type-2 Fuzzy Model Based Controller Design for Neutralization Processes. ISA Trans. 2012, 51, 277–287. [Google Scholar] [CrossRef] [PubMed]
- Walker, C.L.; Walker, E.A. Sets with type-2 operations. Int. J. Approx. Reason. 2009, 50, 63–71. [Google Scholar] [CrossRef]
- Molaeezadeh, S.F.; Moradi, M.H. A 2uFunction representation for non-uniform type-2 fuzzy sets: Theory and Design. Int. J. Approx. Reason. 2013, 54, 273–289. [Google Scholar] [CrossRef]
- Castillo, O.; Amador-Angulo, L.; Castro, J.R.; Garcia-Valdez, M. A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf. Sci. 2016, 354, 257–274. [Google Scholar] [CrossRef]
- Coupland, S.; John, R. New geometric inference techniques for type-2 fuzzy sets. Int. J. Approx. Reason. 2008, 49, 198–211. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Centroid of a type-2 fuzzy set. Inf. Sci. 2001, 132, 195–220. [Google Scholar] [CrossRef]
- Wu, H.; Mendel, J.M. Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2002, 10, 622–639. [Google Scholar]
- Garcia, C.E.; Morari, M. Internal model control. A unifying review and some new result. Ind. Eng. Chem. Process. Des. Dev. 1982, 21, 308–323. [Google Scholar] [CrossRef]
- Liu, D.; Fujii, F. An adaptive interval model control system of a piezo-ceramic actuator with two RBF neural networks. In Proceedings of the 2014 IEEE Interval Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 210–215. [Google Scholar]
- Toshiki, H.; Hiromitsu, O.; Hiroki, S.; Ryo, T.; Yoshihisa, I. Simplified internal model control for time delay processed. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 308–312. [Google Scholar]
- Talange, D.B.; Laware, A.R.; Bandal, V.S. Development of an internal model sliding mode controller for cascade control system. In Proceedings of the 2015 International Conference on Energy Systems and Applications, Pune, India, 30 October–1 November 2015; pp. 51–56. [Google Scholar]
- Sun, Z.P.; Chen, J.; Zhu, X.T. Multi-model internal model control applied in temperature reduction system. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 247–250. [Google Scholar]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Adaptive fuzzy internal model control design with bias term compensator. In Proceedings of the IEEE International Conference on Mechatronics, Kuala Lumpur, Malaysia, 17–19 May 2011; pp. 312–317. [Google Scholar]
- Li, S.; Gu, H. Fuzzy adaptive internal model control schemes for PMSM speed-regulation system. IEEE Trans. Ind. Inform. 2012, 8, 767–779. [Google Scholar] [CrossRef]
- Boukezzoula, R.; Galichet, S.; Folloy, L. Nonlinear internal model control: Application of inverse model based fuzzy control. IEEE Trans. Fuzzy Syst. 2003, 11, 814–829. [Google Scholar] [CrossRef]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Exact inversion of decomposable interval type-2 fuzzy logic systems. Int. J. Approx. Reason. 2013, 54, 253–272. [Google Scholar] [CrossRef]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. An inverse controller design method for interval type-2 fuzzy models. Soft Comput. 2017, 21, 2665–2686. [Google Scholar] [CrossRef]
- Kumbasar, T.; Eksin, I.; Guzelkaya, M.; Yesil, E. Type-2 fuzzy model inverse controller design based on BB-BC optimization method. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 5308–5313. [Google Scholar]
- Zadeh, L.A. Fuzzy Logic. Computer 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Introduction to type-2 fuzzy logic systems. In Proceedings of the IEEE World Congress on IEEE International Conference on Fuzzy Systems, Anchorage, AK, USA, 4–9 May 1998; pp. 915–920. [Google Scholar]
- Babuska, R. Fuzzy Modeling for Control; Springer Science Business Media, LLC.: New York, NY, USA, 1998; pp. 1593–1606. [Google Scholar]
- Zhang, X.Y.; She, H.; Zheng, Y.Y. Operation optimization based on cyber-physical system for smart converter steelmaking. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 6962–6966. [Google Scholar]
| y(k) | u(k) | ||
|---|---|---|---|
| y(k) | u(k) | ||
|---|---|---|---|
| [22.636, 32.915] | [22.636, 32.915] | [22.636, 32.915] | |
| [226.66, 240.02] | [226.66, 240.02] | [226.66, 240.02] | |
| [543.33, 556.66] | [543.33, 556.66] | [543.33, 556.66] | |
| [800.00, 812.59] | [800.00, 812.59] | [800.00, 812.59] | |
| - | RMSE | VAF |
|---|---|---|
| T1-FM | 22.0541 | 0.9816 |
| IT2-FM | 16.2918 | 0.9900 |
| y(k) | u(k) | |||
|---|---|---|---|---|
| - | ISE | IAE | ITAE |
|---|---|---|---|
| T1-MIC | 1.3544 × 107 | 3.3798 × 104 | 2.1988 × 106 |
| IT2-MIC | 1.3241 × 107 | 3.0134 × 104 | 1.3272 × 106 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Li, P.; Cao, J.; Li, T. Interval Type-2 Fuzzy Model Based on Inverse Controller Design for the Outlet Temperature Control System of Ethylene Cracking Furnace. Information 2017, 8, 116. https://doi.org/10.3390/info8040116
Zhao T, Li P, Cao J, Li T. Interval Type-2 Fuzzy Model Based on Inverse Controller Design for the Outlet Temperature Control System of Ethylene Cracking Furnace. Information. 2017; 8(4):116. https://doi.org/10.3390/info8040116
Chicago/Turabian StyleZhao, Taoyan, Ping Li, Jiangtao Cao, and Tian Li. 2017. "Interval Type-2 Fuzzy Model Based on Inverse Controller Design for the Outlet Temperature Control System of Ethylene Cracking Furnace" Information 8, no. 4: 116. https://doi.org/10.3390/info8040116





