Information Extraction Under Privacy Constraints †
Abstract
:1. Introduction
1.1. Our Model and Main Contributions
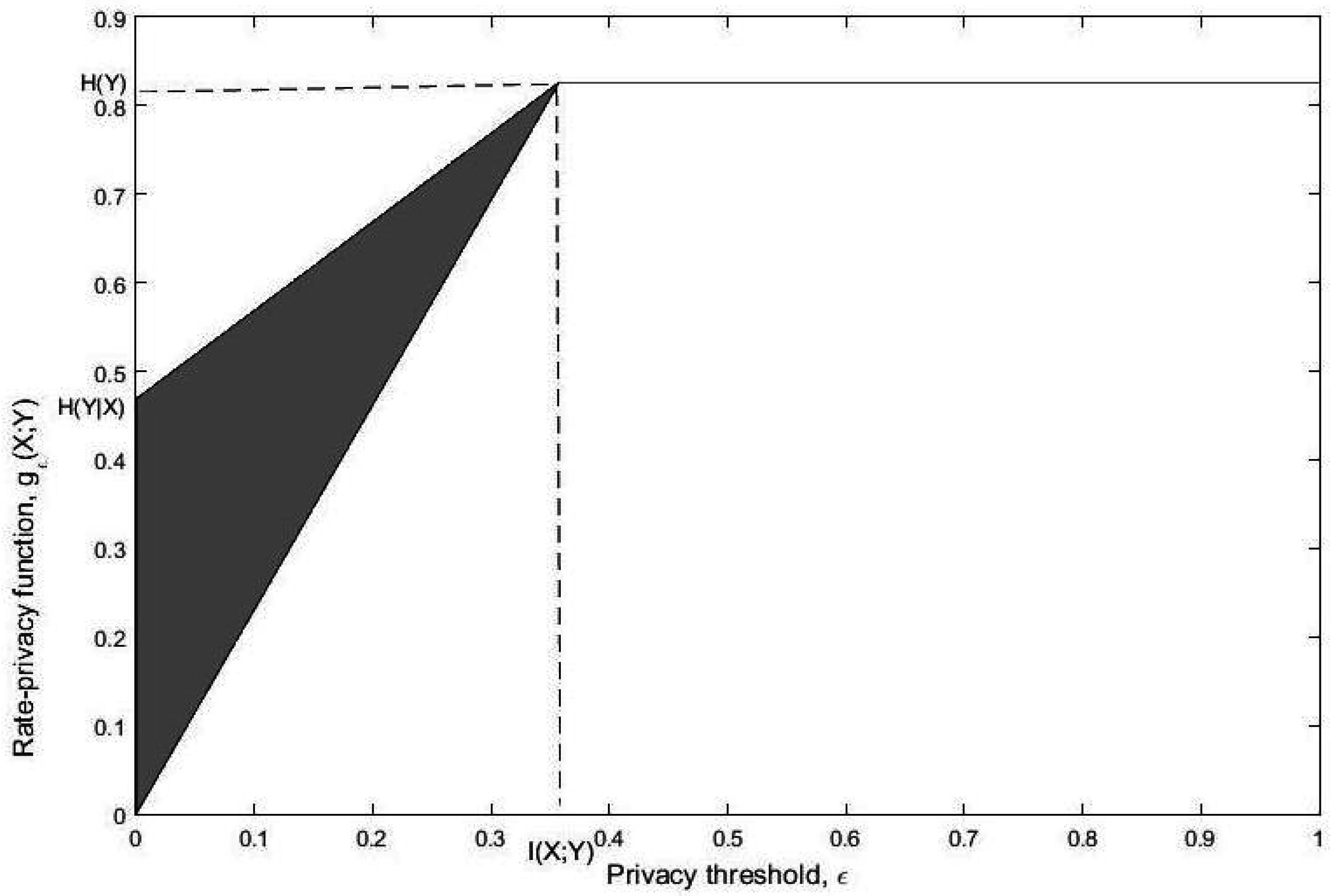
- We study lower and upper bounds of . The lower bound, in particular, establishes a multiplicative bound on for any optimal privacy filter. Specifically, we show that for a given and there exists a channel such that andwhere is a constant depending on the joint distribution . We then give conditions on such that the upper and lower bounds are tight. For example, we show that the lower bound is achieved when Y is binary and the channel from Y to X is symmetric. We show that this corresponds to the fact that both and induce distributions and which are equidistant from in the sense of Kullback-Leibler divergence. We then show that the upper bound is achieved when Y is an erased version of X, or equivalently, is an erasure channel.
- We propose an information-theoretic setting in which appears as a natural upper-bound for the achievable rate in the so-called "dependence dilution" coding problem. Specifically, we examine the joint-encoder version of an amplification-masking tradeoff, a setting recently introduced by Courtade [26] and we show that the dual of upper bounds the masking rate. We also present an estimation-theoretic motivation for the privacy measure . In fact, by imposing , we require that an adversary who observes Z cannot efficiently estimate , for any function f. This is reminiscent of semantic security [27] in the cryptography community. An encryption mechanism is said to be semantically secure if the adversary’s advantage for correctly guessing any function of the privata data given an observation of the mechanism’s output (i.e., the ciphertext) is required to be negligible. This, in fact, justifies the use of maximal correlation as a measure of privacy. The use of mutual information as privacy measure can also be justified using Fano’s inequality. Note that can be shown to imply that and hence the probability of adversary correctly guessing X is lower-bounded.
- We also study the rate of increase of at and show that this rate can characterize the behavior of for any provided that . This again has connections with the results of [25]. Lettingone can easily show that and hence the rate of increase of at characterizes the strong data processing coefficient. Note that here we have .
- Finally, we generalize the rate-privacy function to the continuous case where X and Y are both continuous and show that some of the properties of in the discrete case do not carry over to the continuous case. In particular, we assume that the privacy filter belongs to a family of additive noise channels followed by an M-level uniform scalar quantizer and give asymptotic bounds as for the rate-privacy function.
1.2. Organization
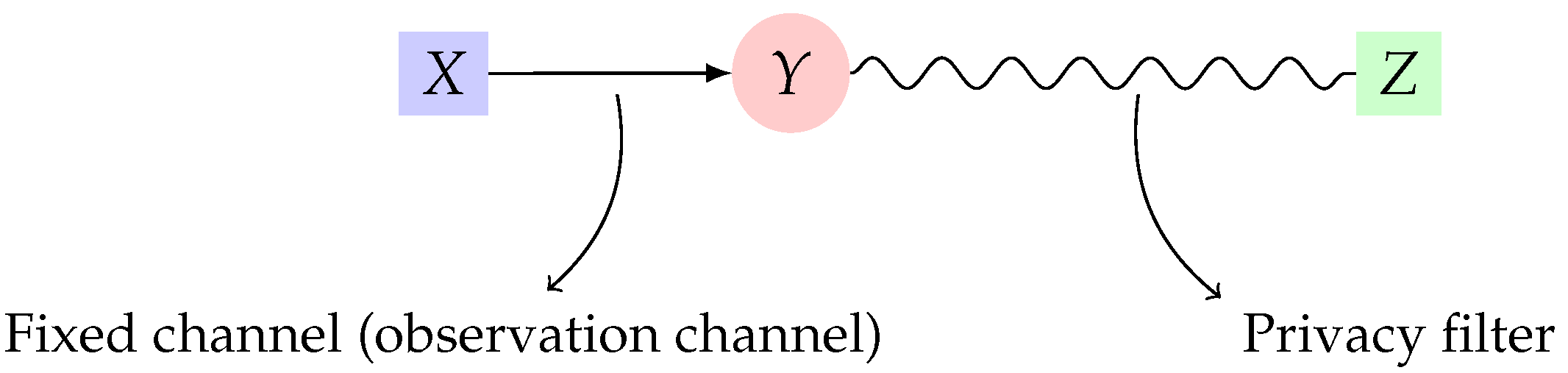
2. Utility-Privacy Measures: Definitions and Properties
2.1. Mutual Information as Privacy Measure
2.2. Maximal Correlation as Privacy Measure
2.3. Non-Trivial Filters For Perfect Privacy
3. Operational Interpretations of the Rate-Privacy Function
3.1. Dependence Dilution
3.2. MMSE Estimation of Functions of Private Information
4. Observation Channels for Minimal and Maximal
4.1. Conditions for Minimal
- (i)
- Y is uniformly distributed,
- (ii)
- is constant for all .
4.2. Special Observation Channels
4.2.1. Observation Channels With Symmetric Reverse
- (i)
- for .
- (ii)
- The initial efficiency of privacy-constrained information extraction is
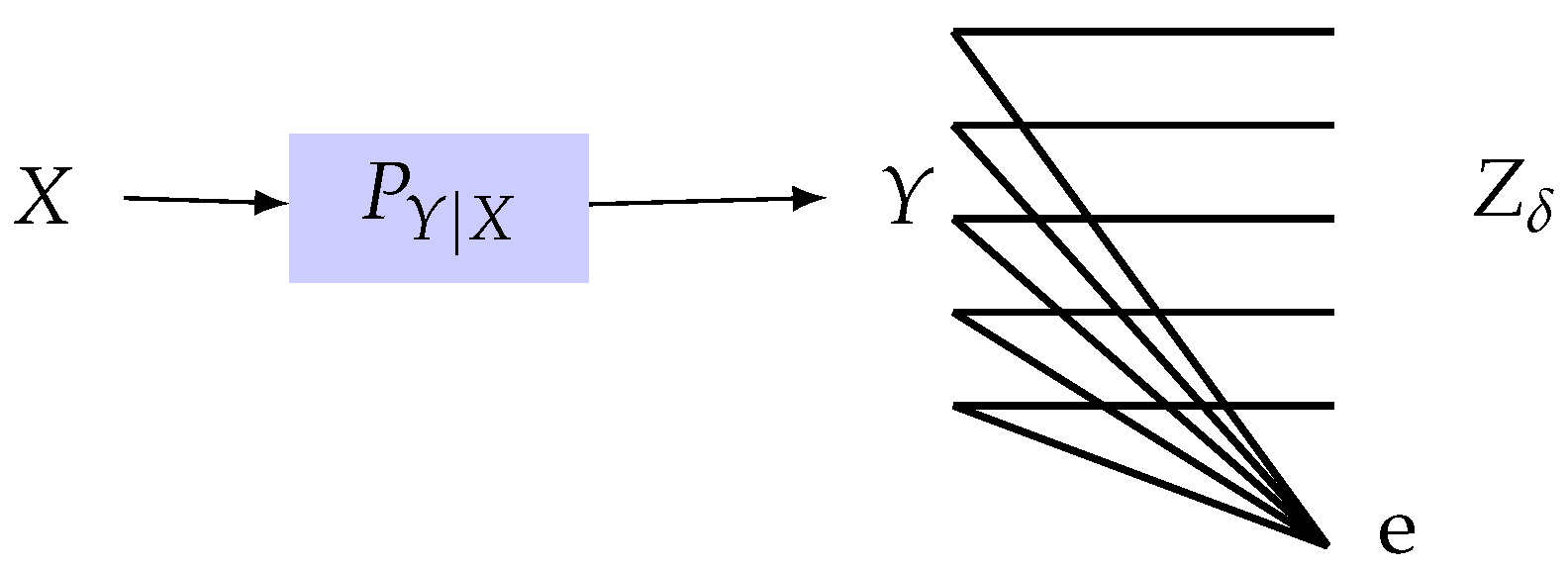
4.2.2. Erasure Observation Channel
5. Rate-Privacy Function for Continuous Random Variables
5.1. General Properties of the Rate-Privacy Function
- (a)
- There exist constants , and bounded function such thatand also for
- (b)
- and are both finite,
- (c)
- the differential entropy of satisfies ,
- (d)
- , where denotes the largest integer ℓ such that .
5.2. Gaussian Information
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemma 19
Appendix B. Completion of Proof of Theorem 25
Appendix C. Proof of Theorems 28 and 29
References
- Asoodeh, S.; Alajaji, F.; Linder, T. Notes on information-theoretic privacy. In Proceedings of the 52nd Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 30 September–3 October 2014; pp. 1272–1278.
- Asoodeh, S.; Alajaji, F.; Linder, T. On maximal correlation, mutual information and data privacy. In Proceedings of the IEEE 14th Canadian Workshop on Information Theory (CWIT), St. John’s, NL, Canada, 6–9 July 2015; pp. 27–31.
- Warner, S.L. Randomized Response: A Survey Technique for Eliminating Evasive Answer Bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Blum, A.; Ligett, K.; Roth, A. A learning theory approach to non-interactive database privacy. In Proceedings of the Fortieth Annual ACM Symposium on the Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 1123–1127.
- Dinur, I.; Nissim, K. Revealing information while preserving privacy. In Proceedings of the Twenty-Second Symposium on Principles of Database Systems, San Diego, CA, USA, 9–11 June 2003; pp. 202–210.
- Rubinstein, P.B.; Bartlett, L.; Huang, J.; Taft, N. Learning in a large function space: Privacy-preserving mechanisms for SVM learning. J. Priv. Confid. 2012, 4, 65–100. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Privacy aware learning. 2014; arXiv: 1210.2085. [Google Scholar]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Proceedings of the Third Conference on Theory of Cryptography (TCC’06), New York, NY, USA, 5–7 March 2006; pp. 265–284.
- Dwork, C. Differential privacy: A survey of results. In Theory and Applications of Models of Computation, Proceedings of the 5th International Conference, TAMC 2008, Xi’an, China, 25–29 April 2008; Agrawal, M., Du, D., Duan, Z., Li, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. Lecture Notes in Computer Science. Volume 4978, pp. 1–19. [Google Scholar]
- Dwork, C.; Lei, J. Differential privacy and robust statistics. In Proceedings of the 41st Annual ACM Symposium on the Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 437–442.
- Kairouz, P.; Oh, S.; Viswanath, P. Extremal mechanisms for local differential privacy. 2014; arXiv: 1407.1338v2. [Google Scholar]
- Calmon, F.P.; Varia, M.; Médard, M.; Christiansen, M.M.; Duffy, K.R.; Tessaro, S. Bounds on inference. In Proceedings of the 51st Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 2–4 October 2013; pp. 567–574.
- Yamamoto, H. A source coding problem for sources with additional outputs to keep secret from the receiver or wiretappers. IEEE Trans. Inf. Theory 1983, 29, 918–923. [Google Scholar] [CrossRef]
- Sankar, L.; Rajagopalan, S.; Poor, H. Utility-privacy tradeoffs in databases: An information-theoretic approach. IEEE Trans. Inf. Forensics Secur. 2013, 8, 838–852. [Google Scholar] [CrossRef]
- Tandon, R.; Sankar, L.; Poor, H. Discriminatory lossy source coding: side information privacy. IEEE Trans. Inf. Theory 2013, 59, 5665–5677. [Google Scholar] [CrossRef]
- Calmon, F.; Fawaz, N. Privacy against statistical inference. In Proceedings of the 50th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 1–5 October 2012; pp. 1401–1408.
- Rebollo-Monedero, D.; Forne, J.; Domingo-Ferrer, J. From t-closeness-like privacy to postrandomization via information theory. IEEE Trans. Knowl. Data Eng. 2010, 22, 1623–1636. [Google Scholar] [CrossRef] [Green Version]
- Makhdoumi, A.; Salamatian, S.; Fawaz, N.; Médard, M. From the information bottleneck to the privacy funnel. In Proceedings of the IEEE Information Theory Workshop (ITW), Hobart, Australia, 2–5 November 2014; pp. 501–505.
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. 2000; arXiv: physics/0004057. [Google Scholar]
- Calmon, F.P.; Makhdoumi, A.; Médard, M. Fundamental limits of perfect privacy. In Proceedings of the IEEE Int. Symp. Inf. Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 1796–1800.
- Wyner, A.D. The Wire-Tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Makhdoumi, A.; Fawaz, N. Privacy-utility tradeoff under statistical uncertainty. In Proceedings of the 51st Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 2–4 October 2013; pp. 1627–1634.
- Li, C.T.; El Gamal, A. Maximal correlation secrecy. 2015; arXiv: 1412.5374. [Google Scholar]
- Ahlswede, R.; Gács, P. Spreading of sets in product spaces and hypercontraction of the Markov operator. Ann. Probab. 1976, 4, 925–939. [Google Scholar] [CrossRef]
- Anantharam, V.; Gohari, A.; Kamath, S.; Nair, C. On maximal correlation, hypercontractivity, and the data processing inequality studied by Erkip and Cover. 2014; arXiv:1304.6133v1. [Google Scholar]
- Courtade, T. Information masking and amplification: The source coding setting. In Proceedings of the IEEE Int. Symp. Inf. Theory (ISIT), Boston, MA, USA, 1–6 July 2012; pp. 189–193.
- Goldwasser, S.; Micali, S. Probabilistic encryption. J. Comput. Syst. Sci. 1984, 28, 270–299. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton Univerity Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Shulman, N.; Feder, M. The uniform distribution as a universal prior. IEEE Trans. Inf. Theory 2004, 50, 1356–1362. [Google Scholar] [CrossRef]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw Hill: New York, NY, USA, 1987. [Google Scholar]
- Gebelein, H. Das statistische Problem der Korrelation als Variations- und Eigenwert-problem und sein Zusammenhang mit der Ausgleichungsrechnung. Zeitschrift f ur Angewandte Mathematik und Mechanik 1941, 21, 364–379. (In German) [Google Scholar] [CrossRef]
- Hirschfeld, H.O. A connection between correlation and contingency. Camb. Philos. Soc. 1935, 31, 520–524. [Google Scholar] [CrossRef]
- Rényi, A. On measures of dependence. Acta Mathematica Academiae Scientiarum Hungarica 1959, 10, 441–451. [Google Scholar] [CrossRef]
- Linfoot, E.H. An informational measure of correlation. Inf. Control 1957, 1, 85–89. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observation. Studia Scientiarum Mathematicarum Hungarica 1967, 2, 229–318. [Google Scholar]
- Zhao, L. Common Randomness, Efficiency, and Actions. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2011. [Google Scholar]
- Berger, T.; Yeung, R. Multiterminal source encoding with encoder breakdown. IEEE Trans. Inf. Theory 1989, 35, 237–244. [Google Scholar] [CrossRef]
- Kim, Y.H.; Sutivong, A.; Cover, T. State mplification. IEEE Trans. Inf. Theory 2008, 54, 1850–1859. [Google Scholar] [CrossRef]
- Merhav, N.; Shamai, S. Information rates subject to state masking. IEEE Trans. Inf. Theory 2007, 53, 2254–2261. [Google Scholar] [CrossRef]
- Ahlswede, R.; Körner, J. Source coding with side information and a converse for degraded broadcast channels. IEEE Trans. Inf. Theory 1975, 21, 629–637. [Google Scholar] [CrossRef]
- Kim, Y.H.; El Gamal, A. Network Information Theory; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Asoodeh, S.; Alajaji, F.; Linder, T. Lossless secure source coding, Yamamoto’s setting. In Proceedings of the 53rd Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 30 September–2 October 2015.
- Raginsky, M. Logarithmic Sobolev inequalities and strong data processing theorems for discrete channels. In Proceedings of the IEEE Int. Sym. Inf. Theory (ISIT), Istanbul, Turkey, 7–12 July 2013; pp. 419–423.
- Geng, Y.; Nair, C.; Shamai, S.; Wang, Z.V. On broadcast channels with binary inputs and symmetric outputs. IEEE Trans. Inf. Theory 2013, 59, 6980–6989. [Google Scholar] [CrossRef]
- Sutskover, I.; Shamai, S.; Ziv, J. Extremes of information combining. IEEE Trans. Inf. Theory 2005, 51, 1313–1325. [Google Scholar] [CrossRef]
- Alajaji, F.; Chen, P.N. Information Theory for Single User Systems, Part I. Course Notes, Queen’s University. Available online: http://www.mast.queensu.ca/math474/it-lecture-notes.pdf (accessed on 4 March 2015).
- Chayat, N.; Shamai, S. Extension of an entropy property for binary input memoryless symmetric channels. IEEE Trans.Inf. Theory 1989, 35, 1077–1079. [Google Scholar] [CrossRef]
- Oohama, Y. Gaussian multiterminal source coding. IEEE Trans. Inf. Theory 1997, 43, 2254–2261. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Linder, T.; Zamir, R. On the asymptotic tightness of the Shannon lower bound. IEEE Trans. Inf. Theory 2008, 40, 2026–2031. [Google Scholar] [CrossRef]
- Rényi, A. On the dimension and entropy of probability distributions. cta Mathematica Academiae Scientiarum Hungarica 1959, 10, 193–215. [Google Scholar] [CrossRef]
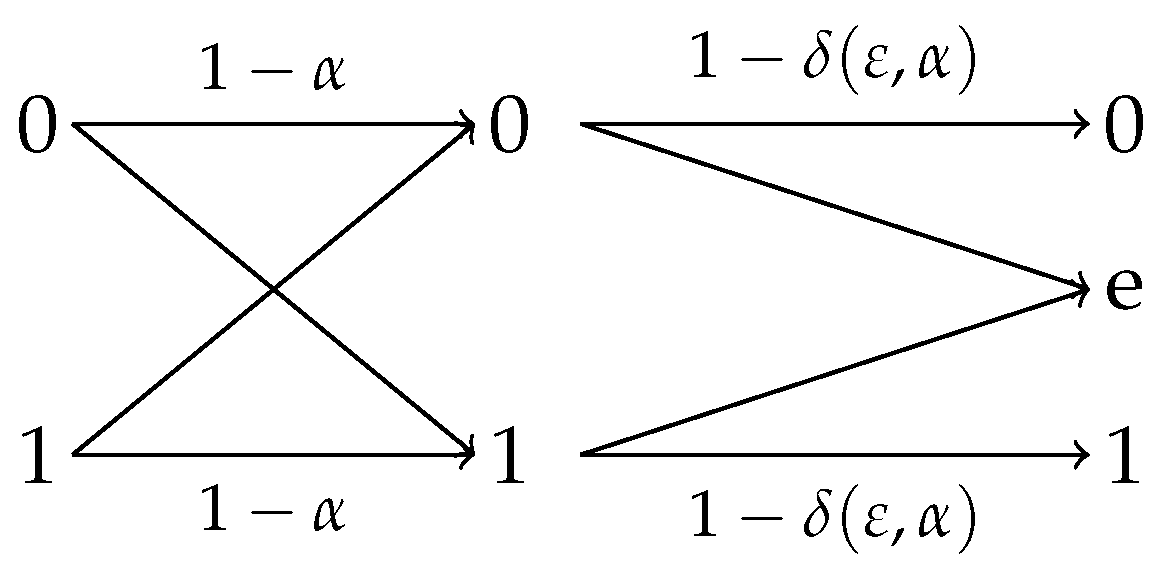
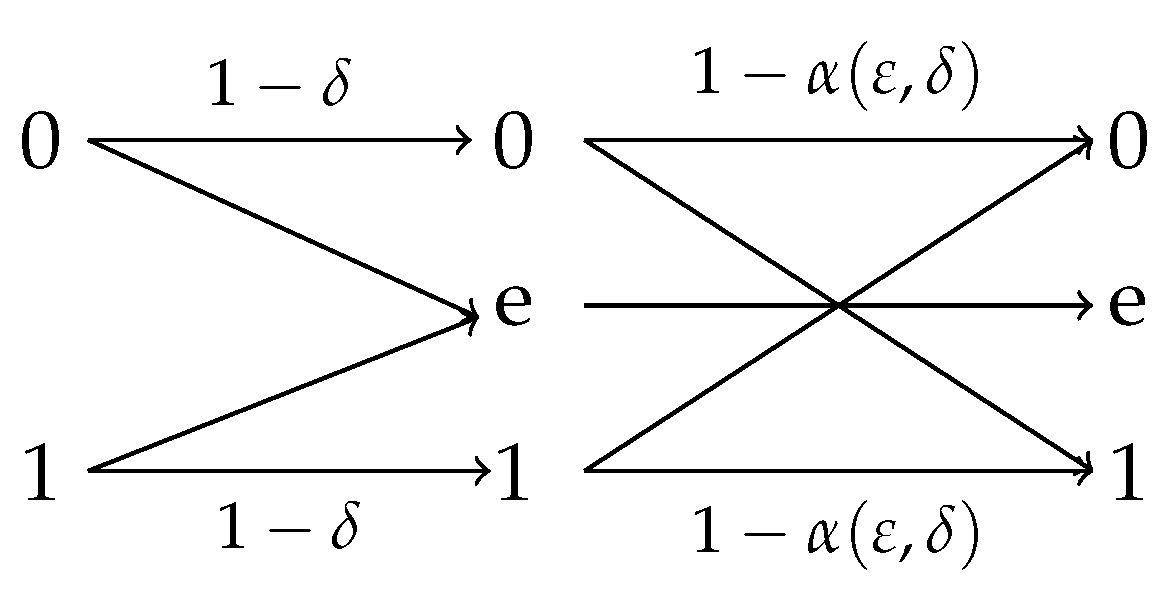
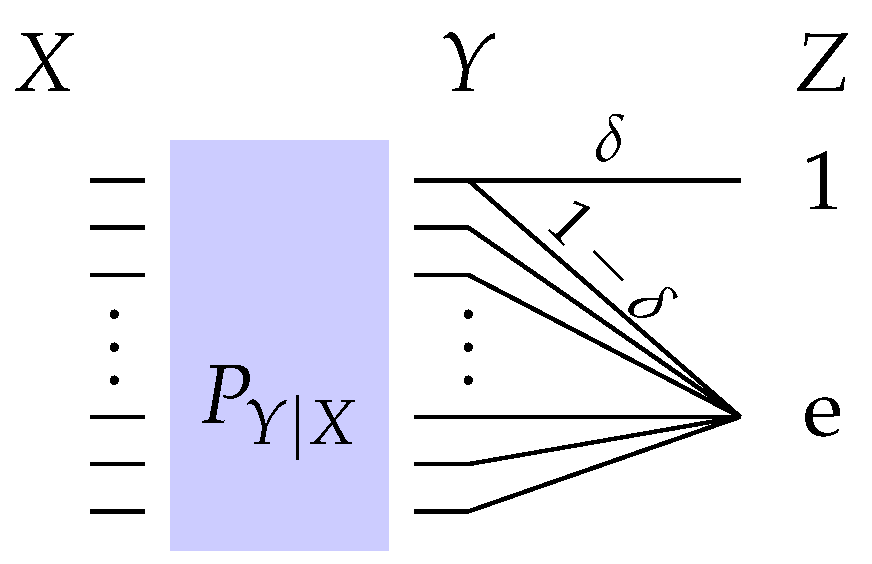
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asoodeh, S.; Diaz, M.; Alajaji, F.; Linder, T. Information Extraction Under Privacy Constraints. Information 2016, 7, 15. https://doi.org/10.3390/info7010015
Asoodeh S, Diaz M, Alajaji F, Linder T. Information Extraction Under Privacy Constraints. Information. 2016; 7(1):15. https://doi.org/10.3390/info7010015
Chicago/Turabian StyleAsoodeh, Shahab, Mario Diaz, Fady Alajaji, and Tamás Linder. 2016. "Information Extraction Under Privacy Constraints" Information 7, no. 1: 15. https://doi.org/10.3390/info7010015




