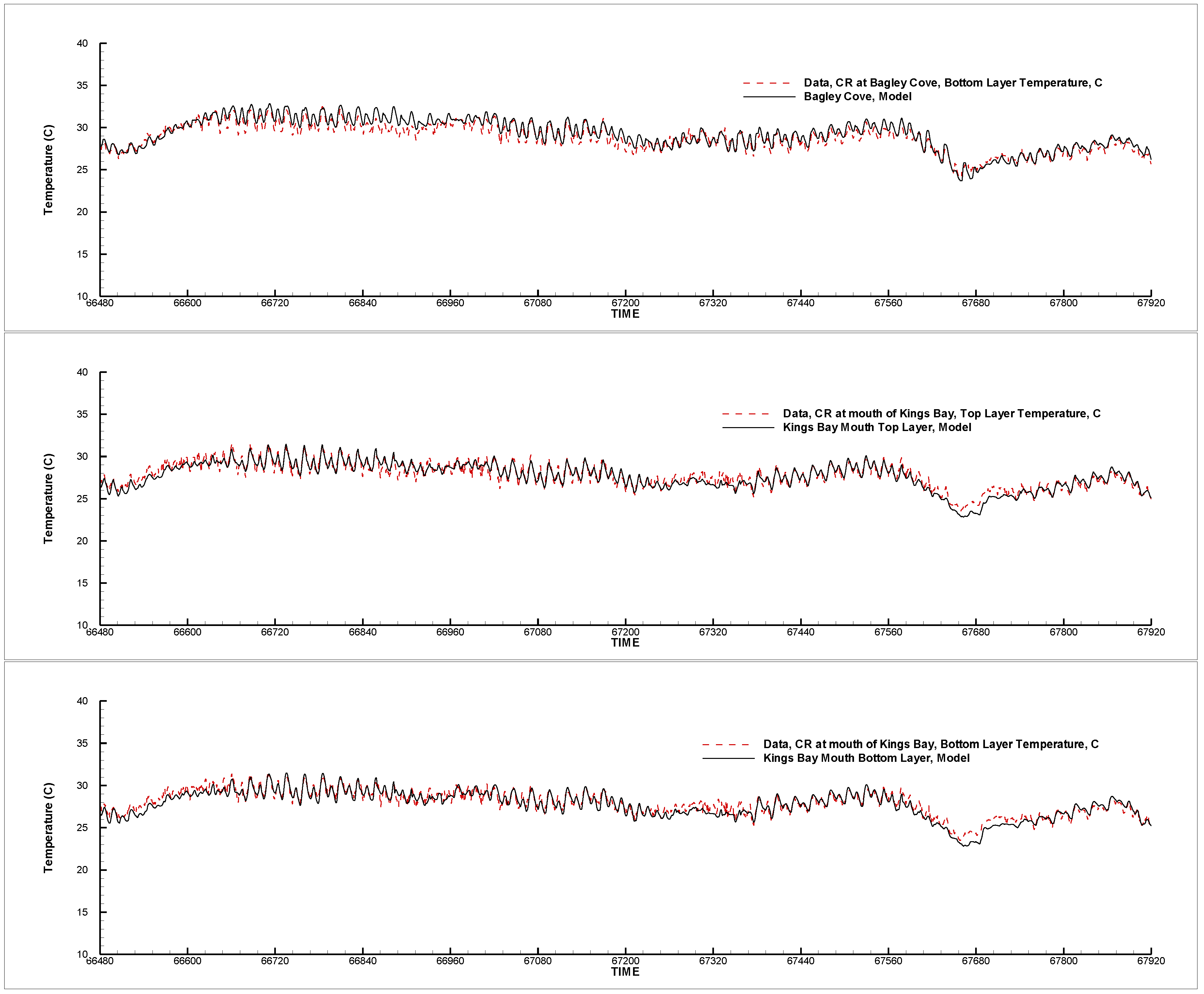
2.1. Data Collection
There exist only limited data collection activities that have tried to quantify flows out of submerged vents in Kings Bay. Rosenau
et al. [
8] measured instantaneous flows and water quality parameters from selected springs that flow into Kings Bay, with a total of 30 reported springs being identified and listed in their report. The same 30 springs in Kings Bay were also listed in a more recent bulletin of Florida Bureau of Geology [
9]. Spring flow rates and water quality in the Crystal River were measured by Seaburn
et al. [
10] in April 1974 to support a water quality modeling study of the system. Yobbi and Knochenmus [
2] estimated the average total spring discharge during 1965–1977 to be about 975 cfs for Kings Bay. In an effort to simulate circulation and flushing characteristics of Kings Bay [
3], the United States Geological Survey (USGS) conducted a flow measurement during 7–8 June 1990 near Bagley Cove (
Figure 1) in the Crystal River. The net flux through this cross section during the tidal cycle was found to be 735 cfs. In a 2D hydrodynamic simulation by Hammett
et al. [
3], 28 major springs in Kings Bay were included in their model based on information from [
8]. In a spring water quality study by the Southwest Florida Water Management District (SWFWMD) during 1993–2004, additional spring vents in Kings Bay were identified.
As none of the aforementioned previous studies of spring discharges to Kings Bay is spatially or temporally comprehensive, it is necessarily to conduct a more extensive data collection study to quantify spring flows and to find out how SGD is affected by tides and the groundwater level in the estuary. For this purpose, a two-phase field investigation in Kings Bay was conducted during 2008–2009. The first phase was a thorough inventory survey, in which all the identifiable spring vents were identified with their locations (latitudes and longitudes) were recorded and configurations, including dimensions (areas) and orientations, were documented. The second phase was to measure discharges out of each spring vent with divers diving to the vents to measure the velocities of spring flows. The discharge was simply the product of the vent area and the velocity. For most of spring vents, multiple field trips were made to measure discharges under various tidal conditions.
During the inventory survey, previously documented spring vents were first visited and validated via snorkeling and SCUBA equipped diving [
11]. The entire Kings Bay was then searched for additional spring vents that were not previously documented. At several spring sites, multiple vents are located in a close proximity, forming a vent cluster that jointly contributes to the overall discharge for the spring. A single set of coordinates was recorded for the vent cluster, which is considered as a single spring. The inventory survey was able to identify a total number of 70 springs, which is more than double the previously documented number of springs.
Figure 1 shows locations of these 70 springs (marked with asterisks). It should be noted that some asterisks appear to be overlapped, because several springs are very close to each other.
After the inventory survey of detectable spring vents was completed, flow measurements were conducted using acoustic Doppler current profiler (ADCP) type meters. Instantaneous discharge measurements for the detectable spring vents were carried out under various tidal conditions (e.g., spring and neap tides) during 28–31 July, 17–20 August, 21–25 September, and 5–8 October 2009. In addition to the flow measurement for each spring vent, a multi-parameter water quality monitoring sonde was used to measure specific conductance and temperature at the same time. Water quality data are not the focus of this paper and thus not discussed in detail in the following discussion.
In order to study effects of tides on spring discharges, two multi-beam ADCPs were deployed to measure real-time cross-sectional fluxes in two channels, each conveying discharges out of a group of spring vents discharge to Kings Bay. In
Figure 2, G1 and G2 denote the locations where Groups 1 and 2 of the springs were gauged, respectively. Group 1 consists of three springs (#8–#10), while Group 2 consists of eight springs (#15, #16, #18–#23). The ADCP measurements of the cross-sectional fluxes through the channel were recorded every 15 minutes and were conducted during a 25-day period between 27 July and 20 August 2009, during which both surface water level data in Kings Bay and groundwater level data at a nearby well were available. The groundwater well is called ROMP TR21-3 and located roughly 2.5 km southeast of the center of Kings Bay (
Figure 1).
Figure 2.
Locations where Group 1 (G1) and Group 2 (G2) spring flows were gauged. Identified springs are marked by white circles with numbers (for mapping purposes, springs in a close proximity are combined together sharing a single number).
Figure 2.
Locations where Group 1 (G1) and Group 2 (G2) spring flows were gauged. Identified springs are marked by white circles with numbers (for mapping purposes, springs in a close proximity are combined together sharing a single number).
2.2. Data Analyses
Results of instantaneous discharge measurements during July–October 2009 are reported elsewhere [
12]. Most spring sites were measured under more than one tidal condition, resulting in multiple discharge samples for these sites. At 11 sites, spring discharges were measured only one time because of their relatively low flow rates, though multiple readings were recorded for each of them to either obtain an average flow rate or get the sum for the spring site if several vents are involved. Similar to the finding reported in previous measurements, the magnitude of the spring flow in Kings Bay varies greatly from one vent to another. About 15 spring sites are second order magnitude springs with mean discharges ranging between 10 and 100 cfs, while two are fifth order magnitude (1–100 gal/min, or 0.0223–0.223 cfs) or less. For the same spring site, the discharge also varies significantly from time to time. For example, a spring vent named H24 in the north portion of Kings Bay was measured on two different days. One was on 23 September 2009 and the other was on 7 October 2009. The first measurement of the discharge was 8.35 cfs, but the second flow measurement was 49.5 cfs, almost six times of the previous measurement. The total of measured mean flows from all the identified vents is about 467 cfs.
Generally, salinity is higher in southern springs than in northern springs. Except for Sites No. 1 and H24 (
Figure 2), most northern springs discharge fresh water, with salinity normally less than 0.5 psu. Site No. 1 is located at the headwater of Miller Creek, which is a short waterway connecting the spring with the Crystal River (
Figure 2), and has an average salinity of 1.75 psu. H24 is connected to Kings Bay through a spring run and has an average salinity of 1.14 psu. Southern springs are brackish and salinities in these springs can be 6 psu or higher (e.g., Spring Sites 38–40). Overall, the flow-weighted salinity in spring flows out of all spring vents is about 1.58 psu.
Spring temperature is generally much more stable than spring salinity in Kings Bay, both in terms of special variation and temporal variation. Most spring flows have a temperature around 23.5. The highest spring temperature was measured at H24 Spring Site, with a value of 24.94 °C. The lowest spring temperature was measured at Spring Site No. 1 located at the headwater of Miller Creek, where the average spring temperature was 22.93 °C. The flow-weighted spring temperature was 23.51 °C for all the springs in Kings Bay during the measurement period. During the coldest days in winter, spring temperature can be about 1 °C lower than in summer.
As mentioned above, real-time cross-sectional fluxes at G1 and G2 shown in
Figure 2 were measured with multi-beam ADCPs during 27 July to 20 August 2009. Because cross-sectional fluxes measured at the two sites also include tidal prisms upstream of the cross sections, net spring discharges from the two groups of springs need to be adjusted as follows
where
qg is the net spring flow of the group,
qm is the cross-sectional flux measured by ADCP,
A is the total water surface area upstream of the cross section,
t is time, and
η is the water surface elevation measured at the mouth of Kings Bay station.
qg and
qm are positive leaving the spring group. The second term on the right hand side in the above equation is the flux due to the tidal prism. Using a geographic information system, the total water surface areas upstream of Groups 1 and 2 are found to be 613,111.20 and 1,785,544.49 square feet at the mean sea level, respectively. Because shorelines in both areas are mostly man-made vertical seawalls, both areas vary around their mean sea level values within a very small range and thus can be treated as constants. The time derivative of water surface elevation can be calculated from measured data at the USGS mouth of Kings Bay station.
Results of Equation (1) for both Groups are presented in
Figure 3, along with measured water level at the USGS mouth of Kings Bay station during the same period. There were some problems with the ADCP measurement at the G1 cross section after about 9.5 days, and thus only the first 9.5 days of Group 1 spring flow data are plotted in
Figure 3.
Figure 3.
Measured spring flows for Group 1 (red short dashed line) and Group 2 (blue long dashed line) during 27 July–20 August 2009. The green solid line is measured water level at the USGS mouth of Kings Bay station during the same period.
Figure 3.
Measured spring flows for Group 1 (red short dashed line) and Group 2 (blue long dashed line) during 27 July–20 August 2009. The green solid line is measured water level at the USGS mouth of Kings Bay station during the same period.
From
Figure 3, one can see that spring flows for both Groups 1 and 2 exhibit strong tidal signals. Mean discharge out of Group 2 spring vents are about twice of that out of Group 1 spring vents; however, the range of discharge variation for Group 2 springs is more than five times of that for Group 1 springs. As shown in
Figure 3, net spring flows from both spring groups are negatively proportional to the surface water elevation. As water level increases, spring flows decrease, and
vice versa. When surface water level in Kings Bay increases to a certain elevation, the net spring flow from Group 2 vents becomes negative. In other words, instead of ground water being discharged out of the springs, estuarine water in Kings Bay flows into these spring vents.
As mentioned above, the inverse relationship between tides and SGD has been reported in many previous studies all over the world, including those for Kings Bay springs [
2,
3]. Based on flow measurement for a single spring (Spring Site 6 in
Figure 2), Hammett
et al. [
3] obtained the following linear regression equation
where
q1, in cfs, is the estimated spring flow for Spring Site 6 in
Figure 2 and
η, in feet NGVD 29, is water level measured at the mouth of Kings Bay station.
Equation (2) suggests that the spring discharge is only a function of water level. This is obviously not the whole story for spring discharges in Kings Bay, because one of the main driving forces that cause springs to discharge flows to Kings Bay, namely the groundwater level, also varies with time.
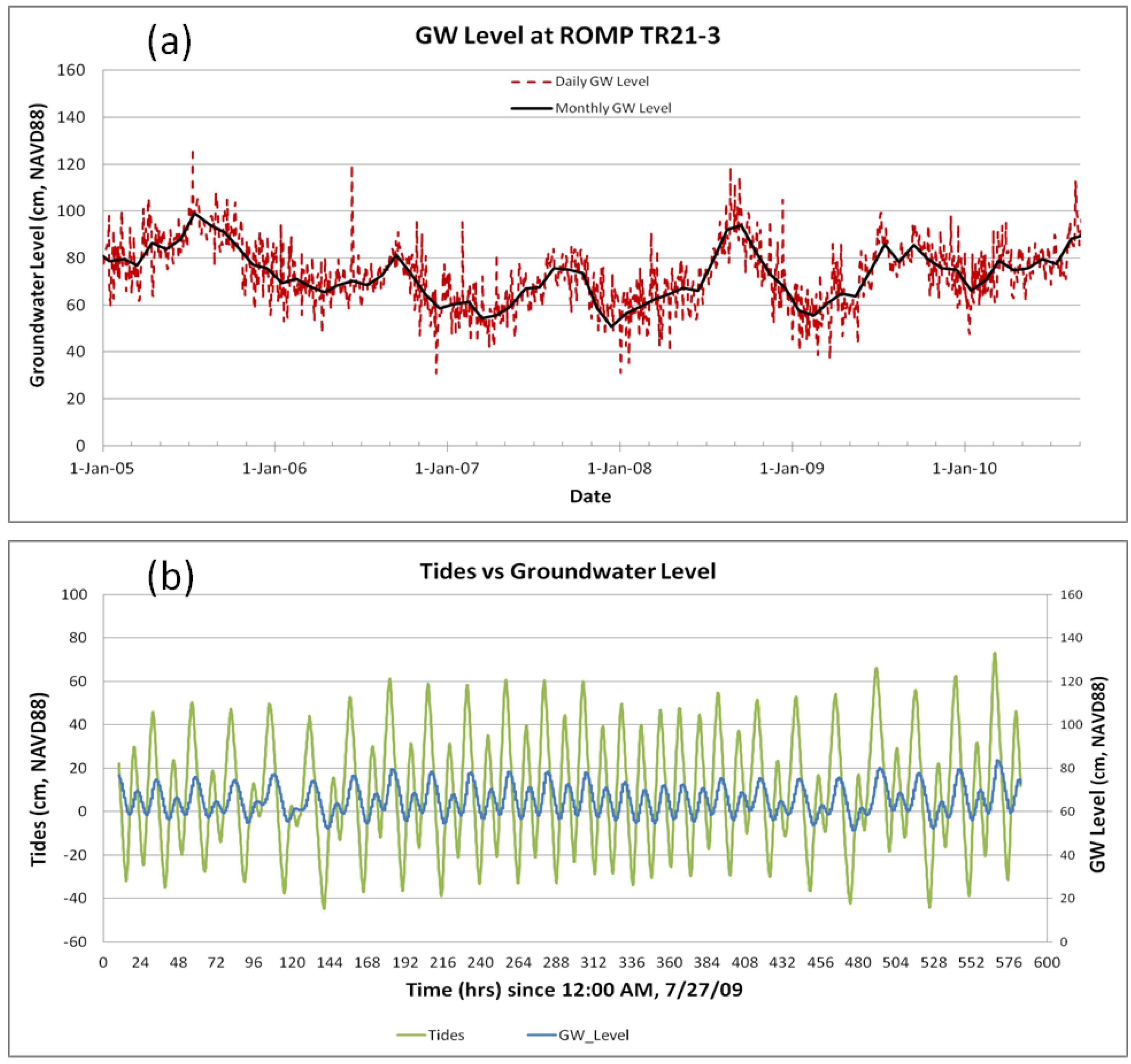
Figure 4a shows measured daily and monthly groundwater level data during 1 January 2005 through 1 September 2010 in a nearby well called ROMP TR21-3 (
Figure 1). A comparison of the water level measured at the USGS mouth of Kings Bay station with measured hourly groundwater level is shown in
Figure 4b. Although the groundwater level is relatively stable in comparison with the tides in the system, it does have tidal signals in it. From
Figure 4, it is clear that groundwater level contains not only high frequency variations but also low frequency variations with a time scale of a year. Hence, the consideration of groundwater level in predicting spring flow is necessary.
Figure 4.
(a) Measured monthly and daily groundwater levels in ROMP TR21-3 during 1 January 2005–1 September 2010. (b) Comparison of measured Kings Bay tides and hourly groundwater level in ROMP TR21-3 during the 25-day continuous recordings of cross-sectional fluxes at G1 and G2.
Figure 4.
(a) Measured monthly and daily groundwater levels in ROMP TR21-3 during 1 January 2005–1 September 2010. (b) Comparison of measured Kings Bay tides and hourly groundwater level in ROMP TR21-3 during the 25-day continuous recordings of cross-sectional fluxes at G1 and G2.
Based on available data, including continuous cross-sectional fluxes at G1 and G2, tides at the USGS mouth of Kings Bay station, and groundwater level data at ROMP TR21-3, it was found that the following linear equation can describe the effects of tides and groundwater level on the spring flow in Kings Bay very well.
where
q denotes the estimated spring flow,
q0 is the long-term mean spring flow,
G represents the groundwater level in ROMP TR21-3, Δ
G is the long-term mean head difference between the groundwater level in ROMP TR21-3 and the surface water level in Kings Bay, and
C1 and
C2 are two parameters which are time-independent and can be determined from measured field data. The time derivative of surface water elevation (∂
η/∂
t) in the above equation not only allows the phase mismatch predicted by the head difference to be eliminated, but also allows higher mode oscillations shown in the measured net spring flows to be correctly matched.
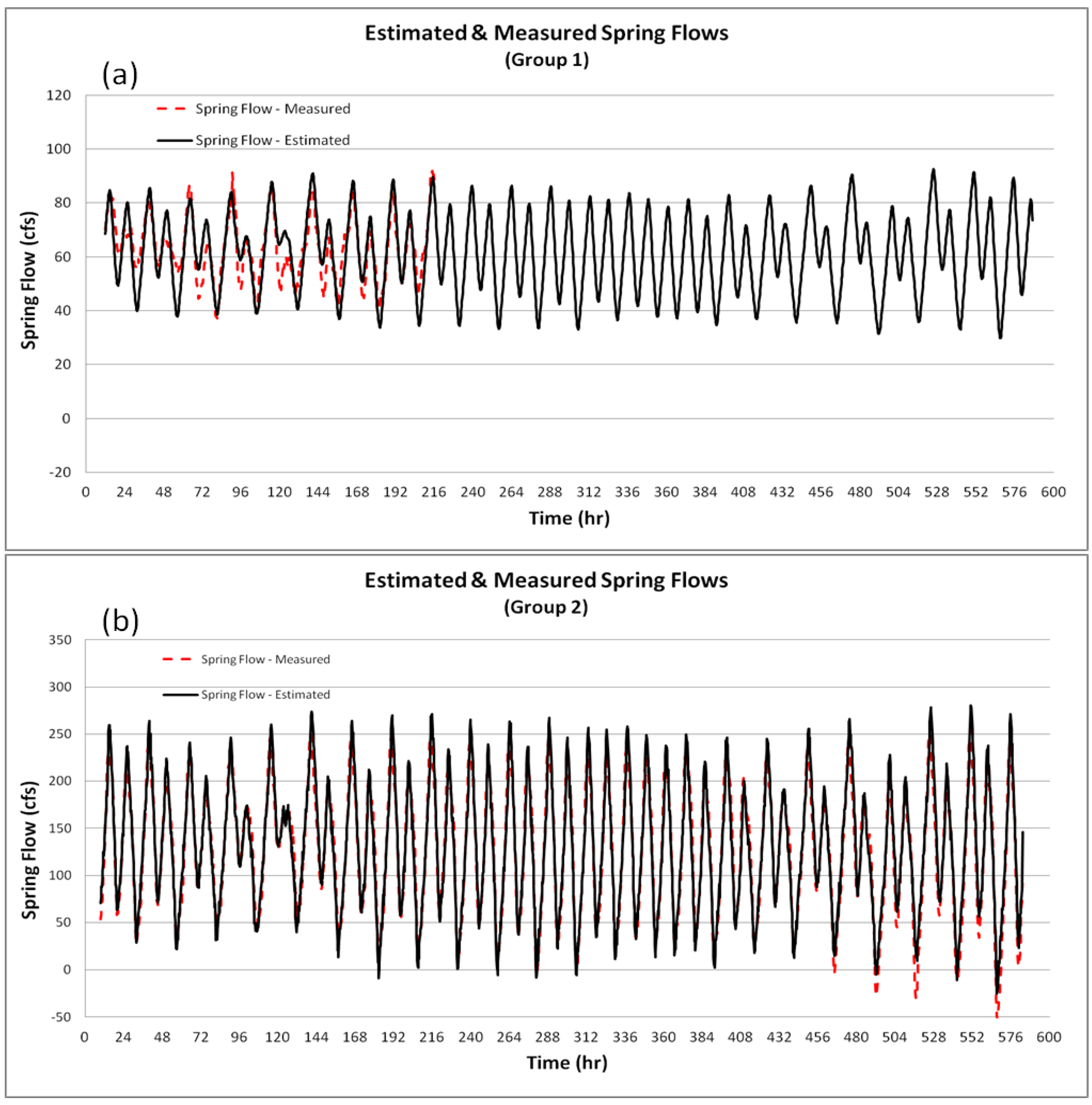
Figure 5 compares time series of measured spring flows with those estimated using Equation (3). As can be seen from the figure, Equation (3) predicts spring flows very well, especially for Group 2 springs. The R
2 values for the match of estimated and measured SGDs are 0.72 and 0.94 for Groups 1 and 2 springs, respectively.
Figure 5.
Time series of estimated and measured spring flows at G1 for Group 1 springs (a) and G2 for Group 2 springs (b) during 27 July–20 August 2009.
Figure 5.
Time series of estimated and measured spring flows at G1 for Group 1 springs (a) and G2 for Group 2 springs (b) during 27 July–20 August 2009.
The three parameters (ΔG, C1, and C2) in Equation (3) were determined through a trial and error process in obtaining the best match between estimated and measured spring flows. This trial and error process yielded two sets of (ΔG, C1, and C2): (70.3 cm, −0.0088 cm−1, 3.9 s cm−1) for Groups 1 and (67.06 cm, −0.0166 cm−1, 79.78 s cm−1) for Group 2. Clearly, for different spring groups, these parameters are quite different, especially C1, and C2.