Multiple-Penalty-Weighted Regularization Inversion for Dynamic Light Scattering
Abstract
:1. Introduction
2. Dynamic Light Scattering and Multiple-Penalty-Weighted Regularization
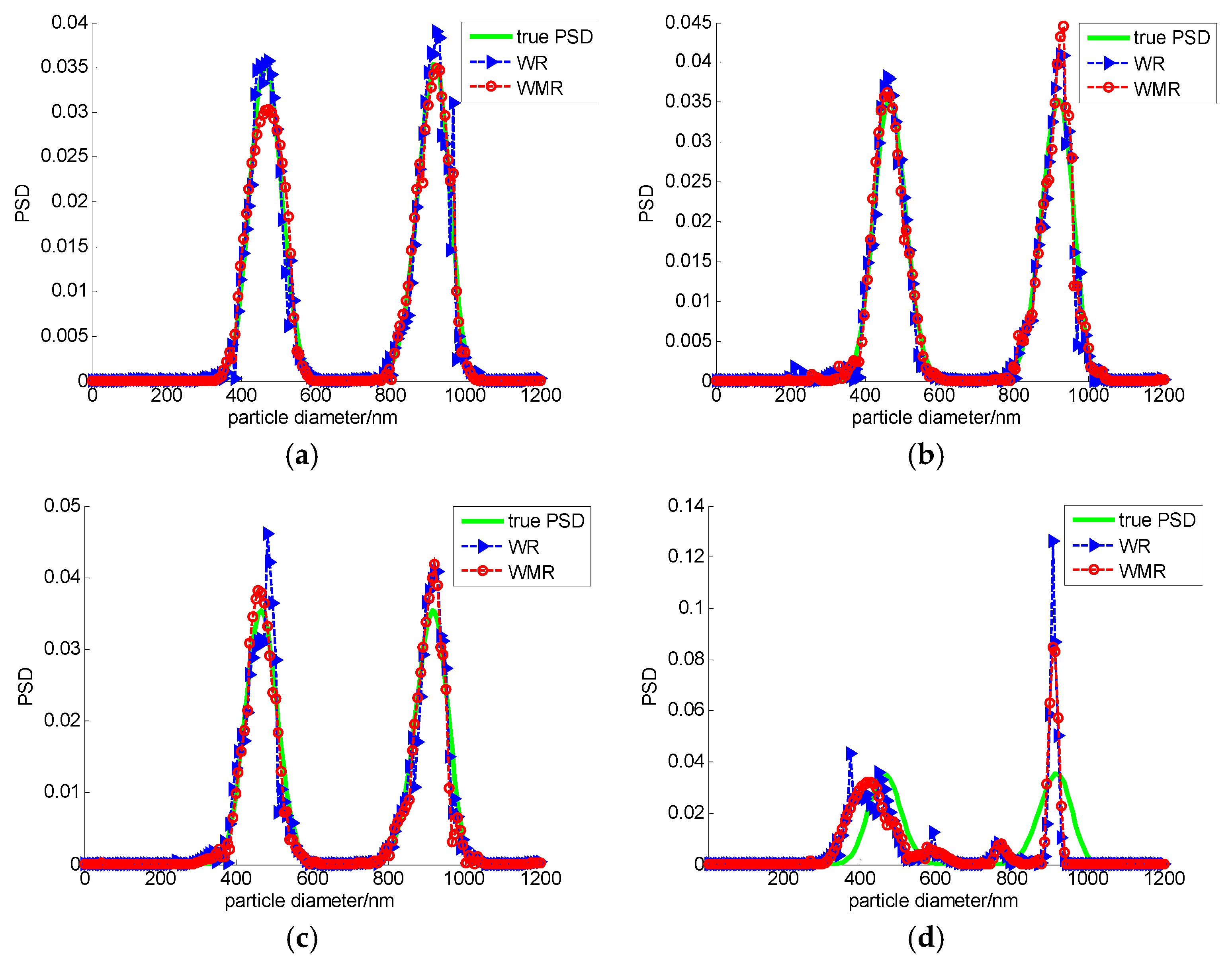
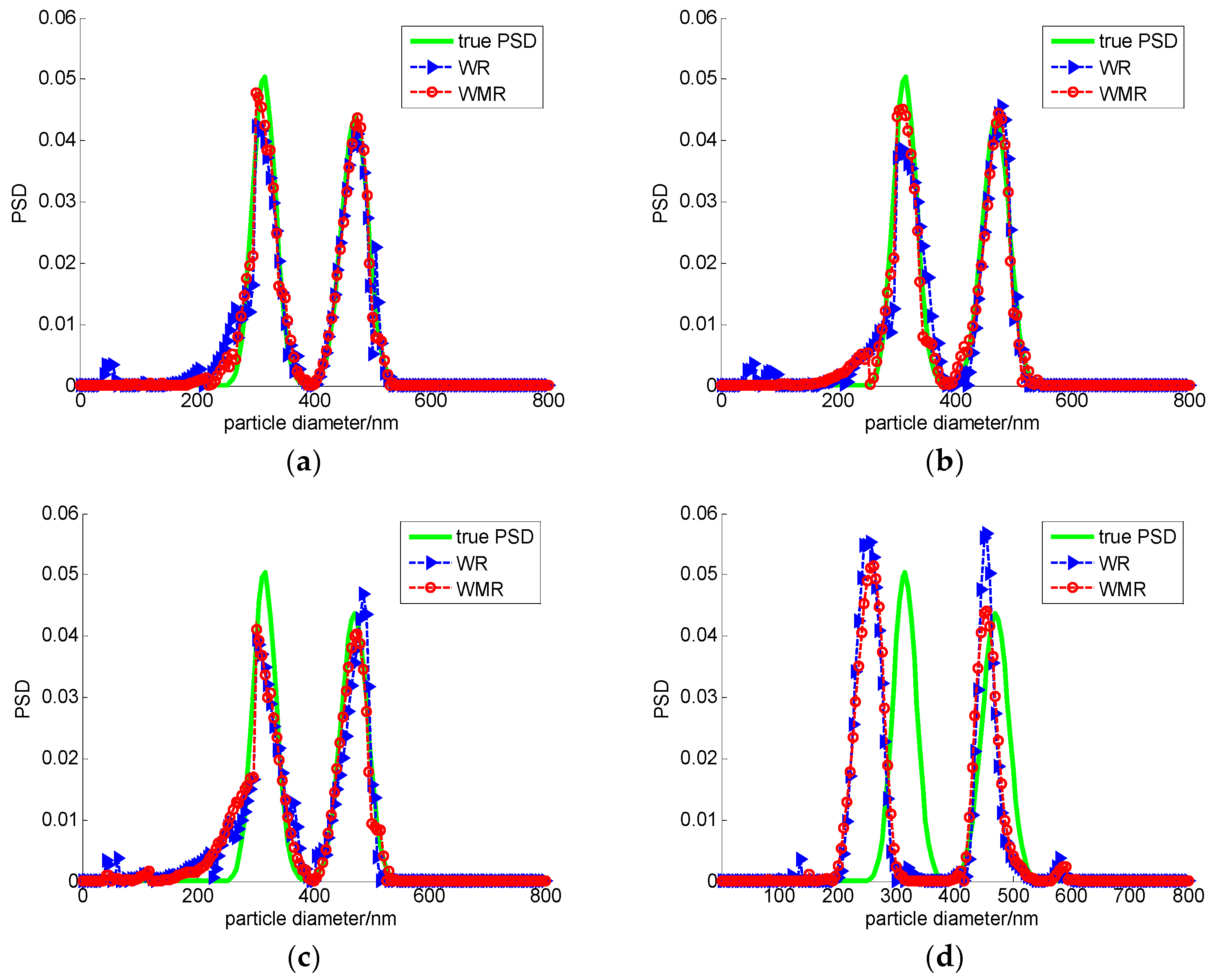
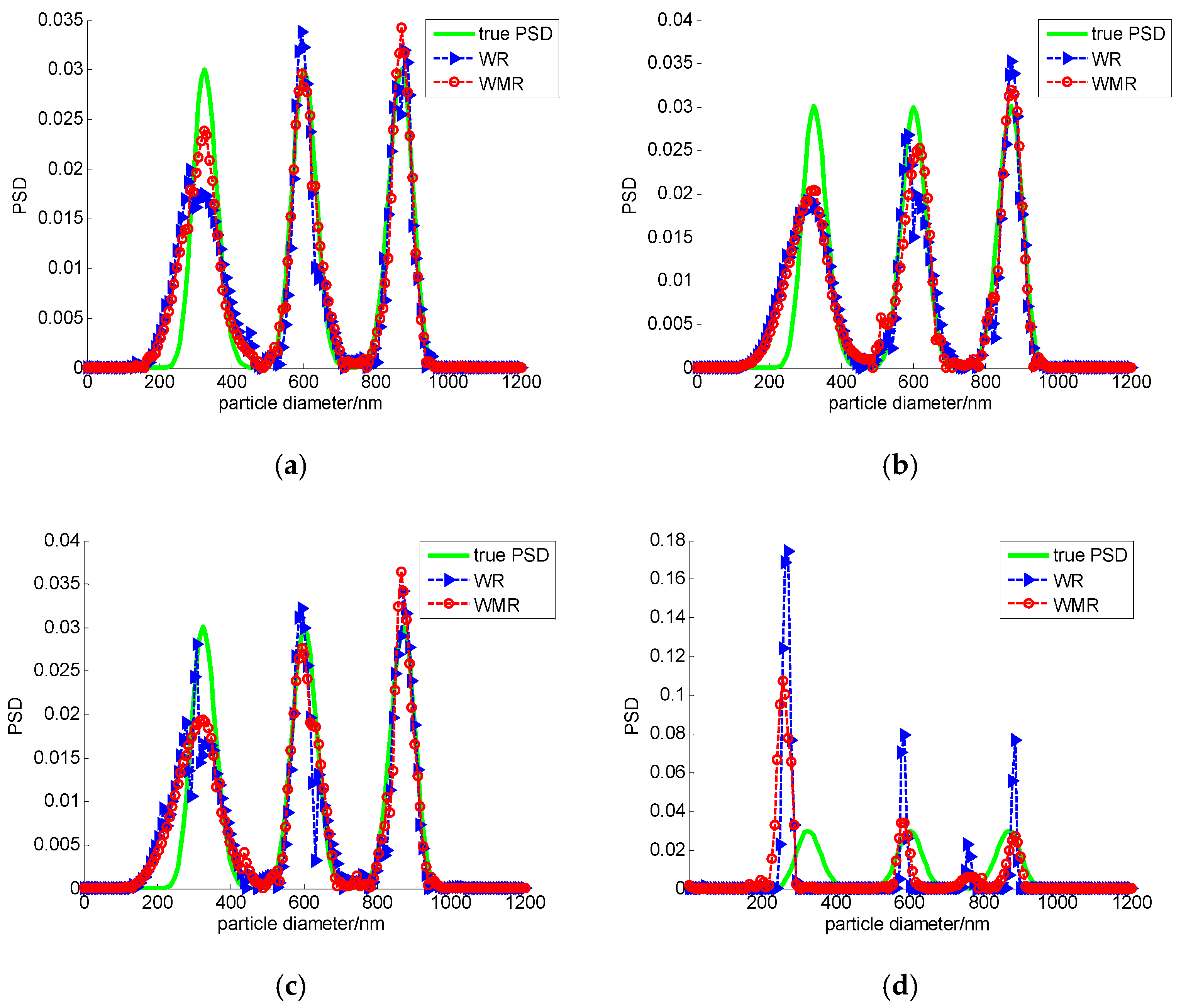
3. Numerical Simulation and Analysis
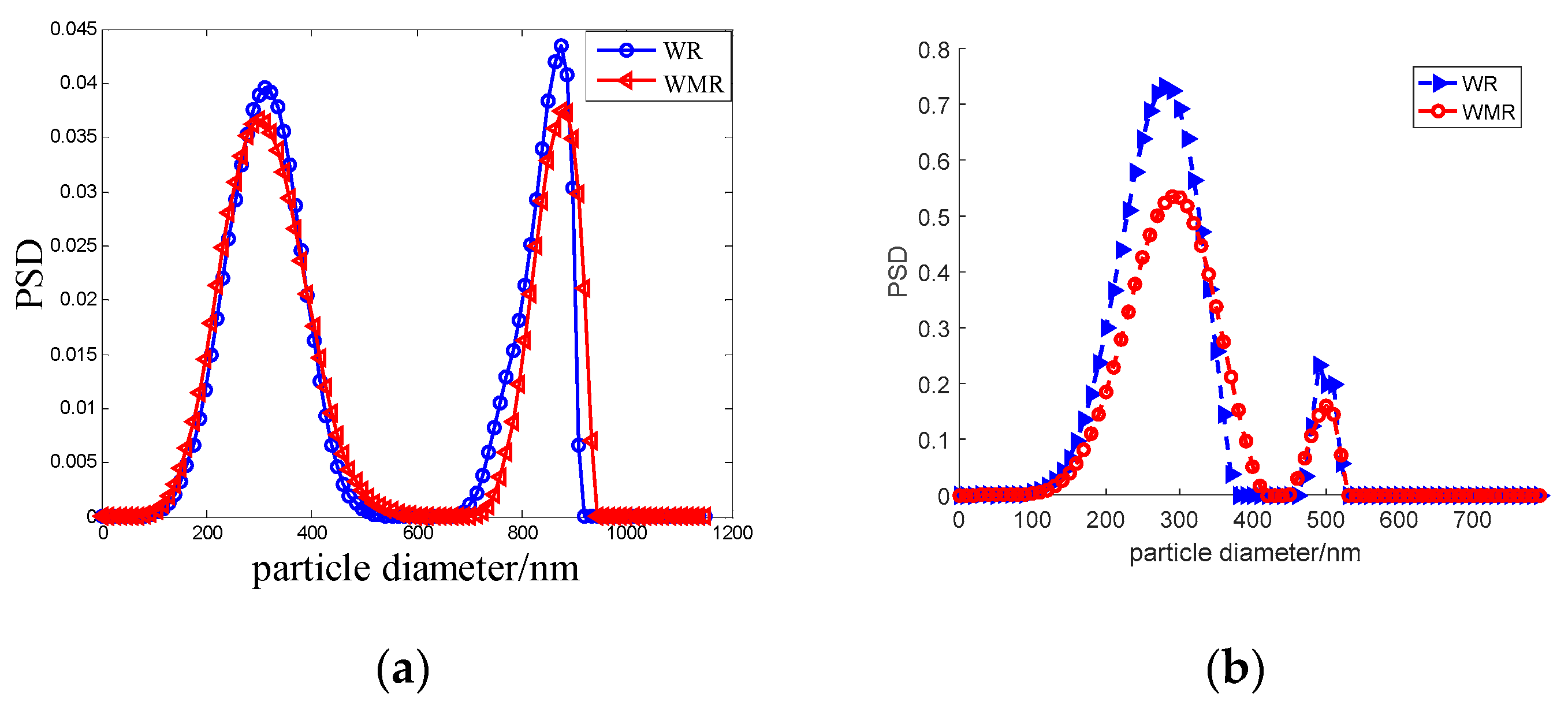
4. Experimental Data Inversion
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Organization for Standardization (ISO). Particle Size Analysis-Photon Correlation Spectroscopy; ISO 13321; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- International Organization for Standardization (ISO). Particle Size Analysis-Dynamic Light Scattering (DLS); ISO 22412; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- International Organization for Standardization (ISO). Particle Size Analysis-Dynamic Light Scattering (DLS); ISO 22412; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Foord, R.; Jakeman, E.; Oliver, C.J.; Pike, E.R.; Blagrove, R.J.; Wood, E.; Peacocke, A.R. Determination of diffusion coefficients of haemocyanin at low concentration by intensity fluctuation spectroscopy of scattered laser light. Nature 1970, 227, 242–245. [Google Scholar] [CrossRef] [PubMed]
- Gulari, E.; Gulari, E.; Tsunashima, Y.; Chu, B. Photon correlation spectroscopy of particle distributions. J. Chem. Phys. 1979, 70, 3965–3972. [Google Scholar] [CrossRef]
- Koppel, D.E. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: The Method of Cumulants. J. Chem. Phys. 1972, 57, 4814–4820. [Google Scholar] [CrossRef]
- McWhirter, J.G.; Pike, E.R. On the numerical inversion of the Laplace transform and similar Fredholm integral equations of the first kind. J. Phys. A Math. Theor. Gen. 1978, 11, 1729–1745. [Google Scholar] [CrossRef]
- Morrison, I.D.; Grabowski, E.F.; Herb, C.A. Improved techniques for particle size determination for quasi-elastic light scattering. Langmuir 1985, 1, 496–501. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Provencher, S.W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- Varah, J.M. On the Numerical Solution of Ill-Conditioned linear systems with applications to Ill-Posed problems. Siam J. Numer. Anal. 1973, 10, 257–267. [Google Scholar] [CrossRef]
- Gugliotta, L.M.; Vega, J.R.; Meira, G.R. Latex particle size distribution by dynamic light scattering: Computer evaluation of two alternative calculation paths. J. Colloid Interface Sci. 2000, 228, 14–17. [Google Scholar] [CrossRef] [PubMed]
- Buttgereit, R.; Roths, T.; Honerkamp, J.; Aberle, L.B. Simultaneous regularization method for the determination of radius distributions from experimental multiangle correlation functions. Phys. Rev. E 2001, 64, 1515–1523. [Google Scholar] [CrossRef] [PubMed]
- Ubera, J.V.; Aguilar, J.F.; Gale, D.M. Reconstruction of particle size distributions from light scattering patterns using three inversion methods. Appl. Opt. 2007, 46, 124–132. [Google Scholar] [CrossRef]
- Frisken, B.J. Revisiting the method of cumulants for analysis of dynamic light scattering data. Appl. Opt. 2001, 40, 4087–4091. [Google Scholar] [CrossRef] [PubMed]
- Hassan, P.A.; Kulshreshtha, S.K. Modification to the cumulant analysis of polydispersity in quasi-elastic light scattering data. J. Colloid Interface Sci. 2006, 300, 744–748. [Google Scholar] [CrossRef] [PubMed]
- Mailer, A.G.; Clegg, P.S.; Pusey, P.N. Particle sizing by dynamic light scattering: Non-linear cumulant analysis. J. Phys. Condens. Matter 2015, 27, 145102. [Google Scholar] [CrossRef] [PubMed]
- Roig, A.R.; Alessandrini, J.L. Particle size distribution from static light scattering with regularized non-negative least squares constraints. Part. Part. Syst. Charact. 2006, 23, 431–437. [Google Scholar] [CrossRef]
- Arias, M.L.; Frontini, G.L. Particle size distribution retrieval from elastic light scattering measurement by a modified regularization method. Part. Part. Syst. Charact. 2006, 23, 374–380. [Google Scholar] [CrossRef]
- Zhu, X.; Shen, J.; Liu, W.; Sun, X.; Wang, Y. Nonnegative least-squares truncated singular value decomposition to particle size distribution inversion from dynamic light scattering data. Appl. Opt. 2010, 49, 6591–6596. [Google Scholar] [CrossRef] [PubMed]
- Ligon, D.A.T.; Chen, W.; Gillespie, J.B. Determination of aerosol parameters light-scattering data using an inverse Monte Carlo technique. Appl. Opt. 1996, 35, 4297–4303. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Wang, S.; Lu, Y. Inversion of particle-size distribution from angular light-scattering data with genetic algorithms. Appl. Opt. 1999, 38, 2677–2685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clementi, L.A.; Vega, J.R.; Gugliotta, L.M. Particle Size Distribution of Multimodal Polymer Dispersions by Multiangle Dynamic Light Scattering. Solution of the Inverse Problem on the Basis of a Genetic Algorithm. Part. Part. Syst. Charact. 2010, 27, 146–157. [Google Scholar] [CrossRef]
- Gugliotta, L.M.; Stegmayer, G.S.; Clementi, L.A.; Gonzalez, V.D.G. A neural network model for estimating the particle size distribution of dilute latex from multiangle dynamic light scattering measurements. Part. Part. Syst. Charact. 2009, 26, 41–52. [Google Scholar] [CrossRef]
- Chicea, D. Using neural networks for dynamic light scattering time series processing. Meas. Sci. Technol. 2017, 28, 055206. [Google Scholar] [CrossRef]
- Cummins, P.G.; Taples, E. Particle size distributions determined by a “multiangle” analysis of photon correlation spectroscopy data. Langmuir 1987, 3, 1109–1113. [Google Scholar] [CrossRef]
- Bryant, G.; Thomas, J.C. Improved particle size distribution measurements using multiangle dynamic light scattering. Langmuir 1995, 11, 2480–2485. [Google Scholar] [CrossRef]
- Vega, J.R.; Gugliotta, L.M.; Gonzalez, V.D.; Meira, G.R. Latex particle size distribution by dynamic light scattering: Novel data processing for multiangle measurements. J. Colloid Interface Sci. 2003, 261, 74–81. [Google Scholar] [CrossRef]
- Liu, X.; Shen, J.; Thomas, J.C.; Shi, S.; Sun, X.; Liu, W. Multiangle dynamic Light scattering analysis using angular intensity weighting determined by iterative recursion. Appl. Opt. 2012, 51, 846–854. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Shen, J.; Song, L. Accurate Retrieval of Bimodal Particle Size Distribution in Dynamic Light Scattering. IEEE Photonics Technol. Lett. 2015, 28, 311–314. [Google Scholar] [CrossRef]
- Xu, M.; Shen, J.; Thomas, J.C.; Huang, Y.; Zhu, X.; Clementi, L.A.; Vega, J.R. Information-weighted constrained regularization for particle size distribution recovery in multiangle dynamic light scattering. Opt. Express 2018, 26, 15–31. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Shen, J.; Huang, Y.; Xu, Y.; Zhu, X.; Wang, Y.; Liu, W.; Gao, M. Information character of particle size and the character weighted inversion in dynamic light scattering. Acta Phys. Sin. 2018, 67, 134201. [Google Scholar] [CrossRef]
- Thomas, J.C. Photon correlation spectroscopy: Technique and instrumentation. In Proceedings of the SPIE—The International Society for Optical Engineering, Los Angeles, CA, USA, 20–25 January 1991; Volume 1430, pp. 2–18. [Google Scholar] [CrossRef]
- Hansen, P.C.; Leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. Siam J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef] [Green Version]
- Rezghi, M.; Hosseini, S.M. A new variant of L-curve for Tikhonov regularization. J. Comput. Appl. Math. 2009, 231, 914–924. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, J.; Wang, Y.; Liu, W.; Sun, X. Influence of initial model on regularized inversion of noisy dynamic light scattering data. High Power Laser Part. Beams 2014, 26, 129003. [Google Scholar] [CrossRef]
- Wang, Z. Multi-parameter Tikhonov regularization and model function approach to the damped Morozov principle for choosing regularization parameters. J. Comput. Appl. Math. 2012, 236, 1815–1832. [Google Scholar] [CrossRef]
- Belge, M.; Kilmer, M.E.; Miller, E.L. Efficient determination of multiple regularization parameters in a generalized L-curve framework. Inverse Probl. 2001, 18, 1161–1183. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. A study of particle size distribution. Powder Technol. 1990, 62, 101–118. [Google Scholar] [CrossRef]
- Gao, S.; Shen, J.; Thomas, J.C.; Yin, Z.; Wang, X.; Wang, Y.; Liu, W.; Sun, X. Effect of scattering angle error on particle size determination by multiangle dynamic light scattering. Appl. Opt. 2015, 54, 2824–2831. [Google Scholar] [CrossRef] [PubMed]
| Sample | d1 | d2 | d3 | µ1 | µ2 | µ3 | σ1 | σ2 | σ3 | a | b | c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AS | 466 | 915 | - | 3 | −6 | - | 6.76 | 5.1 | - | 0.5 | 0.5 | - |
| BS | 316 | 470 | - | 4.1 | −3.1 | - | 9.7 | 8.5 | - | 0.5 | 0.5 | - |
| CS | 324 | 601 | 871 | 7.0 | −1 | −7 | 7.2 | 9.05 | 7.2 | 1/3 | 1/3 | 1/3 |
| Unit | μm | μm | μm | - | - | - | - | - | - | - | - | - |
| Size/nm | Noise Level | WR | WMR | ||||
|---|---|---|---|---|---|---|---|
| V1 | Pmeas/nm | V2 | V1 | Pmeas/nm | V2 | ||
| 466/915 | 0 | 0.0252 | 451/474/923 | 0.0322/0.0172/0.0087 | 0.0195 | 474/923 | 0.0172/0.0087 |
| 10−4 | 0.0231 | 459/923 | 0.0150/0.0087 | 0.0229 | 459/930 | 0.0150/0.0164 | |
| 10−2 | 0.0349 | 481/923 | 0.0322/0.0087 | 0.0254 | 459/923 | 0.0150/0.0057 | |
| 0.08 | 0.1551 | -/908 | -/0.0076 | 0.1297 | 425/908 | 0.0880/0.0076 | |
| Size/nm | Noise Level | WR | WMR | ||||
|---|---|---|---|---|---|---|---|
| V1 | Pmeas/nm | V2 | V1 | Pmeas/nm | V2 | ||
| 316/470 | 0 | 0.0422 | 301/475 | 0.0475/0.0106 | 0.0286 | 301/475 | 0.0475/0.0106 |
| 10−4 | 0.0480 | 306/480 | 0.0316/0.0213 | 0.0380 | 311/475 | 0.0158/0.0106 | |
| 10−2 | 0.0576 | 301/485 | 0.0475/0.0319 | 0.0500 | 301/475 | 0.0475/0.0106 | |
| 0.08 | 0.2113 | 251/455 | 0.2057/0.0319 | 0.1997 | 261/455 | 0.1741/0.0319 | |
| Size/nm | Noise Level | WR | WMR | ||||
|---|---|---|---|---|---|---|---|
| V1 | Pmeas/nm | V2 | V1 | Pmeas/nm | V2 | ||
| 324/601/871 | 0 | 0.0481 | 324/594/878 | 0/0.0116/0.0116 | 0.0326 | 324/594/871 | 0/0.0116/0 |
| 10−4 | 0.0487 | 316/586/608/871 | 0.0247/-/0.0116/0 | 0.0421 | 324/616/871 | 0/0.0250/0 | |
| 10−2 | 0.0523 | 309/339/594/870 | 0.0463/-/0.0116/0.0011 | 0.0419 | 324/594/863 | 0/0.0116/0.0092 | |
| 0.08 | 0.3160 | 271/586/885 | 0.1636/0.0249/0.0161 | 0.2340 | 256/586/885 | 0.2098/0.0249/0.0161 | |
| Size/nm | WR | WMR | ||
|---|---|---|---|---|
| Pmeas/nm | V2 | Pmeas/nm | V2 | |
| 306/974 | 313/874 | 0.0228/0.1027 | 301/886 | 0.0196/0.0903 |
| 300/502 | 280/490 | 0.0667/0.0239 | 290/500 | 0.0333/0.004 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Xiu, W.; Shen, J.; Zhang, W.; Xu, M.; Cao, L.; Ma, L. Multiple-Penalty-Weighted Regularization Inversion for Dynamic Light Scattering. Appl. Sci. 2018, 8, 1674. https://doi.org/10.3390/app8091674
Chen W, Xiu W, Shen J, Zhang W, Xu M, Cao L, Ma L. Multiple-Penalty-Weighted Regularization Inversion for Dynamic Light Scattering. Applied Sciences. 2018; 8(9):1674. https://doi.org/10.3390/app8091674
Chicago/Turabian StyleChen, Wengang, Wenzheng Xiu, Jin Shen, Wenwen Zhang, Min Xu, Lijun Cao, and Lixiu Ma. 2018. "Multiple-Penalty-Weighted Regularization Inversion for Dynamic Light Scattering" Applied Sciences 8, no. 9: 1674. https://doi.org/10.3390/app8091674




