Bloch Oscillations in the Chains of Artificial Atoms Dressed with Photons
Abstract
:1. Introduction
2. Statement of the Problem and Calculation Technique
2.1. Physical System and Model
2.2. Hamiltonian in Wannier-Fock Basis
2.3. Equations of Motion
2.4. Studying Observable Values
- (i)
- inversion density, given byand
- (ii)
- tunneling current density (see Appendix B)
- (iii)
- photonic number distribution
- (iv)
- mean number of photonswhere is given by (11),
- (v)
- photonic number variancewhere is given by relation (12), and
- (vi)
- von Neumann quantum entropywhere are the weights of the various Fock states of the statistical light distribution [44].
3. Approximate Analytical Solution
3.1. Preliminaries
3.2. Details
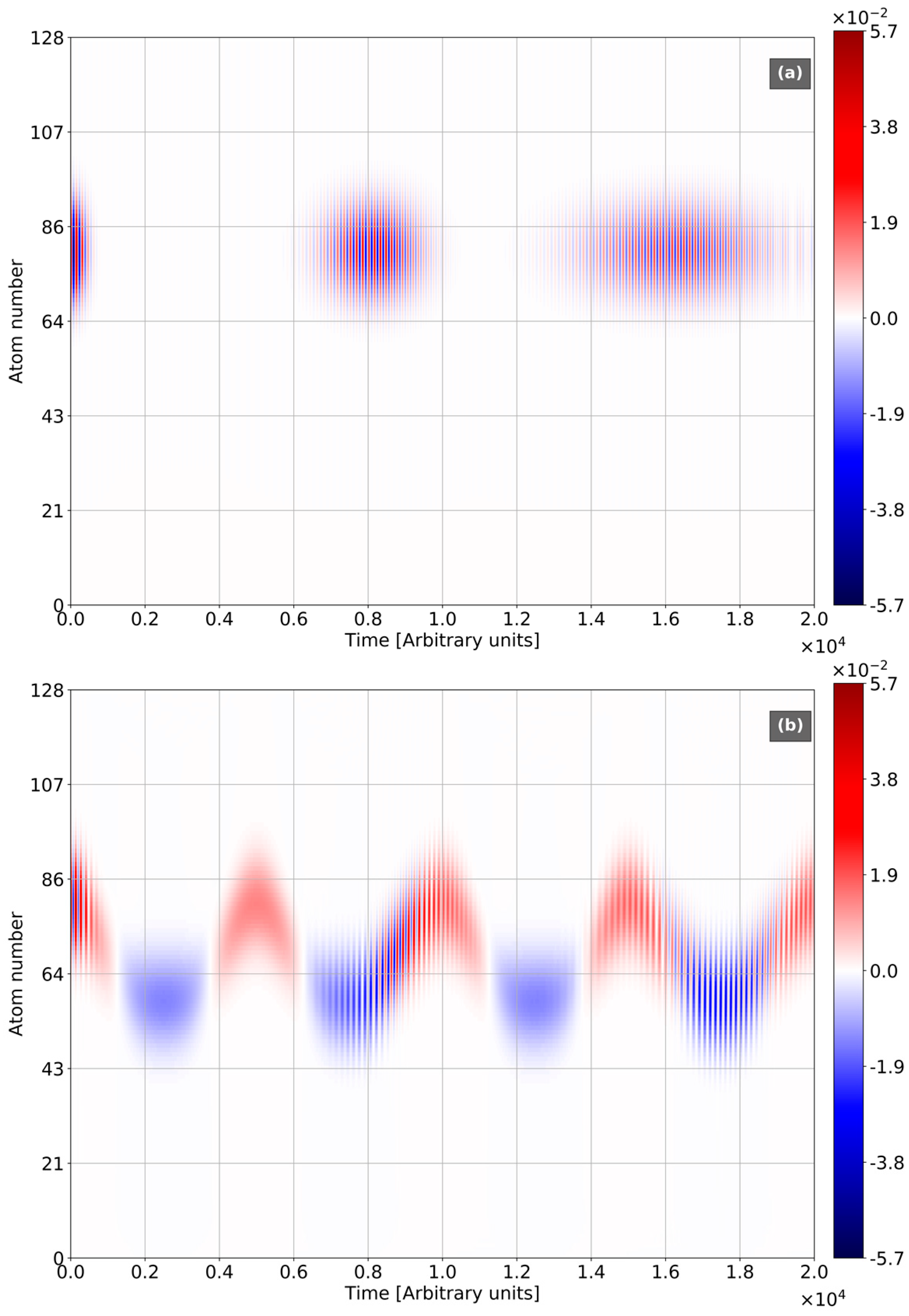
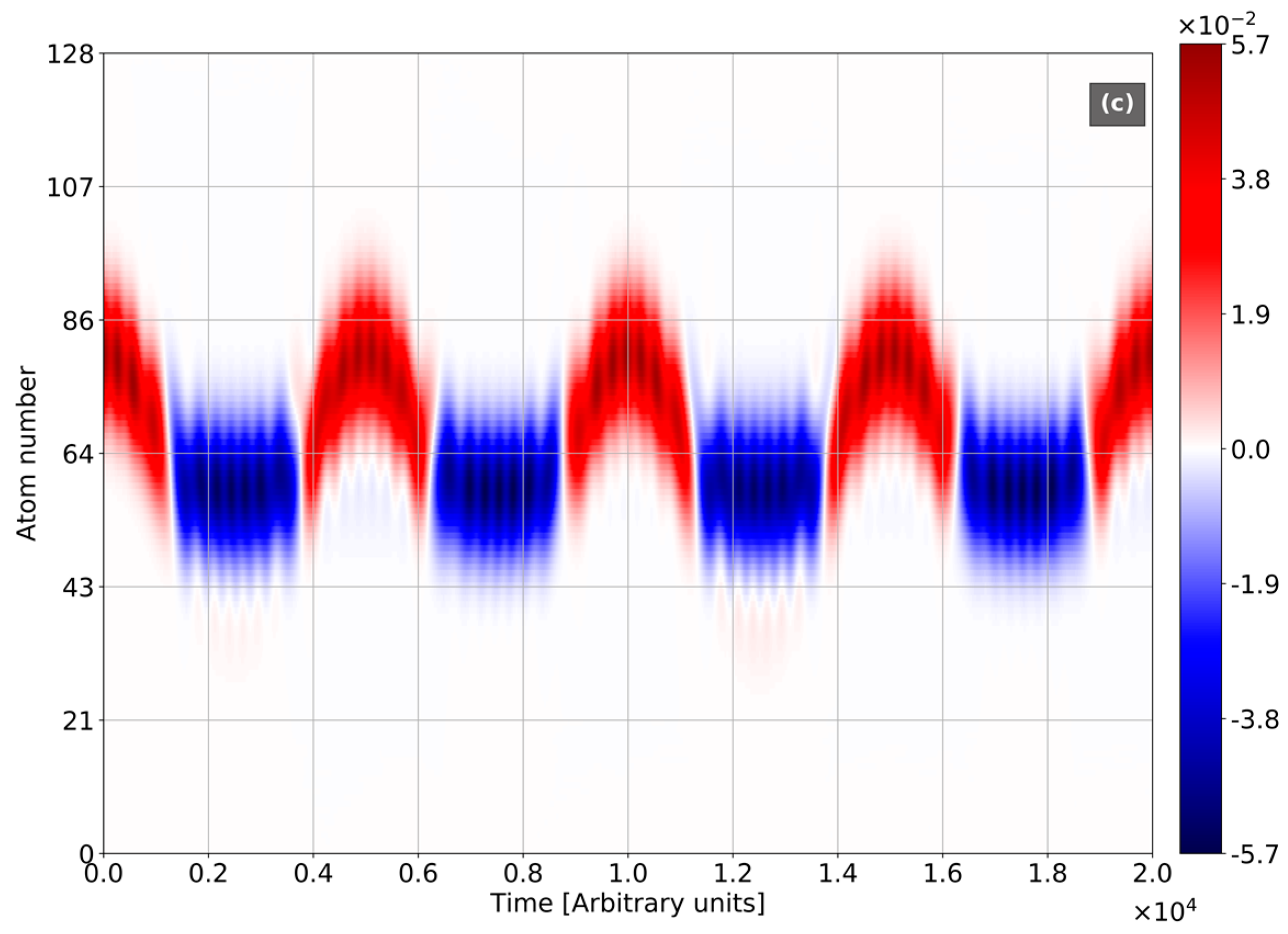
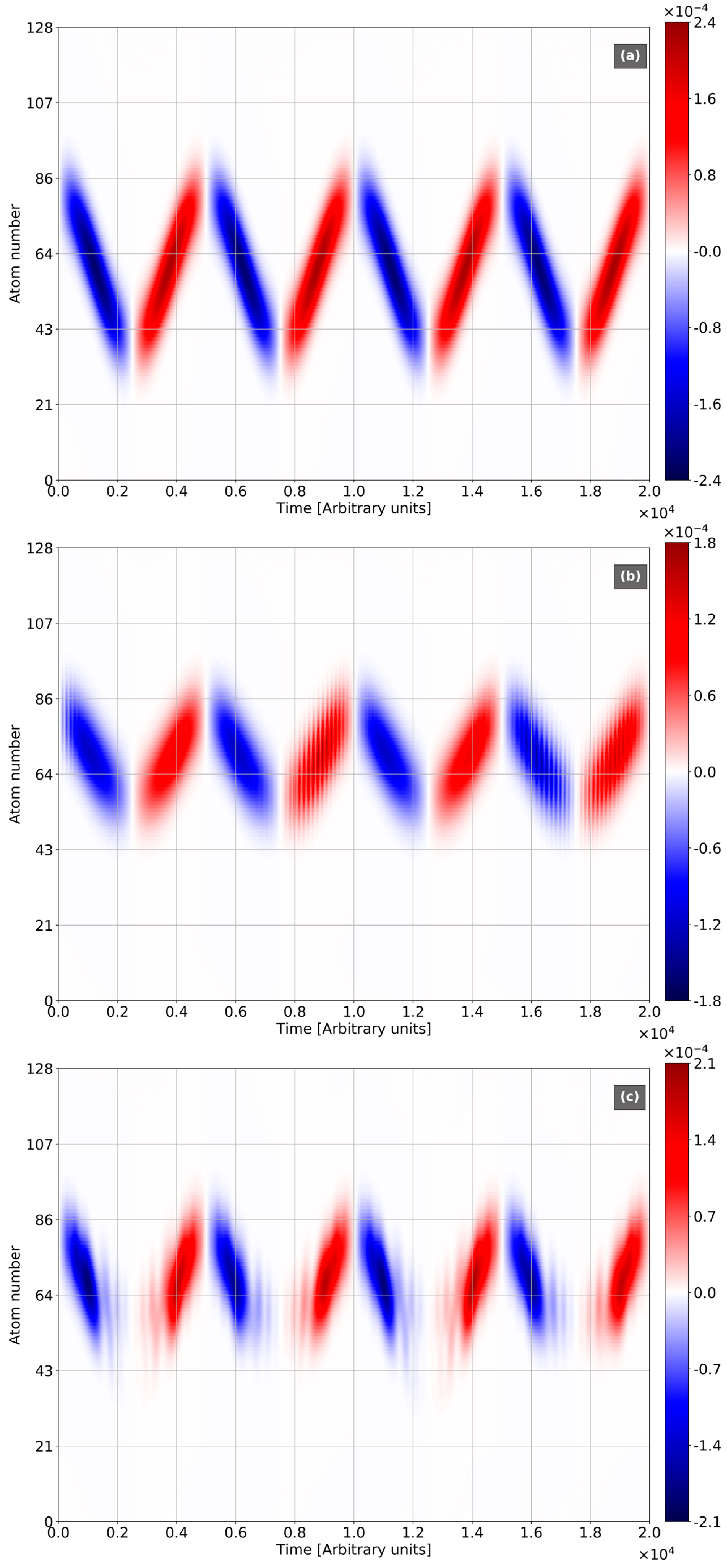
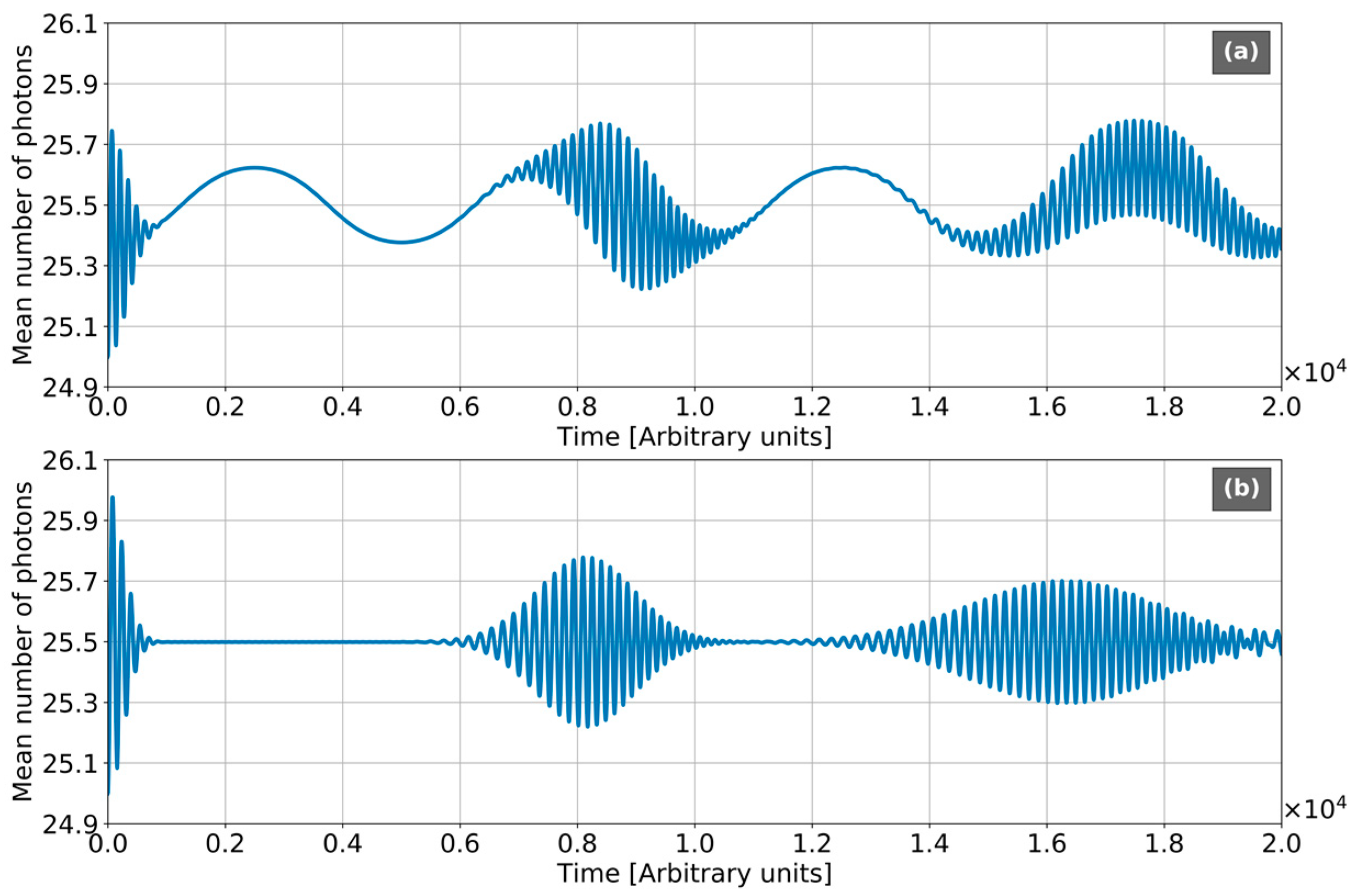
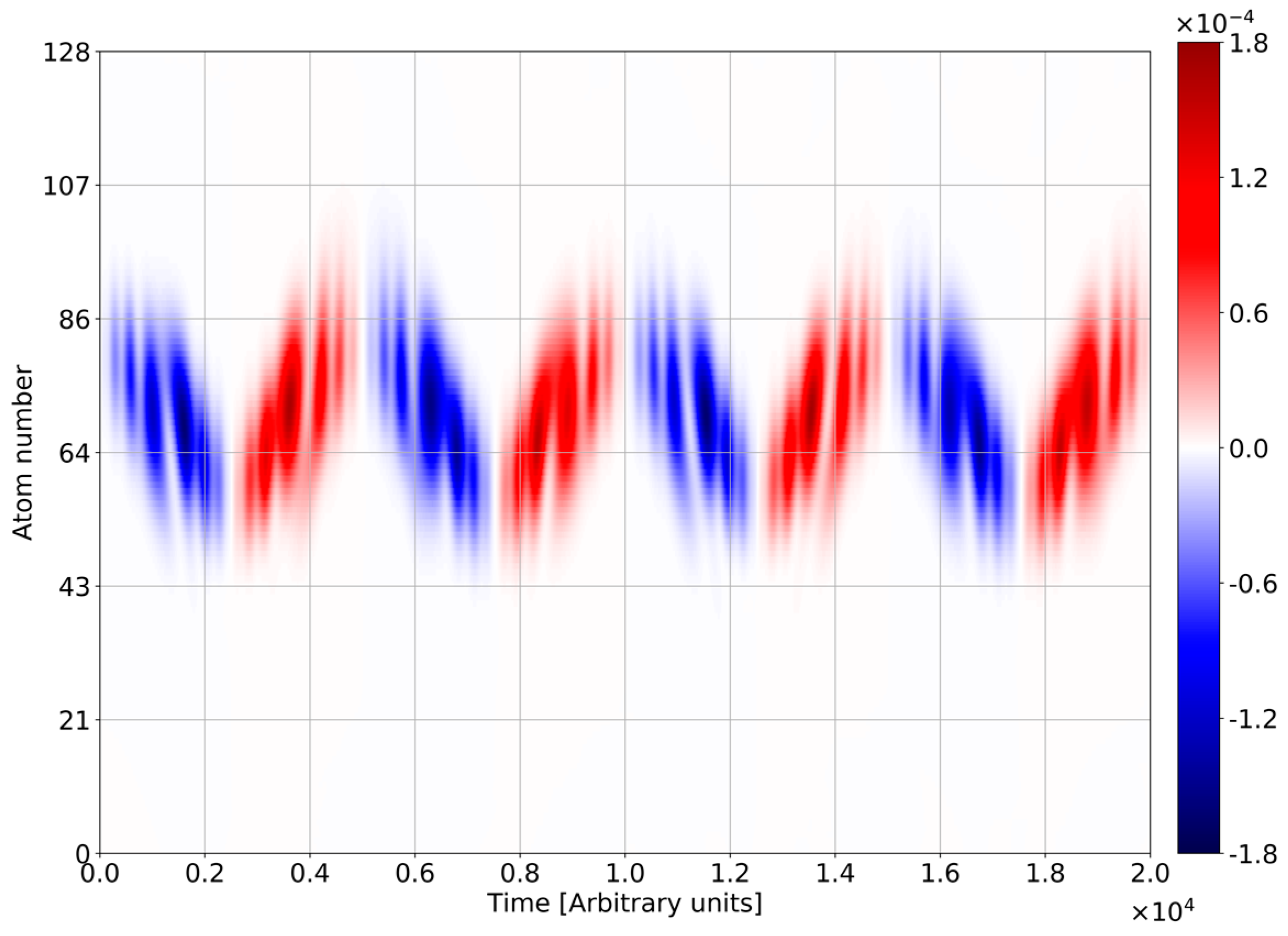
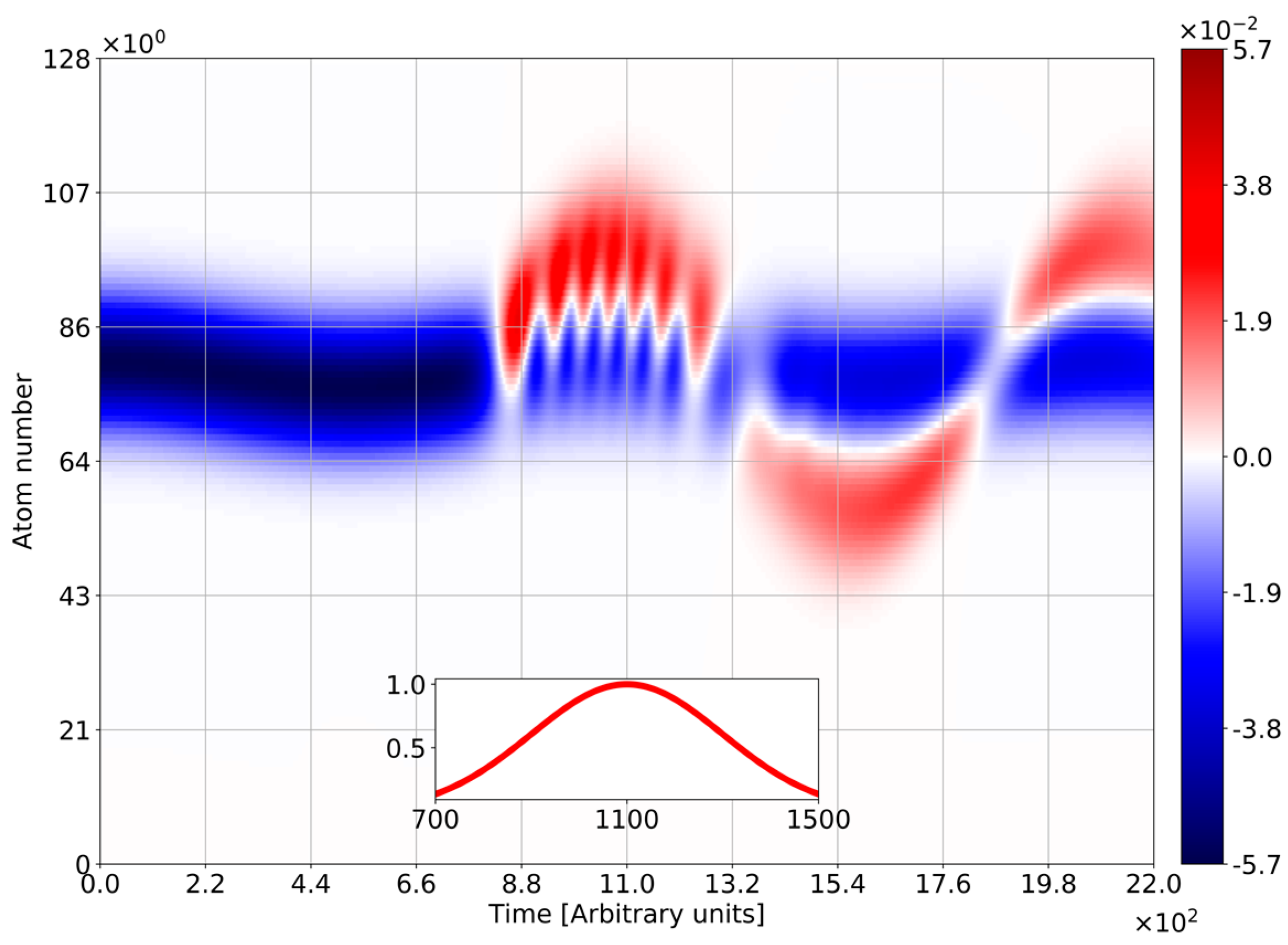
4. Numerical Modelling and Discussion
5. Some Other Potential Experimental Implementations
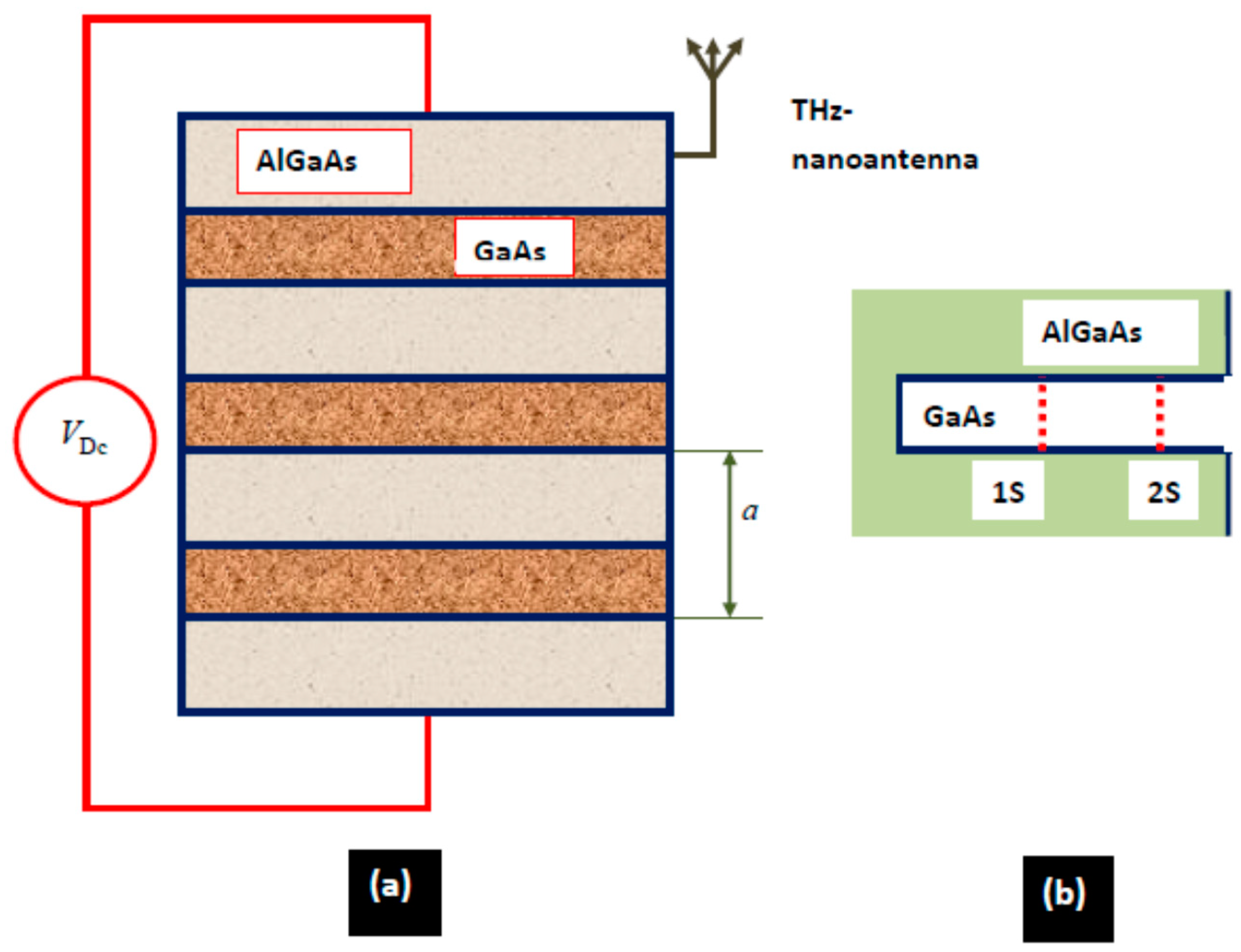
5.1. Semiconductor 2D-Heterostructures
5.2. Josephson Junction
6. Conclusion and Outlook
- (1)
- The case of initial coherent state of the light exhibits the collapse-revival picture, which drifts over the chain (collapses and revivals placed in the different spatial areas). In contrast with Jaynes-Cummings model, the collapse-revival picture is modulated with Bloch frequency;
- (2)
- In the case of initial vacuum state of light, the photon emission and absorption occurs with Bloch frequency, instead of Rabi-frequency in Jaynes-Cummings model. The photonic probabilities are mainly modulated with Bloch frequency, while the contribution of Rabi-components is rather slight. BO strongly squeezes the vacuum state of light entangled with electronic wavepackets;
- (3)
- The electron-photon entanglement dramatically modifies the tunnel current behavior. It becomes modulated agreed with the collapse-revival picture for the case of coherent state of light, and periodically modulated by RO for the case of initial photonic vacuum;
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Hamiltonian in the Wannier-Fock Basis
Appendix B. Derivation of Formula for Tunneling Current
Appendix C. Quantization of Electromagnetic Fields in Wavepackets
References
- Bloch, F. UЁ ber die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Zener, C. A theory of electrical breakdown of solid dielectrics. Proc. R. Soc. Lond. 1934, 145, 523–529. [Google Scholar] [CrossRef]
- Wannier, G.H. Wave functions and effective Hamiltonian for Bloch electrons in an electric field. Phys. Rev. 1960, 117, 432. [Google Scholar] [CrossRef]
- Wannier, G.H. Stark ladder in solids? A reply. Phys. Rev. 1969, 181, 1364. [Google Scholar] [CrossRef]
- Kuehn, W.; Gaal, P.; Reimann, K.; Woerner, M.; Elsaesser, T.; Hey, R. Coherent Ballistic Motion of Electrons in a Periodic Potential. Phys. Rev. Lett. 2010, 104, 146602. [Google Scholar] [CrossRef] [PubMed]
- Waschke, C.; Roskos, H.; Schwedler, R.; Leo, K.; Kurz, H.; Köhler, K. Coherent submillimeter-wave emission from Bloch oscillations in a semiconductor superlattice. Phys. Rev. Lett. 1993, 70, 3319. [Google Scholar] [CrossRef] [PubMed]
- Preiss, P.M.; Ma, R.; Tai, M.E.; Lukin, A.; Rispoli, M.; Zupanic, P.; Lahini, Y.; Islam, R.; Greiner, M. Strongly correlated quantum walks in optical lattices. Science 2015, 347, 1229–1233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gluck, M.; Kolovsky, A.R.; Korsch, H.J. Wannier–Stark resonances in optical and semiconductor superlattices. Phys. Rep. 2002, 366, 103–182. [Google Scholar] [CrossRef] [Green Version]
- Ben Dahan, M.; Peik, E.; Reichel, J.; Castin, Y.; Salomon, C. Bloch Oscillations of Atoms in an Optical Potential. Phys. Rev. Lett. 1996, 76, 4508. [Google Scholar] [CrossRef] [PubMed]
- Madison, K.W.; Fischer, M.C.; Diener, R.B.; Niu, Q.; Raizen, M.G. Dynamical Bloch Band Suppression in an Optical Lattice. Phys. Rev. Lett. 1998, 81, 5093. [Google Scholar] [CrossRef]
- Morsch, O.; Muller, J.H.; Cristiani, M.; Ciampini, D.; Arimondo, E. Bloch Oscillations and Mean-Field Effects of Bose-Einstein Condensates in 1D Optical Lattices. Phys. Rev. Lett. 2011, 87, 140402. [Google Scholar] [CrossRef] [PubMed]
- Bongs, K.; Sengstock, K. Physics with Coherent Matter Waves. Rep. Prog. Phys. 2004, 67, 907. [Google Scholar] [CrossRef]
- Ferrari, G.; Poli, N.; Sorrentino, F.; Tino, G.M. Long-Lived Bloch Oscillations with Bosonic Sr Atoms and Application to Gravity Measurement at the Micrometer Scale. Phys. Rev. Lett. 2006, 97, 060402. [Google Scholar] [CrossRef] [PubMed]
- Battesti, R.; Cladé, P.; Guellati-Khélifa, S.; Schwob, C.; Grémaud, B.; Nez, F.; Julien, L.; Biraben, F. Bloch Oscillations of Ultracold Atoms: A Tool for a Metrological Determination of h/mRb. Phys. Rev. Lett. 2004, 92, 253001. [Google Scholar] [CrossRef] [PubMed]
- Morandotti, R.; Peschel, U.; Aitchison, J.S.; Eisenberg, H.S.; Silberberg, Y. Experimental Observation of Linear and Nonlinear Optical Bloch Oscillations. Phys. Rev. Lett. 1999, 83, 4576. [Google Scholar] [CrossRef]
- Pertsch, T.; Dannberg, P.; Elflein, W.; Bräuer, A.; Lederer, F. Optical Bloch Oscillations in Temperature Tuned Waveguide Arrays. Phys. Rev. Lett. 1999, 83, 4752. [Google Scholar] [CrossRef]
- Peschel, U.; Pertsch, T.; Lederer, F. Optical Bloch oscillations in waveguide arrays. Opt. Lett. 1998, 23, 1701–1703. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.J.; Xiao, J.J.; Yu, K.W. Controllable optical Bloch oscillation in planar graded optical waveguide arrays. Phys. Rev. A 2010, 81, 033829. [Google Scholar] [CrossRef]
- Bromberg, Y.; Lahini, Y.; Silberberg, Y. Bloch Oscillations of Path-Entangle Photons. Phys. Rev. Lett. 2010, 105, 263604. [Google Scholar] [CrossRef] [PubMed]
- Afek, I.; Natan, A.; Ambar, O.; Silberberg, Y. Quantum state measurements using multipixel photon detectors. Phys. Rev. A 2009, 79, 043830. [Google Scholar] [CrossRef]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON States by Mixing Quantum and Classical Light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef] [PubMed]
- Sanchis-Alepuz, H.; Kosevich, Y.A.; Sanchez-Dehesa, J. Acoustic Analogue of Electronic Bloch Oscillations and Resonant Zener Tunneling in Ultrasonic Superlattices. Phys. Rev. Lett. 2007, 98, 134301. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.P.; Kasevich, M.A. Macroscopic quantum interference from atomic tunnel arrays. Science 1998, 282, 1686–1689. [Google Scholar] [CrossRef] [PubMed]
- Kudo, K.; Monteiro, T.S. Theoretical analysis of super–Bloch oscillations. Phys. Rev. A 2011, 83, 053627. [Google Scholar] [CrossRef]
- Hartmann, T.; Keck, F.; Korsch, H.J.; Mossmann, S. Dynamics of Bloch oscillations. New J. Phys. 2004, 6, 2. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom-Photon Interactions: Basis Properties and Applications; Wiley: Chichester, UK, 1998. [Google Scholar]
- Rabi, I.I. Space Quantization in a Gyrating Magnetic Field. Phys. Rev. 1937, 51, 652. [Google Scholar] [CrossRef]
- Hocker, G.B.; Tang, C.L. Observation of the Optical Transient Nutation Effect. Phys. Rev. Lett. 1968, 21, 591. [Google Scholar] [CrossRef]
- Johnson, T.A.; Urban, E.; Henage, T.; Isenhower, L.; Yavuz, D.D.; Walker, T.G.; Saffman, M. Rabi flopping between ground and Rydberg states with dipole-dipole atomic interactions. Phys. Rev. Lett. 2008, 100, 113003. [Google Scholar] [CrossRef] [PubMed]
- Kamada, H.; Gotoh, H.; Temmyo, J.; Takagahara, T.; Ando, H. Exciton Rabi Oscillation in a Single Quantum Dot. Phys. Rev. Lett. 2001, 87, 246401. [Google Scholar] [CrossRef] [PubMed]
- Blais, A.; Huang, R.-S.; Wallraff, A.; Girvin, S.M.; Schoelkopf, R.J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 2004, 69, 062320. [Google Scholar] [CrossRef] [Green Version]
- Gambetta, J.; Blais, A.; Schuster, D.I.; Wallraff, A.; Frunzio, L.; Majer, J.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Qubit-photon interactions in a cavity: Measurement-induced dephasing and number splitting. Phys. Rev. A 2006, 74, 042318. [Google Scholar] [CrossRef] [Green Version]
- Blais, A.; Gambetta, J.; Wallraff, A.; Schuster, D.I.; Girvin, S.M.; Devoret, M.H.; Schoelkopf, R.J. Quantum-information processing with circuit quantum electrodynamics. Phys. Rev. A 2007, 75, 032329. [Google Scholar] [CrossRef] [Green Version]
- Burkard, G.; Imamoglu, A. Ultra-long-distance interaction between spin qubits. Phys. Rev. B 2006, 74, 041307. [Google Scholar] [CrossRef]
- Barrett, S.D.; Milburn, G.J. Measuring the decoherence rate in a semiconductor charge qubit. Phys. Rev. B 2003, 68, 155307. [Google Scholar] [CrossRef]
- Kibis, O.V.; Slepyan, G.Y.; Maksimenko, S.A.; Hoffmann, A. Matter Coupling to Strong Electromagnetic Fields in Two-Level Quantum Systems with Broken Inversion Symmetry. Phys. Rev. Lett. 2009, 102, 023601. [Google Scholar] [CrossRef] [PubMed]
- Slepyan, G.Ya.; Yerchak, Y.D.; Maksimenko, S.A.; Hoffmann, A. Wave propagation of Rabi oscillations in one-dimensional quantum dot chain. Phys. Lett. A 2009, 373, 1374–1378. [Google Scholar] [CrossRef]
- Slepyan, G.Ya.; Yerchak, Y.D.; Maksimenko, S.A.; Hoffmann, A.; Bass, F.G. Mixed states in Rabi waves and quantum nanoantennas. Phys. Rev. B 2012, 85, 245134. [Google Scholar] [CrossRef]
- Yerchak, Y.; Slepyan, G.Y.; Maksimenko, S.A.; Hoffmann, A.; Bass, F. Array of tunneling-coupled quantum dots as a terahertz range quantum nanoantenna. J. Nanophotonics 2013, 7, 073085. [Google Scholar] [CrossRef]
- Slepyan, G.Ya.; Yerchak, Y.D.; Hoffmann, A.; Bass, F.G. Strong electron-photon coupling in a one-dimensional quantum dot chain: Rabi waves and Rabi wave packets. Phys. Rev. B 2010, 81, 085115. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Hadžievski, L.; Slepyan, G.Ya.; Malomed, B.A. Discrete solitons in an array of quantum dots. Phys. Rev. B 2013, 88, 155329. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.-Y.; Argyropoulos, C.; Alù, A. Enhanced nonlinearities using plasmonic nanoantennas. Nanophotonics 2012, 1, 221–233. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Childs, A.M.; Gosset, D.; Webb, Z. Universal computation by multiparticle quantum walk. Science 2013, 339, 791–794. [Google Scholar] [CrossRef] [PubMed]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051. [Google Scholar] [CrossRef]
- Mogilevtsev, D.; Slepyan, G.Y.; Garusov, E.; Kilin, S.Y.; Korolkova, N. Quantum tight-binding chains with dissipative coupling. New J. Phys. 2015, 17, 043065. [Google Scholar] [CrossRef] [Green Version]
- Mogilevtsev, D.; Slepyan, G.Y. Diffusive lossless energy and coherence transfer by noisy coupling. Phys. Rev. A 2016, 94, 012116. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mogilevtsev, D.; Slepyan, G.Y.; Doherty, T.H.; Thomson, R.R.; Korolkova, N. Dissipatively coupled waveguide networks for coherent diffusive photonics. Nat. Commun. 2018, 8, 1909. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.W.; Reimann, K.; Woerner, M.; Elsaesser, T.; Hey, R.; Ploog, K.H. Phase-Resolved Nonlinear Response of a Two-Dimensional Electron Gas under Femtosecond Intersubband Excitation. Phys. Rev. Lett. 2004, 92, 047402. [Google Scholar] [CrossRef] [PubMed]
- Levie, I.; Kastner, R.; Slepyan, G. Rabi-Bloch oscillations in spatially distributed systems: Temporal dynamics and frequency spectra. Phys. Rev. A 2017, 96, 043854. [Google Scholar] [CrossRef]
- Levie, I.; Slepyan, G. The New Concept of Nano-Device Spectroscopy Based on Rabi–Bloch Oscillations for THz-Frequency Range. Appl. Sci. 2017, 7, 721. [Google Scholar] [CrossRef]
- Weißl, T.; Rastelli, G.; Matei, I.; Pop, I.M.; Buisson, O.; Hekking, F.W.J.; Guichard, W. Bloch band dynamics of a Josephson junction in an inductive environment. Phys. Rev. B 2015, 91, 014507. [Google Scholar] [CrossRef]
- Nataf, P.; Ciuti, C. Vacuum Degeneracy of a Circuit QED System in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2010, 104, 023601. [Google Scholar] [CrossRef] [PubMed]
- Guichard, W.; Hekking, F.W.J. Phase-charge duality in Josephson junction circuits: Role of inertia and effect of microwave irradiation. Phys. Rev. B 2010, 81, 064508. [Google Scholar] [CrossRef]
- Manucharyan, V.E.; Masluk, N.A.; Kamal, A.; Koch, J.; Glazman, L.I.; Devoret, M.H. Evidence for coherent quantum phase slips across a Josephson junction array. Phys. Rev. B 2012, 85, 024521. [Google Scholar] [CrossRef]
- Manfra, M.J. Molecular Beam Epitaxy of Ultra-High-Quality AlGaAs/GaAs Heterostructures: Enabling Physics in Low-Dimensional Electronic Systems. Annu. Rev. Condens. Matter Phys. 2014, 5, 347–373. [Google Scholar] [CrossRef]
- Folsch, S.; Martinez-Blanco, J.; Yang, J.; Kanisawa, K.; Erwin, S.C. Quantum dots with single-atom precision. Nat. Nanotechnol. 2014, 9, 505. [Google Scholar] [CrossRef] [PubMed]
- Heiss, M.; Fontana, Y.; Gustafsson, A.; Wüst, G.; Magen, C.; O’Regan, D.D.; Luo, J.W.; Ketterer, B.; Conesa-Boj, S.; Kuhlmann, A.V.; et al. Self-assembled quantum dots in a nanowire system for quantum photonics. Nat. Mater. 2013, 12, 439. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Dover: New York, NY, USA, 1975. [Google Scholar]
- Loudon, R. The Quantum Theory of Light; Clarendon: Oxford, UK, 1983. [Google Scholar]
- Wubs, M.; Suttorp, L.G.; Lagendijk, A. Multiple-scattering approach to interatomic interactions and superradiance in inhomogeneous dielectrics. Phys. Rev. A 2004, 70, 053823. [Google Scholar] [CrossRef]
- Sorensen, M.W.; Sorensen, A.S. Three-dimensional theory for light-matter interaction. Phys. Rev. A 2008, 77, 013826. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 2, Course of Theoretical Physics; Pergamon Press: New York, NY, USA, 1980. [Google Scholar]
- Todorov, Y.; Sirtori, C. Few-Electron Ultrastrong Light-Matter Coupling in a Quantum LC Circuit. Phys. Rev. X 2014, 4, 041031. [Google Scholar]
- Vukics, A.; Grießer, T.; Domokos, P. Fundamental limitation of ultrastrong coupling between light and atoms. Phys. Rev. A 2015, 92, 043835. [Google Scholar] [CrossRef]
- Soriano, A.; Navarro, E.A.; Porti, J.A.; Such, V. Analysis of the finite difference time domain technique to solve the Schrodinger equation for quantum devices. J. Appl. Phys. 2004, 95, 8011–8018. [Google Scholar] [CrossRef]
- Sokolov, V.N.; Zhou, L.; Iafrate, G.J.; Krieger, J.B. Spontaneous emission of Bloch oscillation radiation from a single energy band. Phys. Rev. B 2006, 73, 205304. [Google Scholar] [CrossRef]
- Yu, P.P.; Cardona, M. Fundamentals of Semiconductors: Physics and Material Properties; Springer: Berlin, Germany, 2001. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Course of Theoretical Physics; Pergamon Press: New York, NY, USA, 1965. [Google Scholar]
- Keller, O. Quantum Theory of Near-Field Electrodynamics; Springer: Berlin, Germany, 2011. [Google Scholar]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levie, I.; Slepyan, G. Bloch Oscillations in the Chains of Artificial Atoms Dressed with Photons. Appl. Sci. 2018, 8, 937. https://doi.org/10.3390/app8060937
Levie I, Slepyan G. Bloch Oscillations in the Chains of Artificial Atoms Dressed with Photons. Applied Sciences. 2018; 8(6):937. https://doi.org/10.3390/app8060937
Chicago/Turabian StyleLevie, Ilay, and Gregory Slepyan. 2018. "Bloch Oscillations in the Chains of Artificial Atoms Dressed with Photons" Applied Sciences 8, no. 6: 937. https://doi.org/10.3390/app8060937



