Reverberation-Ray Matrix Analysis and Interpretation of Bending Waves in Bi-Coupled Periodic Multi-Component Beams

Featured Application

The method of reverberation-ray matrix (MRRM) and the interpretation of bending waves proposed in this paper provide respectively analysis method and profound knowledge for bending waves in bi-coupled periodic multi-component beams. These achievements will push forward the applications of bi-coupled periodic multi-component beams in wave filtering and vibration isolation.

Abstract

Most existing research on periodic beams concerns bending waves in mono-coupled and bi-coupled periodic mono-component beams with the unit cell containing only one beam segment, and very few works on bi-coupled periodic multi-component beams with the unit cell containing more than one beam segments study the bending waves in structures with only binary unit cells. This paper presents the method of reverberation-ray matrix (MRRM) as an alternative theoretical method for analyzing the dispersion characteristics of bending waves with the wavelength greater than the size of the cross-sections of all components in bi-coupled periodic multi-component beams. The formulation of MRRM is proposed in detail with its numerically well-conditioned property being emphasized, which is validated through comparison of the results obtained with the counterpart results by other methods for exemplified bi-coupled periodic beams. Numerical examples are also provided to illustrate the comprehensive dispersion curves represented as the relations between any two among three in frequency, wavenumber (wavelength) and phase-velocity for summarizing the general features of the dispersion characteristics of bending waves in bi-coupled periodic multi-component beams. The effects of the geometrical and material parameters of constituent beams and the unit-cell configuration on the band structures are also demonstrated by numerical examples. The most innovative finding indicated from the dispersion curves is that the frequencies corresponding to the Brillouin zone boundary may not be the demarcation between the pass-band and stop-band for bending waves in bi-coupled periodic multi-component beams.

1. Introduction

A periodic structure consists of repeated unit cells which are joined together end-to-end/side-by-side [1]. The most important property determined by this constructional feature is that the frequency domain of the waves falls into pass-bands and stop-bands that correspond respectively to those frequencies at which waves propagate without attenuation and to others at which waves attenuate with no propagation [1,2,3]. Consequently, periodic structures may have wide applications in various fields requiring wave filtering or vibration isolation, which drives the investigations of wave propagation in periodic structures in various scientific fields such as solid-state physics, electrical engineering and mechanical engineering, that are concerned with electron waves, electromagnetic waves, and electric current and elastic waves [2,3].

As one of the most important periodic structures, a periodic beam consists of beam segments possessing frequency bands of bending waves. Since the beam structure is a basic component in engineering and the bending wave is one of the main vibration forms and noise origins in engineering structures [4], the study of bending waves in periodic beams hence provides a method for vibration control and noise reduction in engineering structures, e.g., railway trains and tracks. Using the elastically point-supported, flexibly interconnected periodic beam and Timoshenko beam theory (TBT) or Euler–Bernoulli beam theory (EBT) to model railway train, Sakuma et al. [5] analyzed the harmonic and time-history responses of high-speed trains and train-like articulated systems travelling in confined fluid. Adopting the elastically point-supported periodic beam and based on the TBT, EBT or extended beam theory to model the railway track, Gry and Gontier [6] and Hosking and Milinazzo [7] studied bending-wave propagation together with the forced responses of railway tracks and floating ladder tracks, respectively. Sheng et al. [8] derived the propagation constant equations and used them for ballasted track to study the harmonic responses to steadily moving or static loads [8] and to discuss the propagation and resonance properties [9]. Using the Green’s function approach, Mazilu [10] predicted the interaction between a simple moving vehicle and the infinite periodic Timoshenko tract beam. Employing the elastically point-supported periodic Euler–Bernoulli beam to model the direct fixation track and the periodic beam with a unit cell consisting of a double beam on an elastic foundation to model the floating slab track, Gupta and Degrande [11] computed the transfer functions of the coupled track–tunnel–soil system and the dynamic forces accounting for the interaction between the moving vehicle and the periodic track. Although in recent years active periodic beams with smart components have been proposed on the basis of initially presented passive periodic beams made of only elastic materials in order for the bending-wave bands to be adjusted intelligently for controlling vibration and reducing noise in a more effective way, in this paper we still exclusively consider passive periodic beams in which only the construction of unit cell affects the band properties and the dispersion characteristics remain after the unit cell is determined. This is because there are still pending problems on this research objective, as will be summarized after an extensive literature review.

Passive periodic elastic beams may fall into two categories according to the minimum number of coupling coordinates between the structural beams, i.e., mono-coupled and bi-coupled periodic beams that have one and two minimum coupling coordinates, respectively [1,12]. For example, as the flexible interconnection of the articulated train system in Reference [5] transfers one or two generalized forces, the analysis models are mono-coupled and bi-coupled periodic beams, respectively. Mono-coupled periodic beams are mainly introduced in the form of periodic multi-span beams. There already exist extensive investigations on the bending waves in mono-coupled periodic beams, and without exception periodic multi-span beams [1,4,12,13,14,15,16,17,18,19,20], have led to the very wide applications of these structures in engineering practice, such as periodically supported bridges for instance. Thus, here we focus on bi-coupled periodic beams in this paper. Note that there are five kinds of bi-coupled periodic beams that have been presented so far: (1) a periodic beam composed of a uniform beam periodically attached with elastic supports with/without lumped masses; (2) a periodic beam composed of a uniform beam periodically attached with mass-spring systems (together with lumped masses and/or elastic supports); (3) a periodic beam made of periodically arranged two or more beam segments of different material/geometrical properties; (4) a periodic beam formed by combining the third and the first concepts; (5) a periodic beam formed by combining the third and the second concepts. It should be pointed out that periodic beams formed by combining the first and the second concepts belong to the second kind itself. It should also be emphasized that the second and the fifth kinds of bi-coupled periodic beams introduce a locally resonant mechanism [2] other than the Bragg scattering mechanism [2,3] into the formation of band gaps, so that low-frequency band gaps may possibly provide a new way in controlling low-frequency waves/vibrations without using unrealistically large structures. Note further that the first two kinds of periodic beams all have unit cells containing only one beam segment with attachments, and these structures are referred here to as bi-coupled periodic mono-component beams. In contrast, the last three kinds of periodic beams all have unit cells containing more than one beam segments without or with attachments, which are referred to here as bi-coupled periodic multi-component beams. Up until now, the bending waves in all the five types of bi-coupled periodic beams have been of concern.

First, the bending waves in the first kind of periodic beams have gained attention since the 1960s. Some literature considered the bending wave/vibration properties of infinite/finite periodic beams. For the periodic beams supported by translational/rotational springs: Lin [21] pioneered the analysis of the natural frequencies and modes of finite beams; then, Mead [16] derived the dispersion equation of characteristic bending waves in the infinite beams and discussed the interaction between characteristic bending waves and the alternating pressure field using the receptance method (RM); Zhu and Cheng [22] constructed the mutual variational principle of bending wave propagation in periodic structures, which provided the theoretical basis for the corresponding h-type finite element method (FEM). With the h–p hybrid FEM, Bardell et al. [17] analyzed the phase constant curves of the bending waves in infinite periodic Euler–Bernoulli beams; Romeo and Luongo [23] presented the design of periodic undamped and damped beams aimed at reducing the transmitted vibrations by referring the bi-dimensional analytical maps of the single unit free-wave propagation domains (stop, pass and complex domains) as the optimal choice of the cell properties and ordering. For periodic beams supported by translational/rotational springs with lumped masses: Wei and Petyt [18,19] introduced the extended Rayleigh–Ritz method to analyze the pass band properties and the natural properties of infinite and finite periodic structures, respectively; Brunskog [24] discussed the propagation properties of bending waves. For periodic beams with only added masses, Domadiya et al. [25] investigated numerically and experimentally the dispersion curves and the transmission loss coefficient of infinite and semi-infinite beams, respectively. Others consider the responses of infinite/finite periodic beams under external excitation: Ungar [26] discussed the propagation constants of bending waves in infinite periodic beams supported by translational springs and analyzed the steady-state response at the supported joint under harmonic loads by considering the effect of damping and fluid loads; using Fourier transform, Belotserkovskiy [27] analyzed the transient responses of infinite periodic Euler–Bernoulli beams with translational springs under a concentrated load; Cheng et al. [28,29] presented the wavenumber-harmonic method to analyze the frequency responses and sound radiations of a translational point-spring supported periodic Timoshenko beam subjected to a convected or travelling harmonic loading by considering the fluid-loading effect and discussing the influences of the spring support and the loading speed; Mead and Pujara [30] and Mead and Mallik [31] analyzed the steady-state response of infinite periodic Euler–Bernoulli beams with translational/rotational springs under alternating random loads by the space harmonic method and complex modal method, respectively; Mead [32] proposed a method to analyze the propagation constants of bending waves in infinite-period Timoshenko beams attached with translational/rotational springs and lumped-mass and their responses to an alternating harmonic pressure field; Mead and Yaman [33] analyzed the steady-state responses of infinite periodic beams with translational/rotational spring supports or lumped-mass under harmonic loads based on propagation constants.

Second, the bending waves in the second periodic beams classified above have been studied ever since 2005. The main concerns have been the band gaps and frequency responses of bending waves caused by Bragg scattering and locally resonant in infinite/finite periodic beams. For periodic beams with single DOF (degree-of-freedom) resonators: Yu et al. [34] and Liu et al. [35] analyzed the complex band structures using the transfer matrix method (TMM) based on TBT and EBT, respectively. Yu et al. [34] further analyzed the frequency response function (FRF, i.e., transmission) using the FEM and validated the results by experiments. Liu et al. [35] further analyzed the FRF using TMM, particularly concerning the influence of different local resonators, and summarized some design guidelines for this kind of structure. Xiao et al. [36] analyzed the complex band structures by the spectral element method (SEM) and examined the effects of various system parameters on band-gap behavior. The band formation mechanisms and formulas determining the transition and near-coupling conditions between local resonance and Bragg scattering were obtained. Sharma and Sun [37] studied the attenuation behavior of low-frequency waves in sandwich beams by closed form expression obtained from a phased array approach and verified the results by FEM. For periodic beams with two DOF resonators: Wang et al. [38] analyzed the band structures by TMM and the FRF by FEM, respectively, with a simplified model proposed to determine the edge frequencies of the band gaps and to enhance the understanding of the locally resonant mechanism. Pai et al. [39] calculated the dynamic behaviors by FEM and explained how the spring-mass-damper subsystem created two stopbands and negative effective mass and stiffness. For periodic beams with three DOF resonators: Wang et al. [40] studied the suppression of flexural vibration theoretically and numerically by the dispersion relation obtained using Hamilton’s principle and Bloch’s theorem. For periodic beams with more than three DOF resonators: Wang et al. [41] analyzed the band structures and characteristic modes of infinite periodic beams using the lumped mass method (LMM) and calculated the FRF of finite periodic beams using the FEM, based on three-node triangular plane stress elements. The theoretical FRF was validated by experimental measurements on a finite periodic beam specimen. For bending waves in a uniform beam attached with both translational/rotational spring supports and mass-spring resonators and with/without lumped mass: Lin and McDaniel [42] analyzed the FRF of a finite periodic beam by TMM based on EBT; based on Winkler’s foundation model and EBT, Yu et al. [43] studied the complex band structures and FRF of periodic beams on elastic foundations attached also with a locally-resonant mass-spring system; Raghavan and Phani [44] derived by RM the closed-form expressions for the location and width of sub-Bragg bandgaps, obtained the rigid body modes of the unit cell setting the bounding frequencies for local resonance bandgaps, and validated these results by experiments.

Third, the above-classified third kind of periodic beams have also received much attention. The main concern was the flexural wave/vibration in and frequency response of infinite/finite period beams. For periodic binary beams with two kind of materials: Lee et al. [45] proposed a basis theory of bending wave propagation; Han et al. [46] and Ni et al. [47] introduced a modified transfer matrix method (MTM) by transforming the state parameters of TMM into four initial parameters based on EBT and TBT, respectively; Tao and Liao [48] investigated the effects of the clamped boundary condition and disturbance on the flexural wave propagation using the method of multiple reflections; de Miranda and Dos Santos [49] investigated theoretically using FEM, SEM, the wave finite element method (WFEM), the wave spectral element method (WSEM), the conventional and improved plane wave expansion (PWE) method and experimentally the forced response and band structure based on EBT. Cheng et al. [50] investigated complex dispersion relations and the evanescent wave modes by their developed extended differential quadrature element method (EDQEM). For periodic binary beams with two kinds of cross-sections: Díaz-de-Anda et al. [51] analyzed the normal-mode frequencies and amplitudes of finite beams using TMM based on TBT, which were compared with the results based on EBT and were verified by experimental results from electromagnetic acoustic transducer (EMAT) measurements; Domadiya et al. [25] investigated numerically and experimentally the dispersion curves of periodic beams and the transmission loss coefficient of semi-periodic beams, respectively; Gao et al. [52] used TMM to explore the natural frequencies and the band-gap properties of the periodic beams based on the EBT and TBT, and verified the results by FEM and an experiment, with attention on the influences of the cross-section ratios and the length ratios on the dynamic properties. For periodic binary beams with two kind of materials of different cross-sections: Wen et al. [53,54] calculated the band structures of an infinite periodic beam with the PWE and the vibration attenuation spectra of a corresponding finite sample by FEM. The theoretical results were validated by vibration experiment, and a vibration isolation structure was designed based on these investigations. Xiang and Shi [55] proposed the differential quadrature method (DQM) for the analysis of band structures and properties with comparing the effects of TBT and EBT on the results. The influences of geometrical parameters and material parameters on the band-gap properties were discussed. For periodic beams with continuously changed parameters, Ying and Ni [56] proposed a double-expansion method for the frequency response of finite-length beams under harmonic excitation. For practical engineering applications of periodic binary beams: Richards and Pines [57] analyzed the propagation parameters and the frequency spectra based on EBT using SEM aiming at the reduction of the gear mesh flexural vibration using a periodic drive shaft. The influences of added inertia, boundary conditions and structural configuration were also considered. The analytical results were verified by experimental data, which indicated the real attenuation efficiency. Asiri et al. [58] designed periodic binary beams for supporting the ocean platform to reduce the propagation of the ocean noise to the platform, analyzed with a method based on EBT and TMM the band structure and the frequency response of the infinite and finite periodic binary beams, respectively, and verified the results by comparing them with an experiment of the scaled model of the ocean platform.

Fourth, bending waves in periodic beams of the above-classified fourth kind have been investigated since the 1980s. All the unit cells in the numerical examples considered up to now were binary. As the attachments are lumped, McDaniel and Carroll [20] analyzed the band structure of infinite periodic beams supported by translational springs and discussed the free vibration properties based on the EBT and the TMM. As the attachments are distributed, Tassilly [59] analyzed the band structures of periodic beams with spring and viscously-damped supports based on EBT and Floquet theory. Gei et al. [60] studied the band structures of prestressed periodic perfect and defected beams on an elastic foundation based on EBT, with special attention on the effects of prestress on the position/width of the band-gaps. The band-gap localized modes and effective negative mass effects of periodic perfect beams on an elastic foundation with an additional mass were also discussed using a Green’s function formulation. Xiang and Shi [61] analyzed the band gaps and the dynamic responses of periodic and quasi-periodic beams on a Pasternak foundation based on TBT and using the DQM. Yu et al. [43] studied the complex band structures and FRF of periodic beams on elastic Winkler foundations based on EBT. Also based on EBT, Zhang et al. [62,63] analyzed the vibration band gaps of periodic beams on Winkler and two-parameter foundations by the proposed MTM and by the TMM, respectively. Liu et al. [64] developed the EDQEM to study the effect of initial stress on the attenuation zones and attenuation coefficients of periodic Timoshenko beams resting on a two-parameter elastic foundation.

Fifth, the fifth periodic beams classified above have been devised since 2006. In all the unit cells considered, actually the beam itself was homogenous along the whole structure. In the case of attached two DOF resonators, Yu et al. [65] analyzed the band structures of infinite periodic beams using the TMM based on EBT. The FRF and the characteristic modes of a finite periodic beam were calculated by the FEM. Theoretical results were validated by experimentally measured FRF on a finite periodic beam specimen, with special attention on the material damping in the rubber. Zuo et al. [66] investigated the band gaps by TMM with the results validated by FEM, and observed the effects of band-gap coupling, the intervals, and oscillator parameters. In the case of attached resonators with more finite DOF, Xiao et al. [67] extended the PWE method to study the complex band structures of locally resonant beams attached with multiple periodic arrays of spring-mass resonators based on EBT, which were validated by the FRF obtained with commercial FEM software. Zhu et al. [68] suggested a chiral lattice-based elastic metamaterial beam with multiple embedded local resonators to achieve broadband vibration suppression without sacrificing its load-bearing capacity. In the case of attached resonators with infinite DOF, Wang and Wang [69] investigated the frequency band structure by TMM based on EBT, and showed richer dispersion properties in their proposed periodic beam with distributed DOF than those with the conventional force-only resonators.

Reviewing the above literature, we can summarize the current status of research on bending wave propagation in bi-coupled periodic beams:

(1)

There is plenty of literature on bi-coupled periodic mono-component beams with the unit cell containing only one beam segment. The works on bi-coupled periodic multi-component beams so far mainly have concerned bi-coupled periodic beams with the unit cell containing only two beam segments, particularly in the numerical examples, although most literature has presented the analysis on a unit cell model consisting of an arbitrary number of components. To the best of the authors’ knowledge, only Yan et al. [70] studied the complex band structures, the localization factors, and the characteristic modes of bending waves in periodic fourfold (quaternary) beams by TMM based on EBT. Nevertheless, as revealed by Liu and Hussein [71], the types/properties of periodicity have clear influence on bending wave characteristics. Hence, deducing the properties of bending waves in bi-coupled periodic multi-component beams from those of the adequate studies on similar structures may not be feasible, unless the similarities and differences between them have been obtained.

(2)

Although many methods have been proposed or used in analyzing the bending waves in bi-coupled periodic multi-component beams, such as PWE, TMM, SEM, DQM among the analytical ones and FEM among the numerical ones, effectively analyzing the bending waves at a relatively high frequency range is still challenging due to the essential deficiency in some of the existing methods. For example, the PWE method and the FEM are too computationally inefficient (expensive) for providing satisfactory results at a high frequency range. The TMM suffers from numerical weakness in cases of high frequency and a long transfer path [72].

(3)

The dispersion of bending waves in bi-coupled infinite periodic beams has been monotonously represented by the band structures, i.e., the frequency-wavenumber dispersion curves, in all previous research. There is very little knowledge on the properties of the wavelength and phase velocity of the characteristic bending waves in bi-coupled periodic beams. In particular, the general dispersion characteristics of bending waves in bi-coupled periodic multi-component beams have not been revealed so far.

Considering the pending problems in the aforementioned three aspects, this paper takes bi-coupled periodic multi-component beams with unit cells composed of arbitrary beam segments of different materials and cross-sections. Various periodic binary, ternary and quaternary beams are analyzed in the numerical examples, with special emphasis on the effect of unit-cell configuration on the dispersion curves and properties. The method of reverberation-ray matrix (MRRM) [73,74,75] is introduced as an alternative method for analyzing bending wave propagation in bi-coupled periodic multi-component beams. Note that MRRM compromises somewhat the computational efficiency as compared to the very efficient transfer matrix method (TMM). This is because the global scattering matrix in MRRM is formed by grouping all the element-related scattering matrices as compared to the global transfer matrix in TMM which is formed by the multiplication of all element transfer matrices, and thus the dimension of the system equation in MRRM is four times the element number as compared to the dimension of the system equation in TMM always being four regardless of the element number. However, by avoiding the matrix multiplications in the MRRM formulation, a numerical well-condition is achieved, as will be validated in Section 3.2. The comprehensive dispersion curves have been presented to illustrate the general dispersion characteristics of bending waves in bi-coupled periodic multi-component beams; in particular, the wavelength-related and phase velocity related dispersion curves are newly introduced to represent the dispersion of waves from all viewpoints. The influences of various construction factors in the unit cell, especially the beam component number, on the band structures are studied. We hope that the proposed method and interpretation will push forward better design and optimization of bi-coupled periodic multi-component beams for controlling bending waves and vibration isolation in engineering practice, such as for aircraft/automobile engines [57] and ocean platforms [58]. The outline of the paper is as follows. In Section 2 we derive the formulation of MRRM. The theoretical derivation and the computer program are verified by numerical examples in Section 3, where the advantages of the proposed MRRM as compared to TMM, the general dispersion characteristics, and the influence of various construction factors of the unit cell on the band structures, are discussed. Some conclusions are drawn in Section 4.

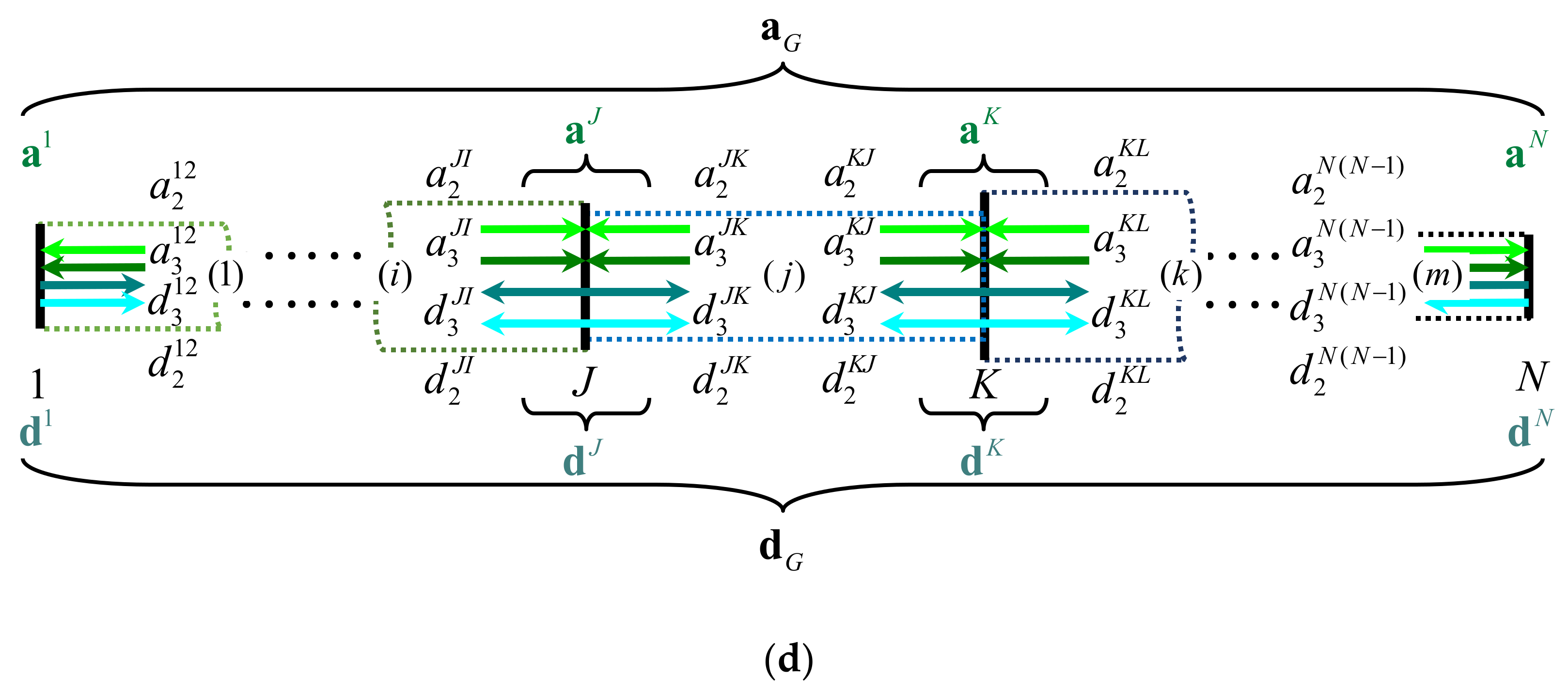
2. The Method of Reverberation-Ray Matrix (MRRM) for the Analysis of Bending Waves in Bi-Coupled Periodic Beams

Consider the bending waves in an infinite periodic structure whose unit cell of length $l$ containing $m$ beams and $n$ ($= m + 1$) joints are depicted in Figure 1. Each constituent beam in the unit cell is rigidly connected to its adjacent beam and is a carrier member of bending waves including the coupled flexural and thickness-shear modes. Thus, each joint in the unit cell has two coupling coordinates, at which the bending waves scatter. Therefore, the structure considered is a bi-coupled periodic beam [1]. Because the infinite periodic structures satisfy the Floquet–Bloch principle [1,2,3], the unit cell model in Figure 1 is adequate for determining the dispersion characteristics of bending waves in the infinite bi-coupled periodic beam as considered.

In the unit cell, any constituent beam is assumed to have a straight axis, homogenous material and uniform cross-section, and is deemed as one structural member. If it does not satisfy this assumption, the beam can always be further re-divided into more members to meet this requirement. In this case, the model in Figure 1 also applies but with enlarged $m$, in which the geometrical parameters $A$, $I$ and $\kappa$ are the area, moment of inertia and shear coefficient of the cross-section, respectively, and the material parameters $\rho$, $E$ and $G$ are the mass density, Young’s modulus and shear modulus, respectively. These geometrical and material parameters are all constant for each member. In addition, the cross-sectional dimensions of each constituent beam are comparatively smaller than the length, so that beam theories such as the Timoshenko or Euler–Bernoulli theory can be adopted to model the bending waves in the member. Thus, the deflection $v$, rotation $\phi$, shear force $Q$ and bending moment $M$ should be the variables to describe the dynamic state of the member. The amplitudes $a_r$ and $d_r$ of the respective backward (arriving) and forward (departing) waves of flexural ($r = 2$) or thickness-shear ($r = 3$) mode are used to represent the bending wave motion in the member. All members from left to right are denoted in turn by numbers $(1)$ to $(m)$ with their lengths signified by $l_{(1)}$ to $l_{(m)}$. In the unit cell, the end joints connecting the current unit cell to its neighbors and the intermediate joints linking the contiguous members are referred to as the exterior joints and the interior joints, respectively. All joints from left to right are signified in sequence as 1 to $N$ ($=n$), which include exterior joints 1, $N$ and interior joints $2$ through $N - 1$.

For an arbitrary member $(j)$ with left joint $J$ and right joint $K$, a pair of dual local coordinate systems ${(x,y,z)}^{JK}$ and ${(x,y,z)}^{KJ}$ of right-handed type are introduced, as shown in Figure 2a, to describe the cross-section and physical variables of this member within the framework of MRRM, and the variables of member $(j)$ in respective coordinates are described by superscripts $JK$ and $KJ$, as shown in Figure 2b–d. By this means, the axial coordinate of any one end cross-section in the local coordinate system with its origin on this cross-section is always zero. Accordingly, the joint coupling equations can be represented in a simple form without exponential functions, and the waves propagating in the same and opposite directions are naturally divided into groups, as indicated in Figure 2d. These advantages of introducing dual local coordinates will be indicated in the following derivations. For all joints, the global right-handed coordinate system $(X,Y,Z)$, as shown in Figure 2a, is set up to describe the physical variables, and the joint label is served as superscript to indicate their affiliation except for the exterior joints. For example, $u_Y^J$ and ${\theta }_Z^J$ in Figure 2b are the translational and rotational displacements of a typical interior joint $J$, respectively, which combine the generalized displacements. No external generalized forces arise at any interior joint since only free bending waves are considered here. The coupling variables including the translational and rotational displacements at the left (right) exterior joint $1$ $(N)$ are denoted by $u_{YL}$ $(u_{YR})$ and ${\theta }_{ZL}$ $({\theta }_{ZR})$, respectively. Meanwhile, the corresponding force and moment are $p_{YL}$ $(p_{YR})$ and $m_{ZL}$ $(m_{ZR})$, respectively. These quantities at exterior joint $1$ $(N)$ represent the interactions between the left (right) neighbor and the current unit cells. The translational displacements and the forces of joints and of members are deemed positive in the forward coordinate direction, and the rotational displacements and the moments are deemed positive around the counter clockwise, as clearly indicated in Figure 2b,c.

2.1. Wave-Based Modeling of Structural Members

For any structural member described in either of its local right-handed coordinates, the governing equations based on the Timoshenko beam theory [76] are:

$$\kappa GA\left(\frac{{\partial }^{2}v}{\partial x^2}-\frac{\partial \phi }{\partial x}\right)=\rho A\frac{{\partial }^{2}v}{\partial t^2}, EI\frac{{\partial }^2\phi }{\partial x^2}+\kappa GA\left(\frac{\partial v}{\partial x}-\phi \right)=\rho I\frac{{\partial }^2\phi }{\partial t^2}.$$

(1)

Assuming time harmonic variation ${\mathrm{e}}^{\mathrm{i}\omega t}$ to the generalized displacements with $\omega$ the circular frequency, Equation (1) can be reduced to the wave equations as:

$$\frac{{\mathrm{d}}^2\widehat{v}}{\mathrm{d}{x}^2}-\frac{\mathrm{d}\widehat{\phi }}{\mathrm{d}x}+\frac{{\omega }^2}{c_t^2}\widehat{v}=0, \frac{{\mathrm{d}}^2\widehat{\phi }}{\mathrm{d}{x}^2}+\frac{A{c}_t^2}{I{c}_l^2}\frac{\mathrm{d}\widehat{v}}{\mathrm{d}x}+\left[\frac{{\omega }^2}{c_l^2}-\frac{A{c}_t^2}{I{c}_l^2}\right]\widehat{\phi }=0,$$

(2)

where $c_l=\sqrt{E/\rho }$ and $c_t=\sqrt{\kappa G/\rho }$ are the velocities of quasi-longitudinal and quasi-transverse waves in the structural beam, respectively; and an over caret signifies the quantities in the frequency domain.

Equation (2) can be solved by virtue of the theory of ordinary differential equations to give the solutions to the generalized displacements as:

$$\begin{gathered} \widehat{v}(x)=(a_2{\mathrm{e}}^{\mathrm{i}{k}_{2}x}+a_3{\mathrm{e}}^{\mathrm{i}{k}_{3}x})+(d_2{\mathrm{e}}^{-\mathrm{i}{k}_{2}x}+d_3{\mathrm{e}}^{-\mathrm{i}{k}_{3}x}), \\ \widehat{\phi }(x)=({\beta }_2{a}_2{\mathrm{e}}^{\mathrm{i}{k}_{2}x}+{\beta }_3{a}_3{\mathrm{e}}^{\mathrm{i}{k}_{3}x})-({\beta }_2{d}_2{\mathrm{e}}^{-\mathrm{i}{k}_{2}x}+{\beta }_3{d}_3{\mathrm{e}}^{-\mathrm{i}{k}_{3}x}), \end{gathered}$$

(3)

where $\mathrm{i}=\sqrt{-1}$ is the imaginary unit. The terms in the former and latter parenthesis of Equation (3), as combined with ${\mathrm{e}}^{\mathrm{i}\omega t}$, signify backward (arriving) and forward (departing) traveling waves. The wavenumbers $k_r$ of flexural ($r=2$) and thickness-shear ($r=3$) modes are related to $\omega$ by:

$$k_{2,3}=\frac{\omega }{\sqrt{2}{c}_l}\sqrt{\left[\left(\frac{c_l^2}{c_t^2}+1\right)\pm \sqrt{{\left(\frac{c_l^2}{c_t^2}-1\right)}^2+4\frac{A{c}_l^2}{I{\omega }^2}}\right]},$$

(4)

where $k_2$ is always purely-real indicating the propagation property of the flexural mode all along the frequency domain, and $k_3$ is first purely-imaginary below ${\omega }_c$ and then purely-real above ${\omega }_c$ manifesting the first attenuation and then propagation property of the thickness-shear mode. ${\omega }_c=\sqrt{\kappa GA/(\rho I)}$ is the cut-off frequency. Note that in order to guarantee the numerically well condition of our formulation, $k_3=-\mathrm{i}\omega \sqrt{-\left[{(c_l^2/c_t^2+1)}^2-\sqrt{{(c_l^2/c_t^2-1)}^2+4A{c}_l^2/(I{\omega }^2)}\right]}/(\sqrt{2}{c}_l)$ should be adopted as $\omega <{\omega }_c$. It is indicated from Equation (3) that the flexural and the thickness-shear waves are coupled to each other, since the solutions to the generalized displacements contain contributions from both waves. ${\beta }_r=[{\omega }^2/c_t^2-k_r^2]/(\mathrm{i}{k}_r)$ representing the contribution of the flexural ($r=2$) or thickness-shear ($r=3$) wave on rotation displacement, is called the influence coefficient of rotation displacement, as the influence coefficients of transverse displacement are both unit. It can also be deduced from Equation (4) that the velocities $c_{2,3}=\omega /k_{2,3}$ of flexural and thickness-shear waves are frequency dependent. This indicates that the flexural and thickness-shear waves are dispersive.

Substituting Equation (3) into the spectral constitutive relations based on the Timoshenko beam theory as follows: $\widehat{Q}=\kappa GA(\mathrm{d}\widehat{v}/\mathrm{d}x-\widehat{\phi })$, $\widehat{M}=EI\mathrm{d}\widehat{\phi }/\mathrm{d}x$ [76], the solutions to the generalized forces are:

$$\begin{gathered} \widehat{Q}(x)=({\zeta }_2{a}_2{\mathrm{e}}^{\mathrm{i}{k}_{2}x}+{\zeta }_3{a}_3{\mathrm{e}}^{\mathrm{i}{k}_{3}x})-({\zeta }_2{d}_2{\mathrm{e}}^{-\mathrm{i}{k}_{2}x}+{\zeta }_3{d}_3{\mathrm{e}}^{-\mathrm{i}{k}_{3}x}), \\ \widehat{M}(x)=({\mu }_2{a}_2{\mathrm{e}}^{\mathrm{i}{k}_{2}x}+{\mu }_3{a}_3{\mathrm{e}}^{\mathrm{i}{k}_{3}x})+({\mu }_2{d}_2{\mathrm{e}}^{-\mathrm{i}{k}_{2}x}+{\mu }_3{d}_3{\mathrm{e}}^{-\mathrm{i}{k}_{3}x}), \end{gathered}$$

(5)

where ${\zeta }_r=(\mathrm{i}{k}_r-{\beta }_r)\kappa GA$ and ${\mu }_r=\mathrm{i}{k}_r{\beta }_{r}EI$ are the influence coefficients of shear force and bending moment corresponding to $r$ wave mode, respectively.

2.2. Wave-Based Modeling of Joints: Scattering Relations

2.2.1. Coupling Conditions between the Beam Elements and Scattering Relations at the Interior Joints

At any interior joint $J$ ($J=2,3,\cdots ,N-1$) where two adjacent structural members in the current unit cell are rigidly connected, the spectral equations of compatibility of displacements and equilibrium of forces should be:

$$-{\widehat{v}}^{JI}(0)={\widehat{u}}_Y^J={\widehat{v}}^{JK}(0), {\widehat{\phi }}^{JI}(0)={\widehat{\theta }}_Z^J={\widehat{\phi }}^{JK}(0); -{\widehat{Q}}^{JI}(0)+{\widehat{Q}}^{JK}(0)=0, {\widehat{M}}^{JI}(0)+{\widehat{M}}^{JK}(0)=0.$$

(6)

Substitute the solutions to the generalized displacements and forces of the members, as given respectively in Equations (3) and (5), into Equation (6), and one obtains the local scattering relation of interior joint $J$ as:

$$A^J(\omega )a^J+D^J(\omega )d^J=0 (J=2,3,\cdots ,N-1),$$

(7)

where $a^J={[a_2^{JI},a_3^{JI},a_2^{JK},a_3^{JK}]}^{\mathrm{T}}$ and $d^J={[d_2^{JI},d_3^{JI},d_2^{JK},d_3^{JK}]}^{\mathrm{T}}$ are the arriving and departing wave vectors of interior joint $J$, respectively, with the superscript $\mathrm{T}$ signifying the transpose of a vector or a matrix here and after. The corresponding coefficient matrices are:

$$A^J=\left[\begin{array}{cccc}1& 1& 1& 1\\ -{\beta }_{2(i)}& -{\beta }_{3(i)}& {\beta }_{2(j)}& {\beta }_{3(j)}\\ -{\zeta }_{2(i)}& -{\zeta }_{3(i)}& {\zeta }_{2(j)}& {\zeta }_{3(j)}\\ {\mu }_{2(i)}& {\mu }_{3(i)}& {\mu }_{2(j)}& {\mu }_{3(j)}\end{array}\right], D^J=\left[\begin{array}{cccc}1& 1& 1& 1\\ {\beta }_{2(i)}& {\beta }_{3(i)}& -{\beta }_{2(j)}& -{\beta }_{3(j)}\\ {\zeta }_{2(i)}& {\zeta }_{3(i)}& -{\zeta }_{2(j)}& -{\zeta }_{3(j)}\\ {\mu }_{2(i)}& {\mu }_{3(i)}& {\mu }_{2(j)}& {\mu }_{3(j)}\end{array}\right]$$

(8)

where ${\Gamma }_{r(i)}$ and ${\Gamma }_{r(j)}$ ($\Gamma =\beta ,\zeta ,\mu$, $r=2,3$) are the influence coefficients of rotation, shear force and bending moment for members $(i)$ and $(j)$ associated with $r$ wave mode, respectively.

2.2.2. Periodic Conditions between the Unit Cells and Scattering Relations at Exterior Joints

At the exterior joint pair $1$ and $N$ where the current unit cell is rigidly connected to the left and right adjacent unit cells, periodic conditions exist between the generalized displacements (forces) of joint pairs due to the Floquet–Bloch principle [1,2,3]. Further considering the coupling conditions between the generalized displacements (forces) of the exterior joint and the corresponding generalized displacements (forces) of the correlated end member at the section of the joint, the spectral periodic conditions between the unit cells [77,78] are written as:

$$\begin{gathered} -{\widehat{v}}^{N(N-1)}(0)={\widehat{u}}_{YR}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{u}}_{YL}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{v}}^{12}(0), {\widehat{\phi }}^{N(N-1)}(0)={\widehat{\theta }}_{ZR}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{\theta }}_{ZL}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{\phi }}^{12}(0); \\ {\widehat{Q}}^{N(N-1)}(0)={\widehat{p}}_{YR}=-{\mathrm{e}}^{\mathrm{i}ql}{\widehat{p}}_{YL}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{Q}}^{12}(0), -{\widehat{M}}^{N(N-1)}(0)={\widehat{m}}_{ZR}=-{\mathrm{e}}^{\mathrm{i}ql}{\widehat{m}}_{ZL}={\mathrm{e}}^{\mathrm{i}ql}{\widehat{M}}^{12}(0); \end{gathered}$$

(9)

where $q$ is the wavenumber of the characteristic wave in the periodic beam, and $l$ is the length of the unit cell. $\mathrm{i}ql=\mu$ is known as the complex propagation constant, with its imaginary part $q_{R}l={\mu }_I$ and real part $-q_{I}l={\mu }_R$ are the well-known phase constant and attenuation constant, respectively.

Introduction of the solutions to the generalized displacements and forces of members provided respectively in Equations (3) and (5) into Equation (9) leads to the local scattering relations of joint pairs $1$ and $N$. These scattering relations are written as:

$$\left[\begin{array}{cc}{A}^1(\omega ,q)& A^{1N}(\omega ,q)\\ A^{N1}(\omega ,q)& A^N(\omega ,q)\end{array}\right]\left\{\begin{array}{c}{a}^1\\ a^N\end{array}\right\}+\left[\begin{array}{cc}{D}^1(\omega ,q)& D^{1N}(\omega ,q)\\ D^{N1}(\omega ,q)& D^N(\omega ,q)\end{array}\right]\left\{\begin{array}{c}{d}^1\\ d^N\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\},$$

(10)

where $a^1={[a_2^{12},a_3^{12}]}^{\mathrm{T}}$ ($a^N={[a_2^{N(N-1)},a_3^{N(N-1)}]}^{\mathrm{T}}$) and $d^1={[d_2^{12},d_3^{12}]}^{\mathrm{T}}$ ($d^N={[d_2^{N(N-1)},d_3^{N(N-1)}]}^{\mathrm{T}}$) are the arriving and departing wave vectors of exterior joint $1$ ($N$), respectively, and the corresponding partitions of the coefficient matrices are:

$$\begin{array}{l}{A}^1={\mathrm{e}}^{\mathrm{i}ql}\left[\begin{array}{cc}1& 1\\ {\beta }_{2(1)}& {\beta }_{3(1)}\end{array}\right], A^{N1}={\mathrm{e}}^{\mathrm{i}ql}\left[\begin{array}{cc}{\zeta }_{2(1)}& {\zeta }_{3(1)}\\ {\mu }_{2(1)}& {\mu }_{3(1)}\end{array}\right], A^{1N}=\left[\begin{array}{cc}1& 1\\ -{\beta }_{2(m)}& -{\beta }_{3(m)}\end{array}\right], A^N=\left[\begin{array}{cc}-{\zeta }_{2(m)}& -{\zeta }_{3(m)}\\ {\mu }_{2(m)}& {\mu }_{3(m)}\end{array}\right];\\ D^1={\mathrm{e}}^{\mathrm{i}ql}\left[\begin{array}{cc}1& 1\\ -{\beta }_{2(1)}& -{\beta }_{3(1)}\end{array}\right], D^{N1}={\mathrm{e}}^{\mathrm{i}ql}\left[\begin{array}{cc}-{\zeta }_{2(1)}& -{\zeta }_{3(1)}\\ {\mu }_{2(1)}& {\mu }_{3(1)}\end{array}\right],D^{1N}=\left[\begin{array}{cc}1& 1\\ {\beta }_{2(m)}& {\beta }_{3(m)}\end{array}\right], D^N=\left[\begin{array}{cc}{\zeta }_{2(m)}& {\zeta }_{3(m)}\\ {\mu }_{2(m)}& {\mu }_{3(m)}\end{array}\right]\end{array}$$

(11)

with ${\Gamma }_{r(1)}$ and ${\Gamma }_{r(m)}$ ($\Gamma =\beta ,\zeta ,\mu$, $r=2,3$) denoting the influence coefficients of rotation, shear force and bending moment for members $(1)$ and $(m)$ associated with $r$ wave mode, respectively.

2.2.3. Global Scattering Relation

Grouping the scattering relations of all joints as provided typically in Equations (7) and (10) in order of the joint label, one obtains the global scattering relation:

$$A(\omega ,q)a+D(\omega ,q)d=0,$$

(12)

where $a$ and $d$ are, respectively, the global arriving and departing wave vectors composed of:

$$a={[{(a^1)}^{\mathrm{T}},{(a^2)}^{\mathrm{T}},\cdots ,{(a^J)}^{\mathrm{T}},\cdots ,{(a^N)}^{\mathrm{T}}]}^{\mathrm{T}}, d={[{(d^1)}^{\mathrm{T}},{(d^2)}^{\mathrm{T}},\cdots ,{(d^J)}^{\mathrm{T}},\cdots ,{(d^N)}^{\mathrm{T}}]}^{\mathrm{T}},$$

(13)

and the corresponding $4 m \times 4 m$ square coefficient matrices $A$ and $D$ are formed as:

$$A=\left[\begin{array}{ccccccc}{A}^1& 0& \cdots & 0& \cdots & 0& A^{1N}\\ 0& A^2& \cdots & 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & A^J& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& \cdots & A^{N-1}& 0\\ A^{N1}& 0& \cdots & 0& \cdots & 0& A^N\end{array}\right], D=\left[\begin{array}{ccccccc}{D}^1& 0& \cdots & 0& \cdots & 0& D^{1N}\\ 0& D^2& \cdots & 0& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & D^J& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& \cdots & D^{N-1}& 0\\ D^{N1}& 0& \cdots & 0& \cdots & 0& D^N\end{array}\right].$$

(14)

It should be emphasized that the exponential functions in the solutions to generalized displacements and forces of members as shown in Equations (3) and (5) do not appear in the local and global scattering relations, as can be inferred from Equations (8) and (11), because the axial coordinate of the end cross-section of every correlated structural member at any joint is always zero in the utilized local coordinate system. This is one of the main advantages of introducing the dual local coordinates in the MRRM for structural members.

2.3. Spectral System Equation and Dispersion Relation

The global scattering relation (12) gives altogether $4 m$ equations for the $4 m$ unknown arriving wave amplitudes and the $4 m$ unknown departing wave amplitudes in vectors $a$ and $d$, respectively. Obviously, another $4 m$ equations should be supplemented for solving the wave problem. Fortunately, the global phase relation $a=P(\omega )\tilde{\mathbf{d}}=P(\omega )Ud$ exactly provides another $4 m$ equations for the global arriving and departing wave vectors $a$ and $d$, whose derivation is detailed in Appendix A. Substitution of this global phase relation into the global scattering relation (12) gives the spectral system equation:

$$\left[A(\omega ,q)P(\omega )U+D(\omega ,q)\right]d=R_d(\omega ,q)d=0,$$

(15)

where $R_d=APU+D$ is the $4 m \times 4 m$ system matrix. Equation (15) in fact poses a non-linear and implicit eigenproblem with the eigenvector $d$ and the eigenvalue ${\mathrm{e}}^{\mathrm{i}ql}$ as the frequency $\omega$ is specified or the eigenvalue $\omega$ in case of given wavenumber $q$.

For an existing non-trivial solution to the system Equation (15), the determinant of the system matrix should vanish to give

$$\det [R_d(\omega ,q)]=\det \left[A(\omega ,q)P(\omega )U+D(\omega ,q)\right]=0,$$

(16)

which is a transcendental dispersion equation determining the dispersion characteristics of bending waves in the infinite bi-coupled periodic beams. In practice, except for the closed-form transcendental dispersion equation provided in Reference [74] for simply configured bi-coupled periodic beams with a binary unit cell having only two constituent beams, the concrete dispersion equation is difficult to write out in closed-form for the general bi-coupled periodic multi-component beams. This is because complicated operations of matrix multiplication and matrix determinant are involved in deriving the closed-form of Equation (16). Consequently, the dispersion equation is usually solved numerically. If any one among three in frequency $\omega$, wavenumber $q$ (or wavelength $\lambda =2\pi /q$) and phase velocity $c=\omega /q$ is specified within a prescribed range, the other two can be determined by properly searching the root of Equation (16). The solving process and the adopted techniques are summarized as follows:

(1)

Initially preset a beginning value and the increment to the known quantity. In later circulation computations, add an increment to the current value of the known quantity to give it an updated value.

(2)

Specify two tentative values to the requested quantity. The first tentative value should be specified at the initial computation and obtained from step (6) during the later calculations. The second tentative value is obtained from the first tentative value by adding a specified increment. Based on the golden section method, the two golden points between the first and the second tentative values are calculated. Then, the wavenumbers $q$ and frequencies $\omega$ can be computed corresponding to the value of known quantity and the four values of requested quantity including two tentative values and two golden section values.

(3)

Substitute the resulting four ($q$,$\omega$) groups into the pertinent formulas and matrices to form the system matrices associated with the four values of requested quantities. Then calculate the determinants of the system matrices in these four cases.

(4)

According to the golden section method and referring to the determinant amplitudes of the four system matrices, decide whether there is a root to the requested quantity within the two tentative values. If there is not, directly go to step (6); If there is, search the root by virtue of the dichotomizing method through inspecting the real or imaginary parts of the determinants or finish the root searching by the golden section method by observing the amplitudes of the determinants.

(5)

Judge if adequate numbers of the requested quantity have been obtained or judge if the second tentative value is exceeding the required range. If so, go to step (7). If not, go to the next step.

(6)

Assign the second tentative value as the first one and then return to step (2).

(7)

Judge if adequate numbers of root have been obtained for the current value of known quantity or judge if the current value of known quantity exceeds the required range. If not, start the calculation from step (1) again. If yes, terminate the calculation.

After all the roots within the required range of the requested quantity have been obtained for all the specified values of known quantity with a given range, the dispersion spectra between the known and requested quantities in the corresponding area can be plotted. These dispersion curves represent the dispersion properties of the characteristic waves from a viewpoint.

It should be emphasized that the involved exponential functions in system Equation (15) and the dispersion Equation (16) are ${\mathrm{e}}^{\mathrm{i}ql}$ from the global scattering relation (12) and ${\mathrm{e}}^{-\mathrm{i}{k}_{r(j)}{l}_{(j)}}$ from the global phase relation (A3), respectively. Since the elaborately chosen $k_{r(j)}$ has guaranteed $\mathrm{Re}[-\mathrm{i}{k}_{r(j)}{l}_{(j)}]\le 0$, thus ${\mathrm{e}}^{-\mathrm{i}{k}_{r(j)}{l}_{(j)}}$ is always an exponentially decaying function. Comparatively, the other analytical methods like the well-known transfer matrix method (TMM) contain both ${\mathrm{e}}^{-\mathrm{i}{k}_{r(j)}{l}_{(j)}}$ and ${\mathrm{e}}^{\mathrm{i}{k}_{r(j)}{l}_{(j)}}$ in its formulation, and thus inevitably both exponentially decaying and growing functions are involved, which will lead to a numerically ill-condition problem as discussed in Ref. [79]. Our MRRM formulation, however, should be numerically well-conditioned as long as $\mathrm{Re}[\mathrm{i}ql]\le 0$ satisfies or $\mathrm{Re}[\mathrm{i}ql]$ is not too big. These conditions are relatively easy to guarantee since in the wave problem studied here the eigenvalue $[\mathrm{i}ql]$ is symmetrical with respect to $q=0$, i.e., the characteristic waves in opposite directions should give the same dispersion property. Thus, our proposed MRRM is applicable for accurate calculation of the dispersion curves until a relatively high frequency where the Timoshenko beam theory still holds for modeling structural members. With regard to the aforementioned numerically well-conditioned property, the advantage of our MRRM as compared to TMM will be illustrated by numerical examples in Section 3.2.

It should also be pointed out that our proposed MRRM formulation based on the Timoshenko beam theory in this section can actually be degenerated to a counterpart formulation for the bi-coupled periodic Euler–Bernoulli beam structures, as long as $c_t=\infty$, ${\beta }_r=\mathrm{i}{k}_r$, ${\zeta }_r=-{(\mathrm{i}{k}_r)}^{3}EI$, ${\mu }_r={(\mathrm{i}{k}_r)}^{2}EI$, $k_2=k=\sqrt[4]{{\omega }^{2}A/(c_l^{2}I)}$ and $k_3=-\mathrm{i}{k}_2=-\mathrm{i}k$ are adopted [76] in all the above related formulas. Again, the MRRM formulation in this case is valid as long as the Euler–Bernoulli beam theory is effective.

3. Numerical Examples

Bi-coupled periodic multi-component beams with five kinds of unit cell, including two binary, two ternary and one quaternary unit cells, have been considered in all the numerical examples to validate our proposed MRRM, to illustrate the advantages of our MRRM compared to TMM, to demonstrate the general dispersion characteristics of bending waves in bi-coupled periodic multi-component beams, and to study the influences of various construction factors of the unit cell on the band structures. The configurations of these five kinds of unit cells are listed in

Table 1. The configuration of five kinds of unit cell in our exemplified bi-coupled periodic beams.

Unit Cell Type	Configuration of the Unit Cell
Binary-I	1.0 m Concrete beam + 1.0 m Steel beam
Binary-II	1.0 m Aluminum beam + 1.0 m Epoxy beam
Ternary-I	0.5 m Aluminum beam + 1.0 m Concrete beam + 0.5 m Steel beam
Ternary-II	0.5 m Aluminum beam + 1.0 m Epoxy beam + 0.5 m Steel beam
Quaternary	0.5 m Aluminum beam + 0.5 m Concrete beam + 0.5 m Steel beam + 0.5 m Epoxy beam

, with the parameters of all the four involved materials provided in

Table 2. The material constants of the four materials involved.

Material	Young’s Modulus E (GPa)	Shear Modulus G (GPa)	Mass Density ρ (kg·m−3)
Concrete	25	9.40	2300
Steel	210	78.95	7850
Aluminum	77.56	28.87	2730
Epoxy	4.35	1.59	1180

. In all the following calculations, the Timoshenko beam theory and the shear coefficient $5/6$ are used for all of the constituent beams in the unit cells. Nevertheless, in Section 3.1 the Euler–Bernoulli beam theory is also exploited to model the structural member for the sake of observing the effect of beam theories on the dispersion curves. Except for the different geometric parameters of the exemplified periodic beams in Section 3.2 and Section 3.4.1, the cross-sectional area and the cross-sectional inertia moment of all constituent beams in the unit cell are given as $0.1{\mathrm{m}}^2$ and $2.083\times {10}^{-3}{\mathrm{m}}^4$ for the exemplified periodic beams in all the other sections of this part.

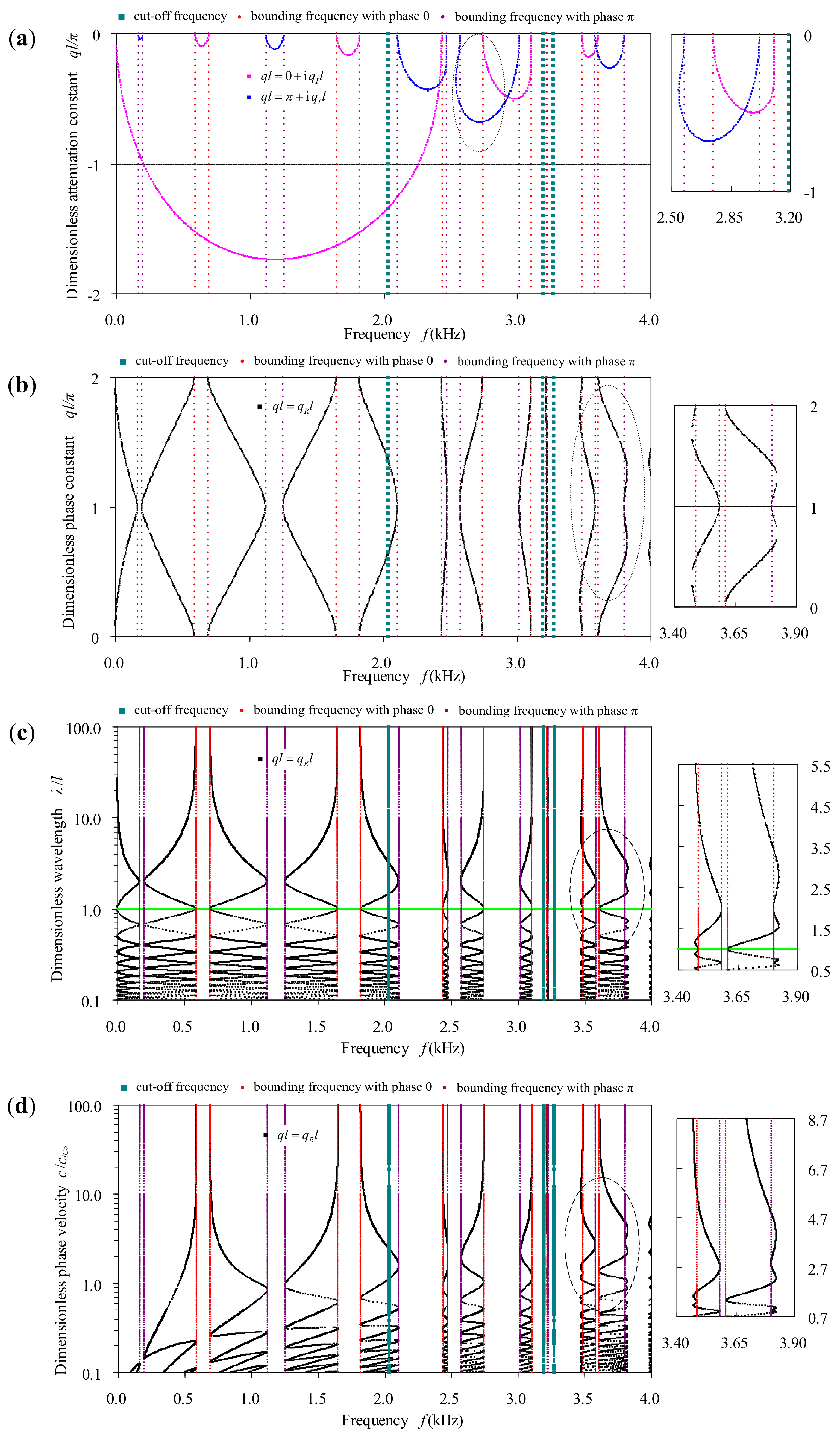
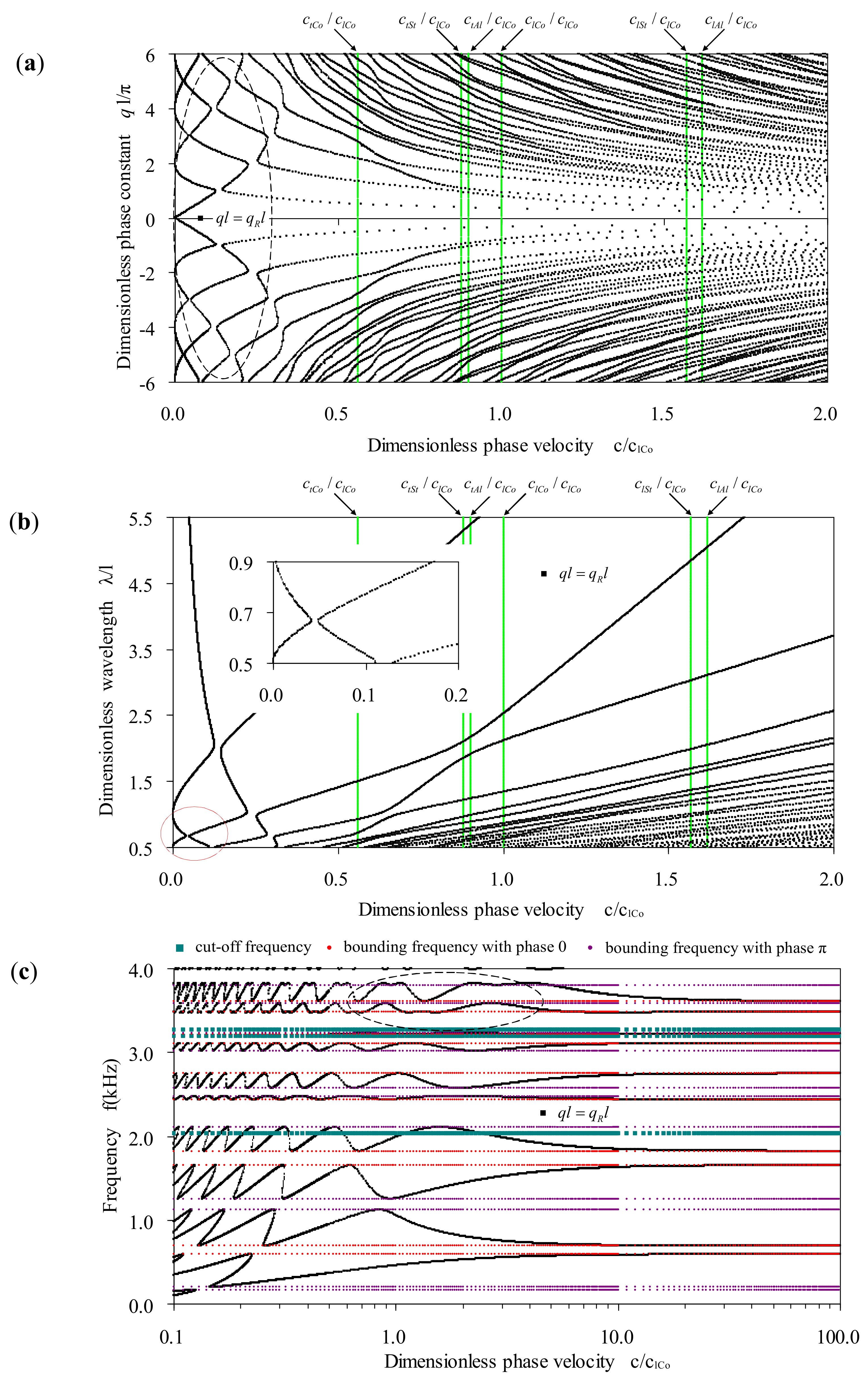
Adopting the aforementioned parameters, the comprehensive dispersion curves of the five exemplified bi-coupled periodic multi-component beams are calculated by our proposed MRRM, containing the frequency-attenuation constant, the frequency-phase constant, the frequency-wavelength, the frequency-phase velocity dispersion curves that are in group called as the frequency-related spectra and the phase velocity-phase constant, the phase velocity-wavelength, and the phase velocity-frequency dispersion curves that are called the phase velocity-related dispersion curves in group. For the convenience of plotting these dispersion curves and also for the ease of discussing the corresponding dispersion characteristics, the engineering frequency $f=\omega /(2\pi )$, the dimensionless wavenumber (phase/attenuation constant) $ql/\pi$, the dimensionless wavelength $\lambda /l$ and the dimensionless phase velocity $c/c_{lRf}$ are used with $c_{lRf}=\sqrt{E_{Rf}/{\rho }_{Rf}}$ as the wave speed of longitudinal mode in the referred constituent beam. If the unit cell of the considered periodic beam contains a concrete beam member, then it is taken as the referred beam. Otherwise, the aluminum beam is deemed as the referred beam.

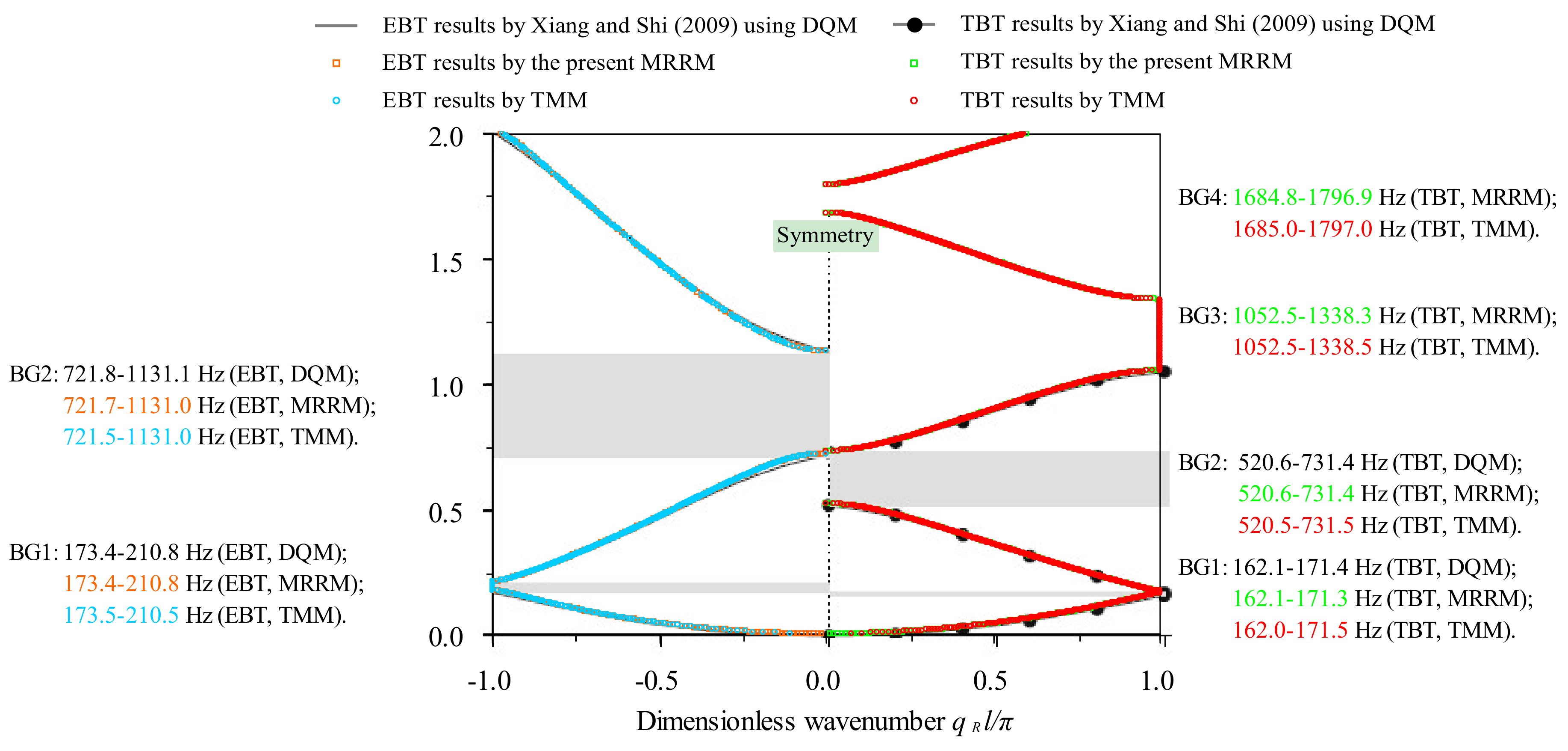
3.1. Validation of the Proposed MRRM

Consider the bi-coupled periodic beam with Binary-I unit cell. The first several phase-constant spectra below $2.0\mathrm{kHz}$ obtained by proposed MRRM based on the Timoshenko beam theory (TBT) are shown in the right half-part of Figure 3. Also provided are the counterpart results by TMM obtained by ourselves and by DQM in Ref. [55]. The comparison of the boundary frequencies of the first four band gaps obtained by the aforementioned three methods are also listed in Figure 3. In order to also validate the proposed MRRM based on the EBT and for the sake of illustrating the effects of rotary inertia and shear deformation on the phase constant spectra and boundary frequencies of band gaps, the calculations are also conducted based on the EBT. In the left half part of Figure 3, the results by the MRRM, TMM and DQM are depicted corresponding to the right half part.

In both cases of TBT and EBT, the good agreement between the results by the MRRM, TMM and DQM validates our formulation. Moreover, the good agreement between the first spectrum by TBT and EBT indicates both EBT and TBT work well in the relatively low frequency range. But the discrepancy between the second upwards spectra and the boundary frequencies of band gaps based on TBT and EBT becomes more and more distinct with the increasing of spectra order, which indicates that the rotary inertia and shear deformation have more and more obvious influences on the phase constant spectra and boundary frequencies of band gaps with the increasing frequency. EBT, which neglects the effects of rotary inertia and shear deformation, ceases to be effective in a somewhat high-frequency range above the second pass-bands.

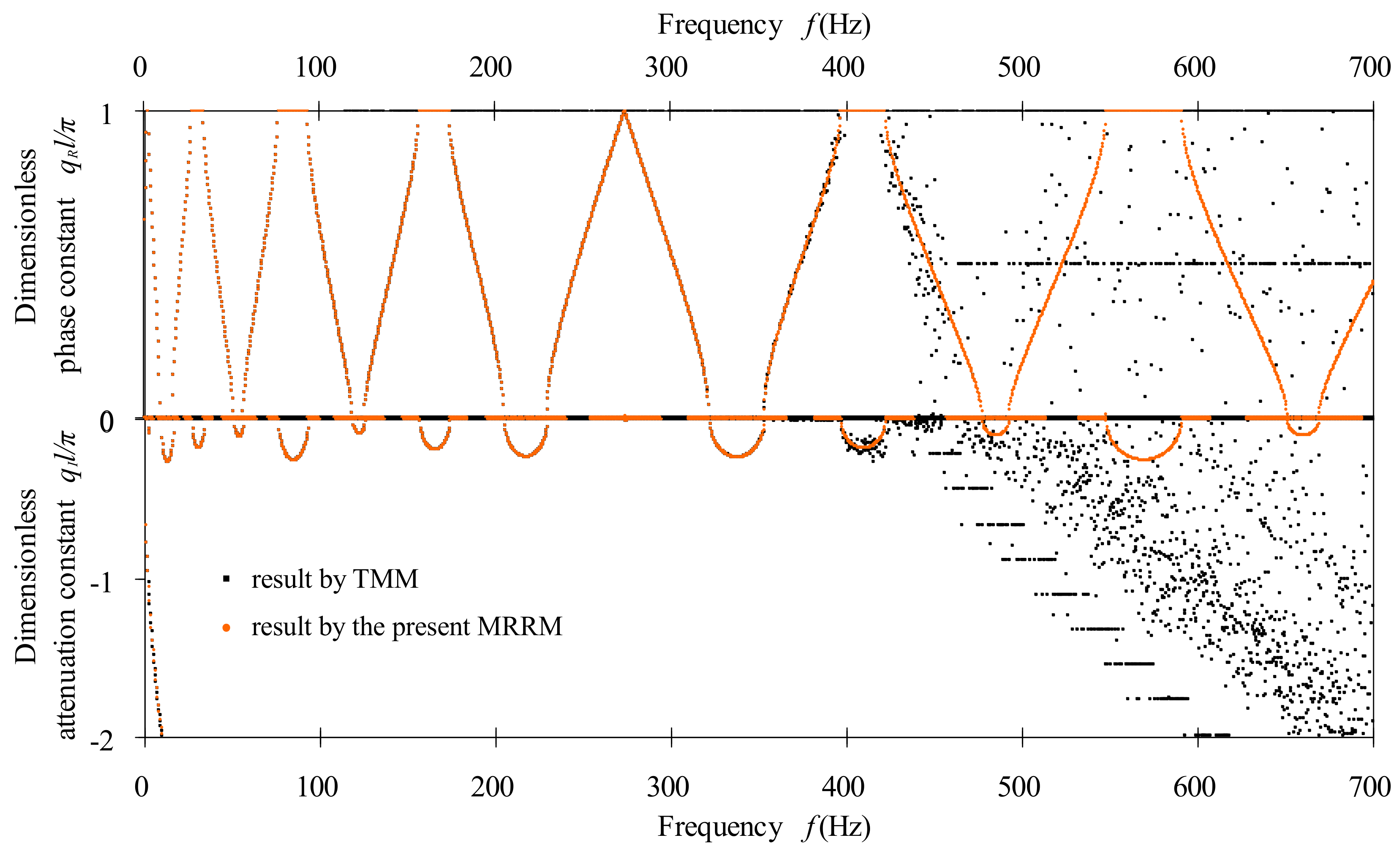
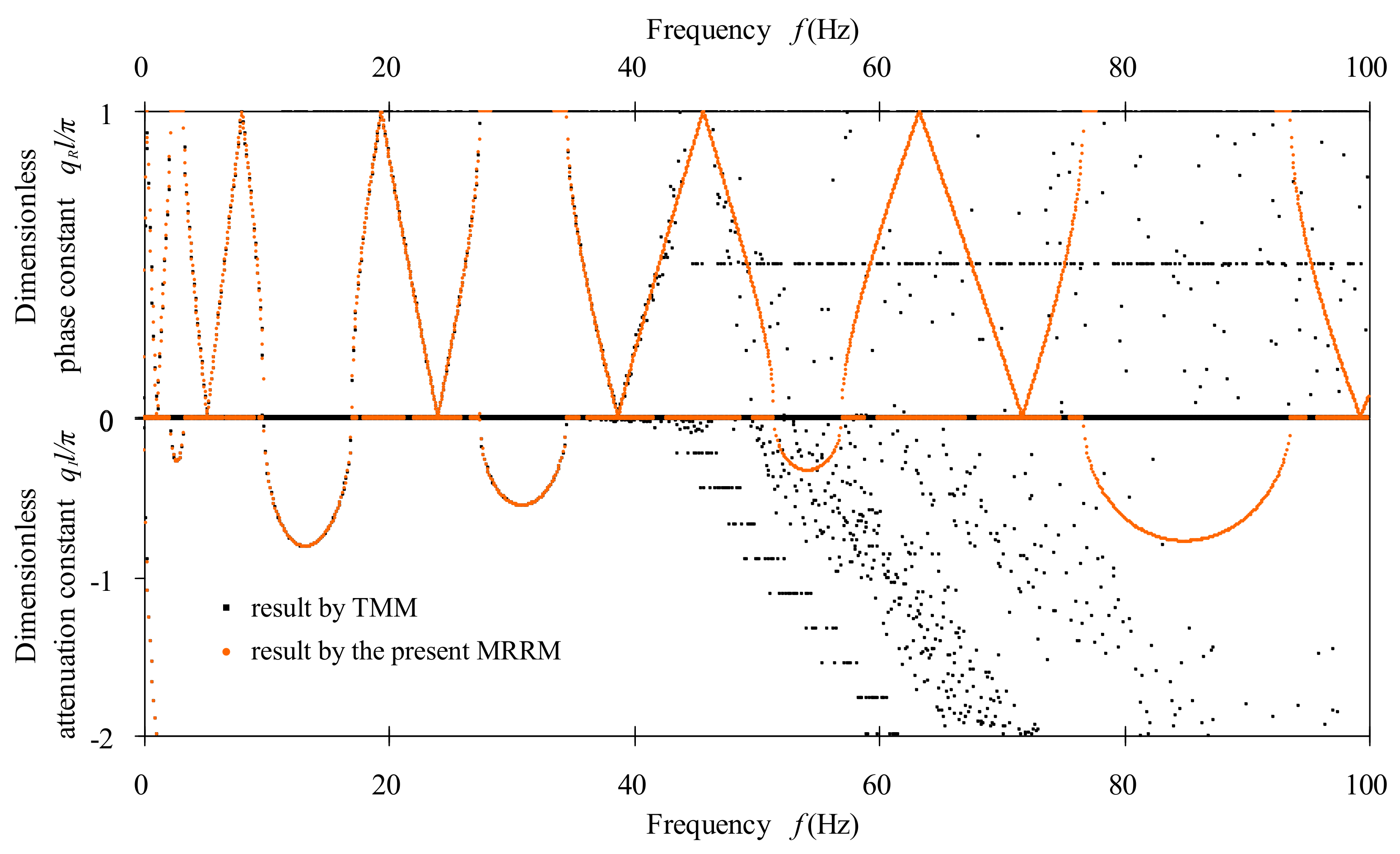
3.2. The Advantages of the Proposed MRRM as Compared to the Transfer Matrix Method (TMM)

Consider the bi-coupled periodic beams with one Binary-II as the unit cell and three Binary-IIs as the super cell. The cross-sectional area and the cross-sectional inertia moment of all constituent beams are $A=2\times {10}^{-4}{\mathrm{m}}^2$ and $1/6\times {10}^{-8}{\mathrm{m}}^4$ in the respective unit/super cell of the above two exemplified periodic beams. The phase and attenuation constant spectra of these two periodic beams are computed by the proposed MRRM and the well-known TMM. These band structures of the periodic beam with one Binary-II as the unit cell are given and compared in 0–700 Hz, while those of the periodic beam with three Binary-IIs as the super cell are provided and contrasted in Figure 4 within 0–100 Hz.

Figure 4 and Figure 5 indicates that the classical TMM formulation is ill-conditioned, as the frequency is above $380\mathrm{Hz}$ and $40\mathrm{Hz}$ for the exemplified periodic beam with one Binary-II as the unit cell and the periodic beam with three Binary-IIs as the super cell under consideration, respectively. The comparison between Figure 4 and Figure 5 demonstrate that the increasing of transfer path will reduce the critical frequency above which the TMM will be ill-conditioned. These findings illustrate the possible ill-condition problem of the TMM in cases of relatively high frequency and long transfer path. However, our proposed MRRM formulation is always well-conditioned for both exemplified periodic beams within the respectively considered frequency ranges. This serves as the main advantages of the MRRM as compared to TMM.

3.3. The General Dispersion Characteristics of Bending Waves in Bi-Coupled Periodic Multi-Component Beams

Among all kinds of dispersion curves, the corresponding ones of bending waves in the five exemplified bi-coupled periodic multi-component beams illustrate qualitatively identical features although they show quantitatively different shapes and positions. As a representative, the first several frequency-related dispersion curves and the first several phase velocity-related dispersion curves of the bending waves in a bi-coupled periodic beam with Ternary-I unit cell are exhibited respectively in Figure 6 and Figure 7. Figure 8 depicts those frequency-related dispersion curves within the frequency range 500–505 kHz of bending waves in the same bi-coupled periodic ternary beam, which again indicates that the present MRRM formulation is well-conditioned within the considered high frequency range.

The comparison of the corresponding subfigures in Figure 6 and Figure 8 verifies that the frequency related dispersion curves illustrate similar features at low and relatively high frequency ranges. In addition, when the bending-wave dispersion curves in Figure 6, Figure 7 and Figure 8 are compared to the counterpart longitudinal-wave dispersion curves in a periodic multi-component rod [75], a typical mono-coupled periodic structure, features that are alike and unlike may be sought out.

The features that are alike include: (1) among the diversified dispersion curves representing the propagation characteristics, only those frequency-related dispersion curves reflect the band property; (2) in the frequency-wavenumber spectra, the phase and the attenuation constant spectra are both symmetrical about $ql=0$, since $+ql$ and $-ql$ denoting a pair of characteristic waves in opposite directions should have the same propagation property. Within each pass-band, the phase constant spectrum is periodic about wavenumber with the minimum positive period being $ql/\pi =2$. Within each stop-band, the attenuation constant spectrum is a closed loop and non-periodic about the wavenumber; (3) in the frequency-wavelength spectra, the wavelength associated with a given frequency in pass-band is multi-valued. As we take $\lambda /l=1$ as the dividing line, the spectra below it become more and more intensive with the decrease of dimensionless wavelength, while those above it are sparse. The frequency-wavelength spectra within the second and higher pass-bands take the bounding frequencies with phase $0$ as their asymptotes as the wavelength tends to infinity. This means that near $ql=0$ all the unit cells are displaced in the same direction without phase delay, thus the periodic structure displaces as a whole; (4) in the frequency-phase velocity spectra, the phase velocity associated with a given frequency in pass-band are also multi-valued. There is not any cut-off value for phase velocity in the second and higher order pass-bands. The spectra become more and more intensive as the phase velocity decreases. By contrast with the frequency-wavelength spectra, the frequency-velocity spectra do not have clear division between the intensive and sparse regions. The frequency-velocity spectra also take the bounding frequencies with phase $0$ as their asymptotes as the phase velocity tends to infinity; (5) the phase velocity-related dispersion curves show the dispersion properties of the frequency-related dispersion curves in different viewpoints. As observed from the phase-velocity related dispersion curves, the spectrum in the first pass-band has cut-off phase velocity, but does not have cut-off wavelength, as noted in Figure 6c.

The special features of bending-wave dispersion curves in bi-coupled periodic multi-component beams, as compared to the longitudinal-wave dispersion-curves in a mono-coupled periodic multi-component rod, include: (A) the frequency-related dispersion curves in some pass-bands may not be entirely constrained between the bounding frequencies corresponding to $ql=0$ and $ql=\pi$, which means that the frequencies corresponding to the Brillouin zone boundary may not be the demarcation between pass-band and stop-band. This should be the most innovative dispersion feature for bending waves in bi-coupled periodic multi-component beams, which never exist in mono-coupled periodic structures; (B) the pass-bands and stop-bands no longer appear alternately due to the existence of two kinds of characteristic bending waves. There may be frequency regions that are pass-bands/stop-bands for both characteristic modes, because in these regions the phase/attenuation constant spectra associated with different characteristic modes may overlap. There are regions that have neither phase constant spectra nor attenuation constant spectra, in which the wavenumbers are neither purely real nor purely imaginary, but are complex; (C) since the attenuation spectra in some stop-bands are concave, more than one forms of attenuations at a given frequency occur in this case; (D) the cut-off phase velocity should be obtained by setting $ql=\pi$, which is different from the determination of the cut-off phase velocity in the mono-coupled periodic multi-component rods by setting $ql=0$ ($\omega =0$).

3.4. Influences of Various Construction Factors of the Unit Cell on the Band Structures

In what follows, the effects of various construction factors of the unit cell (with fixed length $2\mathrm{m}$) on the band structures, including the geometrical and material parameters of the constituent beams and the unit-cell configuration, are studied on the bi-coupled periodic beams with the Ternary-I unit cell. The referred geometrical parameters to all the constituent beams are $A=0.1{\mathrm{m}}^2$ and $I=2.083\times {10}^{-3}{\mathrm{m}}^4$. During the research on the influences of geometrical and material parameters, only the considered parameters of the concrete beam in the Ternary-I unit cell are altered, while the other parameters of this beam and all parameters of the other constituent beams remain unchanged. The degree of alteration is represented by the ratio of these parameters defined by the updated value of the varied beam divided by the original value of the previous beam. These ratios are specified during our study. Except for the shape and position of the band structures, particularly emphasized are the effects of the geometrical and material parameters on the newly found novel dispersion property, i.e., the frequencies corresponding to the Brillouin zone boundaries may not be the demarcation between pass-bands and stop-bands for bending waves in bi-coupled periodic multi-component beams.

3.4.1. Effect of the Geometrical Parameters of Constituent Beams on the Band Structures

The involved geometrical parameters of the constituent beams are the cross-sectional area and the cross-sectional inertia moment. The cross-sectional area or the cross-sectional inertia moment of the altered beam is changing independently on each other. The ratio of cross-sectional area ${\gamma }_A$ has been specified as three values $0.25$, $1$ and $4$. Similarly, the ratio of cross-sectional inertia moment are specified as the same three values ${\gamma }_I=0.25$, ${\gamma }_I=1$ and ${\gamma }_I=4$. Figure 9 and Figure 10 depict respectively the phase/attenuation constant spectra of the resulting periodic beams with Ternary-I unit cell as the cross-sectional area and the cross-sectional inertia moment change independently.

Figure 9 and Figure 10 indicate that both the phase and the attenuation constant spectra are sensitive to the variation of the cross-sectional area and the cross-sectional inertia moment. From Figure 9, it can be noticed that the band structures generally move to the lower frequency side with the increase of the cross-sectional area. As the cross-sectional inertia moment decreases, Figure 10 shows the same phenomena. The highlighted regions of phase constant spectra in Figure 9 and Figure 10 indicate that with the alterations of ${\gamma }_A$ or ${\gamma }_I$, the novel dispersion property, i.e., the feature that the frequencies corresponding to the Brillouin zone boundaries may not be the demarcation between pass-bands and stop-bands, will probably disappear or re-occur. It seems that there is not a general rule for this phenomenon.

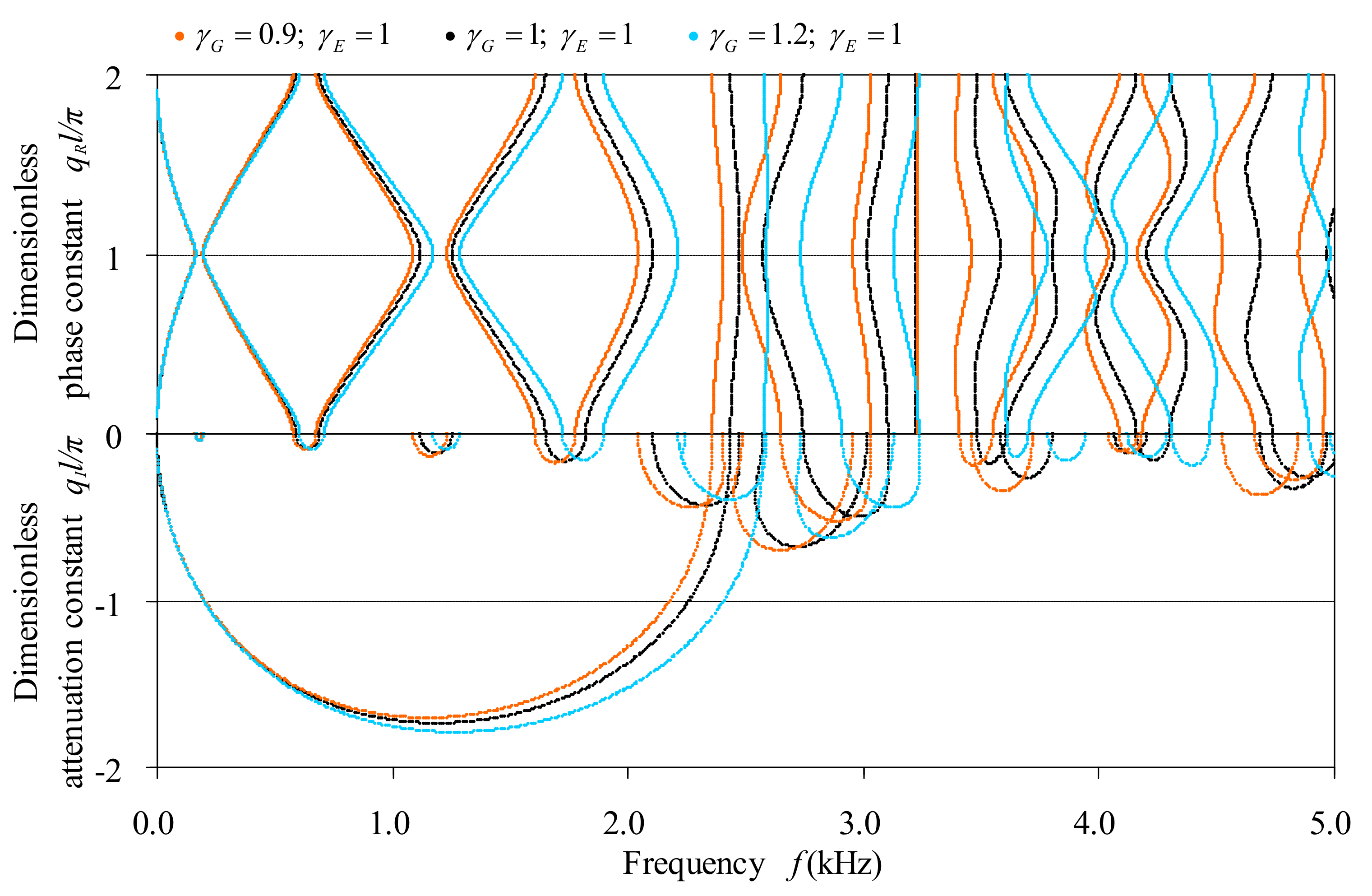
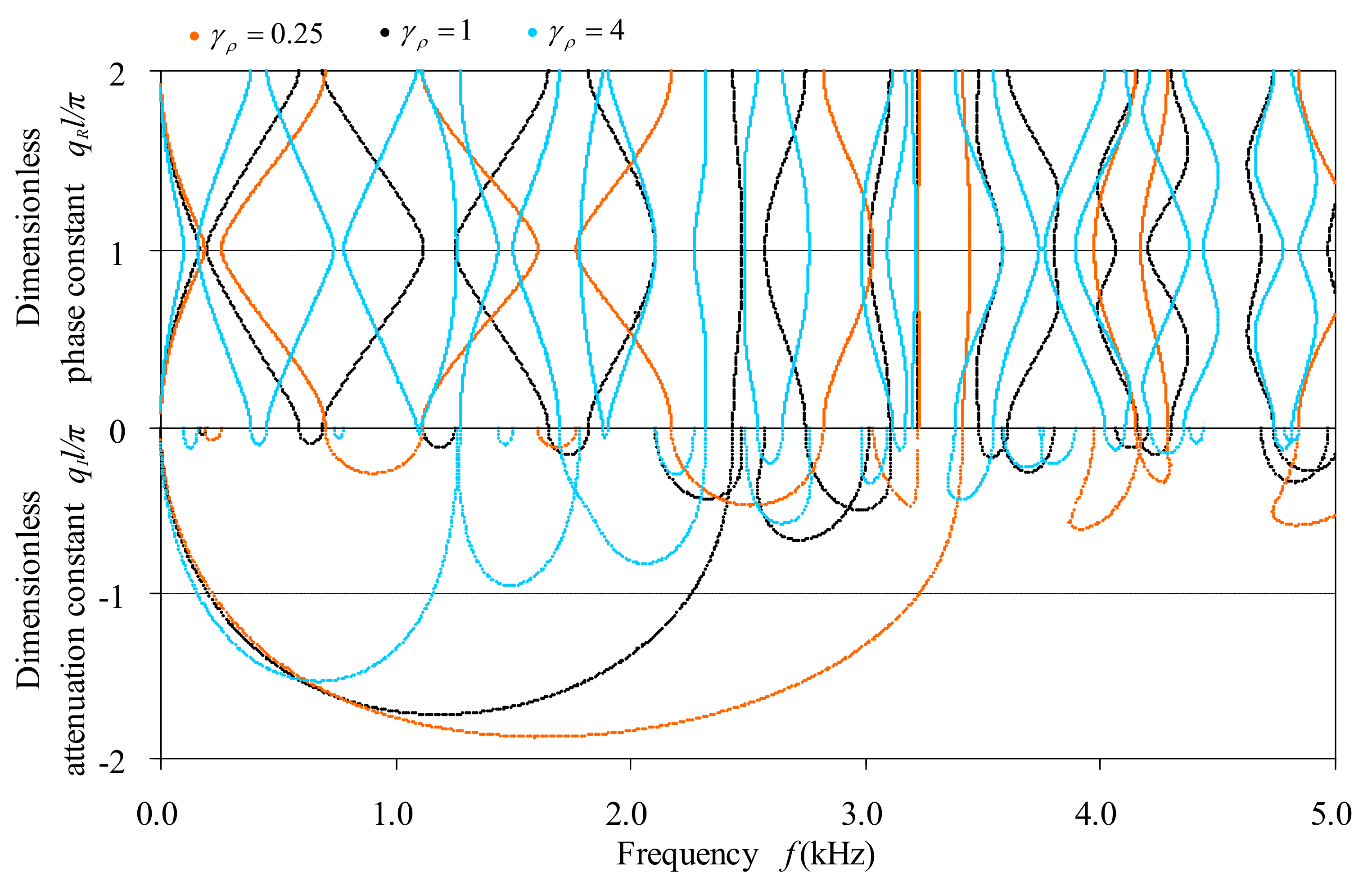
3.4.2. Effect of the Material Parameters of Constituent Beams on the Band Structures

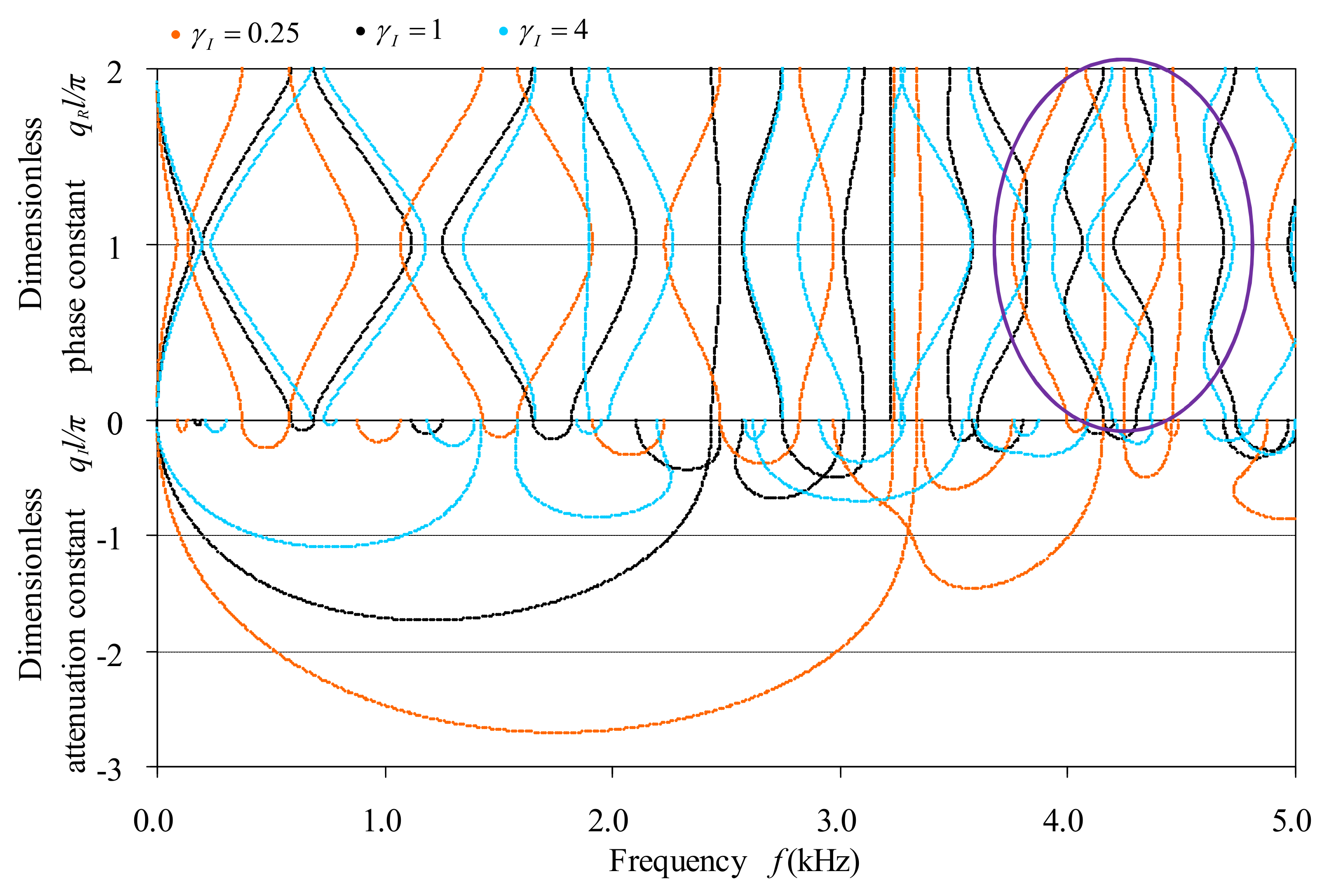
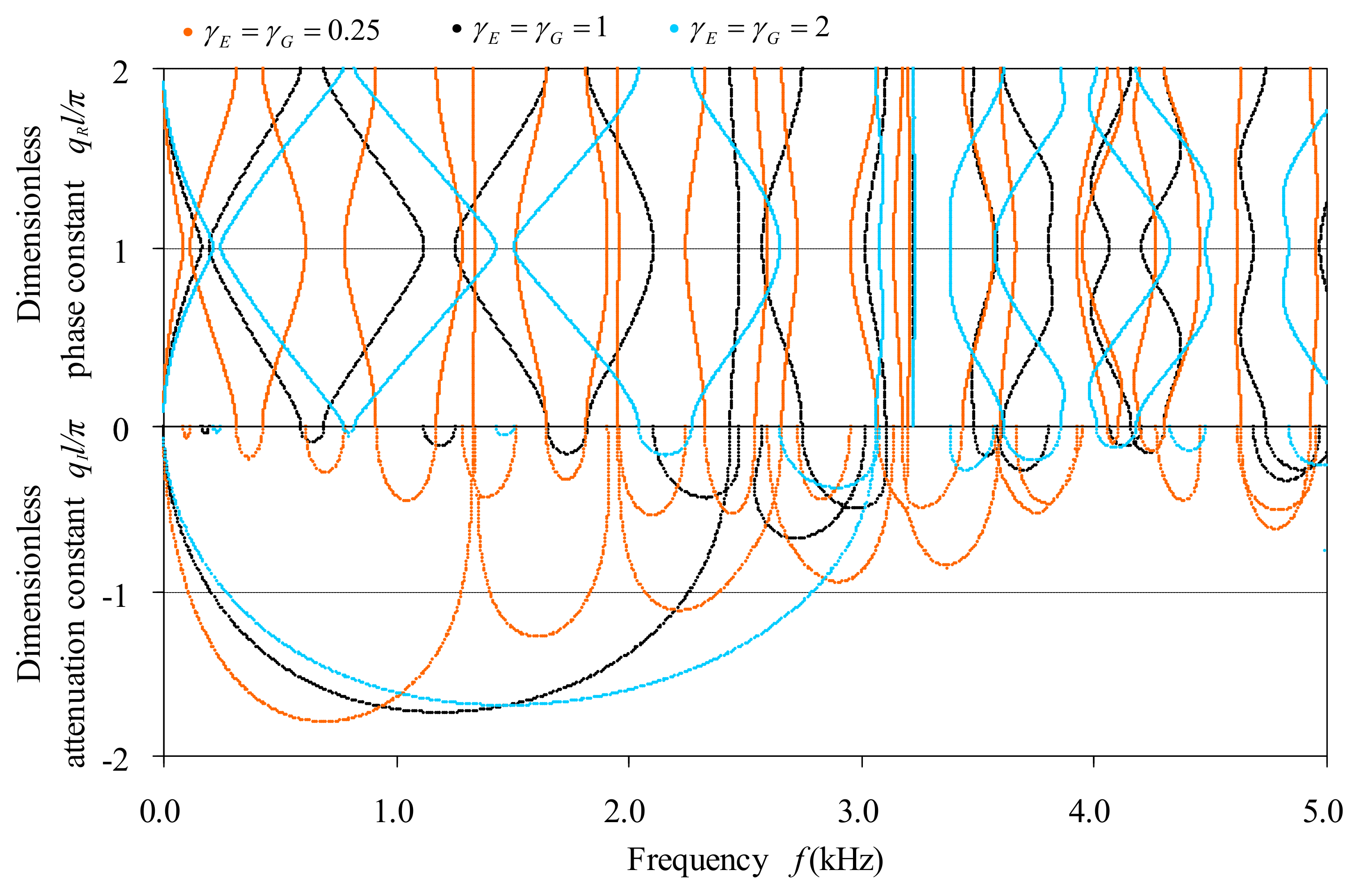
The material parameters involved include the Young’s modulus, the shear modulus and the mass density. The Young’s modulus and the shear modulus are not independent, and are related by the Poisson’s ratio. To inspect the effect of the modulus, we fixed the Poisson’s ratio and let both the Young’s modulus and the shear modulus change synchronously. The specified ratios are ${\gamma }_E={\gamma }_G=0.25$, ${\gamma }_E={\gamma }_G=1$ and ${\gamma }_E={\gamma }_G=2$, and the band structures of the corresponding periodic beams are depicted in Figure 11. To observe the effects of the Poisson’s ratio, the Young’s modulus remains fixed and the shear modulus changes, because the variation of the Poisson’s ratio is equivalent to changing the shear modulus as the Young’s modulus fixes. Three cases of the shear modulus are considered, i.e., ${\gamma }_G=0.9$, ${\gamma }_G=1$ and ${\gamma }_G=1.2$, with the corresponding band structures provided in Figure 12. For the sake of investigating the effect of mass density on the band structures, the ratio of mass density ${\gamma }_{\rho }$ is assumed as ${\gamma }_{\rho }=0.25$, ${\gamma }_{\rho }=1$ and ${\gamma }_{\rho }=4$ with the corresponding band structures shown in Figure 13.

In general, Figure 11, Figure 12 and Figure 13 indicate that the decreasing of modulus, the decreasing of Poisson’s ratio and the increasing of density have similar effects on the variation of band structures of bending waves in bi-coupled periodic multi-component beams, which are also similar to the increasing of cross-sectional area and the decreasing of cross-sectional inertia moment as these figures are compared to Figure 9 and Figure 10. In the cases of these changes, the first pass-bands all appear at higher frequency and the phase spectra all become sparser in a specified frequency range. From the attenuation constant spectra, it is indicated that not only the central frequencies and widths of the stop-bands but also the attenuation values in the stop-bands are influenced by these changes.

3.4.3. Effect of the Unit-Cell Configuration on the Band Properties

Just as the comparisons of the results in Section 3.3 have indicated, the five bi-coupled periodic beams have quantitatively and slightly different dispersion curves and band properties, which exactly reflect the influence of the unit-cell configuration.

Table 3. The bounding frequencies of the first 10 pass-bands of bending waves in the five exemplified bi-coupled periodic multi-component beams.

Pass-Bands		Periodic Binary Beams		Periodic Ternary Beams		Periodic Quaternary Beam
Order	Bounding Frequencies (Hz)	Binary-I	Binary-II	Ternary-I	Ternary-II	Quaternary
First	Lower	0.00	0.00	0.00	0.00	0.00
	Upper	162.13	102.88	165.24	83.63	88.54
Second	Lower	171.35	126.66	196.46	107.72	141.59
	Upper	520.61	353.47	589.39	296.93	340.82
Third	Lower	731.37	484.77	690.65	472.36	497.86
	Upper	1052.51	686.77	1120.80	617.87	673.13
Fourth	Lower	1338.31	893.94	1253.65	885.74	937.24
	Upper	1684.79	1040.70	1650.56	984.39	1096.64
Fifth	Lower	1796.83	1348.76	1822.11	1335.82	1238.31
	Upper	2075.91	1500.30	2105.90	1443.82	1349.03
Sixth	Lower	2479.84	1515.88	2437.78	1525.62	1909.45
	Upper	2506.23	1535.84	2475.43	1541.03	1910.74
Seventh	Lower	2638.36	1713.27	2574.76	1648.44	2063.38
	Upper	2687.30	1863.85	2745.19	1735.87	2139.10
Eighth	Lower	2869.99	2038.70	3018.43	2038.54	2422.14
	Upper	3005.43	2203.39	3105.16	2110.07	2498.37
Ninth	Lower	3468.91	2203.39	3221.10	2234.20	2968.38
	Upper	3542.20	2268.12	3224.44	2262.24	3010.78
Tenth	Lower	3622.93	2540.88	3473.08	2545.36	3068.38
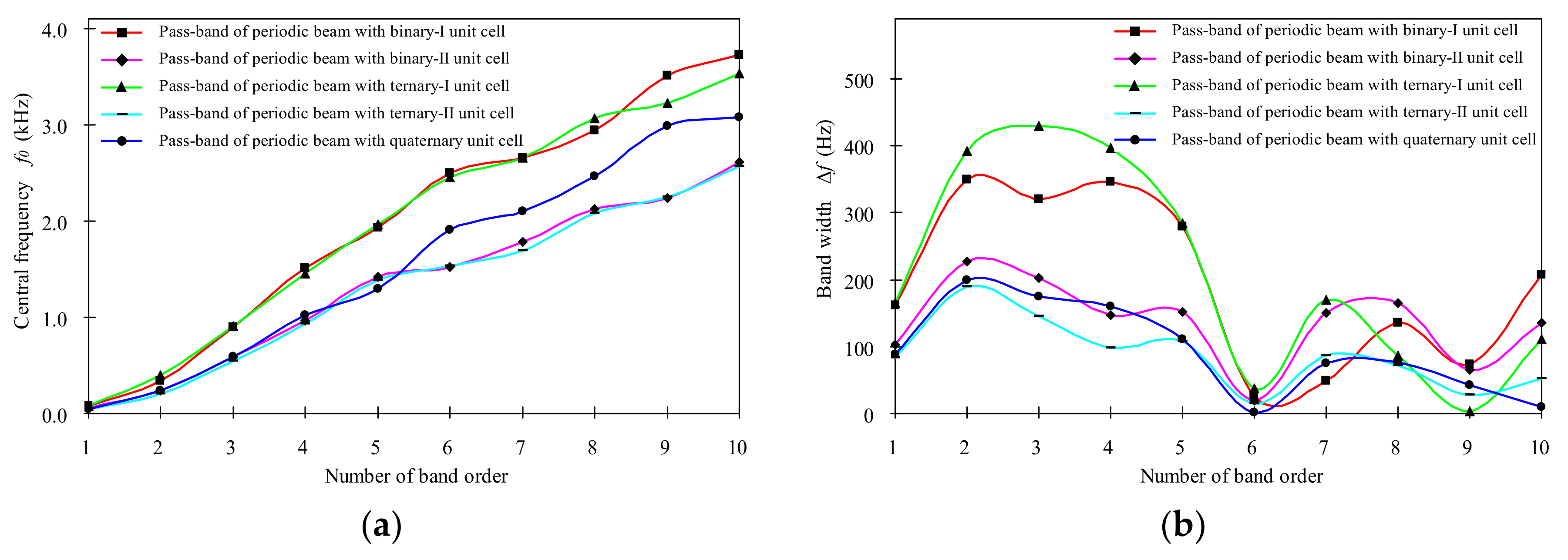
	Upper	3830.39	2677.25	3584.17	2597.76	3077.64

lists the bounding frequencies of the first 10 pass-bands, and the bounding frequencies of the first 10 stop-bands can be easily written out accordingly. Figure 14 shows the contrast of the central frequencies and the bandwidths of these pass-bands as the unit-cell configuration is the observing factor.

Figure 14 infers that the minimum bandwidth appears at the sixth pass-band for all the five periodic beams. From Table 3 and Figure 14, we see that the number and arrangement of constituent beams in the unit cell can be used to adjust the quantitative properties of the frequency bands, which provides an effective way for designing and optimizing bi-coupled periodic multi-component beams according to specific wave-controlling requirements in engineering practice.

4. Conclusions

The method of reverberation-ray matrix (MRRM) is formulated based on analytical beam theory and matrix operation for analyzing the dispersion characteristics of bending waves (coupled flexural and thickness-shear waves) in bi-coupled periodic multi-component beams. It entails a numerically well-condition so as to be an accurate and uniform method, especially applicable for relatively high frequency analysis, where the wavelength is still larger than the size of beam cross-section and where other methods often cease to be effective. Through plentiful numerical examples on the dispersion curves and band properties of bending waves in exemplified periodic multi-component beams, the proposed MRRM formulation has been validated and its advantages as compared to the classical transfer matrix method have been illustrated. Special attention is paid to the comprehensive dispersion characteristics represented as the relationship between any two among three in frequency, wavenumber (or wavelength) and phase velocity. The dependence of band structures (properties) on the geometrical and material parameters of the constituent beams and the unit-cell configuration are studied as well. The investigation in this paper leads to the following conclusions:

(1)

MRRM is an analytical method based on a distributed-parameter model and yields a unified formulation possessing a numerically well condition. It provides an alternative accurate method for analyzing bending waves in bi-coupled periodic multi-component beams. The method is effective as long as the adopted beam theory, such as the Timoshenko or Euler–Bernoulli beam theory, is valid for modeling the structural members. The advantages of MRRM as compared to TMM should be the consistently well-condition of MRRM, even in cases of relatively high frequency and long unit cell where TMM is ill-conditioned and may fail to give reasonable results.

(2)

Being different from the dispersion curves of longitudinal waves in periodic multi-component rods, essentially a kind of mono-coupled periodic structure, the dispersion curves of the bending waves in bi-coupled periodic multi-component beams no longer show alternately distributed pass-bands and stop-bands due to the existence of two characteristic wave modes. Pass-bands and stop-bands for both characteristic wave modes may arise due to the overlaps of the dispersion curves of different wave modes in the same regions. The wavenumber of the characteristic waves may be complex in some frequency ranges other than purely real or purely imaginary in other ranges. In some stop-bands, the attenuation constants may be multi-valued. The most innovative finding is that the bounding frequencies corresponding to the Brillouin zone boundary are not always the demarcations between the pass-band and stop-band. The cut-off phase velocity should be obtained by setting $ql=\pi$ rather than $ql=0$ (or $\omega =0$).

(3)

The cross-sectional area and the cross-sectional inertia moment as involved in the geometrical parameters, the modulus, the Poisson’s ratio and the density as involved on the material parameters, as well as the unit-cell configuration, all affect both the central frequencies and the widths of the frequency bands. In particular, the increasing (decreasing) of the cross-sectional area and the density have similar effects on the variation of band structures with the decreasing (increasing) of the cross-sectional inertia moment, the modulus and the Poisson’s ratio, which all push the band structures toward the lower frequency side and vice versa. The unit cell configuration does have an effect on the band structures and properties, but there seems not to be any general influence rule. All these findings can guide the adjustment of bending wave propagation/attenuation characteristics.

In summary, we believe the presented MRRM and the deep understanding of bending-wave dispersion curves in this paper will push forward the quantitative design and optimization of bi-coupled periodic multi-component beams for wave filtering and vibration isolation applications.