The NARX Model-Based System Identification on Nonlinear, Rotor-Bearing Systems

Abstract

In practice, it is usually difficult to obtain the physical model of nonlinear, rotor-bearing systems due to uncertain nonlinearities. In order to solve this issue to conduct the analysis and design of nonlinear, rotor-bearing systems, in this study, a data driven NARX (Nonlinear Auto-Regressive with exogenous inputs) model is identified. Due to the lack of the random input signal which is required in the identification of a system′s NARX model, for nonlinear, rotor-bearing systems, a new multi-harmonic input based model identification approach is introduced. Moreover, the identification results of NARX models on the nonlinear, rotor-bearing systems are validated under different conditions (such as: low speed, critical speed, and over critical speed), illustrating the applicability of the proposed approach. Finally, an experimental test is conducted to identify the NARX model of the nonlinear rotor test rig, showing that the NARX model can be used to reproduce the characteristics of the underlying system accurately, which provides a reliable model for dynamic analysis, control, and fault diagnosis of the nonlinear, rotor-bearing system.

1. Introduction

The rotor-bearing system is the main component of large-scale, rotatable equipment such as, e.g., aircraft engines and gas turbines, etc., and most of the rotor-bearing systems are significantly affected by nonlinearities [1]. In order to investigate the properties of nonlinear, rotor-bearing systems, mathematical models are important [2]. The mathematical models can generally be divided into two categories: the numerical model and the physical model [3]. For nonlinear, rotor-bearing systems, the systems are usually simplified into physical models based on mechanical or electrical-related theories [4,5]. For example, Hu et al. [6] established a 5 degree of freedom (5DOF) physical model about the aircraft engine spindle dual-rotor system. Zhou and Chen [7] introduced a dual rotor-ball and bearing-stator coupling dynamic system. However, those physical models are relatively simple to describe complex, nonlinear, rotor-bearing systems such as, e.g., large centrifugal compressors and steam turbines, etc., where strong nonlinearities have to be taken into account [8]. Moreover, in practice, it is also difficult to establish the physical model of a system due to its complexity and the lack of physical knowledge [9]. Fortunately, it is possible to build a data-driven model by using only input and output signals, which is widely applied in system analysis, design, and control for the advantages of efficiency and the capacity of tracking changes of the system [10].

In 1980s, the NARX (Nonlinear Auto-Regressive with Exogenous Inputs) model was introduced by Billings as a new representation for a wide class of discrete, nonlinear systems [11]. The Volterra series model [12], the block-structured model [13], and many neural network architectures [14] can all be considered as subsets of the NARX model [15]. In practice, many systems have been investigated by using the NARX model [16,17,18]. For example, Peng et al. [19] established a NARX model of aluminum plate with structure damage and then detected the location of damage by frequency domain analysis, which provided a theoretical support for structural damage detection in practical engineering. Besides, the NARX model can also be used in other industrial scenarios such as modeling the large horizontal axis wind turbine [20] and large horizontal lathes [21]. Considering the nonlinear, rotor-bearing system, Tang et al. [22] established a Volterra series model by using date sets of the vibration response under different positions; based on this model, the fault modes were identified. Jiang et al. [23] developed the Volterra series model to detect the crack of the two discs in the rotor-bearing system.

In general, a random signal is selected as the system input in the traditional NARX modeling process. This is because the random signal contains different frequency and amplitude characteristics, and by using this, different properties of the system can be tested when the knowledge about system parameters and model structures is absent [24]. However, in practice, it is impossible to produce random input excitations when identifying rotor-bearing systems [25]. To address the aforementioned issue, in this study, a multi-harmonic signal generated by a speed-up process is applied as the system input to establish the NARX model. Moreover, a new approach to determine the NARX model by using the speed-up harmonic signal is introduced. Many researchers have analyzed the rotor-bearing system based on the speed-up process. For example, Li et al. [26] and Zhu et al. [27] extracted fault features of the rotor-bearing system by using the speed-up process, based on which the fault modes were identified. In this paper, the approach of identifying the NARX model of the nonlinear, rotor-bearing system is proposed by using the speed-up harmonic signal. The accuracy of the identified model is validated by using both numerical and experimental methods, and the results indicate that the NARX model of the nonlinear, rotor-bearing system can be used to represent different system characteristics, which contribute to the analysis, design, and fault diagnosis of the rotor-bearing system.

This paper is organized as follows. In Section 2, a typical nonlinear, rotor-bearing system is established and the inherent characteristics of the system are revealed. Section 3 introduces a new approach of identifying the NARX model of nonlinear systems based on a multi-harmonic input, which is discussed under different working conditions (such as: low speed, critical speed, and over critical speed). The NARX model is evaluated by two different validation methods and an error criterion. An experimental validation is discussed in Section 4, in which a test rig connected with the Labview test system and two eddy current displacement sensors are used. Finally, the three main conclusions are presented in Section 5, which provide an efficient method for numerical modeling of nonlinear, rotor-bearing system.

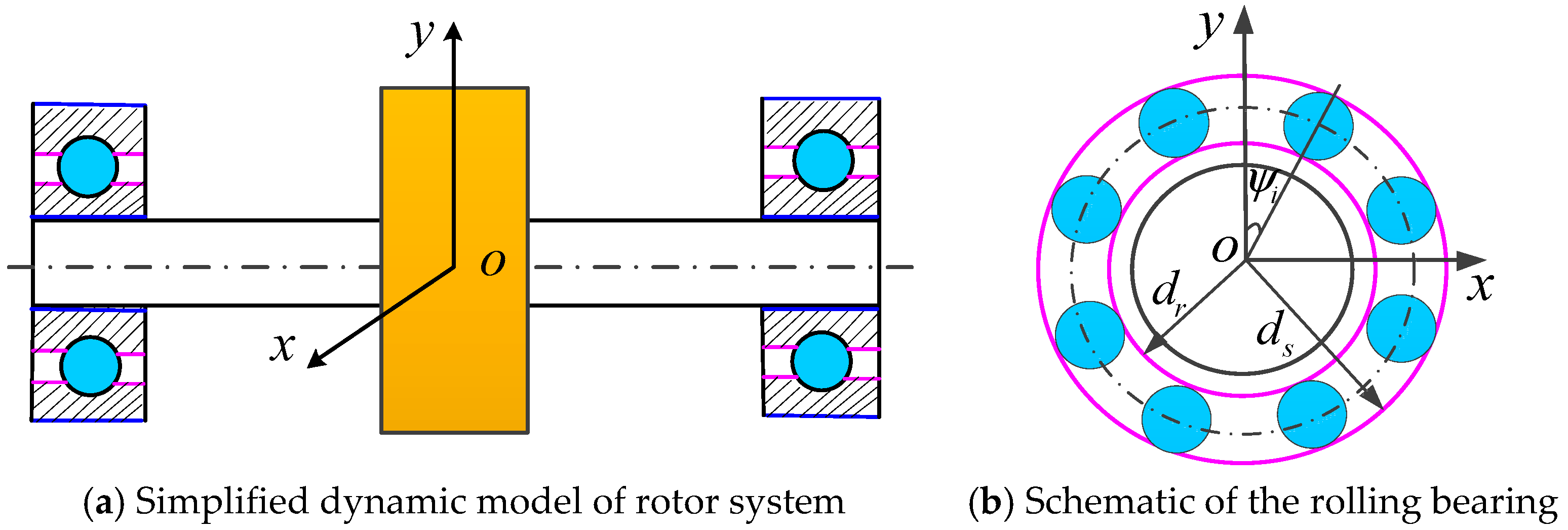
2. Nonlinear, Rotor-Bearing System Structure

2.1. System Structure

Considering the nonlinear contact force, the rotor-bearing system, placed horizontally with an unbalanced disc, is simplified (as the rotor is rigid) and supported by two symmetrical rolling bearings with the same parameters.

A simplified dynamic model of the rotor system is shown in Figure 1a, while the schematic of the rolling bearing is shown in Figure 1b. In Figure 1a, x-axis is the horizontal direction, and y-axis is the vertical direction; and in Figure 1b, $d_s,$ and $d_r$ are the diameters of the outer race and inner race, respectively, and ${\psi }_i$ is the angle location of the ith ball.

The dynamic differential equation of the rotor-bearing system in Figure 1 can be defined as:

$$\{\begin{array}{c}m\ddot{x}+C\dot{x}+F_x=me{\omega }^2\sin \left(\omega t\right)\\ m\ddot{y}+C\dot{y}+F_y=me{\omega }^2\cos \left(\omega t\right)+F^{\prime }\end{array}$$

(1)

where $m$ is the equivalent mass of the rotor and the inner race at the disc; $C$ is the damping coefficient of the rotor at the disc and rolling bearing; $\omega$ is the rotor angular velocity; $F\text{'}$ is the sum of the radial external force and the gravity of the rotor; $e$ is the rotor eccentricity distance; and $F_x,F_y$ are the supporting force components in the x and y directions, respectively. According to Hertzian contact theory, the forces generated from the rolling bearing are defined as [28]:

$$\{\begin{array}{c}{F}_x=K_b{\displaystyle {\displaystyle \sum }_{i=1}^{N_b}}{\left(y\cos {\phi }_i+x\sin {\phi }_i-{\gamma }_0\right)}^{1.5}\sin {\phi }_i\\ F_y=K_b{\displaystyle {\displaystyle \sum }_{i=1}^{N_b}}{\left(y\cos {\phi }_i+x\sin {\phi }_i-{\gamma }_0\right)}^{1.5}\cos {\phi }_i\end{array}$$

(2)

where $K_b$ represents the Hertzian contact stiffness; ${\gamma }_0$ is the rolling bearing radial clearance; and $y\cos {\phi }_i+x\sin {\phi }_i-{\gamma }_0$ is the contact deformation between the ith ball and the races. Also, the ith ball angle location ${\phi }_i$ is:

$${\phi }_i=\frac{2\pi }{N_b}\left(i-1\right)+\frac{d_r}{d_r+d_s}\omega t$$

(3)

where $N_b$ is the number of balls of the rolling bearing.

2.2. System Inherent Characteristics

In system (1), given m = 1 kg, C = 200 Ns/m, $K_b$ = 7.055 × 10⁵ N/m, $N_b$ = 9, e = 2 mm, $d_s$ = 28.262 mm, $d_r$ = 18.783 mm, ${\lambda }_0$ = 3 × 10⁻⁴ m. The first-order critical speed of the system can be obtained as ${\omega }_0$ = 320 rad/s, which is shown in Figure 2.

Three cases of the low speed ($\omega$ = 100 rad/s), the critical speed ($\omega$ = 320 rad/s), and the over critical speed ($\omega$ = 500 rad/s) are discussed separately, as follows. The time domain and frequency domain responses of the rotor-bearing system are shown in Figure 3, Figure 4 and Figure 5, respectively.

As can be seen from Figure 3, Figure 4 and Figure 5, the second harmonics is the significant component under the three cases due to the effect of the nonlinear bearing force. Therefore, in the following section, the NARX model to the second order is identified based on the nonlinear, rotor-bearing system.

3. NARX Model on the Rotor-Bearing System

3.1. Identification of the NARX Model

A broad range of nonlinear systems can be described using NARX models, which can be expressed as [29]:

$$y\left(k\right)=F\left[y\left(k-1\right)\cdots ,y\left(k-n_y\right),u\left(k-1\right),\cdots u\left(k-n_u\right)\right]$$

(4)

where $F\left[\right]$ is some nonlinear function, $n_y$ and $n_u$ are the maximum time lag for the system output and input, respectively, and $y\left(k\right)$ and $u\left(k\right)$ are the output and input sequence of the system, respectively.

The NARX model has several forms, among which the power polynomial representation is most commonly used in nonlinear system identification. Function $F$ in equation (4) is defined as the following polynomial expression:

$$\begin{gathered} y\left(k\right)={\theta }_0+{\displaystyle \sum }_{i_1=1}^n{\theta }_{i_1}{x}_{i_1}\left(k\right)+{\displaystyle \sum }_{i_1=1}^n{\displaystyle \sum }_{i_2=i_1}^n{\theta }_{i_1}{\theta }_{i_2}{x}_{i_1}\left(k\right)x_{i_2}\left(k\right)+\cdots \\ +{\displaystyle \sum }_{i_1=1}^n\cdots {\displaystyle \sum }_{i_l=l-1}^n{\theta }_{i_1{i}_{2\cdots }{i}_l}{x}_{i_1}\left(k\right)x_{i_2}\left(k\right)\cdots x_{i_l}\left(k\right) \end{gathered}$$

(5)

where:

$$x_m\left(k\right)=\{\begin{array}{c}y\left(k-m\right)1\le m\le n_y\\ u\left(k-\left(m-n_y\right)\right)n_y+1\le m\le n_y+n_u\end{array}$$

(6)

where ${\theta }_i$ are model coefficients; $L$ is the degree of polynomial nonlinearity; n = $n_u$ + $n_y$.

Consider a generic linear-in-parameters representation of model (5) as:

$$y\left(k\right)={\displaystyle \sum }_{m=1}^M{\theta }_m{p}_m\left(k\right)$$

(7)

where ${\theta }_m$ is the model coefficient of the mth term; $M$ is the number of all possible model terms, M = (n + l)!/(n!l!); $p_m\left(k\right)$ is the regression which is formed by some combinations of the predetermined model variables, which are orderly chosen from the following vector $x\left(k\right)=\left[1,y\left(k-1\right),L,y\left(k-n_y\right),u\left(k-1\right),L,u\left(k-n_u\right)\right]$.

The NARX model can be obtained by using FROLS (Forward Regression Orthogonal Least Squares) algorithm [30], which is a recursive algorithm based on ERR (Error Reduction Ratio) criterion to select significant model terms. The steps of FROLS are as follows:

● Step 1: Orthogonalization of model:

The NARX model (7) can be rewritten into a matrix form:

$$y=P\theta$$

(8)

where $P=\left[p_1,p_2,L,p_M\right]$ is the regression matrix with the column vectors $p_m={\left[p_m\left(1\right),L,p_m\left(N\right)\right]}^T,\left(m=1,L,M\right)$ which consist of the values $p_m\left(k\right),\left(m=1,K,N\right)$ over the time history; $N$ is the number of sampling observations; $\theta ={\left[{\theta }_1,{\theta }_2,L,{\theta }_M\right]}^T$ is the coefficient vector.

Based on the Schmidt′s orthogonalization, the model (8) can be orthogonalized into [15]:

$$y=P\theta =WG$$

(9)

where $W=\left[w_1,w_2,L,w_M\right]$ is the orthogonalized matrix of $P,G={\left[g_1,g_2,L,g_M\right]}^T$ is the corresponding coefficients vector, where:

$$w_m=p_m-{\displaystyle \sum }_{i=1}^{m-1}\frac{<p_m,w_i>}{<w_i,w_i>}{w}_i$$

(10)

$$g_m=\frac{<y,w_m>}{<w_m,w_m>}$$

(11)

● Step 2: Model term selection:

A.

Given $w_m^{\left(1\right)}=p_m$, where the superscript (1) represents the first selecting step. $g_m^{\left(1\right)}$ can be calculated based on Equation (11).

The ERR value of the mth model term is given as [31]:

$$ER{R}_m^{\left(1\right)}=\frac{{(g_m^{\left(1\right)})}^2<w_m^{\left(1\right)},w_m^{\left(1\right)}>}{<y,y>}\times 100\%$$

(12)

Then obtain the column $S_{1,}$ which has the largest ERR value:

$$s_1=argmax\left\{ER{R}_m^{\left(1\right)}\right\},1\le m\le M$$

(13)

where $\arg max\left\{\right\}$ represents the value of the argument when the function reaches the maximum.

Given the corresponding term vector as the first model term vector of the orthogonalized matrix in (9), which means $w_1=w_{S_1}^{\left(1\right)}$, and given ${\beta }_1=p_{S_1}$.

B.

When the selection goes to step l, define $m\ne S_1{{\displaystyle \cap }}^{\text{}}m\ne S_2{{\displaystyle \cap }}^{\text{}}L{{\displaystyle \cap }}^{\text{}}m\ne S_{l-1}$, and based on the selected orthogonalized model term vectors $\widetilde{w_1},\widetilde{w_2},\cdots \widetilde{w_{l-1}}$, the lth model term vector is given as:

$$w_m^{\left(l\right)}=p_m-{\displaystyle \sum }_{i=1}^{l-1}\frac{<p_m,\widetilde{w_i}>}{<\widetilde{w_i},\widetilde{w_i}>}\widetilde{w_i}$$

(14)

The ERR value of each vector and the one with maximum ERR value are obtained as:

$$ER{R}_m^{\left(l\right)}=\frac{{(g_m^{\left(l\right)})}^2<w_m^{\left(l\right)},w_m^{\left(l\right)}>}{<y,y>}\times 100\%$$

(15)

$$s_l=argmax\left\{ER{R}_m^{\left(l\right)}\right\}$$

(16)

Based on (16), one obtains the lth model term vector of the orthogonalized matrix in (9), which means $w_l=w_{S_l}^{\left(l\right)}$, and given ${\beta }_l=p_{S_l}$.

C.

The algorithm will stop selecting at the M’th step when the model structure satisfies the following condition:

$$1-{\displaystyle \sum }_{i=1}^{M^{\prime }}\left\{ER{R}_{l_i}^{\left(i\right)}\right\}\le \rho$$

(17)

where $\rho$ is the threshold; M’ represents the total number of the selected model terms.

Based on (15)–(17), the M’th selected model term is given as $w_{M\prime }=w_{S_{M\prime }}^{\left(M\prime \right)}$.

The orthogonalized NARX model is given as:

$$y={\displaystyle \sum }_{i=1}^{M^{\prime }}\widetilde{w_i}\widetilde{g_i}$$

(18)

● Step 3: Calculation of model coefficients:

Based on (18), the final NARX model can be written as [15]:

$$y={\displaystyle \sum }_{i=1}^{M^{\prime }}{\beta }_i\widetilde{{\theta }_i}$$

(19)

where:

$$\widetilde{{\theta }_i}=\widetilde{g_i}-{\displaystyle \sum }_{n=i+1}^{M^{\prime }}\frac{<{\beta }_n,\widetilde{w_i}>}{<\widetilde{w_i},\widetilde{w_i}>}\widetilde{{\theta }_n},1\le i\le M^{\prime },i+1\le n\le M^{\prime }$$

(20)

As for model validation, there are two different methods, defined as OSA (One Step Ahead) and MPO (Model Predicted Output). It is difficult to give a general conclusion as to method should be used in a specific situation [32].

The concept of OSA validation can be explained by using a simple second-order NARX model:

$$y\left(k\right)=ay\left(k-1\right)+by\left(k-2\right)+cu\left(k-1\right)y\left(k-1\right)$$

(21)

Assume that a number of values if system input u(k) and y(k) are available. The OSA validation processes, starting from step 3, are then given as:

$$\{\begin{array}{c}\widehat{y}\left(3\right)=ay\left(2\right)+by\left(1\right)+cu\left(2\right)y\left(2\right)\\ ⋮\\ \widehat{y}\left(k\right)=ay\left(k-1\right)+by\left(k-2\right)+cu\left(k-1\right)y\left(k-1\right)\end{array}$$

(22)

By comparison, the calculation of model output by the MPO method is completely different from the OSA method. Consider again the NARX model (21), for which the MPO can be defined as:

$$\{\begin{array}{c}\widehat{y}\left(1\right)=y\left(1\right)\\ \widehat{y}\left(2\right)=y\left(2\right)\\ ⋮\\ \widehat{y}\left(k\right)=a\widehat{y}\left(k-1\right)+b\widehat{y}\left(k-2\right)+cu\left(k-1\right)\widehat{y}\left(k-1\right)\end{array}$$

(23)

In this paper, the results are evaluated by time domain and spectrum graph, as well as RMSE (root mean square error (RMSE). The RMSE is given as:

$$RMSE=\surd \frac{{{\displaystyle \sum }}_{i=1}^N{\left(\widehat{y_i}-y_i\right)}^2}{N}$$

(24)

where $\widehat{y_i}$ and $y_i$ are the predicted output and actual output, respectively; N is the number of sampling observations.

3.2. NARX Model Subjected to Multi-Harmonic Excitation

NARX approach is used in the system identification of the rotor-bearing system which is shown in Figure 1, where the system is subjected to unbalanced force $me{\omega }^2\sin \left(\omega t\right)$ in the horizontal direction. Considering the advantages of the speed-up process which have been discussed in the introduction, the multi-harmonic signal $\sin \left(\omega t\right),\omega \in \left[1,450\right]$ rad/s is defined as the system input excitation, and the output of the system is defined as the horizontal vibration response of the unbalanced disc.

The NARX model for the rotor-bearing system in Figure 1 is identified as:

$$\begin{array}{c}y\left(k\right)={\displaystyle \sum }_{i=1}^{15}{\beta }_i\left(k\right)\widetilde{{\theta }_i}\\ =1.5806y\left(k-1\right)-0.4635y\left(k-2\right)+2.9713\times {10}^{-4}u\left(k-2\right)+\cdots \\ -8.0035\times {10}^{-4}u\left(k-9\right)u\left(k-9\right)\end{array}$$

(25)

The 15 selected model terms, ranked in order of significance, are shown in

Table 1. Identification result of the example.

Step	Term	Coefficient	ERR%
1	$y\left(k-1\right)$	1.5806	89.2521
2	$y\left(k-2\right)$	−0.4635	10.3201
3	$u\left(k-2\right)$	2.9713 × 10−4	0.0963
4	$y\left(k-6\right)$	0.0931	0.0349
5	$u\left(k-7\right)$	−2.2028 × 10−4	0.0227
6	$u\left(k-1\right)$	−3.7178 × 10−4	0.0158
7	$y\left(k-1\right)y\left(k-5\right)$	−5.3027	0.0119
8	$y\left(k-3\right)$	−0.2637	0.0052
9	$y\left(k-9\right)$	−0.0418	0.0078
10	$u\left(k-3\right)$	3.2374 × 10−4	0.0021
11	$u\left(k-9\right)$	1.8632 × 10−4	0.0023
12	$y\left(k-2\right)u\left(k-1\right)$	−0.0091	0.0008
13	$y\left(k-5\right)u\left(k-7\right)$	0.0301	0.0009
14	$u\left(k-8\right)$	−1.7955 × 10−4	0.0004
15	$u\left(k-9\right)u\left(k-9\right)$	−8.0035 × 10−4	0.0004
Total	-	-	99.7728

.

In the following study, the NARX model (25) is validated under the excitations of the low speed ($\omega$ = 100 rad/s), the critical speed ($\omega$ = 320 rad/s), and the over critical speed ($\omega$ = 500 rad/s), respectively. The predicted output responses by the NARX model are compared with the simulation results in both the time and the frequency domain. Moreover, the OSA and the MPO methods are also discussed. The results are shown in Figure 6, Figure 7 and Figure 8. Also, the model is also evaluated by RMSE, which is shown in

Table 2. Root square mean error (RMSE) of MPO and OSA method in a large frequency range.

Frequency Range (rad/s)	RMSE of MPO Method (m)	RMSE of OSA Method (m)
Low speed	3.1582 × 10−6	2.9461 × 10−7
Critical speed	5.2704 × 10−6	4.7590 × 10−7
Over critical speed	1.4032 × 10−6	2.0754 × 10−6

.

Figure 6, Figure 7 and Figure 8 and Table 2 indicate that the NARX model over a wide frequency range can be accurately predicted by using the OSA method. However, by using the MPO method, the output predictions have significant errors over the whole frequency range. Therefore, in practice, the NARX model identified over a wide frequency range cannot be used to reproduce the structure of the nonlinear, rotor-bearing system.

To address this issue, in the following study, NARX models are separately identified under, a more narrow frequency range, such as the low frequency range, the natural frequency range, or the high frequency range, respectively.

3.3. NARX Model under Different Frequency Ranges

In this section, three different NARX models are separately established by using the speed-up input signal over different frequency ranges, and the results are validated by using the MPO method, which indicates that the NARX model of the rotor-bearing system covering a relatively narrow frequency range can reflect the system characteristic accurately.

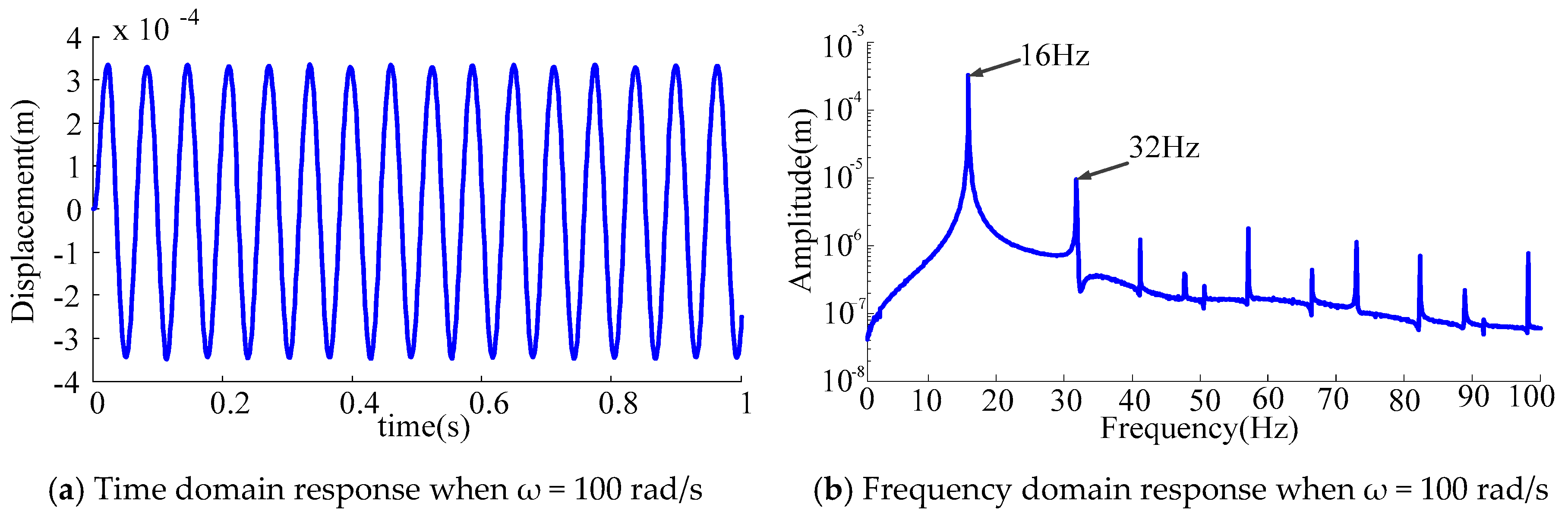
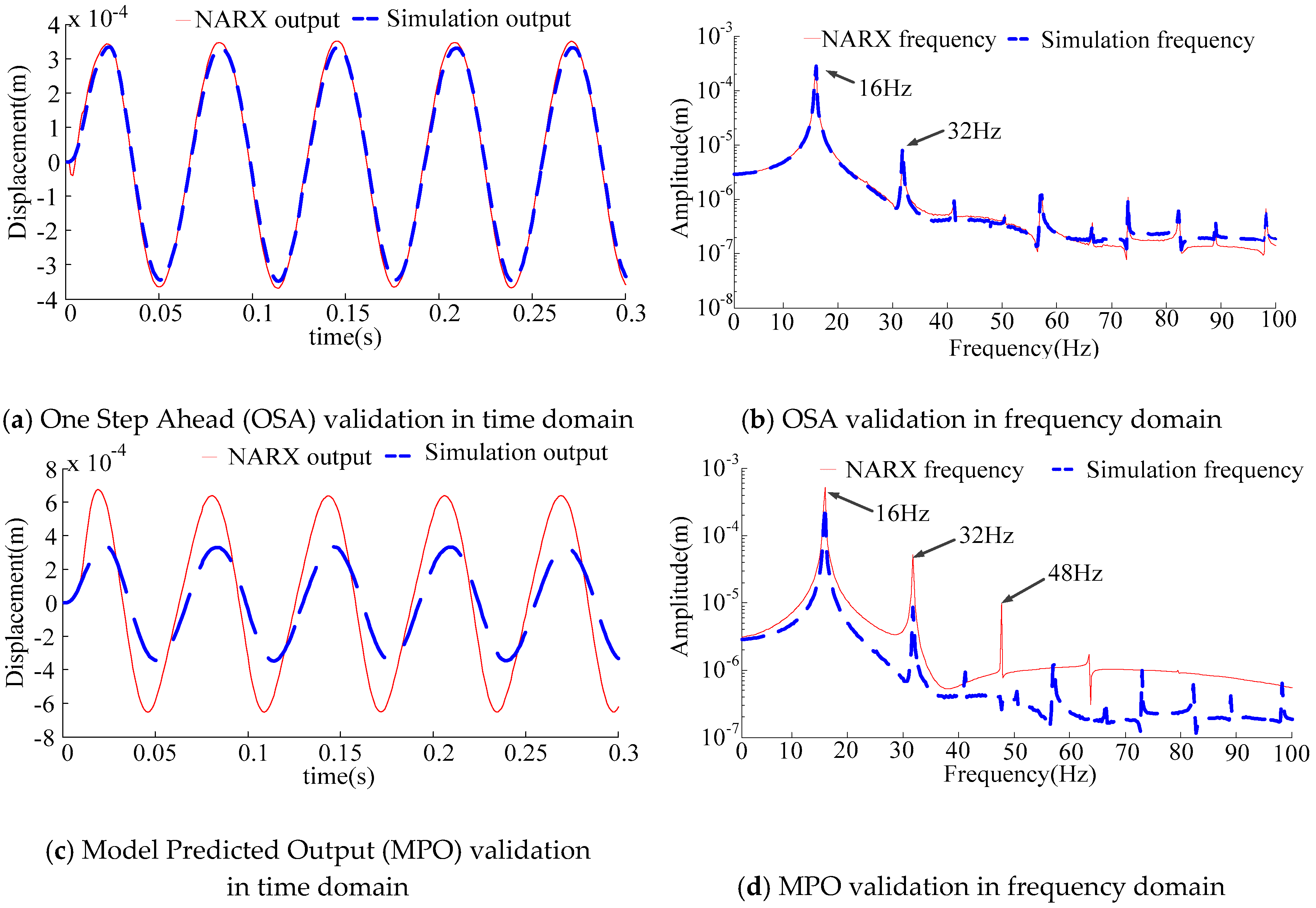
3.3.1 Under the Low-Speed Condition

When the input signal contains the frequency of ${\omega }_{low}\in \left[1,200\right]$ rad/s, the NARX model can be identified as:

$$\begin{array}{c}y\left(k\right)={\displaystyle {\displaystyle \sum }_{i=1}^{15}}{\beta }_i\left(k\right)\widetilde{{\theta }_i}\\ =1.36296y\left(k-1\right)-0.1352y\left(k-3\right)+4.5869\times {10}^{-5}u\left(k-3\right)\\ +\cdots -8.0035\times {10}^{-4}u\left(k-9\right)u\left(k-9\right)\end{array}$$

(26)

where the harmonic input with $\omega$ = 100 rad/s is used to test the model in both the time and the frequency domain, shown in Figure 9. Also, the RMSE is 9.0925 × 10⁻⁷ m.

Figure 9 indicates that the NARX model identified in the low frequency range provides a more accurate prediction result than that of (25). Also, the RMSE is better than 3.1582 × 10⁻⁶ m, which is presented in Table 2.

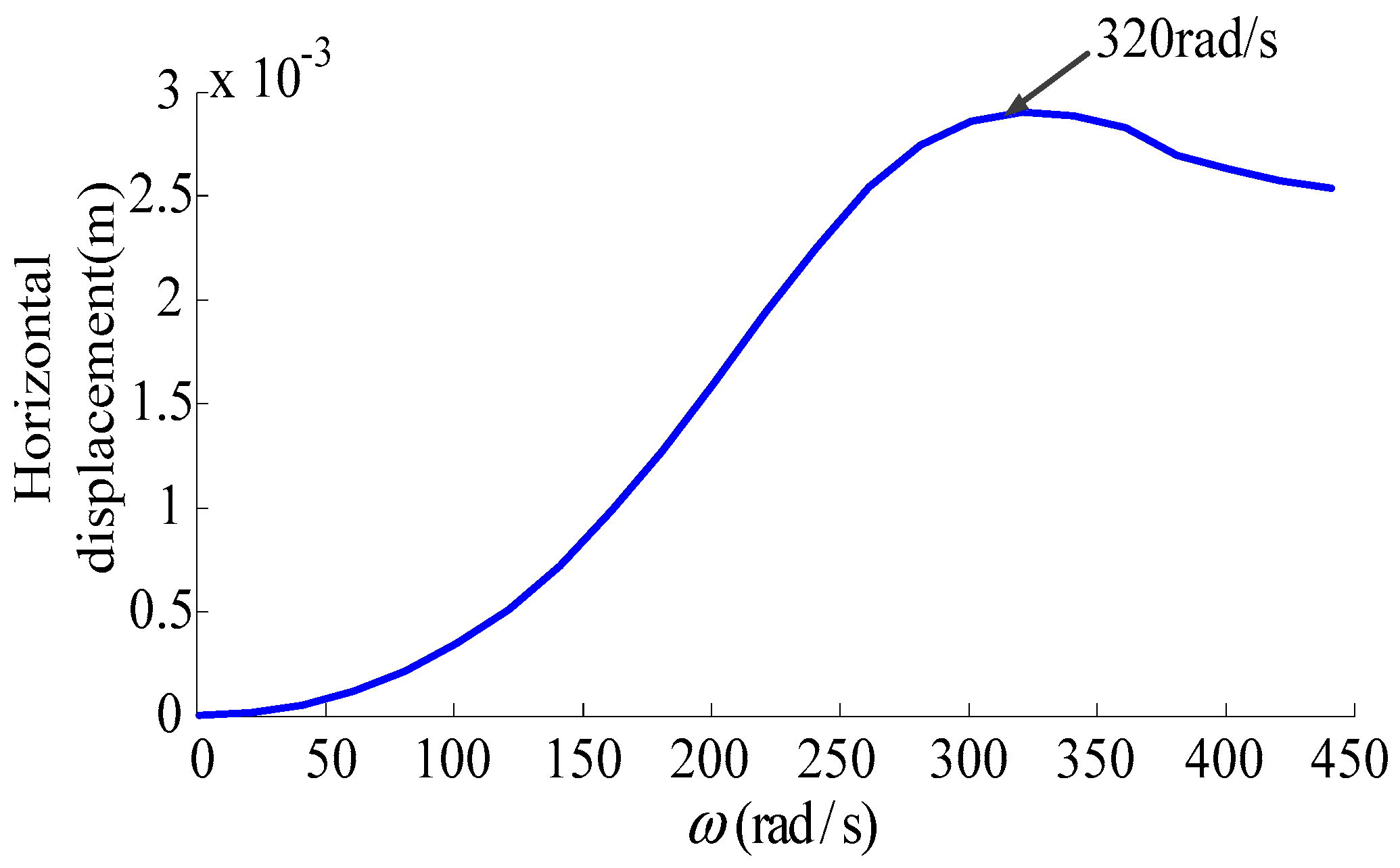
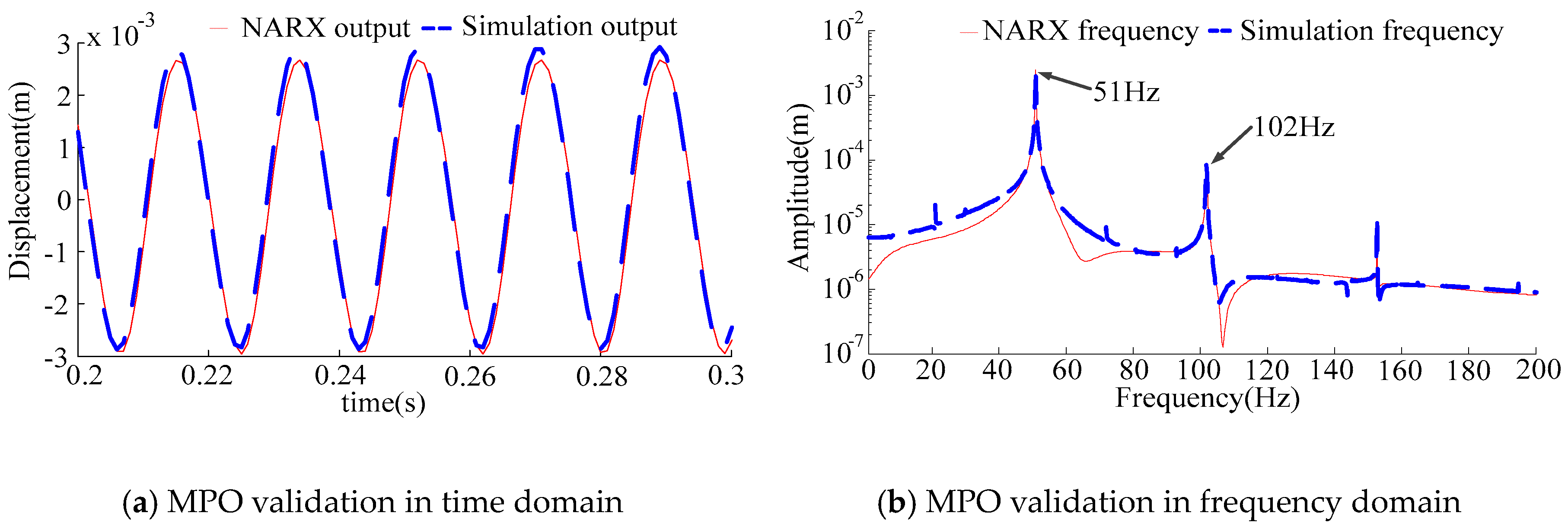
3.3.2 Under the Critical Speed Condition

When the input signal contains the frequency of ${\omega }_{critical}\in \left[200,350\right]$ rad/s, the NARX model can be identified as:

$$\begin{array}{c}y\left(k\right)={\displaystyle {\displaystyle \sum }_{i=1}^{15}}{\beta }_i\left(k\right)\widetilde{{\theta }_i}\\ =6.8641\times {10}^{-6}u\left(k-6\right)\\ +1.2448y\left(k-1\right)\\ +0.1446y\left(k-3\right)\cdots +6.3439\times y\left(k-7\right)y\left(k-7\right)\end{array}$$

(27)

where the harmonic input with $\omega$ = 320 rad/s is used to test the model in both the time and the frequency domain, shown in Figure 10. Also, the RMES is 2.4703 × 10⁻⁶ m.

Figure 10 indicates that the NARX model identified in the low frequency range provides a more accurate prediction result than that of (25). Also, the RMSE is smaller than 5.2704 × 10⁻⁶ m, which is shown in Table 2.

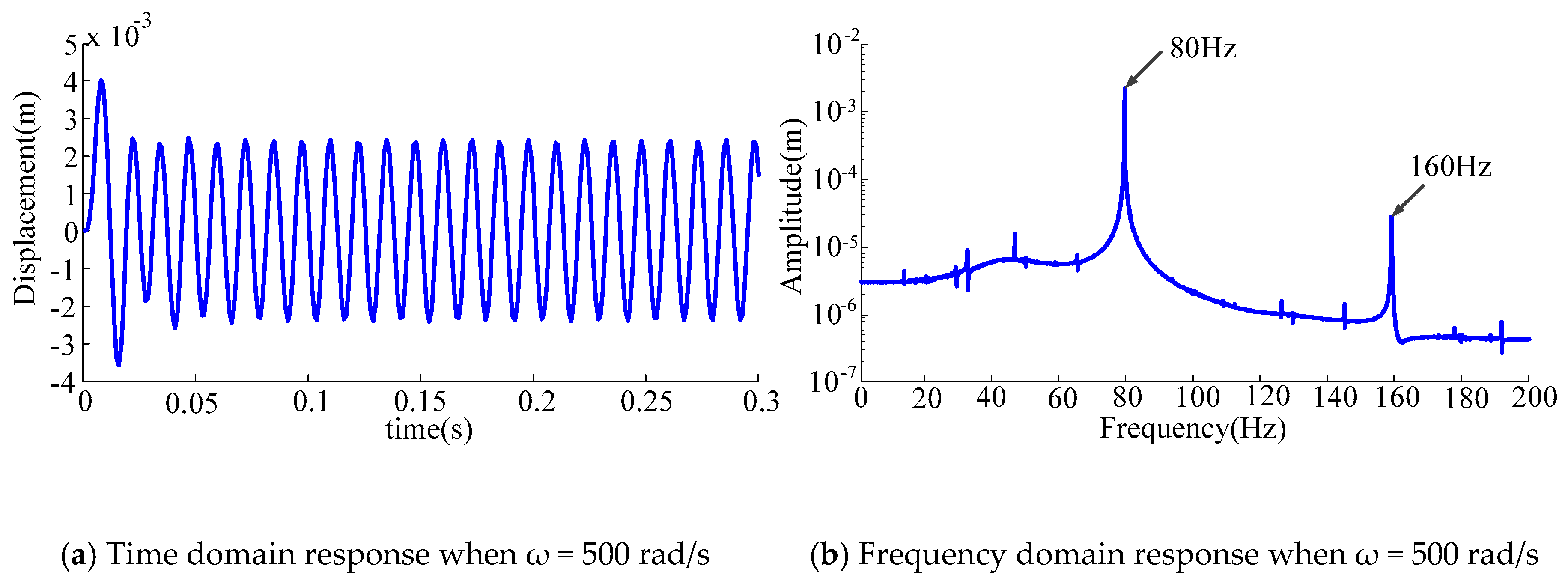
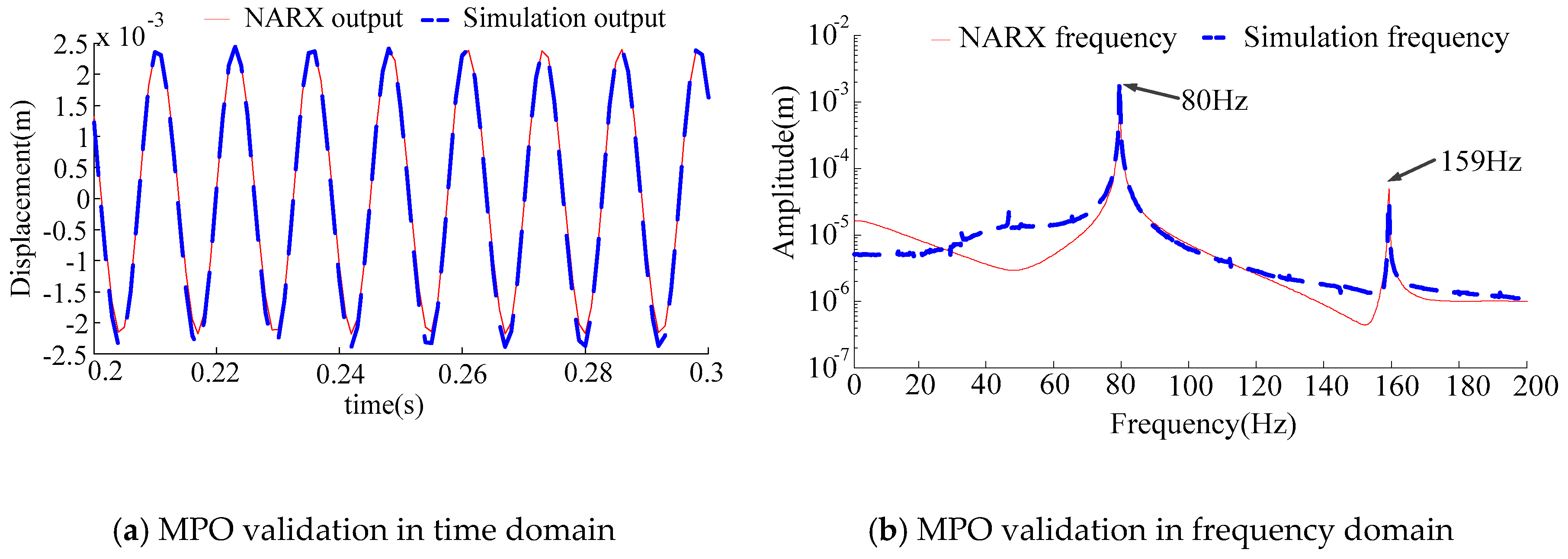
3.3.3. Under the Over-Critical Speed Condition

When the input signal contains the frequency of ${\omega }_{overcritical}\in \left[350,450\right]$ rad/s, the NARX model can be identified as:

$$\begin{array}{c}y\left(k\right)={\displaystyle {\displaystyle \sum }_{i=1}^{10}}{\beta }_i\left(k\right)\widetilde{{\theta }_i}\\ =-2.7421\times {10}^{-5}u\left(k-6\right)\\ +1.3522y\left(k-1\right)+2.3854\\ \times {10}^{-5}u\left(k-6\right)+\cdots 0.0190y\left(k-8\right)\end{array}$$

(28)

where the harmonic input with $\omega$ = 500 rad/s is used to test the model in both the time and the frequency domain, presenting in Figure 11. And the RMES is 6.4411 × 10⁻⁶ m.

Figure 11 indicates that the NARX model identified in the low frequency range provides a more accurate prediction result than that of (25). Also, the RMSE is better than 1.4032 × 10⁻⁵ m, as shown in Table 2.

As the above three sections indicate, both the graphs and the values of RMSE show a better accuracy than that of Section 3.2. That is, from both a qualitative and quantitative point of view, the method of narrowing the frequency range of input excitations can optimize the NARX model and make the model perform better.

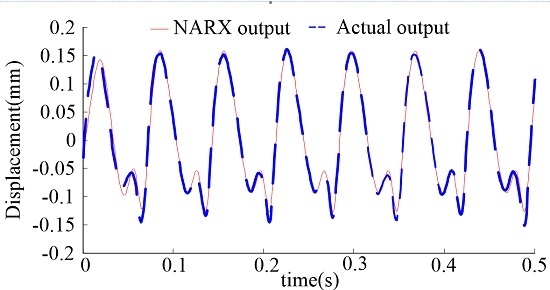
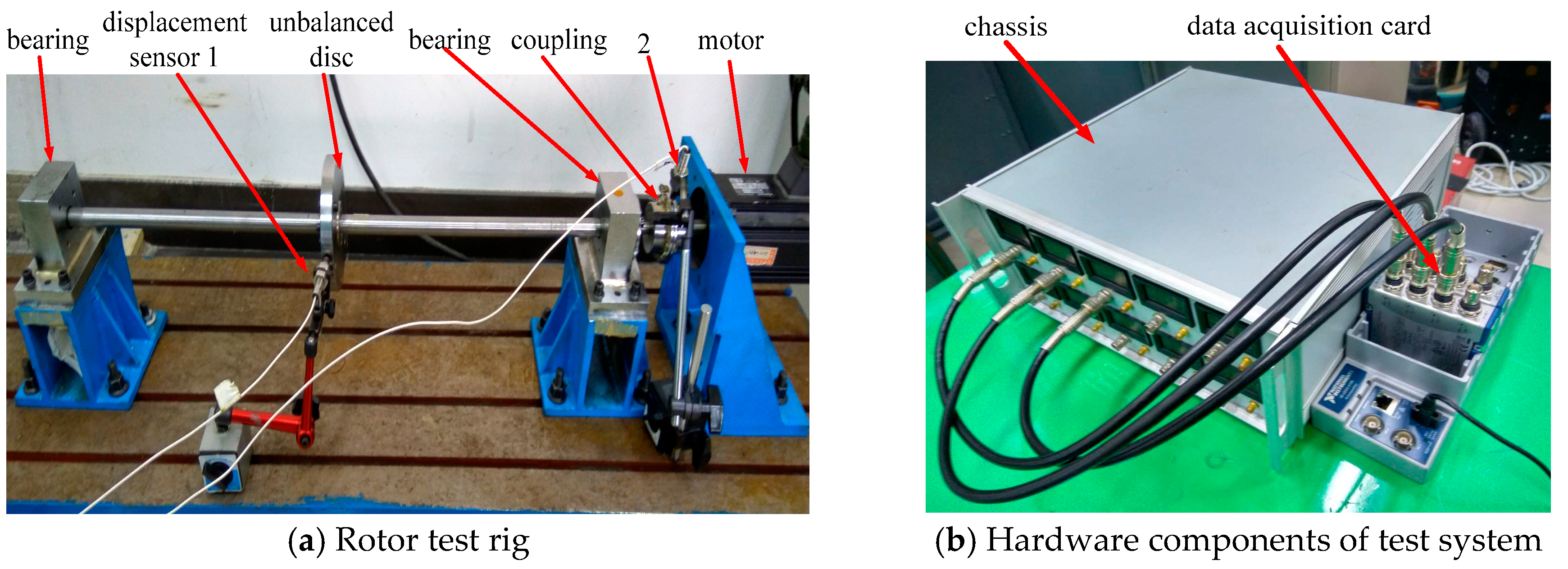
4. Experimental Verification

In order to validate the proposed identification method of the nonlinear, rotor-bearing system, a rotor test rig is taken for verification, where the eddy current displacement sensor is arranged to measure the response, and the added bolt is expected to reinforce unbalanced force, as shown in Figure 12a. The test rig is connected with the Labview test system, as shown in Figure 12b.

Concerned with safeness, the test rig, which has a critical speed of 229 rad/s, is operated under low speed case. Define the multi-harmonic $\sin \left(\omega t\right),\omega \in \left[84,89\right]$ rad/s as the system input excitation, and the output of the system is considered as the horizontal vibration response.

The NARX model of the rotor test rig is established with the test data of 84, 85, 86, 87, and 88 rad/s. Based on FROLS algorithm, a 3 order NARX model is identified as follow (

Table 3. Identification result of the test.

Step	Term	Coefficient	ERR%
1	$y\left(k-1\right)$	1.8444	99.4393
2	$y\left(k-2\right)$	−0.8595	0.5177
3	$u\left(k-2\right)u\left(k-2\right)$	0.1788	0.0027
4	$u\left(k-1\right)u\left(k-2\right)$	−0.2439	0.0017
5	$u\left(k-1\right)u\left(k-1\right)$	0.0642	0.0138
6	$y\left(k-2\right)y\left(k-2\right)$	0.6580	0.0003
7	$y\left(k-1\right)u\left(k-1\right)$	0.1268	0.0006
8	$y\left(k-1\right)y\left(k-2\right)y\left(k-2\right)$	−0.5515	0.0003
9	$u\left(k-2\right)$	−0.0243	0.0003
10	$y\left(k-1\right)y\left(k-2\right)$	−0.7159	0.0001
11	$y\left(k-1\right)u\left(k-2\right)$	−0.1019	0.0001
12	$u\left(k-1\right)$	0.0250	0.0001
13	$u\left(k-2\right)u\left(k-2\right)$	−0.0020	0.0001
14	$y\left(k-1\right)u\left(k-1\right)u\left(k-1\right)$	0.1688	0.0002
15	$y\left(k-2\right)u\left(k-1\right)u\left(k-2\right)$	−0.1482	0.0005
Total	-	-	99.9778

):

The input excitation $\omega$ = 89 rad/s is used to verify the identified NARX model in both the time and frequency domains by using the MPO method, and the results are shown in Figure 13. At the same time, the RMSE is calculated as 8.2272 × 10⁻⁶ m.

As Figure 13 implies, the NARX model shows satisfying accuracy. It indicates that the NARX model of the rotor test rig can predict the system output and reflect the system dynamic characteristics. Therefore, the NARX model provides a theoretical basis for analysis, design, and fault diagnosis of the nonlinear, rotor-bearing system.

5. Conclusions

• Mathematical models are important in the analysis, design, and fault diagnose of rotor-bearing systems. However, due to the complex structure and other factors, it is impossible to establish an accurate physical model. Thus, in this paper, an identification method of the nonlinear, rotor-bearing system based on NARX model is proposed.
• The experimental results indicate that the NARX model can reproduce the underlying nonlinear, rotor-bearing system accurately. Furthermore, the method enriches the nonlinear, rotor-bearing modeling theory and provides a reliable model for dynamic analysis, design, and fault diagnosis of the rotor-bearing system, which is of practical significance.
• The NARX model under multi-harmonic excitation can reflect a broad range of system characteristics. The MPO and OSA methods are used in model validation. The results indicate that it is inappropriate to use the OSA method when establishing the nonlinear, rotor-bearing system.