A Statistical Model Updating Method of Beam Structures with Random Parameters under Static Load

Abstract

This paper presents a new statistical model updating method of beam structures with random parameters under static load. The new updating method considers structural parameters and measurement errors to be random. To reduce the unmeasured degrees of freedom in the finite element model, a static condensation technique is used in this method. A statistical model updating equation with respect to element updated factors is established afterwards. The element updated factors are expanded as random multivariate power series. Using a high-order perturbation technique, the statistical model updating equation can be solved to obtain the coefficients of the power series expansions of the element updated factors. The results of two numerical examples show that for the solution of the statistical model updating equation, the accuracy of the proposed method agrees with that of the Monte Carlo simulation method very well. The static responses obtained by the updated finite element model coincide with the measured results very well. Finally, a series of static load tests of the concrete beam are conducted to testify the effectiveness of the proposed method.

1. Introduction

In recent years, structural health monitoring and safety assessment have been a hot research topic which has attracted the attention of numerous researchers. In structural health monitoring, the damage identification of the structure is a key point. However, to realize the damage identification, an initial referenced model must be established. Due to the influence of various factors, e.g., environment, construction styles etc., there is a difference between the finite element simulation model and the actual structure. To reduce the impact of these factors, it is necessary to update the simulation model to make it coincide with the actual structure using measured data. In this regard, one can consider the structural responses (e.g., displacements, strains, and dynamic characteristics, etc.) as the indicators, and update the parameters and boundary conditions of the initial simulation model based on the measured data. This process is generally named as the model updating. In this way, an eligible referenced model can be obtained so as to further achieve the structural damage identification. Therefore, the model updating will provide a reliable basis for the structural safety assessment [1,2,3,4].

Much research has been conducted on the model updating method in accordance with the structural measured data. The measured data may be displacements, strains, or dynamic characteristics of the structures. Since the static test equipment required is relatively cheap and the static displacements or strains of structures can be measured economically and accurately, the static model updating methods have attracted the attention of many researchers. For instance, Sanayei et al. [5,6,7] presented the analytical methods to identify the structural element stiffness using the applied forces and measured displacements. Subsequently, the static displacements and static strains are used to successfully evaluate the unknown stiffness parameters of the structural components. Liu et al. [8] proposed a superelement-based virtual distortion method to improve the efficiency of the finite element model updating of large-scaled bridges by using static information. Ren et al. [9] presented a method for updating a finite-element model based on the measured static responses of structures with the aid of the response surface methodology. Li et al. [10] proposed a method based on the meta-model for updating the finite element model of bridges by using measured static and dynamic results. Sanayei et al. [11] collected strain data during the load test to calibrate a detailed baseline finite element model in an effort to represent the 3D system behavior of a bridge.

For the above research, the uncertainty of the measurement errors is seldom involved. Considering the measurement errors as random quantities, many statistical approaches have been developed to update the parameters of structures based on the measured data. These approaches include the stochastic perturbation methods [3,12,13,14,15,16], the Monte Carlo simulation methods [17,18], the Bayesian updating methods [19,20,21,22,23,24,25,26] and so on. For example, Jacquelin et al. [12] proposed a random matrix approach to derive the closed-form expressions for the mean matrix and the covariance matrix of the updated stiffness matrix by the perturbation technique. Husain et al. [13] considered the statistical properties of experimental data and updating parameters as random variables, and used the perturbation method to update the parameters. Combined with the sensitive method, Hua et al. use a Monte Carlo simulation method to solve the updating parameters [18]. Although the results from the Monte Carlo simulation methods are traditionally regarded as the exact solution of random problems, these methods generally require much greater computational efforts to obtain an accurate solution, and are impractical in the case of large-scale problems. Zárate et al. [23] studied the behaviour of the Bayesian updating framework when both static and dynamic data are used to update the model. However, all these studies mainly focus on using dynamic data to update structural models. Although some researchers have tried to use different random solution methods based on the finite element model to conduct statistical model updating, few investigations involve the direct use of random finite element methods to perform this work with static data. In light of the evidence, it is clear that further research is needed in this area.

In this paper, a new statistical model updating method of beam structures with random parameters under static load is proposed. This new model updating method considers structural parameters and measurement errors as random quantities. A static condensation technique is used to reduce the unmeasured degrees of freedom in the random finite element model of the beam. Then, a statistical model updating equation with respect to element updated factors is established. The element updated factors are expanded as random multivariate power series. Using the high-order perturbation technique, the statistical model updating equation can be solved to determine the coefficients of the power series expansions of the element updated factors. The results of two numerical examples show that for the solution of the statistical model updating equation, the accuracy of the proposed method agrees with that of the Monte Carlo simulation method very well. The static responses obtained by the updated finite element model coincide with the measured results very well. Finally, static load tests of a concrete beam are conducted to testify the effectiveness of the proposed method.

2. New Statistical Model Updating Method

2.1. Initial Equilibrium Equations

Consider one N degrees of freedom of beam structure under the external static load. The static equilibrium equation of the beam structure at initial simulation state is written as:

$$K_a{x}_a=F$$

(1)

where $K_a$ is an N × N dimensional stiffness matrix, $x_a$ is an N × 1 dimensional displacement response vector of the structure under N × 1 dimensional static load vector $F$.

Considering the translational and rotational degrees of freedom of the structure, Equation (1) can be rewritten as:

$$\left[\begin{array}{cc}{K}_{att}& K_{at\theta }\\ K_{a\theta t}& K_{a\theta \theta }\end{array}\right]\left\{\begin{array}{c}{x}_{at}\\ x_{a\theta }\end{array}\right\}=\left\{\begin{array}{c}{F}_{at}\\ 0\end{array}\right\}$$

(2)

where ${\mathbf{K}}_{att}$ and ${\mathbf{K}}_{a\theta t}$ are respectively sub-matrices, which are related to the translational degrees of freedom of the initial stiffness matrix; $K_a$, ${\mathbf{K}}_{at\theta }$ and ${\mathbf{K}}_{a\theta \theta }$ are sub-matrices of ${\mathbf{K}}_a$ with respect to the rotation degrees of freedom, which are not measured in this paper. $x_{at}$ and $x_{a\theta }$ are displacement vectors related to the translational and rotation degrees of freedom of the initial structure respectively. $F_{at}$ is the concentrated vertical force vector.

According to the static condensation method, which is also used in literature [5] by Sanayei et al., the rotational degrees of freedom of the stiffness matrix in the static equilibrium Equation (2) can be eliminated. In this way, Equation (2) can be condensed as:

$$K_{at}{x}_{at}=F_{at}$$

(3)

where $K_{at}=K_{att}-K_{at\theta }{K}_{a\theta \theta }^{-1}{K}_{a\theta t}$.

Of course, in the same manner, other unmeasured displacements can be removed.

2.2. Statistical Model Updating Equation

Without losing the generality, it is assumed here that the mass of the structural simulation model is invariable compared with the actual structure [27], and the discrepancy between the simulation model and the actual beam structure is mainly due to the variation of the structural stiffness, which is represented as:

$$\Delta K={\displaystyle \sum _{i=1}^n{\alpha }_i}{K}_i$$

(4)

where $n$ is the number of the structural elements; ${\alpha }_i$ is the element updated factor of the ith element of the beam structure, which is the variation ratio of a structural parameter such as the bending rigidity of the beam; $K_i$ is an N × N dimensional expanded matrix of the ith element stiffness matrix, where all elements in expanded parts are zero.

In regard to the stiffness matrix of the initial simulation model, the updated stiffness matrix, $K_m$ can be expressed as follows:

$$K_m=K_a+{\displaystyle \sum _{i=1}^n{\alpha }_i{K}_i}$$

(5)

Similar to the initial simulation model, the updated stiffness matrix can be condensed as:

$$K_{mt}=K_{mtt}-K_{mt\theta }{K}_{m\theta \theta }^{-1}{K}_{m\theta t}$$

(6)

where $K_{mtt}$, $K_{mt\theta }$, $K_{m\theta t}$ and $K_{m\theta \theta }$ are sub-matrices of $K_m$, which are related to the translational and rotational degrees of freedom of the updated finite element model respectively like the situation at the initial simulation state.

Equations (5) and (6) can be rewritten as:

$$K_{mt}=(K_{att}+{\displaystyle \sum _{i=1}^n{\alpha }_i{K}_{itt}})-(K_{at\theta }+{\displaystyle \sum _{i=1}^n{\alpha }_i{K}_{it\theta }}){(K_{a\theta \theta }+{\displaystyle \sum _{i=1}^n{\alpha }_i{K}_{i\theta \theta }})}^{-1}(K_{a\theta t}+{\displaystyle \sum _{i=1}^n{\alpha }_i{K}_{i\theta t}})$$

(7)

where $K_{itt}$, $K_{it\theta }$, $K_{i\theta t}$ and $K_{i\theta \theta }$ are sub-matrices of the expanded matrix $K_i$, which corresponds to the sub-matrices of the updated stiffness matrix.

Taking the first-order partial derivatives of $K_{mt}$ with respect to ${\alpha }_i$, there is:

$${\frac{\partial K_{mt}}{\partial {\alpha }_i}|}_{{\alpha }_i=0}=K_{itt}-K_{it\theta }{K}_{a\theta \theta }^{-1}{K}_{a\theta t}-K_{at\theta }{K}_{a\theta \theta }^{-1}{K}_{i\theta t}+K_{at\theta }{K}_{a\theta \theta }^{-1}{K}_{i\theta \theta }{K}_{a\theta \theta }^{-1}{K}_{a\theta t}$$

(8)

It is worth pointing out that in the sensitive methods as presented by Mottershead et al. in the literature [28,29], the calculation steps similar to the above are used to obtain the partial derivatives of the mass matrix and stiffness matrix with respect to updating parameters based on the first-order Taylor expansion.

Since the applied load is the same for the initial model and the updated model, the product of the updated stiffness matrix $K_{mt}$ and the measured displacement vector $x_{mt}$ should equal to the concentrated force vector $F_{at}$. Note that this principle is different from that presented in literature [5] by Sanayei et al., where a displacement equation error function is defined and minimized to determine the updating parameters. Using Equation (3), the following equation can be obtained:

$$K_{at}{x}_{at}=({K_{mt}|}_{\alpha =0}+{\displaystyle \sum _{i=1}^n{\alpha }_i{\frac{\partial K_{mt}}{\partial {\alpha }_i}|}_{{\alpha }_i=0}})x_{mt}$$

(9)

where ${K_{mt}|}_{\alpha =0}=K_{at}$ the translational part of the stiffness matrix of the initial simulation model.

Letting $K_{ti}={\frac{\partial K_{mt}}{\partial {\alpha }_i}|}_{{\alpha }_i=0}$ and $\Delta x_t=x_{at}-x_{mt}$, Equation (9) can be rewritten as:

$${\displaystyle \sum _{i=1}^n{\alpha }_i{K}_{ti}}{x}_{mt}=K_{at}\Delta x_t$$

(10)

Actually, Equation (10) is the model updating equation with respect to the element updated factors ${\alpha }_i$ (i = 1, …, n). If the measured displacements or $x_{mt}$ contain the measurement errors, and these errors are considered as random quantities, the element updated factors will also be random. In this regard, Equation (10) is named as the statistical model updating equation in this paper.

2.3. Solution of Statistical Model Updating Equation

Assuming that the measurement errors of the beam structure under static load are random, the measured displacement vector of the actual structure can be expressed as:

$$x_{mt}=x_{mt0}+{\displaystyle \sum _{i=1}^l{\beta }_i{x}_{mti}}$$

(11)

where l is the number of random factors affecting the measurement, and equals to 1 given that the measurement errors are completely dependent. $x_{mt0}$ is the mean of the measured displacement vector, ${\beta }_i$ is the independent random variable, and $x_{mti}$ is the adjoint vector of the random variable ${\beta }_i$.

Using the multivariable power series to expand the element updated factors ${\alpha }_i$ (i = 1, …, n), one can have

$${\alpha }_i={\alpha }_{i0}+{\displaystyle \sum _{j=1}^l{\alpha }_{ij}{\beta }_j+{\displaystyle \sum _{j=1}^l{\displaystyle \sum _{k=1}^j{\alpha }_{ijk}{\beta }_j{\beta }_k+{\displaystyle \sum _{j=1}^l{\displaystyle \sum _{k=1}^j{\displaystyle \sum _{p=1}^k{\alpha }_{ijkp}{\beta }_j{\beta }_k{\beta }_p}}}}}}+...$$

(12)

where ${\alpha }_{i0}$, ${\alpha }_{ij}$, ${\alpha }_{ijk}$ and ${\alpha }_{ijkp}$ are respectively the zero-order to third-order of unknown expansion coefficients of the multivariable power series (12).

Substituting Equation (12) for Equation (10) leads to:

$$K_{at}(x_{at}-(x_{mt0}+{\displaystyle \sum _{i=1}^l{\beta }_i{x}_{mti}}))={\displaystyle \sum _{i=1}^n({\alpha }_{i0}+{\displaystyle \sum _{j=1}^l{\alpha }_{ij}{\beta }_j+{\displaystyle \sum _{j=1}^l{\displaystyle \sum _{k=1}^j{\alpha }_{ijk}{\beta }_j{\beta }_k+\cdots )}}}{K}_{ti}}(x_{mt0}+{\displaystyle \sum _{i=1}^l{\beta }_i{x}_{mti}})$$

(13)

Obviously, Equation (13) is a random algebraic equation with unknown expansion coefficients ${\alpha }_{i0}$, ${\alpha }_{ij}$, ${\alpha }_{ijk}$, etc. A high-order perturbation technique, which has been successfully used to determine the random frequencies of a large span cable-stayed bridge in the literature [27], is suggested to solve Equation (13). Using the high-order perturbation technique, the expansion coefficients ${\alpha }_{i0}$, ${\alpha }_{ij}$, ${\alpha }_{ijk}$ and ${\alpha }_{ijkp}$, which correspond to the power polynomials 1, ${\beta }_j$, ${\beta }_j{\beta }_k$ and ${\beta }_j{\beta }_k{\beta }_p$ respectively, can be recursively determined. At first, for the zero-order polynomial term, there is:

$${\alpha }_{i0}=A_0^{-1}(K_{at}{x}_{at}-K_{at}{x}_{mt0})$$

(14)

where $A_0=[K_{t1}{x}_{mt0},K_{t2}{x}_{mt0},...,K_{tn}{x}_{mt0}]$.

Next, for the first-order power polynomial ${\beta }_j$, one has:

$${\alpha }_{ij}=-A_0^{-1}(K_{at}{x}_{mti}+A_1{\alpha }_{i0})$$

(15)

where $A_1=[K_{t1}{x}_{mtj},K_{t2}{x}_{mtj},...,K_{tn}{x}_{mtj}]$.

Then, considering the second-order power polynomial, ${\beta }_j{\beta }_k$ results in:

$${\alpha }_{ijk}=-A_0^{-1}{A}_2{\alpha }_{ij}$$

(16)

where $A_2=[K_{t1}{x}_{mtk},K_{t2}{x}_{mtk},...,K_{tn}{x}_{mtk}]$.

For the third-order power polynomial ${\beta }_j{\beta }_k{\beta }_p$, the expansion coefficient ${\alpha }_{ijkp}$ is obtained as:

$${\alpha }_{ijkp}=-A_0^{-1}{A}_3{\alpha }_{ijk}$$

(17)

where $A_3=[K_{t1}{x}_{mtp},K_{t2}{x}_{mtp},...,K_{tn}{x}_{mtp}]$.

In the same way, the fourth- to the higher-order of expansion coefficients can be determined. Taking into account the balance between the accuracy and the efficiency, up to the fourth-order of coefficients are used in this paper. Further, by the power polynomial expansion solved, the statistics of the element updated factors can be obtained easily. Note that many random methods, such as the Monte Carlo simulation methods, the spectral stochastic finite element methods (SSFEM), etc., can be used to solve the statistical model updating Equation (10). However, although SSFEMs have exhibited relatively high accuracy for many elastic mechanical problems [30], the calculation effectiveness or CPU time of the methods is not satisfactory for complex problems due to the exponential increase of the number of polynomial terms. Compared with these random methods, the proposed method is very efficient only with a little loss of the accuracy in some cases; it is therefore very suitable for solving large-scale engineering problems. For convenience, this paper denotes the proposed statistical model updating method (SMUM) as HP-SMUM, where HP means high-order perturbation.

Since the multivariate power series expansion has been obtained, Equation (1) can be rewritten as:

$$[K_a+{\displaystyle \sum _{i=1}^n({\alpha }_{i0}+{\displaystyle \sum _{j=1}^l{\alpha }_{ij}{\beta }_j+{\displaystyle \sum _{j=1}^l{\displaystyle \sum _{k=1}^j{\alpha }_{ijk}{\beta }_j{\beta }_k}+\cdots )K_i}}}]x_a=F_a$$

(18)

Using the high-order perturbation technique or other generally used methods, such as the spectral random finite element methods, the Monte Carlo simulation methods and so on, the statistical vertical displacements of the updated model can be obtained by Equation (18). Of course, facing the large-scale model updating problems, the high-order perturbation technique is still a very competitive solution method.

3. Numerical Examples

3.1. A Simply Supported Beam

Consider a simply supported beam with a rectangular section as shown in Figure 1. The length of the beam $l=6.0\mathrm{m}$, the elastic modulus $E=2.8\times {10}^{10}\mathrm{Pa}$, the sectional area $A=0.3\mathrm{m}\times 0.8\mathrm{m}$, and the sectional inertia moment $I=0.0128{\mathrm{m}}^4$. The simply supported beam is divided into six elements with seven nodes, and each node includes the vertical deflection and rotation. A concentrated load $P=200\mathrm{kN}$ is applied in the middle of the beam. The rotational degrees of freedom at all nodes are eliminated using the static condensation method.

It is assumed that for the elastic modulus of the 4th element of the beam, a 10% reduction happens, which is due to the discreteness of the elastic modulus of concrete. According to the deterministic mechanical parameters given, the mean values of the assumed measurement deflections are simulated in this case. Considering the uncertainty of the measurement deflections, it is assumed that the coefficients of variation of the measured displacements at all nodes are 0.01 according to our experimental results which are 0.01~0.03, and the displacements are of Beta distributions.

By the simulated measurement data, the proposed HP-SMUM and the Monte Carlo simulation method with 100,000 samples are used to solve the statistical model updating equation to modify the original simulation model. The statistical results of the element updated factors are plotted in Figure 2. From Figure 2, it is found that the means and standard deviations of the element updated factors from the proposed method are in good agreement with those of the Monte Carlo simulation method. Furthermore, the mean value of the element updated factor of the 4th element indicates that the updated result consists of the assumed case where the 10% reduction of the elastic modulus of the 4th element is produced. Especially, from Figure 2c, it is observed that the probability density functions of the 4th element selected from the two calculation methods coincide with each other very well. These results illustrate that the proposed HP-SMUM is a very accurate solution for the statistical model updating equation. Meanwhile, by using the Monte Carlo simulation method to solve Equation (18), the means and standard deviations of the node deflections of the updated beam structure are obtained and shown in Figure 3. From Figure 3, it is found that the first two moments of deflections and the probability density function (pdf) of the deflection in the mid-span determined by the updated finite element model match with the assumed measurement values very well. For the mean of deflection, actual calculated relative errors are less than 1.38%. On the other hand, for the standard deviation of deflection, the relative errors at all nodes are close to zero. These results demonstrate that the proposed method has very good updated effectiveness.

3.2. A Two-Span Continuous Beam

Consider a two-span continuous beam as shown in Figure 4. The mechanical parameters of the continuous beam are the same as those of the simply supported beam in Section 3.1. The concentrated load $P=200\mathrm{kN}$ is applied in the middle of the left span of the continuous beam. Here, the 10% reduction of the elastic modulus of the 3rd and 4th element is assumed. Additionally, it is assumed that the coefficients of variation of the measured displacements at all nodes are 0.01, and they are of Beta distributions.

By the simulated measurement data, the proposed HP-SMUM and the Monte Carlo simulation method with 100,000 samples are used to obtain the statistics of the element updated factors, and the results are plotted in Figure 5. From Figure 5, it is found that the means and standard deviations of the element updated factors from the proposed HP-SMUM are in good agreement with those of the Monte Carlo simulation method. Furthermore, the means of the 3rd and 4th element shown in Figure 5a testify that a 10% reduction of the element stiffness has happened.

However, the probability density function of the 4th element selected from the proposed method is little different from the results of the Monte Carlo simulation method. This may be attributed to the non-symmetry of the continuous beam. Meanwhile, using the obtained element updated factors to solve Equation (10), the statistics of deflections of the updated continuous beam can be determined and shown in Figure 6 which shows that the first two moments of deflections by the updated finite element model match with the assumed measurement values very well. For the mean of deflection, actual calculated relative errors at all nodes are less than 0.54%. On the other hand, for the standard deviation of deflection, the relative errors are less than 7%. In addition, the pdf of the deflection in the mid-span by the updated model hardly deviates from the measured result.

4. Model Updating Test

A simply supported concrete beam under static load is shown in Figure 7a. The section of the reinforced concrete beam is 150 mm × 250 mm, and the length of the span is 1900 mm. For the distributive girder of static load, the length of the span is 950 mm. The grade of concrete strength is C25. This test was implemented according to a test standard as illustrated in literature [31].

The tested simply supported beam is divided into eight elements with nine nodes, as shown in Figure 7b. The concentrated load P is 15 kN. The deflections of seven nodes are measured several times so that the statistic values of the deflections are obtained. The statistics of the measured deflections at seven nodes are listed in

Table 1. Statistics of measured deflections of seven nodes.

Node	2	3	4	5	6	7	8
Mean (mm)	0.192	0.357	0.454	0.488	0.455	0.358	0.196
Standard deviation (×10−2 mm)	0.576	1.071	1.362	1.464	1.365	1.074	0.588

where the node deflections are assumed to be of Beta distributions. Based on the measured data, the proposed HP-SMUM is applied to update the concrete beam.

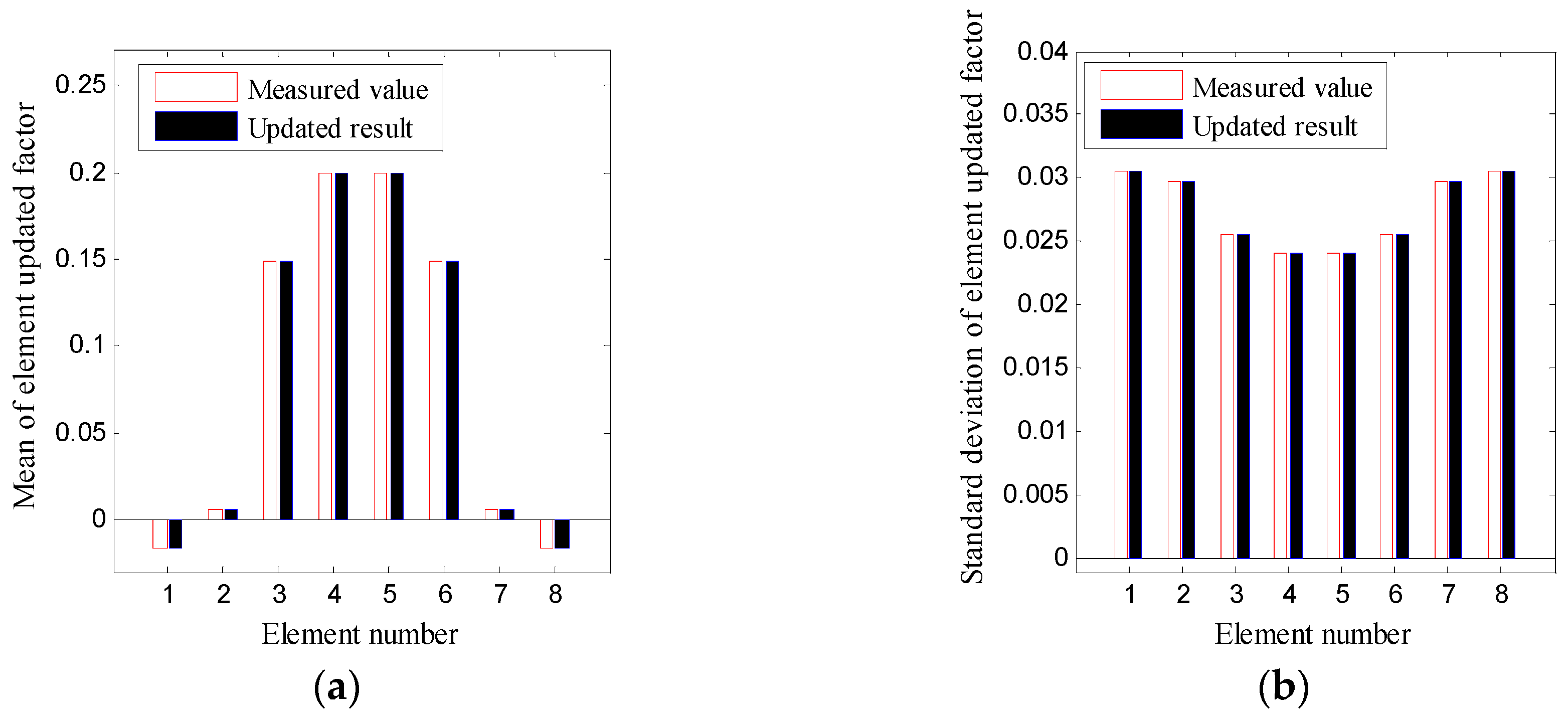
The means and standard deviations of the element updated factors are plotted in Figure 8 which shows that some degree of damage exists in the middle of the beam, and this result confirms the true case where small cracking happens in the concrete beam under the load.

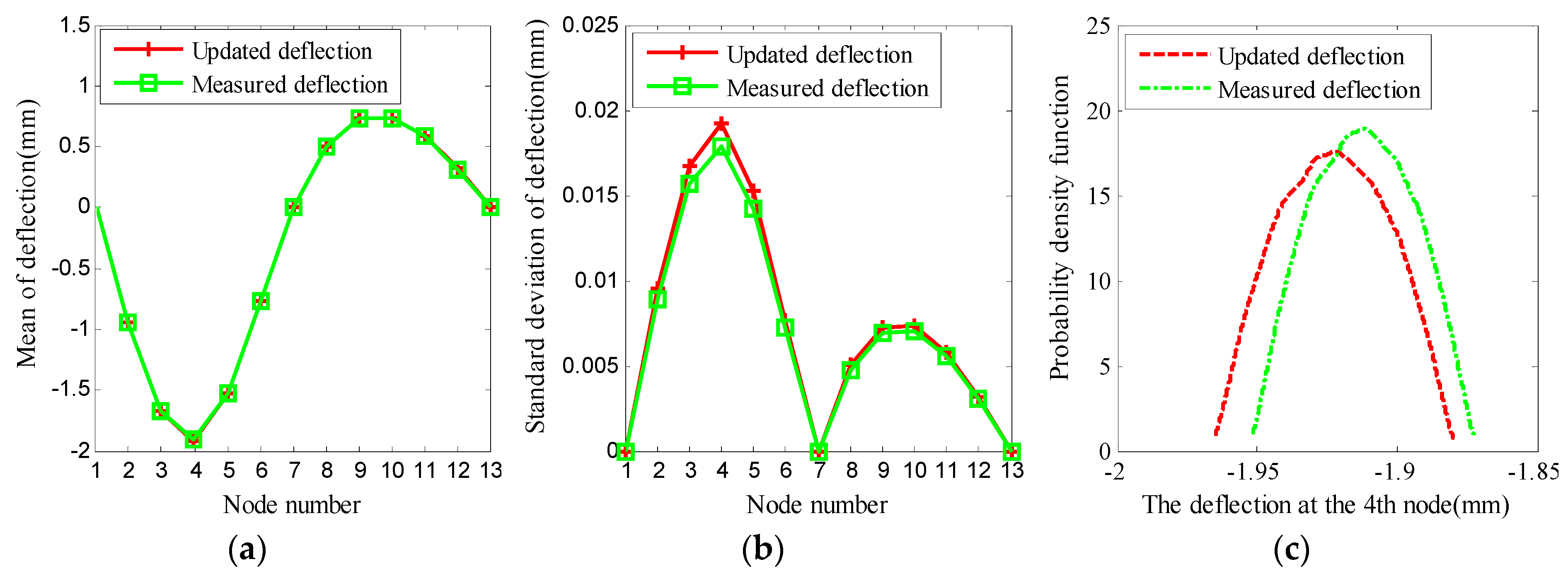
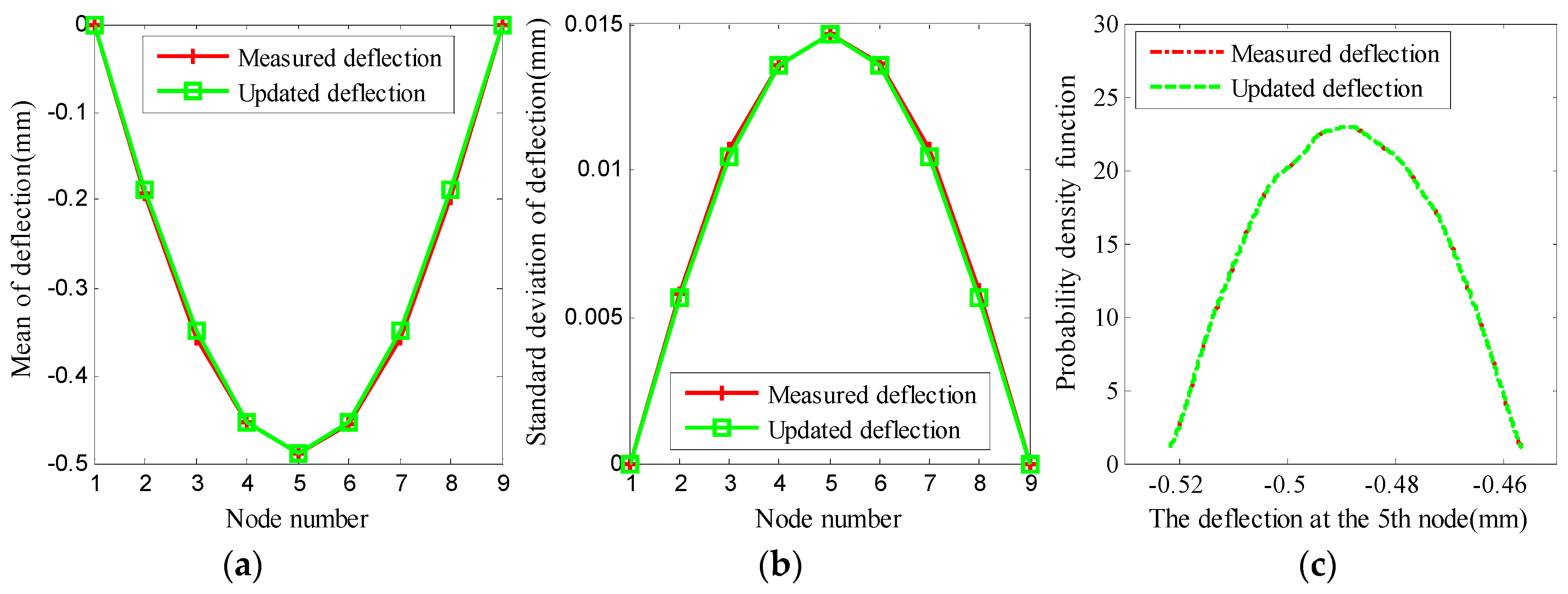
Further, using the obtained element updated factors, the deflections of the concrete beam are calculated by means of Equation (18), and the results are shown in Figure 9. From Figure 9, it is found that the statistics of calculated deflections of the updated concrete beam coincide with the actual measured data very well. This result testifies the effectiveness of the proposed statistical model updating method once again.

5. Conclusions

A new statistical model updating method has been developed for modifying the beam structures with random parameters under static load. The new updating method considered the uncertainty of structural parameters and measurement errors. A static condensation technique is used to reduce the unmeasured degrees of freedom in the finite element model. A statistical model updating equation with respect to element updated factors has been established afterwards. Using the high-order perturbation technique, the statistical model updating equation has been solved to obtain the statistics of the element updated factors. The results of two numerical examples show that the accuracy of the proposed method is very good. The static responses obtained by the updated finite element model coincide with the measured results very well. Further, the updated results of the concrete beam based on static load tests testified the effectiveness of the proposed method.