Numerical Simulation of Red Blood Cell-Induced Platelet Transport in Saccular Aneurysms
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.1.1. Conservation of Mass
2.1.2. Conservation of Linear Momentum
2.1.3. Conservation of Platelets Concentration
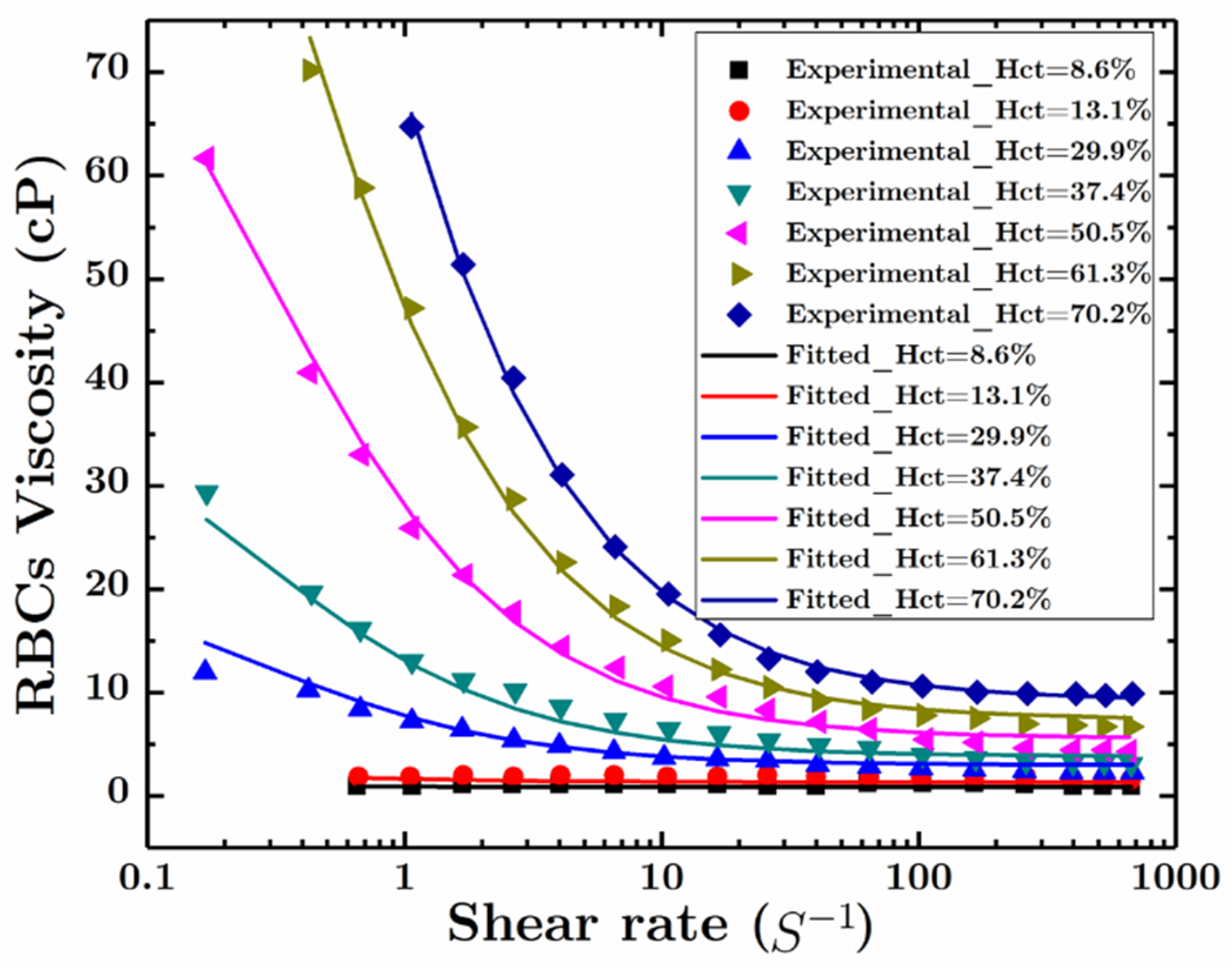
2.2. Constitutive Relations
2.2.1. Stress Tensor of the Plasma
2.2.2. Stress Tensor of the RBCs
2.2.3. Interaction Forces between Plasma and RBCs
2.2.4. The Diffusive Flux of the Platelets
3. Results and Discussions
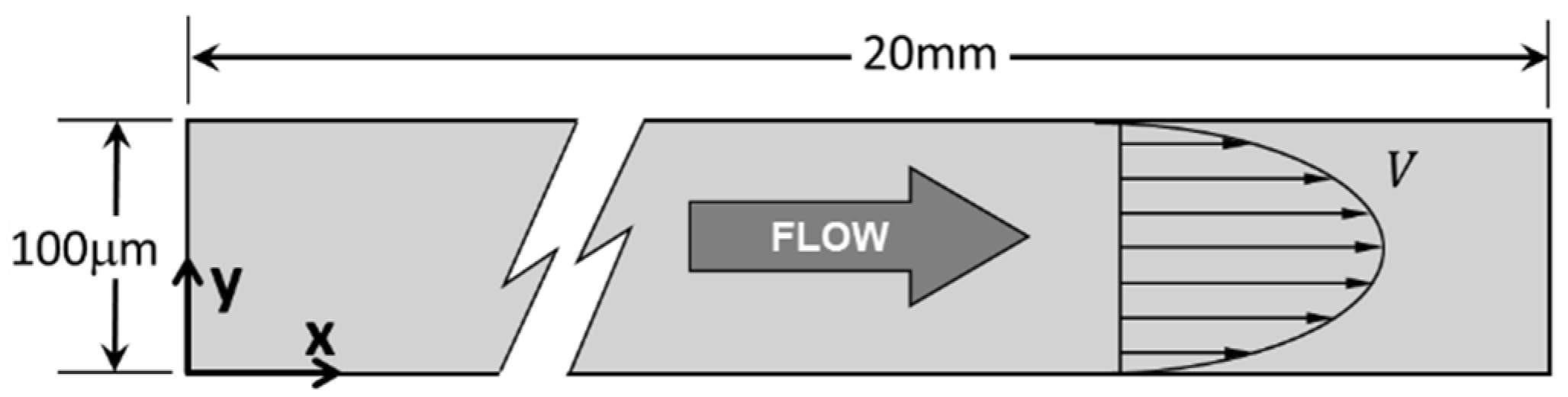
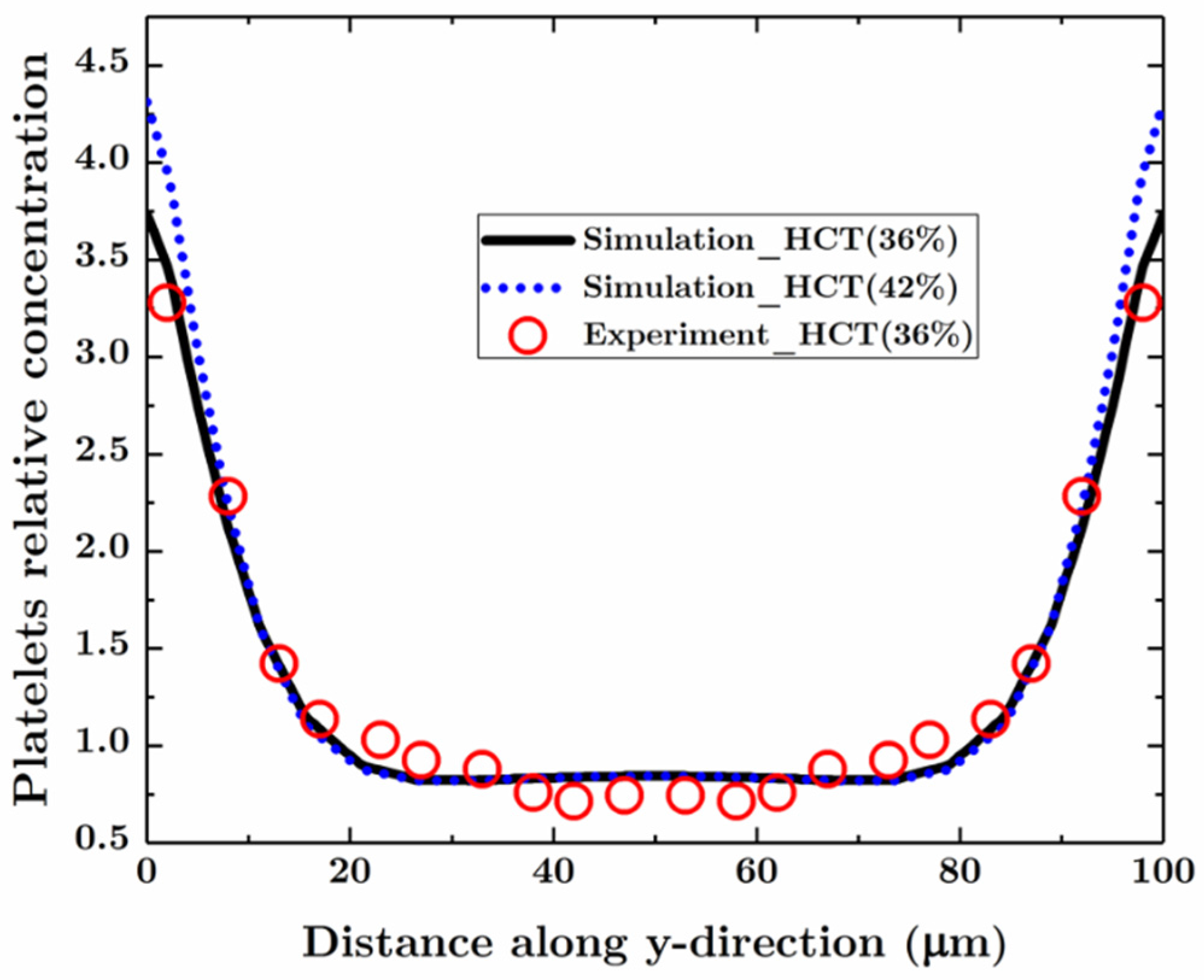
3.1. Blood Flow and Platelets Migration in a Parent Vessel without an Aneurysm
3.2. Blood Flow and Platelets Migration in Aneurysms
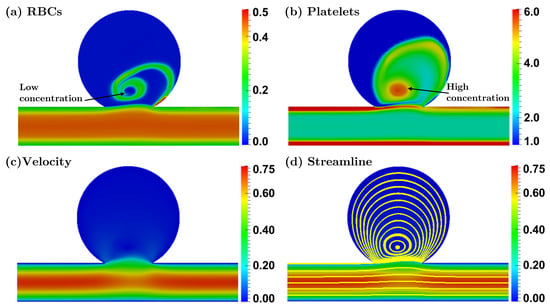
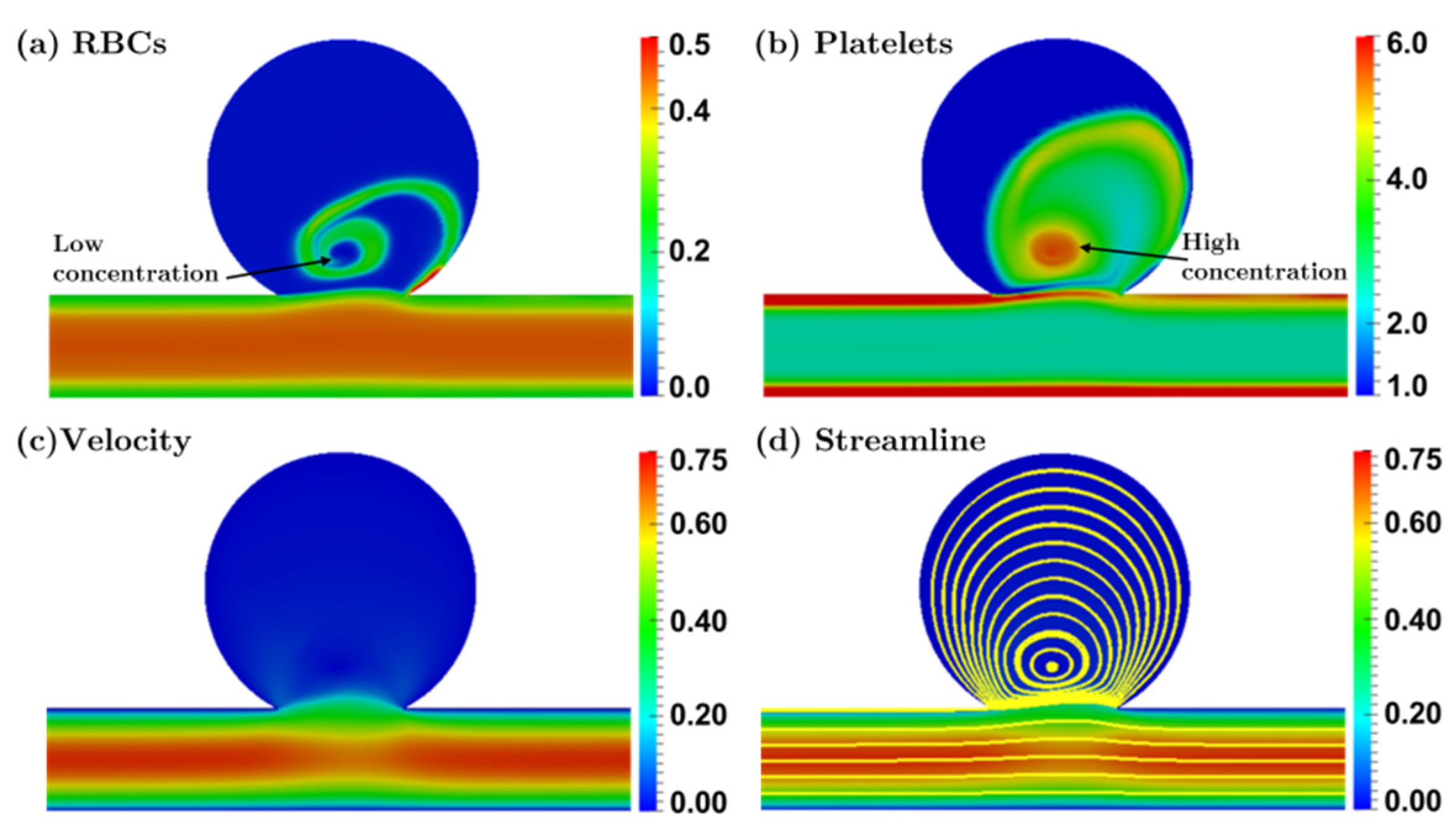
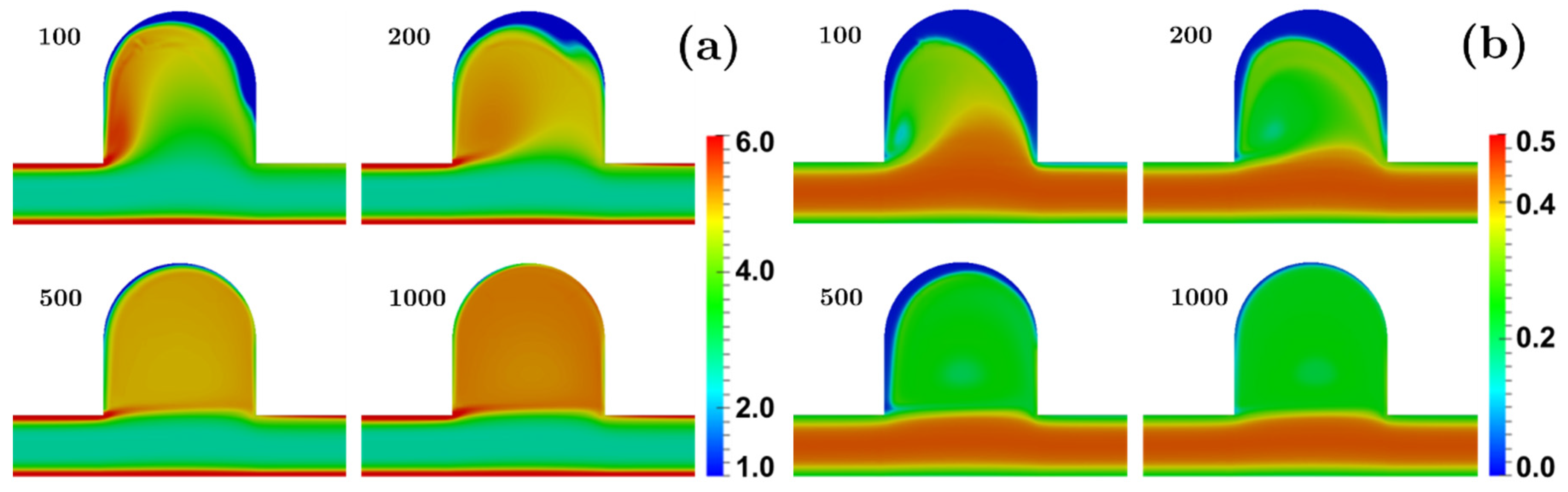
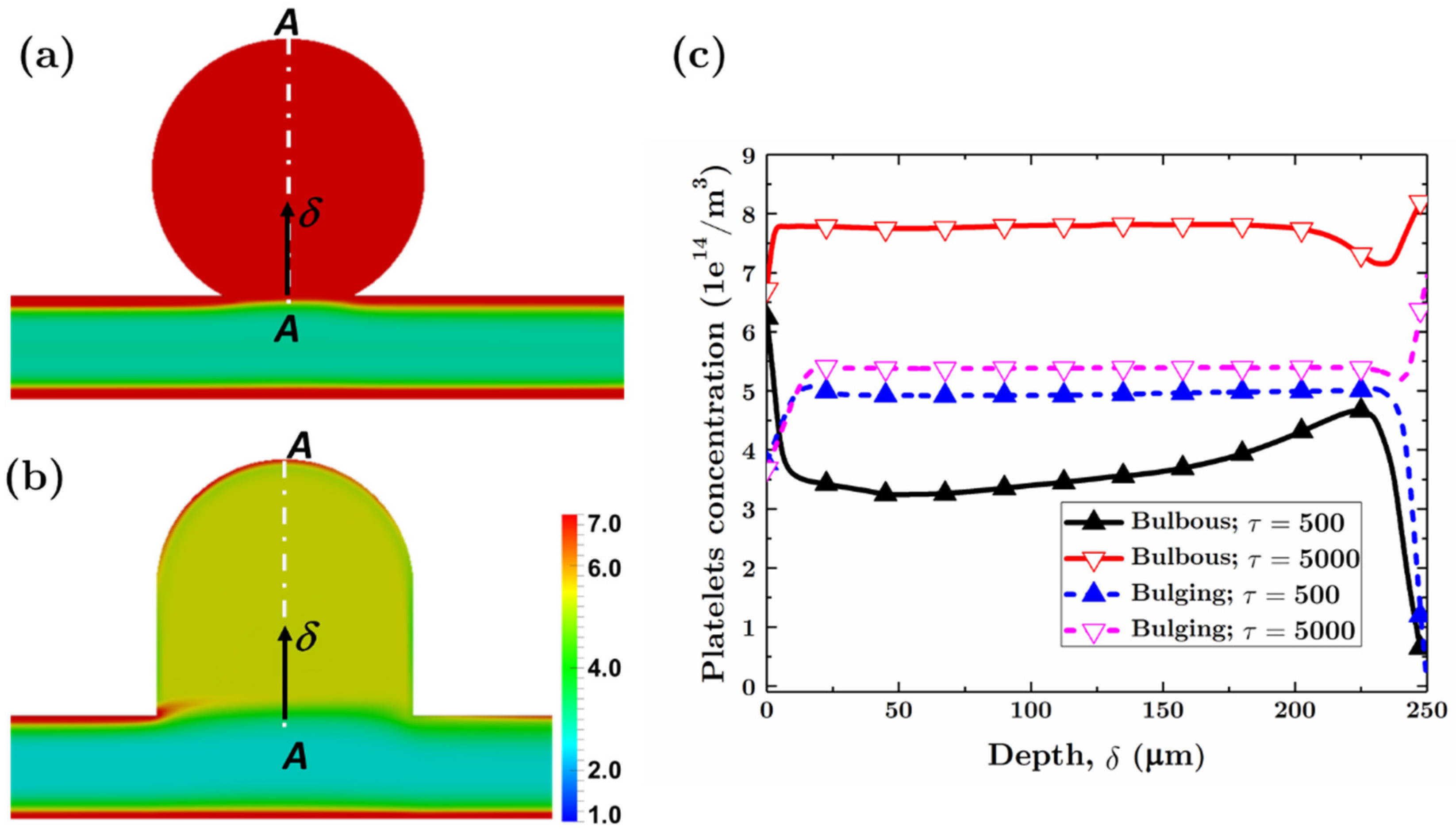
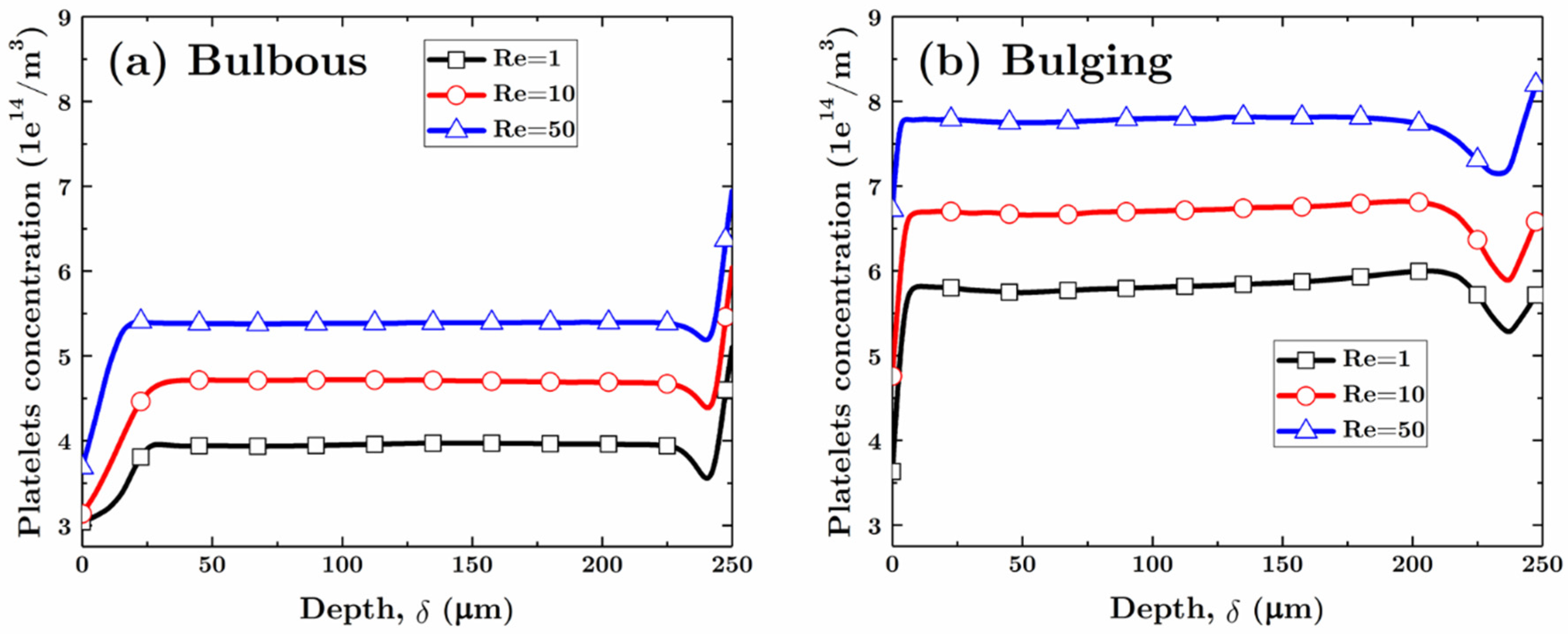
3.2.1. Bulbous Saccular Aneurysm
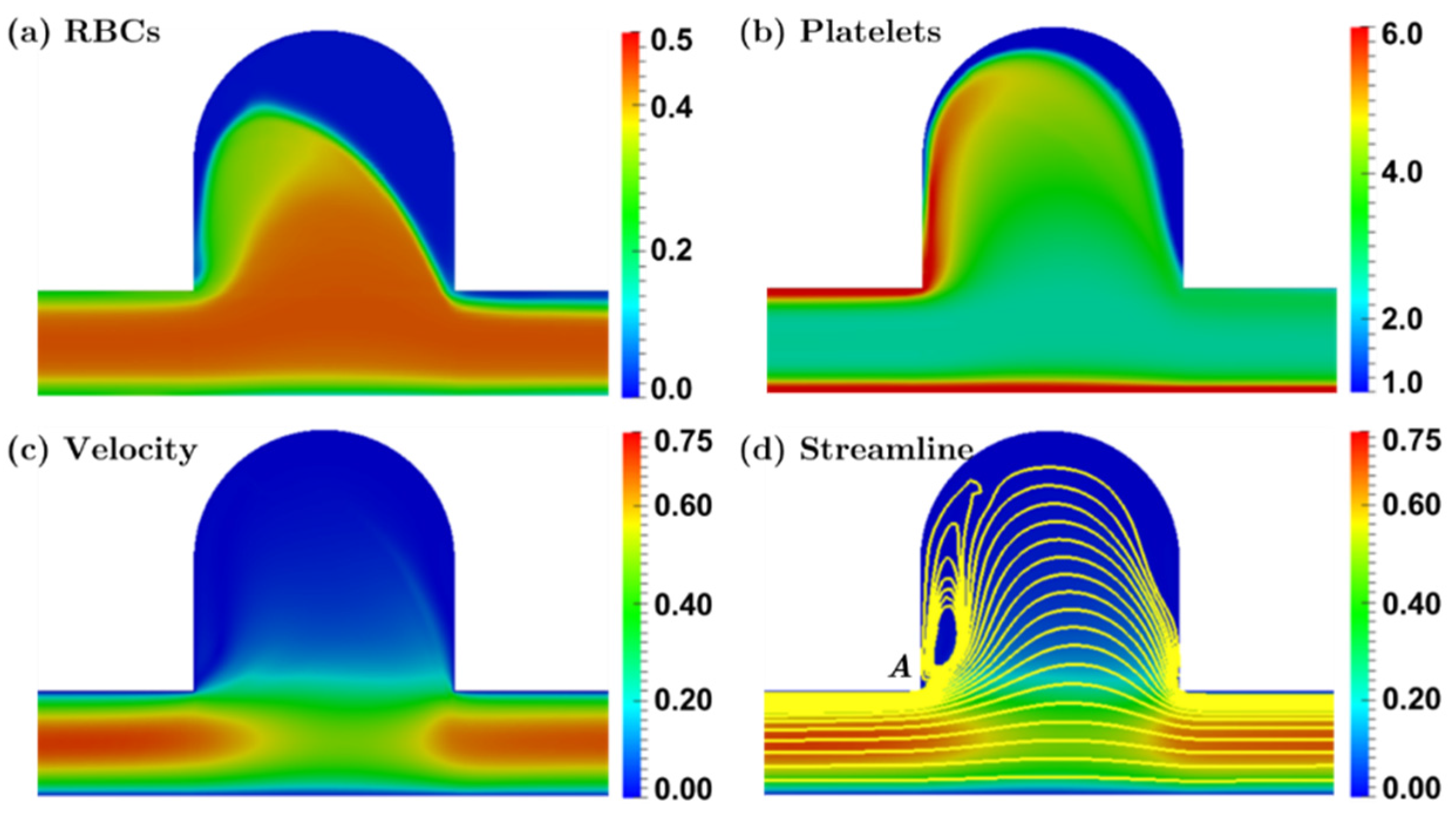
3.2.2. Bulging Saccular Aneurysm
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hirabayashi, M.; Ohta, M.; Rüfenacht, D.A.; Chopard, B. Characterization of flow reduction properties in an aneurysm due to a stent. Phys. Rev. E 2003, 68, 21918. [Google Scholar] [CrossRef] [PubMed]
- Mountrakis, L.; Lorenz, E.; Hoekstra, A.G. Where do the platelets go? A simulation study of fully resolved blood flow through aneurysmal vessels. Interface Focus 2013, 3, 20120089. [Google Scholar] [CrossRef] [PubMed]
- Whittle, I.R.; Dorsch, N.W.; Besser, M. Spontaneous thrombosis in giant intracranial aneurysms. J. Neurol. Neurosurg. Psychiatry 1982, 45, 1040–1047. [Google Scholar] [CrossRef] [PubMed]
- Weir, B. Unruptured intracranial aneurysms: A review. J. Neurosurg. 2002, 96, 3–42. [Google Scholar] [CrossRef] [PubMed]
- Badimon, L.; Badimon, J.J.; Turitto, V.T.; Fuster, V. Thrombosis: Studies under flow conditions. Ann. N. Y. Acad. Sci. 1987, 516, 427–540. [Google Scholar] [CrossRef]
- Badimon, L.; Turitto, V.; Rosemark, J.A.; Badimon, J.J.; Fuster, V. Characterization of a tubular flow chamber for studying platelet interaction with biologic and prosthetic materials: Deposition of indium 111-labeled platelets on collagen, subendothelium, and expanded polytetrafluoroethylene. J. Lab. Clin. Med. 1987, 110, 706–718. [Google Scholar] [PubMed]
- Adams, P.C.; Fuster, V.; Badimon, L.; Badimon, J.J.; Chesebro, J.H. Platelet/Vessel wall interactions, rheologic factors and thrombogenic substrate in acute coronary syndromes: Preventive strategies. Am. J. Cardiol. 1987, 60, G9–G16. [Google Scholar] [CrossRef]
- Merino, A.; Cohen, M.; Badimon, J.J.; Fuster, V.; Badimon, L. Synergistic action of severe wall injury and shear forces on thrombus formation in arterial stenosis: Definition of a thrombotic shear rate threshold. J. Am. Coll. Cardiol. 1994, 24, 1091–1097. [Google Scholar] [CrossRef]
- Sing, C.E.; Alexander-Katz, A. Elongational flow induces the unfolding of von Willebrand factor at physiological flow rates. Biophys. J. 2010, 98, L35–L37. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Jamiolkowski, M.A.; Wagner, W.R.; Aubry, N.; Massoudi, M.; Antaki, J.F. Multi-Constituent Simulation of Thrombus Deposition. Sci. Rep. 2017, 7, 42720. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Yang, F.; Wu, J.; Aubry, N.; Massoudi, M.; Antaki, J.F. High fidelity computational simulation of thrombus formation in Thoratec HeartMate II continuous flow ventricular assist device. Sci. Rep. 2016, 6, 38025. [Google Scholar] [CrossRef] [PubMed]
- Goldsmith, H.L.; Turitto, V.T. Rheological aspects of thrombosis and haemostasis: Basic principles and applications. ICTH-Report--Subcommittee on Rheology of the International Committee on Thrombosis and Haemostasis. Thromb. Haemost. 1986, 55, 415–435. [Google Scholar] [PubMed]
- Turitto, V.T.; Benis, A.M.; Leonard, E.F. Platelet Diffusion in Flowing Blood. Ind. Eng. Chem. Fundam. 1972, 11, 216–223. [Google Scholar] [CrossRef]
- AlMomani, T.; Udaykumar, H.S.; Marshall, J.S.; Chandran, K.B. Micro-scale dynamic simulation of erythrocyte–platelet interaction in blood flow. Ann. Biomed. Eng. 2008, 36, 905–920. [Google Scholar] [CrossRef] [PubMed]
- Cadroy, Y.; Hanson, S.R. Effects of red blood cell concentration on hemostasis and thrombus formation in a primate model. Blood 1990, 75, 2185–2193. [Google Scholar] [PubMed]
- Joist, J.H.; Bauman, J.E.; Sutera, S.P. Platelet adhesion and aggregation in pulsatile shear flow: Effects of red blood cells. Thromb. Res. 1998, 92, S47–S52. [Google Scholar] [CrossRef]
- Peerschke, E.I.; Silver, R.T.; Weksler, B.B.; Yin, W.; Bernhardt, B.; Varon, D. Examination of platelet function in whole blood under dynamic flow conditions with the cone and plate(let) analyzer: Effect of erythrocytosis and thrombocytosis. Am. J. Clin. Pathol. 2007, 127, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Turitto, V.T.; Weiss, H.J. Red blood cells: Their dual role in thrombus formation. Science 1980, 207, 541–543. [Google Scholar] [CrossRef] [PubMed]
- Reasor, D.A.; Mehrabadi, M.; Ku, D.N.; Aidun, C.K. Determination of critical parameters in platelet margination. Ann. Biomed. Eng. 2013, 41, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Skorczewski, T.; Erickson, L.C.; Fogelson, A.L. Platelet motion near a vessel wall or thrombus surface in two-dimensional whole blood simulations. Biophys. J. 2013, 104, 1764–1772. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Aubry, N.; Massoudi, M.; Kim, J.; Antaki, J.F. A numerical study of blood flow using mixture theory. Int. J. Eng. Sci. 2014, 76, 56–72. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Yang, F.; Antaki, J.F.; Aubry, N.; Massoudi, M. Study of blood flow in several benchmark micro-channels using a two-fluid approach. Int. J. Eng. Sci. 2015, 95, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Bowen, R.M. Theory of Mixtures; Academic Press Inc.: New York, NY, USA, 1976; Volume 3. [Google Scholar]
- Bridges, C.; Karra, S.; Rajagopal, K.R. On modeling the response of the synovial fluid: Unsteady flow of a shear-thinning, chemically-reacting fluid mixture. Comput. Math. Appl. 2010, 60, 2333–2349. [Google Scholar] [CrossRef]
- Massoudi, M.; Uguz, A.K. Chemically-reacting fluids with variable transport properties. Appl. Math. Comput. 2012, 219, 1761–1775. [Google Scholar] [CrossRef]
- Wu, W.-T.; Massoudi, M. Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid. Fluids 2016, 1, 4. [Google Scholar] [CrossRef]
- Hund, S.J.; Antaki, J.F. An extended convection diffusion model for red blood cell-enhanced transport of thrombocytes and leukocytes. Phys. Med. Biol. 2009, 54, 6415–6435. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Massoudi, M.; Antaki, J.F.; Gandini, A. Removal of malaria-infected red blood cells using magnetic cell separators: A computational study. Appl. Math. Comput. 2012, 218, 6841–6850. [Google Scholar] [CrossRef] [PubMed]
- Brooks, D.E.; Goodwin, J.W.; Seaman, G.V. Interactions among erythrocytes under shear. J. Appl. Physiol. 1970, 28, 172–177. [Google Scholar] [PubMed]
- Johnson, G.; Massoudi, M.; Rajagopal, K.R. Flow of a fluid—Solid mixture between flat plates. Chem. Eng. Sci. 1991, 46, 1713–1723. [Google Scholar] [CrossRef]
- Massoudi, M. Constitutive relations for the interaction force in multicomponent particulate flows. Int. J. Non-Linear Mech. 2003, 38, 313–336. [Google Scholar] [CrossRef]
- Rusche, H.; Issa, R.I. The Effect of Voidage on the Drag Force on Particles, Droplets and Bubbles in Dispersed Two-Phase Flow. In Proceedings of the 2nd Japanese-European Two-Phase Flow Group Meeting, Tsukuba, Japan, 25–29 September 2000. [Google Scholar]
- Wu, W.-T.; Aubry, N.; Massoudi, M. On the coefficients of the interaction forces in a two-phase flow of a fluid infused with particles. Int. J. Non-Linear Mech. 2014, 59, 76–82. [Google Scholar] [CrossRef]
- Massoudi, M.; Antaki, J.F. An Anisotropic Constitutive Equation for the Stress Tensor of Blood Based on Mixture Theory. Math. Probl. Eng. 2008, 2008, 1–30. [Google Scholar] [CrossRef]
- Zhao, R.; Marhefka, J.N.; Shu, F.; Hund, S.J.; Kameneva, M.V.; Antaki, J.F. Micro-flow visualization of red blood cell-enhanced platelet concentration at sudden expansion. Ann. Biomed. Eng. 2008, 36, 1130–1141. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Wootton, D.M.; Ku, D.N. Fluid mechanics of vascular systems, diseases, and thrombosis. Annu. Rev. Biomed. Eng. 1999, 1, 299–329. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Aubry, N.; Antaki, J.F.; Massoudi, M. Transport of platelets induced by red blood cells based on mixture theory. arXiv Prepr. 2017. [Google Scholar]
- OpenCFD. OpenFOAM Programmer’s Guide Version 2.1.0; OpenCFD, Ed.; Free Software Foundation, Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Zhao, R.; Marhefka, J.N.; Antaki, J.F.; Kameneva, M.V. Drag-reducing polymers diminish near-wall concentration of platelets in microchannel blood flow. Biorheology 2010, 47, 193–203. [Google Scholar] [PubMed]
- Drew, D.A.; Segel, L.A. Averaged equations for two-phase flows. Stud. Appl. Math. 1971, 50, 205–231. [Google Scholar] [CrossRef]
- Müller, I. A thermodynamic theory of mixtures of fluids. Arch. Ration. Mech. Anal. 1968, 28, 1–39. [Google Scholar] [CrossRef]
- Pranay, P.; Henríquez-Rivera, R.G.; Graham, M.D. Depletion layer formation in suspensions of elastic capsules in Newtonian and viscoelastic fluids. Phys. Fluids 2012, 24, 61902. [Google Scholar] [CrossRef]
- Grandchamp, X.; Coupier, G.; Srivastav, A.; Minetti, C.; Podgorski, T. Lift and down-gradient shear-induced diffusion in red blood cell suspensions. Phys. Rev. Lett. 2013, 110, 108101. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Graham, M.D. Mechanism of margination in confined flows of blood and other multicomponent suspensions. Phys. Rev. Lett. 2012, 109, 108102. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.-T.; Li, Y.; Aubry, N.; Massoudi, M.; Antaki, J.F. Numerical Simulation of Red Blood Cell-Induced Platelet Transport in Saccular Aneurysms. Appl. Sci. 2017, 7, 484. https://doi.org/10.3390/app7050484
Wu W-T, Li Y, Aubry N, Massoudi M, Antaki JF. Numerical Simulation of Red Blood Cell-Induced Platelet Transport in Saccular Aneurysms. Applied Sciences. 2017; 7(5):484. https://doi.org/10.3390/app7050484
Chicago/Turabian StyleWu, Wei-Tao, Yubai Li, Nadine Aubry, Mehrdad Massoudi, and James F. Antaki. 2017. "Numerical Simulation of Red Blood Cell-Induced Platelet Transport in Saccular Aneurysms" Applied Sciences 7, no. 5: 484. https://doi.org/10.3390/app7050484